Advances in Pure Mathematics
Vol.3 No.9A(2013), Article ID:40871,12 pages DOI:10.4236/apm.2013.39A1005
On Decay of Solutions and Spectral Property for a Class of Linear Parabolic Feedback Control Systems
Department of Applied Mathematics, Graduate School of System Informatics, Kobe University, Kobe, Japan
Email: nambu@kobe-u.ac.jp
Copyright © 2013 Takao Nambu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Takao Nambu. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received September 4, 2013; revised October 4, 2013; accepted October 11, 2013
Keywords: Stabilization of linear parabolic systems; decay of functionals; dynamic feedback scheme; spectral structures of composite systems; complete observability of systems
ABSTRACT
Unlike regular stabilizations, we construct in the paper a specific feedback control system such that 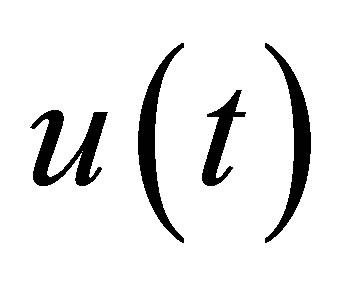 decays exponentially with the designated decay rate, and that some non-trivial linear functionals of
decays exponentially with the designated decay rate, and that some non-trivial linear functionals of 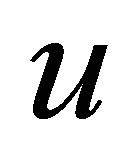 decay exactly faster than
decay exactly faster than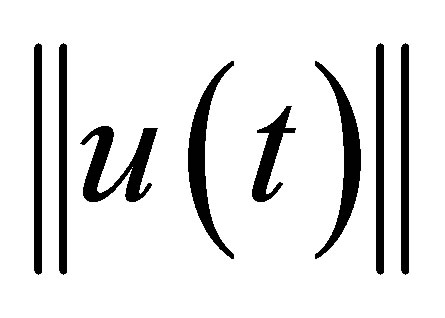 . The system contains a dynamic compensator with another state
. The system contains a dynamic compensator with another state 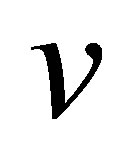 in the feedback loop, and consists of two states
in the feedback loop, and consists of two states  and
and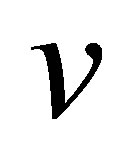 . This problem entirely differs from the one with static feedback scheme in which the system consists only of a single state
. This problem entirely differs from the one with static feedback scheme in which the system consists only of a single state . To show the essential difference, some specific property of the spectral subspaces associated with our control system is studied.
. To show the essential difference, some specific property of the spectral subspaces associated with our control system is studied.
1. Introduction
Stabilization problems for linear parabolic control systems have the history of more than three decades. Although some difficult problems are left unresolved, it seems that the study has reached a degree of maturity in a sense. The so-called dynamic compensators are introduced in the feedback loop to cope with the most difficult case such as the scheme of boundary observation/boundary input (see the literature, e.g., [1-6]). In [2-4,6], no Riesz basis is assumed, corresponding to the coefficient elliptic operators with complicated boundary operators (see (1) below). Let  be a separable Hilbert space with the inner product
be a separable Hilbert space with the inner product  and the norm
and the norm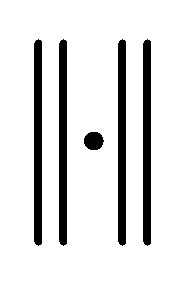 . A standard control system with state
. A standard control system with state ,
,  consists of a finite number of inputs
consists of a finite number of inputs ,
,  , and outputs
, and outputs ,
,  , and is described by the following linear differential equation in
, and is described by the following linear differential equation in :
:
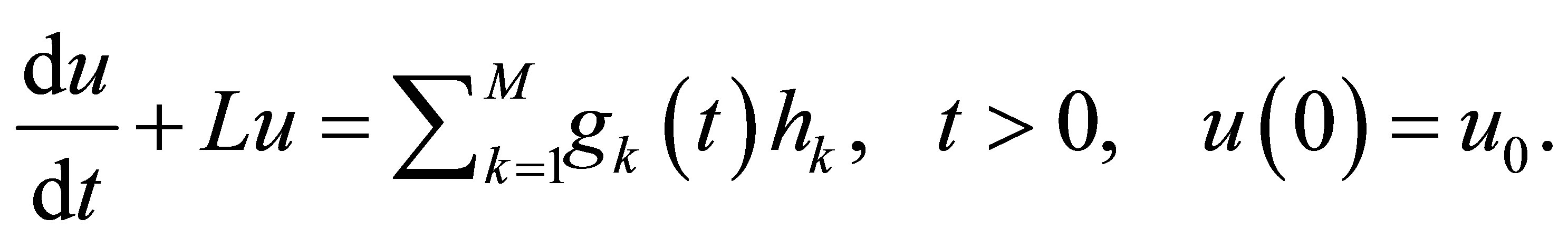
Here, 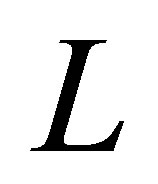 denotes a linear closed operator with dense domain
denotes a linear closed operator with dense domain 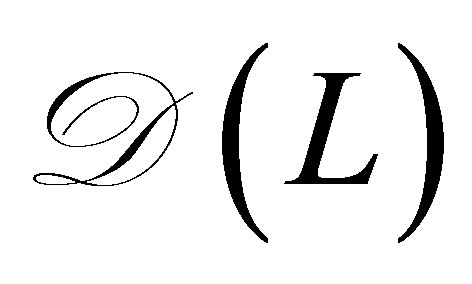 such that the resolvent
such that the resolvent 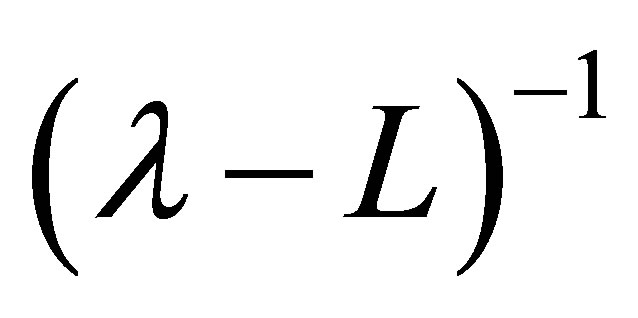 is compact;
is compact;  actuators through which the scalarvalued inputs
actuators through which the scalarvalued inputs 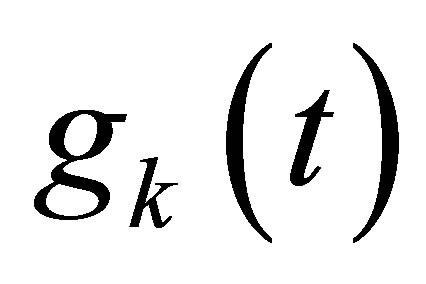 are inserted in the equation; and
are inserted in the equation; and 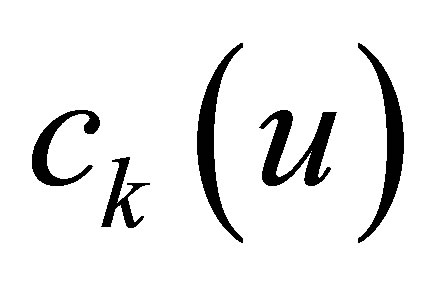 linear functionals of
linear functionals of  which allow unboundedness but are subordinate to
which allow unboundedness but are subordinate to . The control system also reflects boundary feedback schemes by interpreting
. The control system also reflects boundary feedback schemes by interpreting  and the differential equation in weaker topologies. In general stabilization studies, the inputs
and the differential equation in weaker topologies. In general stabilization studies, the inputs 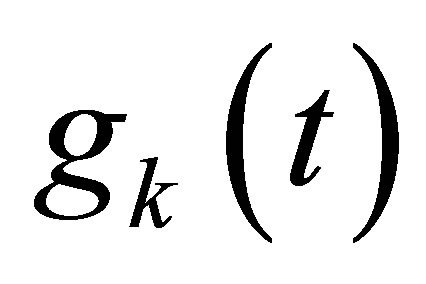 are designed as a suitable feedback of the outputs
are designed as a suitable feedback of the outputs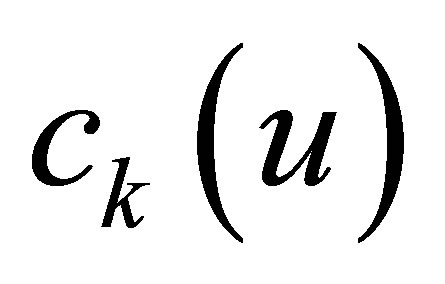 , so that the state
, so that the state 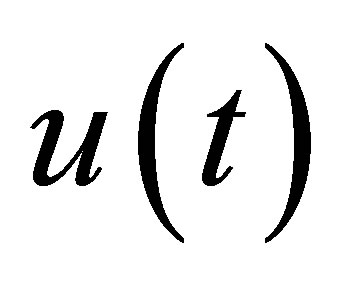 could be stabilized as
could be stabilized as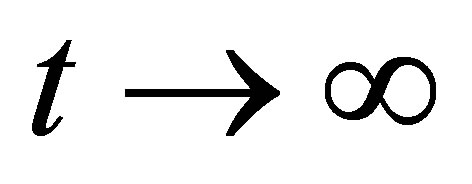 . Then every linear functional of
. Then every linear functional of 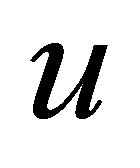 also decays at least with the same decay rate. This is true in the case where the functional is unbounded and subordinate to
also decays at least with the same decay rate. This is true in the case where the functional is unbounded and subordinate to .
.
We then raise a question: can we find a nontrivial linear functional which decays faster than ? The purpose of the paper is to construct a specific feedback control system such that
? The purpose of the paper is to construct a specific feedback control system such that 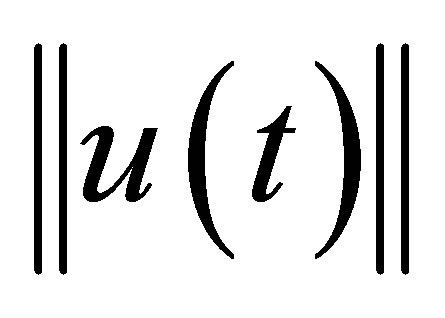 decays exponentially with the designated decay rate, and that some nontrivial linear functionals of
decays exponentially with the designated decay rate, and that some nontrivial linear functionals of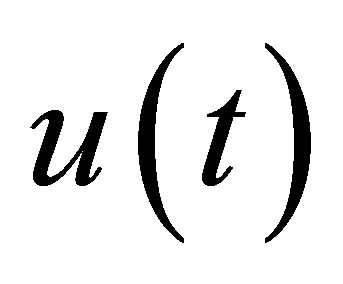 , say
, say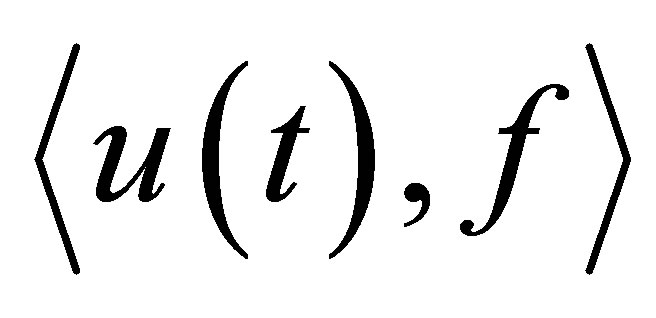 , decay definitely faster than
, decay definitely faster than  for any initial state. To achieve this property, our control scheme contains a dynamic compensator with state
for any initial state. To achieve this property, our control scheme contains a dynamic compensator with state  in another separable Hilbert space
in another separable Hilbert space  in the feedback loop to connect
in the feedback loop to connect 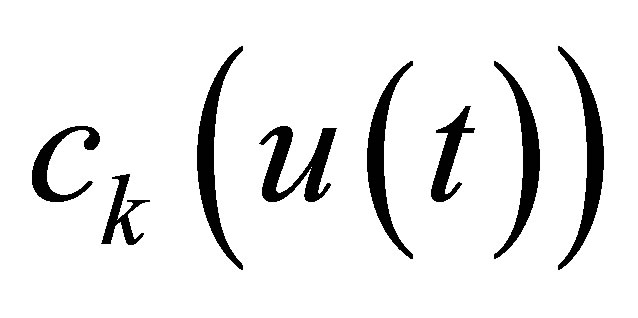 and
and . Thus the control system has state
. Thus the control system has state  in the product space
in the product space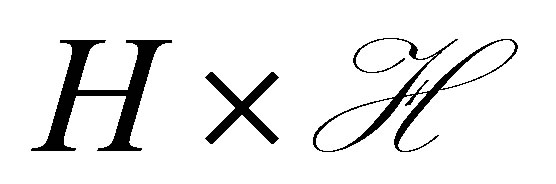 . We note that the above decay property is achieved in a straightforward manner in the static feedback control scheme in which we set
. We note that the above decay property is achieved in a straightforward manner in the static feedback control scheme in which we set 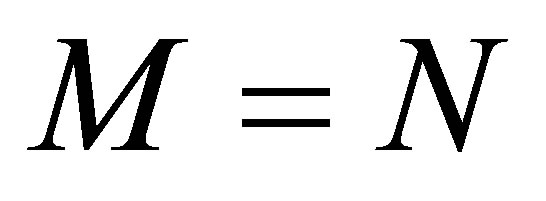 and
and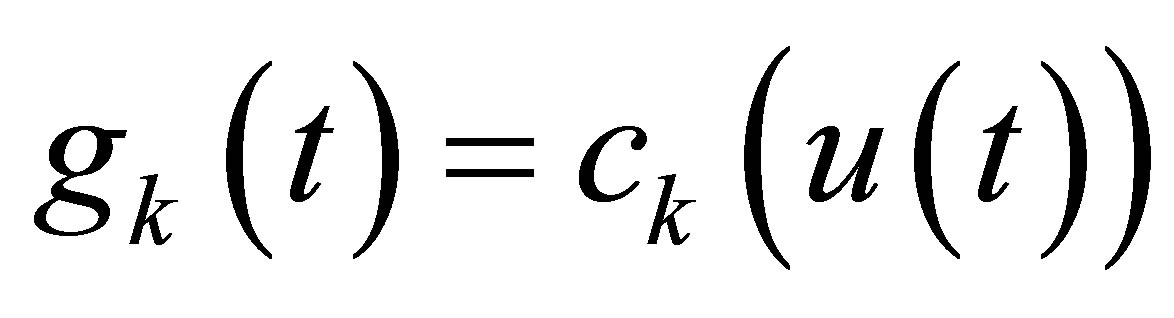 ,
,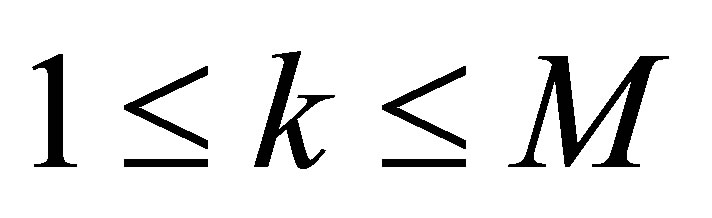 . In fact, the static feedback system contains a single state
. In fact, the static feedback system contains a single state 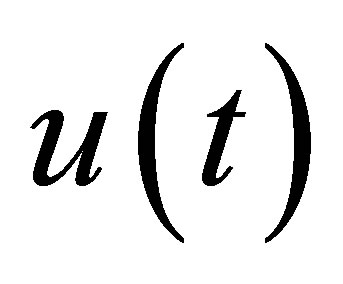 only, and the so-called spectral decomposition of
only, and the so-called spectral decomposition of  associated with the elliptic operator enables us to find such an
associated with the elliptic operator enables us to find such an  in some spectral subspace. Such typical examples are the Fourier coefficients corresponding to higher frequencies. In our control system, however, it is indispensable in the spectral decomposition method to ensure a vector of the form
in some spectral subspace. Such typical examples are the Fourier coefficients corresponding to higher frequencies. In our control system, however, it is indispensable in the spectral decomposition method to ensure a vector of the form 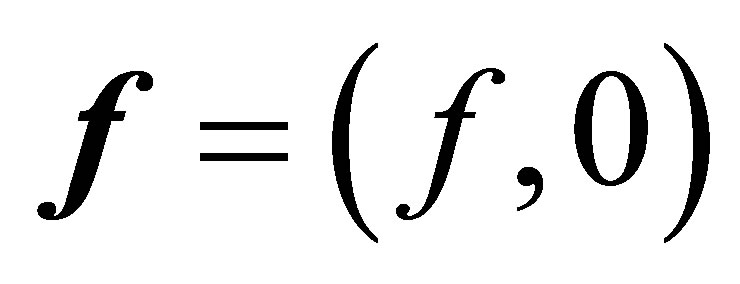 in the spectral subspace of
in the spectral subspace of 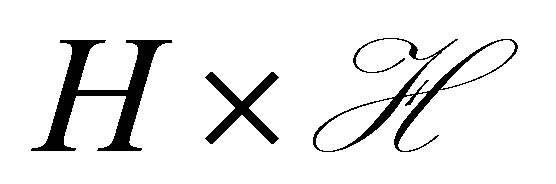 to achieve a faster decay of
to achieve a faster decay of , where
, where  1. It is very unlikely and almost denied to find such a vector
1. It is very unlikely and almost denied to find such a vector 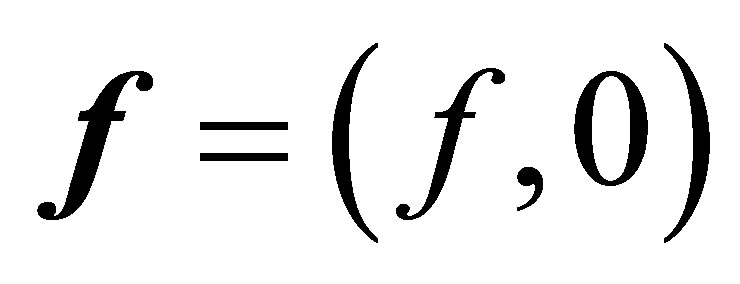 in our control system with state
in our control system with state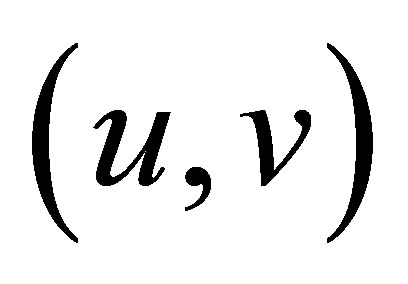 . To make the paper clearer and more readable, unlikeliness of the above vector
. To make the paper clearer and more readable, unlikeliness of the above vector  is discussed in detail in Section 3, which turns out to be a new spectral feature of the control system, and has never appeared in the literature; this spectral property also justifies the relevance of our problem setting.
is discussed in detail in Section 3, which turns out to be a new spectral feature of the control system, and has never appeared in the literature; this spectral property also justifies the relevance of our problem setting.
Let us begin with the characterization of the controlled plant. Let  denote a bounded domain in
denote a bounded domain in 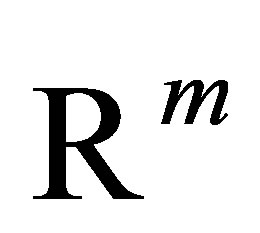 with the boundary
with the boundary  which consists of a finite number of smooth components of
which consists of a finite number of smooth components of 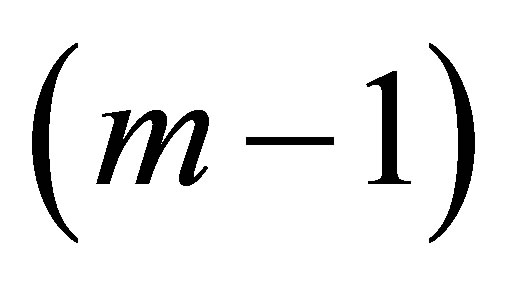 -dimension. Let
-dimension. Let 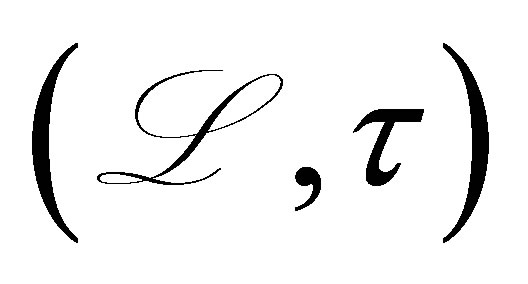 be a pair of linear operators defined by
be a pair of linear operators defined by
 (1)
(1)
where 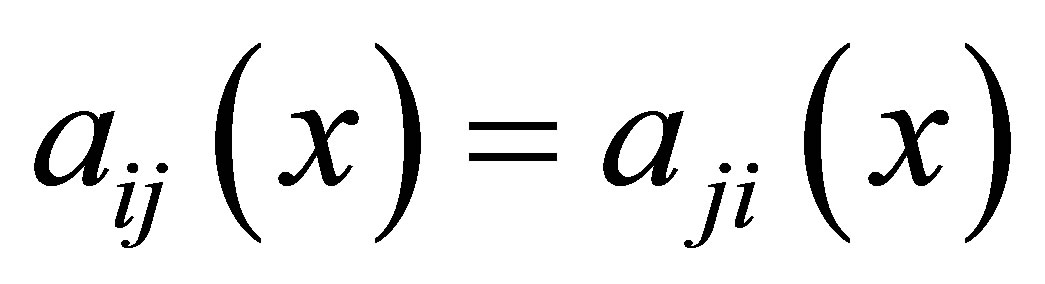 for
for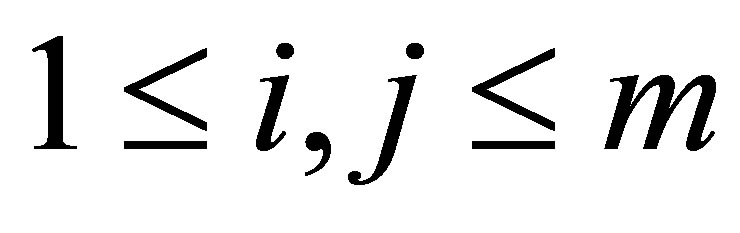 ,
,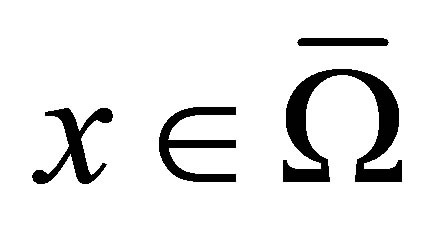 ;
;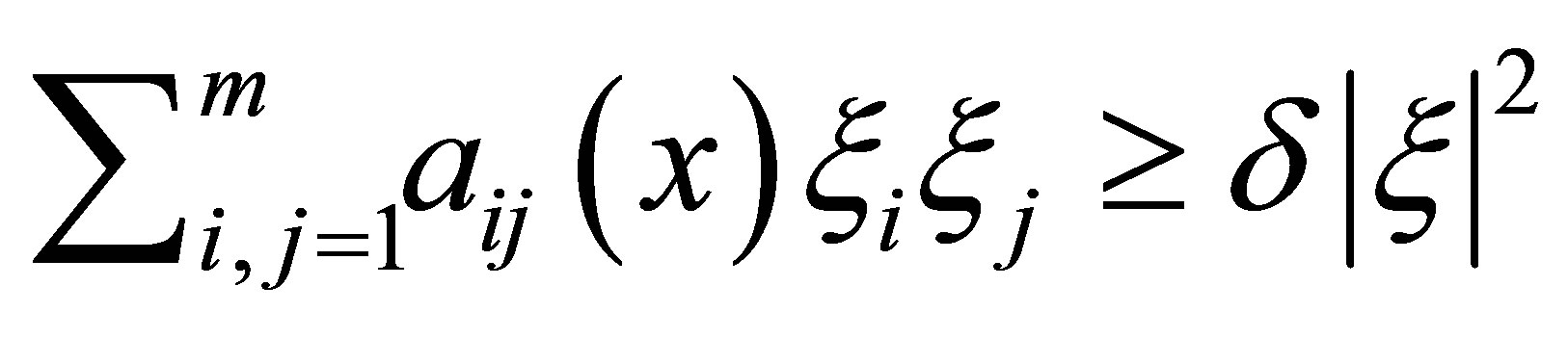 ,
, 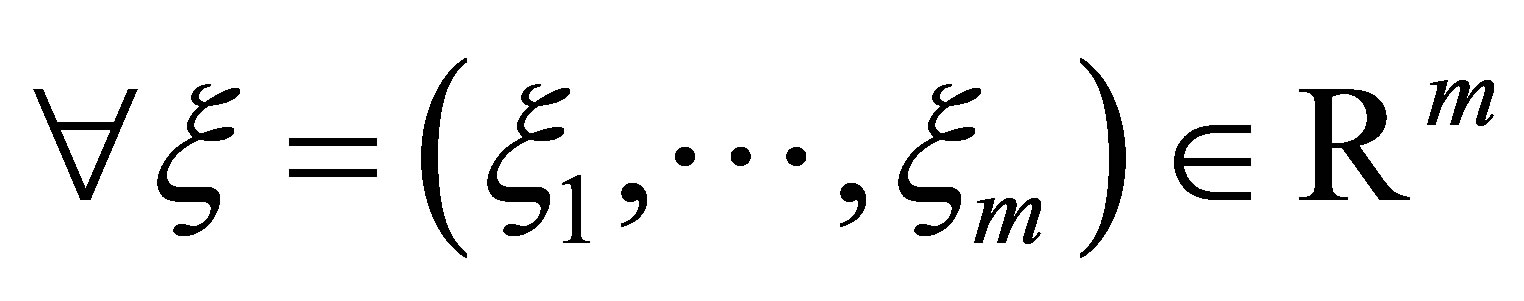 ,
, 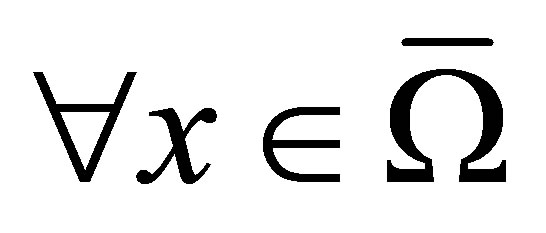 for some positive
for some positive  and
and
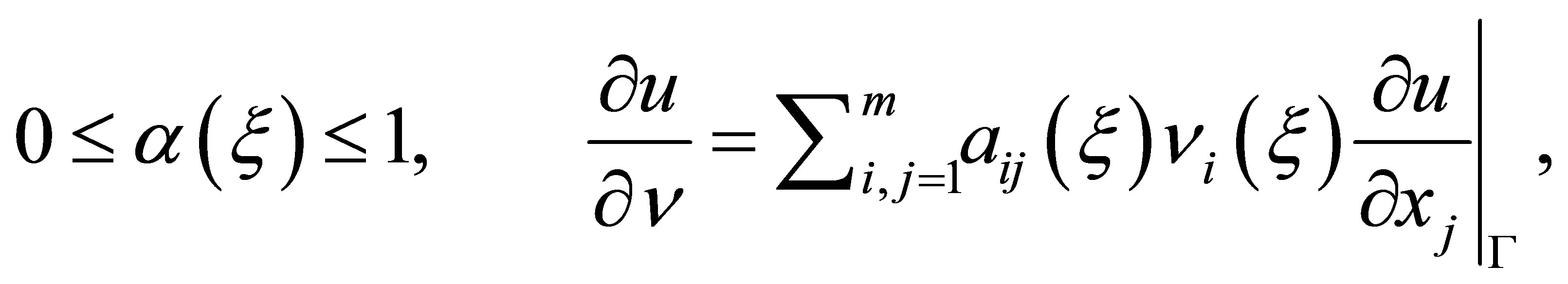
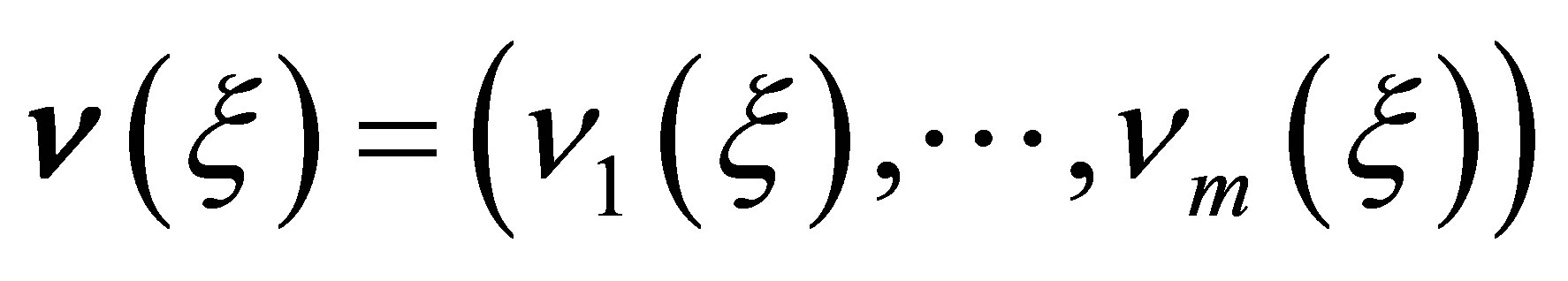 being the unit outer normal at
being the unit outer normal at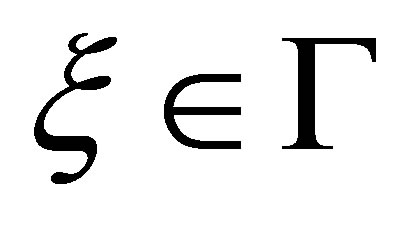 . Henceforth set
. Henceforth set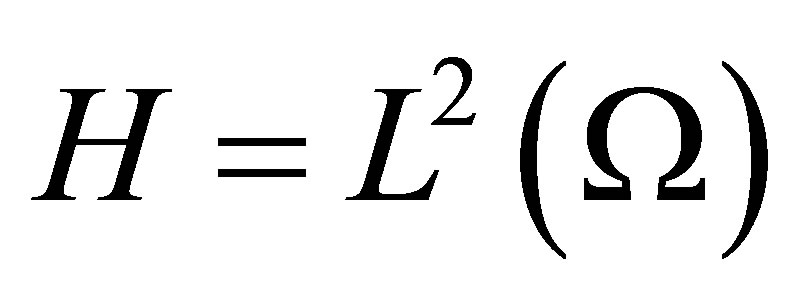 . The pair
. The pair 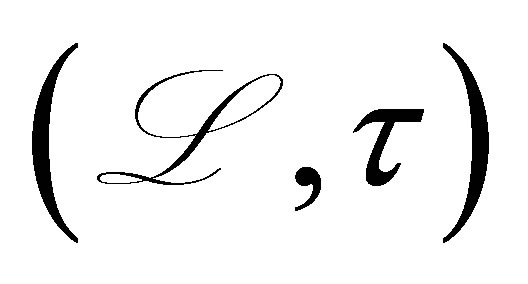 defines an operator
defines an operator 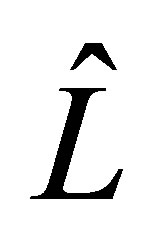 closable in
closable in  as
as 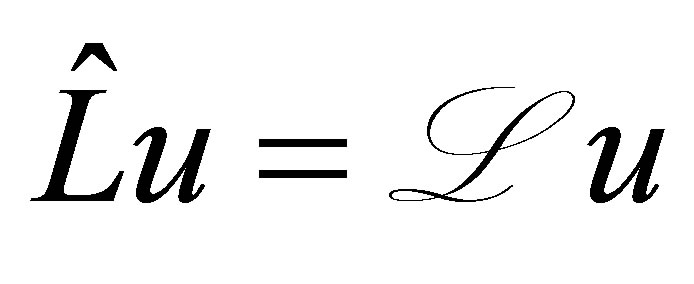 for
for
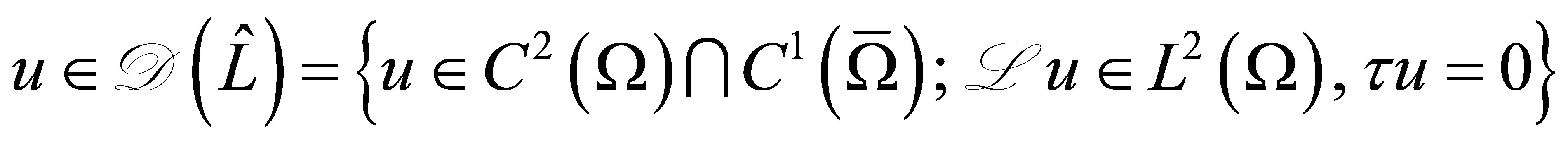 .
.
The closure of  is denoted as
is denoted as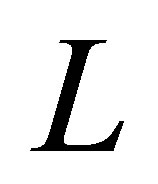 . It is well known (see [7]) that
. It is well known (see [7]) that 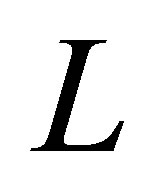 has a compact resolvent
has a compact resolvent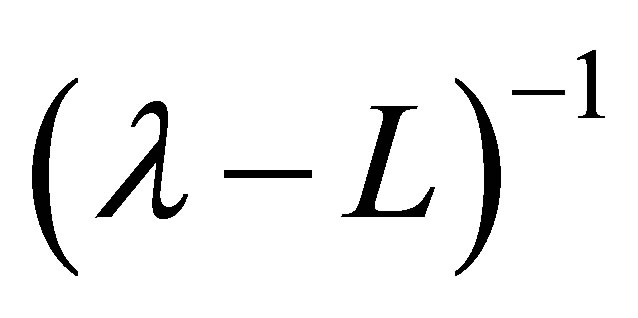 ; that the spectrum
; that the spectrum 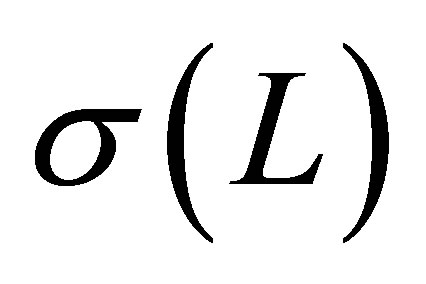 lies in the complement
lies in the complement 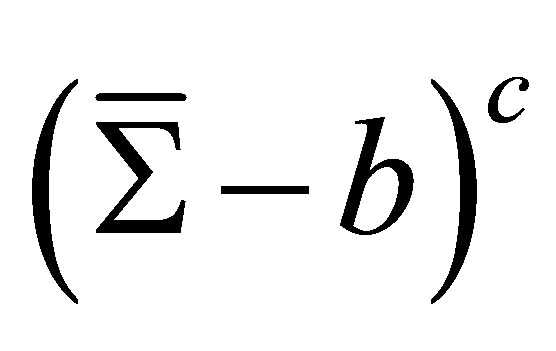 of some sector
of some sector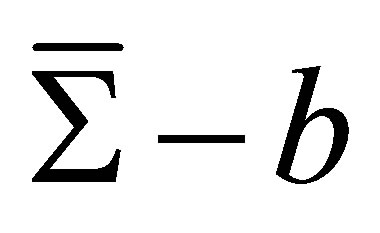 , where
, where 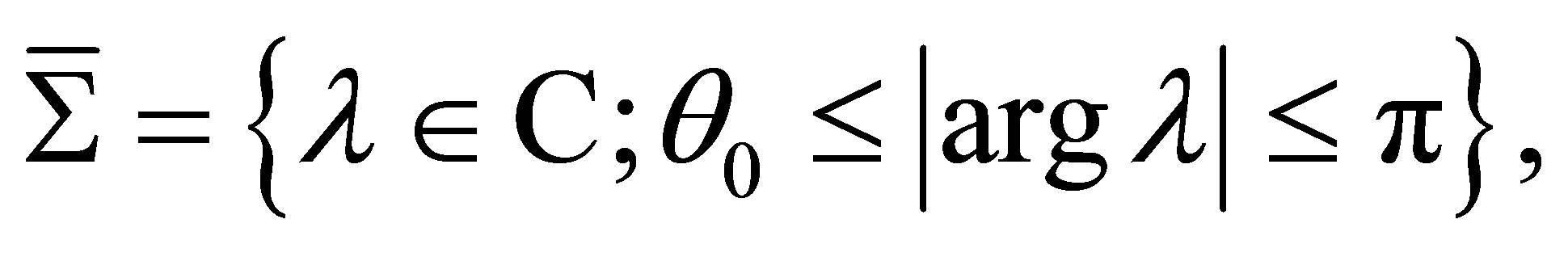
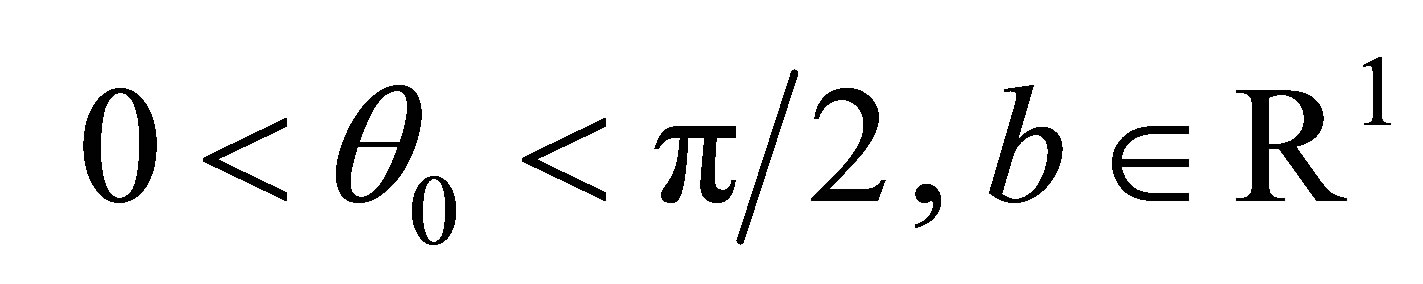 ; and that the following estimates hold:
; and that the following estimates hold:
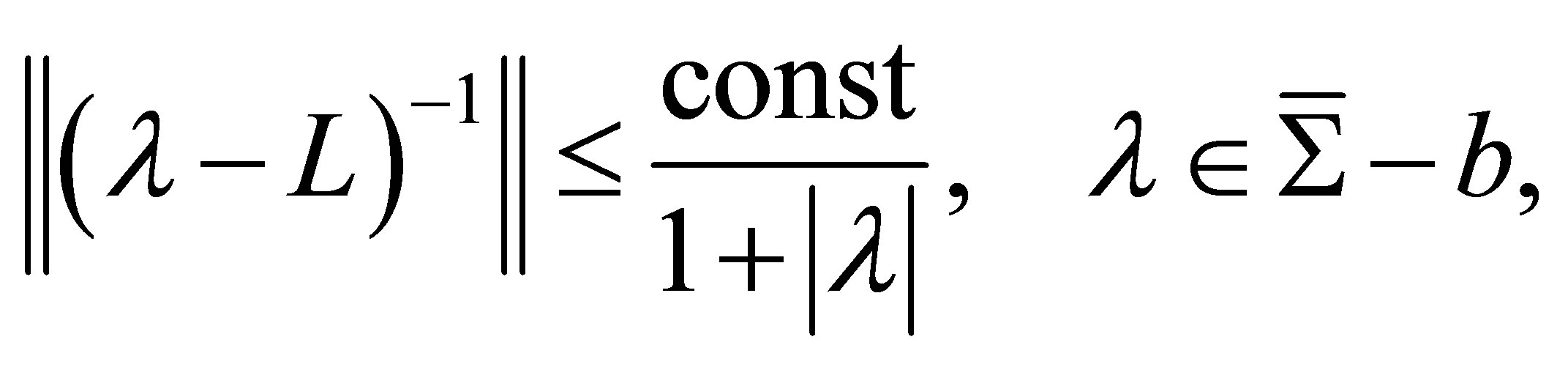 (2)
(2)
where the symbol  also denotes the
also denotes the 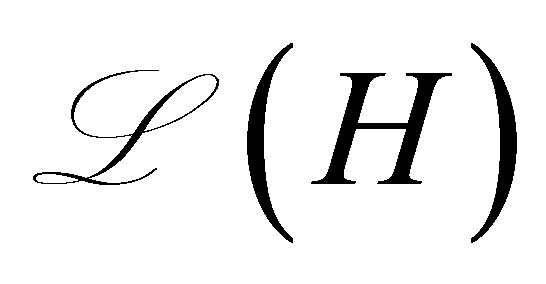 -norm. Thus
-norm. Thus 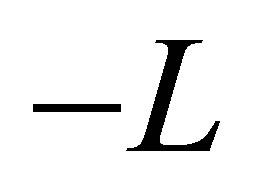 is an infinitesimal generator of an analytic semigroup
is an infinitesimal generator of an analytic semigroup ,
,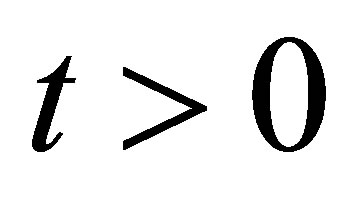 . The fractional powers
. The fractional powers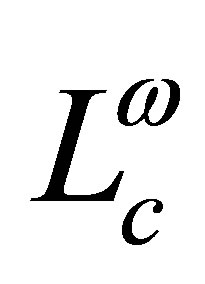 ,
,  are defined in a standard manner, where
are defined in a standard manner, where  and
and  is sufficiently large. It is not very clear on how the domain
is sufficiently large. It is not very clear on how the domain  is characterized by the fractional Sobolev spaces, since the Dirichlet boundary is continuously connected by the Robin boundary. Such a characterization is, however, neither essential nor necessary in our study. There is a set of generalized eigenpairs
is characterized by the fractional Sobolev spaces, since the Dirichlet boundary is continuously connected by the Robin boundary. Such a characterization is, however, neither essential nor necessary in our study. There is a set of generalized eigenpairs 
such that
1)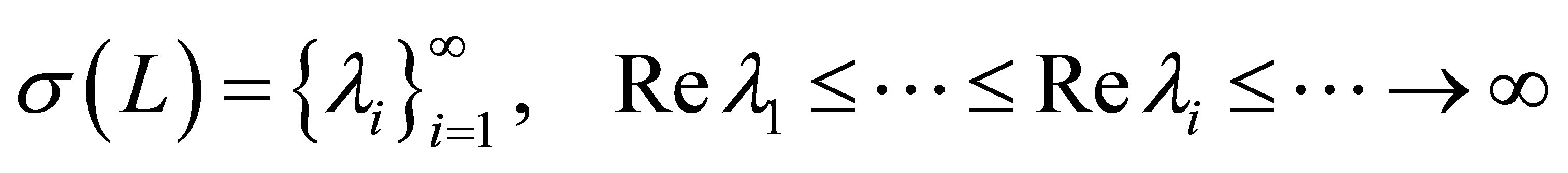 ;
; 2) for
for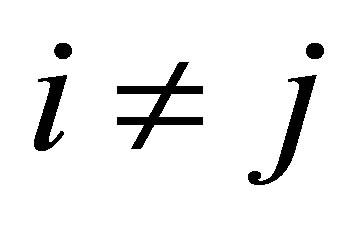 ; and
; and
3) .
.
It is well known (see, e.g., page 285 of [8]) that the set  spans
spans , but does not necessarily form a Riesz basis for
, but does not necessarily form a Riesz basis for . Let
. Let 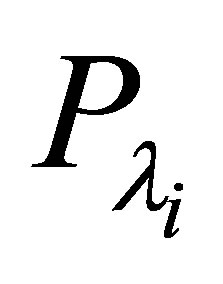 be the (not necessarily orthogonal) projector corresponding to the eigenvalue
be the (not necessarily orthogonal) projector corresponding to the eigenvalue . The restriction of
. The restriction of 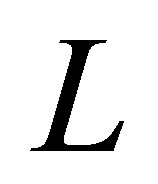 onto the invariant subspace
onto the invariant subspace 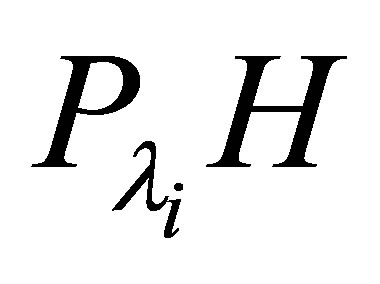 is, according to the basis
is, according to the basis , equivalent to the
, equivalent to the 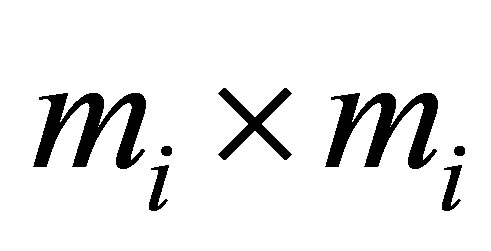 upper triangular matrix
upper triangular matrix :
:
 (3)
(3)
By setting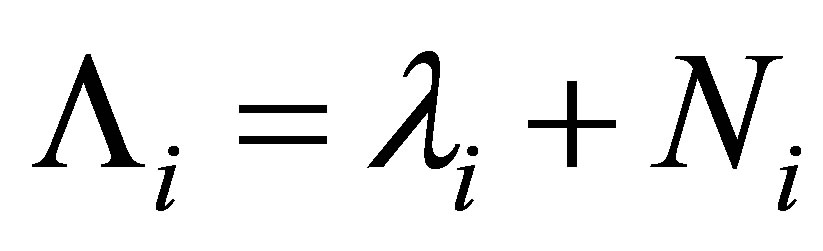 , the matrix
, the matrix 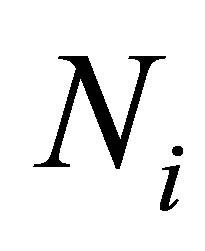 is nilpotent, that is,
is nilpotent, that is, . The minimum integer
. The minimum integer 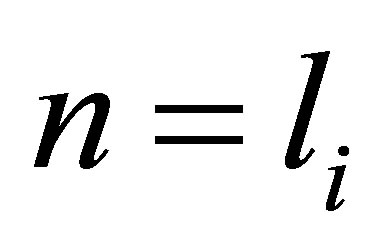 such that
such that 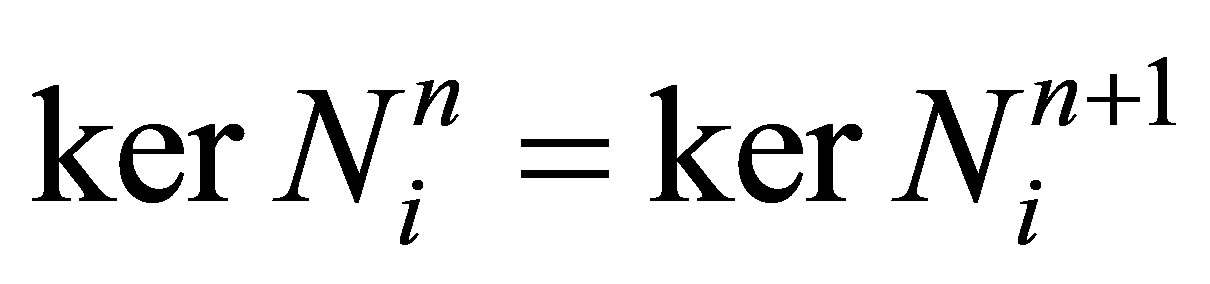 is called the ascent of
is called the ascent of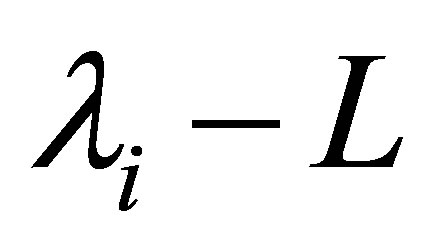 . It is well known that the ascent
. It is well known that the ascent 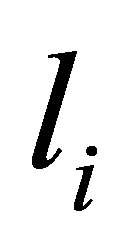 coincides with the order of the pole
coincides with the order of the pole 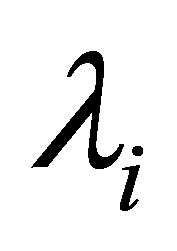 of
of 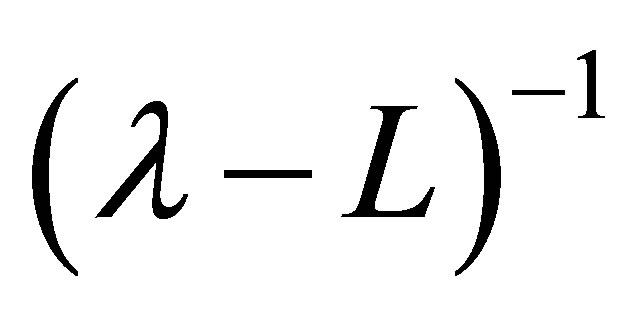 (see Theorem 5.8-A of [9] for more details). Let
(see Theorem 5.8-A of [9] for more details). Let  be the formal adjoint of
be the formal adjoint of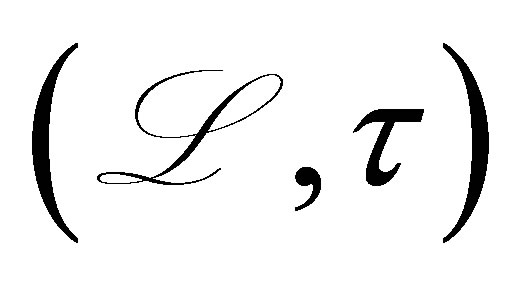 :
:
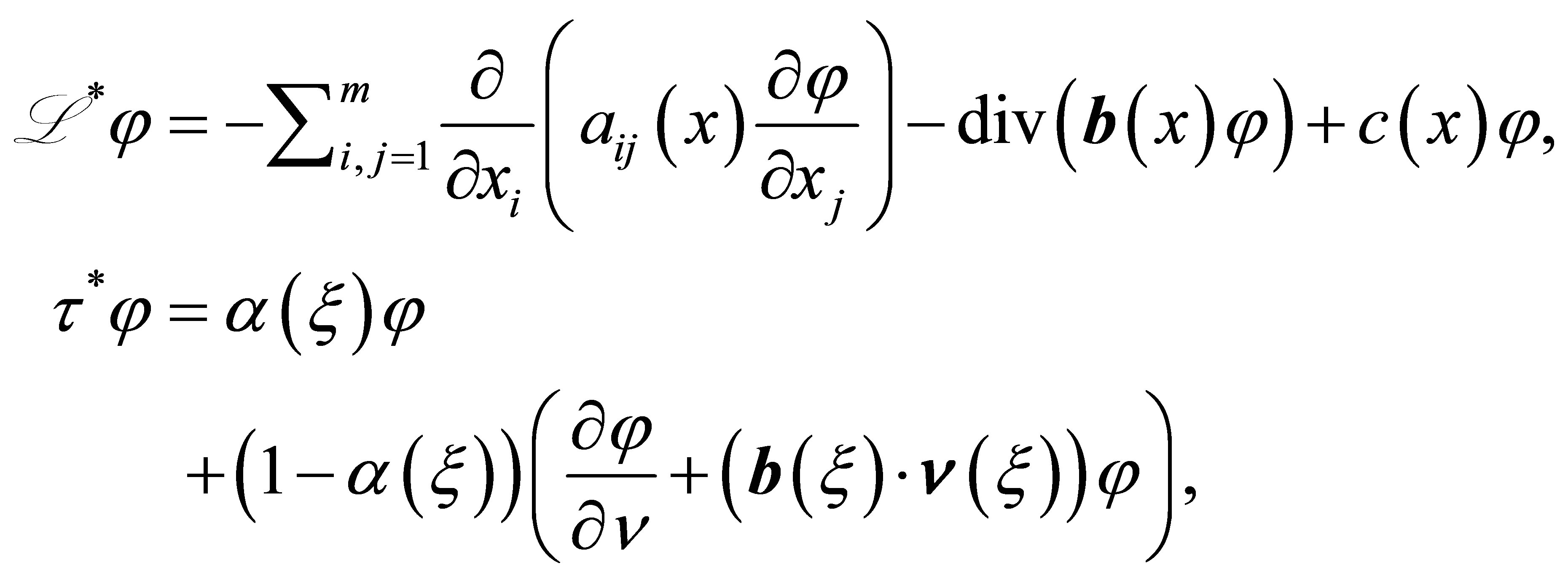 (4)
(4)
where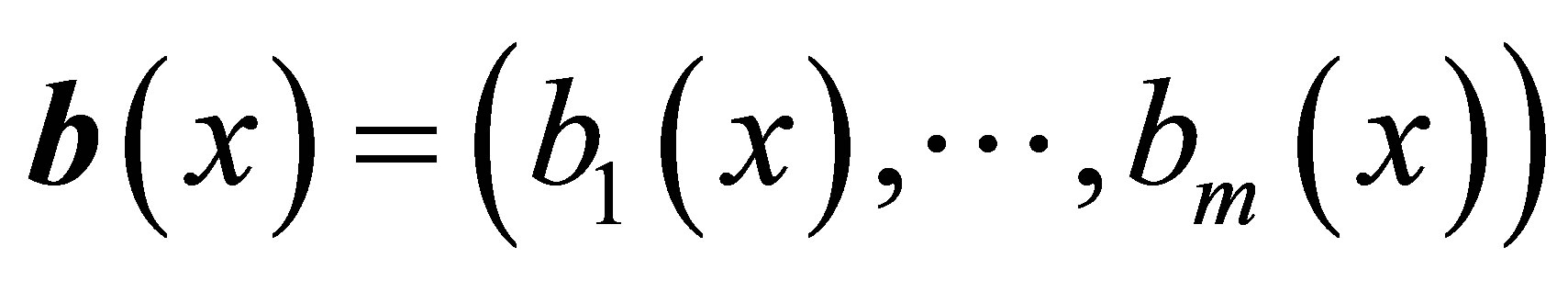 . The pair
. The pair 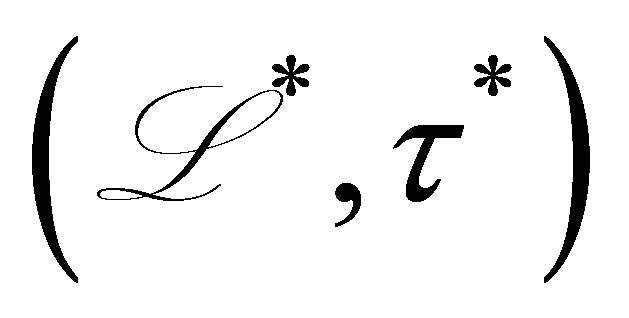 defines an operator
defines an operator  just as the above
just as the above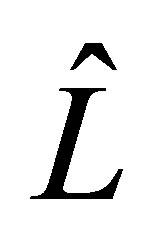 . Then the adjoint of
. Then the adjoint of , denoted by
, denoted by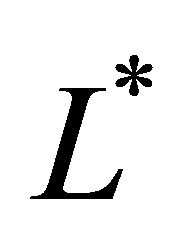 , is given as the closure of
, is given as the closure of  in
in . There is a set of generalized eigenpairs
. There is a set of generalized eigenpairs 
such that
1)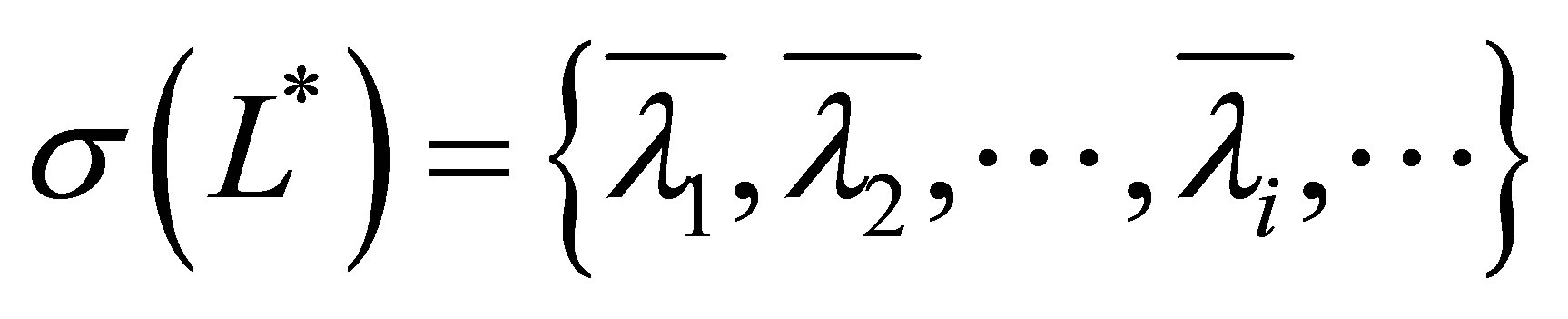 ; and
; and
2)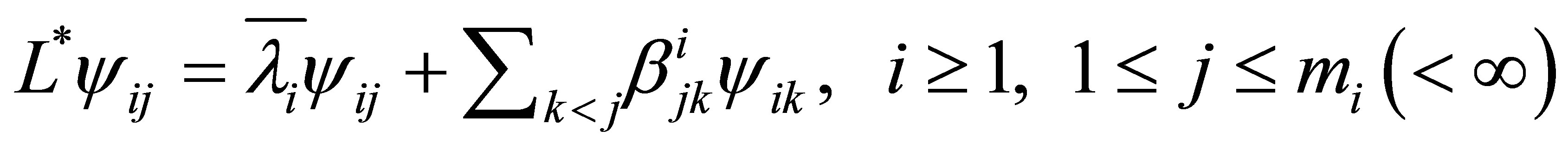 .
.
Similarly, the set 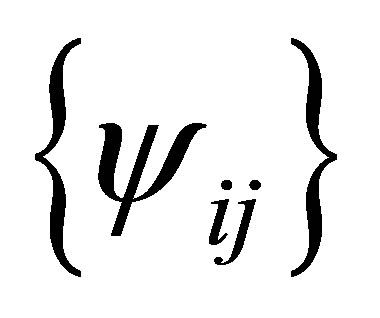 spans
spans . Setting
. Setting 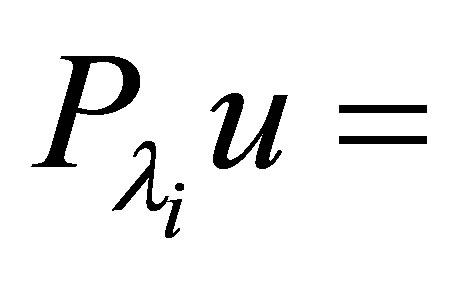
 , we have the relationship:
, we have the relationship:
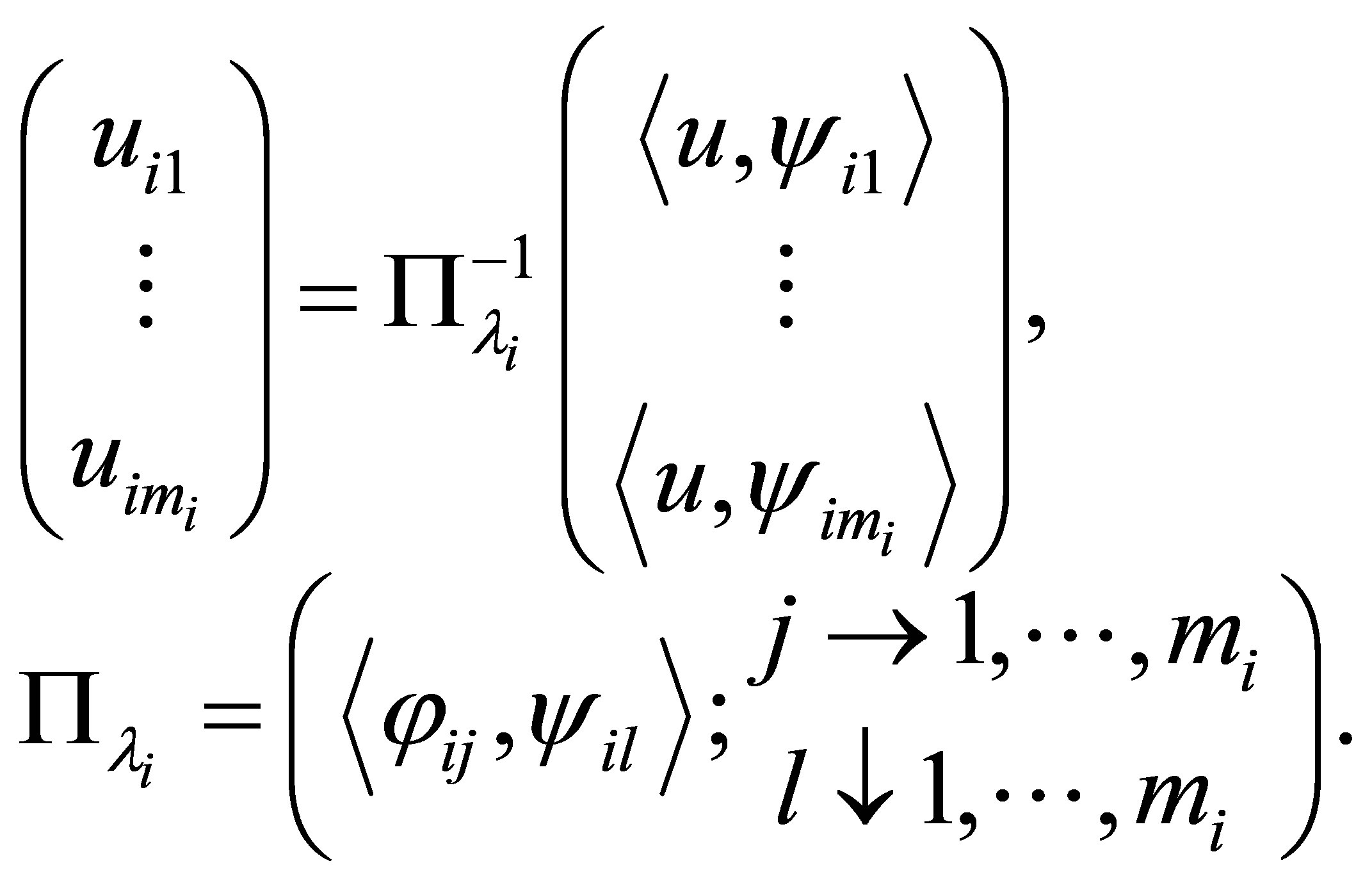 (5)
(5)
Let us turn to the characterization of a dynamic compensator. Let  be any separable Hilbert space with inner product
be any separable Hilbert space with inner product  and norm
and norm . Relabelling an orthonormal basis for
. Relabelling an orthonormal basis for , let
, let 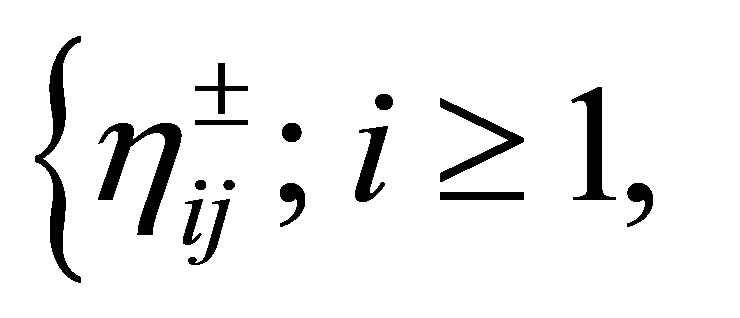
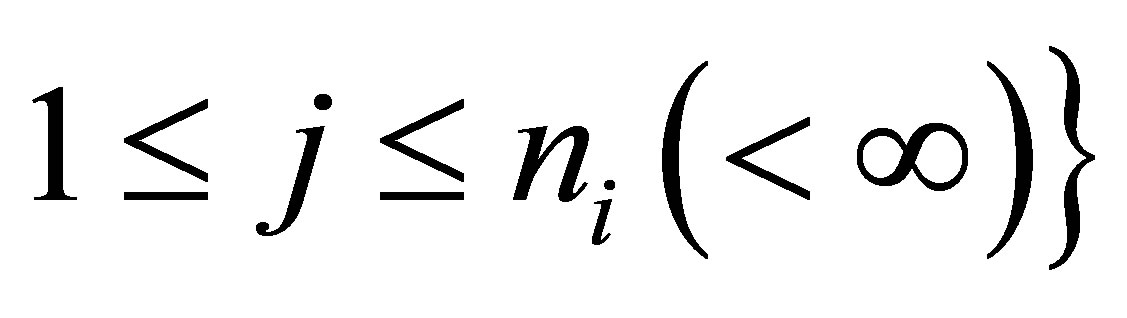 be a new orthonomal basis for
be a new orthonomal basis for . Every vector
. Every vector  is then expressed in terms of the basis
is then expressed in terms of the basis 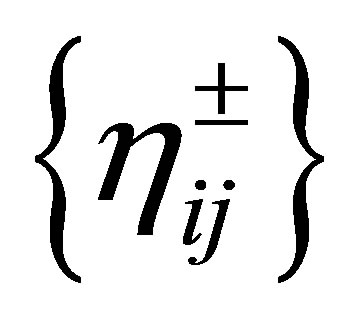 as a Fourier series:
as a Fourier series: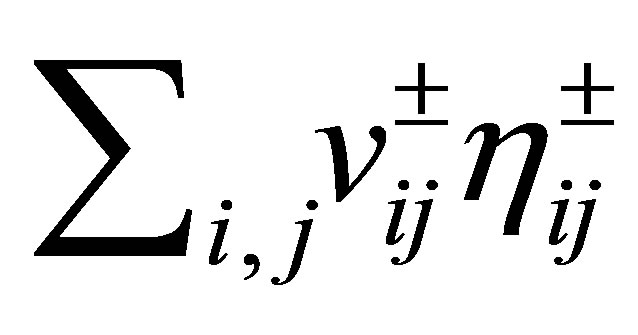
 ,
, . Let
. Let  be a sequence of increasing positive numbers:
be a sequence of increasing positive numbers: , and set
, and set , where
, where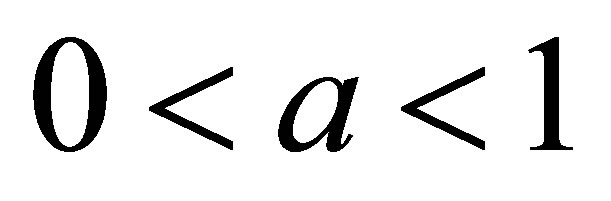 . Let
. Let 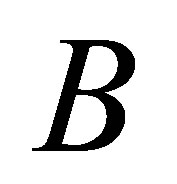 be a linear closed operator defined as
be a linear closed operator defined as
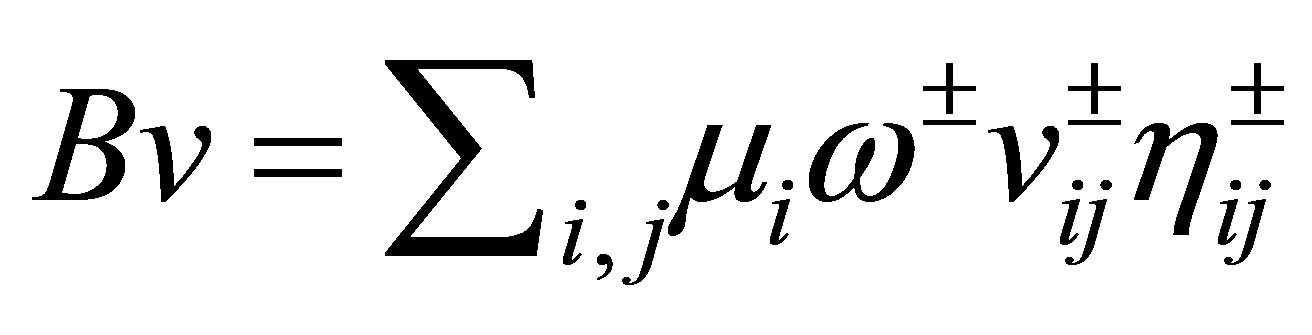 (6)
(6)
with dense domain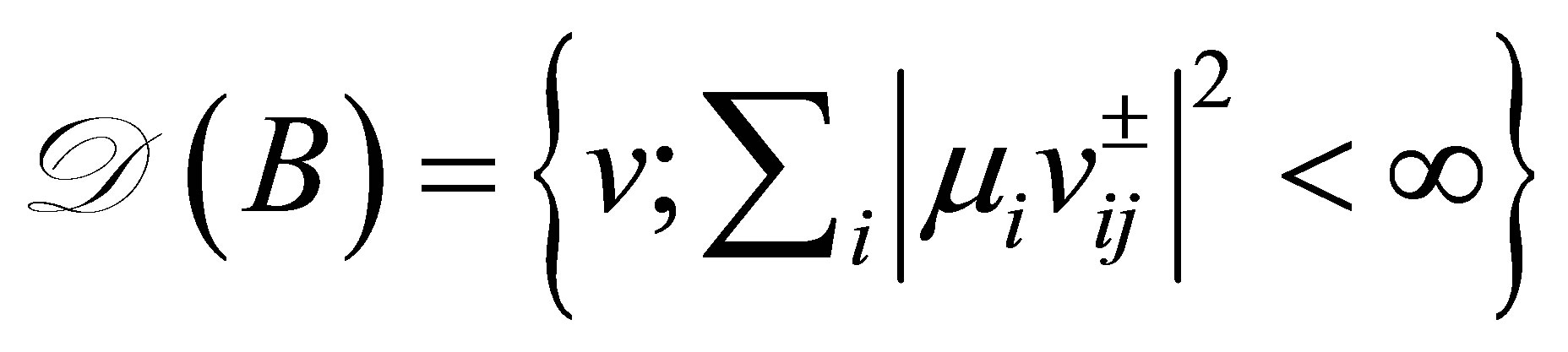 . Then, 1)
. Then, 1)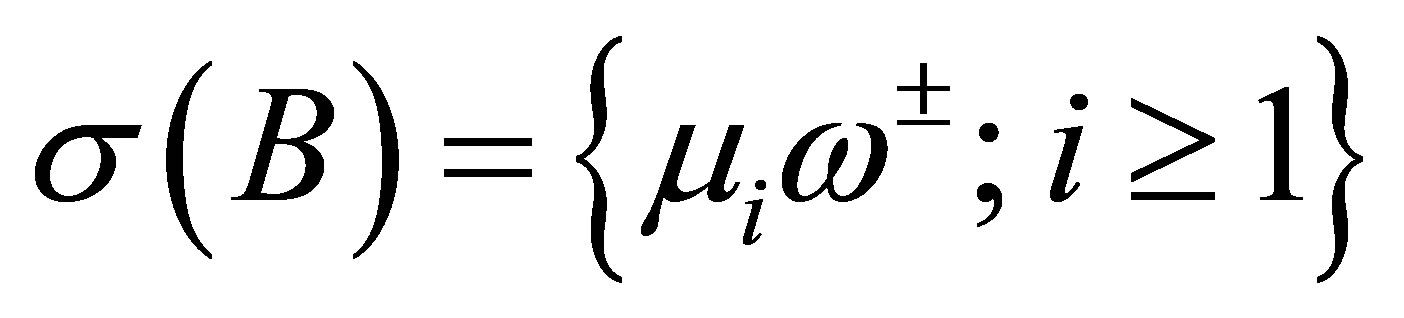 ; and 2)
; and 2) ,
,  ,
,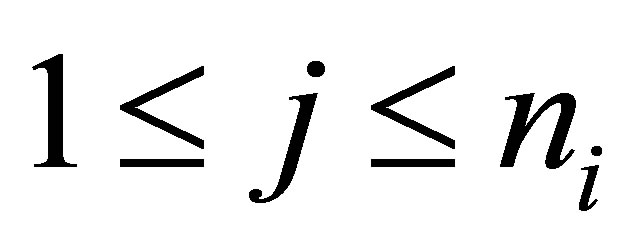 . Thus
. Thus  is the infinitesimal generator of an analytic semigroup
is the infinitesimal generator of an analytic semigroup , which is expressed by
, which is expressed by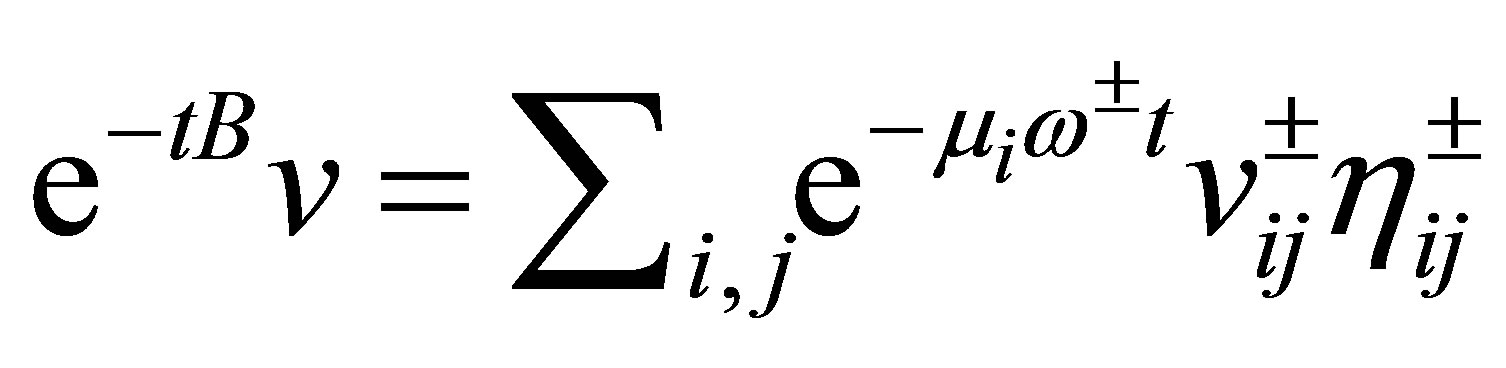 . The semigroup
. The semigroup 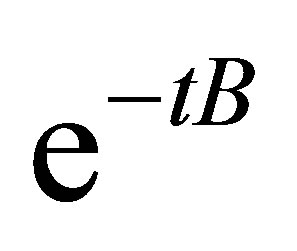 satisfies the decay estimate
satisfies the decay estimate
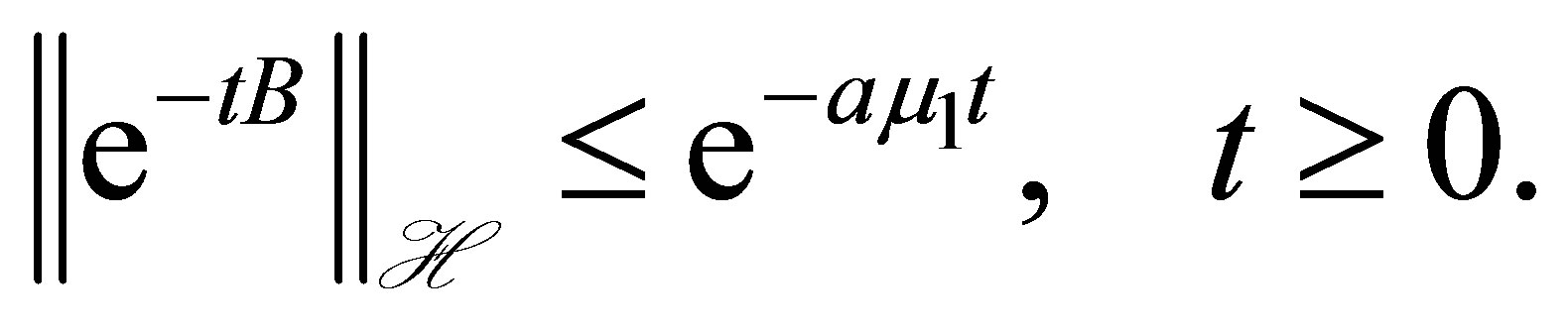 (7)
(7)
The adjoint operator 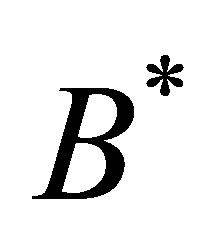 of
of 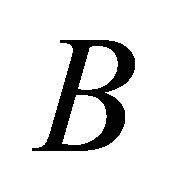 is described as
is described as
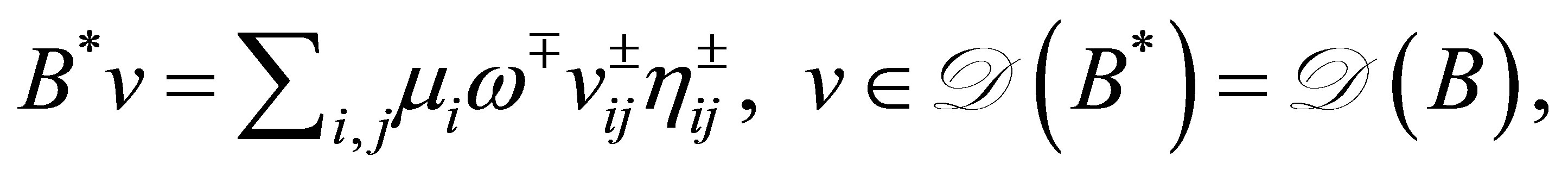 (8)
(8)
and thus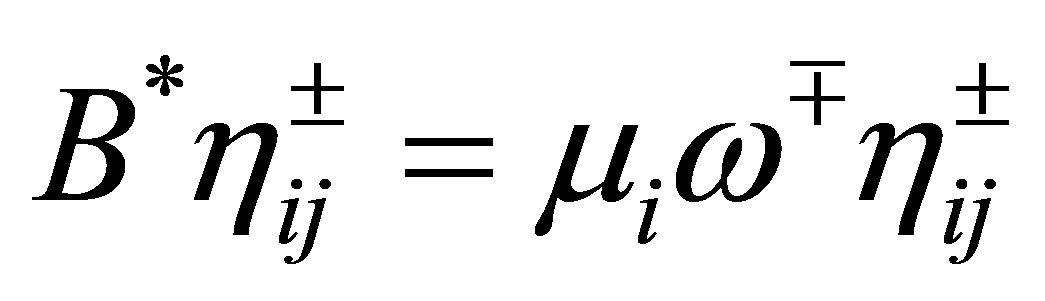 . Let
. Let ,
,  be the projector in
be the projector in  such that
such that .
.
Our control system has state , and is described as a differential equation in
, and is described as a differential equation in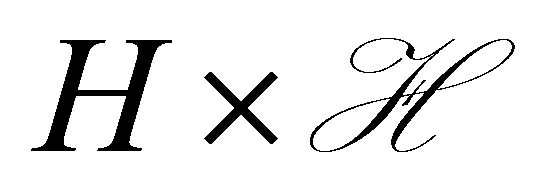 :
:
 (9)
(9)
The equation with state 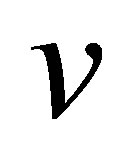 means a dynamic compensator equipped with a set of outputs
means a dynamic compensator equipped with a set of outputs 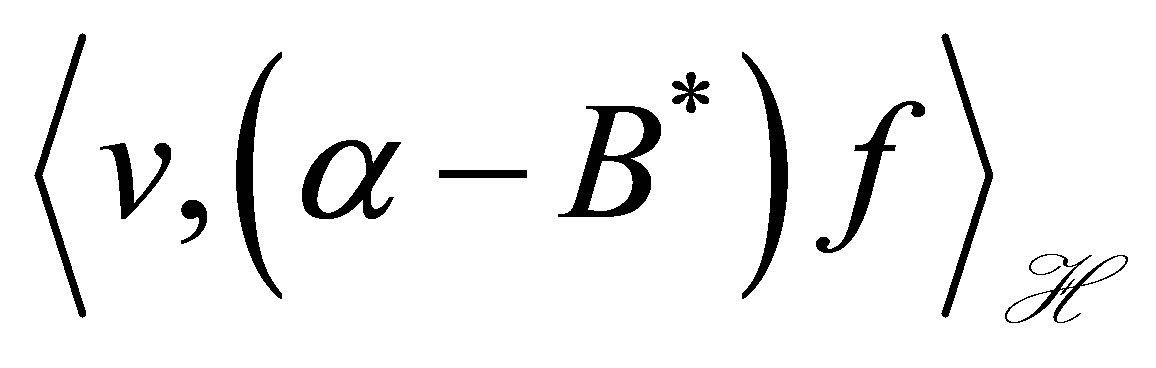 and
and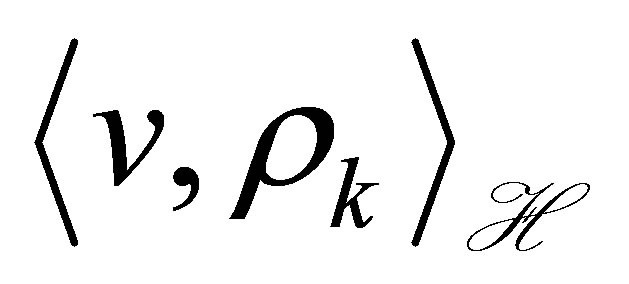 ,
, 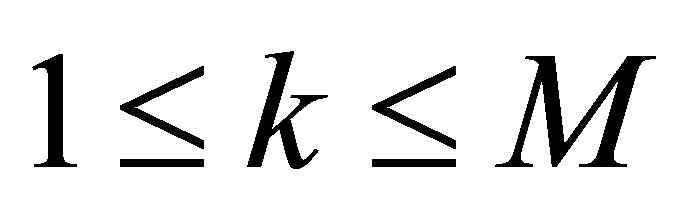 , where α > 0. The parameters
, where α > 0. The parameters 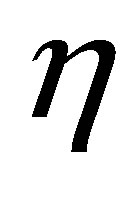 and
and 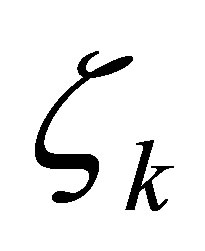 denote given actuators of the controlled plant, and
denote given actuators of the controlled plant, and  actuators of the compensator to be designed. The outputs
actuators of the compensator to be designed. The outputs 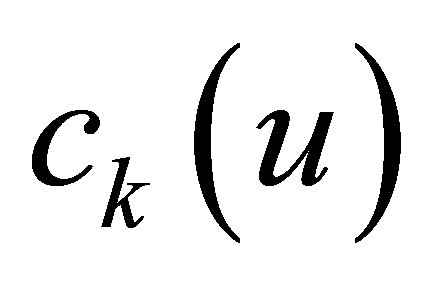 of the controlled plant are considered on the boundary, and defined as
of the controlled plant are considered on the boundary, and defined as
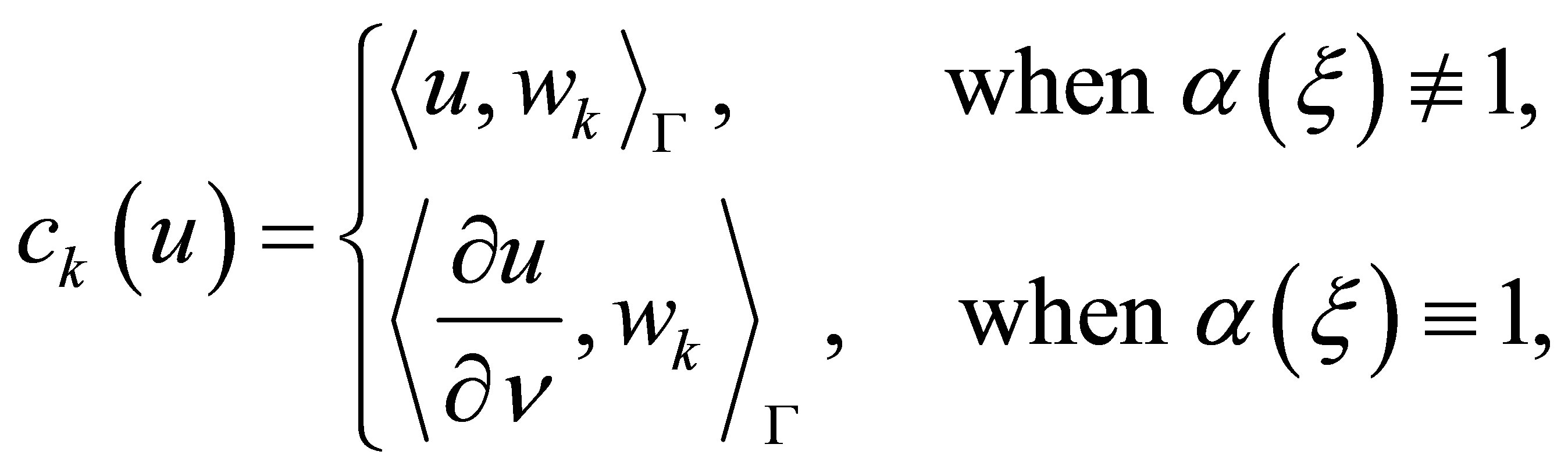 (10)
(10)
where 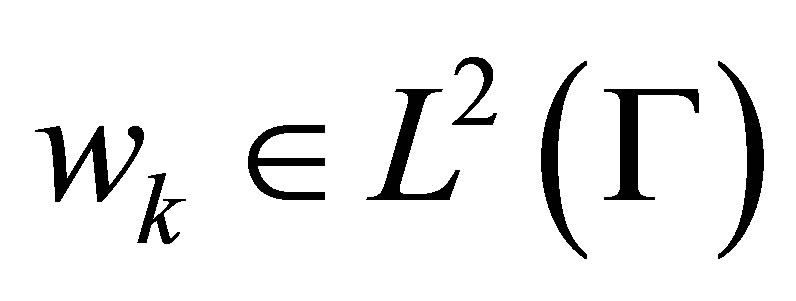 denotes observation weights. The operator
denotes observation weights. The operator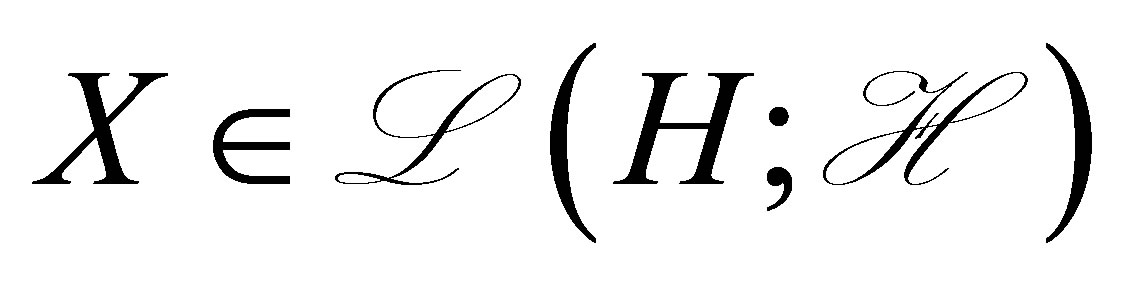 , specified later, denotes a unique solution to the operator equation on
, specified later, denotes a unique solution to the operator equation on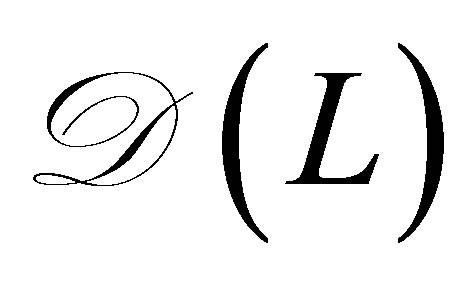 ,
,
 (11)
(11)
Given a suitable vector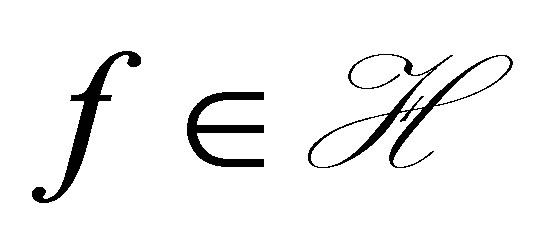 , the control law is to construct such that the number
, the control law is to construct such that the number 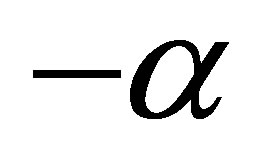 determines the decay rate of a functional
determines the decay rate of a functional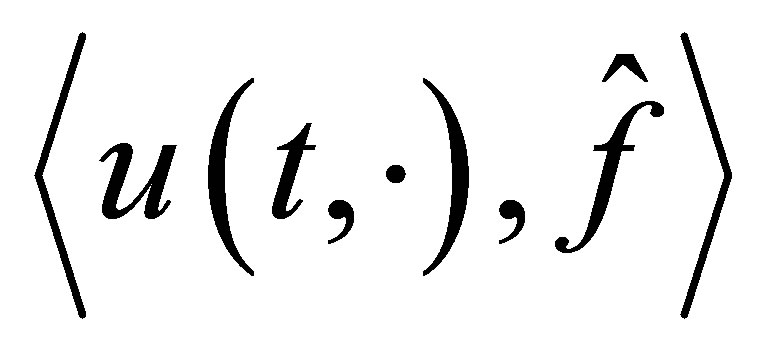 , where
, where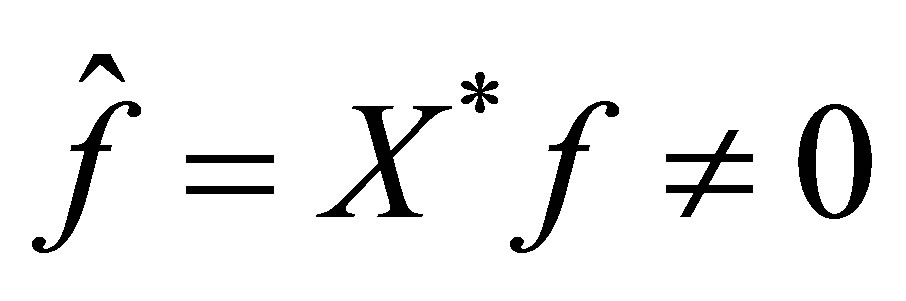 . As we see later, the roles of the outputs
. As we see later, the roles of the outputs 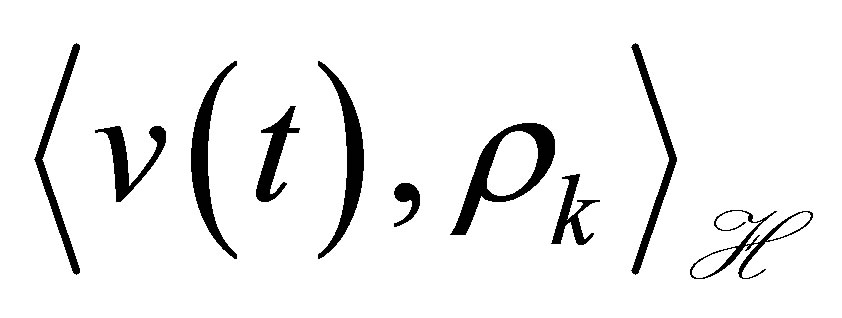 and
and 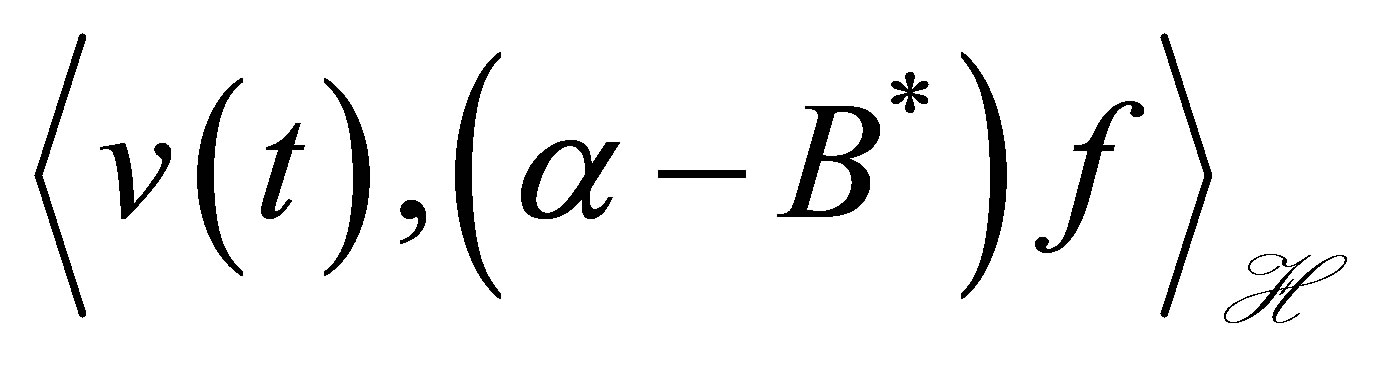 are, respectively, to determine the decay of
are, respectively, to determine the decay of  and the decay of
and the decay of . In state stabilization problems only, the output
. In state stabilization problems only, the output 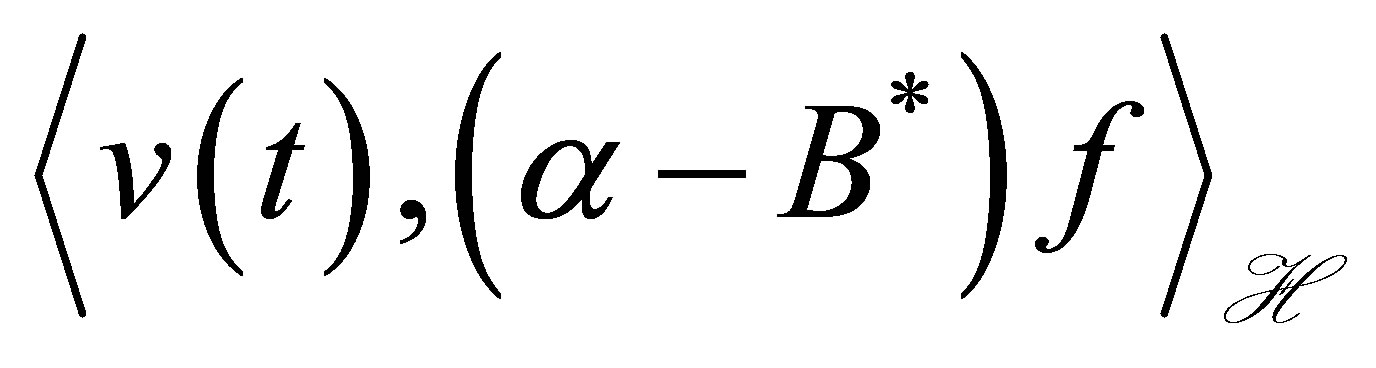 does not appear. More precisely, let
does not appear. More precisely, let 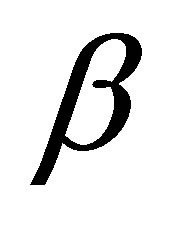 be a number such that
be a number such that . We seek a new feedback scheme such that the decay estimates
. We seek a new feedback scheme such that the decay estimates
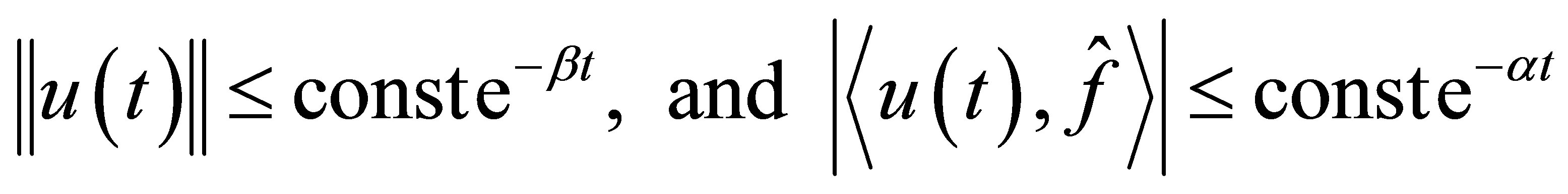 (12)
(12)
hold for every initial value and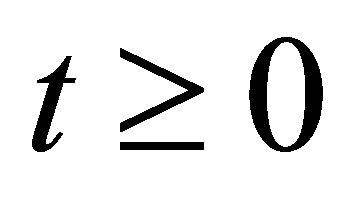 , such that the decay of
, such that the decay of  is no longer improved. To achieve the non-standard decay (12), introduce a new operator
is no longer improved. To achieve the non-standard decay (12), introduce a new operator
 (13)
(13)
and assume conditions in terms of . These conditions have never appeared in the literature. Note that conditions are posed on
. These conditions have never appeared in the literature. Note that conditions are posed on 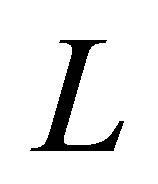 for state stabilization.
for state stabilization.
The functional 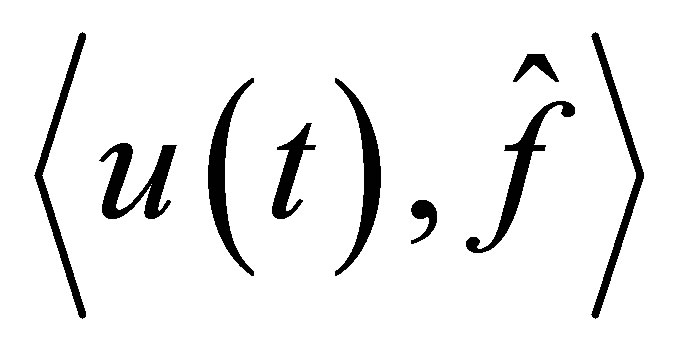 may be regarded as a kind of output of the system. It is worthwhile to refer to our previous results on output stabilization [10-13]: In [10], the decay of outputs is discussed with lack of observability conditions, but the relationship of the decay between
may be regarded as a kind of output of the system. It is worthwhile to refer to our previous results on output stabilization [10-13]: In [10], the decay of outputs is discussed with lack of observability conditions, but the relationship of the decay between 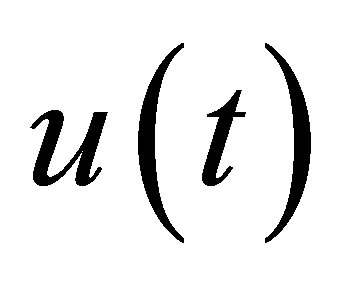 and the outputs is unclear. In [11-13], the problem is discussed, based on a different principle, i.e., a finitedimensional pole assignment theory with constraint. The controlled plants are, however, limited to those equipped with Riesz basis, and the actuators of the controlled plant, corresponding to our
and the outputs is unclear. In [11-13], the problem is discussed, based on a different principle, i.e., a finitedimensional pole assignment theory with constraint. The controlled plants are, however, limited to those equipped with Riesz basis, and the actuators of the controlled plant, corresponding to our , are restrictive, and must be subject to a strong constraint: the actuators have to be designed so that their spectral elements in each spectral subspace are orthogonal to the weights of the outputs at infinity. As we have seen, the controlled plants in the present paper do not necessarily allow a Riesz basis, although a somewhat stronger condition, i.e., complete observability, is assumed. An example of systems equipped with complete observability is illustrated in the end of Section 2.
, are restrictive, and must be subject to a strong constraint: the actuators have to be designed so that their spectral elements in each spectral subspace are orthogonal to the weights of the outputs at infinity. As we have seen, the controlled plants in the present paper do not necessarily allow a Riesz basis, although a somewhat stronger condition, i.e., complete observability, is assumed. An example of systems equipped with complete observability is illustrated in the end of Section 2.
The feedback law in (9) contains parameters: ,
, 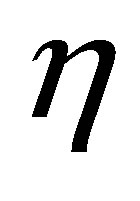 ,
, 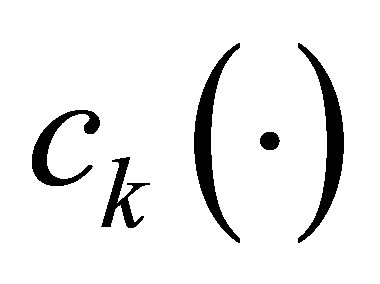 ,
,  ,
, 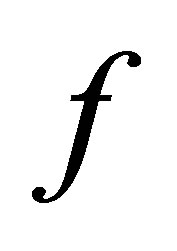 ,
,  , and
, and 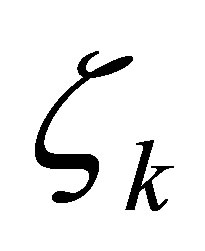 to achieve the nonstandard decays (12). They are designed in the following manner: 1) The actuator
to achieve the nonstandard decays (12). They are designed in the following manner: 1) The actuator 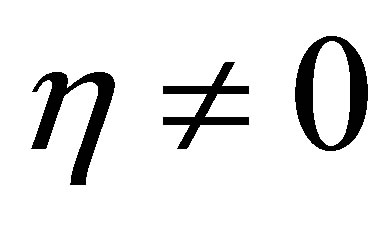 is given in advance arbitrarily. 2) Given the parameters
is given in advance arbitrarily. 2) Given the parameters 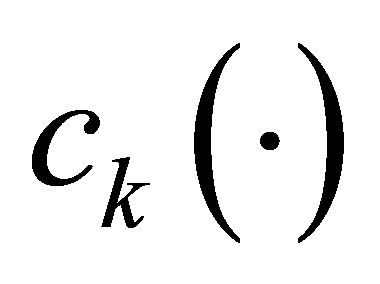 and
and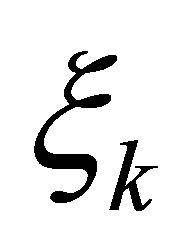 , the operator solution
, the operator solution 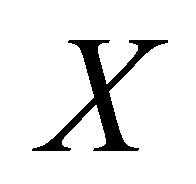 is ensured. 3) Then, a vector
is ensured. 3) Then, a vector 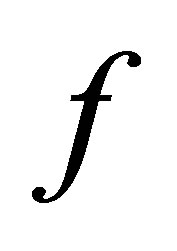 is chosen among a very wide range of sets in
is chosen among a very wide range of sets in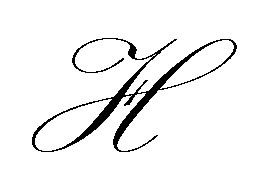 . 4) Finally,
. 4) Finally, 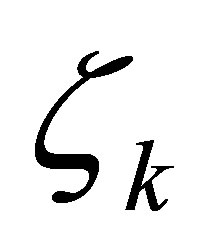 , as well as
, as well as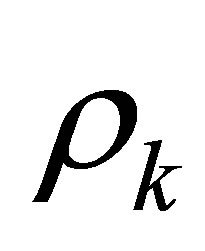 , are designed to satisfy a finite number of controllability conditions associated with the new operator
, are designed to satisfy a finite number of controllability conditions associated with the new operator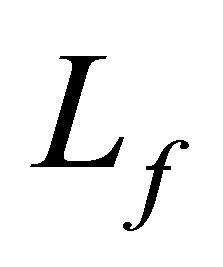 . It is generally desirable to pose less restrictive assumptions on the actuators of the controlled plant. In fact,
. It is generally desirable to pose less restrictive assumptions on the actuators of the controlled plant. In fact,  is arbitrary, and, as we see later that the conditions on
is arbitrary, and, as we see later that the conditions on 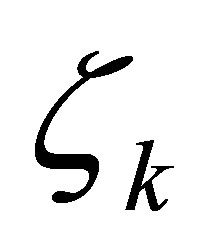 are much less restrictive than those in our preceding works above. In fact,
are much less restrictive than those in our preceding works above. In fact, 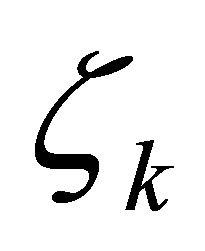 only have to be designed, belonging to an infinite dimensional subspace of
only have to be designed, belonging to an infinite dimensional subspace of .
.
Our main results consist of Theorem 4 in Section 2 and a series of assertions in Section 3 (Theorem 7, Propositions 8, and Theorem 9): The former is on the control law ensuring the non-standard decays (12), and the latter on the relevance of the problem setting with Equation (8), which discusses a spectral property of the invariant subspaces in  associated with the coefficient operator in (9), that is, unlikeliness of a vector of the form,
associated with the coefficient operator in (9), that is, unlikeliness of a vector of the form, 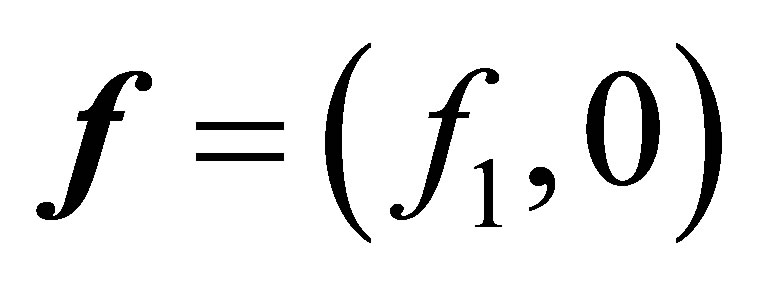 in these subspaces. In Section 3, the spectrum of the coefficient operator is characterized (Theorem 9). To the best of the author’s knowledge, the latter has never been discussed so far, and clarifies a new property of internal structures of control systems.
in these subspaces. In Section 3, the spectrum of the coefficient operator is characterized (Theorem 9). To the best of the author’s knowledge, the latter has never been discussed so far, and clarifies a new property of internal structures of control systems.
2. Decay Estimates of Solutions
To ensure well-posedness of our control system (8), let us begin with the operator Equation (10). Adjusting 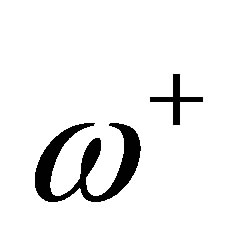 and
and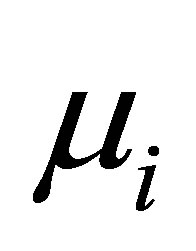 ,
, 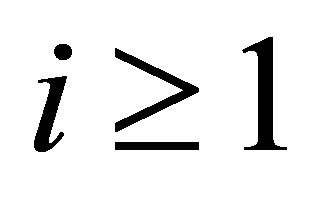 , we may assume that
, we may assume that
 (14)
(14)
(see (2) for ). In (9), let us express the actuators
). In (9), let us express the actuators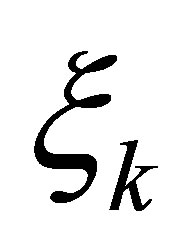 ,
, 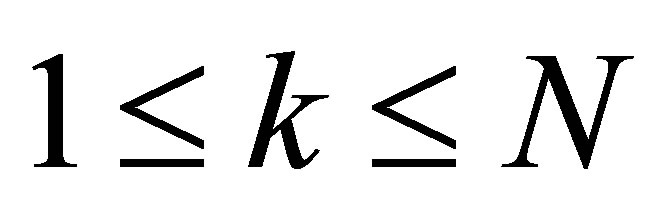 as Fourier series in terms of
as Fourier series in terms of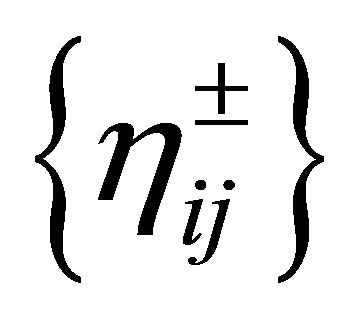 :
:
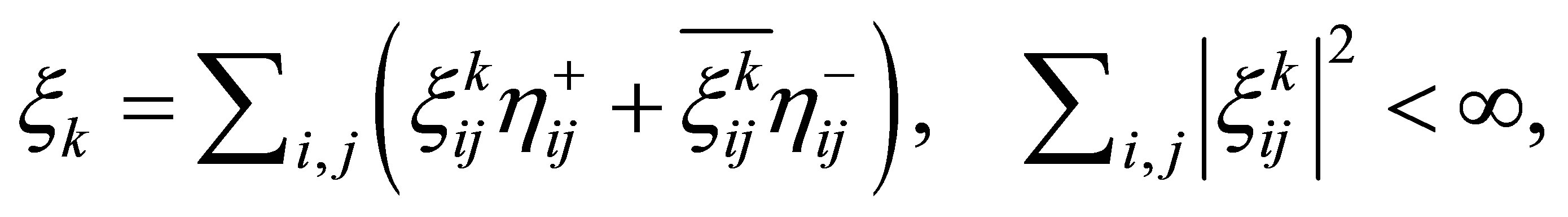
where the overline denotes the complex conjugate. Before stating our first result, let us define the matrices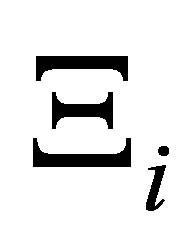 , and
, and ,
,  by
by
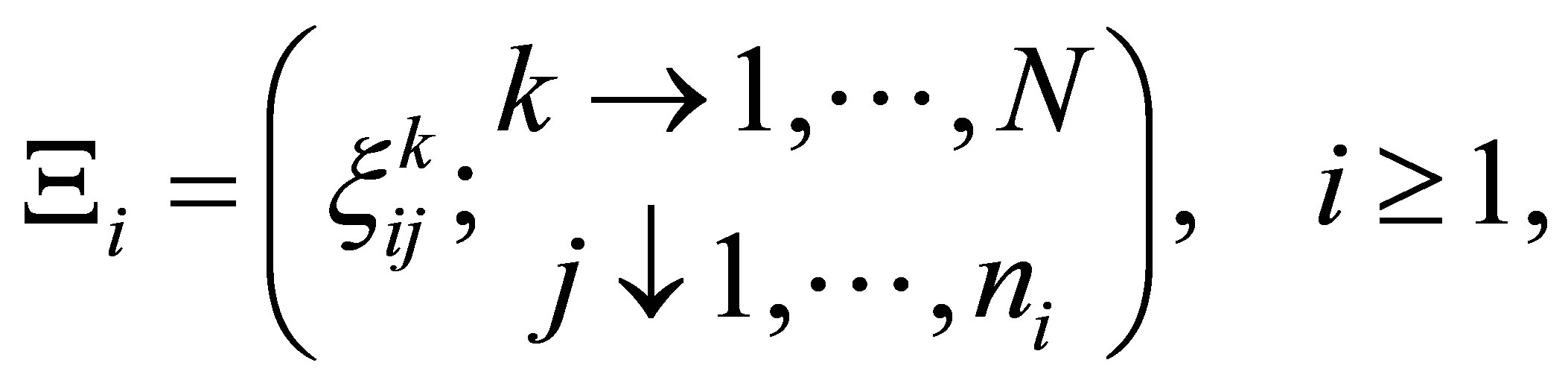 (15)
(15)
and
 (16)
(16)
respectively. Then our first result is stated as follows:
Theorem 1. 1) By assuming (14), the operator equation (11) on 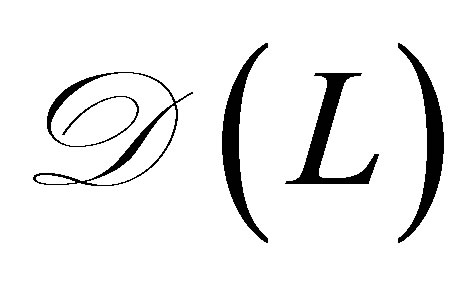 admits a unique operator solution
admits a unique operator solution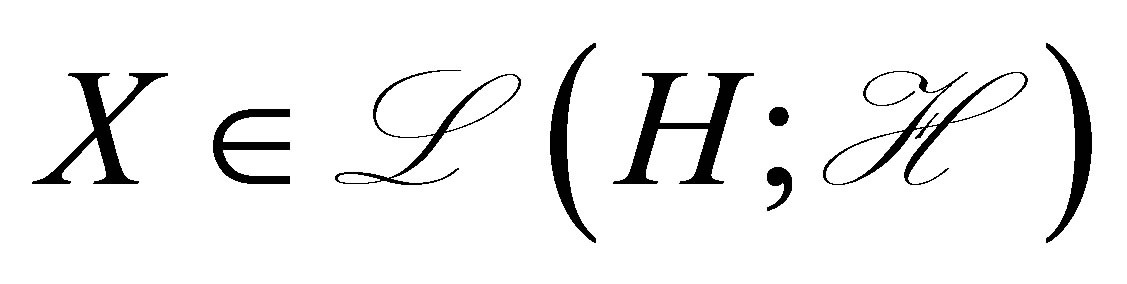 , which is expressed as
, which is expressed as
 (17)
(17)
2) Assume further that
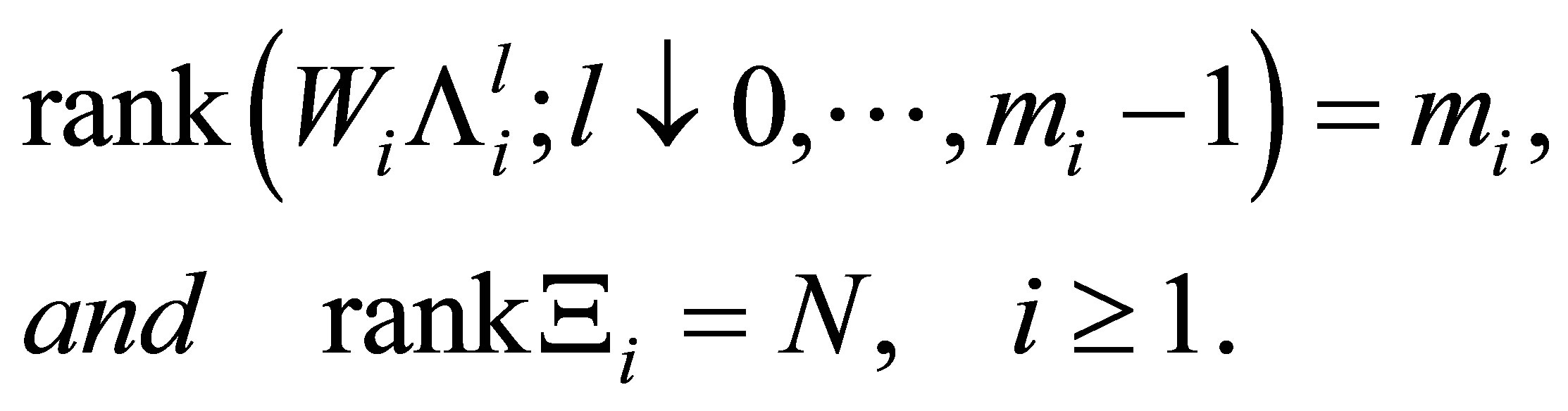 (18)
(18)
Then we have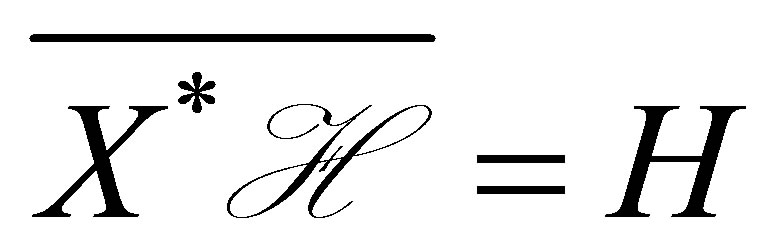 . Here,
. Here, 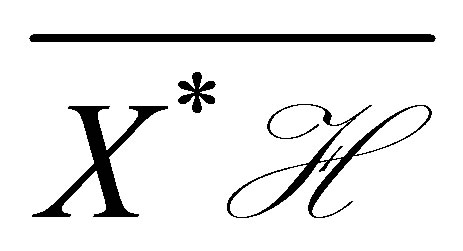 denotes the closure of
denotes the closure of  in
in .
.
Remark. 1) The first condition in (18), called the complete observability condition, is fulfilled with  in the case where
in the case where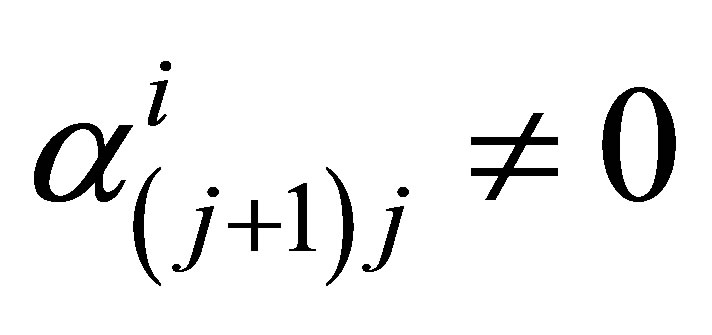 ,
,  ,
,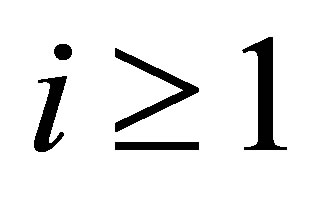 . Actually, by choosing the
. Actually, by choosing the 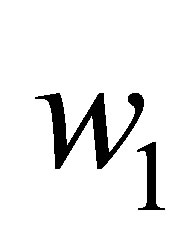 with
with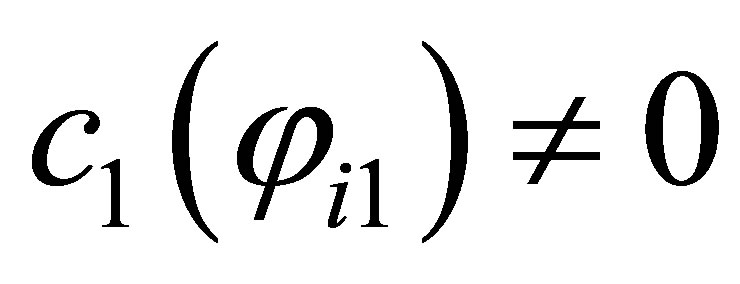 ,
, 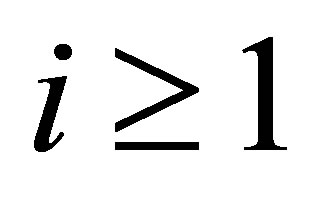 , the condition is fulfilled. In the case where
, the condition is fulfilled. In the case where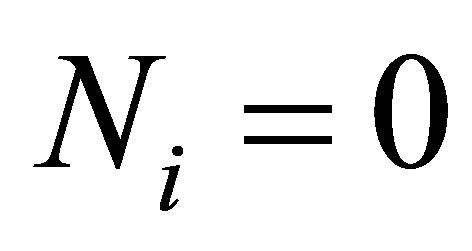 ,
, 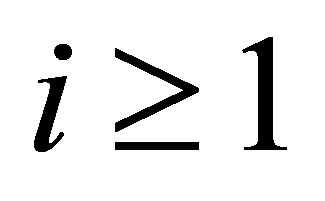 , however, the condition means that
, however, the condition means that ,
, 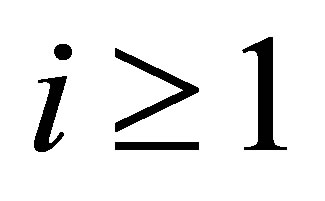 , which requires that
, which requires that 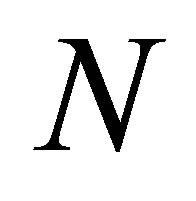 be equal to or greater than
be equal to or greater than : this is the case, for example, where
: this is the case, for example, where  is selfadjoint.
is selfadjoint.
2) The condition: 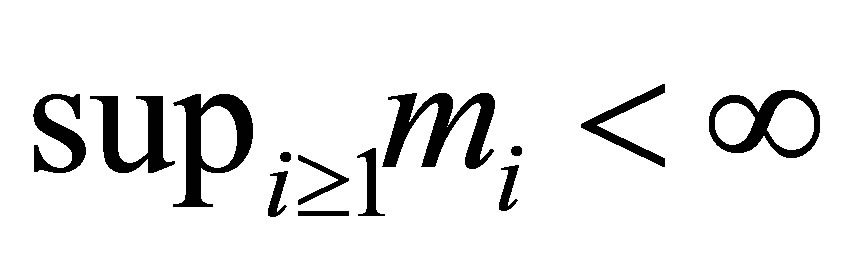 is the so called finite multiplicity condition. In the case of
is the so called finite multiplicity condition. In the case of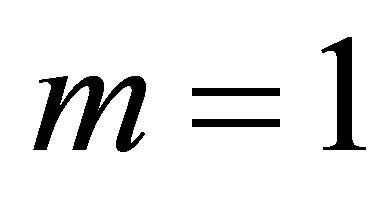 , we know that
, we know that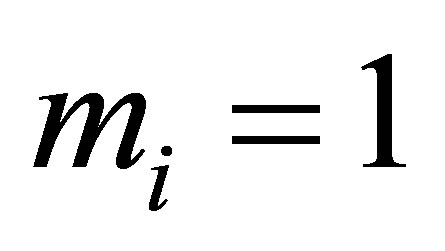 ,
,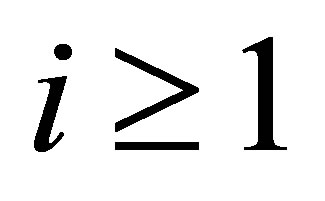 . Thus, by choosing
. Thus, by choosing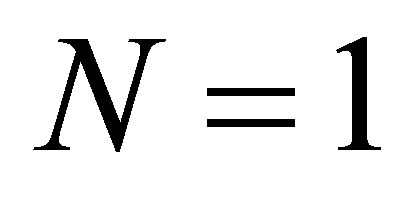 , the complete observability condition is automatically fulfilled. As another example, let
, the complete observability condition is automatically fulfilled. As another example, let  be a self-adjoint operator defined by
be a self-adjoint operator defined by  in
in  equipped with the Dirichlet boundary. The eigenvalues of
equipped with the Dirichlet boundary. The eigenvalues of 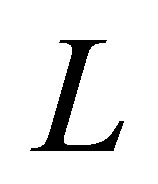 consist of
consist of ,
,  ,
, 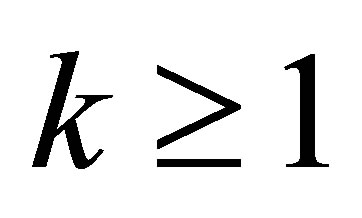 , where
, where 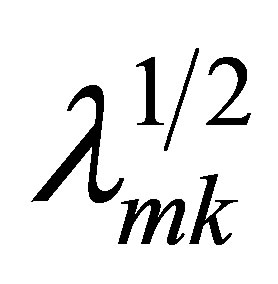 are the zeros of the Bessel functions
are the zeros of the Bessel functions 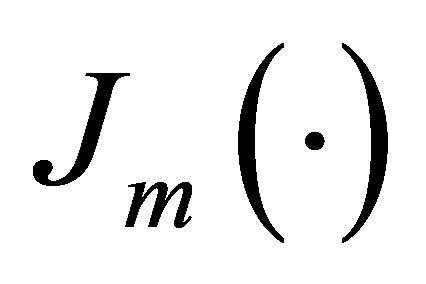 of m-th order. It is expected that
of m-th order. It is expected that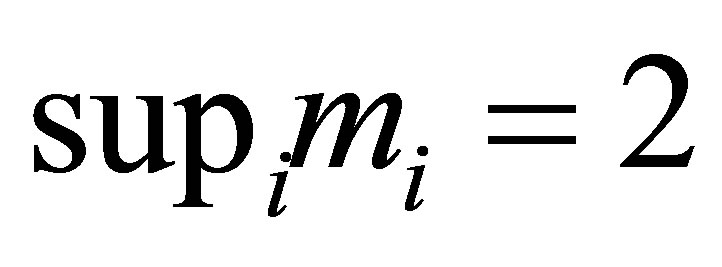 , if the well known Bourget’s hypothesis (see pp. 484-485 of [14]) is proven. As long as the author knows, this conjecture has not been proven so far.
, if the well known Bourget’s hypothesis (see pp. 484-485 of [14]) is proven. As long as the author knows, this conjecture has not been proven so far.
Proof. The result is a version of the results in [2-5], so that we give here only an outline of the proof. 1) Expression (17) and uniqueness of 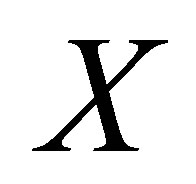 are examined in a straightforward manner.
are examined in a straightforward manner.
2) Relation  is equivalent to
is equivalent to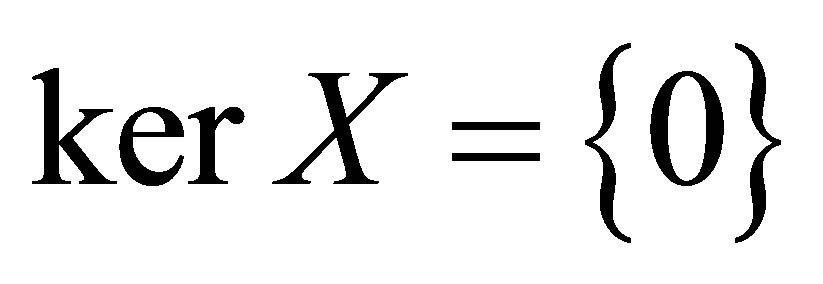 . Assuming that
. Assuming that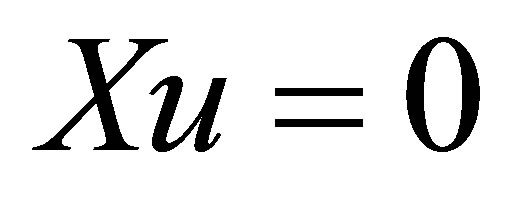 , we see by (17) that
, we see by (17) that
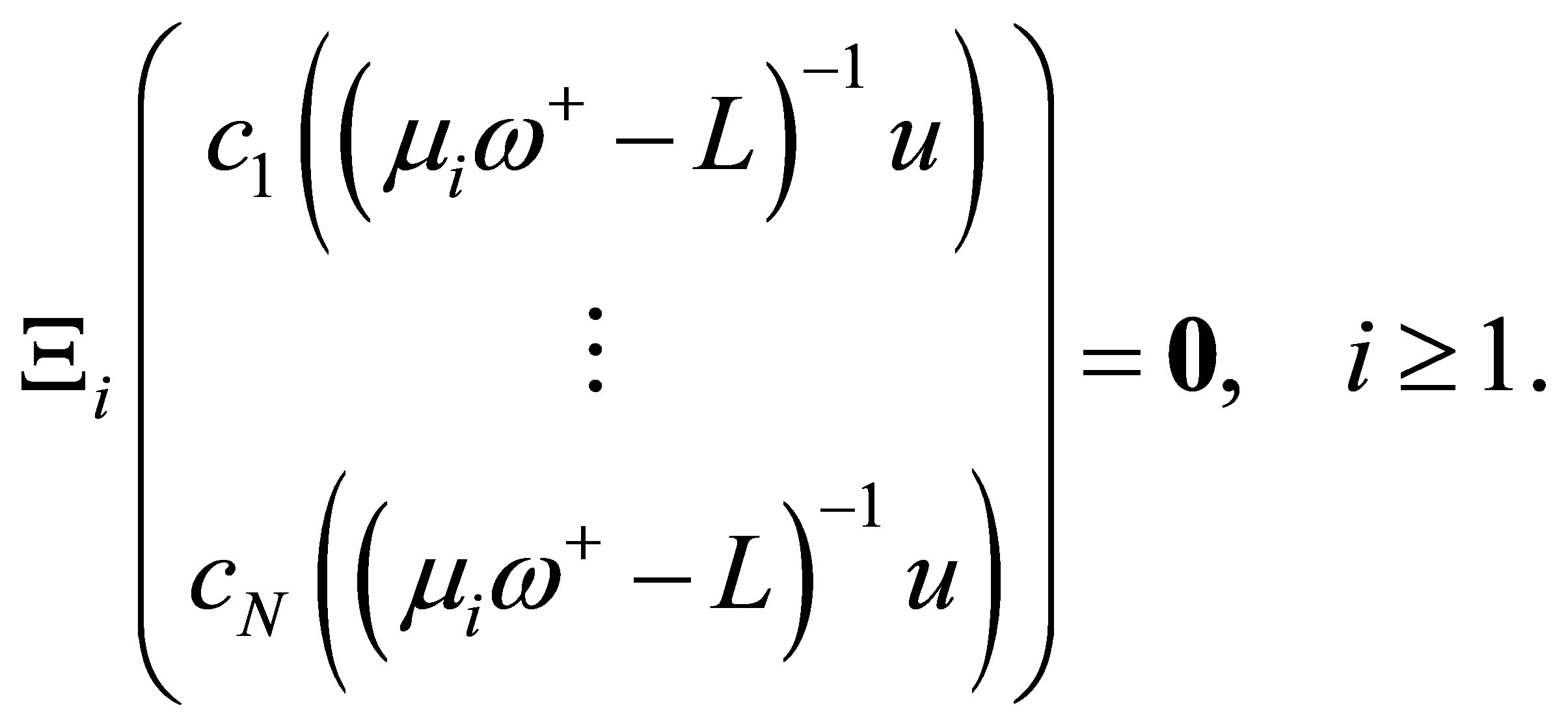
Since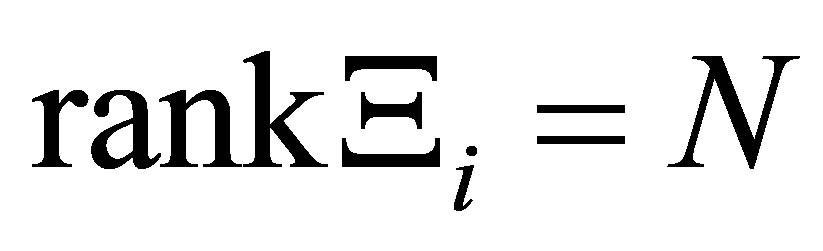 , we see that
, we see that 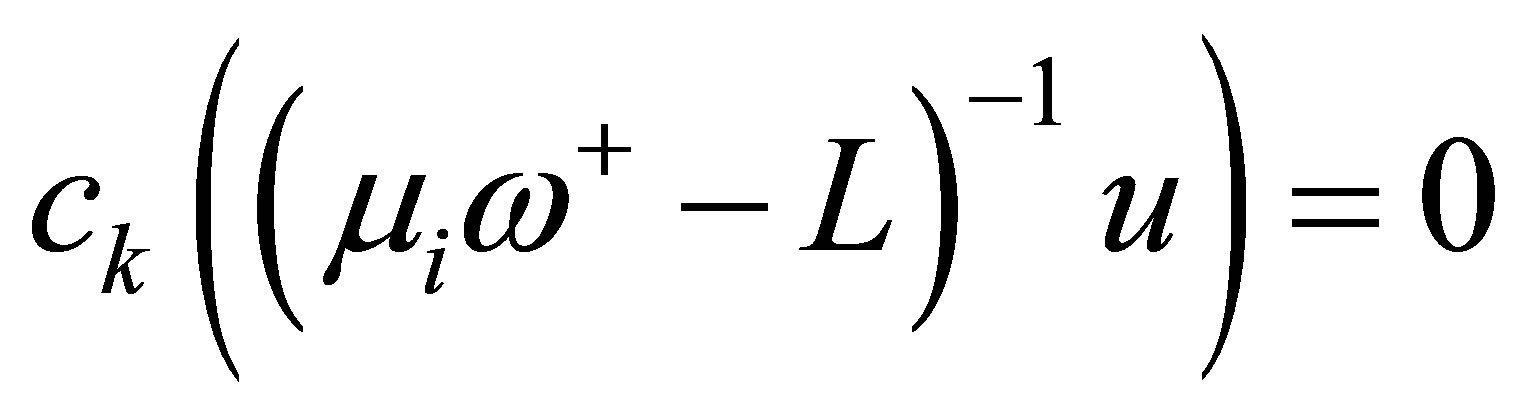 for
for  and
and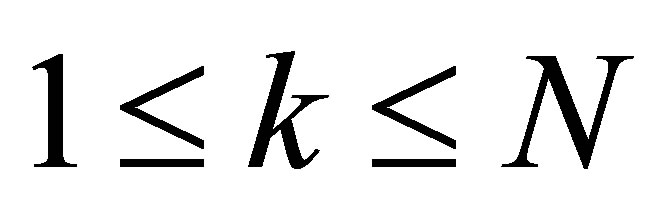 .
.
For a 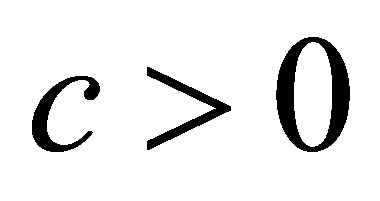 such that
such that  and each
and each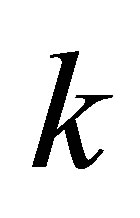 , we introduce a series of meromorphic functions
, we introduce a series of meromorphic functions ,
,  by the recursion formula:
by the recursion formula:
 (19)
(19)
Each function  has the properties: 1) It has at least the zeros
has the properties: 1) It has at least the zeros ,
, ; and 2) the algebraic growth rate
; and 2) the algebraic growth rate 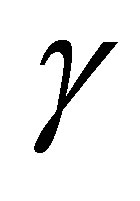 of these zeros,
of these zeros, 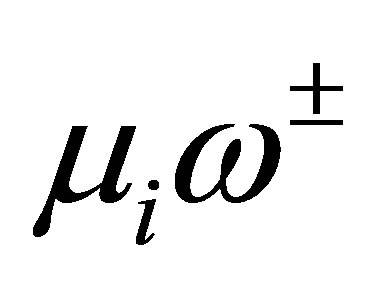 is smaller than 2 by (14). These properties combined with Carleman’s theorem [15,16] imply that
is smaller than 2 by (14). These properties combined with Carleman’s theorem [15,16] imply that 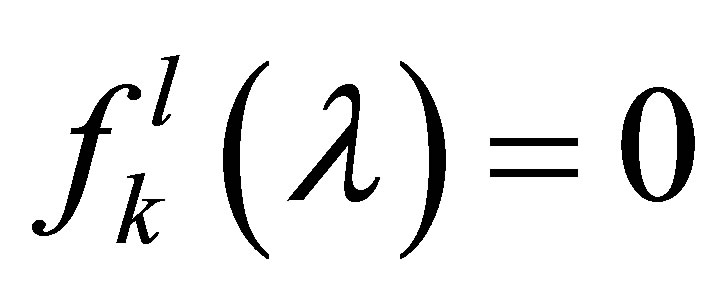 for
for ,
, 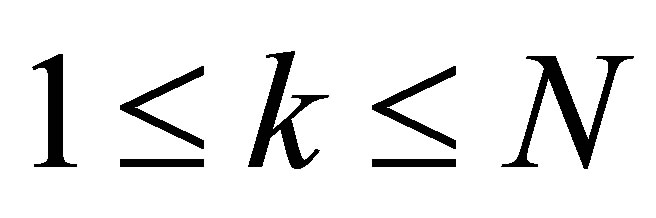 ,
,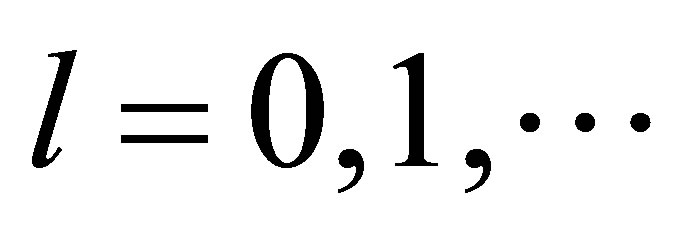 . Following [5], we calculate the residue at each
. Following [5], we calculate the residue at each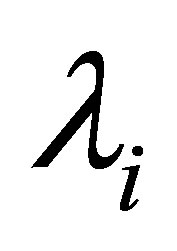 . Then, we see that
. Then, we see that
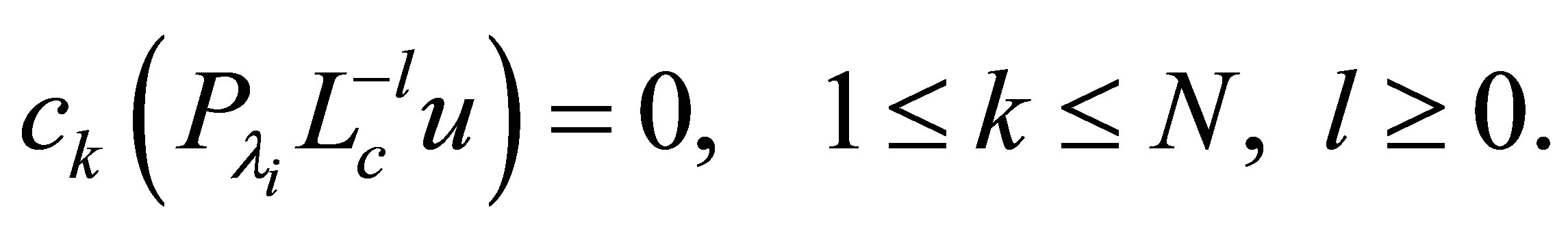 (20)
(20)
Let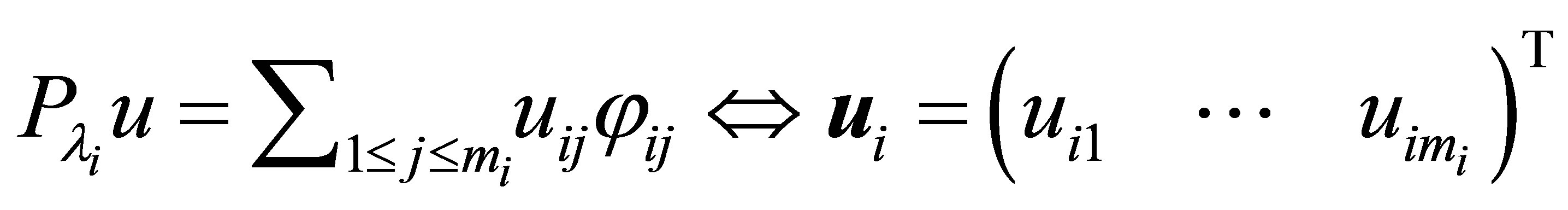 . Note that the restriction of
. Note that the restriction of 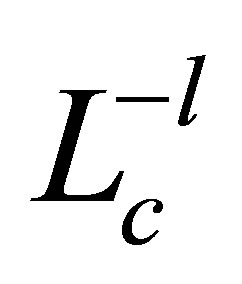 on
on 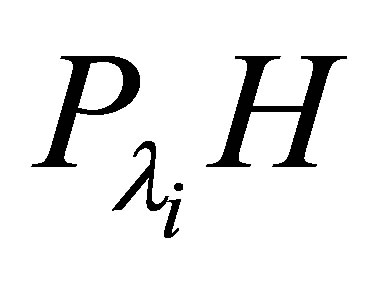 is equivalent to the matrix
is equivalent to the matrix , and thus,
, and thus,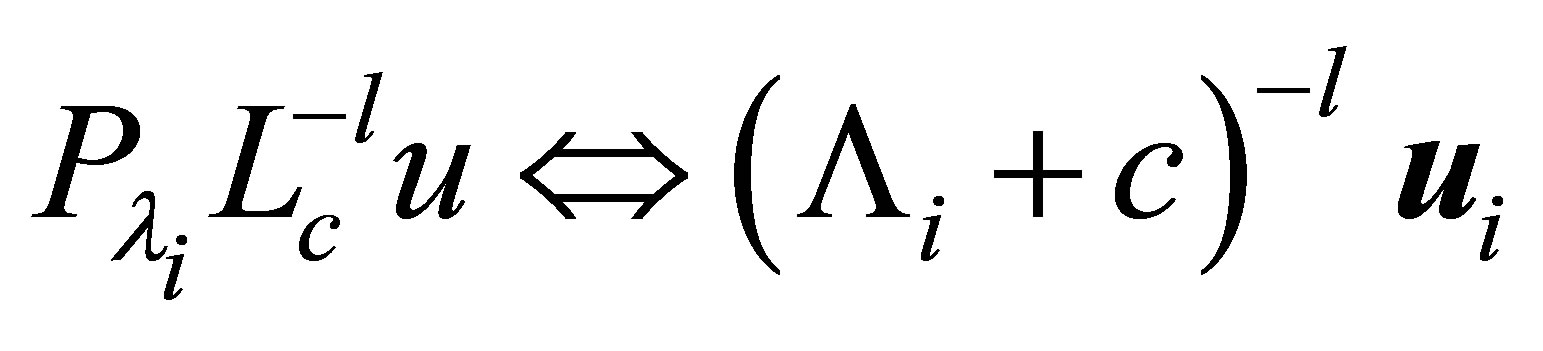 . The relation (20) is rewritten as
. The relation (20) is rewritten as
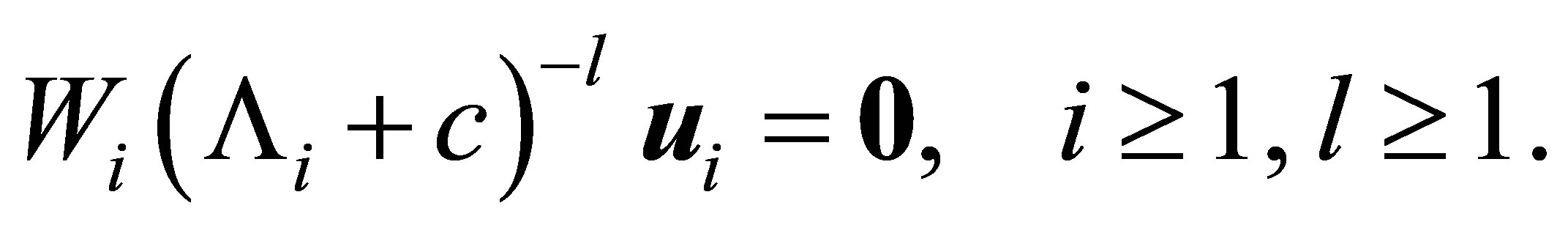 (21)
(21)
The complete observability in (18) implies that  for
for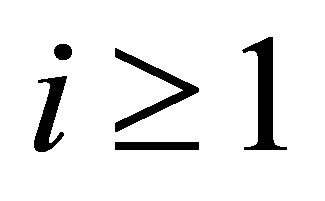 . In view of (5), we see that
. In view of (5), we see that 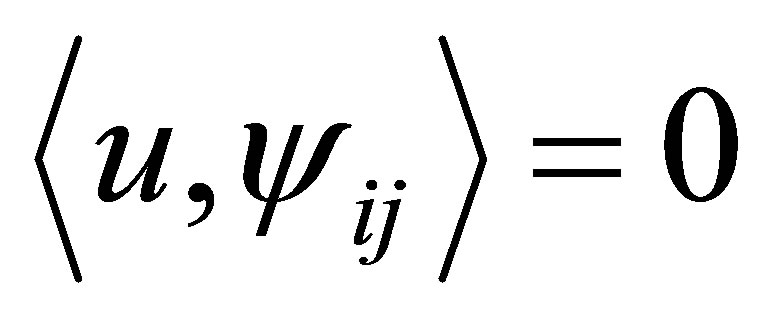 for every
for every  and
and . Since the set
. Since the set 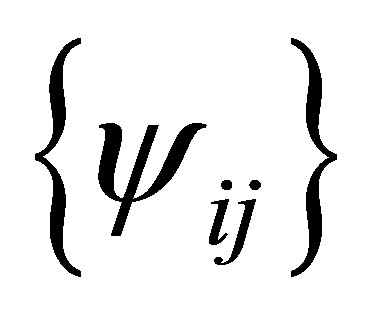 spans the whole space
spans the whole space , we conclude that
, we conclude that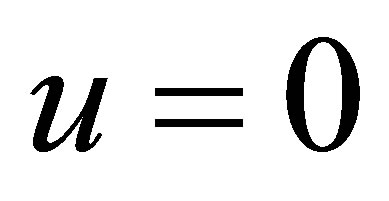 . Q.E.D.
. Q.E.D.
Decay of solutions to Equation (9): In view of (11), it is easily seen that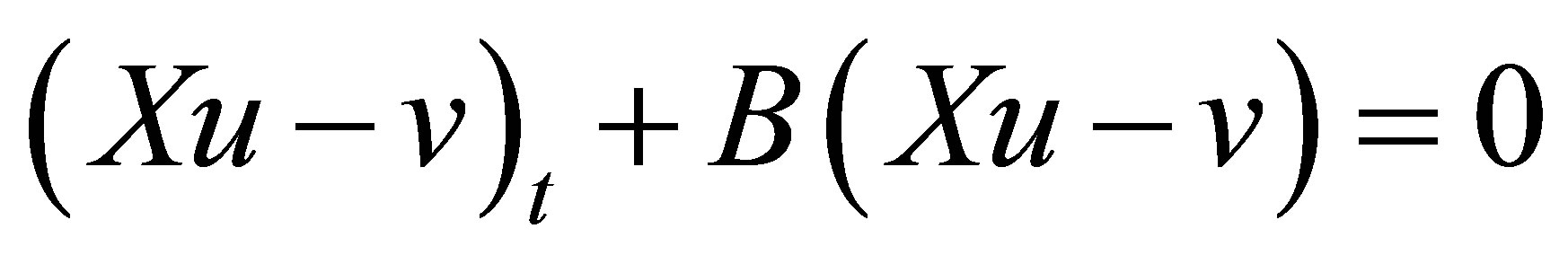 ,
, 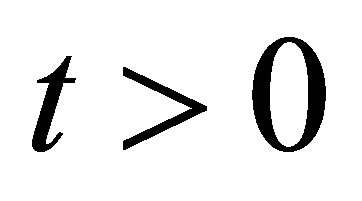 , or
, or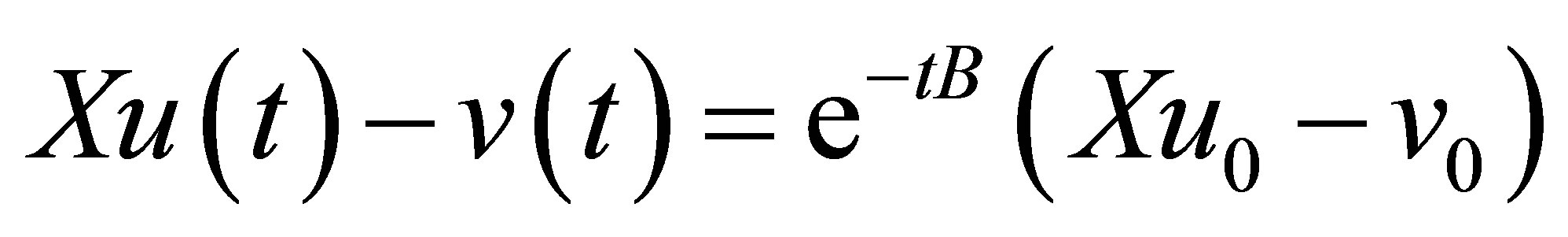 . Thus,
. Thus,
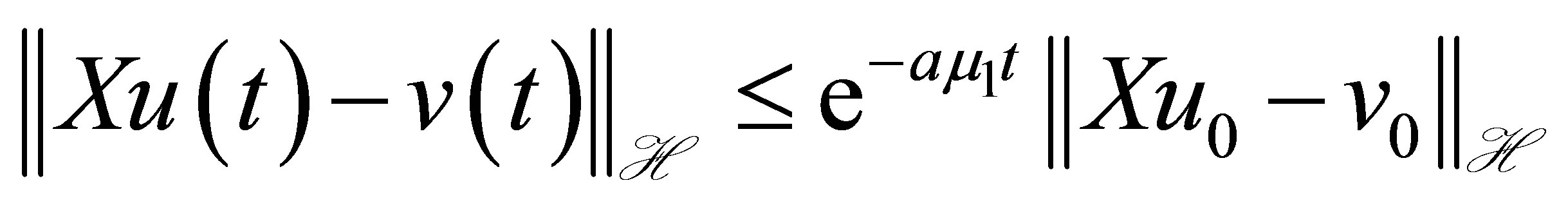 (22)
(22)
for . In (9). let
. In (9). let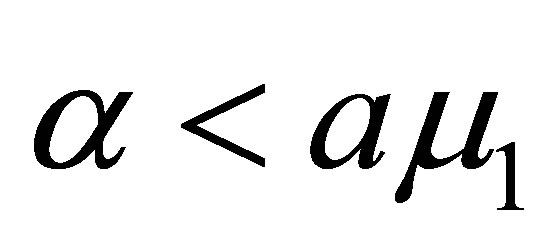 , and
, and 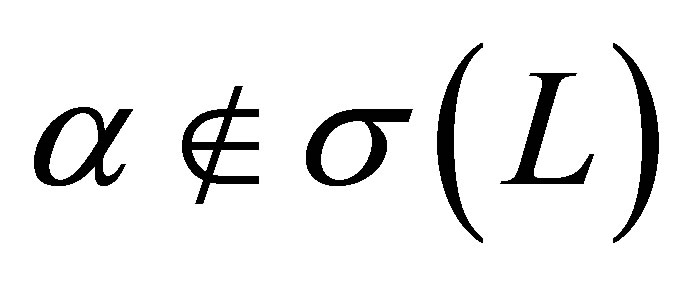 (see Proposition 2). Equation (9) contains various parameters:
(see Proposition 2). Equation (9) contains various parameters: ,
, 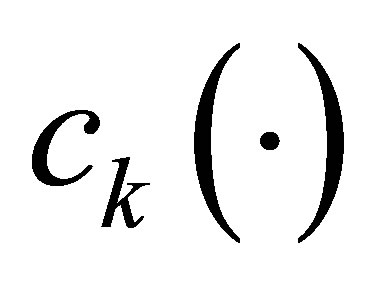 ,
, 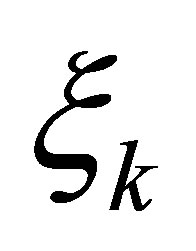 ,
, 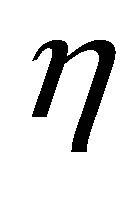 ,
, 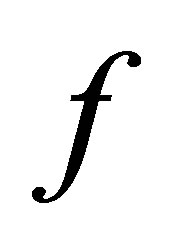 ,
,  , and
, and , among which
, among which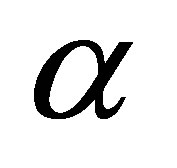 ,
, 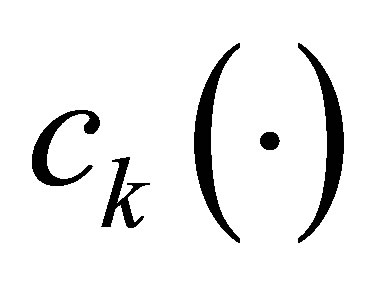 and
and 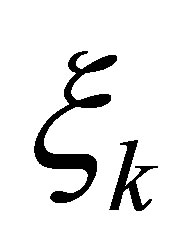 are already determined in Theorem 1. Let a non-trivial
are already determined in Theorem 1. Let a non-trivial 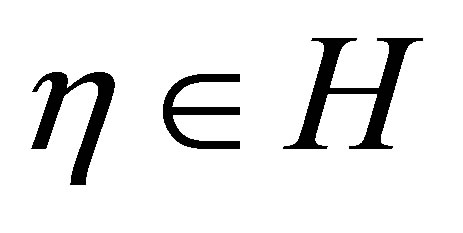 be given arbitrarily. Then,
be given arbitrarily. Then, 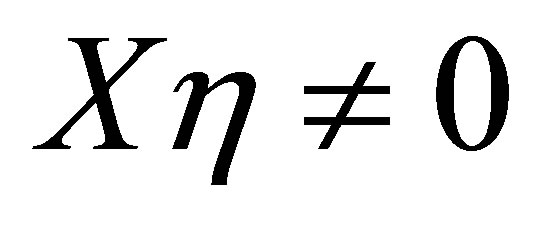 by Theorem 1. We find a non-trivial vector
by Theorem 1. We find a non-trivial vector 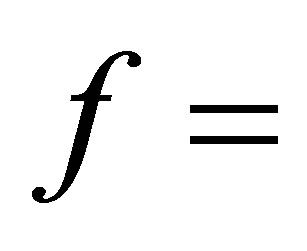
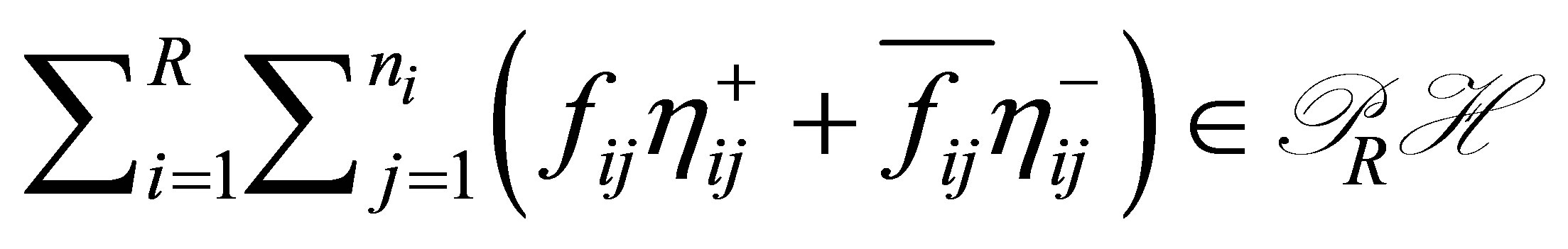 such that
such that
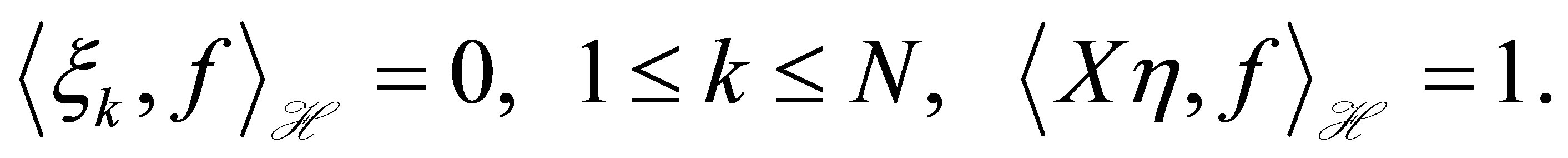 (23)
(23)
There is a variety of choice of such an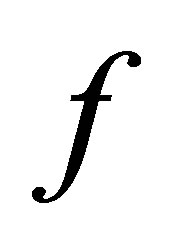 . In fact, this is simply possible, e.g., by finding
. In fact, this is simply possible, e.g., by finding 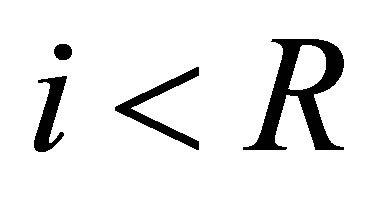 such that
such that

for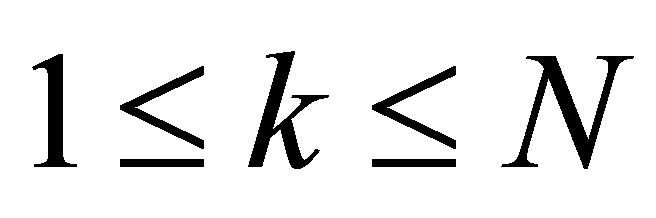 . Then
. Then 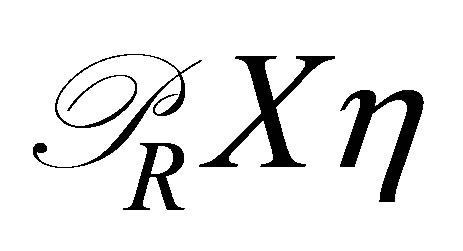 does not belong to the space spanned by
does not belong to the space spanned by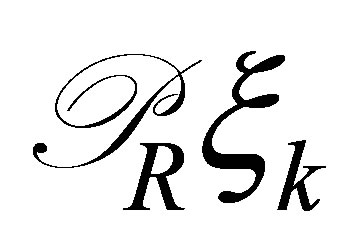 ,
,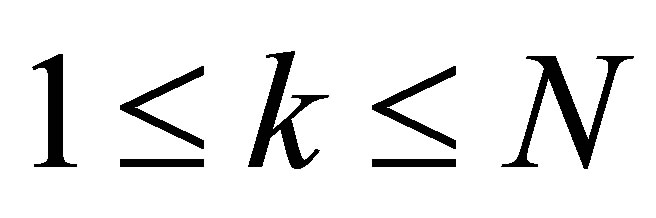 . The integer
. The integer 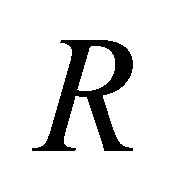 may be chosen arbitrarily large. The vectors
may be chosen arbitrarily large. The vectors 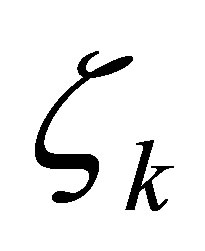 will be determined in terms of the operator
will be determined in terms of the operator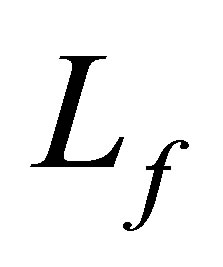 .
.
The state 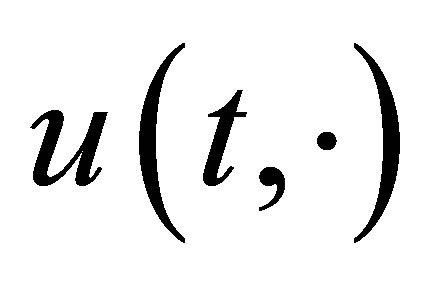 in (9) satisfies the equation:
in (9) satisfies the equation:
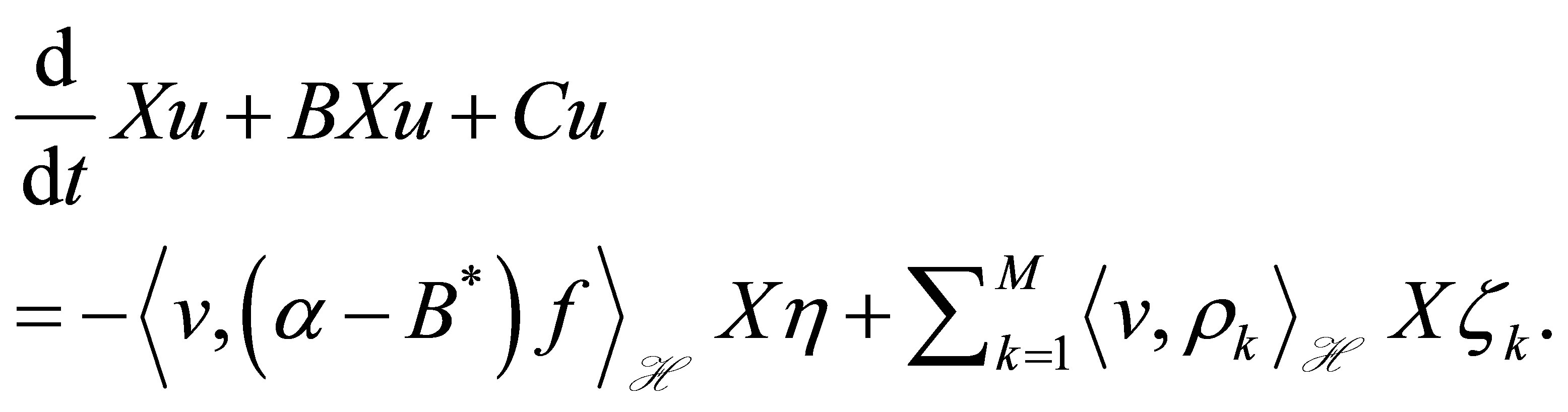
Actuators 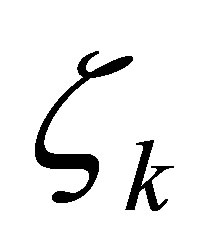 are chosen so that
are chosen so that ,
,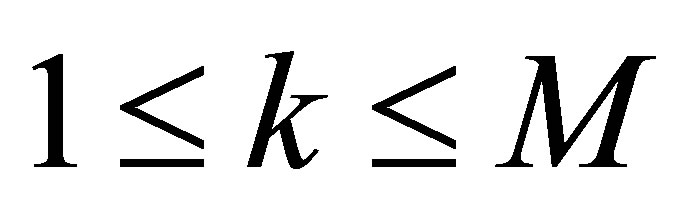 . An assumption on these
. An assumption on these  will be discussed later (see (28)). Then, it is immediately seen that
will be discussed later (see (28)). Then, it is immediately seen that
 (24)
(24)
By the decay (22), we obtain the estimate:
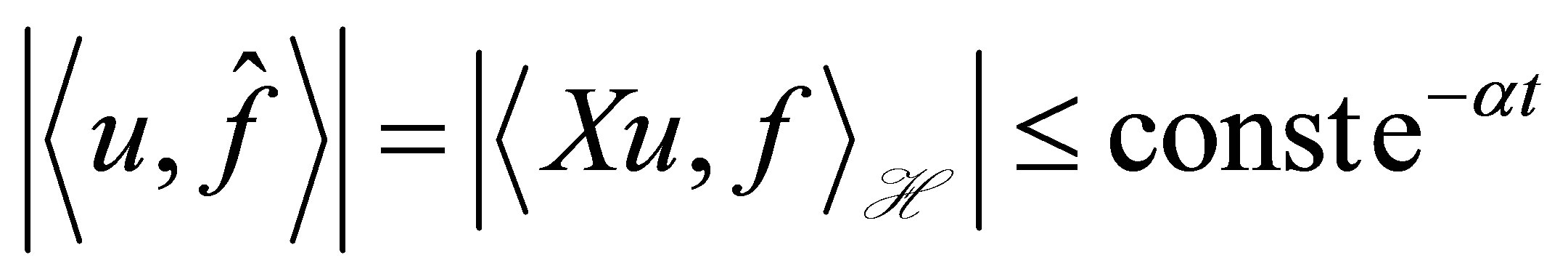 (25)
(25)
for . Here,
. Here, 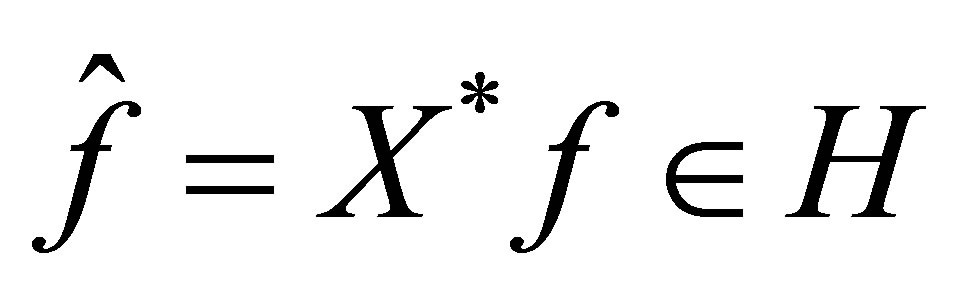 is non-trivial.
is non-trivial.
The operator 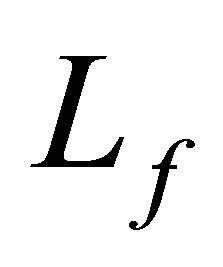 defined in (13) has a compact resolvent, and
defined in (13) has a compact resolvent, and  consists only of eigenvalues. Let
consists only of eigenvalues. Let
 (26)
(26)
where  and
and  for i ≠ j. Each
for i ≠ j. Each 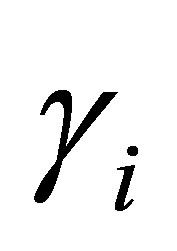 may admit generalized eigenfunctions. Let
may admit generalized eigenfunctions. Let 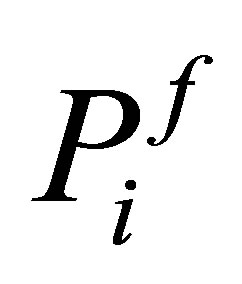 be the projector corresponding to the eigenvalue
be the projector corresponding to the eigenvalue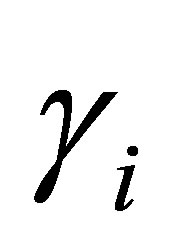 which is calculated as
which is calculated as , Ci
, Ci
being the small counterclockwise circle with center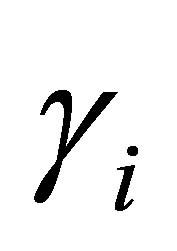 . Then
. Then
Proposition 2. 1) The number 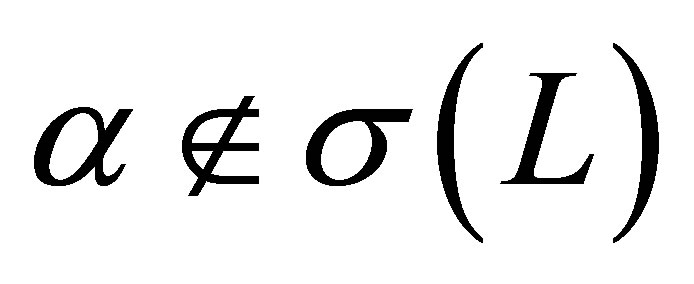 belongs to
belongs to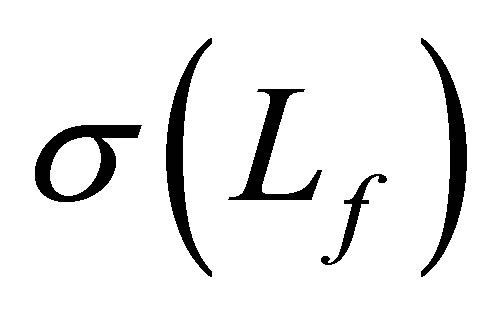 . 2) Any generalized eigenfunction of
. 2) Any generalized eigenfunction of 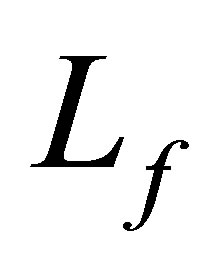 in
in 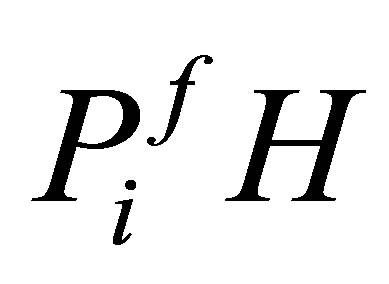
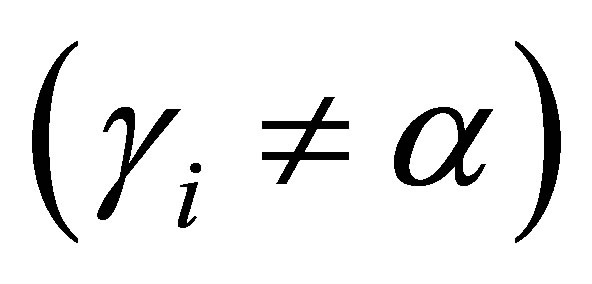 and
and 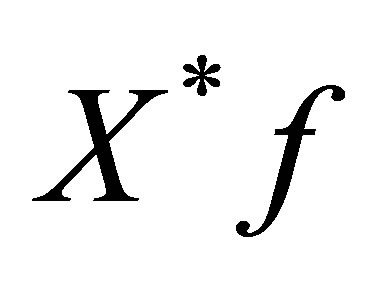 are orthogonal to each other.
are orthogonal to each other.
Proof. 1) Suppose that there is a 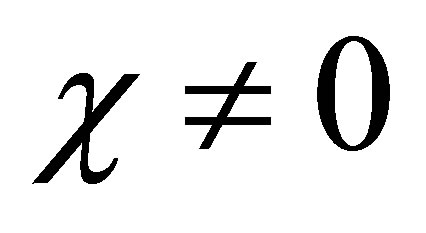 such that
such that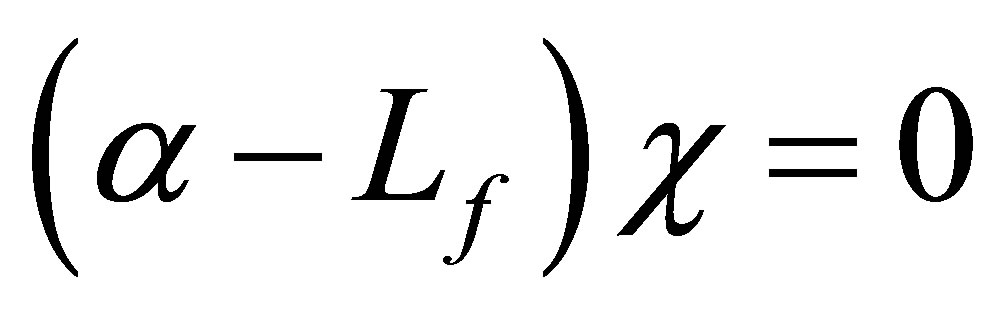 . Then,
. Then,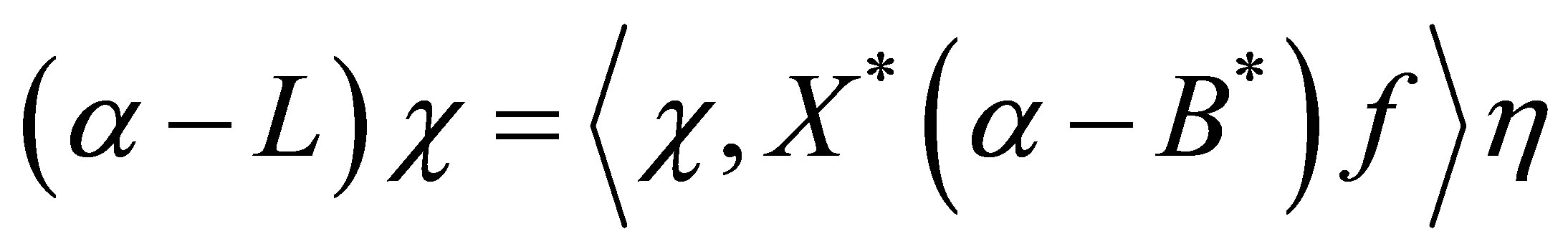 . Thus we have, as a necessary condition,
. Thus we have, as a necessary condition,
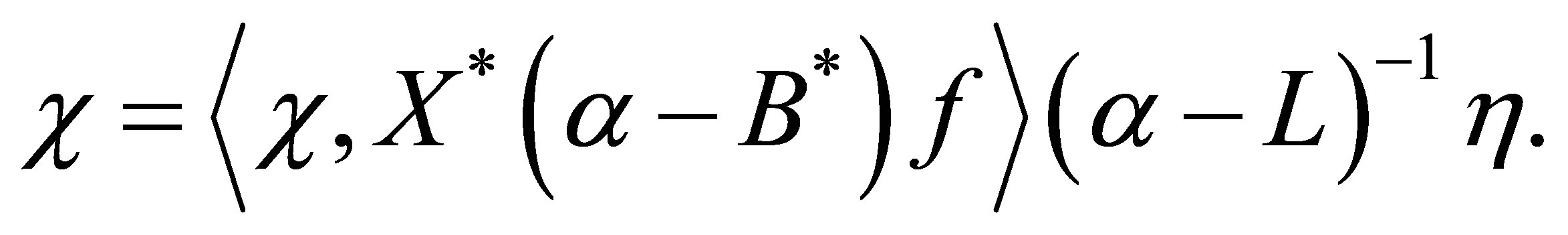
Now set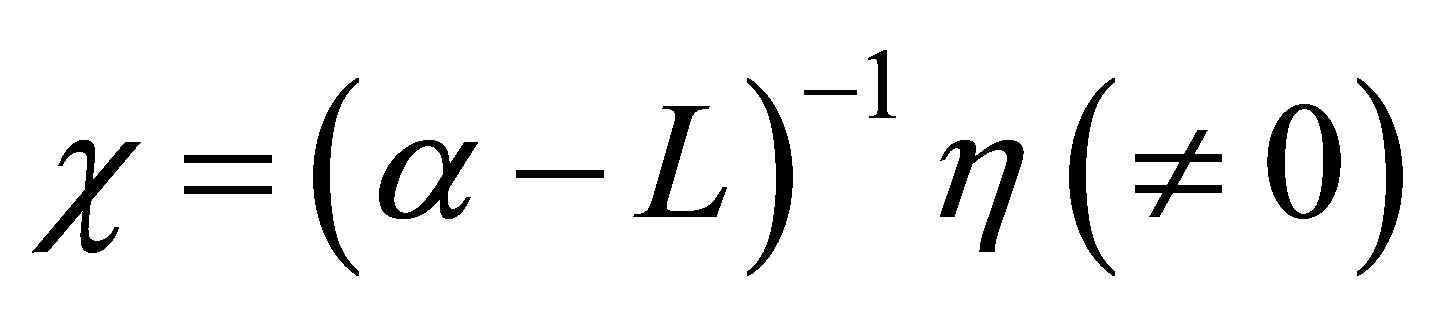 , and calculate as
, and calculate as
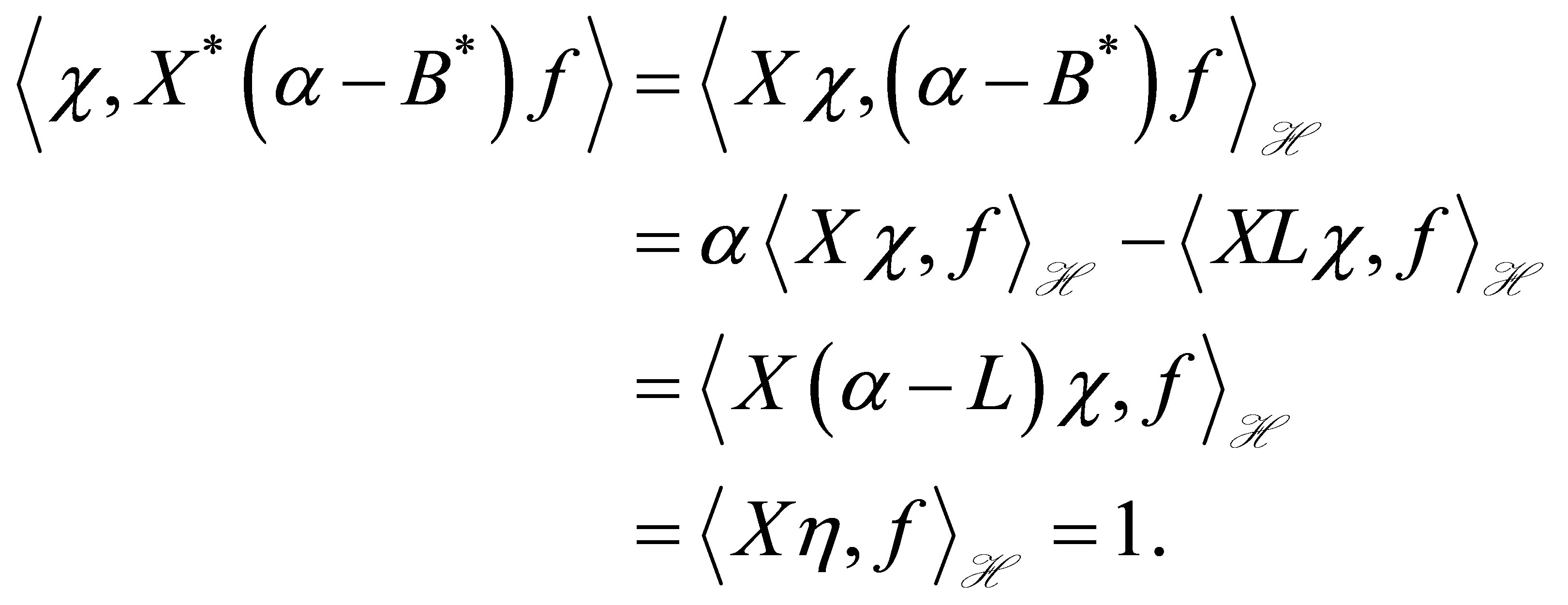
Thus we see that
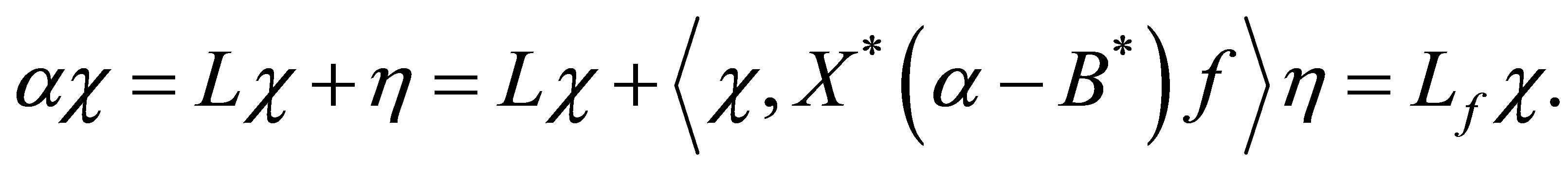
2) Let ,
,  , and
, and  ,
, 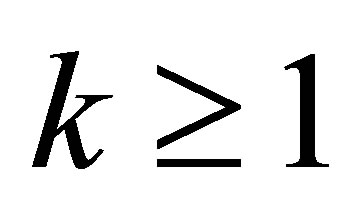 , possible generalized eigenspaces of
, possible generalized eigenspaces of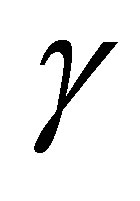 . For a
. For a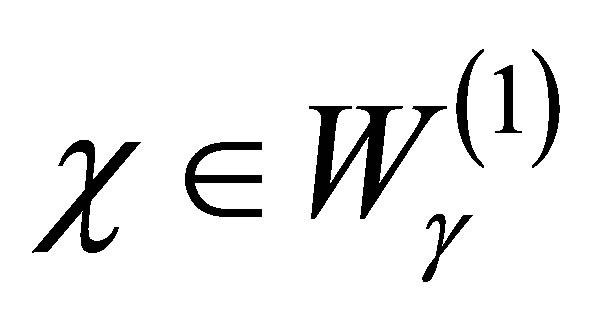 , we calculate by (23) as
, we calculate by (23) as
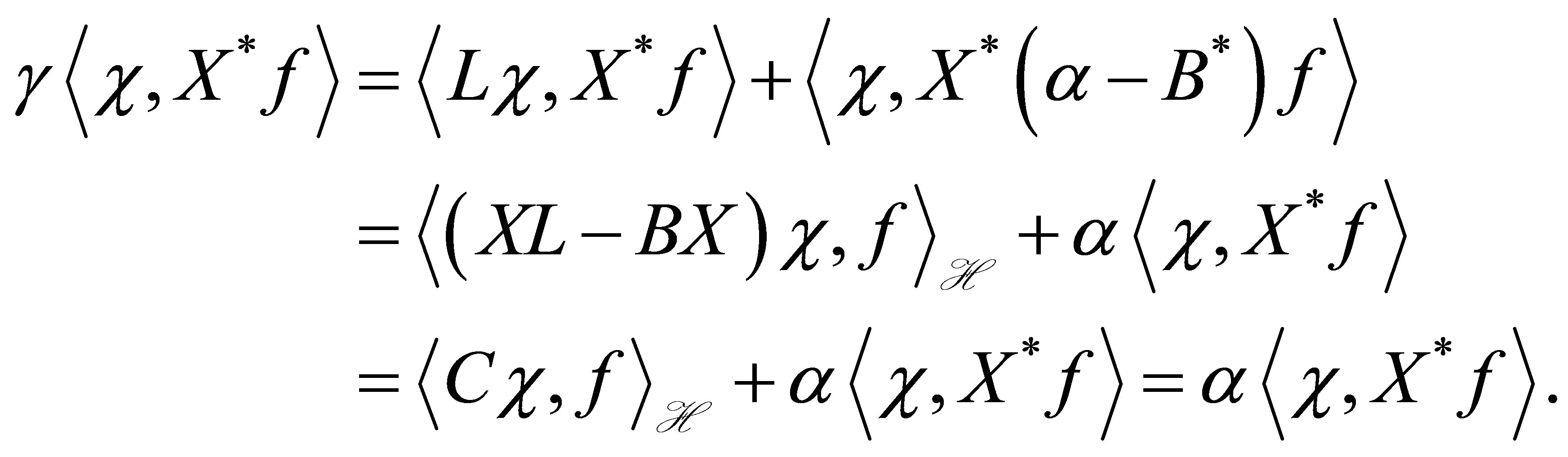
This implies that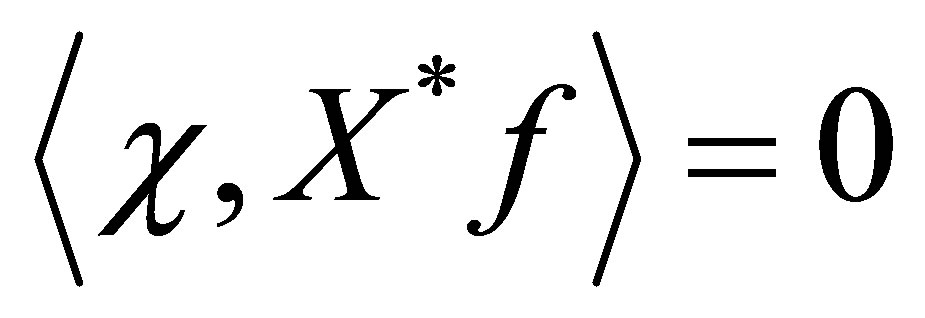 , or
, or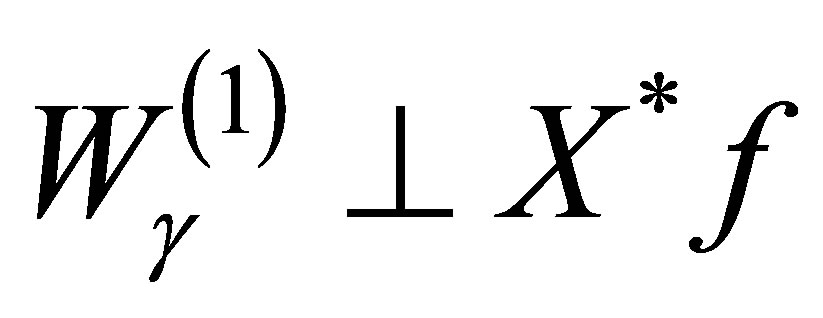 . Suppose then that
. Suppose then that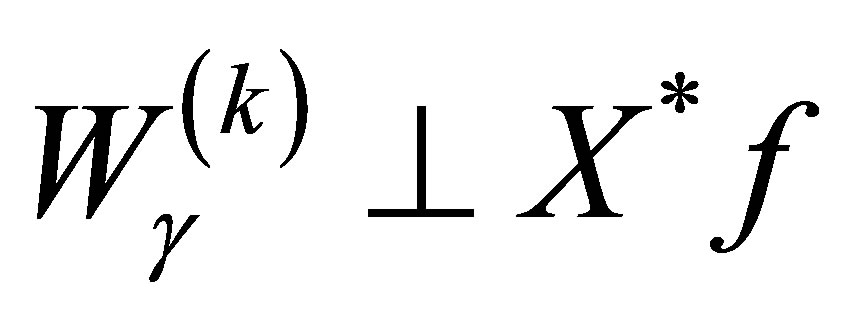 ,
,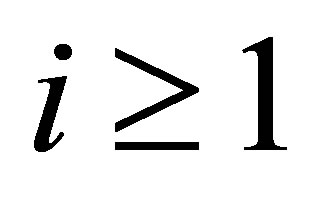 . For a
. For a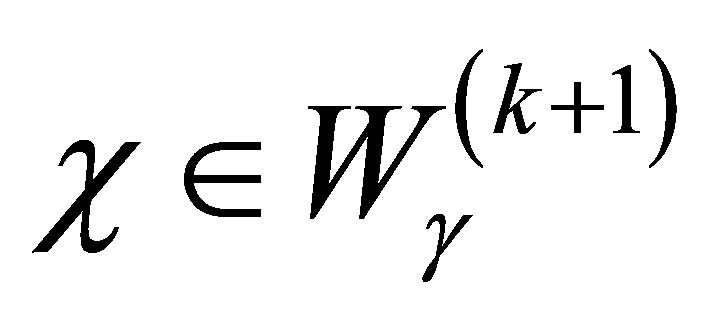 , the function
, the function 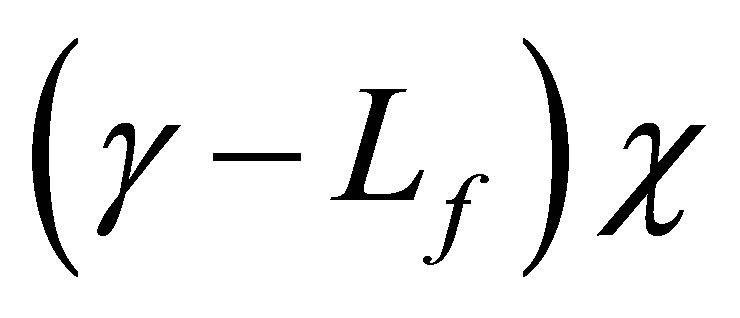 is in
is in , and
, and  . The same calculation as above immediately shows that
. The same calculation as above immediately shows that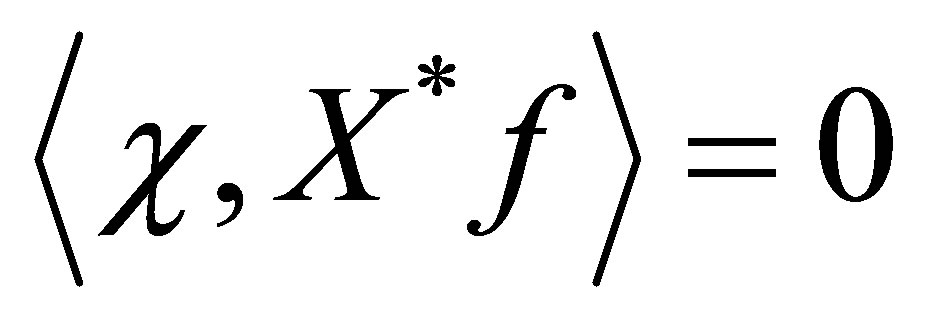 . Thus,
. Thus,
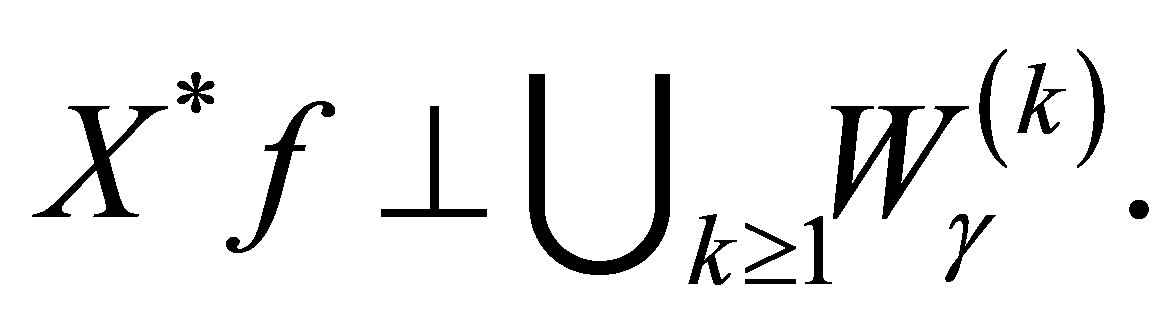 (27)
(27)
The integer 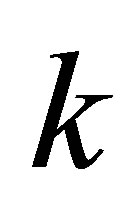 varies over a finite set of positive integers depending on
varies over a finite set of positive integers depending on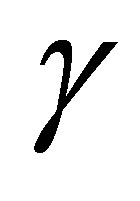 . Q.E.D.
. Q.E.D.
We now choose the actuators 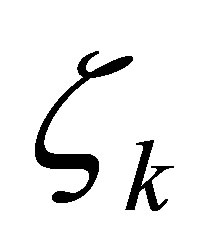 in (9) such that
in (9) such that
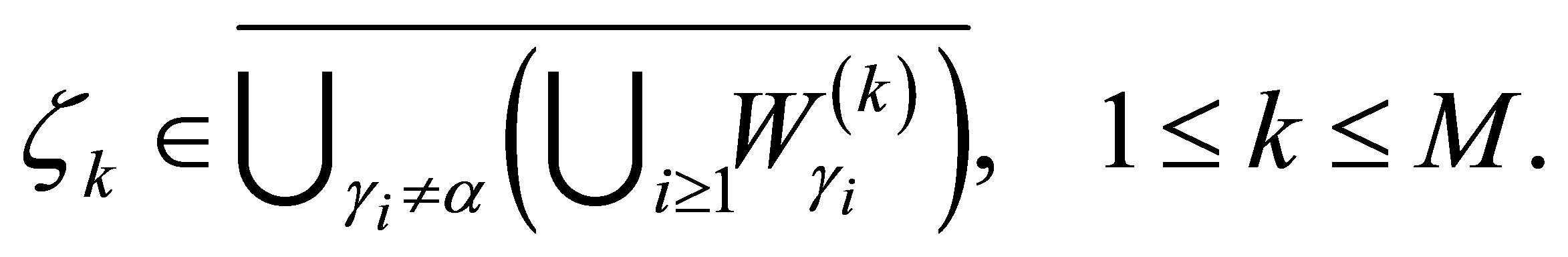 (28)
(28)
Then, 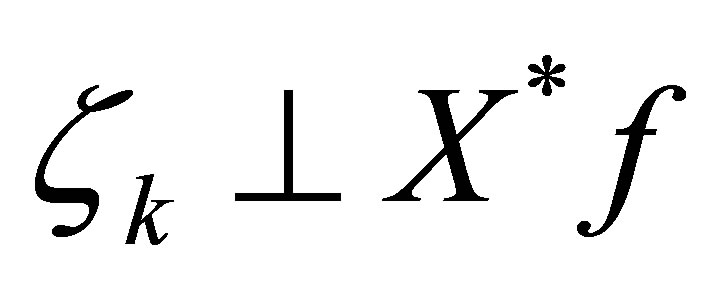 by the above proposition. All parameters except for
by the above proposition. All parameters except for 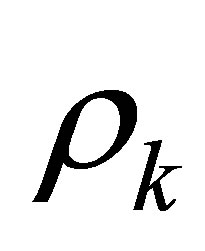 in (9) are determined.
in (9) are determined.
Rewrite the equation for  in (9) as
in (9) as
 (29)
(29)
Let us introduce an operator 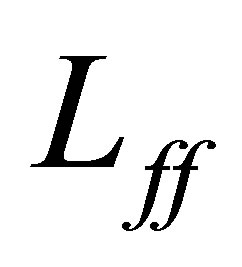 as
as
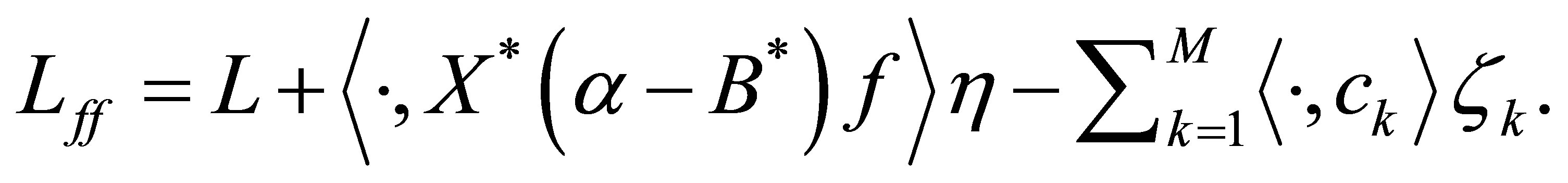
Let the integer 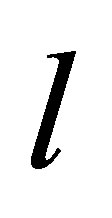 be such that
be such that . Then,
. Then, 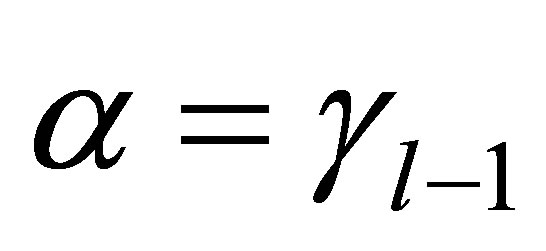 ,
, . The following proposition is just a simple version of the result in [17].
. The following proposition is just a simple version of the result in [17].
Proposition 3. Let 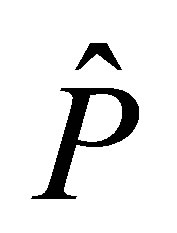 be the projector defined by
be the projector defined by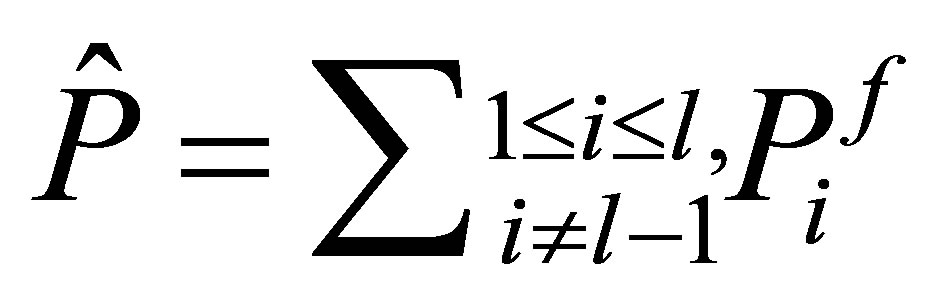 . Choose a
. Choose a 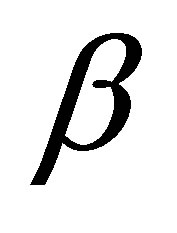 such that
such that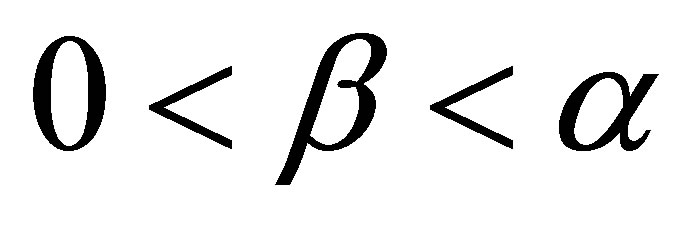 . Suppose that the pair
. Suppose that the pair 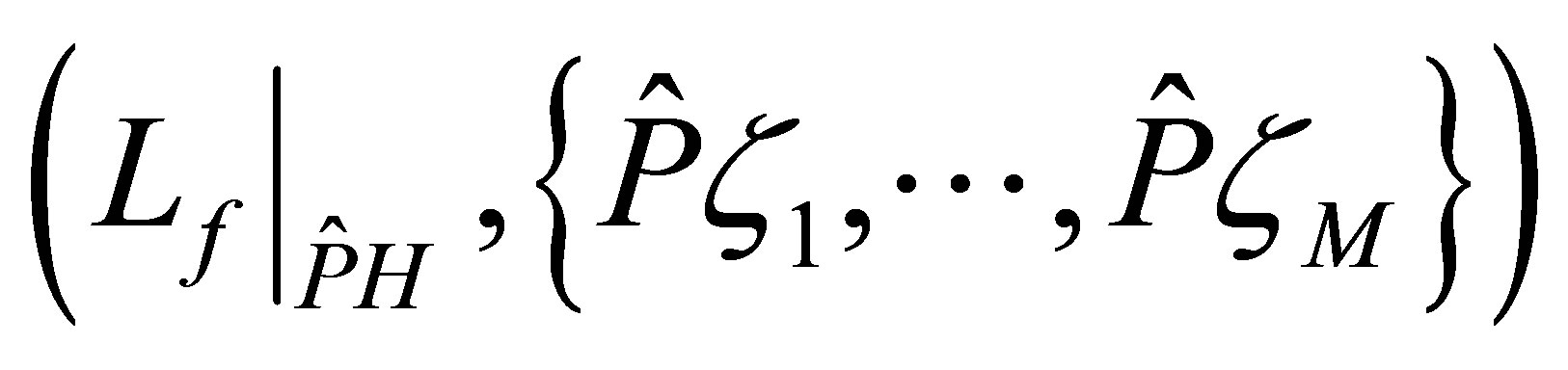 is a controllable one. Then we find
is a controllable one. Then we find 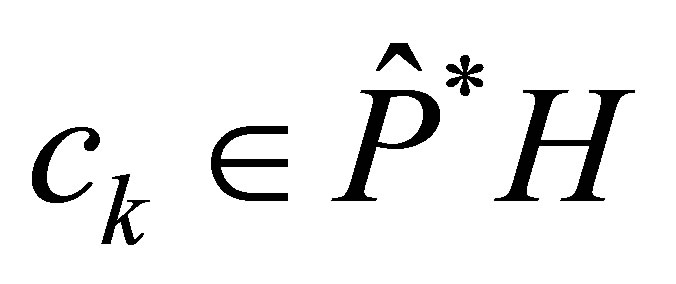 such that
such that
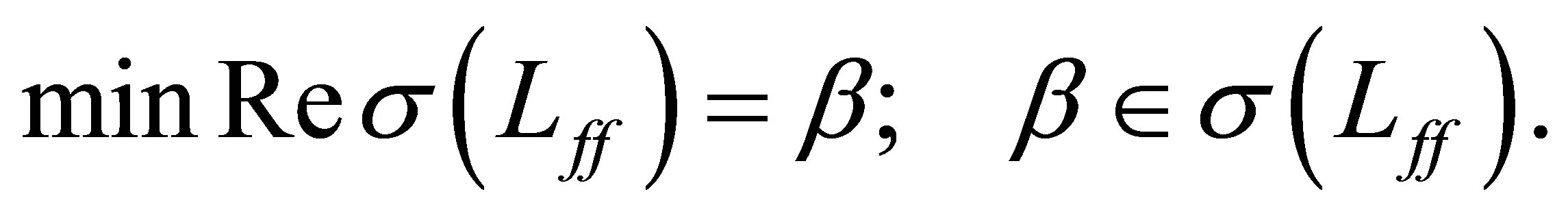
Thus, 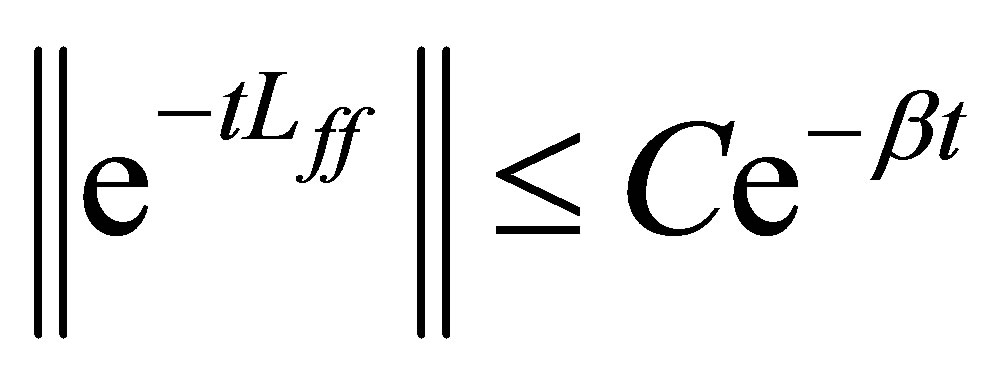 ,
, . We are ready to state the non-standard deay of solutions to Equation (9).
. We are ready to state the non-standard deay of solutions to Equation (9).
Theorem 4. Let 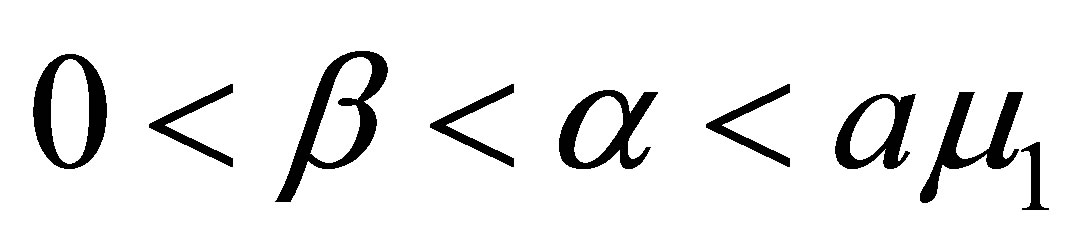 such that
such that . Suppose that
. Suppose that
1)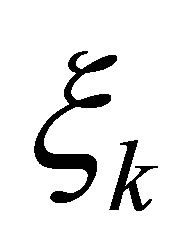 and
and 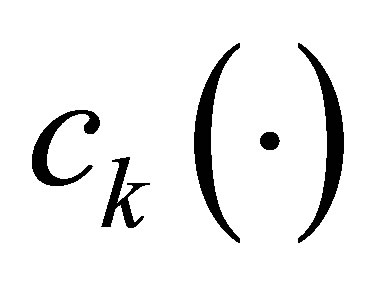 satisfy the rank conditions (18);
satisfy the rank conditions (18);
2)  is arbitrarily given;
is arbitrarily given;
3) 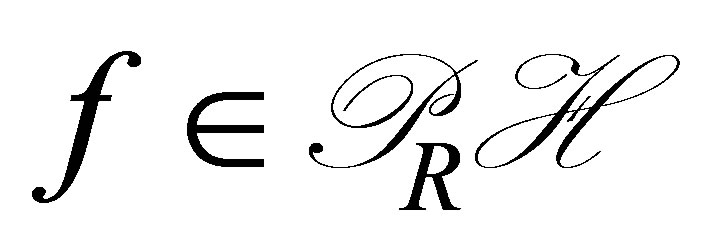 is chosen to satisfy (23); and 4)
is chosen to satisfy (23); and 4) 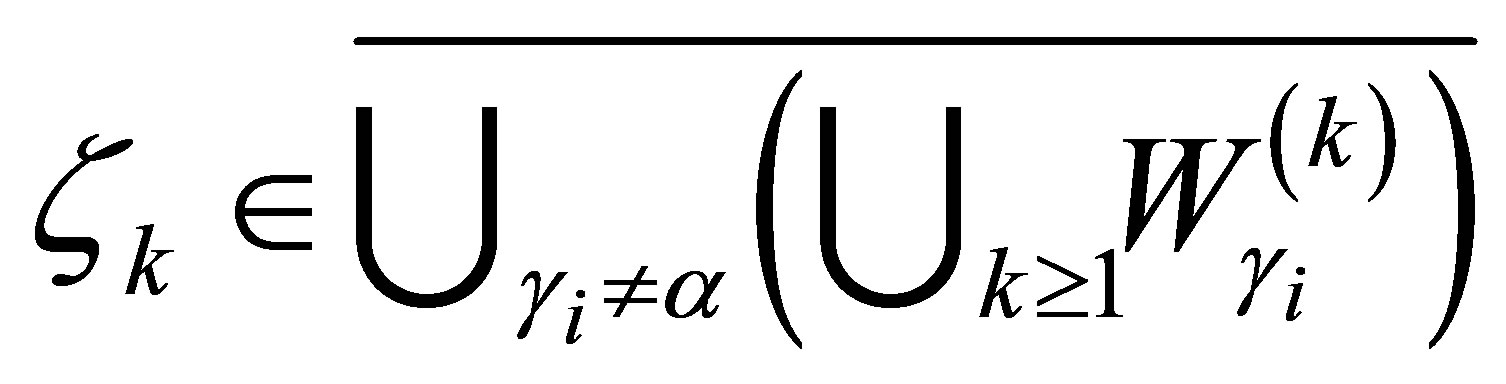 satisfiy the controllability condition in Proposition 3.
satisfiy the controllability condition in Proposition 3.
Then we find a large integer ; vectors
; vectors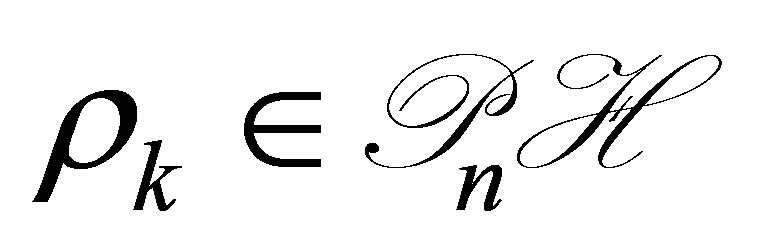 ; and a postive
; and a postive  close to
close to , and subsequently the control system in the product space
, and subsequently the control system in the product space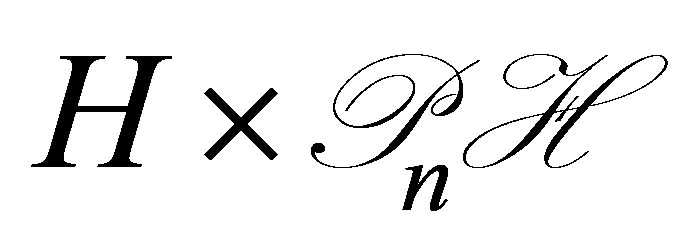 ;
;
 (30)
(30)
where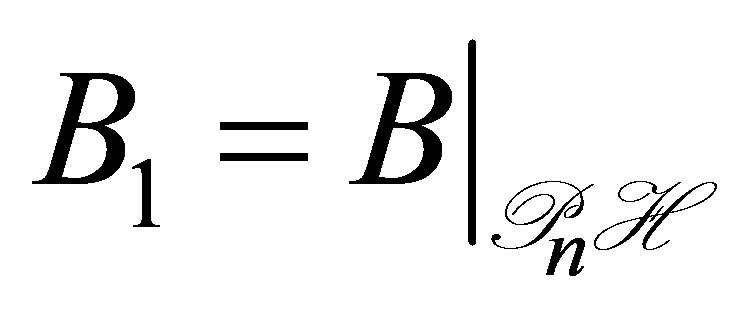 . Every solution
. Every solution 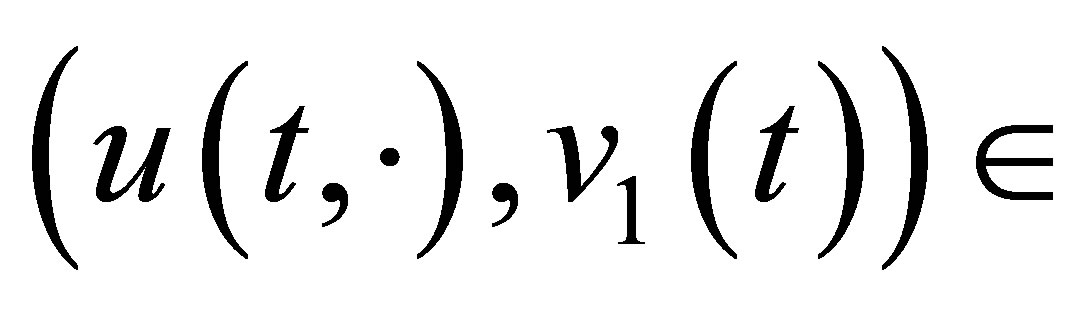
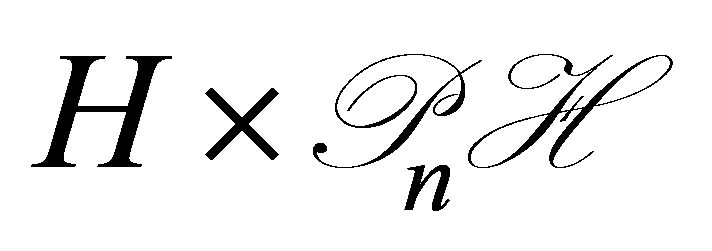 satisfies the decay estimate:
satisfies the decay estimate:
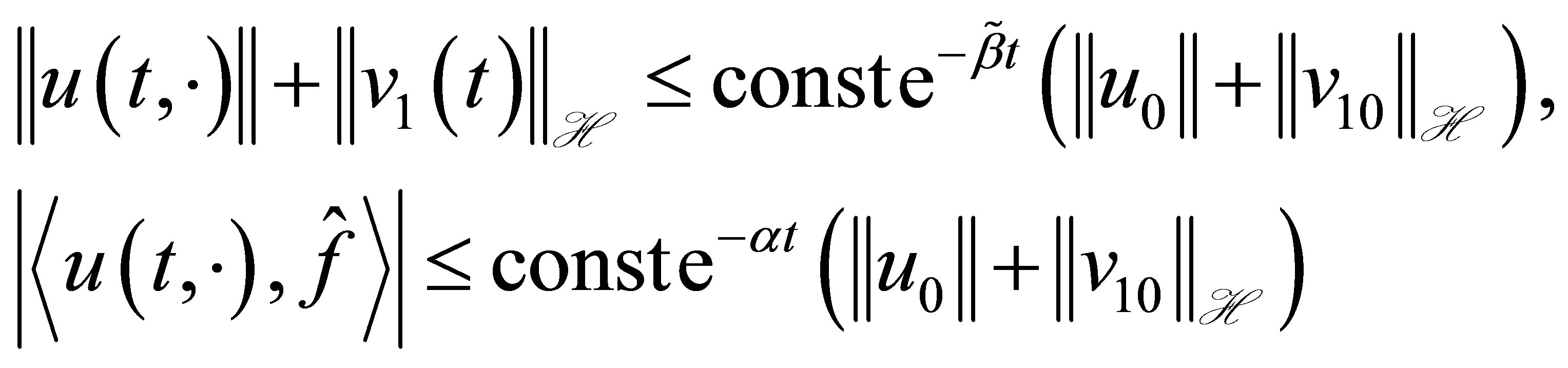 (31)
(31)
for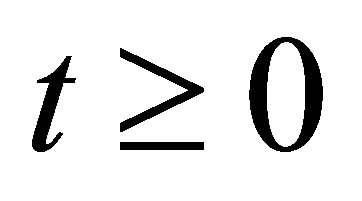 . The estimates for
. The estimates for  and
and 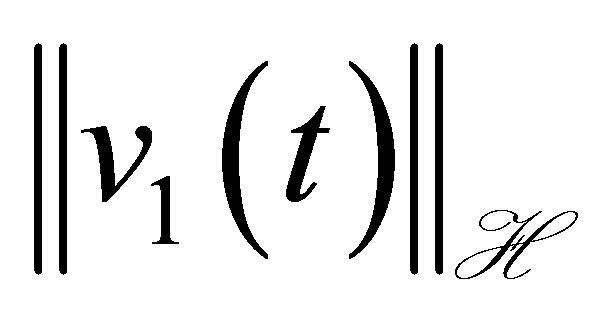 can be no longer improved.
can be no longer improved.
Proof. Choose the functions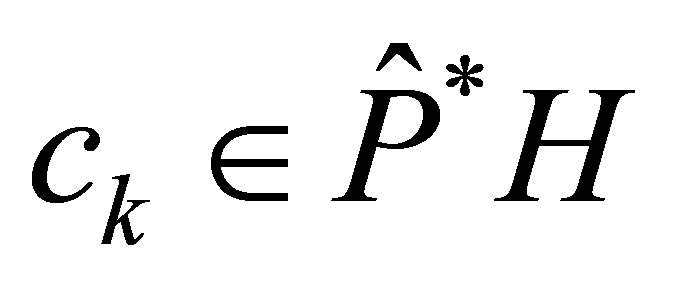 ,
, 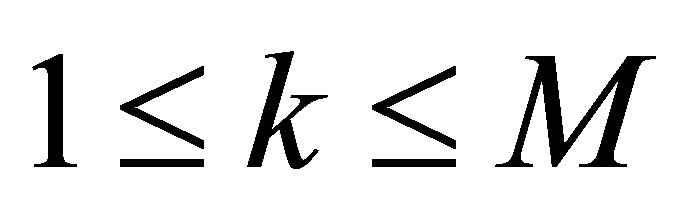 stated in Proposition 3. In view of Theorem 1, we find
stated in Proposition 3. In view of Theorem 1, we find 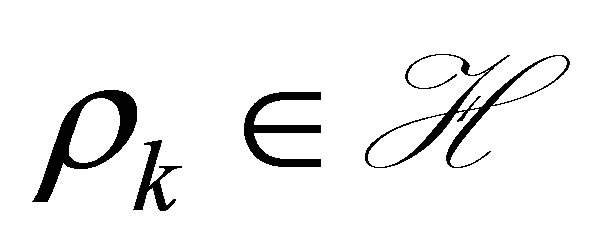 such that
such that 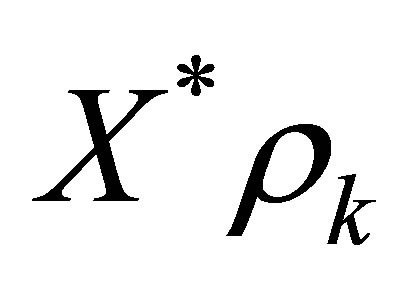 arbitrarily approximate
arbitrarily approximate  in the topology of
in the topology of . Since
. Since 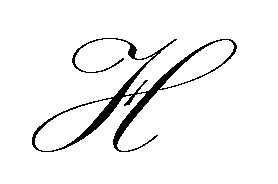 is separable, we may assume with no loss of generality that these
is separable, we may assume with no loss of generality that these 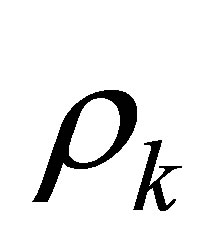 are constructed in
are constructed in  for an enough large
for an enough large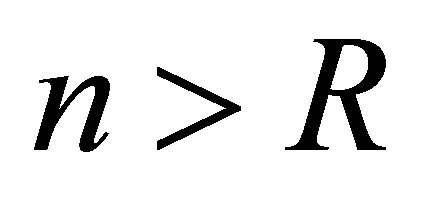 .
.
Let us consider the operator 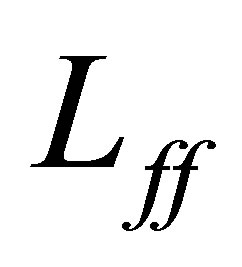 and the perturbed
and the perturbed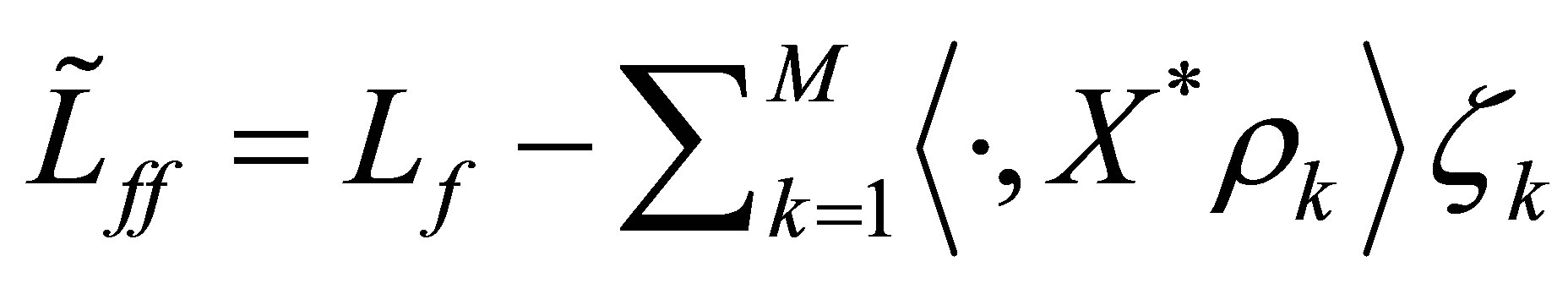 . The right-hand side of (29) is dominated by the decay estimate (22). Since
. The right-hand side of (29) is dominated by the decay estimate (22). Since  are chosen close to
are chosen close to , the semigroup
, the semigroup  is stable, and satisfies the standard estimate:
is stable, and satisfies the standard estimate:
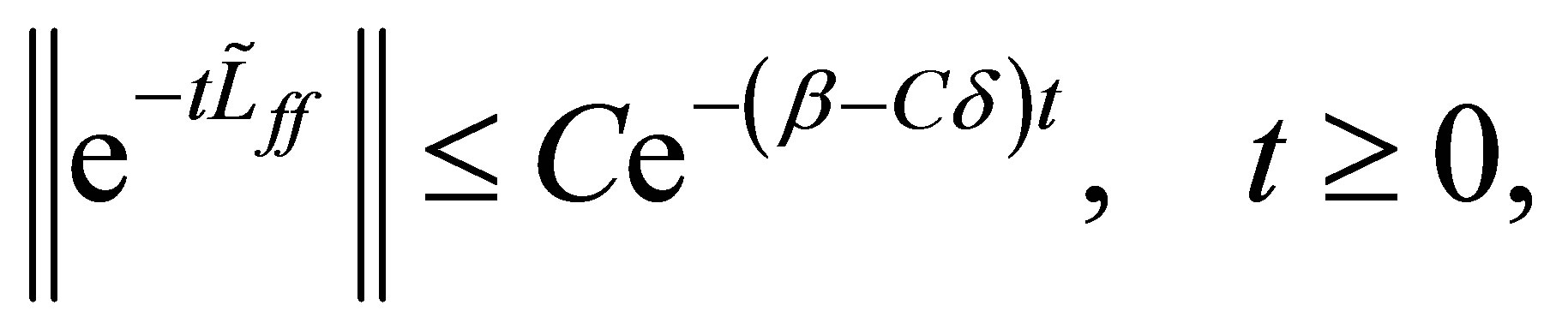 (32)
(32)
where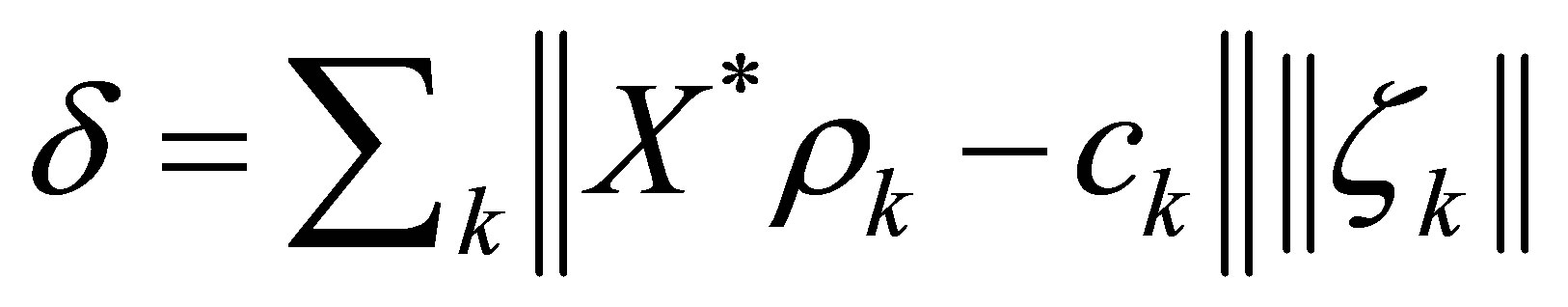 . Thus every solution
. Thus every solution  to Equation (9) satisfies the estimate:
to Equation (9) satisfies the estimate:
 (33)
(33)
where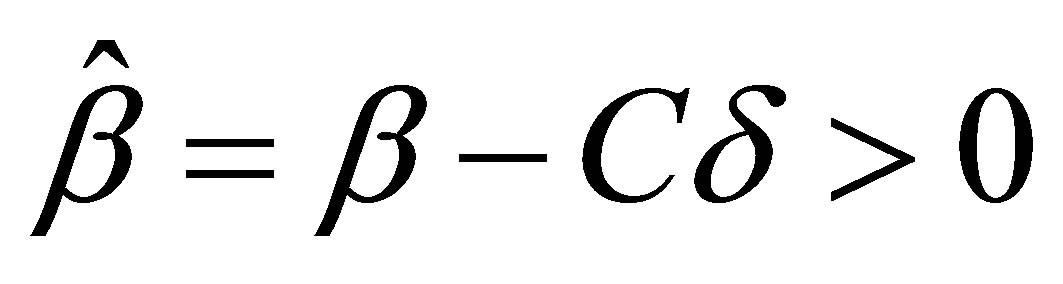 . The decay estimate for the functional
. The decay estimate for the functional 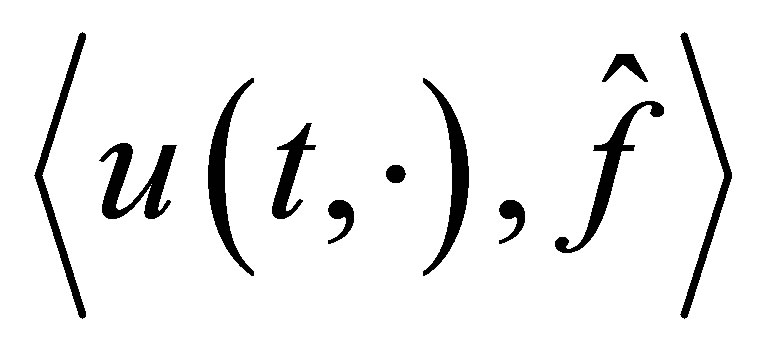 is already obtained in (25).
is already obtained in (25).
The control system (30) is derived in the following manner: Set , and apply the projector
, and apply the projector 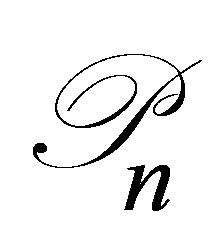 to the equation for
to the equation for 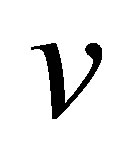 in (9). By noting that
in (9). By noting that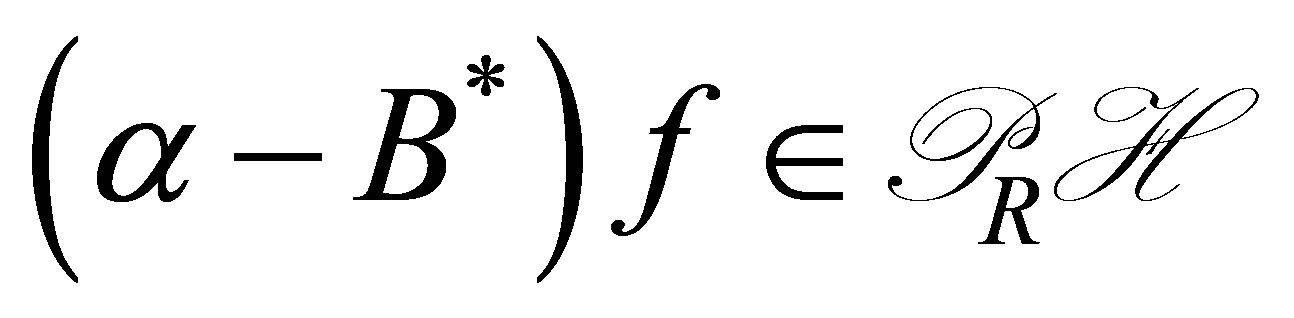 , then, (30) is immediately obtained. Equation (30) is clearly well posed in
, then, (30) is immediately obtained. Equation (30) is clearly well posed in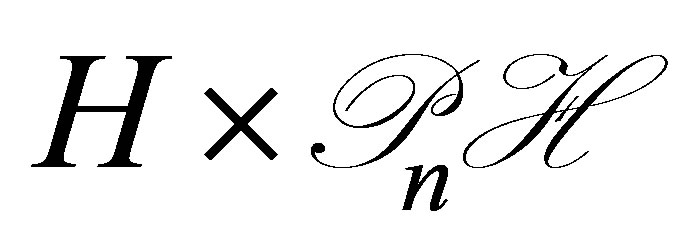 : Thus every solution to (30) is derived from the solution
: Thus every solution to (30) is derived from the solution 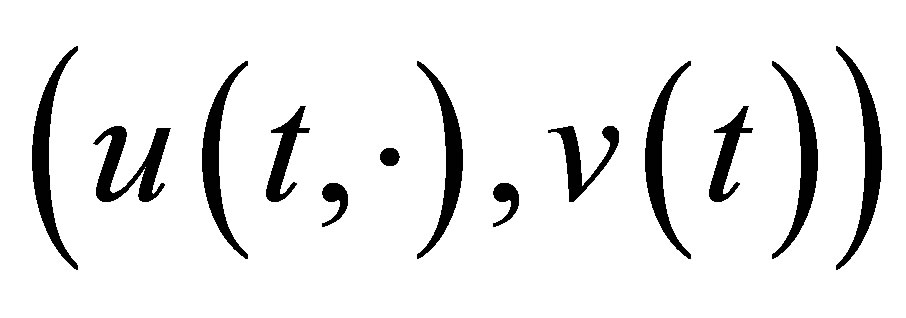 to (9) with initial value
to (9) with initial value 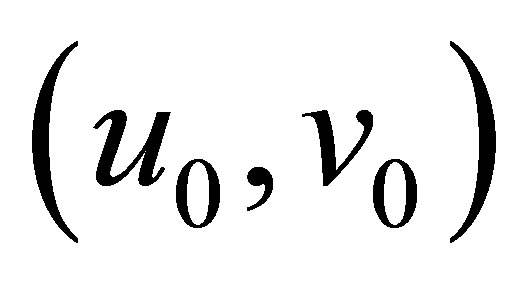 such that
such that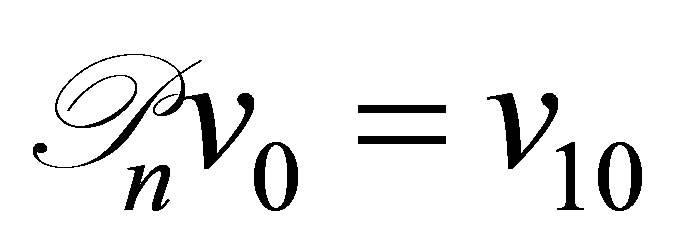 , by setting
, by setting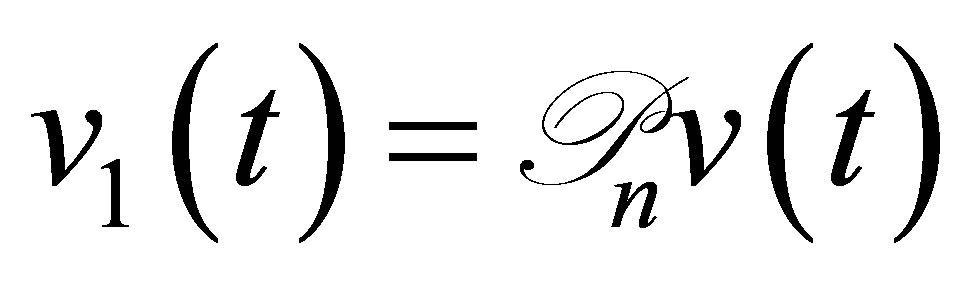 . Thus the first estimate of (31) is derived from (33). The second estimate of (31) is clear by (25).
. Thus the first estimate of (31) is derived from (33). The second estimate of (31) is clear by (25).
Finally we show that the first estimate of (31) for 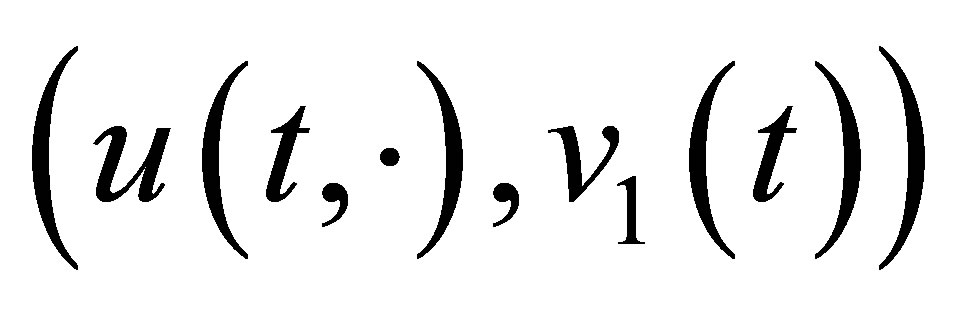 is no more improved. The spectrum
is no more improved. The spectrum 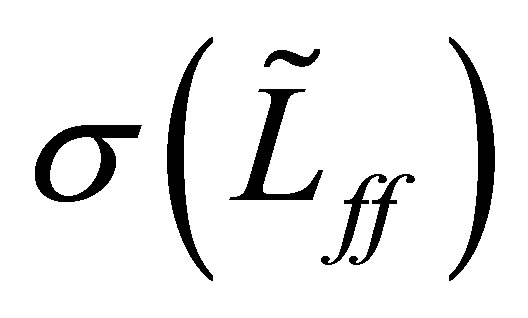 of the perturbed operator
of the perturbed operator  consists only of eigenvalues. It is expected that the value of
consists only of eigenvalues. It is expected that the value of 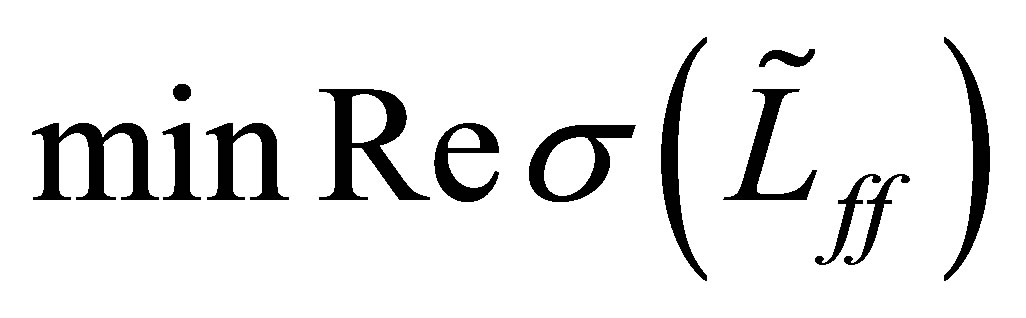 would be close to
would be close to  as long as
as long as 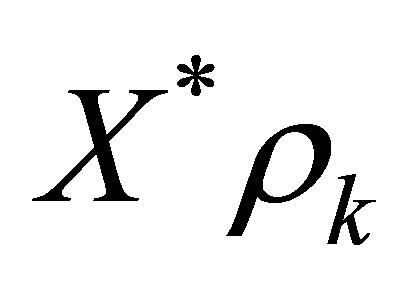 are close to
are close to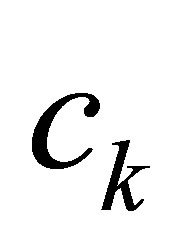 : When both
: When both  and
and  are selfadjoint, it is well known—via the min-max principle (see [18])—that each eigenvalue of
are selfadjoint, it is well known—via the min-max principle (see [18])—that each eigenvalue of 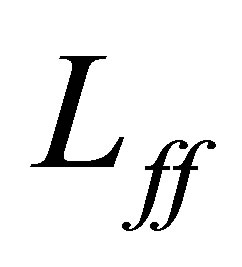 is continuous relative to the coefficient parameters. In our problem, the following result holds:
is continuous relative to the coefficient parameters. In our problem, the following result holds:
Proposition 5. The minimum of  is continuous relative to
is continuous relative to ,
,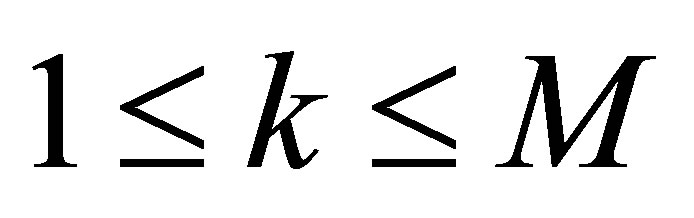 .
.
Proof. Set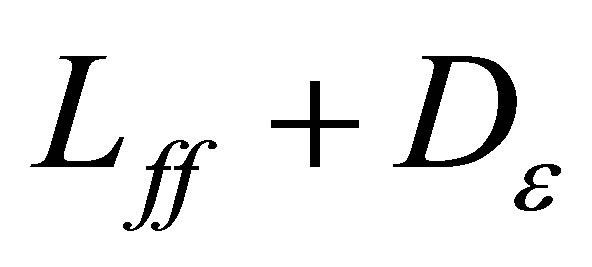
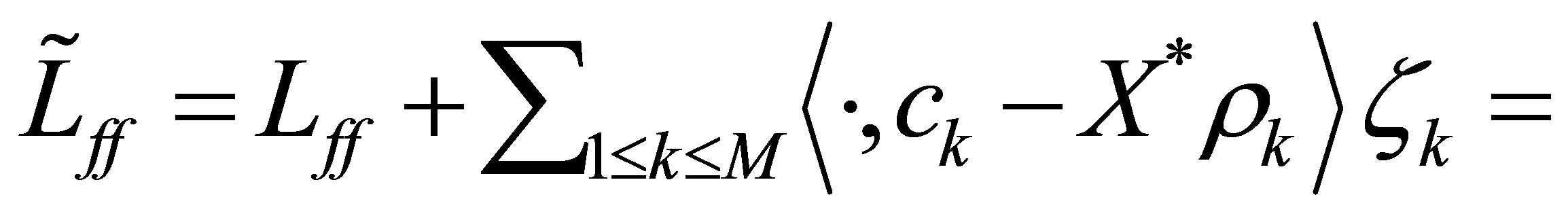 . In view of (32), the left half-plane:
. In view of (32), the left half-plane: 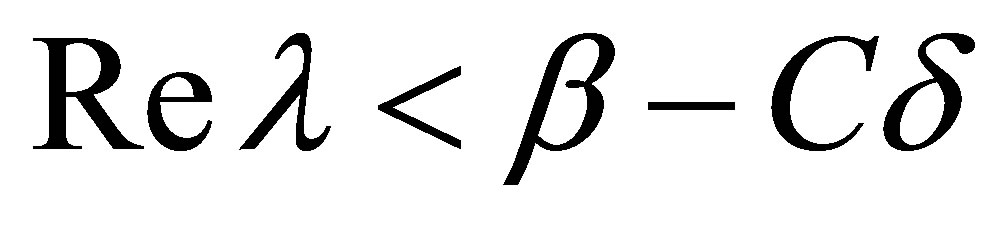 is contained in
is contained in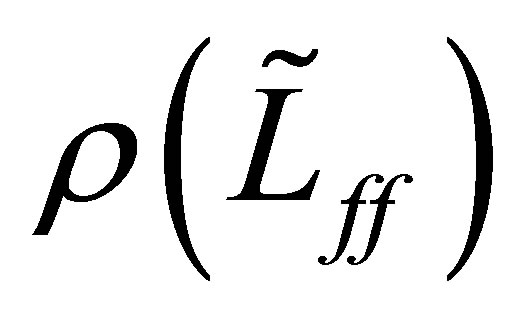 . Thus we see that
. Thus we see that 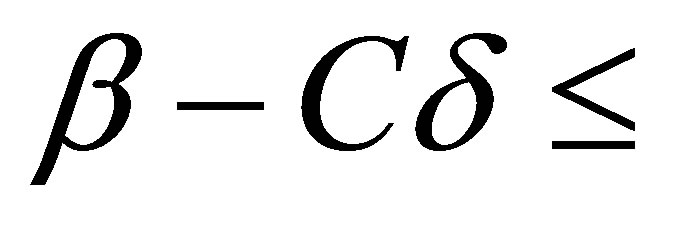
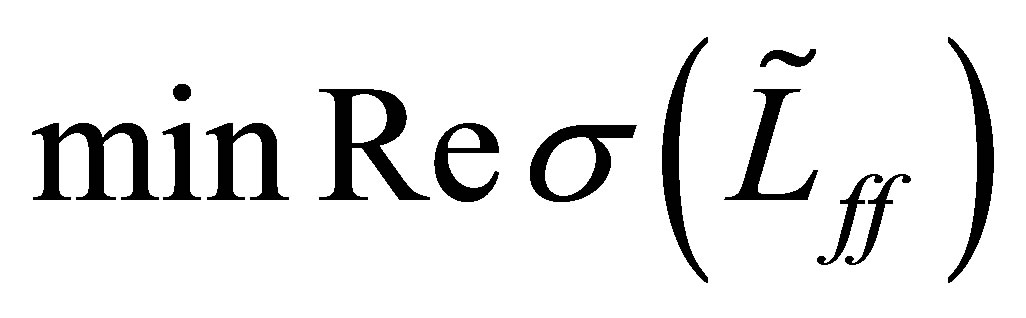 . Choose an
. Choose an 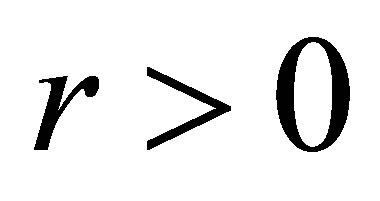 enough small so that
enough small so that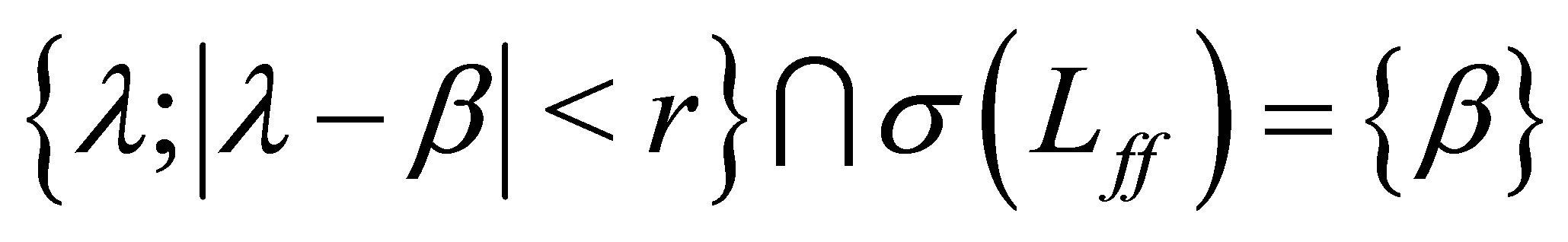 . Let
. Let  be the counterclockwise circle:
be the counterclockwise circle: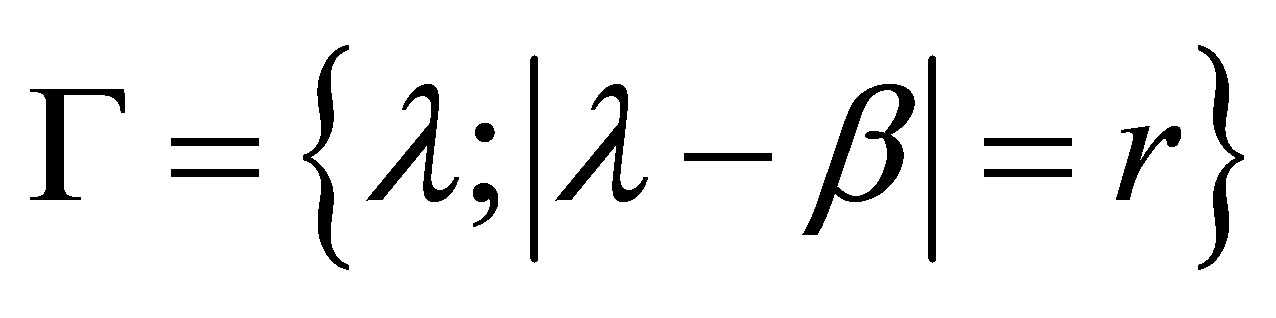 , and suppose that
, and suppose that
 for
for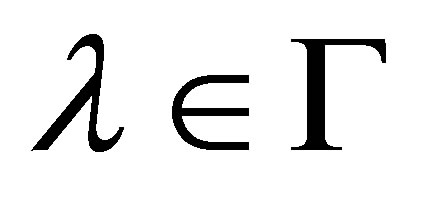 . Choose
. Choose 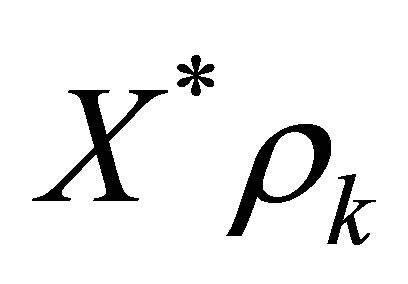 such that
such that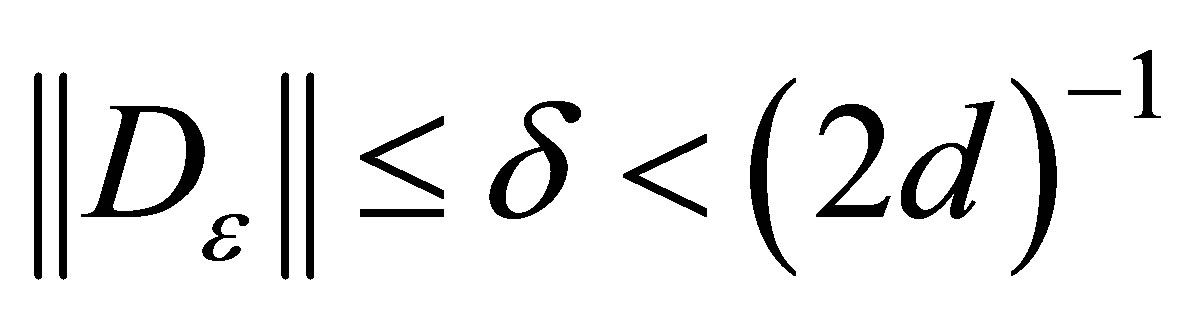 . Then,
. Then,  belongs to
belongs to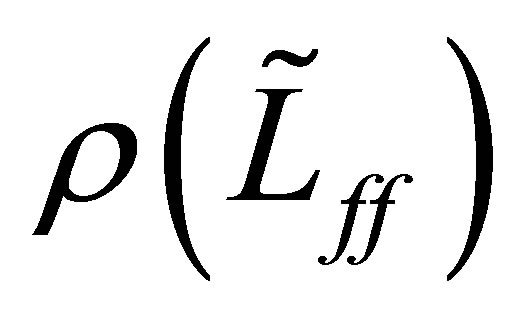 . In fact, we have the relation:
. In fact, we have the relation:
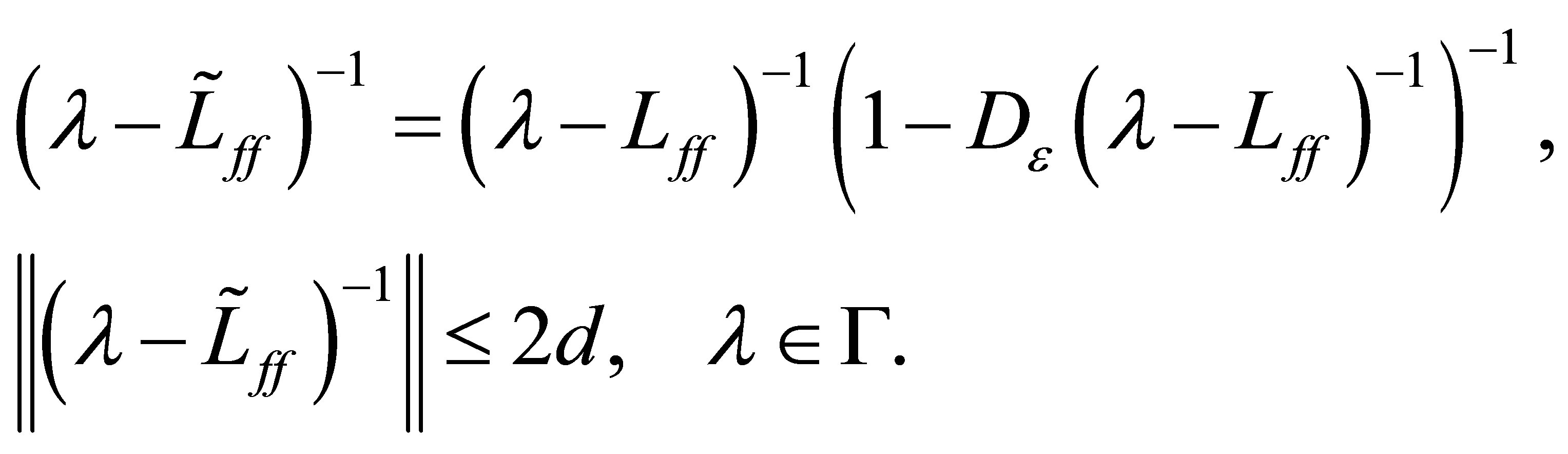 (34)
(34)
Recall that, for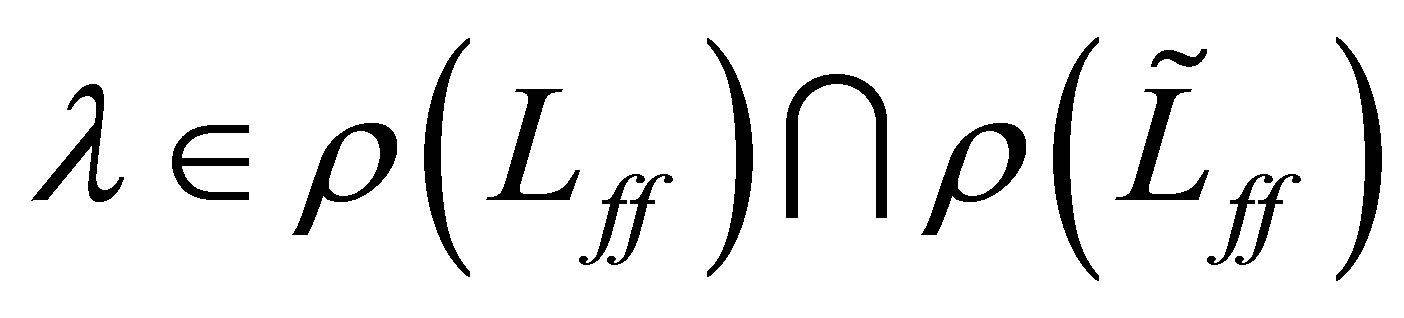 , the (second) resolvent equation:
, the (second) resolvent equation:
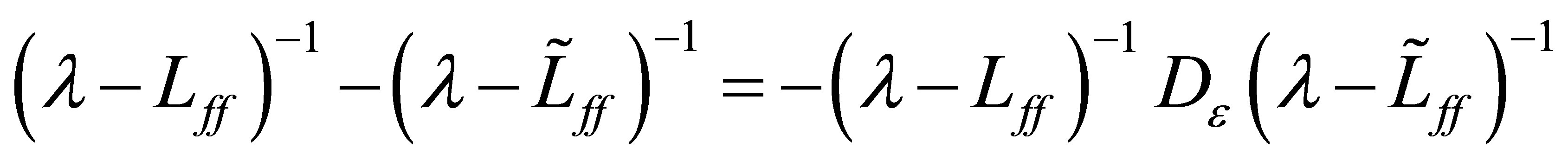
holds. Then we see that
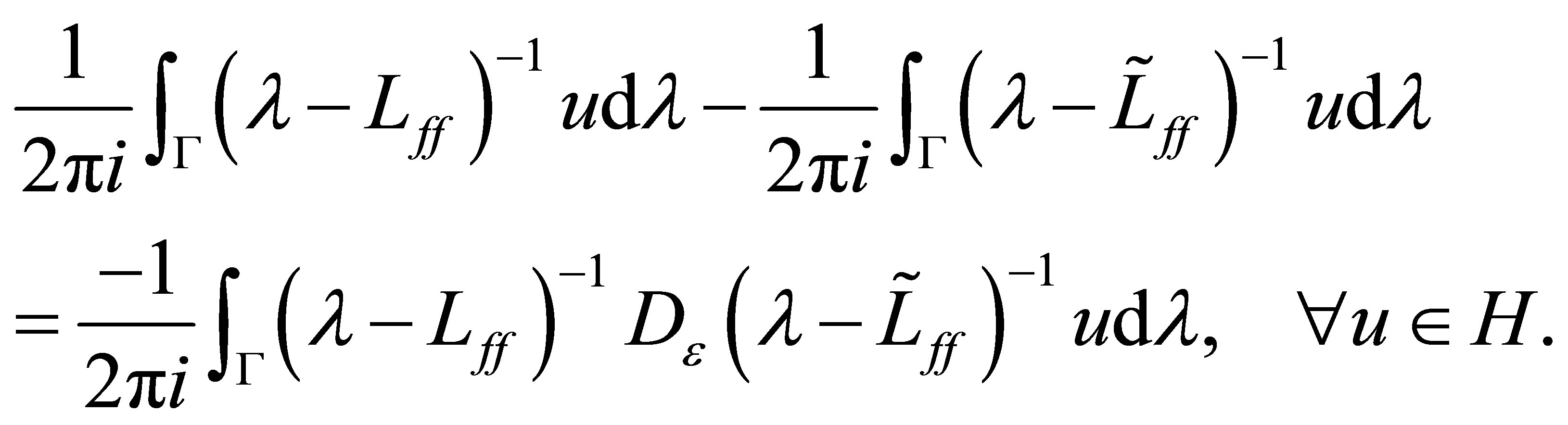 (35)
(35)
The first term of the above left-hand side of (35) is the projector, corresponding to the eigenvalue 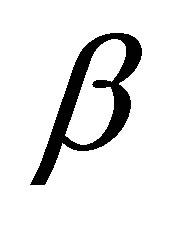 of
of . Choose
. Choose 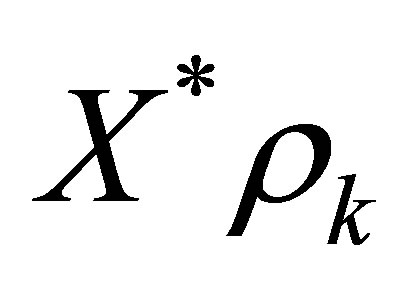 closer to
closer to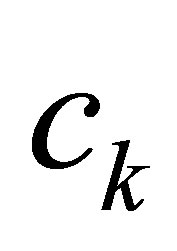 , if necessary, so that
, if necessary, so that

Supposing that 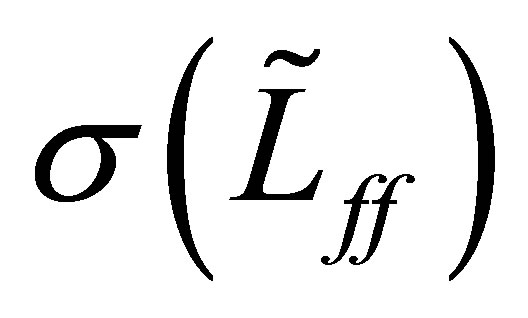 is contained in the half-plane:
is contained in the half-plane: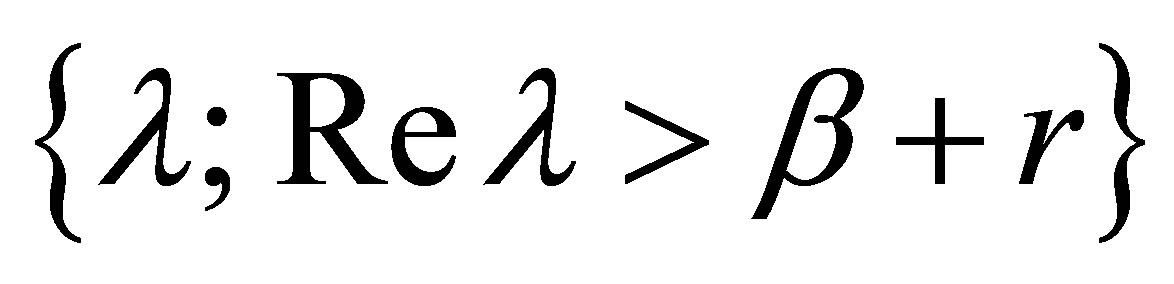 , we then derive a contradiction. If so, the resolvent
, we then derive a contradiction. If so, the resolvent 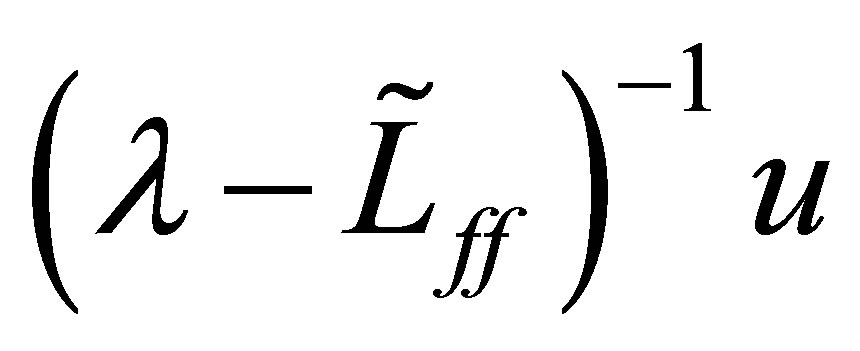 is analytic inside and on
is analytic inside and on . Thus the second term of the left-hand side of (35) must be equal to 0. Let
. Thus the second term of the left-hand side of (35) must be equal to 0. Let  be an eigenfunction of
be an eigenfunction of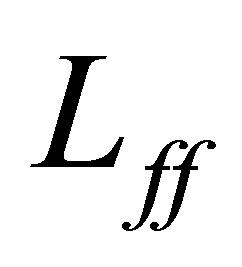 , corresponding to the eigenvalue
, corresponding to the eigenvalue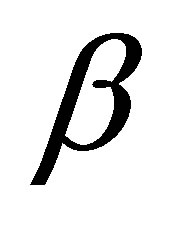 . Then,
. Then,
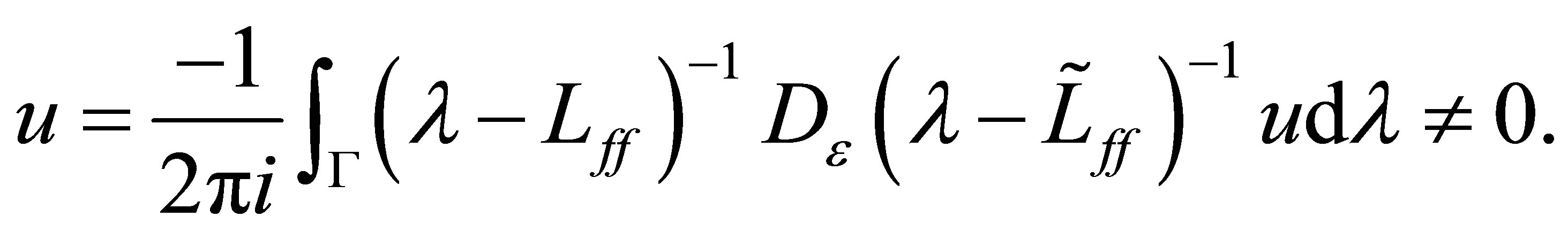
The right-hand side is, however, estimated as follows:
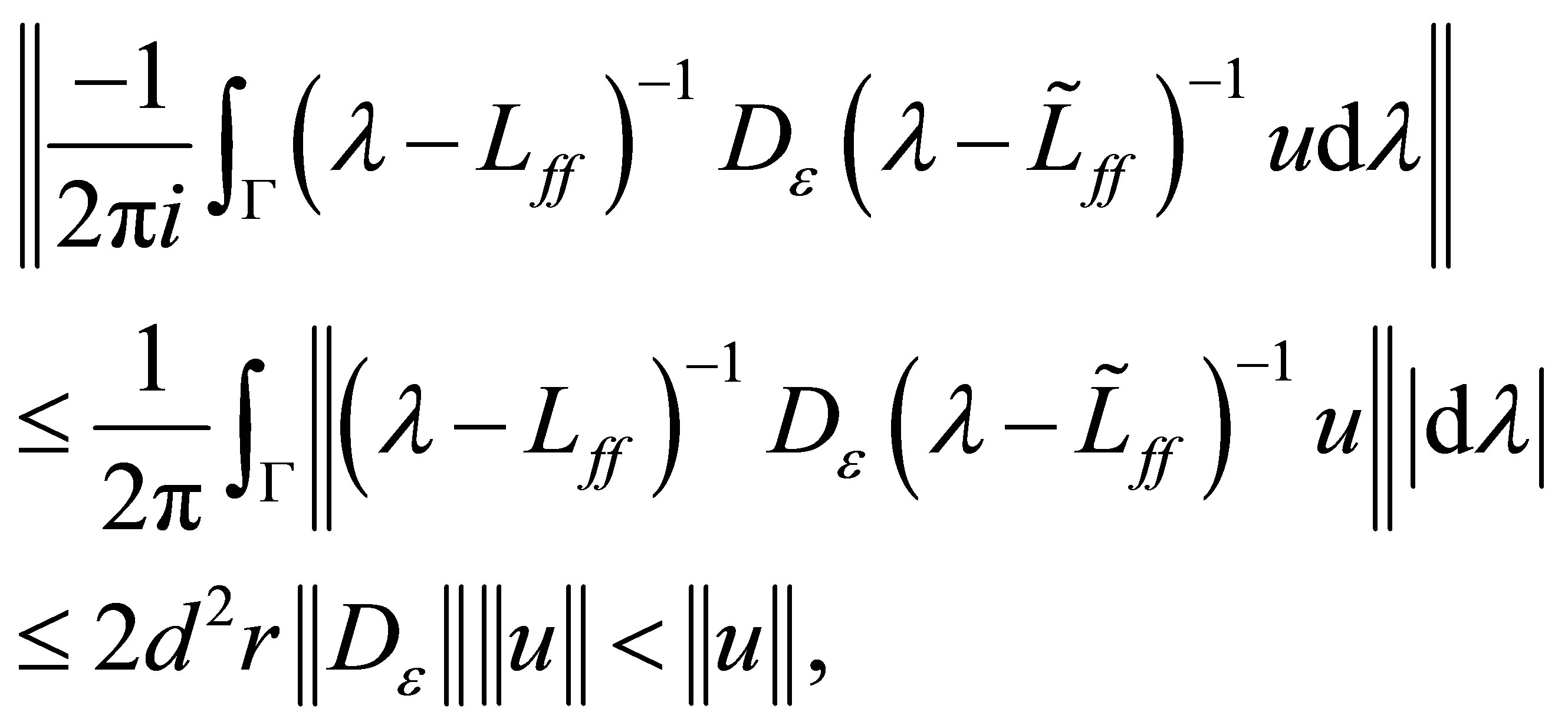
which is a contradiction. Therefore, the spectrum 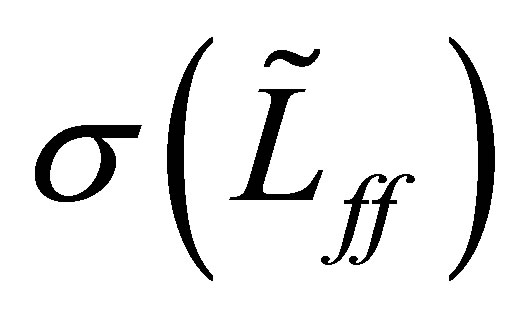 also lies in the left-half plane:
also lies in the left-half plane: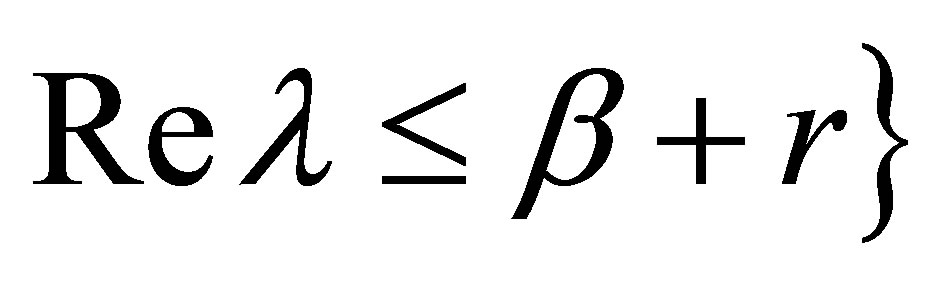
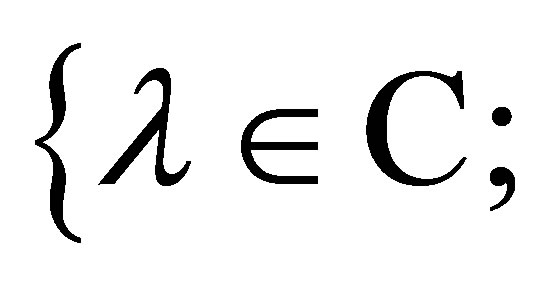 . As a conclusion, the minimum of
. As a conclusion, the minimum of 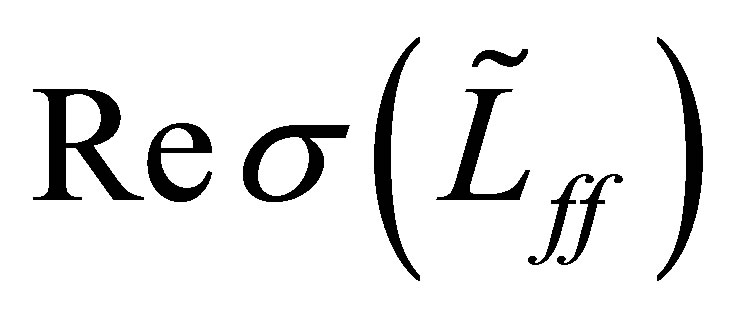 satisfies the estimate:
satisfies the estimate:
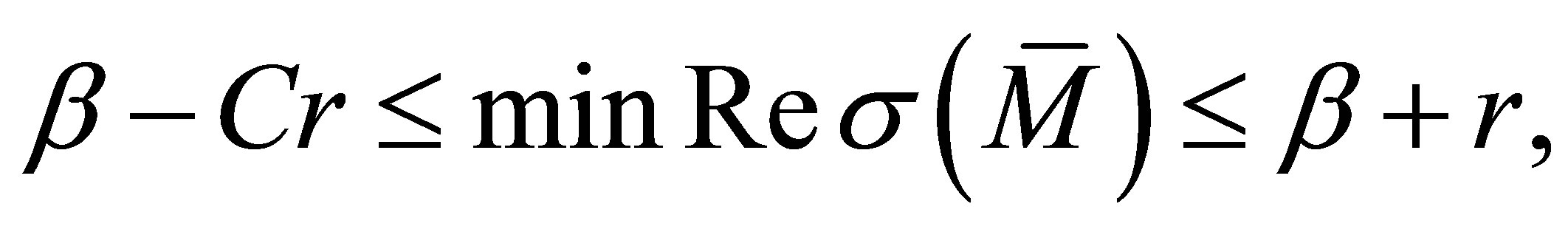
as long as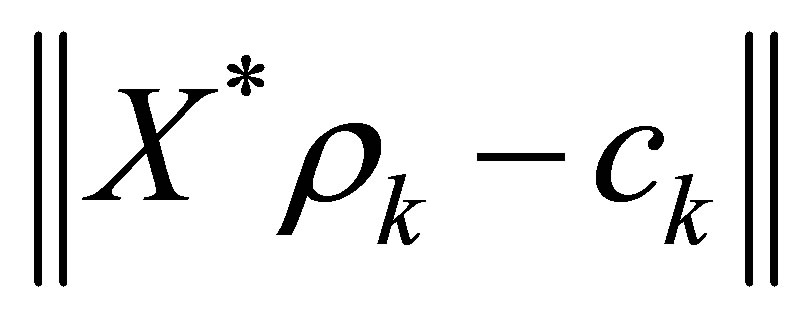 ,
, 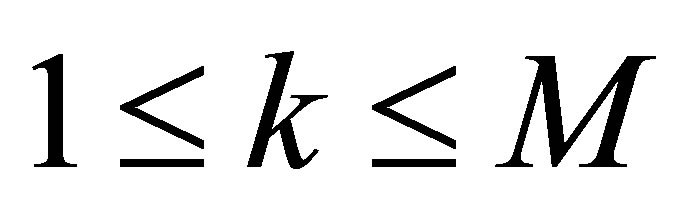 are small. Q.E.D.
are small. Q.E.D.
Let us turn to the proof of Theorem 4. Choose an 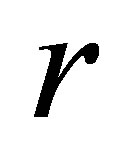 in Proposition 5 such that
in Proposition 5 such that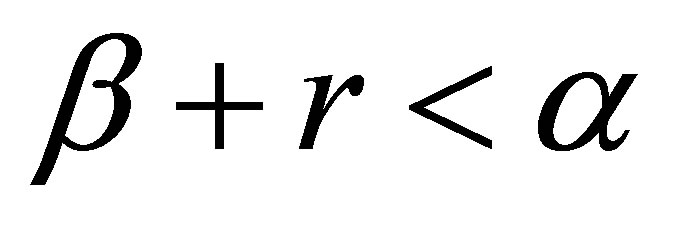 . Let
. Let 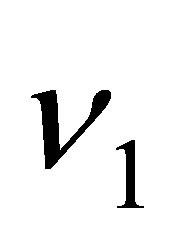 be the eigenvalue of
be the eigenvalue of 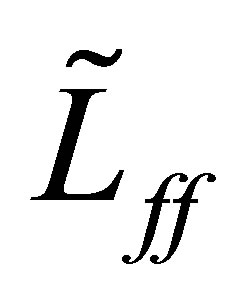 such that
such that , and
, and
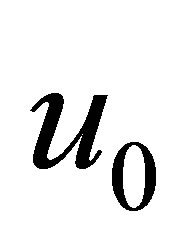 a corresponding eigenfunction:
a corresponding eigenfunction:
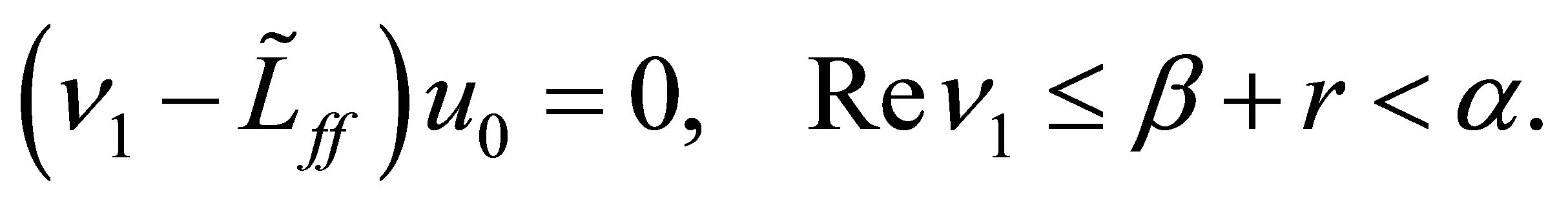
Set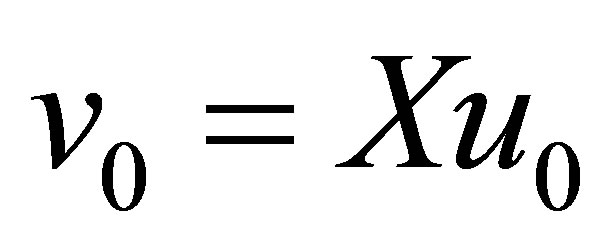 . As easily seen from Equation (29), the function
. As easily seen from Equation (29), the function 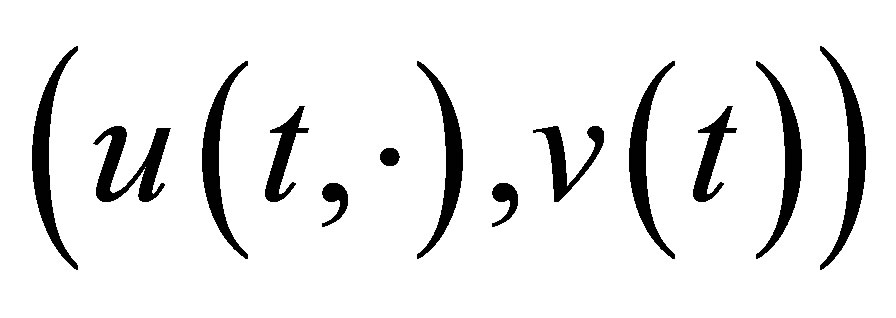 given by
given by

is the solution to Equation (9) with the initial value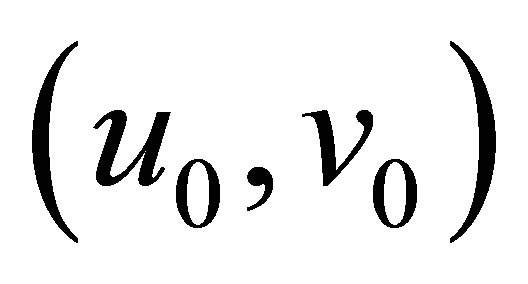 . In view of the reduction process to Equation (30), the function
. In view of the reduction process to Equation (30), the function 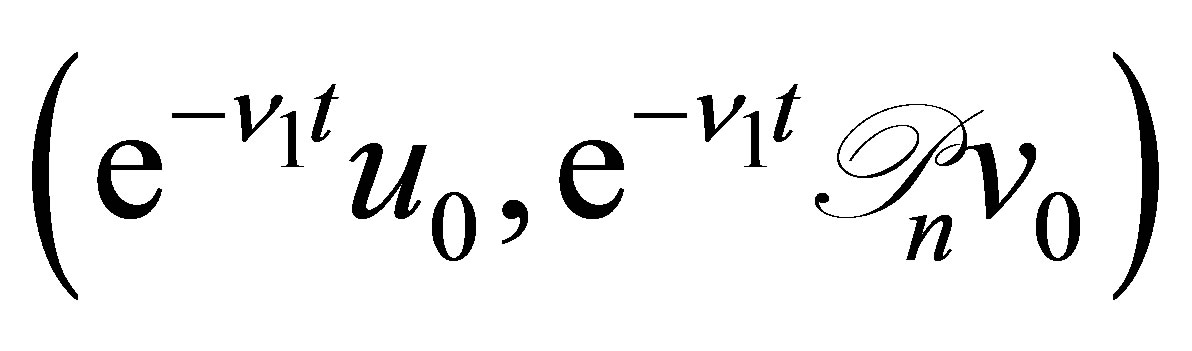 is thus a non-trivial solution to (30). This shows that the decay (31) for
is thus a non-trivial solution to (30). This shows that the decay (31) for 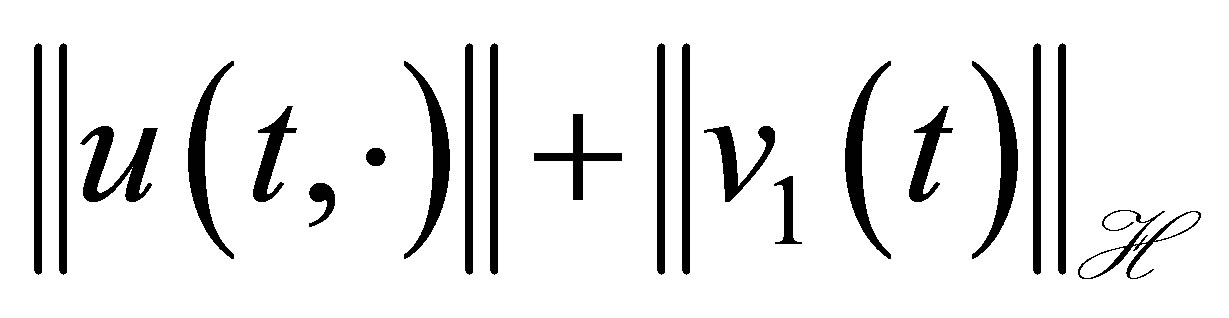 is no longer improved. This finishes the proof of Theorem 4. Q.E.D.
is no longer improved. This finishes the proof of Theorem 4. Q.E.D.
Example. In (1), let us consider the case where  is a bounded interval
is a bounded interval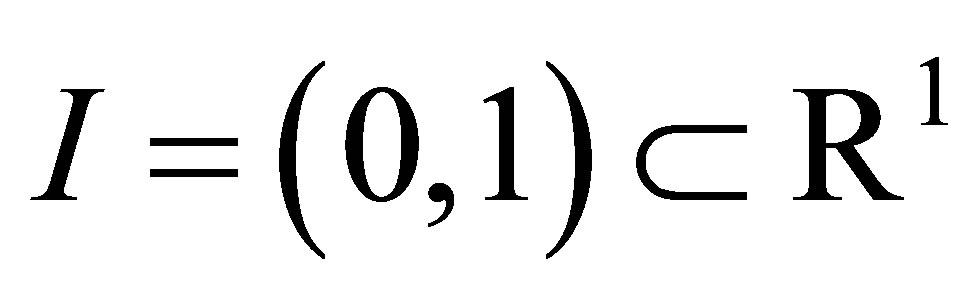 . The pair of differential operators
. The pair of differential operators  is then rewritten as
is then rewritten as
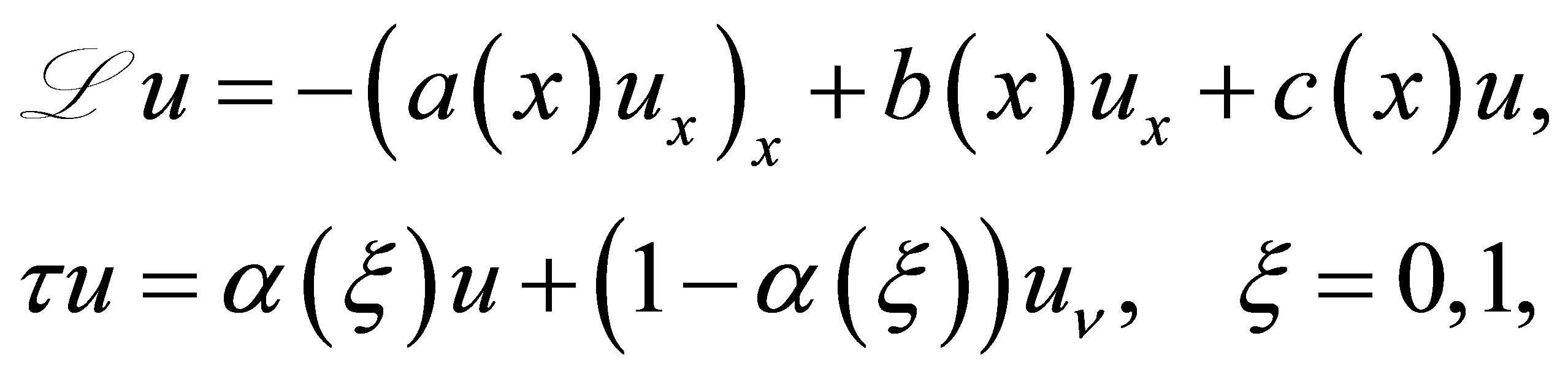 (36)
(36)
where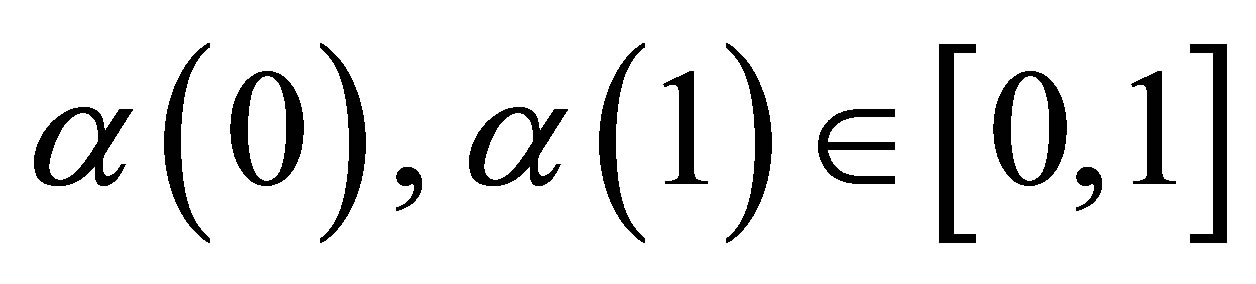 , and
, and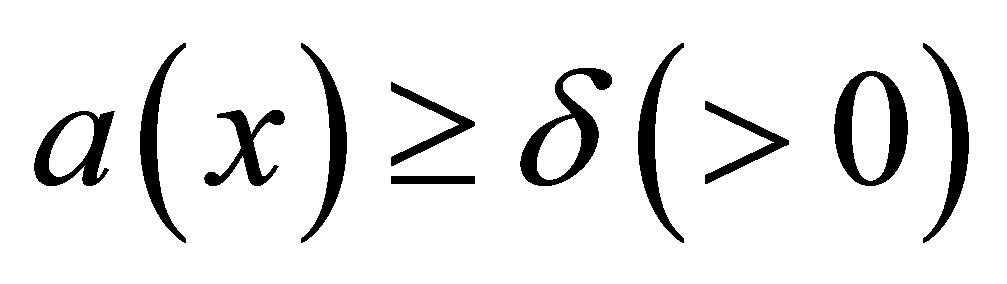 . Let
. Let 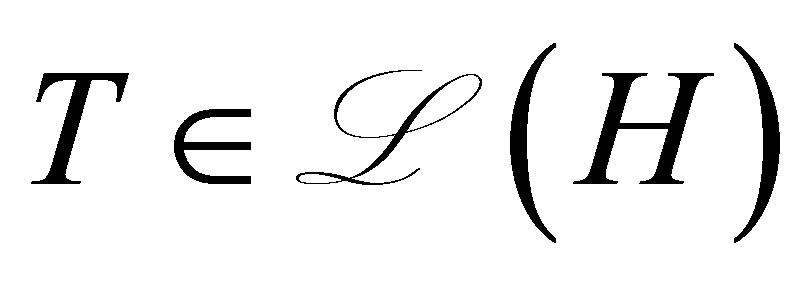 be an operator defined, for
be an operator defined, for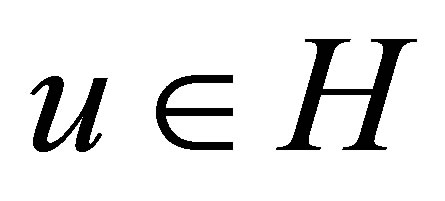 , by
, by

Clearly 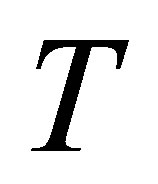 defines an isomorphism in
defines an isomorphism in . Let us consider the case where
. Let us consider the case where  is of the third kind, i.e.,
is of the third kind, i.e.,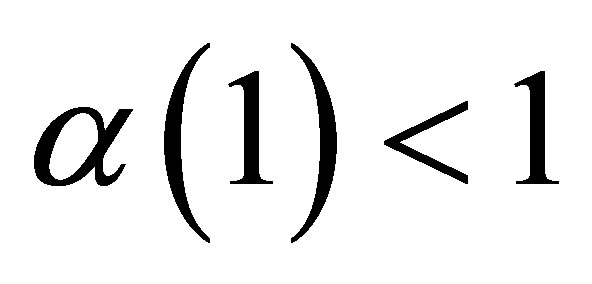
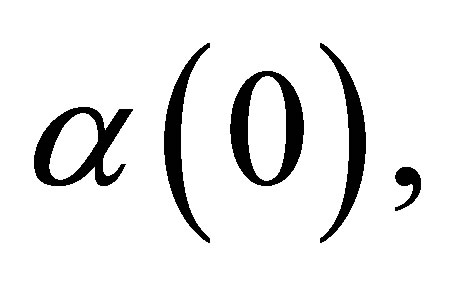 . Then,
. Then, 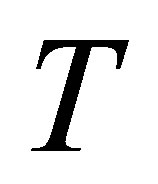 transforms
transforms 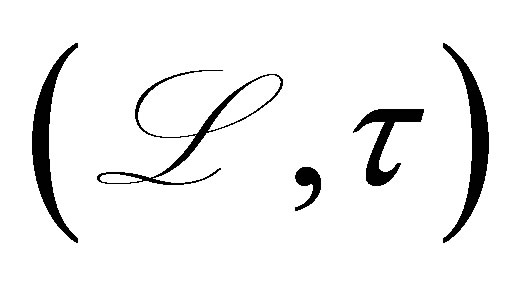 into another pair
into another pair , which defines a self-adjoint operator
, which defines a self-adjoint operator 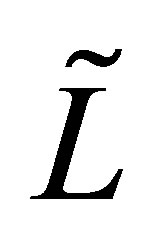 with dense domain
with dense domain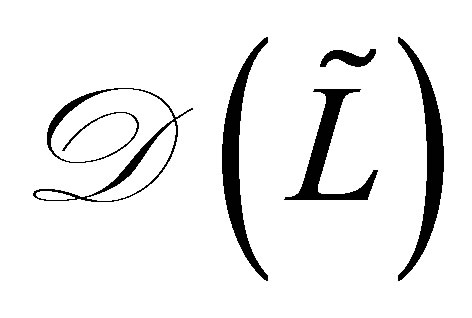 . In
. In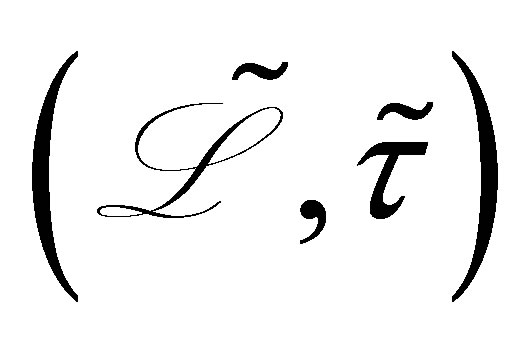 ,
,  is unchanged;
is unchanged;  and
and  are changed, respectively, to 0 and
are changed, respectively, to 0 and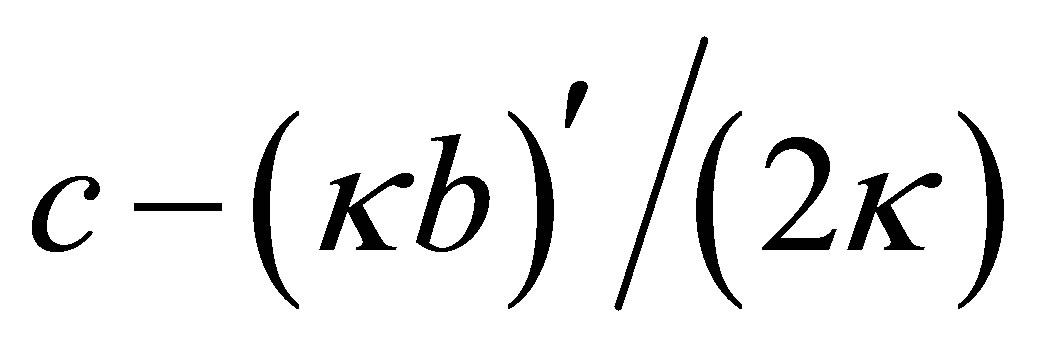 ; and
; and  of the third kind. The idea is a slightly modified version of the well known result (see page 292 of [18]). Based on this, we have
of the third kind. The idea is a slightly modified version of the well known result (see page 292 of [18]). Based on this, we have
Proposition 6. 1) The spectrum 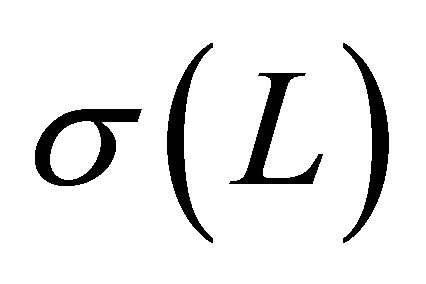 consists of real and simple eigenvalues:
consists of real and simple eigenvalues: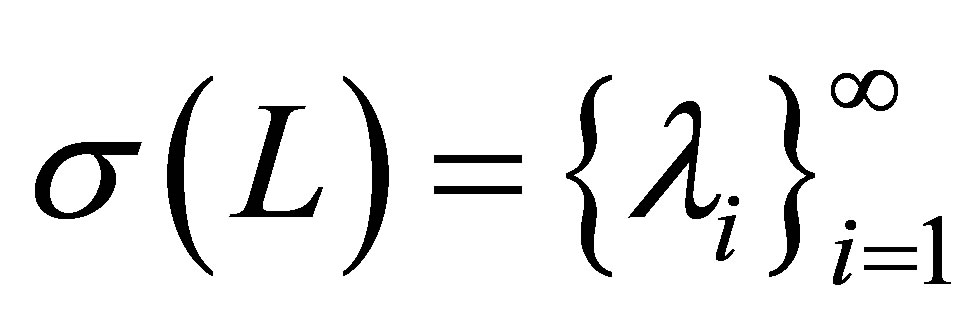 ,
,
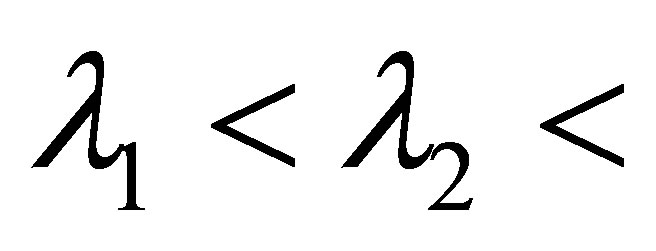 .
.
2) The eigenfunctions 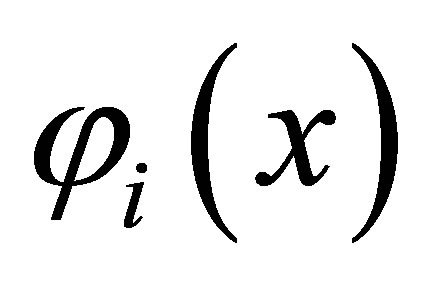 of
of 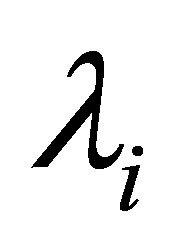 forms a Riesz basis. Any
forms a Riesz basis. Any 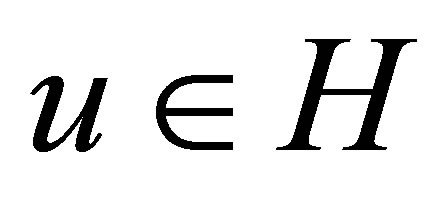 is uniquely expressed as
is uniquely expressed as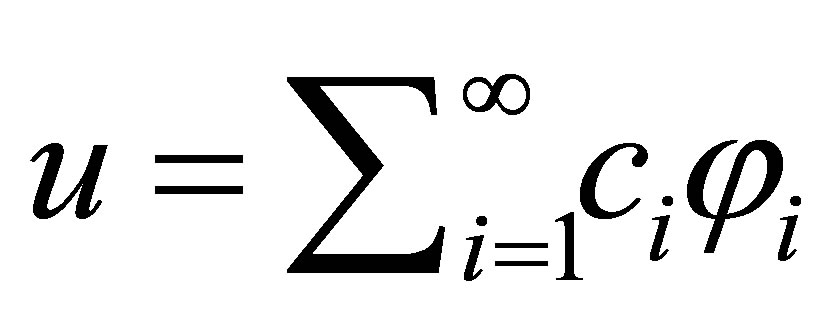 .
.
In our problem, we know that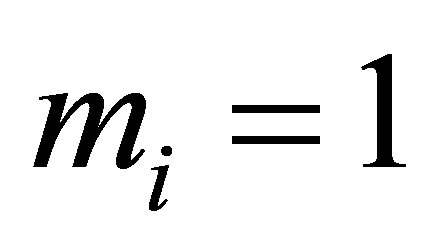 ,
,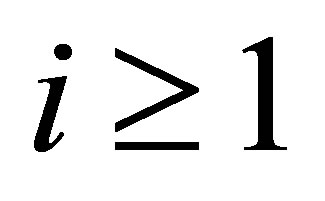 . Thus we choose
. Thus we choose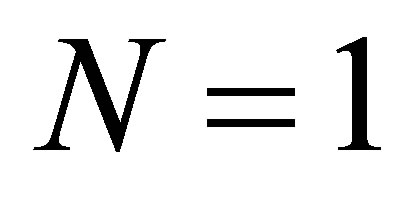 , so that the output of the system is a single observation at the end point
, so that the output of the system is a single observation at the end point 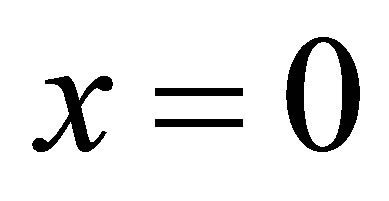 as
as
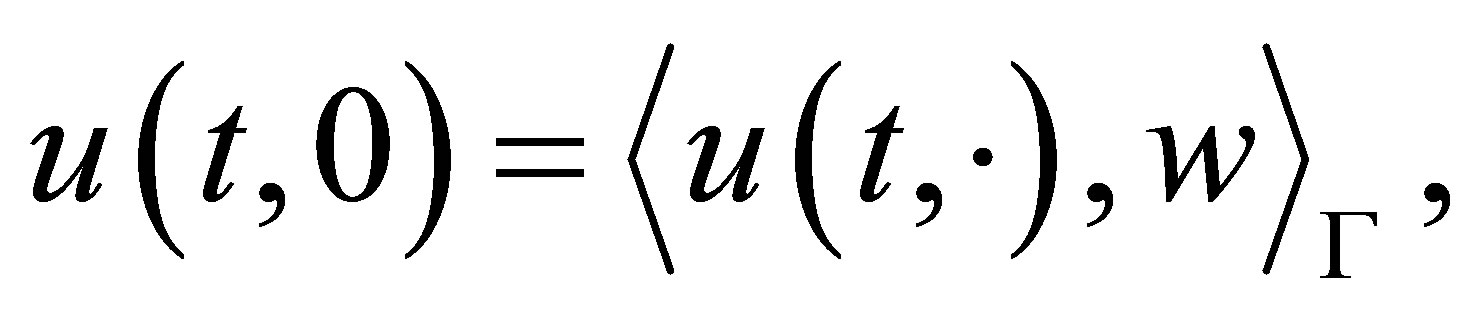 (37)
(37)
that is,  ,
,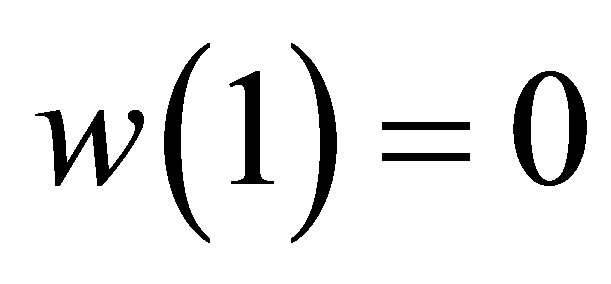 . Let us examine some assumptions in Theorem 4 in this example. Most important is the complete observability (18). The matrices
. Let us examine some assumptions in Theorem 4 in this example. Most important is the complete observability (18). The matrices 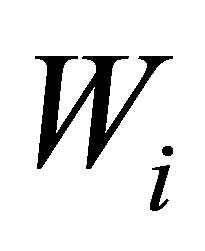 in (16) are now
in (16) are now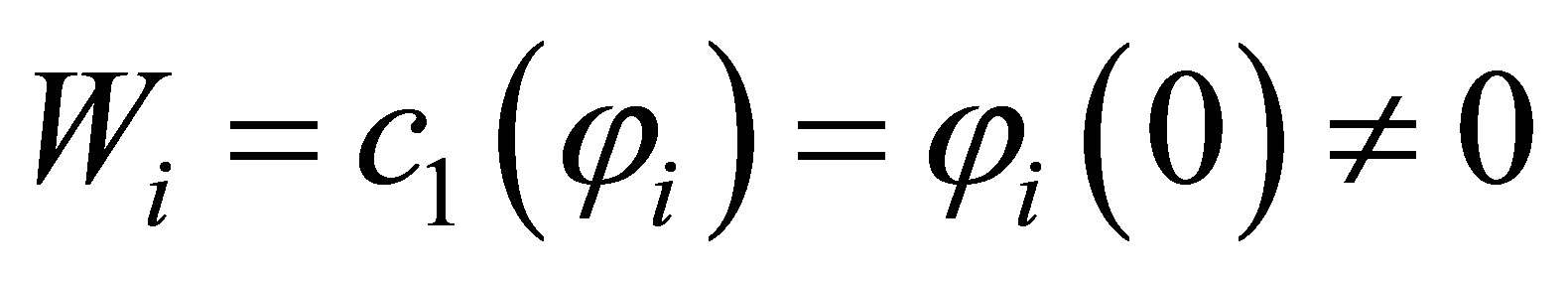 ,
, . Thus, we see that the complete observability is satisfied. Since
. Thus, we see that the complete observability is satisfied. Since 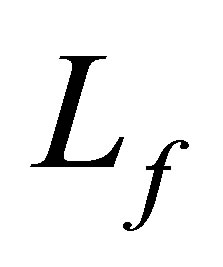 in (13) is a one dimensional operator, the multiplicities of the eigenvalues
in (13) is a one dimensional operator, the multiplicities of the eigenvalues 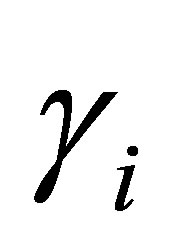 are equal to 1. This enables us to choose
are equal to 1. This enables us to choose  in (9). In Proposition 3, the controllability condition on the actuator
in (9). In Proposition 3, the controllability condition on the actuator 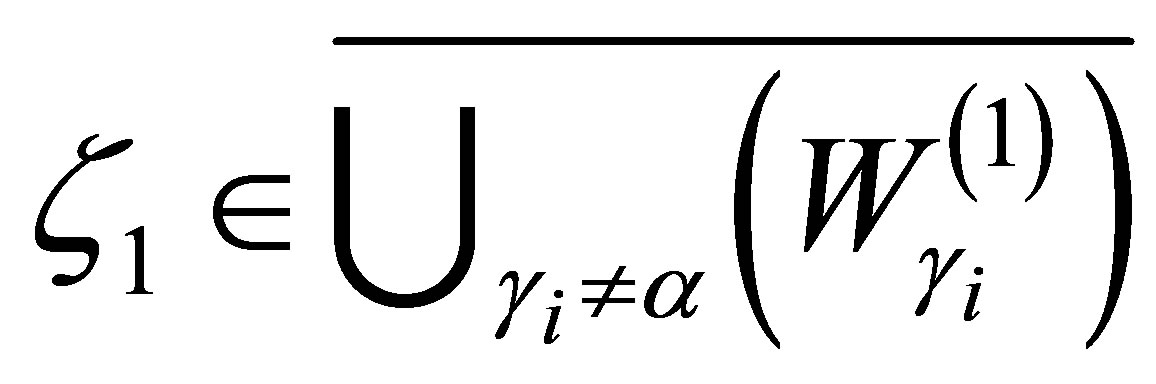 is stated as follows: let
is stated as follows: let 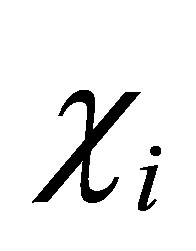 be eigenfunctions of
be eigenfunctions of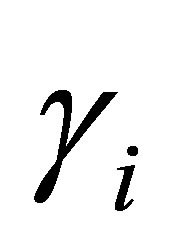 . By setting
. By setting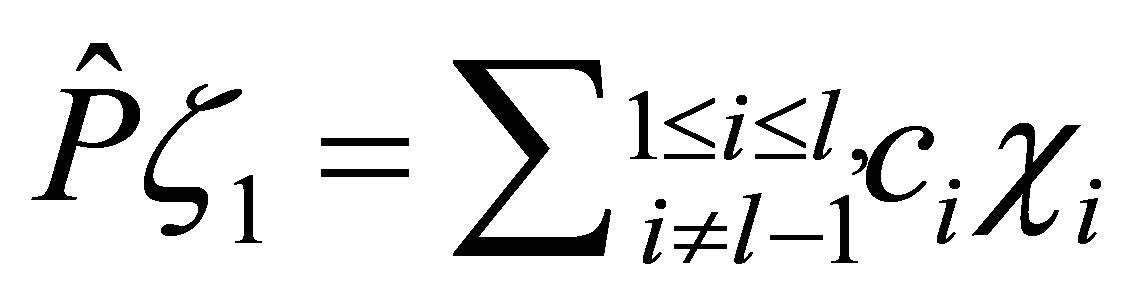 , the controllability condition is simply that
, the controllability condition is simply that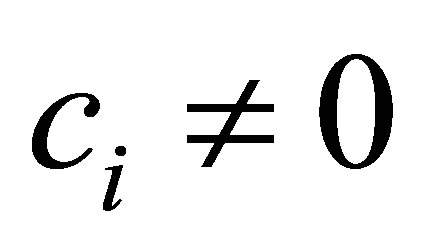 ,
, 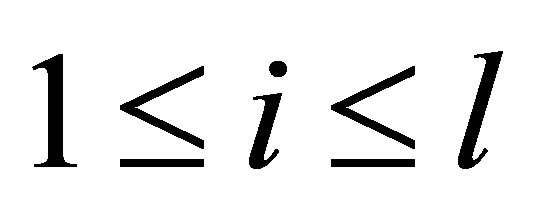 ,
,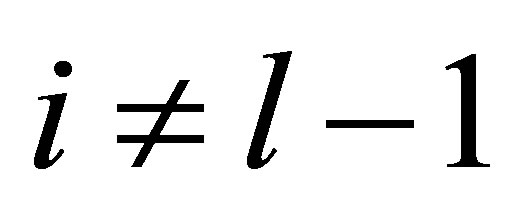 .
.
In the case where  is of the first kind, the output is a single observation at the end point
is of the first kind, the output is a single observation at the end point 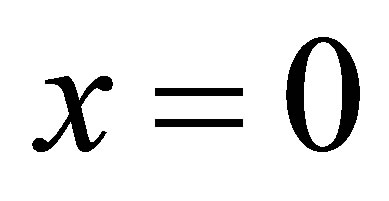 as
as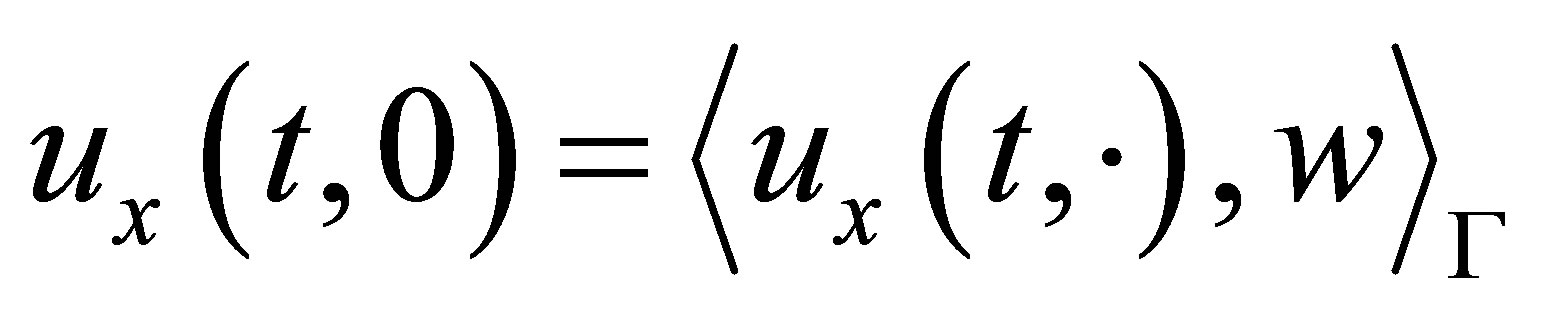 . Proposition 6 also holds in this case. Since
. Proposition 6 also holds in this case. Since ,
, 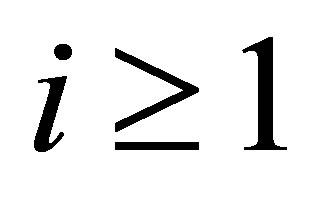 , the complete observability is similarly satisfied.
, the complete observability is similarly satisfied.
3. Spectral Property of the Coefficient Operator
We go back to the problem raised in Section 1: Unlikeliness of a vector of the form . The basic control system is Equation (30) in the product space
. The basic control system is Equation (30) in the product space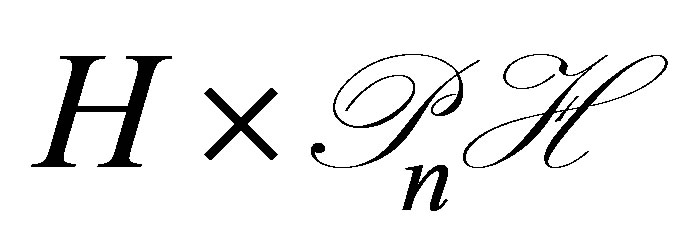 . To avoid any unnecessary technical complexity, we limit ourselves to the simple case of one dimensioanl equations raised in (36),
. To avoid any unnecessary technical complexity, we limit ourselves to the simple case of one dimensioanl equations raised in (36),  being of the third kind. In the setting of the space
being of the third kind. In the setting of the space  as well as
as well as  in (6), we can choose
in (6), we can choose ,
,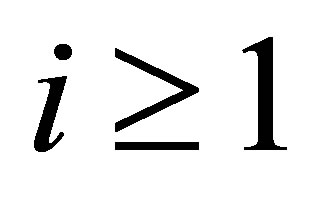 . Thus,
. Thus,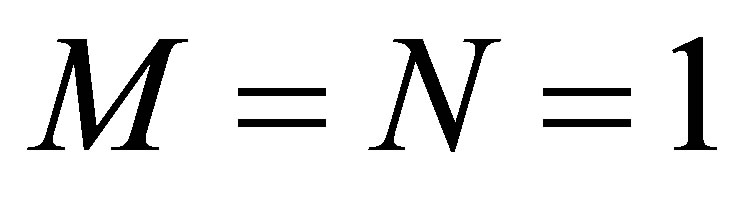 . Equation (30) is simply rewritten as
. Equation (30) is simply rewritten as
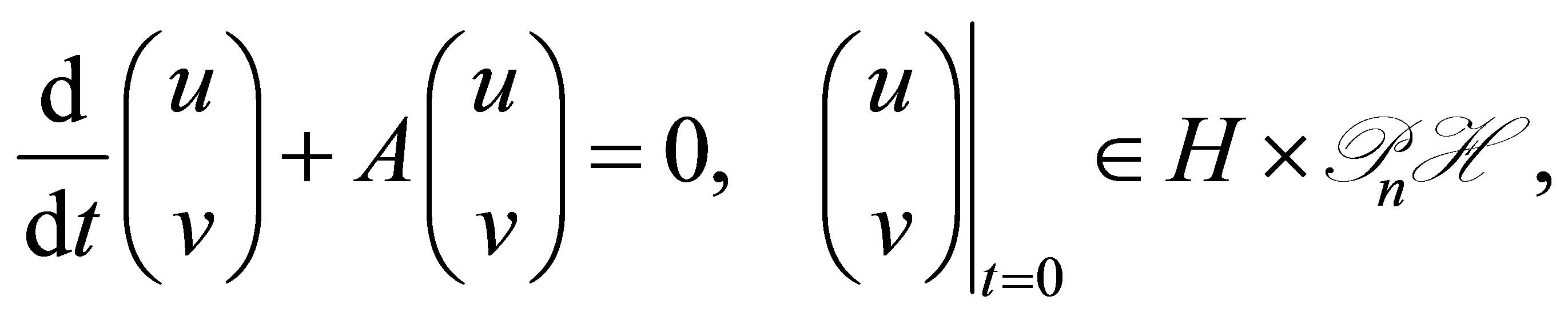 (38)
(38)
where  is defined as
is defined as
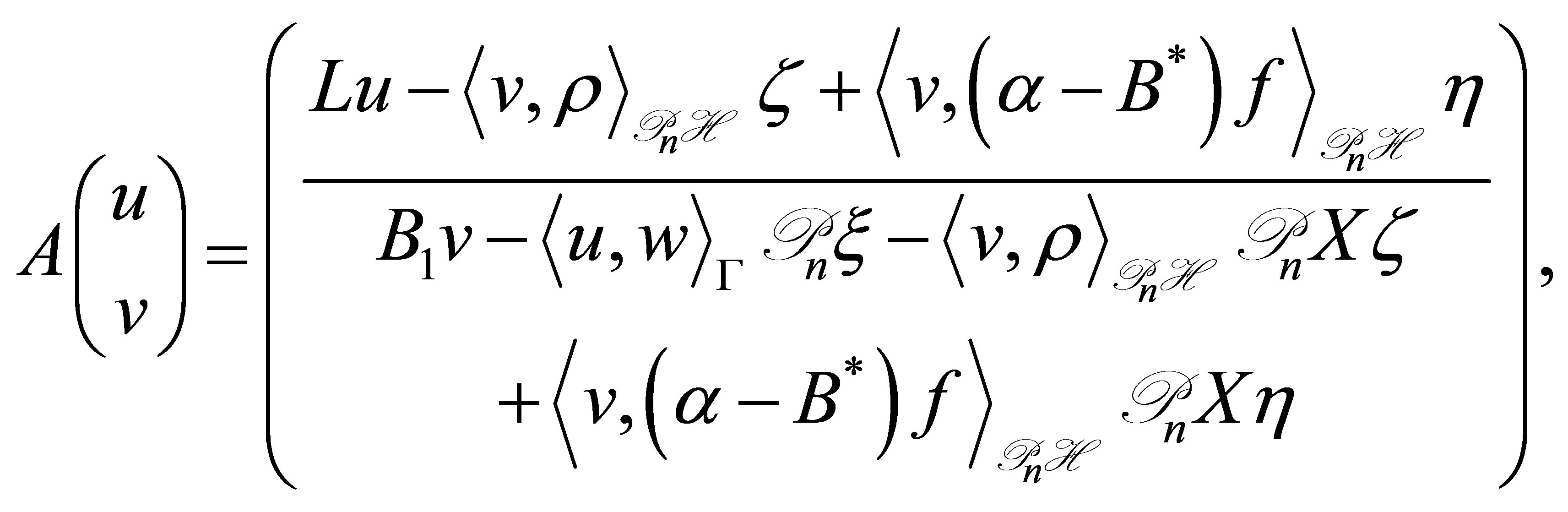 (39)
(39)
and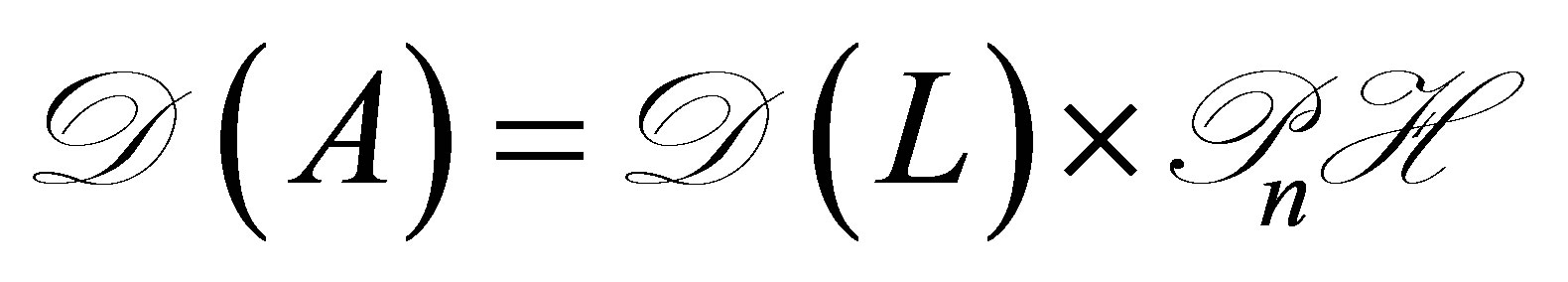 . Here,
. Here, 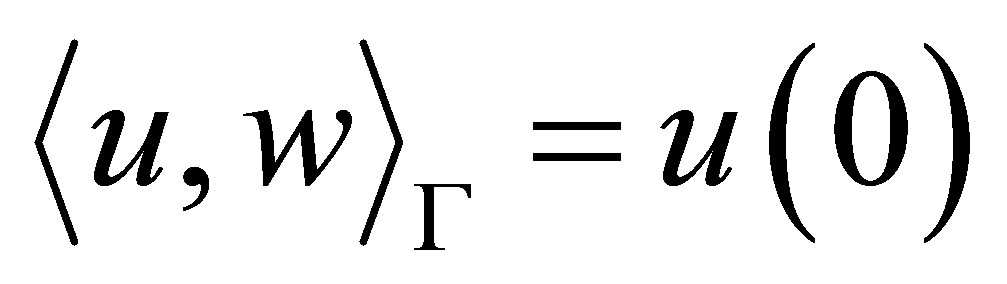 (see
(see
(37)). The operator  is sectorial, and every solution to (30) or (38) is expressed as
is sectorial, and every solution to (30) or (38) is expressed as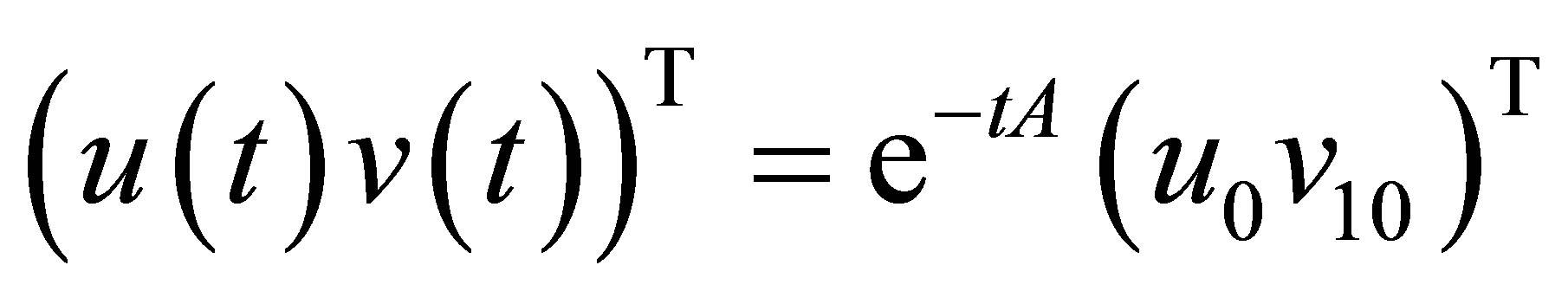 ,
,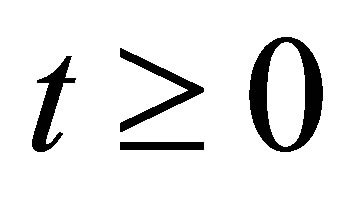 . Let
. Let 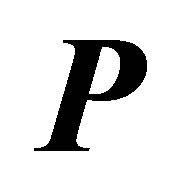 be the projector corresponding to a
be the projector corresponding to a 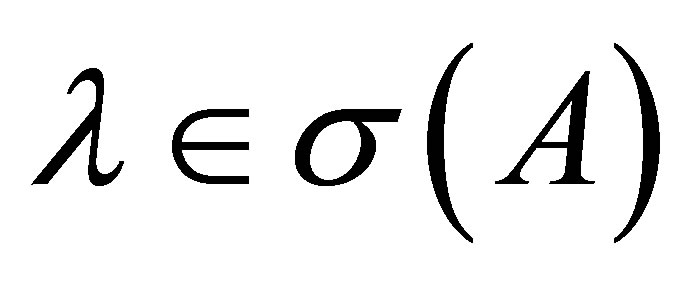 with
with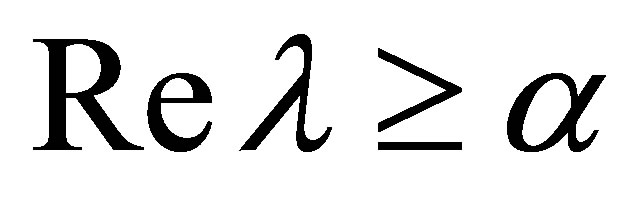 . In view of the relation:
. In view of the relation:
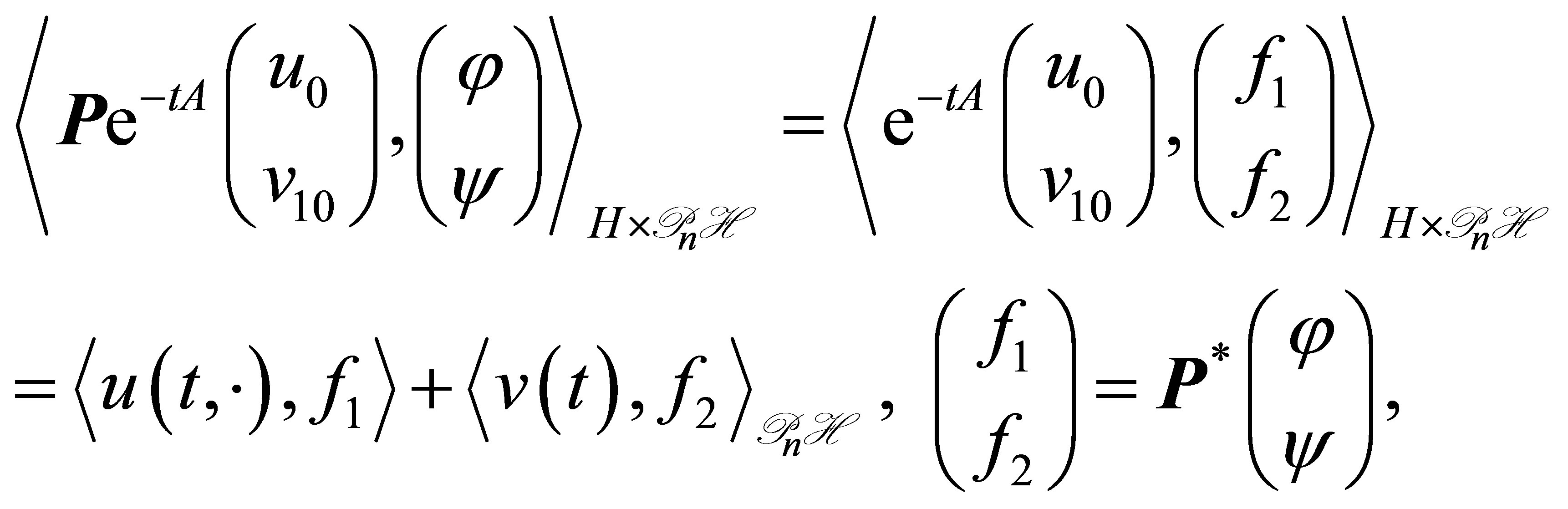
the right-hand side of which decays as 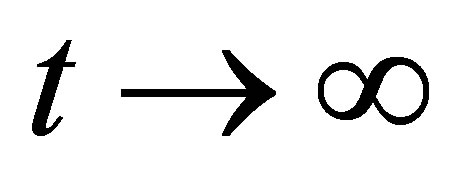 with decay rate
with decay rate 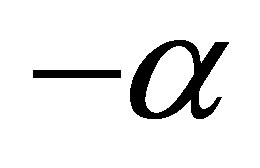 for every initial state. Now we ask: Does the range of the
for every initial state. Now we ask: Does the range of the  contain a vector of the form
contain a vector of the form ? This problem immediately leads to the structure of the eigenspaces of the operator
? This problem immediately leads to the structure of the eigenspaces of the operator . In the operator
. In the operator , the vectors
, the vectors 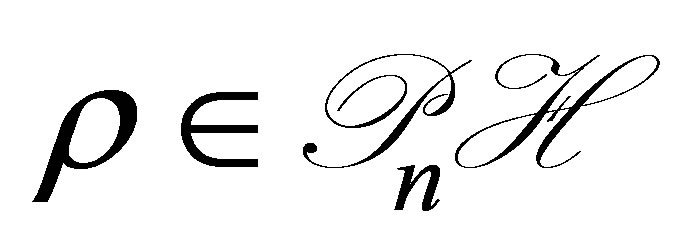 and
and  of the compensator are the parameters to be designed
of the compensator are the parameters to be designed . In designing these parameters, they are generally influenced by small perturbations. It is thus implausible to assume that some Fourier coefficients of these parameters would be designed to be
. In designing these parameters, they are generally influenced by small perturbations. It is thus implausible to assume that some Fourier coefficients of these parameters would be designed to be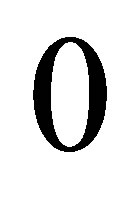 : such conditions are very easily broken. Thus we may henceforth assume that
: such conditions are very easily broken. Thus we may henceforth assume that
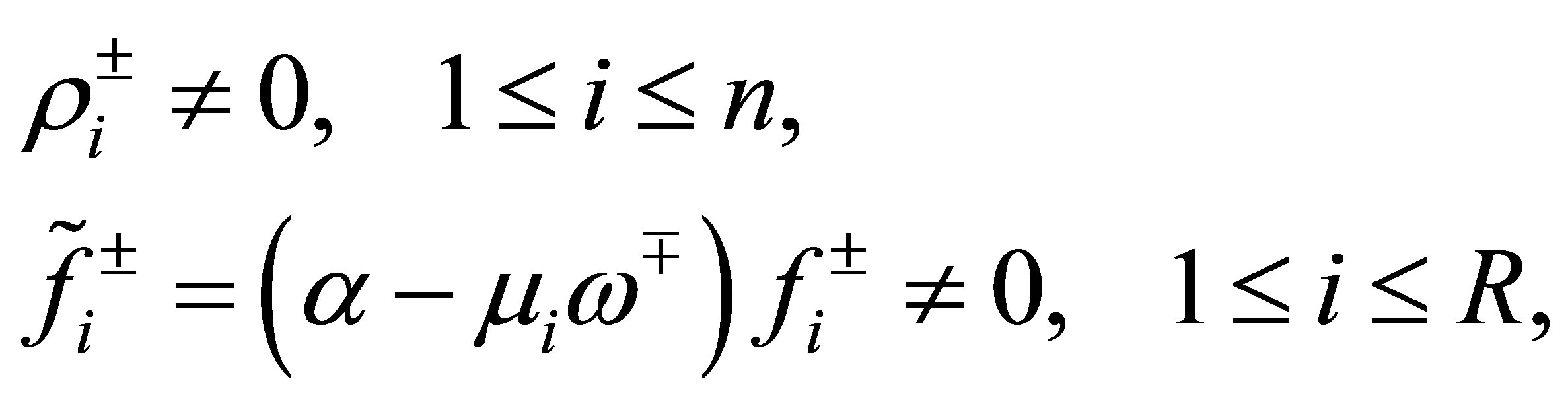 (40)
(40)
where  and
and  denote, respectively,
denote, respectively, 
and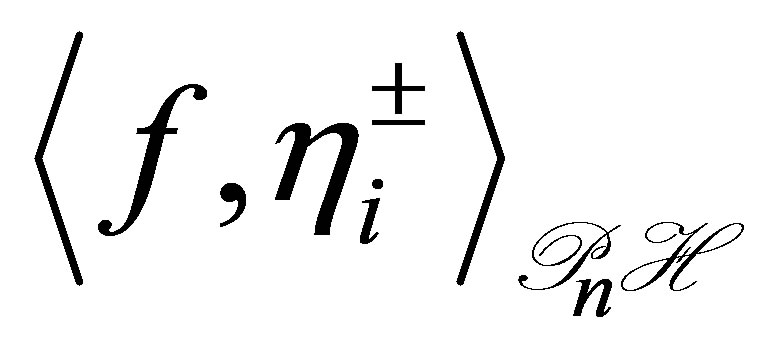 . The actuators
. The actuators  and
and 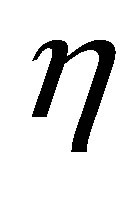 of the controlled plant are the given parameters in advance. It is also implausible to assume that some Fourier coefficients of
of the controlled plant are the given parameters in advance. It is also implausible to assume that some Fourier coefficients of  and
and 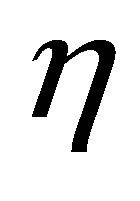 relative to
relative to  might be equal to 0. Thus we may also assume that
might be equal to 0. Thus we may also assume that
 (41)
(41)
The main results in this section are Theorem 7, Proposition 8, and Theorem 9 stated just below. The proof of these results will be given later.
Theorem 7. Let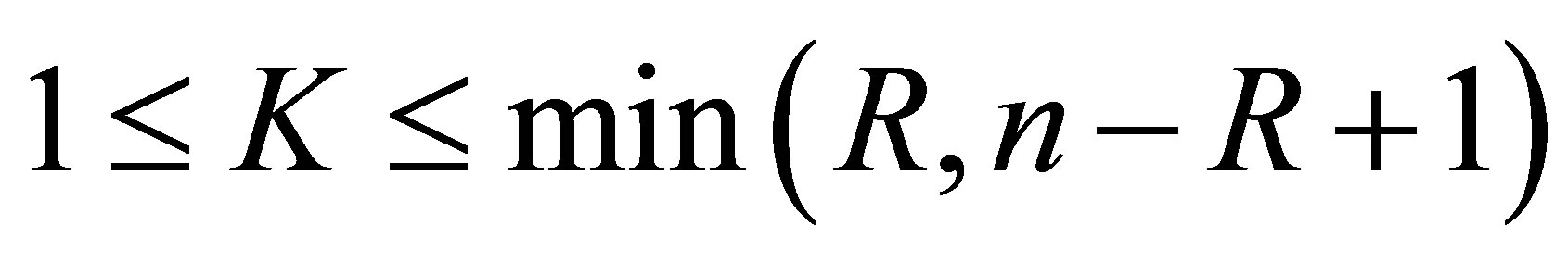 . Suppose that
. Suppose that 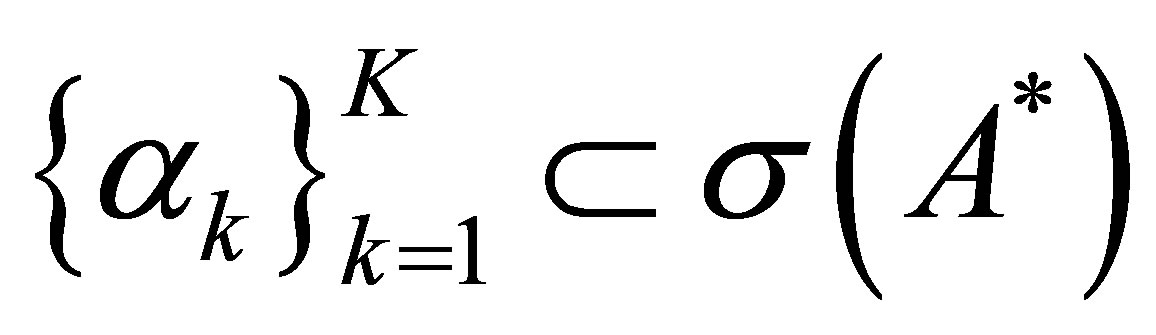 and that
and that
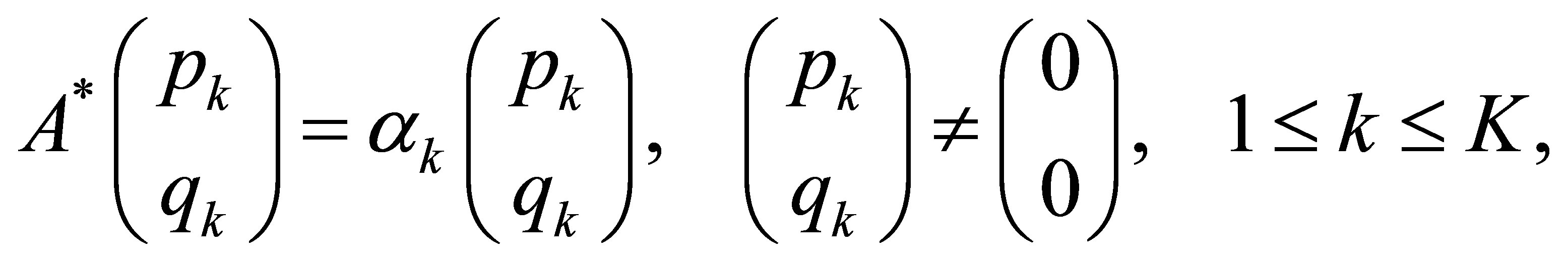 (42)
(42)
where 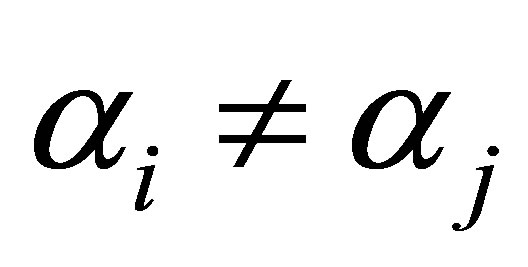 for
for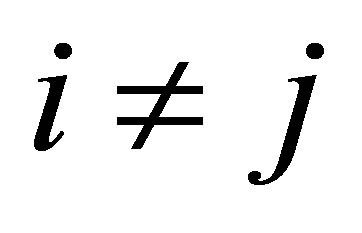 . Then any linear combination of these eigenvectors
. Then any linear combination of these eigenvectors 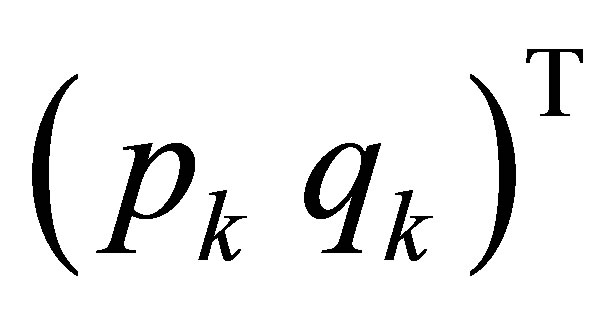 of
of  cannot generate a vector of the form,
cannot generate a vector of the form, 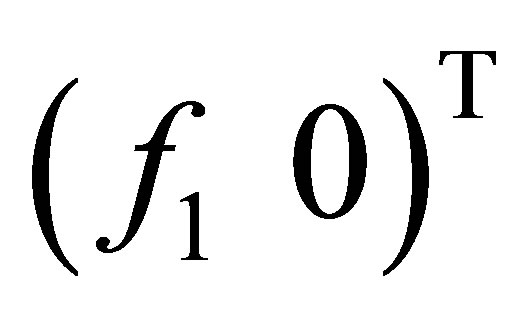 ,
,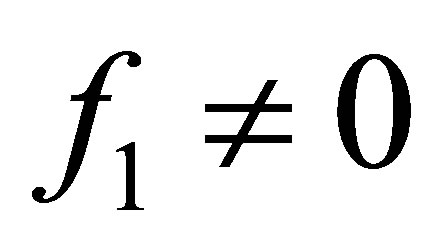 .
.
Remark. The adjoint operator  will be characterized later in (49). Theorem 7 also asserts that there is no eigenvector of the form,
will be characterized later in (49). Theorem 7 also asserts that there is no eigenvector of the form,  ,
,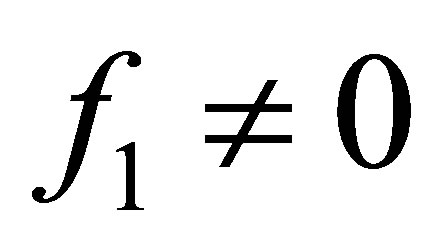 . The restriction on
. The restriction on 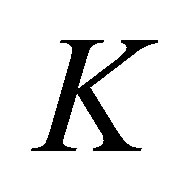 is derived from our setting of the operator
is derived from our setting of the operator  in (39): The setting is made for constructing a finitedimensional compensator. In the original equation (9), however, the parameters are constructed in a more general setting. The operator
in (39): The setting is made for constructing a finitedimensional compensator. In the original equation (9), however, the parameters are constructed in a more general setting. The operator  is then replaced by
is then replaced by
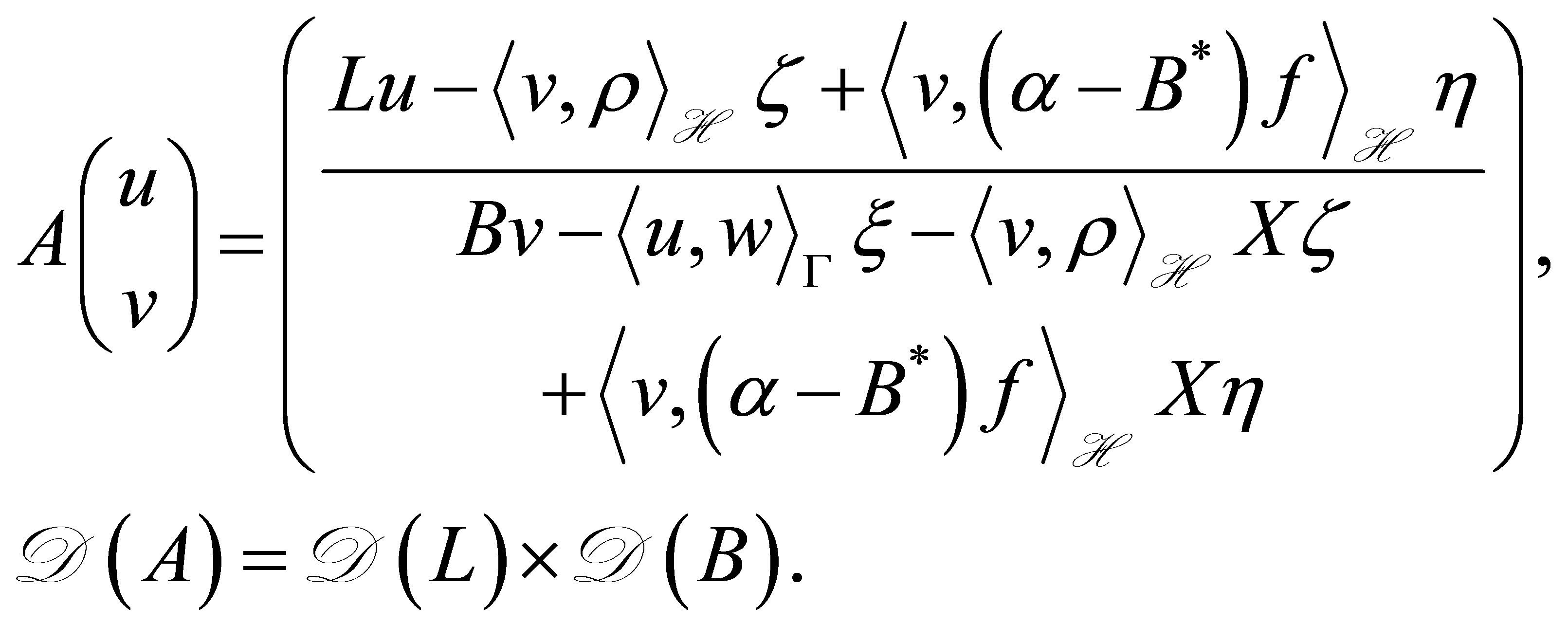 (39')
(39')
Then, the above restriction on the  is removed: In fact, the integer
is removed: In fact, the integer 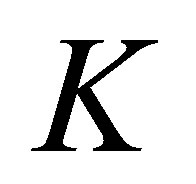 may be chosen arbitrarily large.
may be chosen arbitrarily large.
We hope to know more on . The following proposition partly gives concrete informations on what
. The following proposition partly gives concrete informations on what 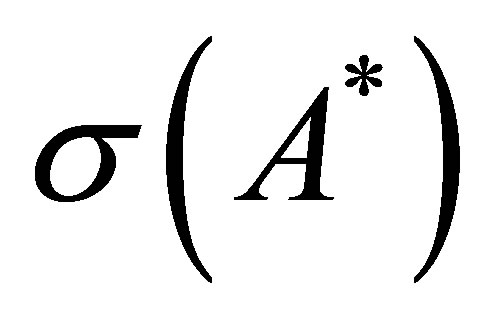 consists of. It shows that
consists of. It shows that 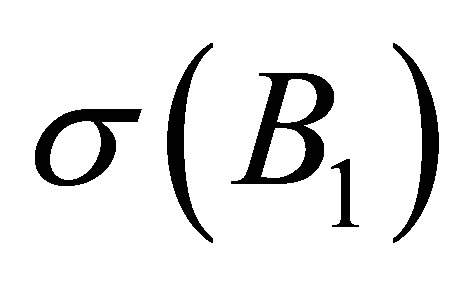 is contained in
is contained in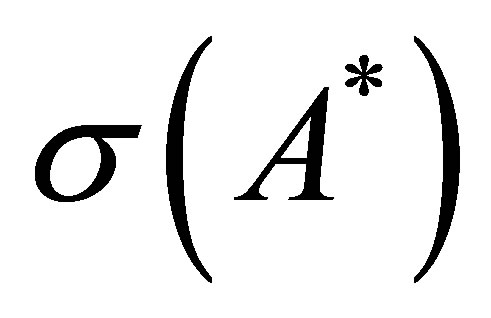 , regardless of the assumptions (40) and (41).
, regardless of the assumptions (40) and (41).
Proposition 8. The numbers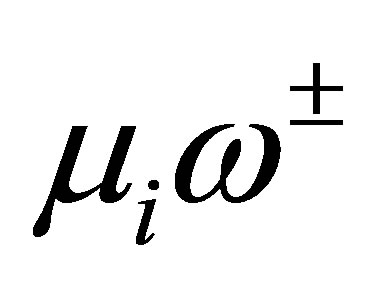 ,
, 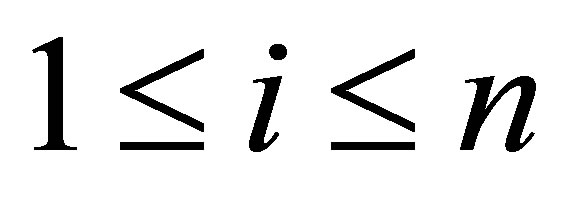 belong to
belong to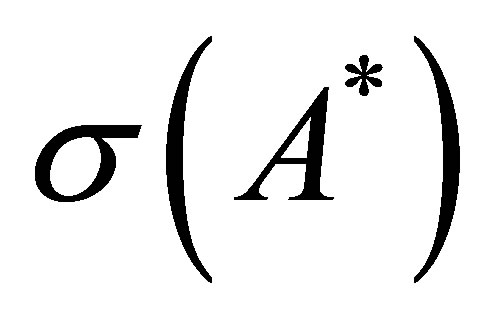 . Actually we have the relations:
. Actually we have the relations:
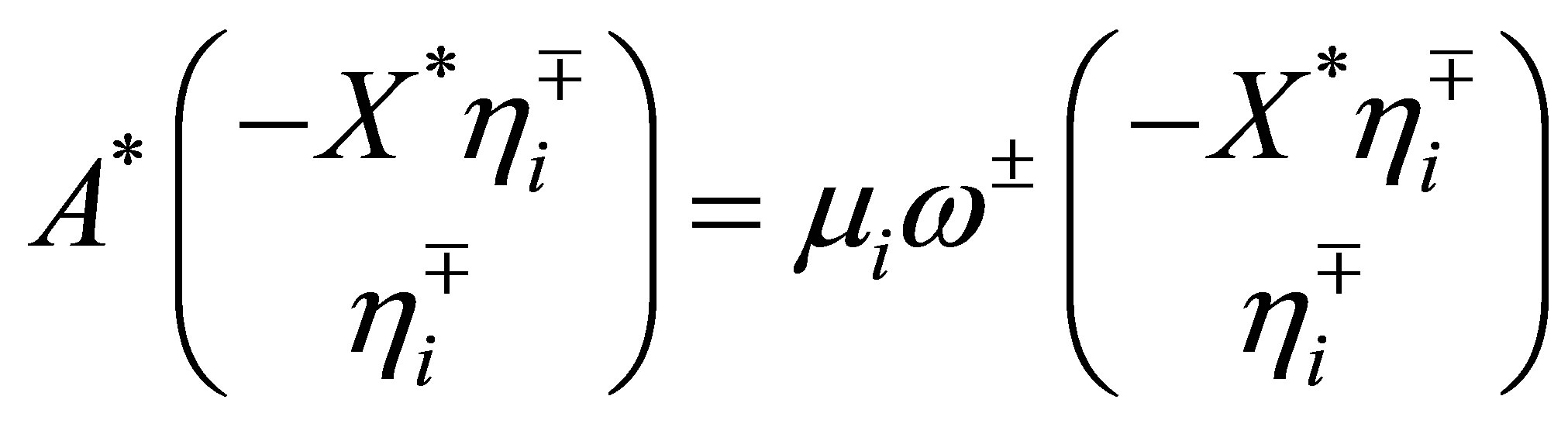 (43)
(43)
for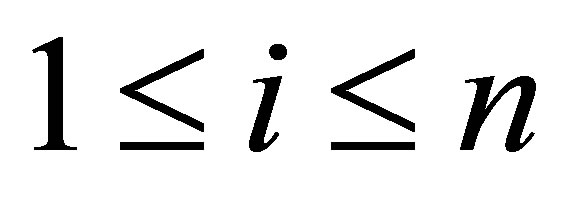 . Since the set
. Since the set 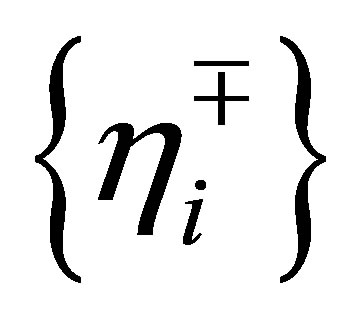 forms an orthonormal system for
forms an orthonormal system for , any linear combinations of these eigenvectors cannot generate a vector of the form,
, any linear combinations of these eigenvectors cannot generate a vector of the form,  ,
,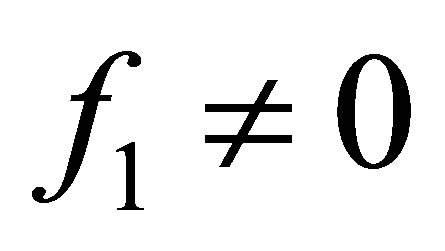 .
.
To seek eigenvalues of  other than
other than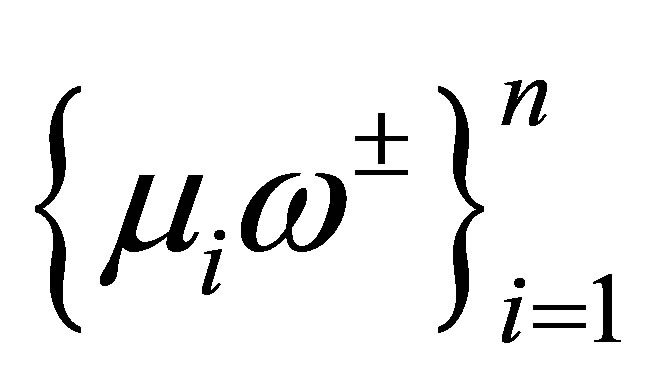 , let us recall the operator
, let us recall the operator 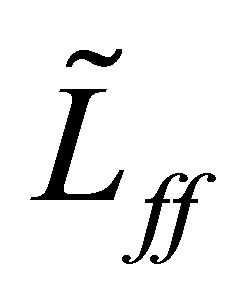 which appeared in (32), where
which appeared in (32), where
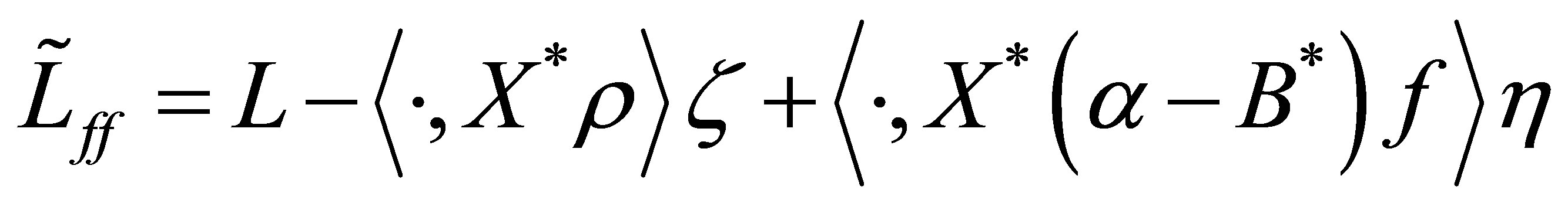 with
with 
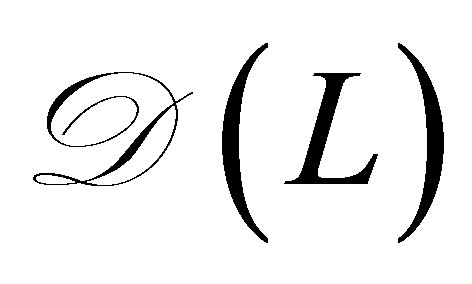 . The adjoint operator
. The adjoint operator  is clearly given by
is clearly given by 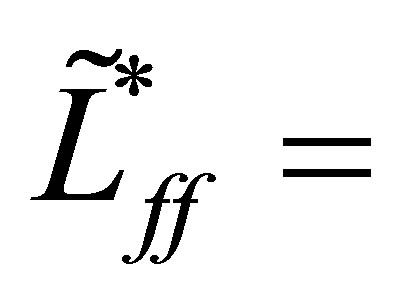
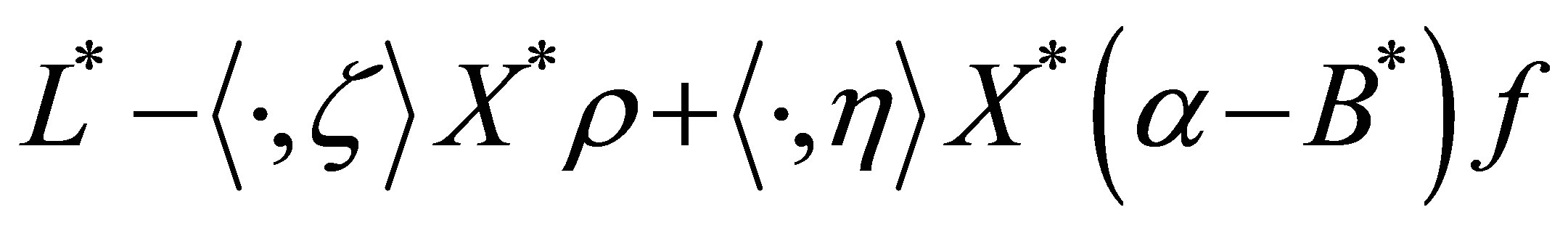 with
with 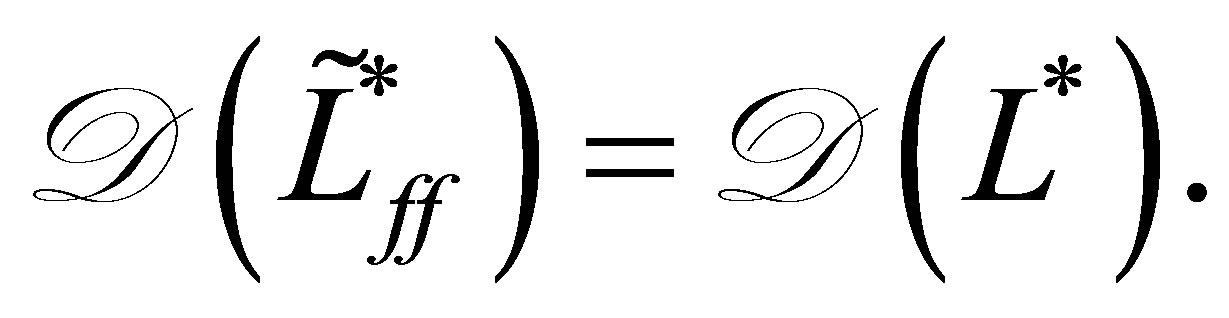
In the following result, we characterize  by introducing an operator
by introducing an operator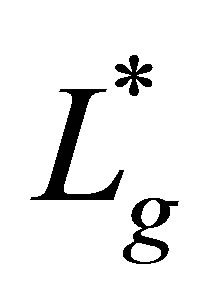 , a slightly perturbed operator of
, a slightly perturbed operator of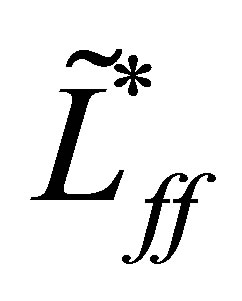 :
:
Theorem 9. Let 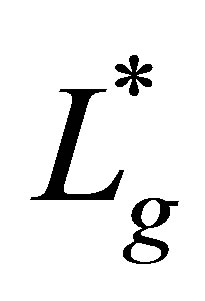 be an operator defined as
be an operator defined as
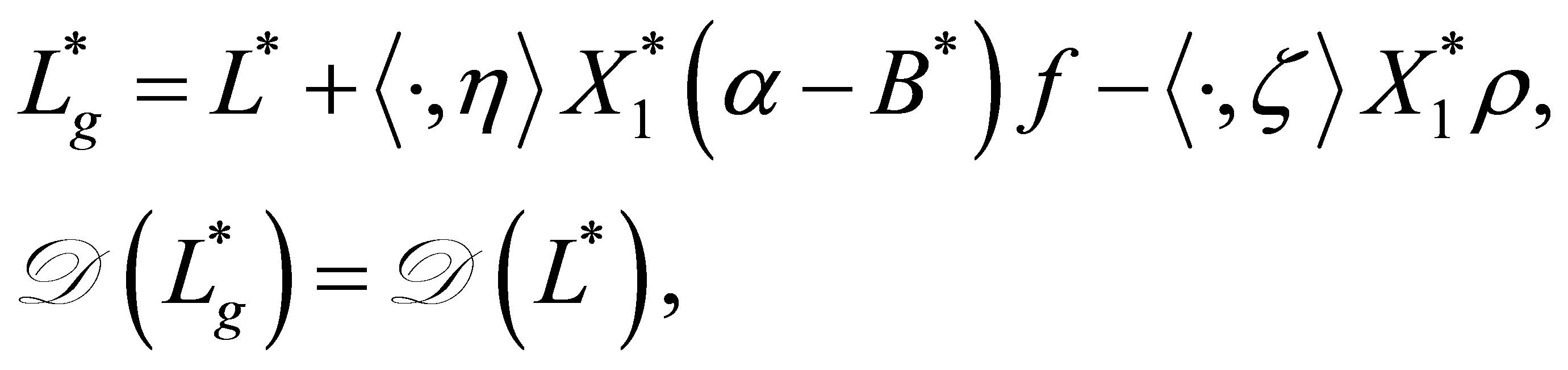 (44)
(44)
where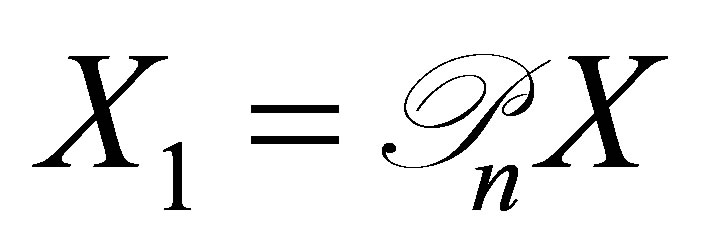 . Then, we have the relation
. Then, we have the relation
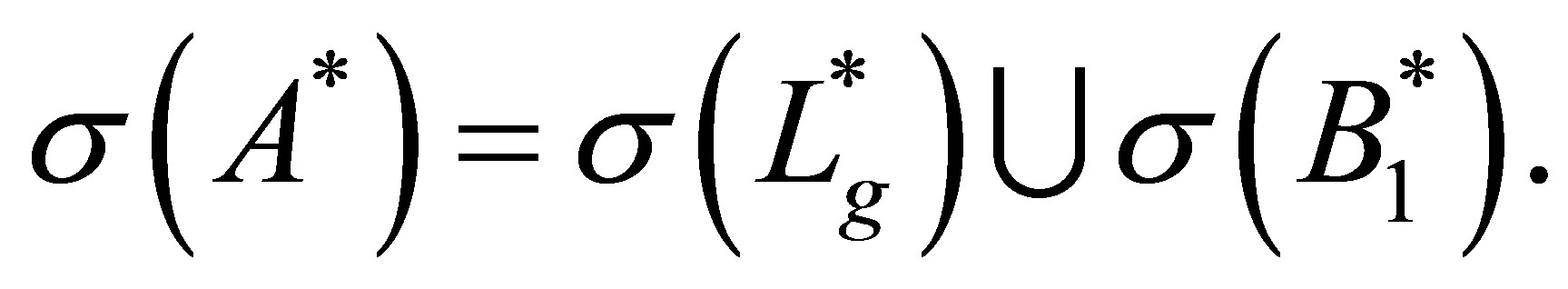 (45)
(45)
Let 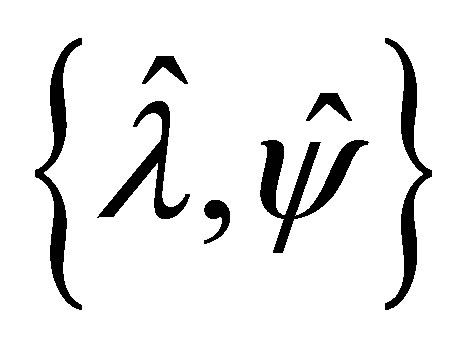 be an arbitrary eigenpair of
be an arbitrary eigenpair of 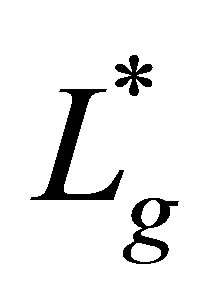 such that
such that 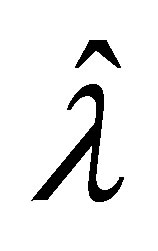 is not contained in
is not contained in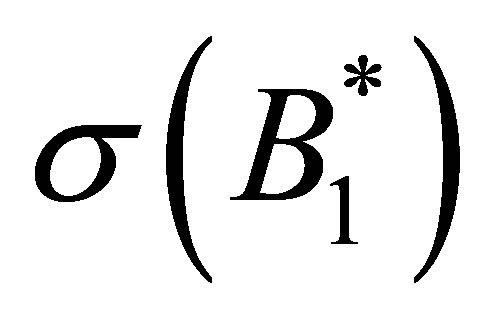 . Then, the corresponding eigenvector
. Then, the corresponding eigenvector 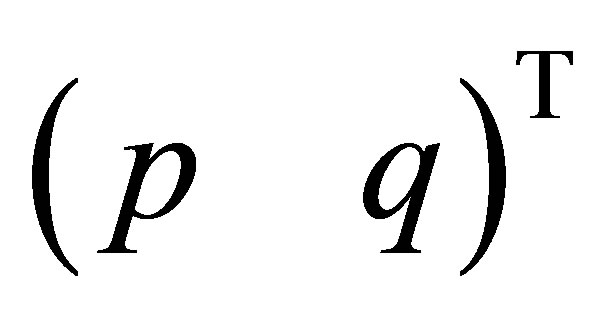 of
of  is given by
is given by
 (46)
(46)
where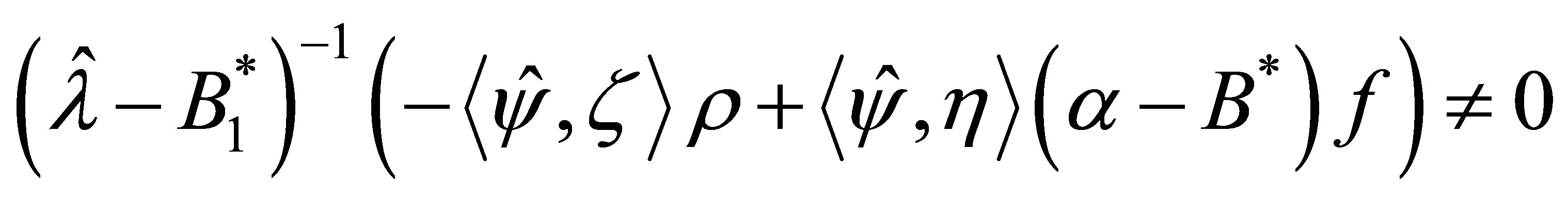 .
.
In the above assertions, we need to characterize the adjoint operator , which will be described later by (51). To seek the structure of
, which will be described later by (51). To seek the structure of , let us begin with the operator equation:
, let us begin with the operator equation:
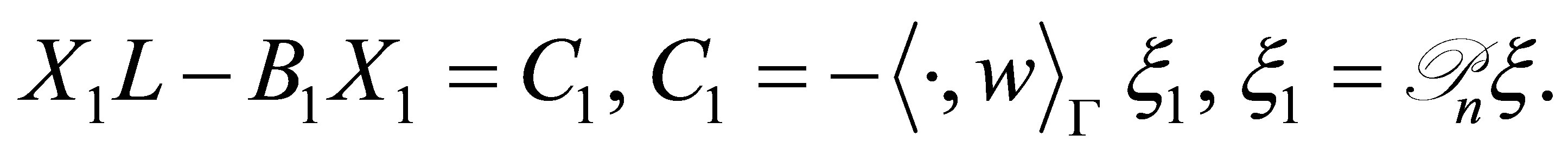 (47)
(47)
It is clear that (47) admits a unique solution , and that the solution is expressed as
, and that the solution is expressed as  (see (17)). Let
(see (17)). Let 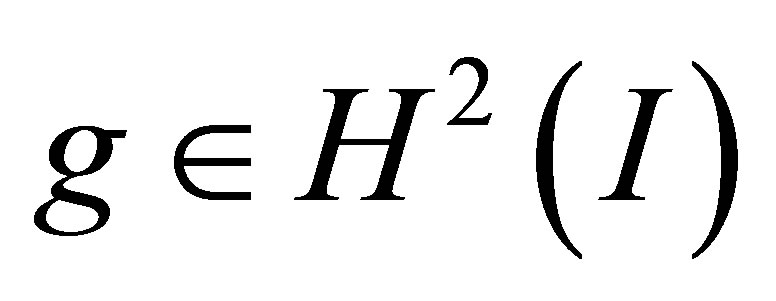 be a unique solution to the boundary value problem:
be a unique solution to the boundary value problem: 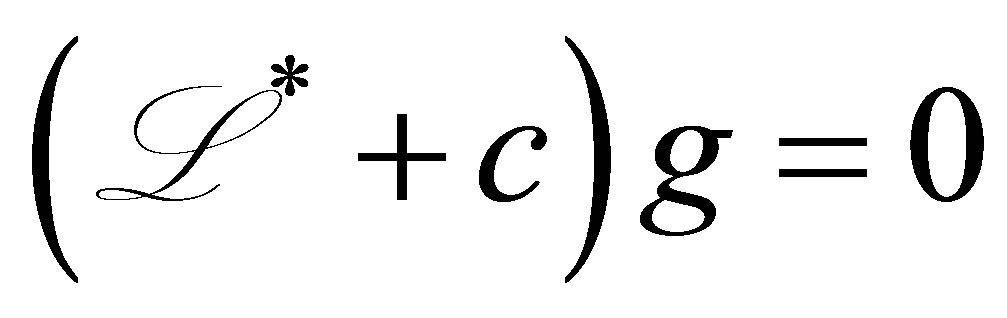 in
in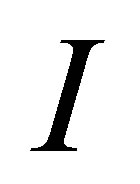 ,
, 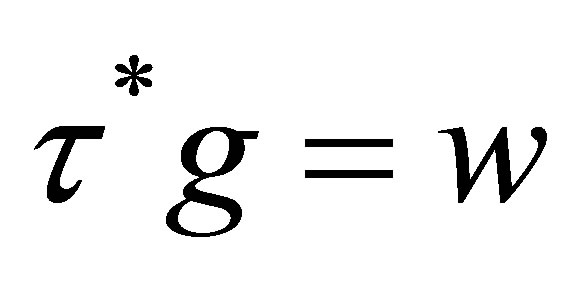 on
on . We note that
. We note that  remains bounded when
remains bounded when  (this fact will be used in Lemma 10 below). For any
(this fact will be used in Lemma 10 below). For any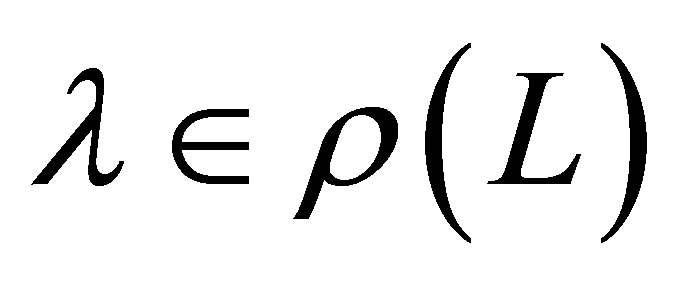 , note that
, note that
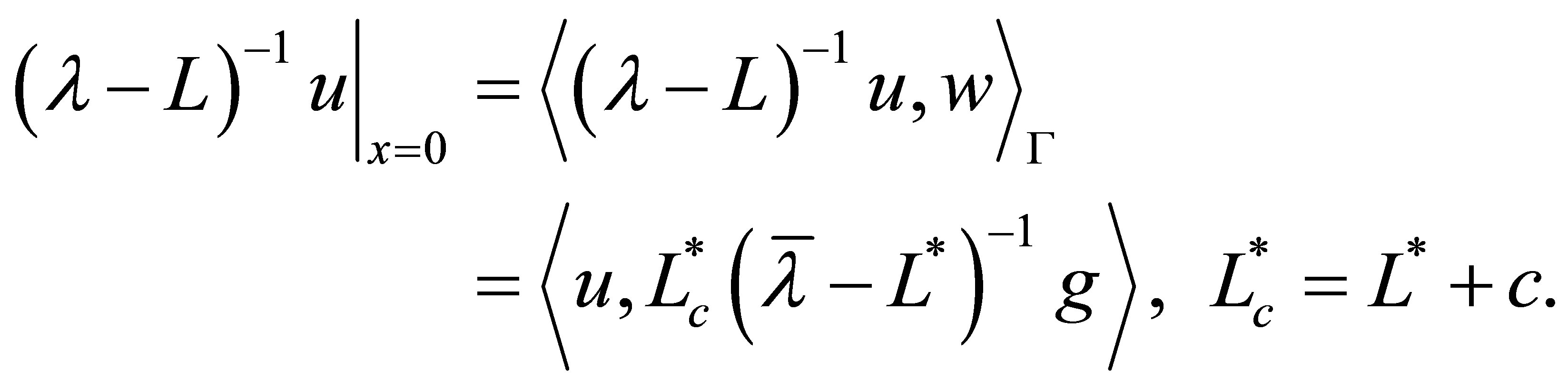
Then the adjoint 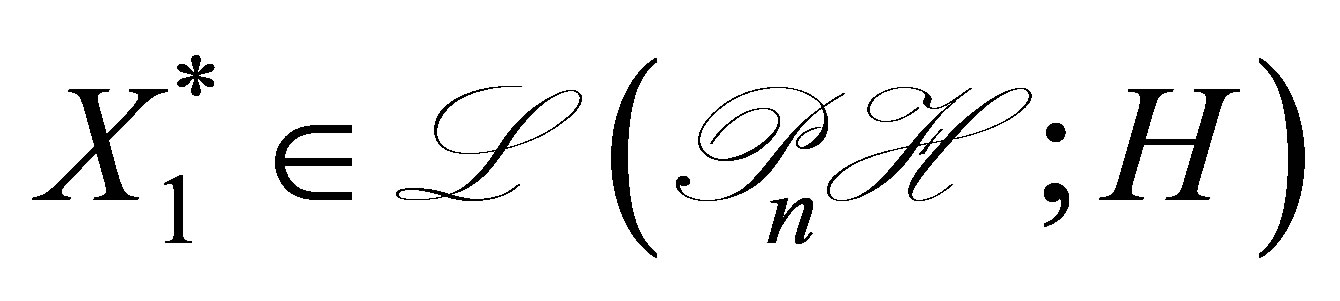 is expressed as
is expressed as
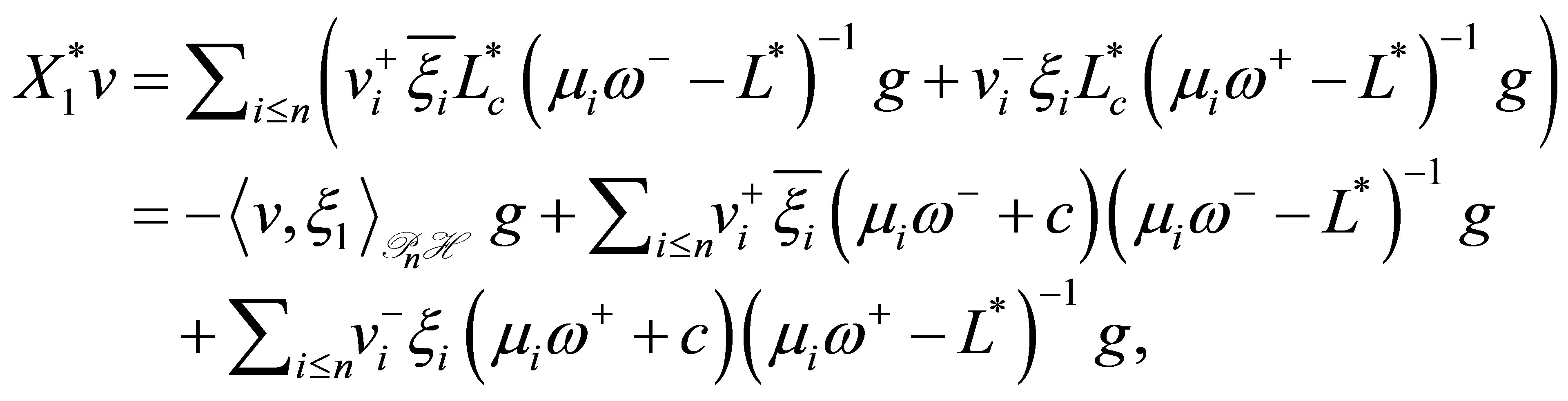
where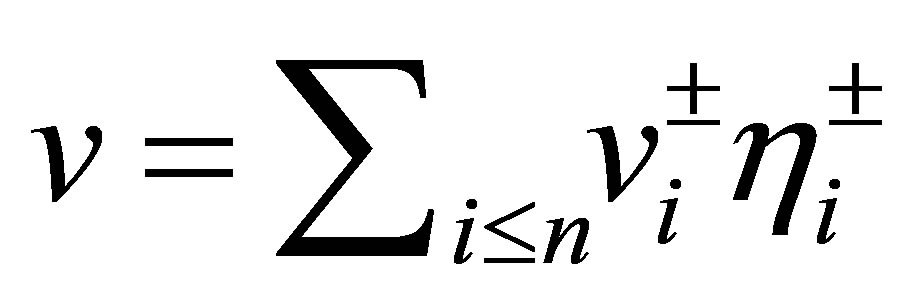 ,
,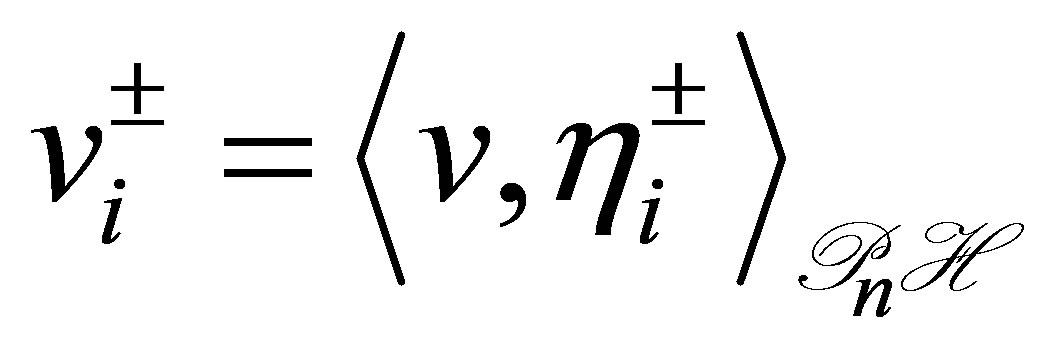 . Thus,
. Thus,
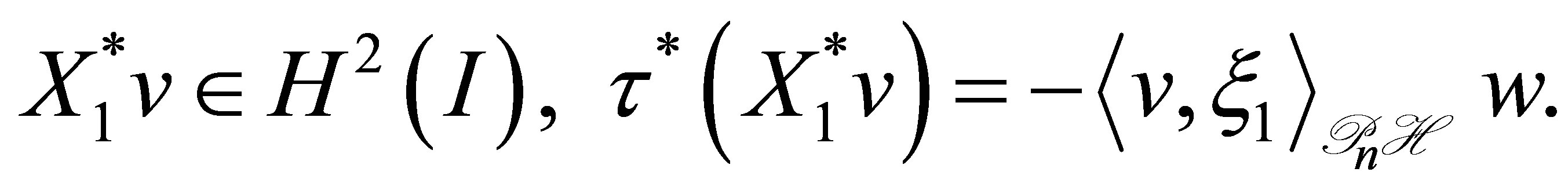 (48)
(48)
Let us find the equation for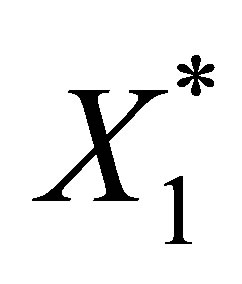 . For
. For 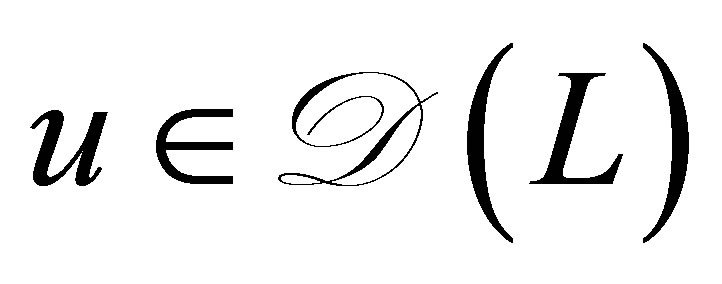 and
and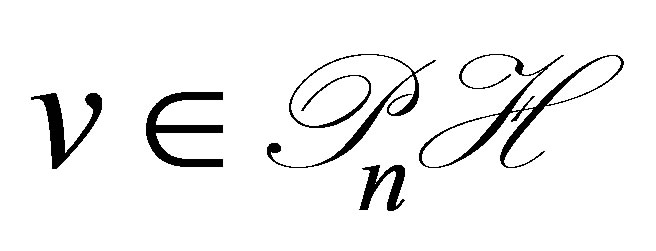 , we calculate through Green’s formula, (47), and the boundary condition (48) as
, we calculate through Green’s formula, (47), and the boundary condition (48) as
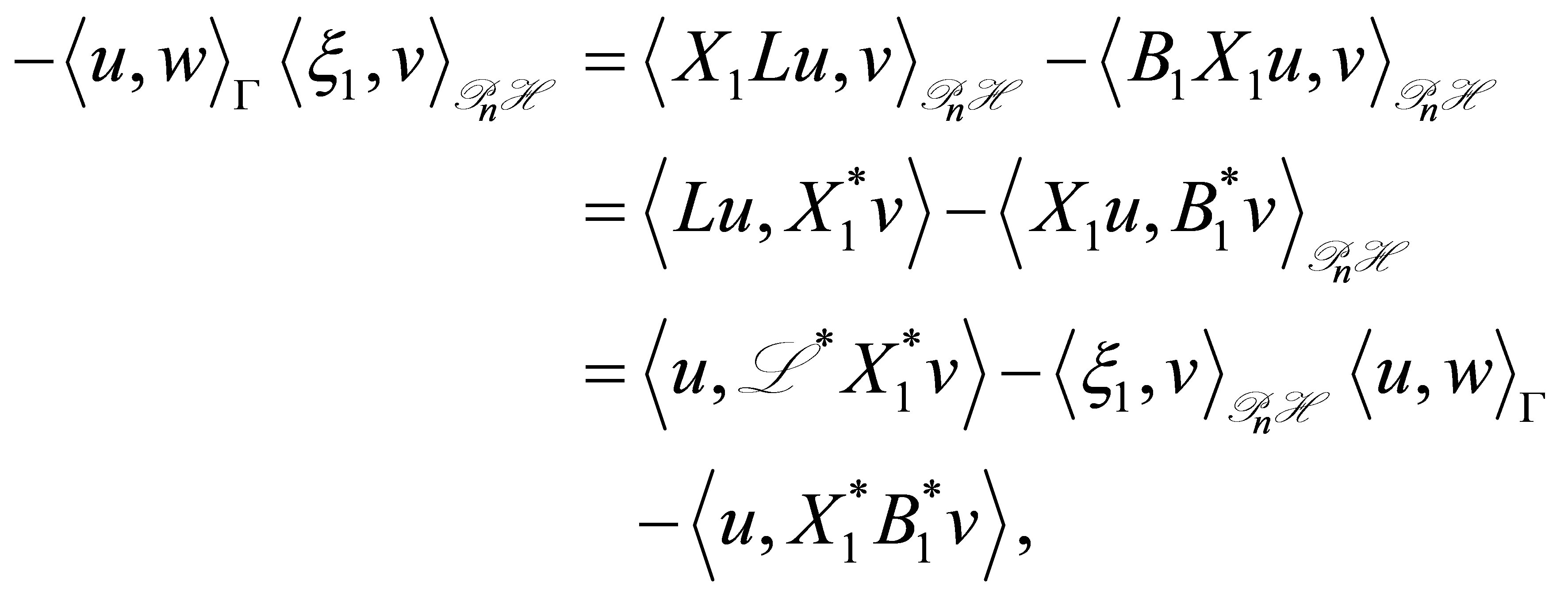
and thus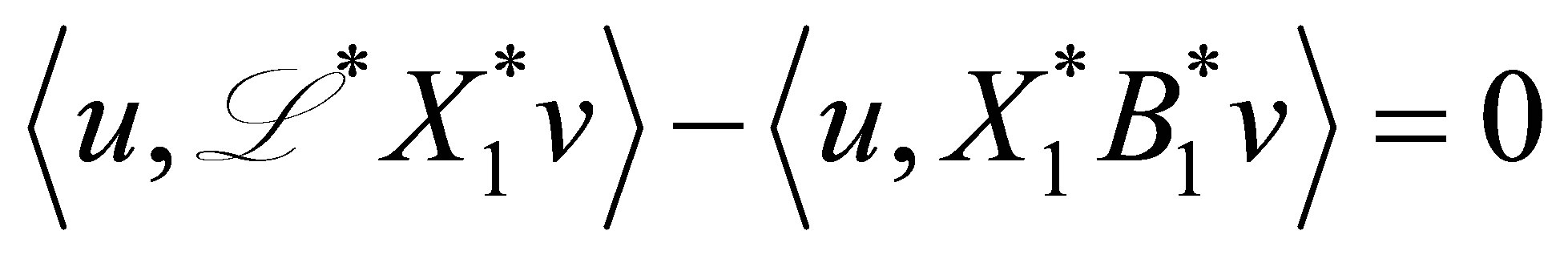 . Since
. Since 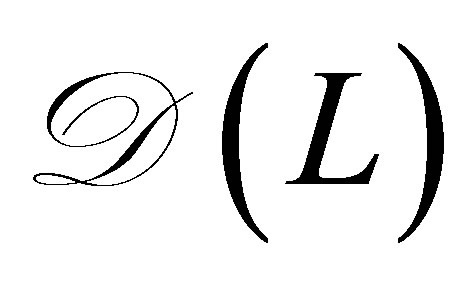 is dense in
is dense in , we see that
, we see that
 (49)
(49)
Let us calculate the adjoint . By assuming that
. By assuming that  is in
is in 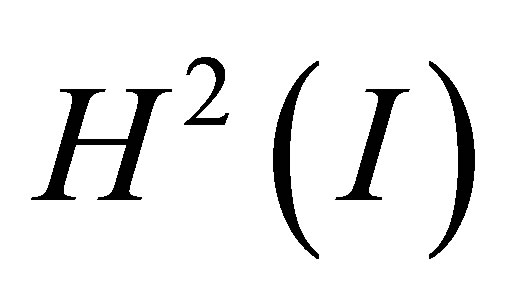 and satisfies the boundary condition:
and satisfies the boundary condition: 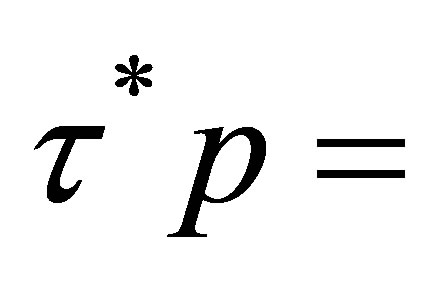
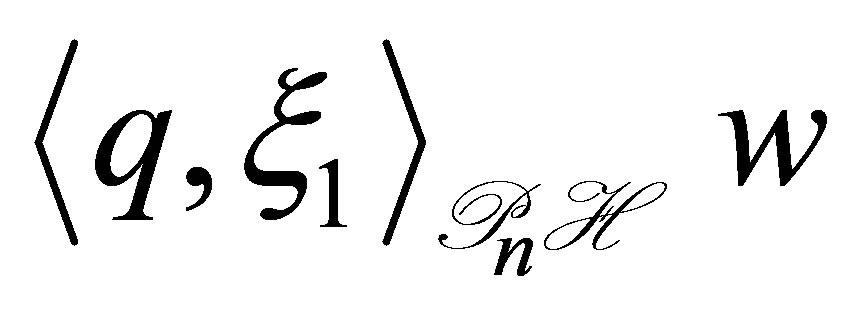 ,
,  is calculated as
is calculated as

where 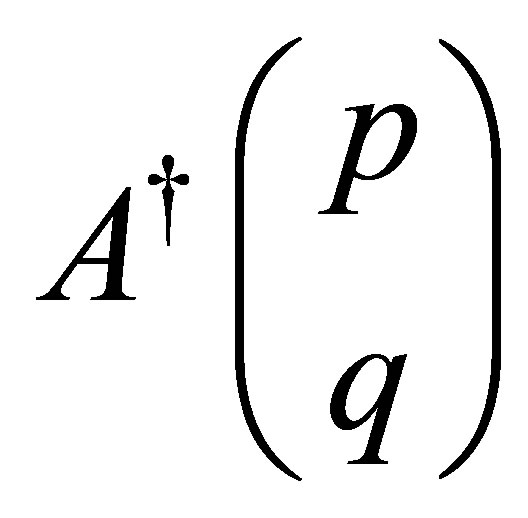 is given by
is given by
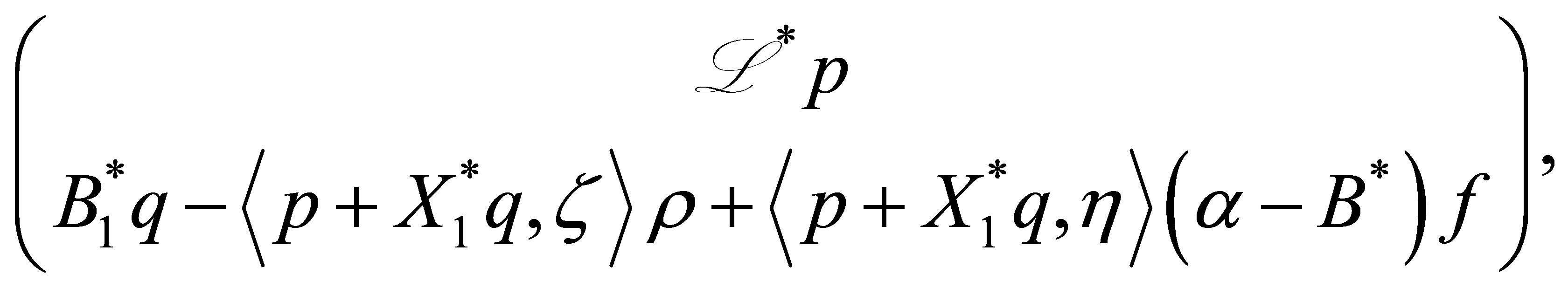 (50)
(50)
and 
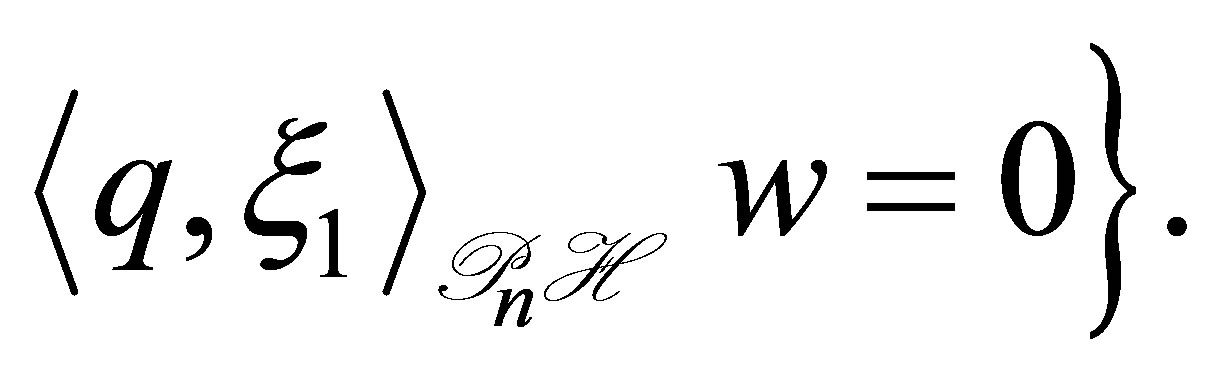 We see that
We see that , and thus
, and thus . In order to show that
. In order to show that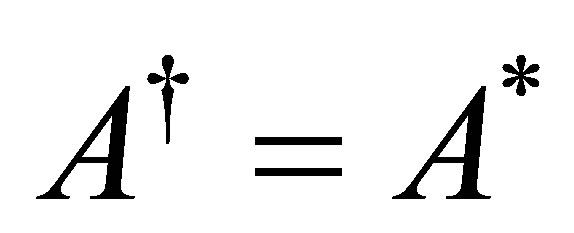 , we need the following elementary result:
, we need the following elementary result:
Lemma 10. The operator  is densely defined, and the bounded inverse,
is densely defined, and the bounded inverse, 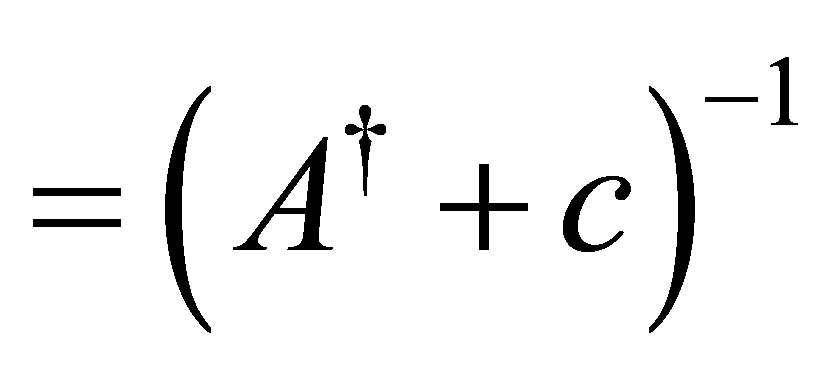
 exists for a sufficiently large
exists for a sufficiently large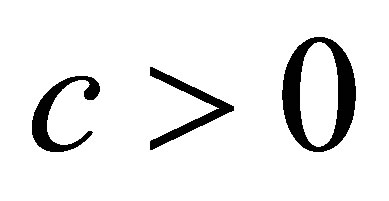 .
.
Proof. Given a , we solve the equation:
, we solve the equation: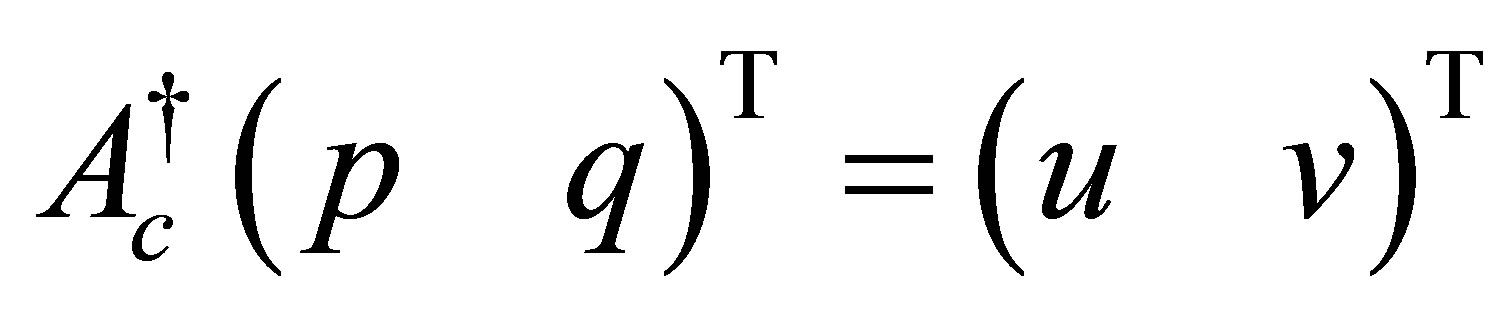 , where
, where . Set
. Set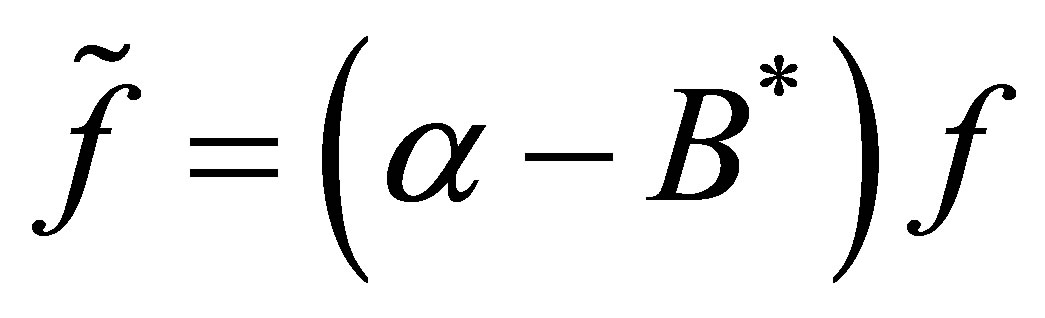 , and define an operator
, and define an operator  as
as
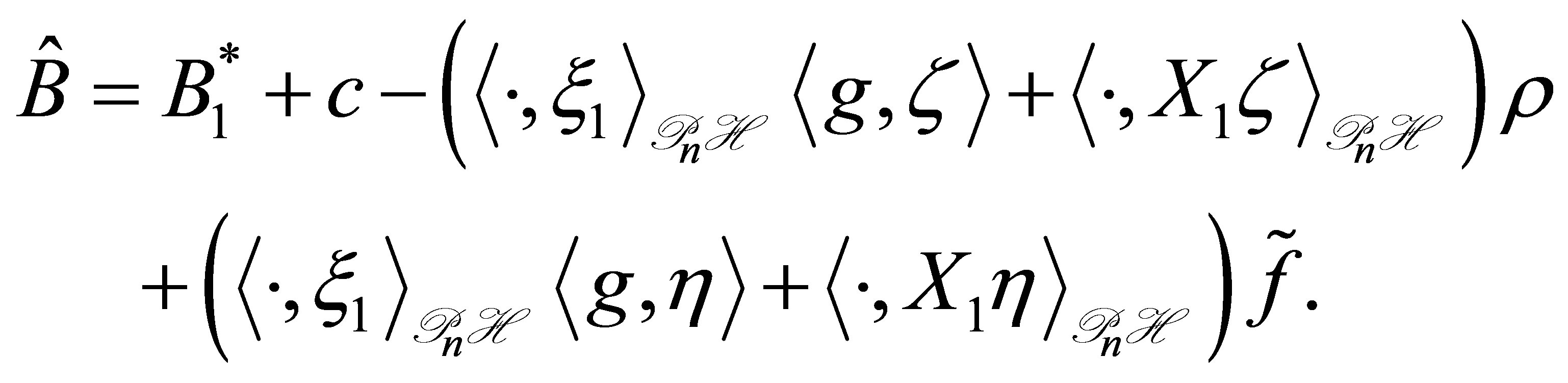
The function 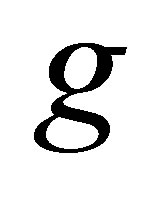 depends on
depends on . However, since
. However, since 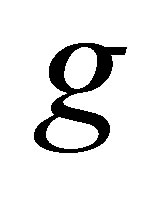 remains bounded as
remains bounded as , there is a bounded inverse:
, there is a bounded inverse: 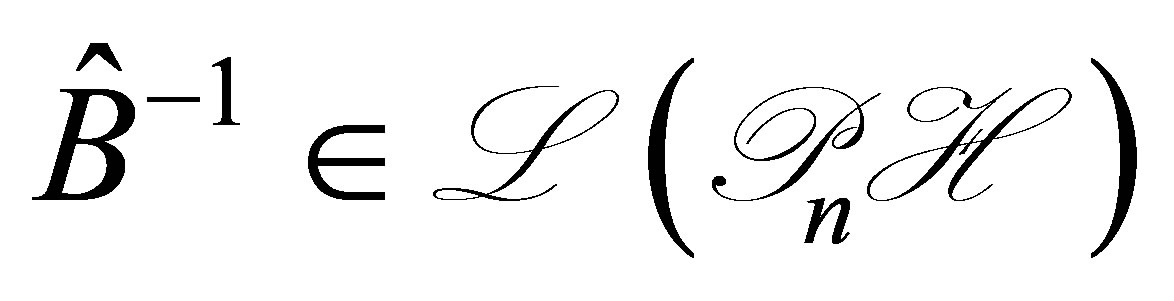 for a sufficiently large
for a sufficiently large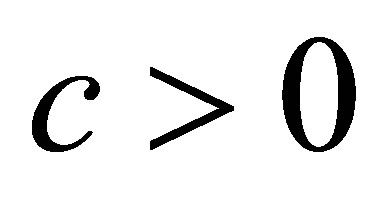 . A straightforward calculation shows that
. A straightforward calculation shows that 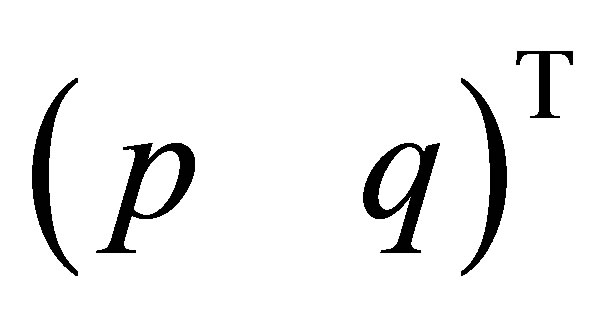 defined by
defined by 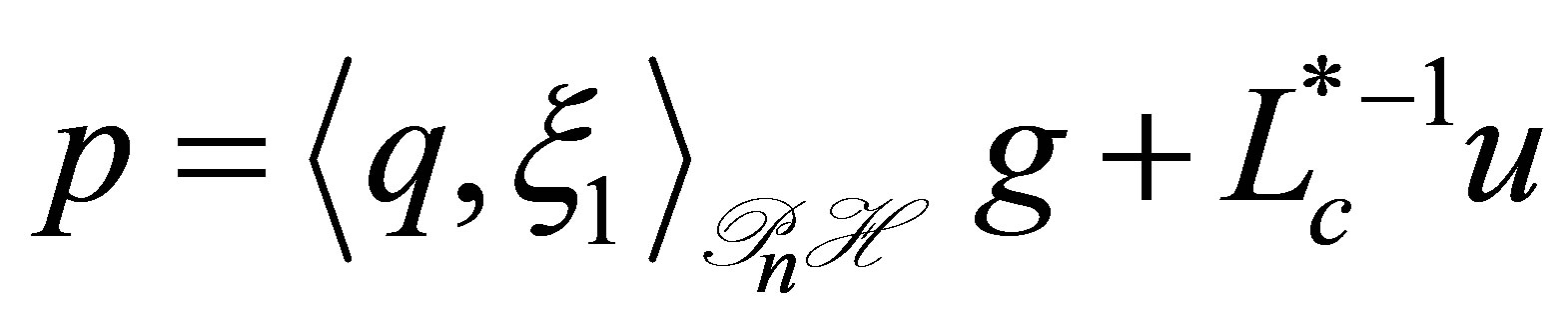 and
and 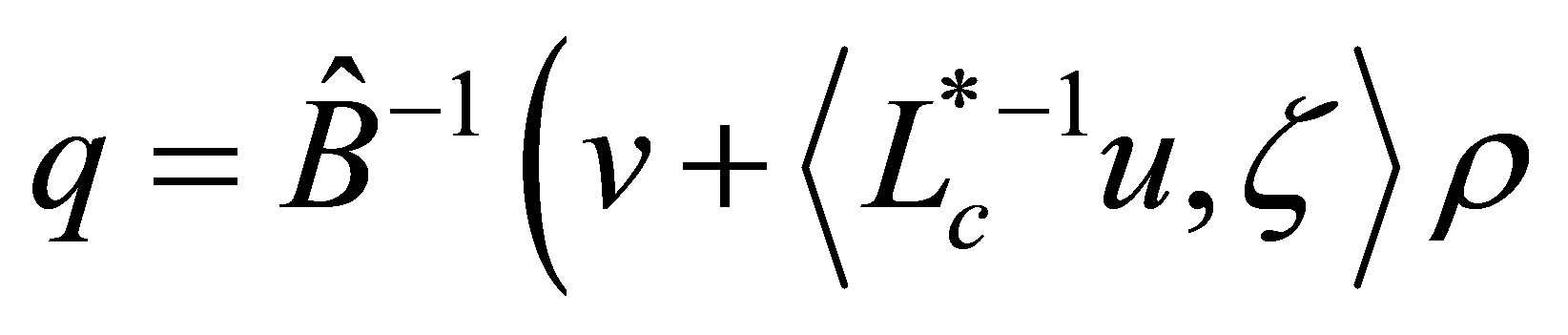
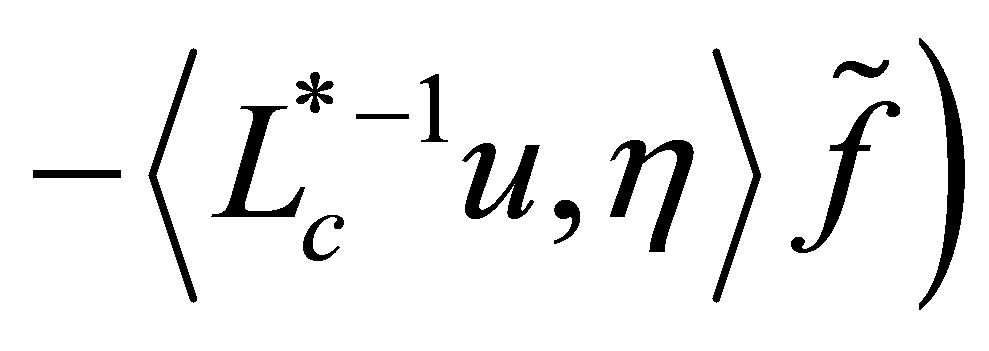 uniquely solves the above equation. Thus the bounded inverse
uniquely solves the above equation. Thus the bounded inverse 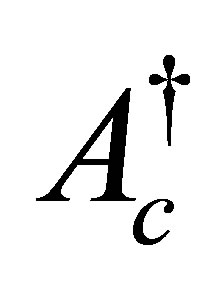 exists.
exists.
Denseness of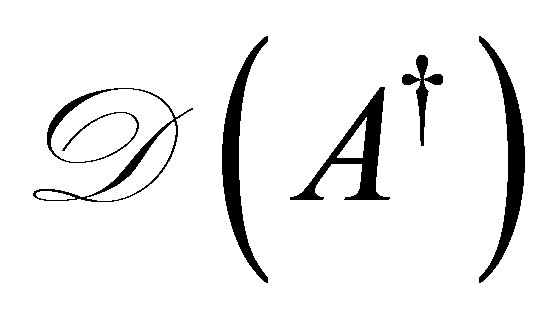 : it is enough to show that
: it is enough to show that
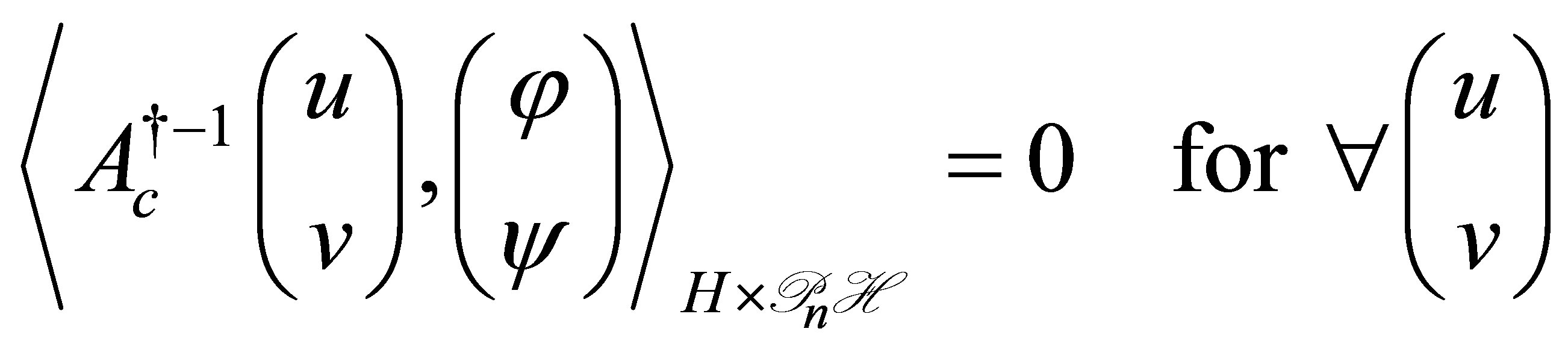
implies . The above left-hand side is calculated for every
. The above left-hand side is calculated for every 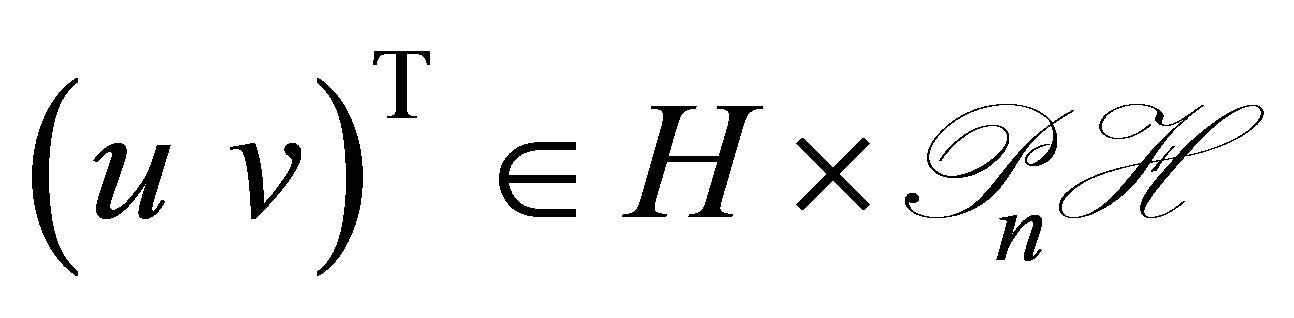 as
as
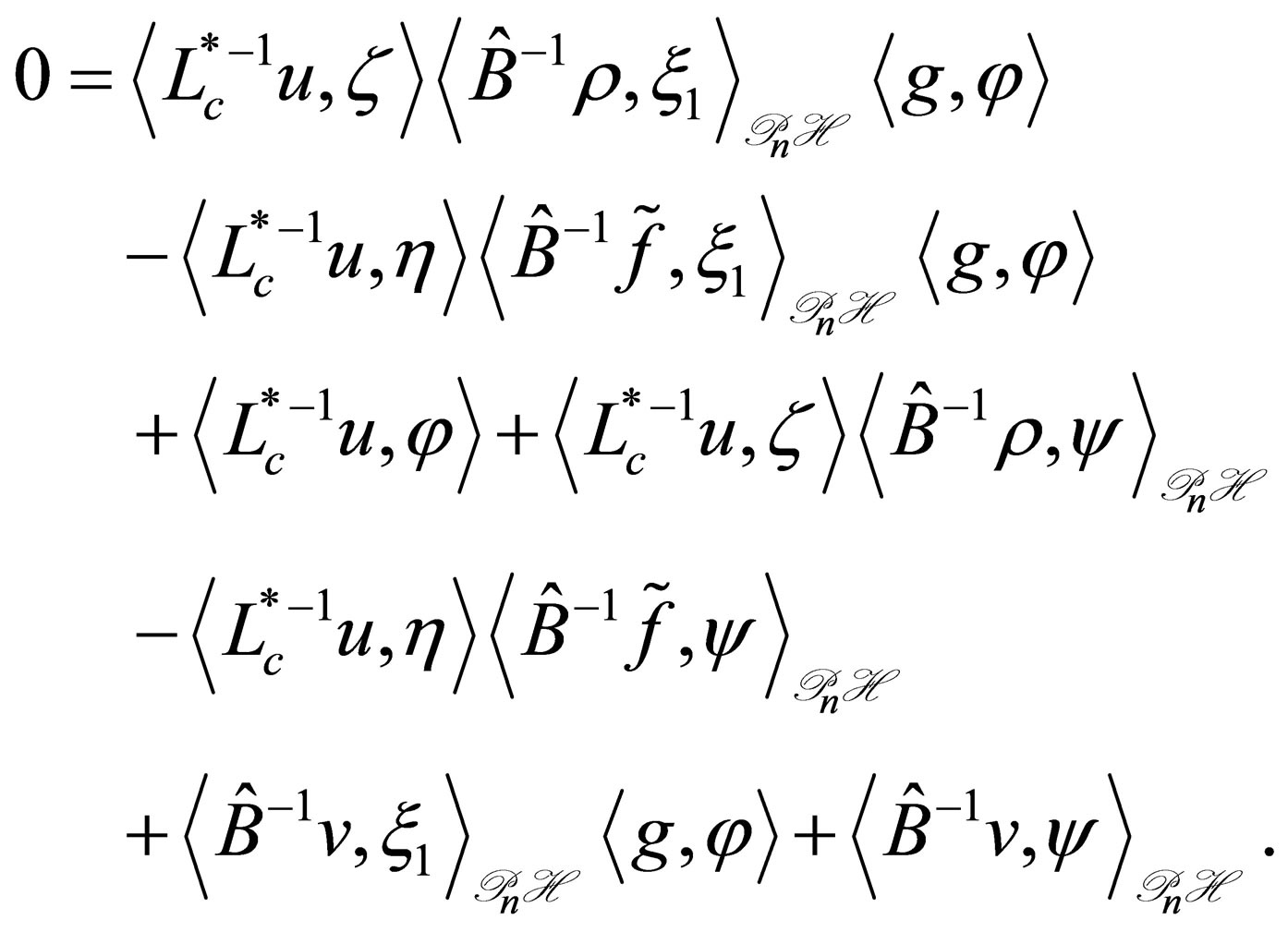
Since  is dense, this means that
is dense, this means that

and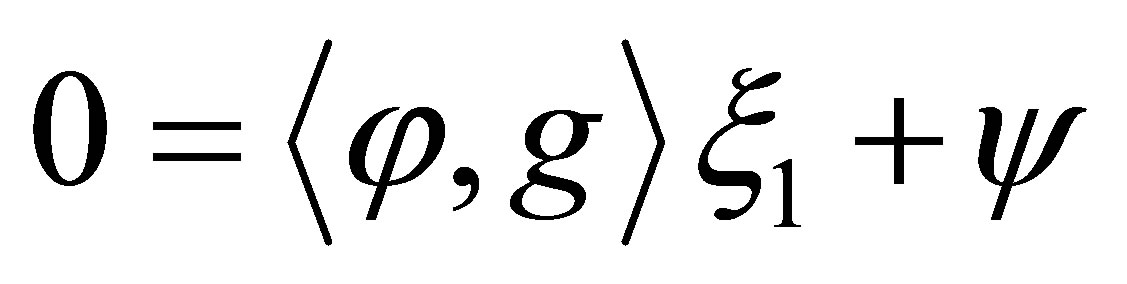 , from which we conclude that
, from which we conclude that 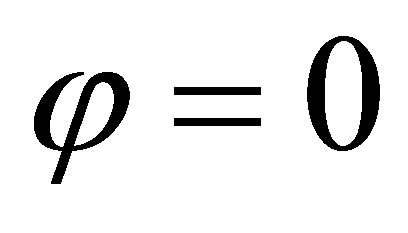 and
and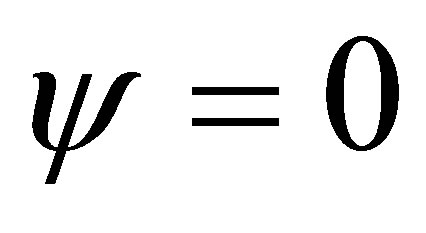 . Q.E.D.
. Q.E.D.
In view of the fact that both  and
and 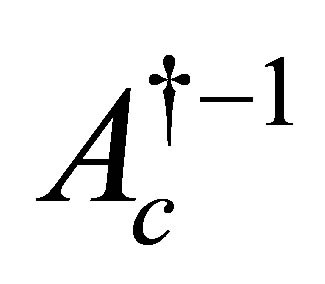 exist as a bounded inverse, it is immediate that
exist as a bounded inverse, it is immediate that 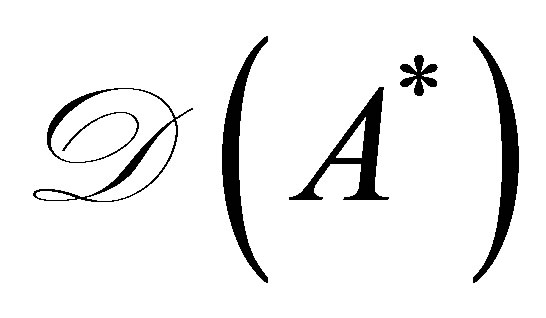 is contained in
is contained in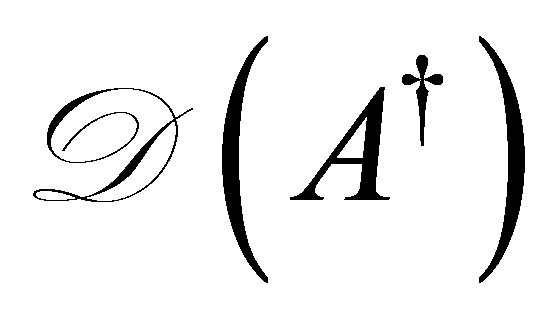 . We have proven that
. We have proven that
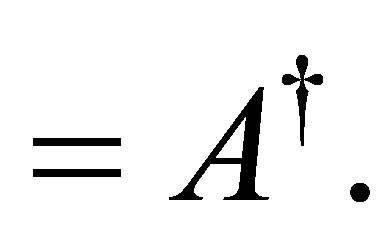
 (51)
(51)
Proof of Proposition 8. By setting 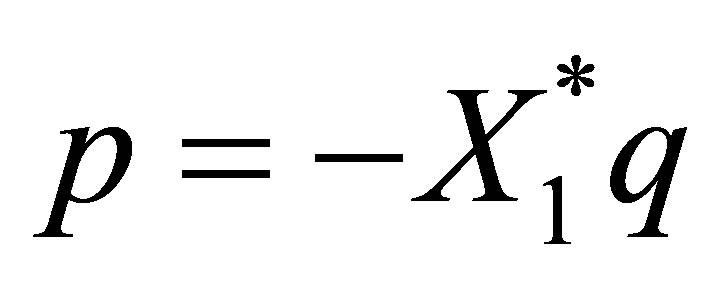 and
and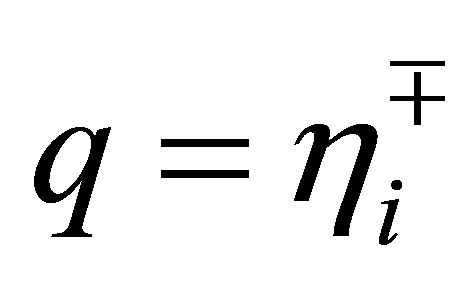 ,
, 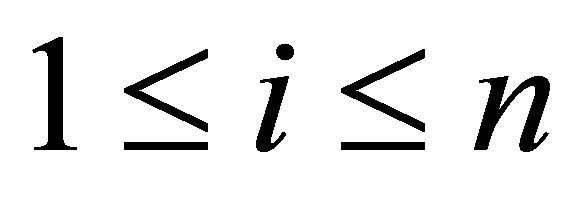 ,
, 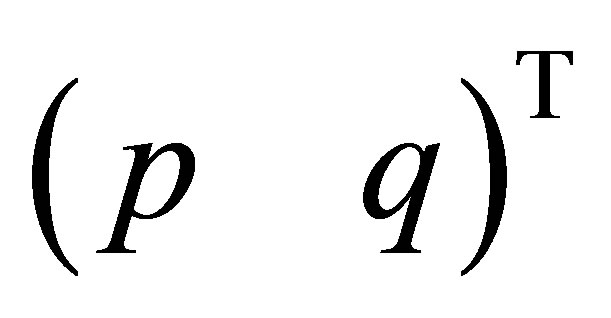 belongs to
belongs to . By (49), we see that
. By (49), we see that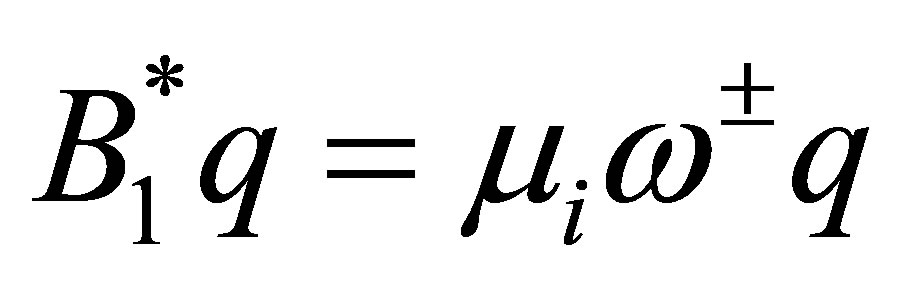 , and
, and 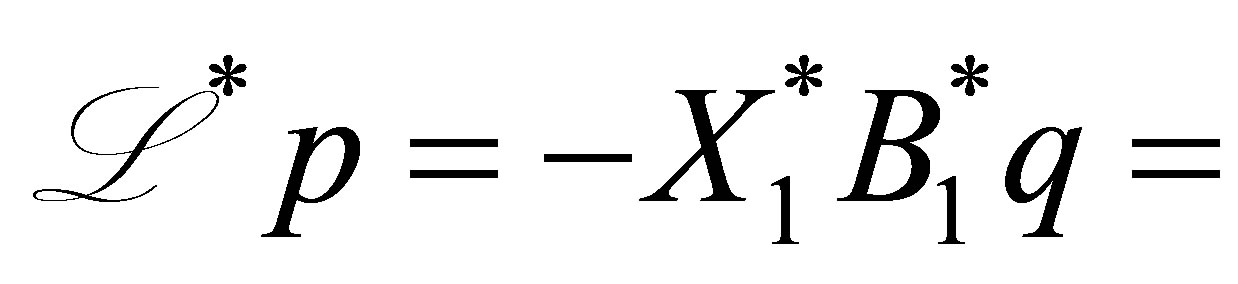
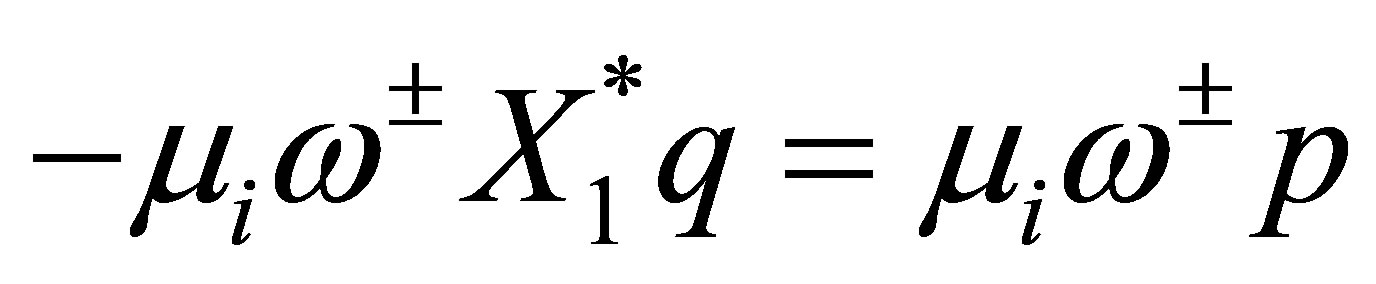 , which shows (43) Q.E.D.
, which shows (43) Q.E.D.
Proof of Theorem 7. Assuming that 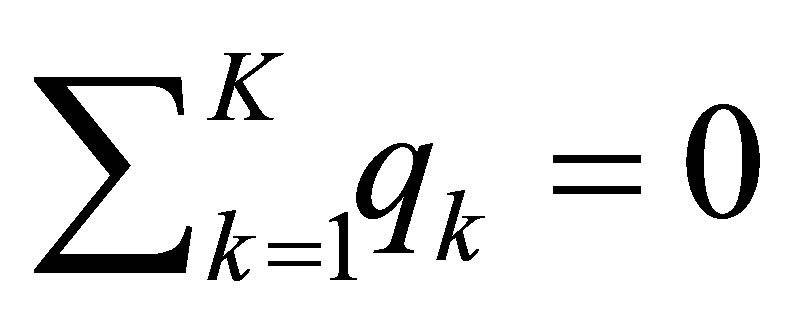 in (42), we derive a contradiction. In (42), adding the equations of
in (42), we derive a contradiction. In (42), adding the equations of 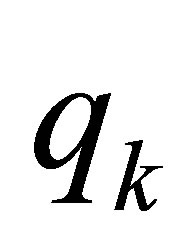 over 1 through
over 1 through , we see that
, we see that
 (52)
(52)
where ,
,  , and
, and . The Fourier coefficients of these vectors relative to the orthonormal system
. The Fourier coefficients of these vectors relative to the orthonormal system 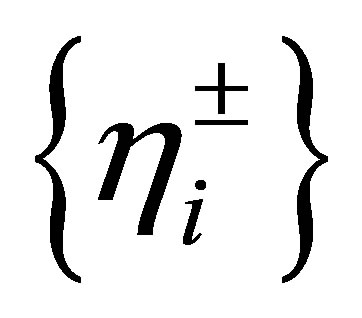 satisfy
satisfy
 (53)
(53)
where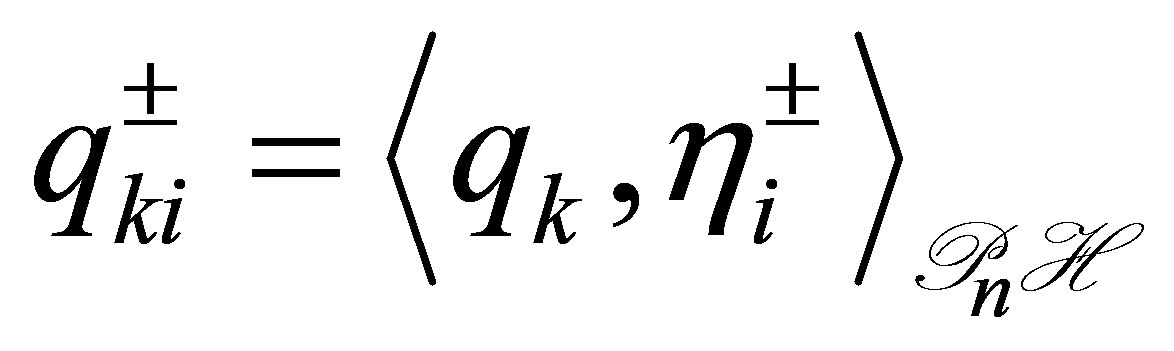 . Note that
. Note that 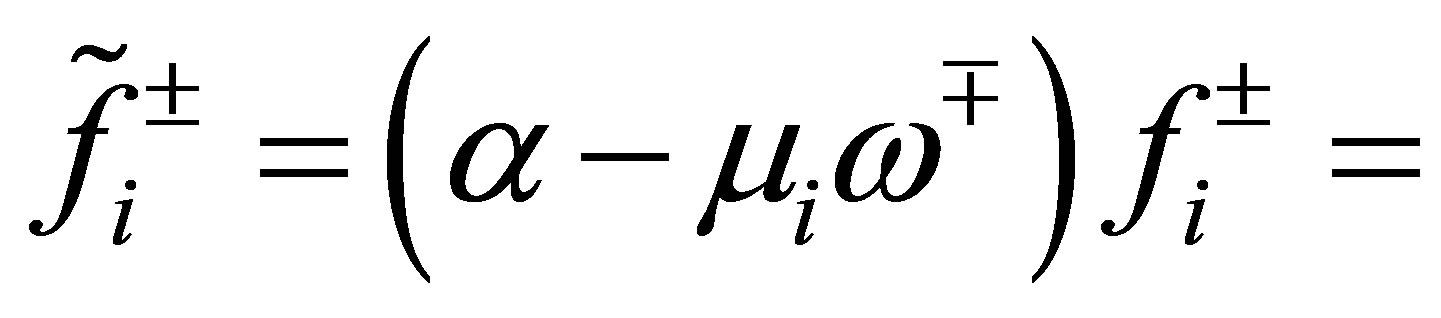
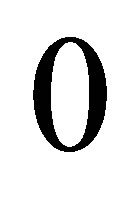 for
for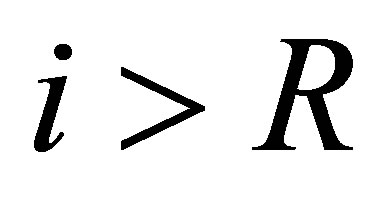 . We show that
. We show that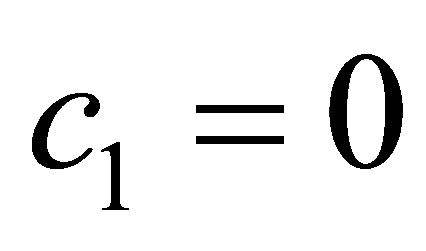 . Supposing the contrary, we must have
. Supposing the contrary, we must have
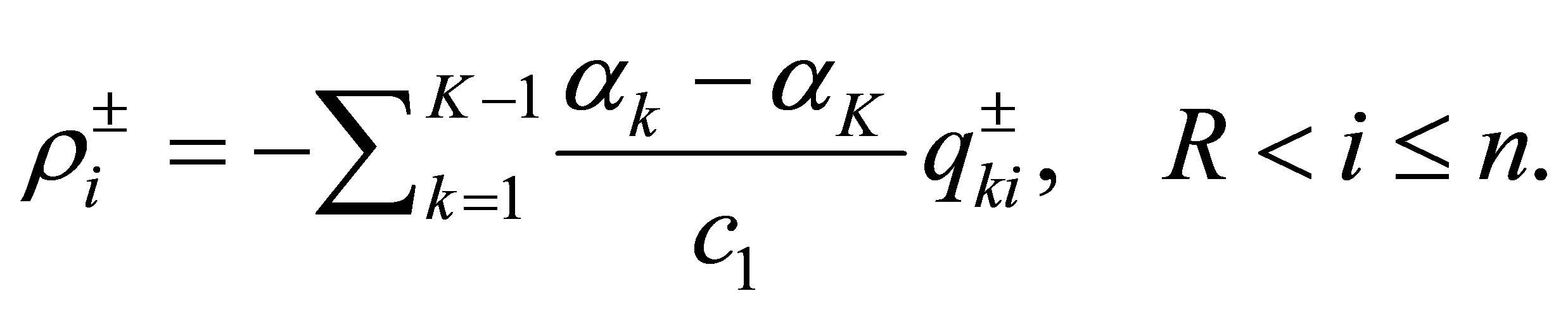 (54)
(54)
Set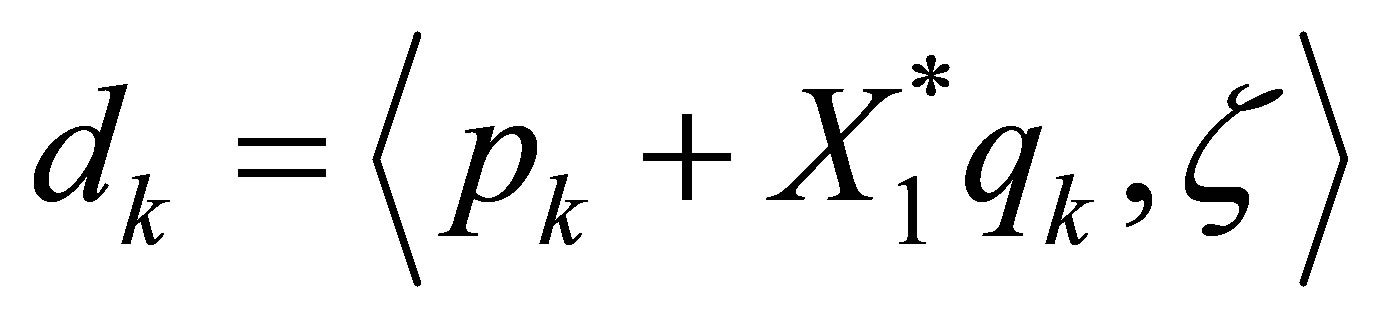 ,
,  for simplicity. Then,
for simplicity. Then,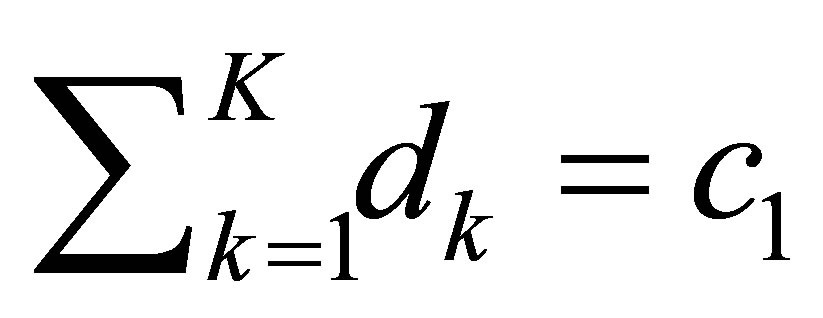 . In the equation for
. In the equation for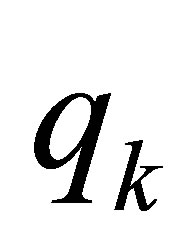 ,
, 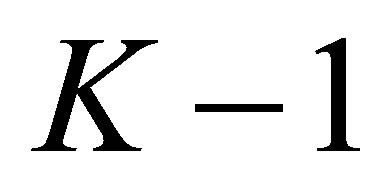
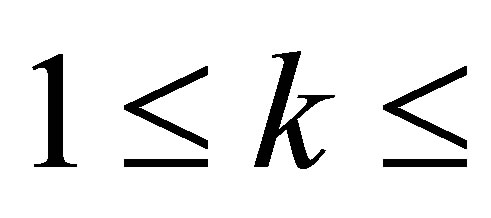 , we see that
, we see that
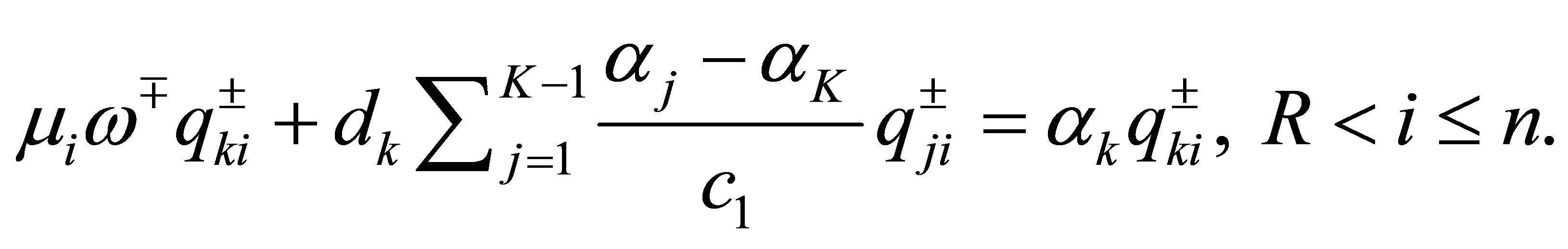
The number of these  is
is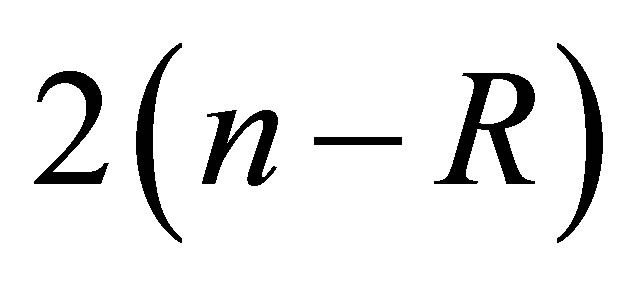 . Consider the algebraic equation in
. Consider the algebraic equation in :
:
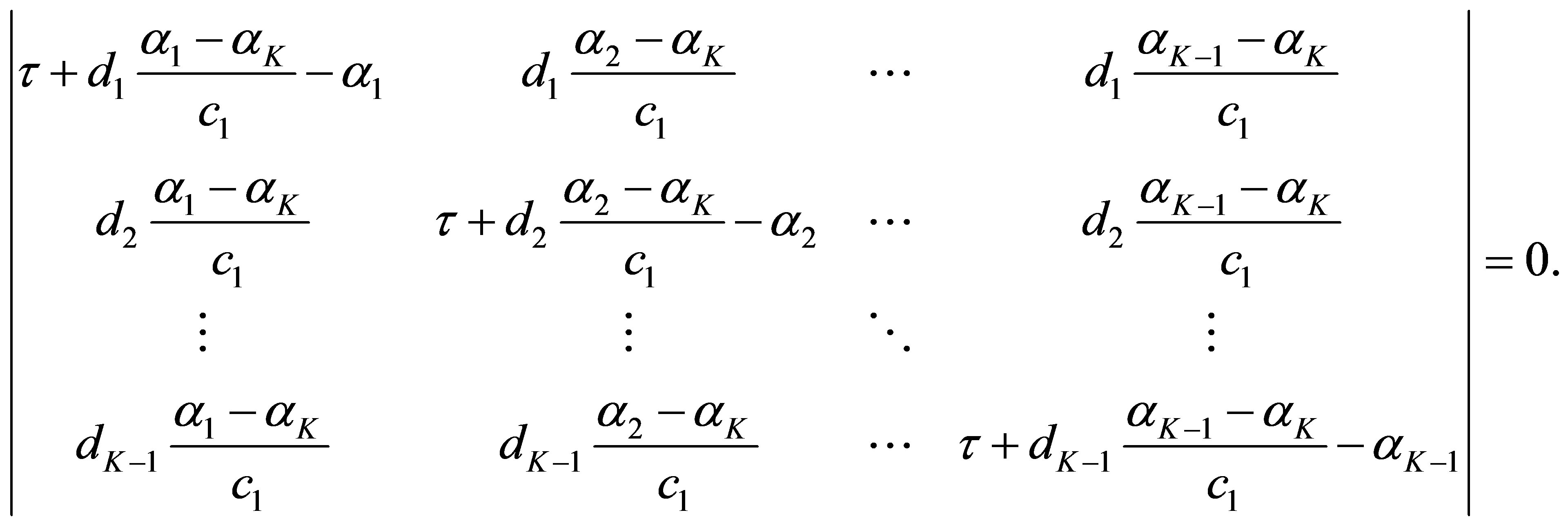
The equation admits 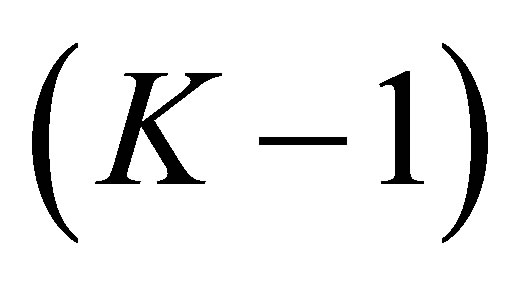 solutions. The number of the solutions
solutions. The number of the solutions  which agree with one of the
which agree with one of the 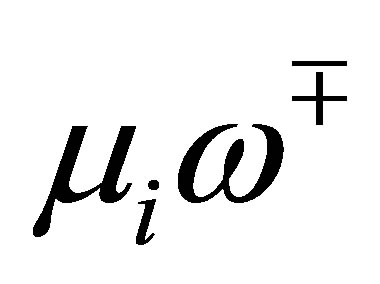 is at most
is at most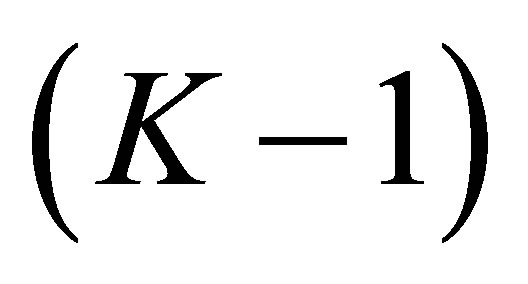 . In other words, the determinant is not equal to 0 for the other
. In other words, the determinant is not equal to 0 for the other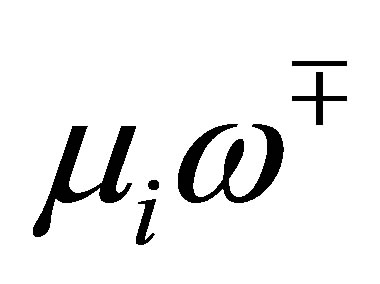 , the number of which is atleast
, the number of which is atleast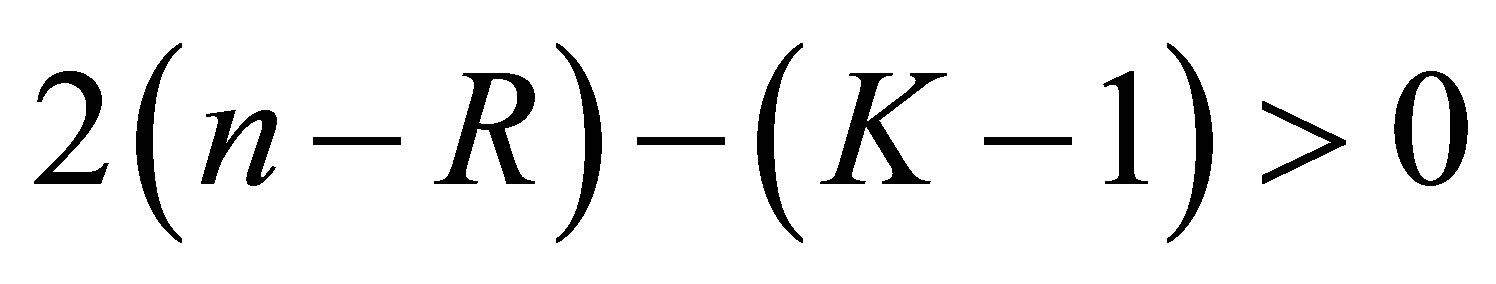 . Thus for these
. Thus for these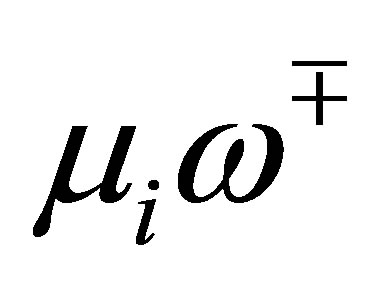 , we must have
, we must have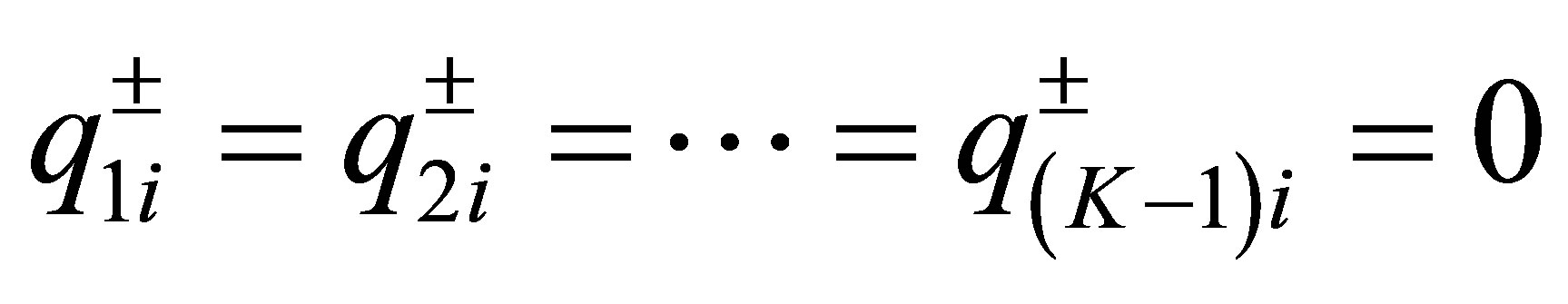 . By (53), this implies that
. By (53), this implies that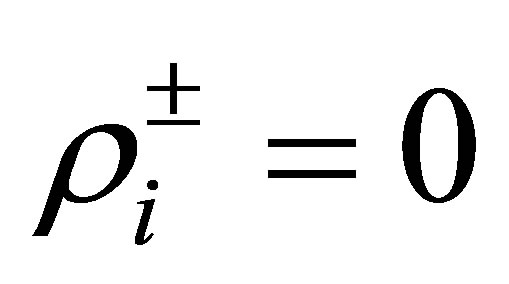 , which contradicts our assumption (40). We have shown that
, which contradicts our assumption (40). We have shown that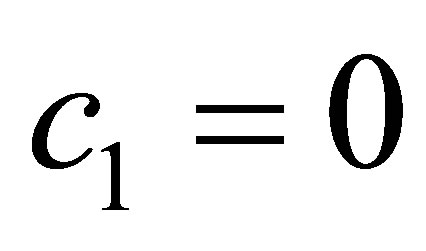 . Thus we have, for
. Thus we have, for ,
,
 (55)
(55)
Comparing the Fourier coefficients in the equations to  in (42), we see that
in (42), we see that
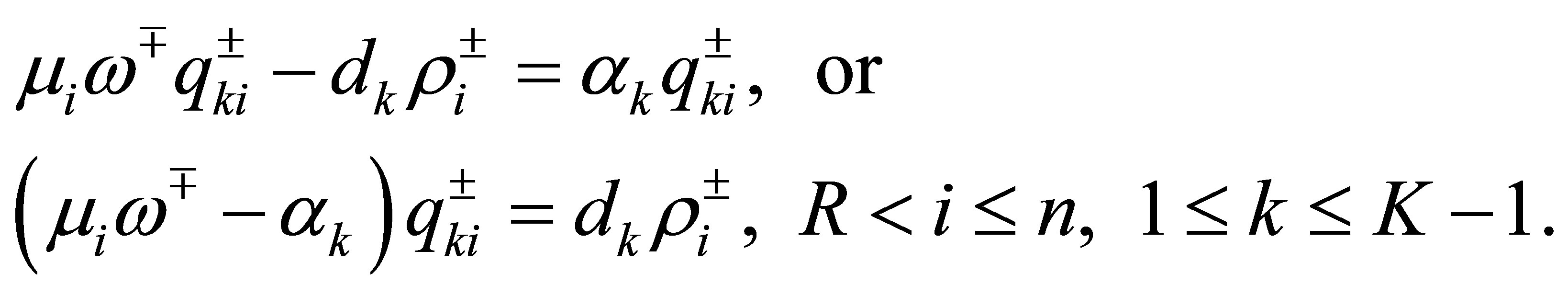
The number of the eigenvalues  which agree with one of the
which agree with one of the 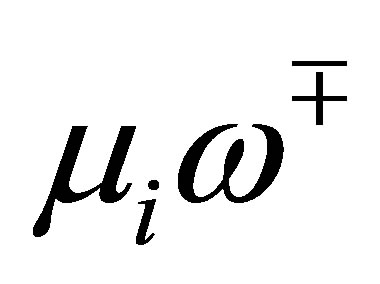 is at most
is at most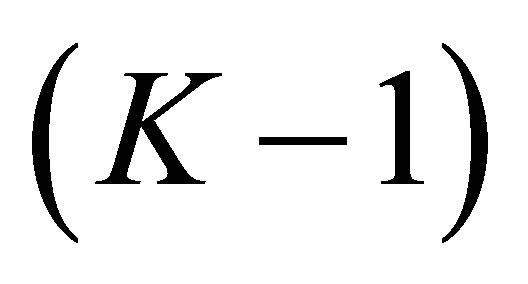 . In other words, the number of the
. In other words, the number of the 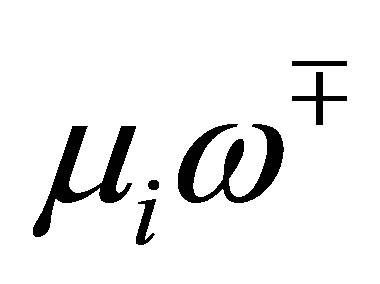 which does not agree with any of the
which does not agree with any of the  is at least
is at least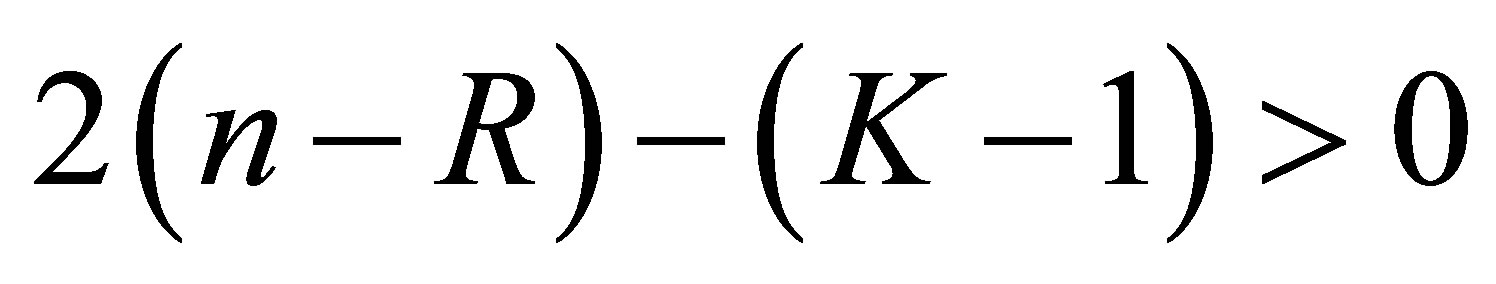 . For these
. For these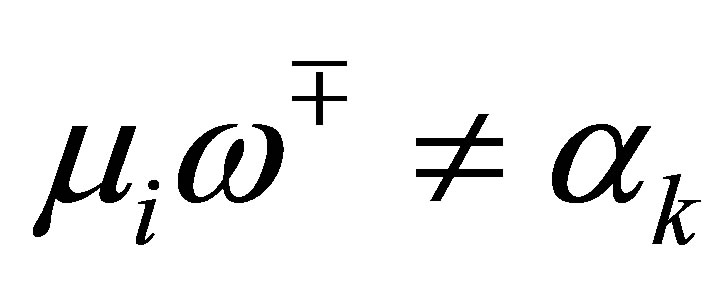 , we see from (55) that
, we see from (55) that
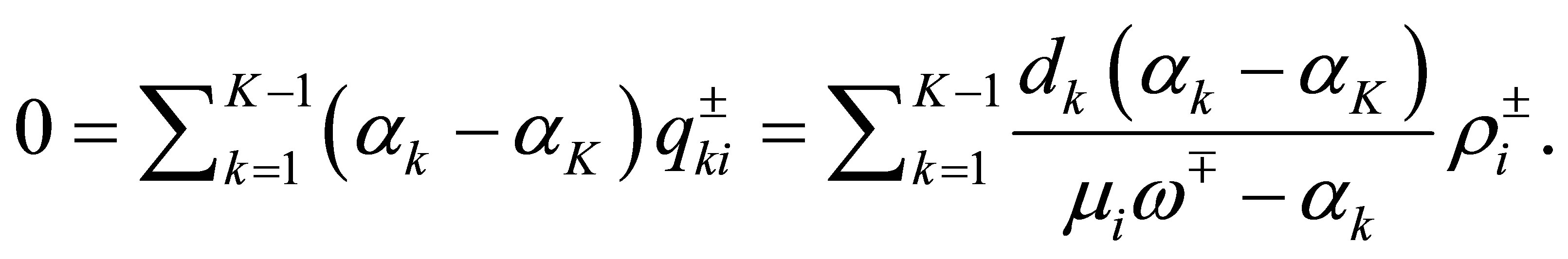
Since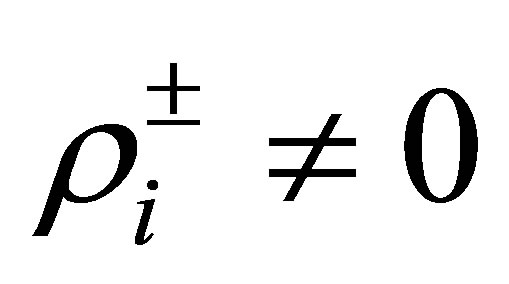 , this means that the relation in
, this means that the relation in :
:
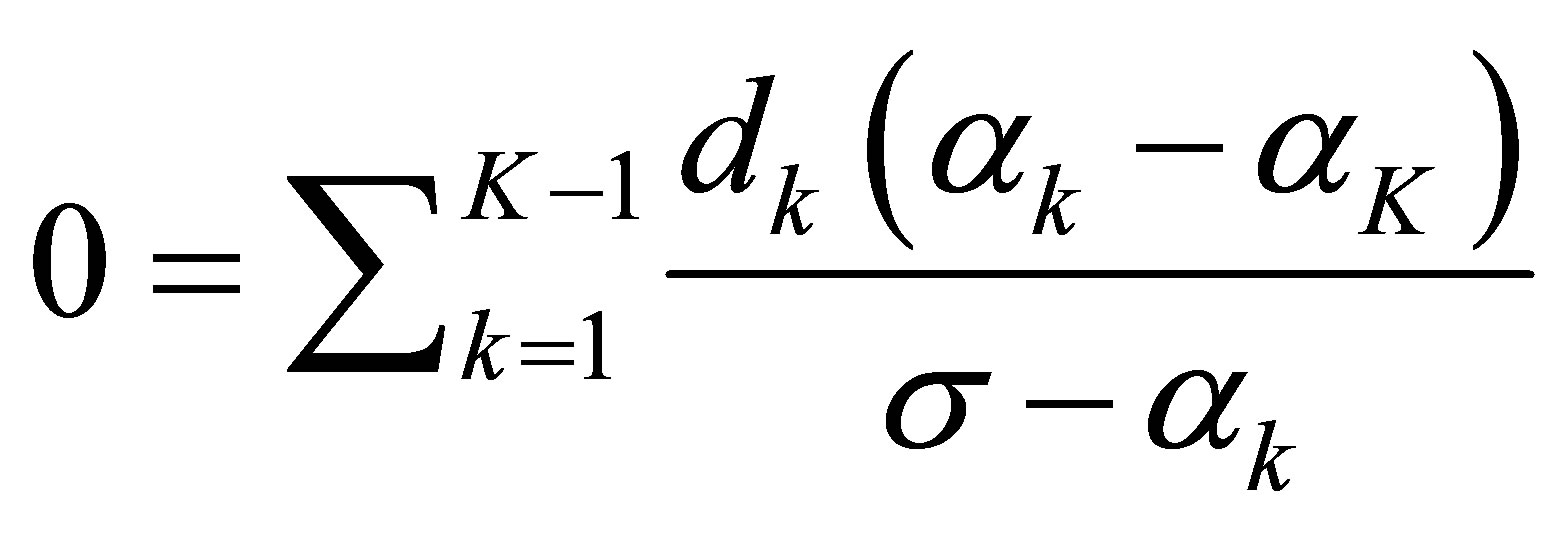 (56)
(56)
holds for the above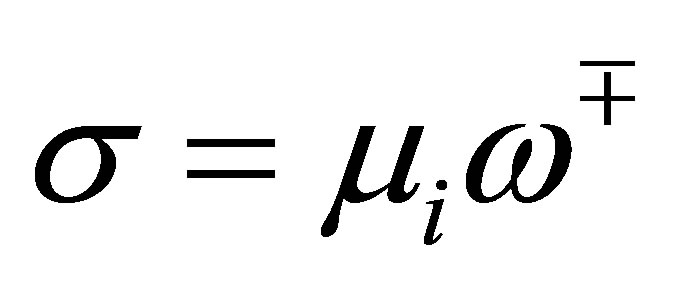 , the distinct number of which is at least
, the distinct number of which is at least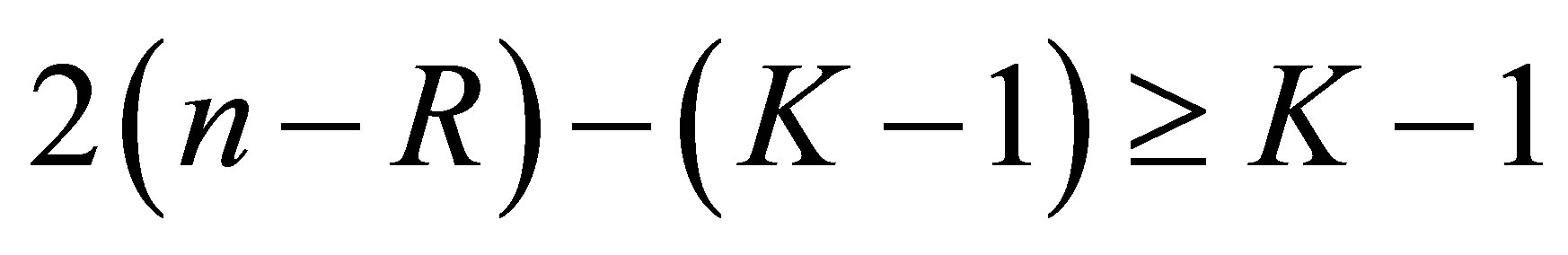 . This implies that the relation (56) holds for any
. This implies that the relation (56) holds for any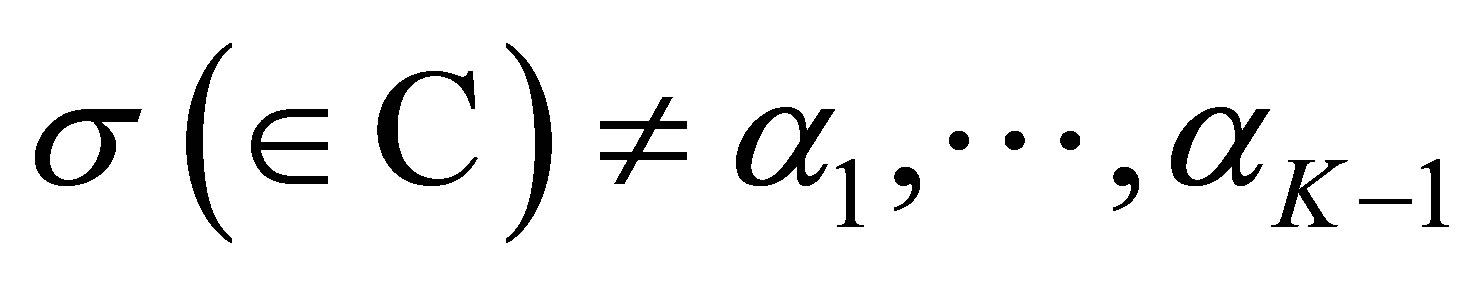 . calculating the residue at each
. calculating the residue at each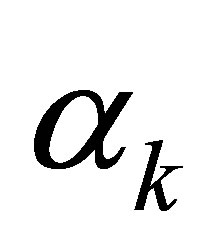 , we find that
, we find that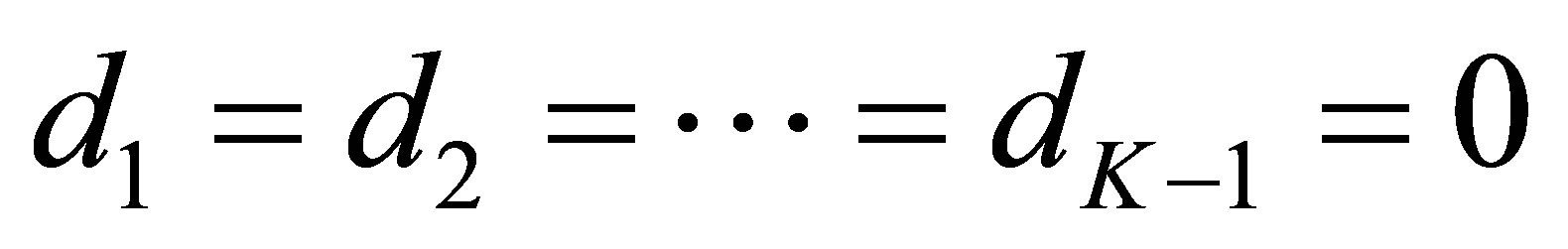 , and thus
, and thus , too.
, too.
We go back to the equations to 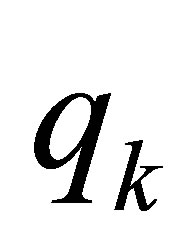 in (42) again. Since
in (42) again. Since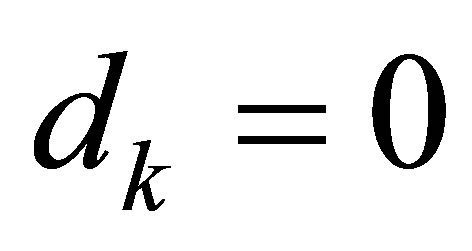 ,
,  , we have
, we have
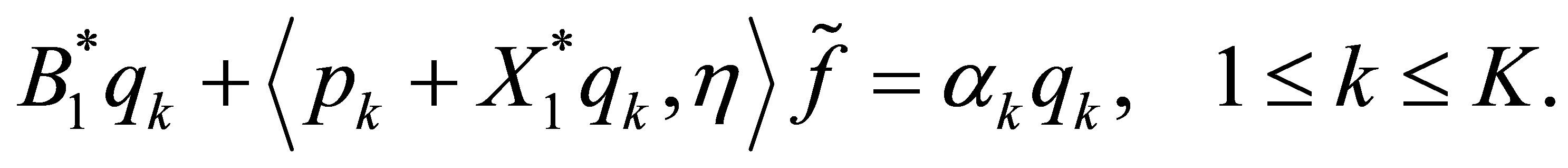
Set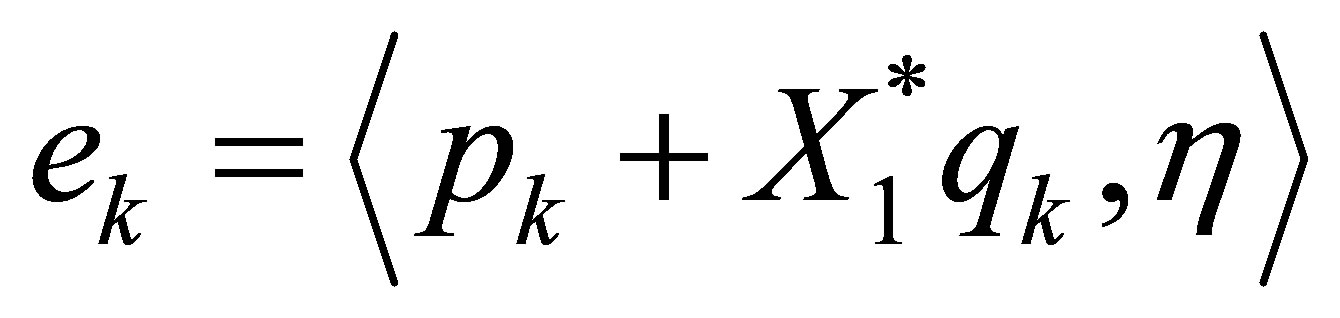 . Then,
. Then,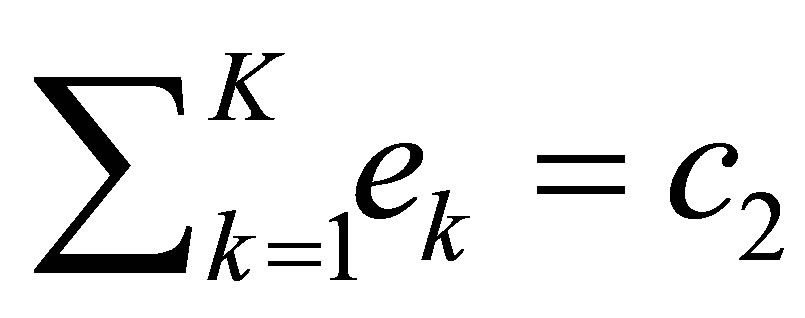 . Calculating the Fourier coefficients, we have
. Calculating the Fourier coefficients, we have

The numbers of these  and
and 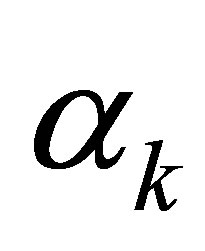 are
are 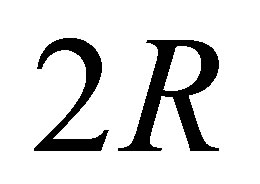 and
and , respectively. Thus, the number of
, respectively. Thus, the number of 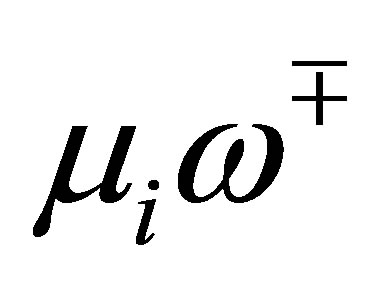 which does not agree with any of
which does not agree with any of 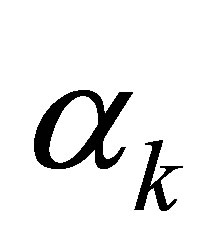 is at least
is at least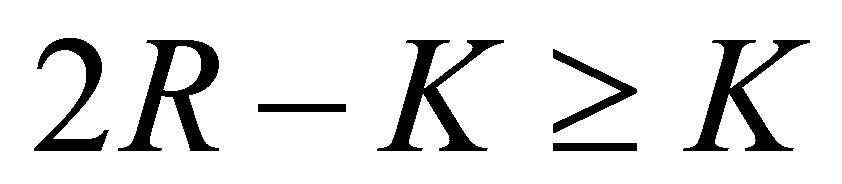 . For these
. For these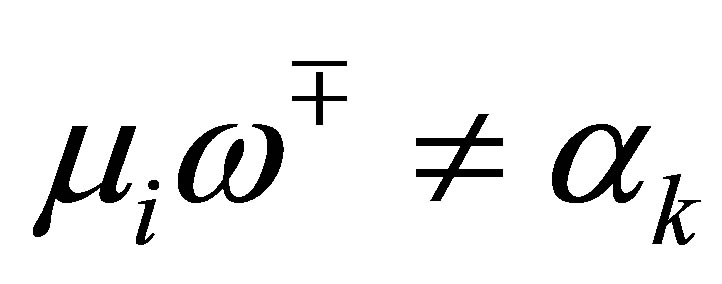 , we see by the relation (54) that
, we see by the relation (54) that
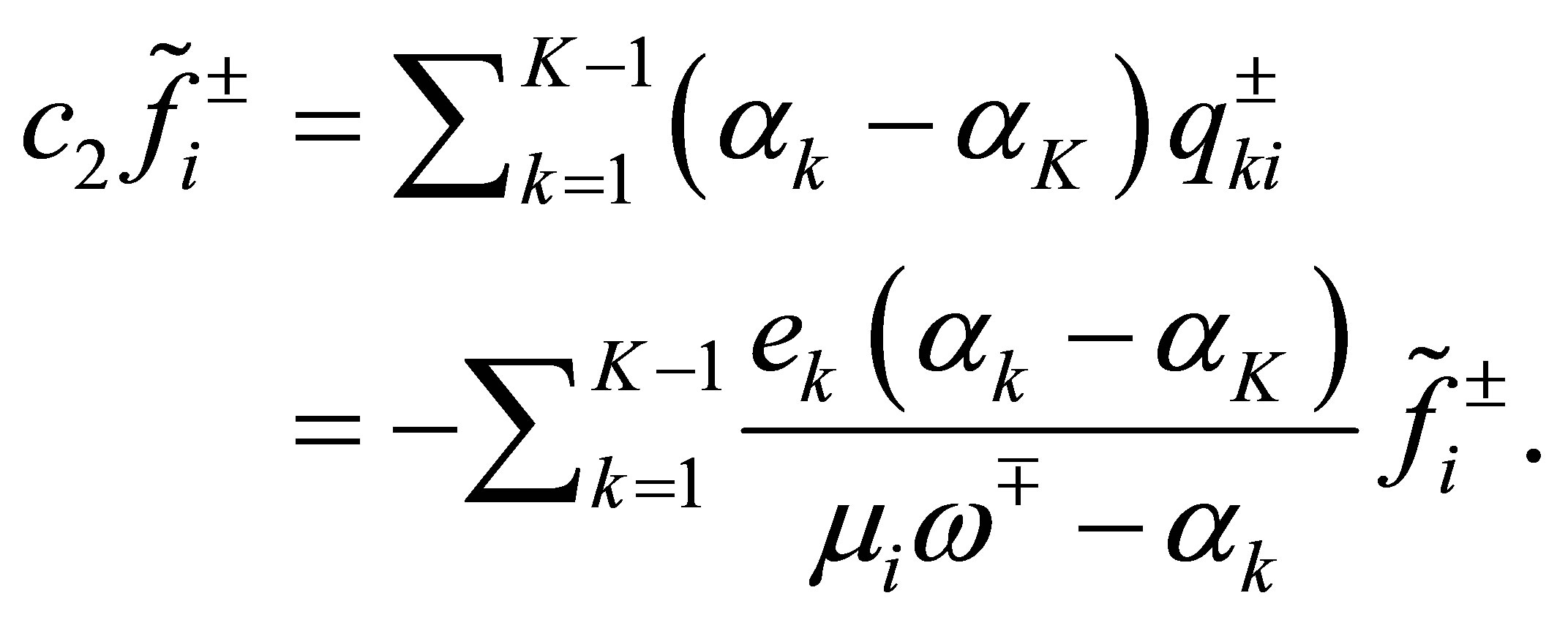
But, since 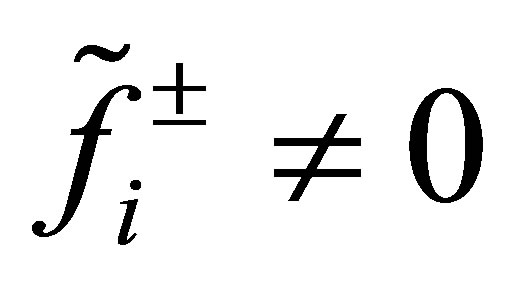 by (40), this means that the relation in
by (40), this means that the relation in :
:
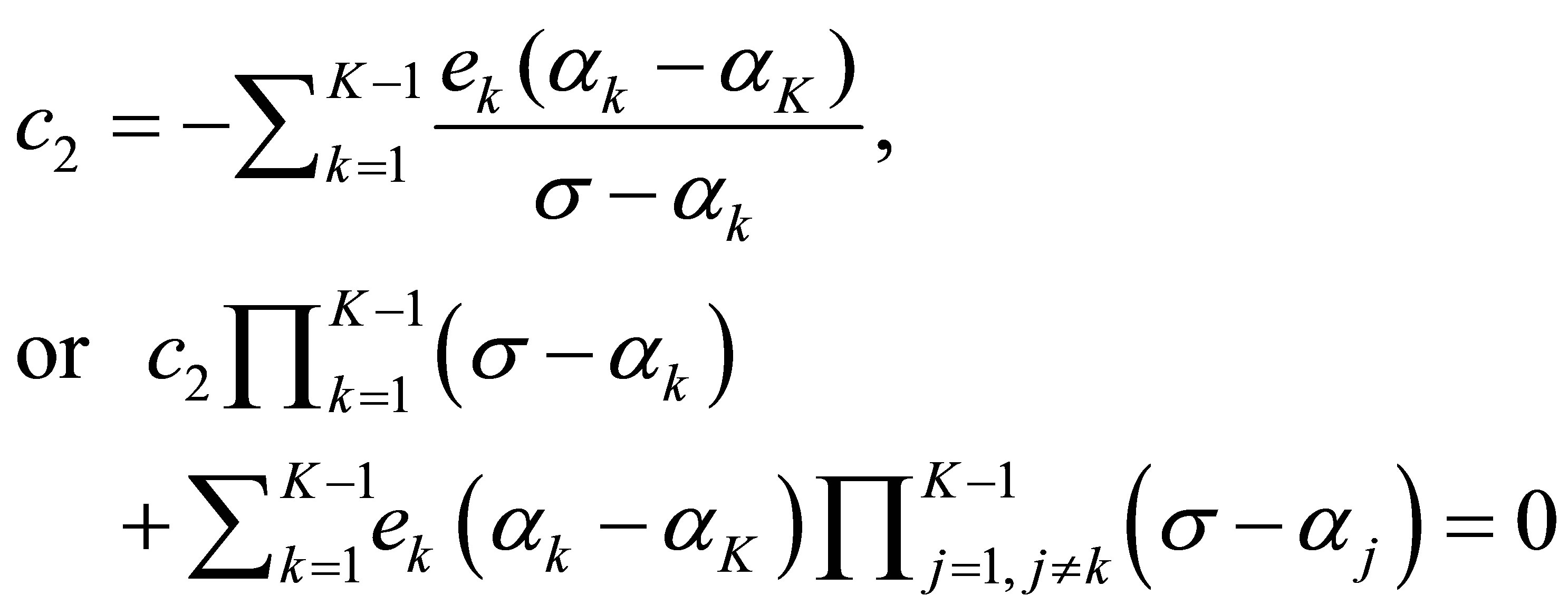 (57)
(57)
holds for the above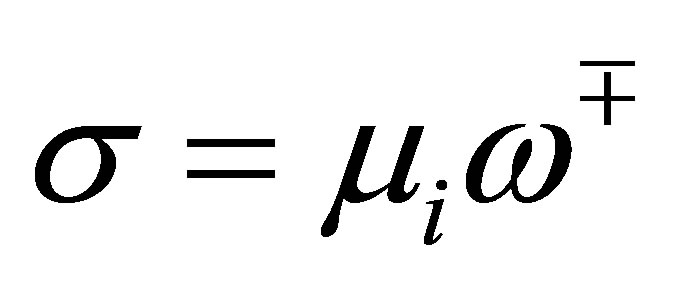 , the distinct number of which is at least
, the distinct number of which is at least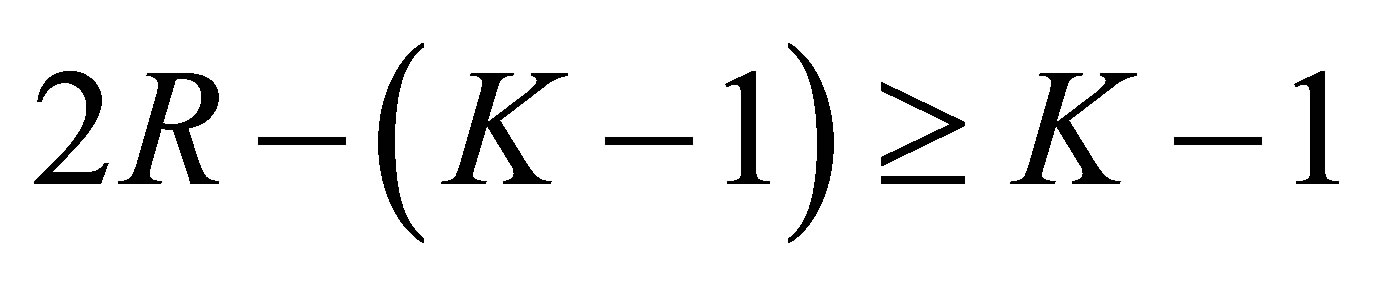 . The situation is the same as in (56). Thus the relation (57) holds for any
. The situation is the same as in (56). Thus the relation (57) holds for any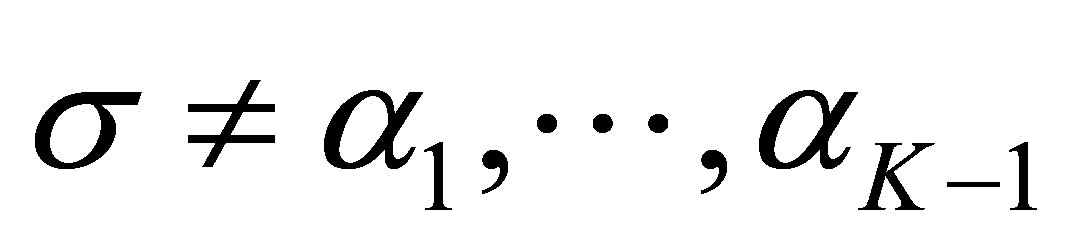 . Calculating the residue at each
. Calculating the residue at each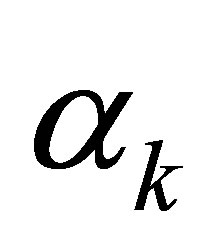 , we similarly find that
, we similarly find that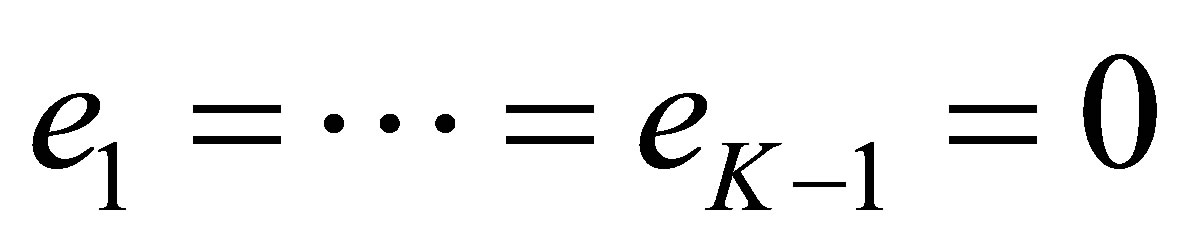 ,
, 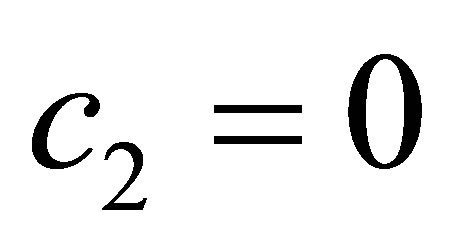 , and thus
, and thus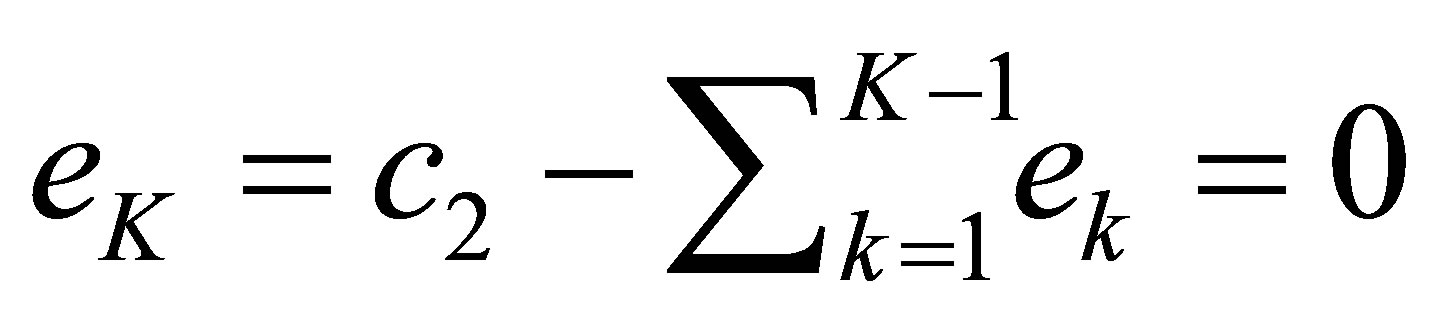 , too. Since
, too. Since ,
, 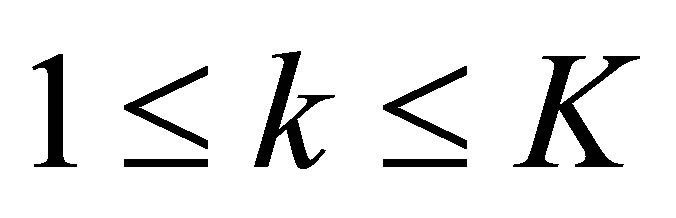 , we have finally obtained from (42) and (55) that
, we have finally obtained from (42) and (55) that 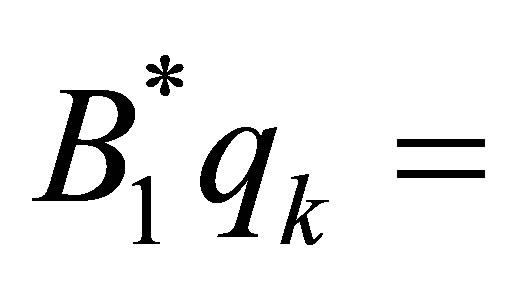
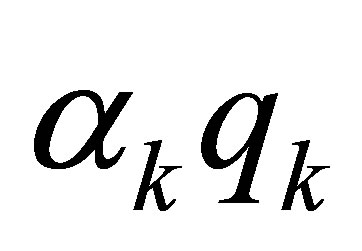 ,
, 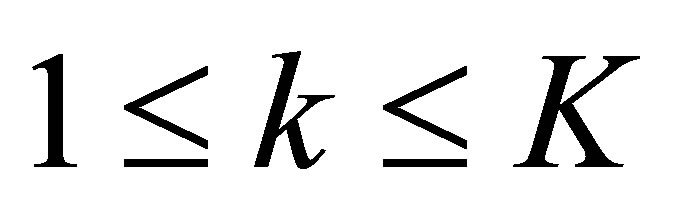 , and
, and
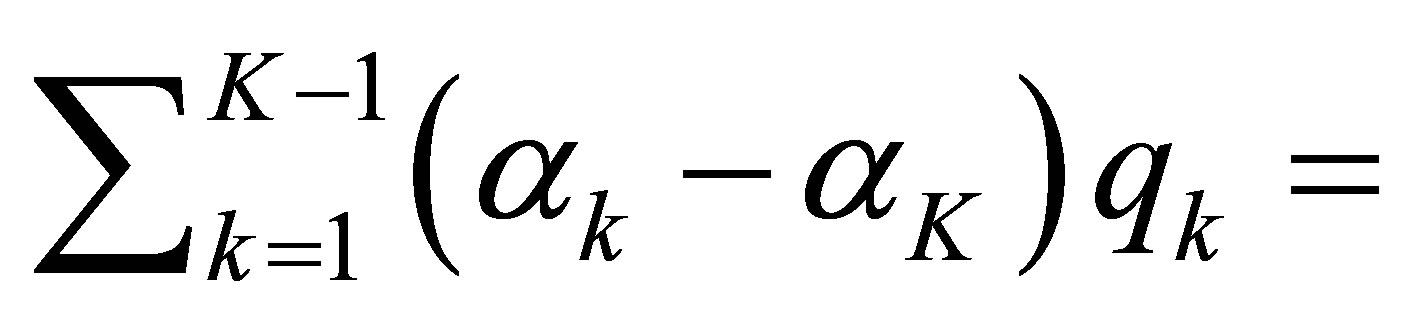 . Applying
. Applying 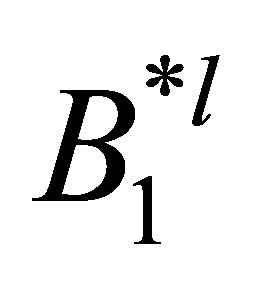 to the both sides of the above second equation, we see that, for
to the both sides of the above second equation, we see that, for ,
,
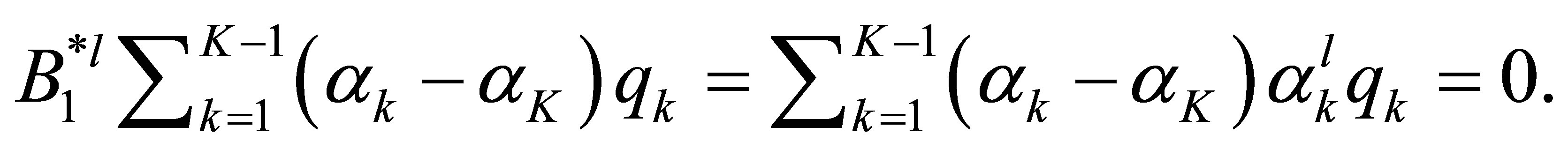
In other words, we have the relation:
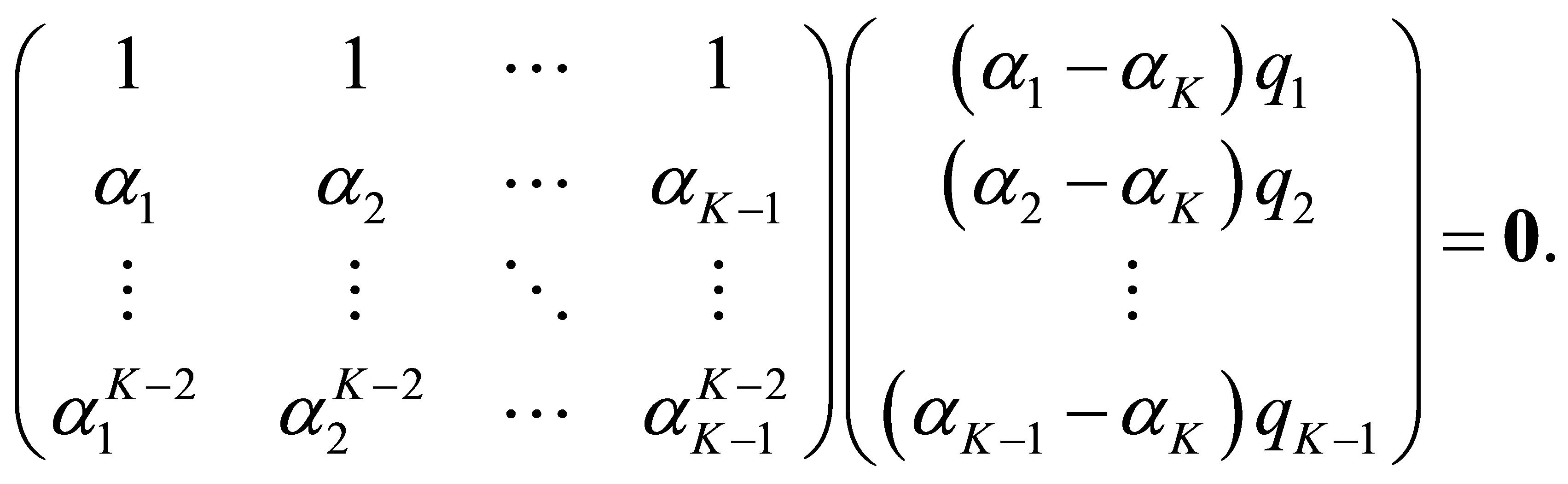
But 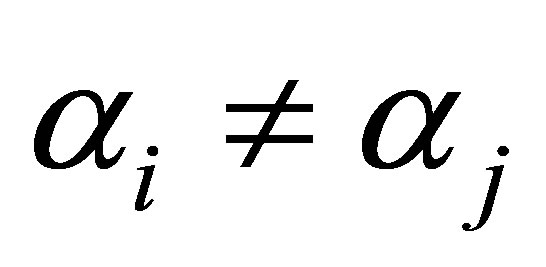 for
for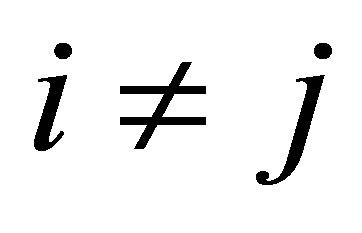 . Thus, we immediately find that
. Thus, we immediately find that ,
,  , i.e.,
, i.e., 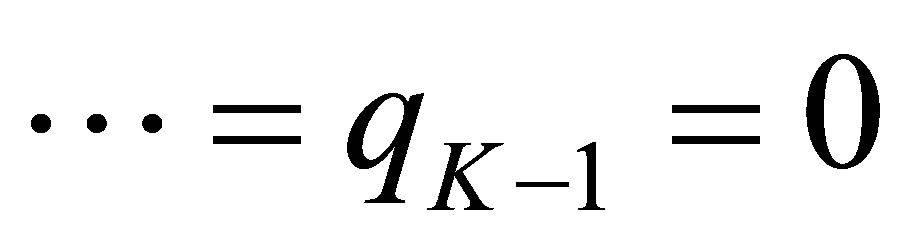
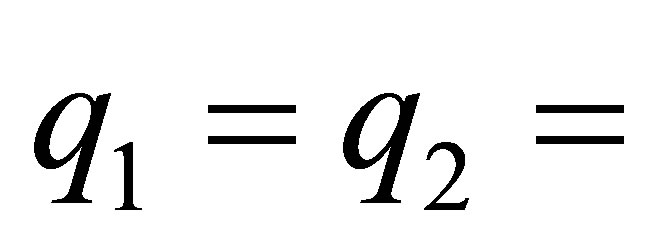 , and that
, and that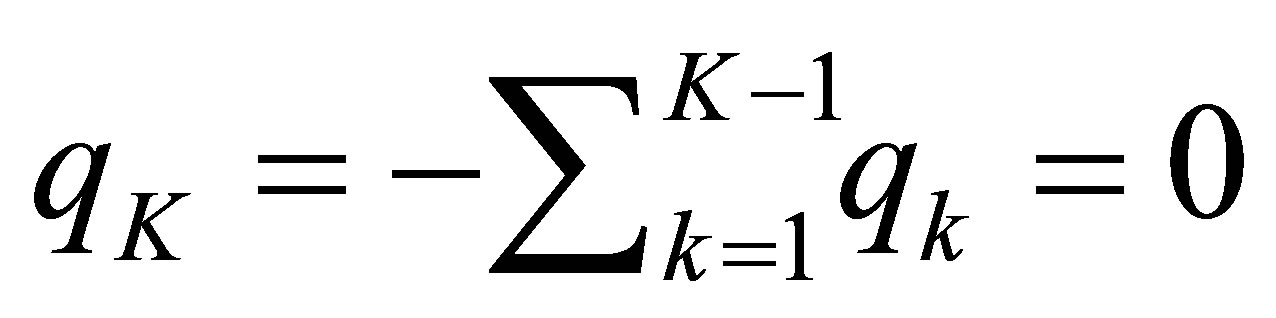 .
.
Recall that ,
,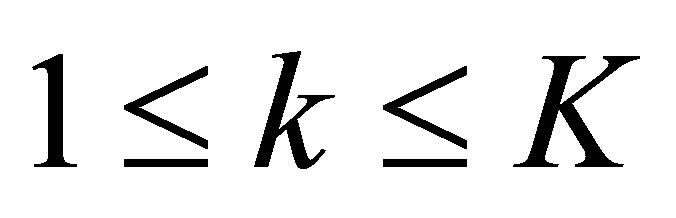 . Thus,
. Thus, 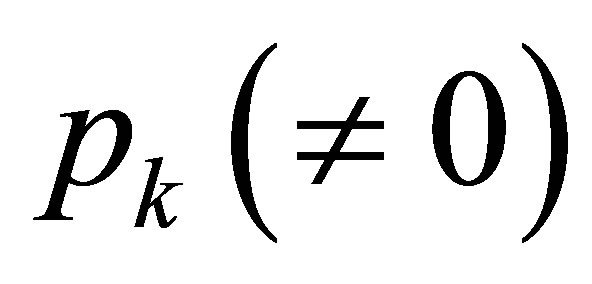 belongs to
belongs to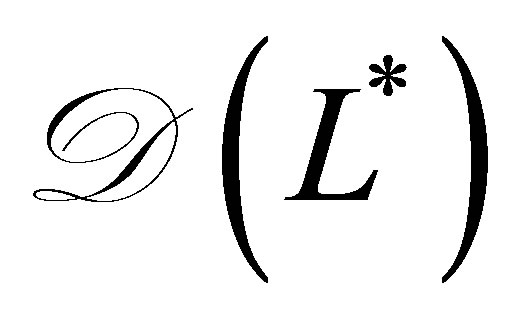 , and
, and 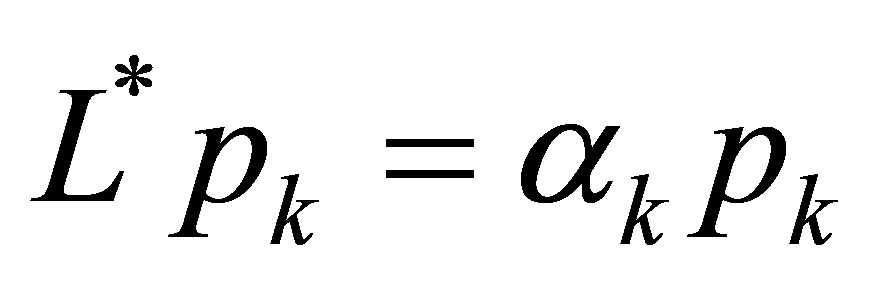 by (42). Each
by (42). Each  is found an eigenvalue of
is found an eigenvalue of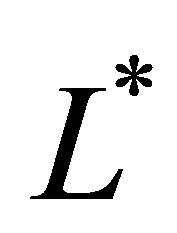 , and
, and 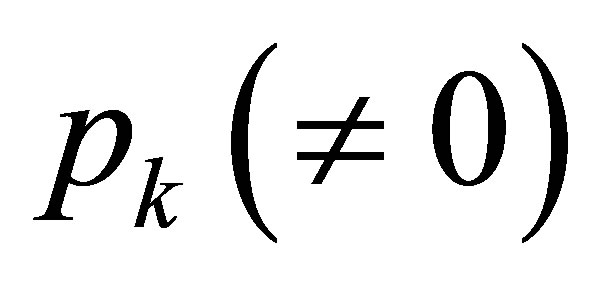 must be an eigenfunction. In addition,
must be an eigenfunction. In addition,
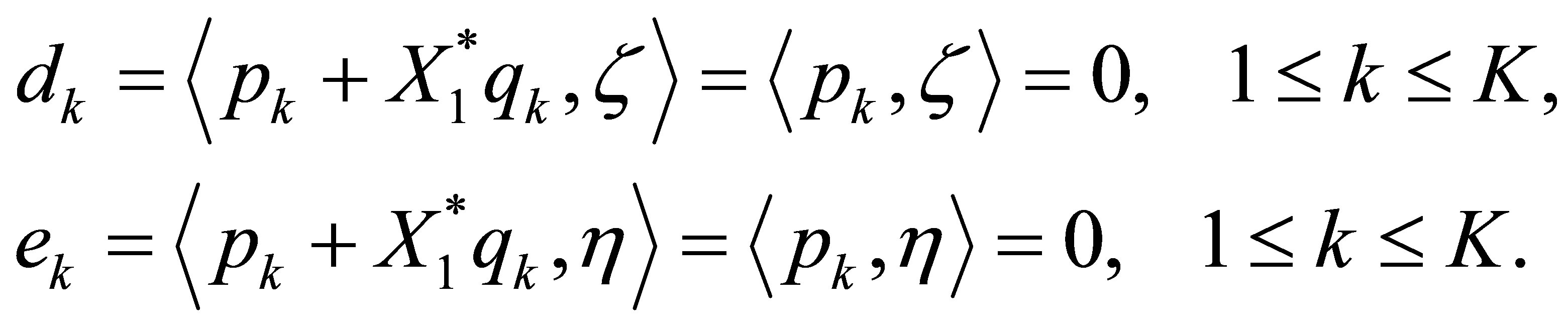
But, this contradicts our assumption (41). Q.E.D.
Proof of Theorem 9. We already know that 
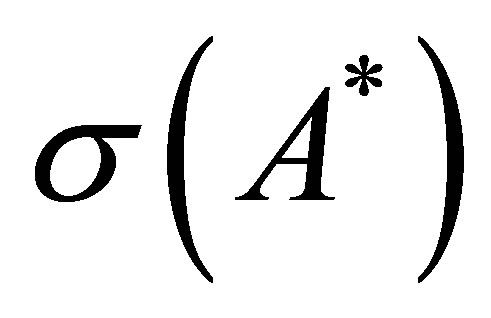 by Proposition 8. Let
by Proposition 8. Let 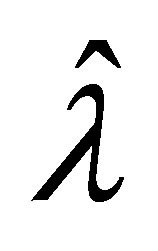 be in
be in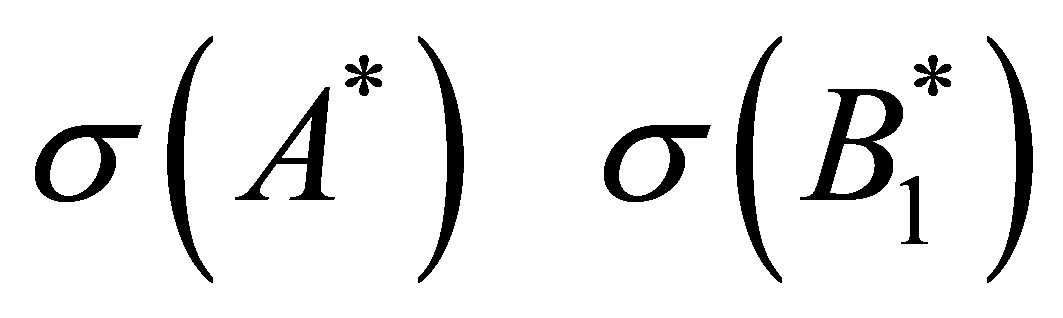 .
.
In view of (51), the relation: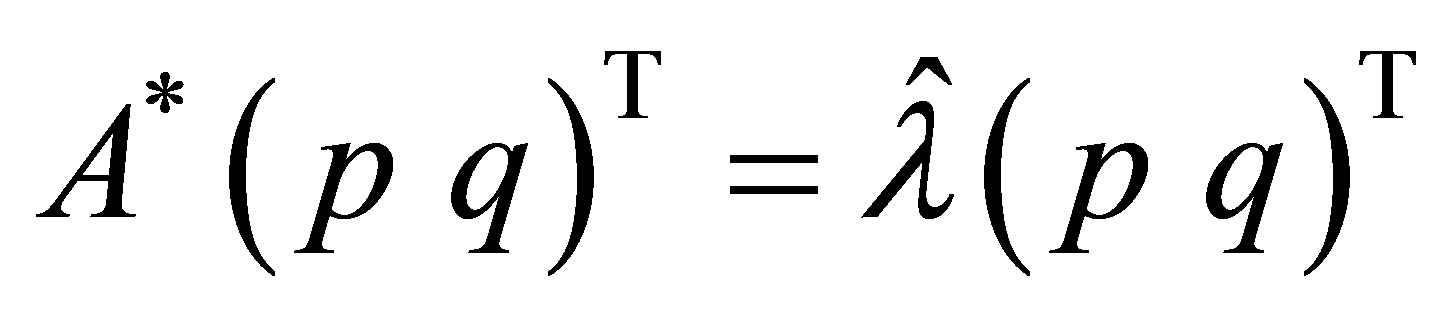 ,
, 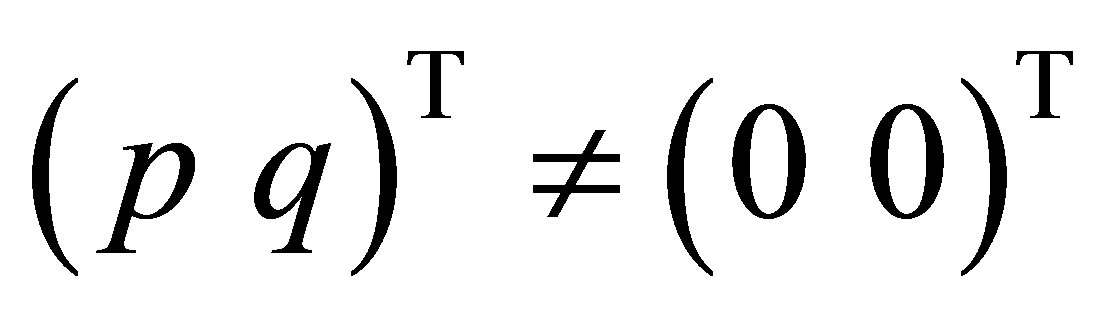 means that
means that
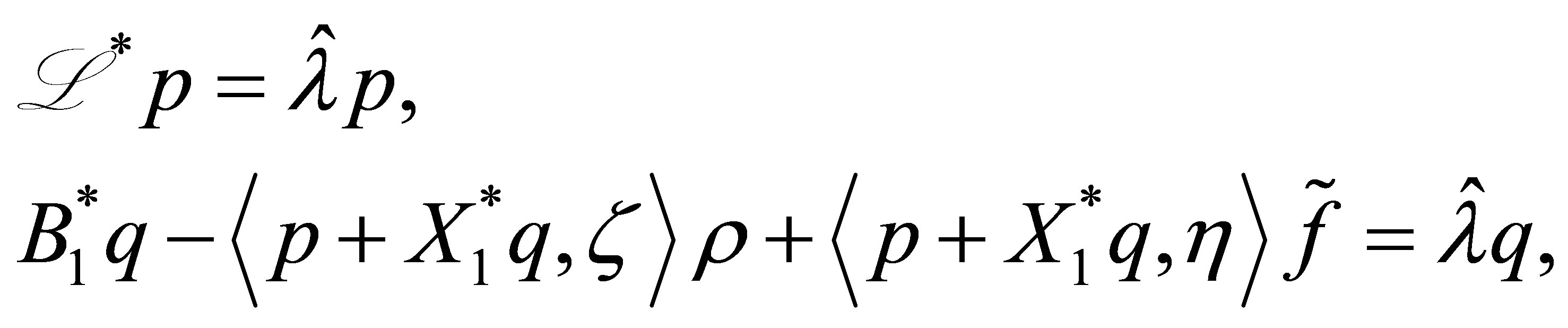 (58)
(58)
where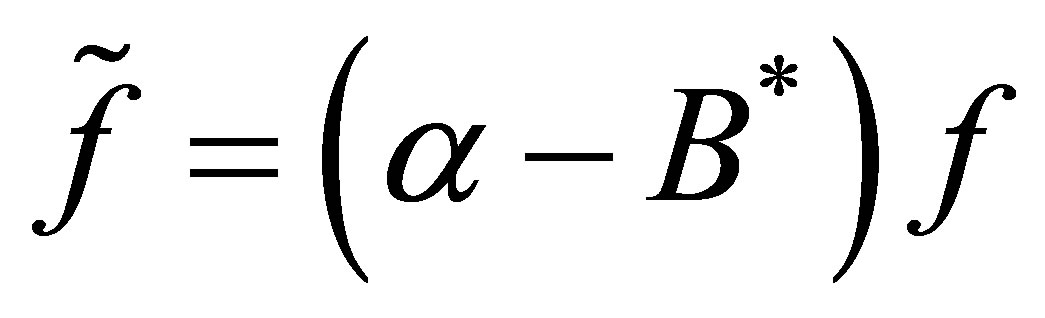 . The calculation of: (the first equation) +
. The calculation of: (the first equation) + 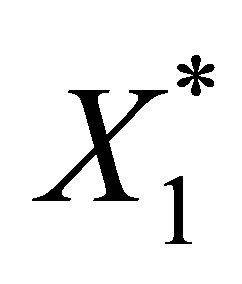 × (the second equation) yields that
× (the second equation) yields that

By noting that 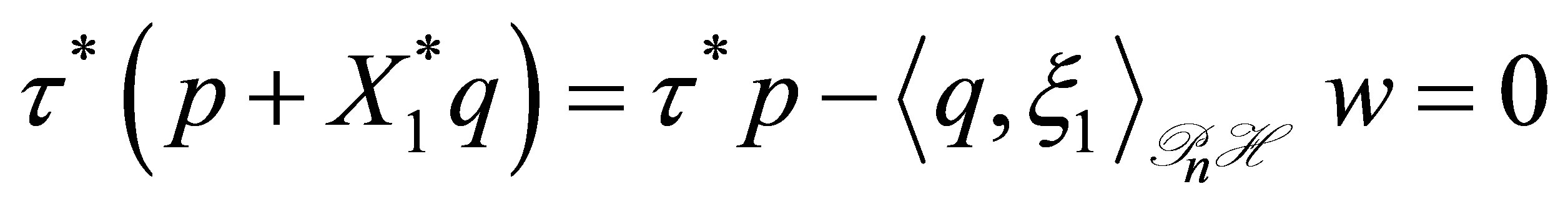 (see (48)), the function
(see (48)), the function 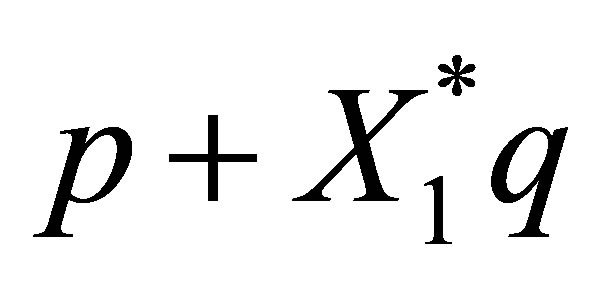 belongs to
belongs to 
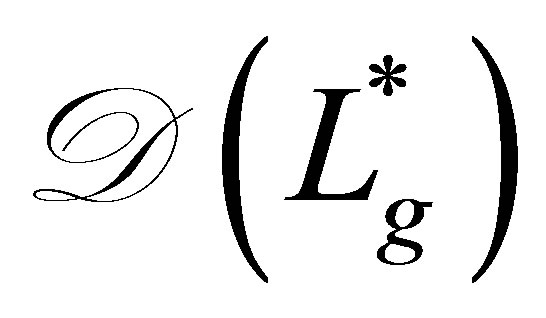 . Thus we see that
. Thus we see that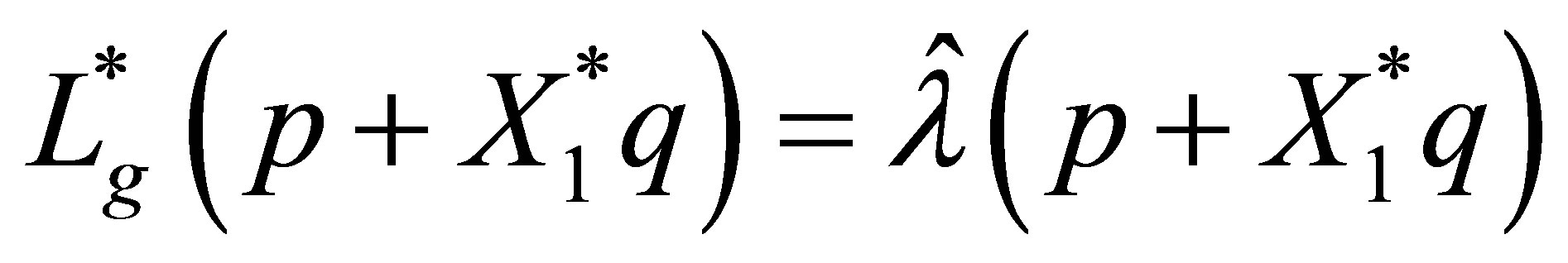 . Supposing that
. Supposing that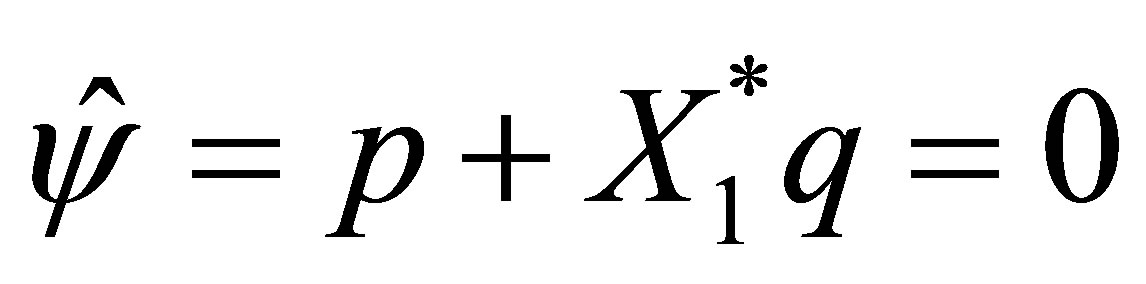 , we show a contradiction. In fact, if so, the second equation of (58) becomes
, we show a contradiction. In fact, if so, the second equation of (58) becomes . Since
. Since , however, we see that
, however, we see that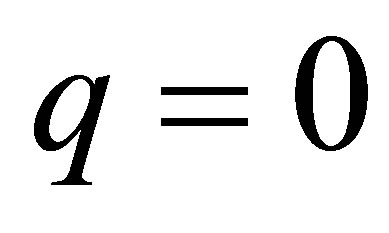 , and
, and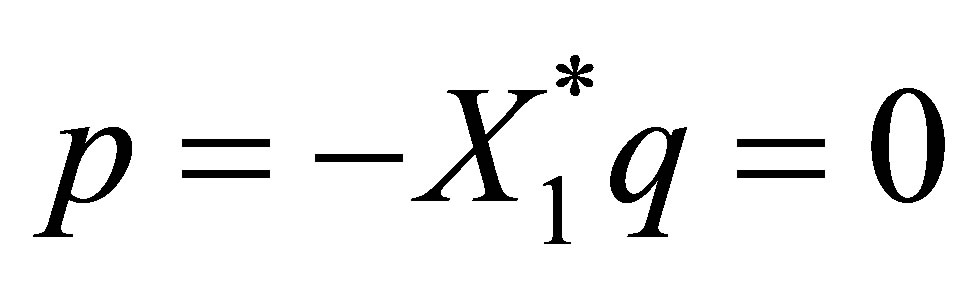 , or
, or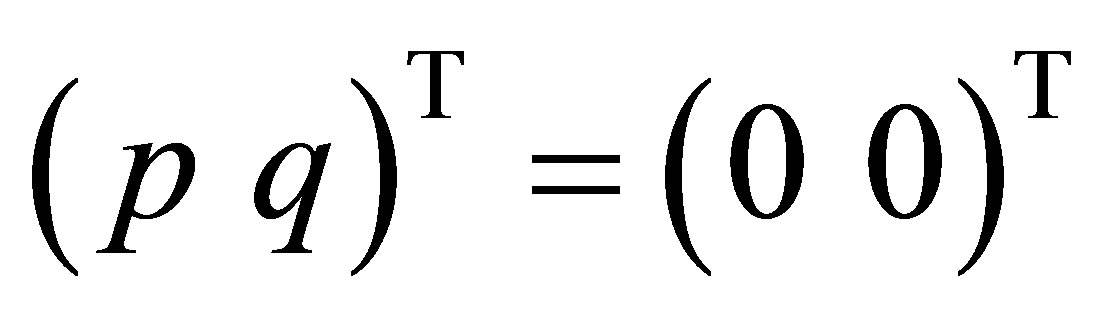 . Thus,
. Thus, 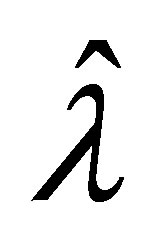 belongs to
belongs to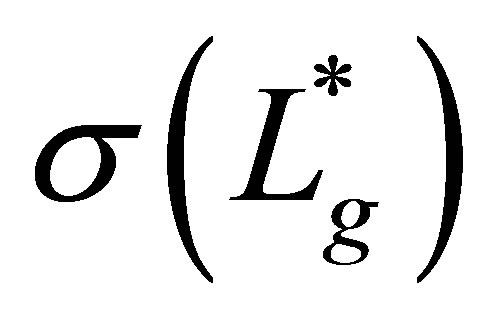 , and the corresponding eigenvector of
, and the corresponding eigenvector of  is given by the form
is given by the form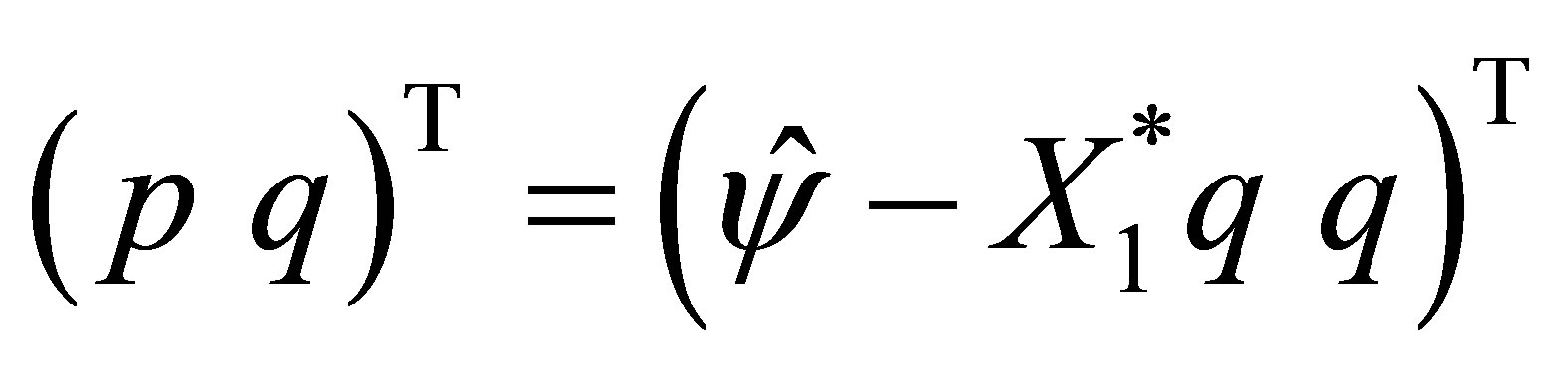 , where
, where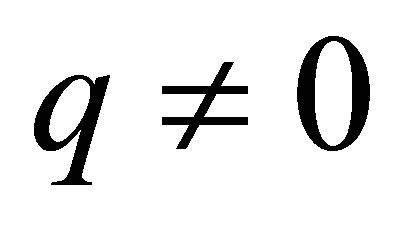 . We have also shown that
. We have also shown that 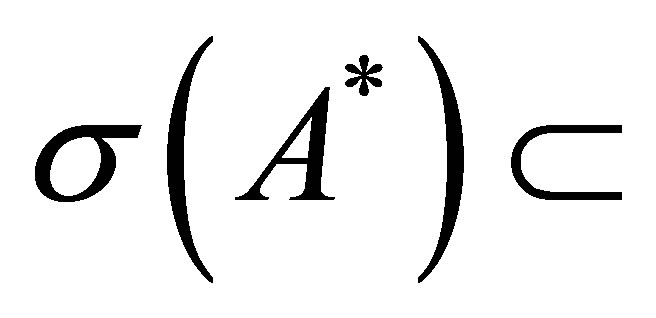
 .
.
Conversely, let  be an arbitrary eigenpair of
be an arbitrary eigenpair of  such that
such that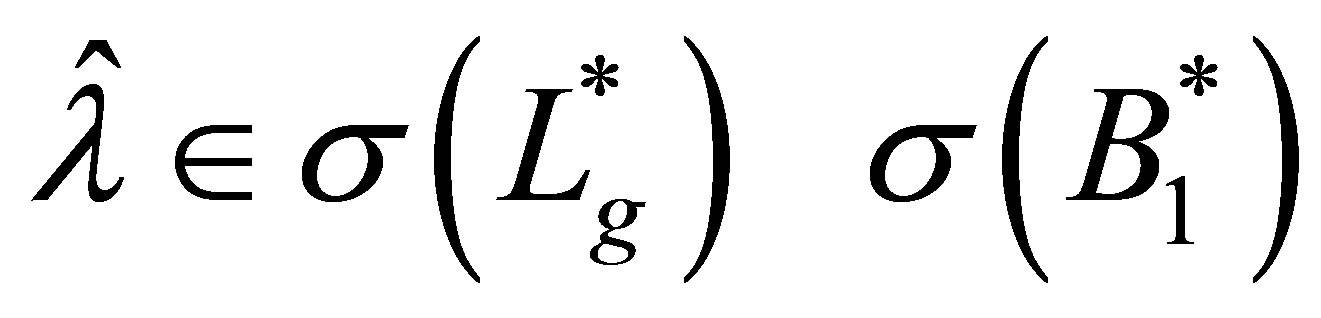 . Then we solve the equation:
. Then we solve the equation: 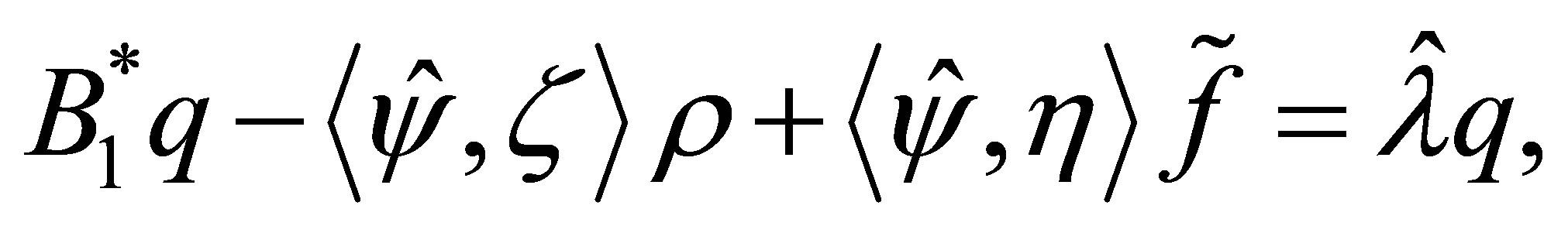 the unique solution of which is given by
the unique solution of which is given by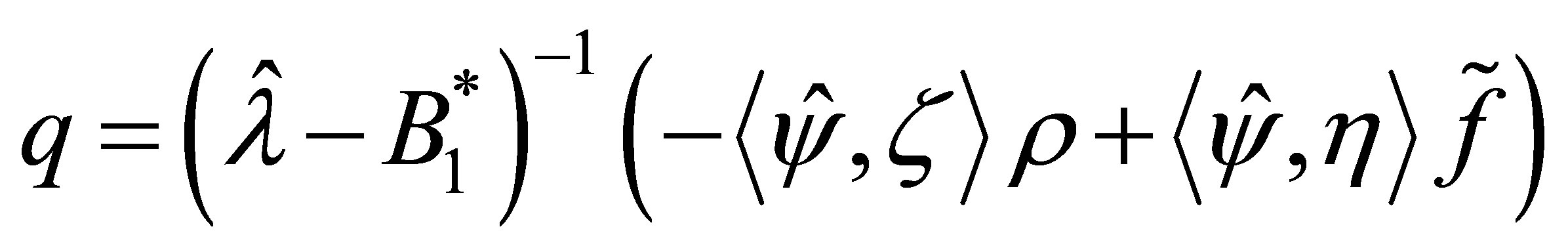 .
.
By setting , the vector
, the vector  means (46), and clearly satisfies the relation:
means (46), and clearly satisfies the relation: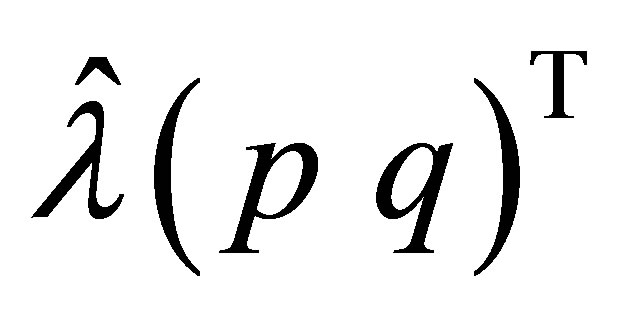
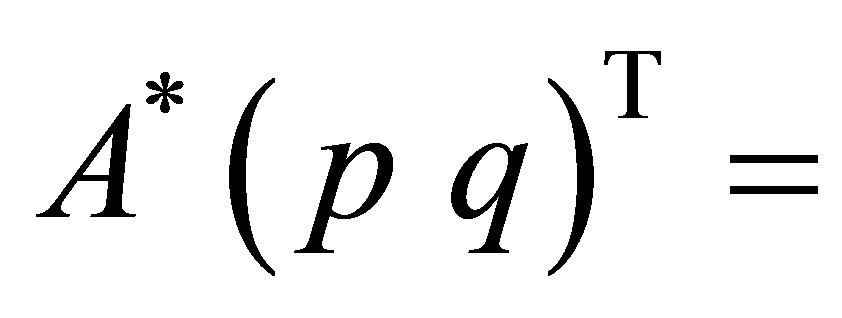 .To show that
.To show that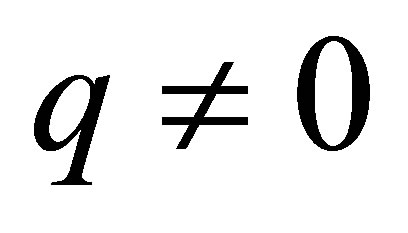 , we suppose the contrary:
, we suppose the contrary: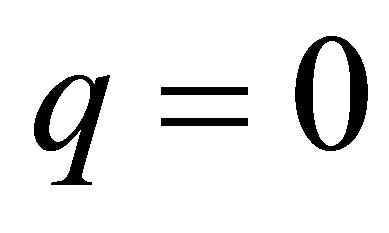 , or
, or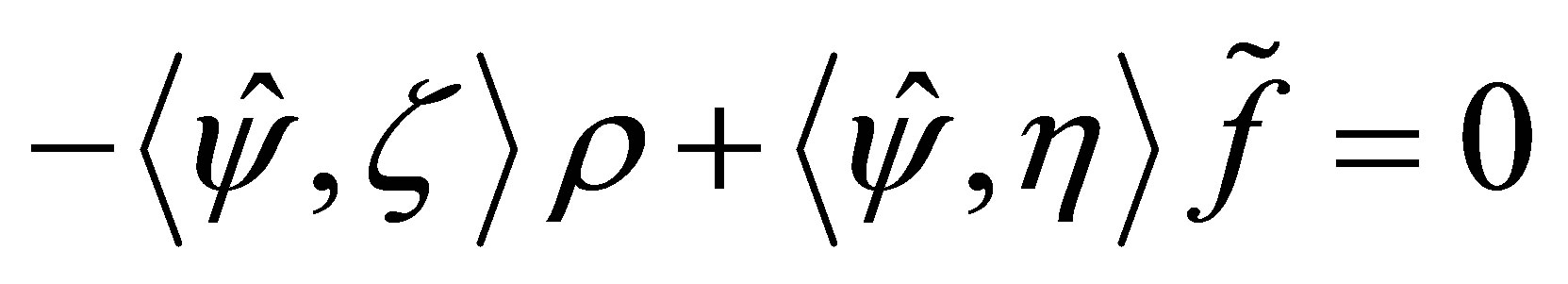 . Then,
. Then, 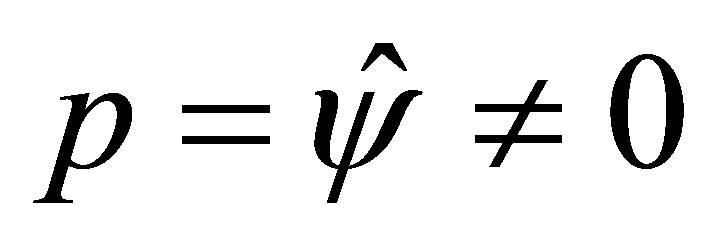 , and
, and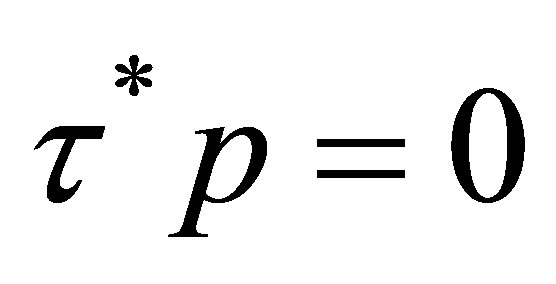 . Thus,
. Thus,  must be an eigenpair of
must be an eigenpair of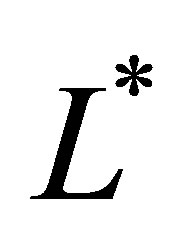 . But, this contradicts the assumptions (40) and (41). We have shown that
. But, this contradicts the assumptions (40) and (41). We have shown that 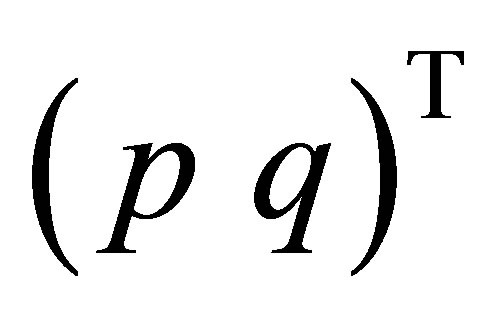 given by (46) is an eigenvector of
given by (46) is an eigenvector of . Q.E.D.
. Q.E.D.
Remark. In (45), it is not certain if . This problem seems a pathological one. If
. This problem seems a pathological one. If 
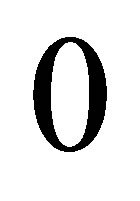 ,
, 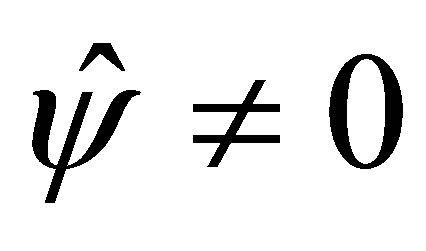 for some
for some ,
,  , and, in addition,
, and, in addition, 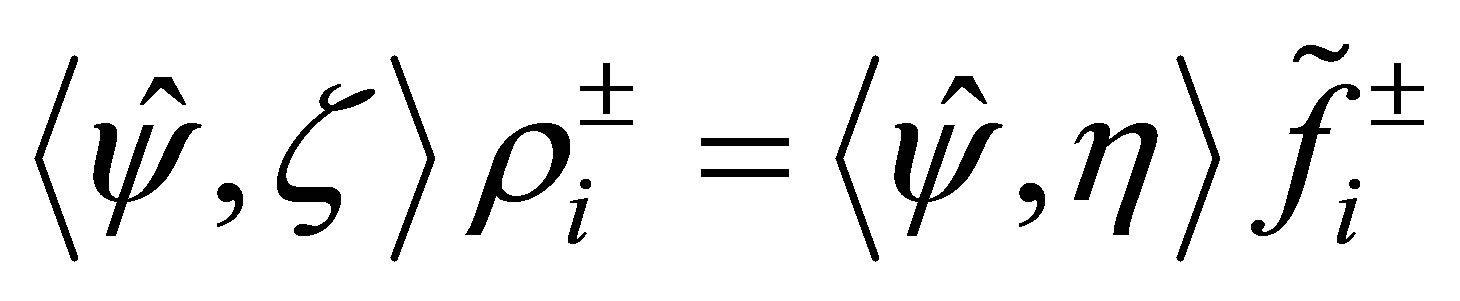 , then the equation
, then the equation 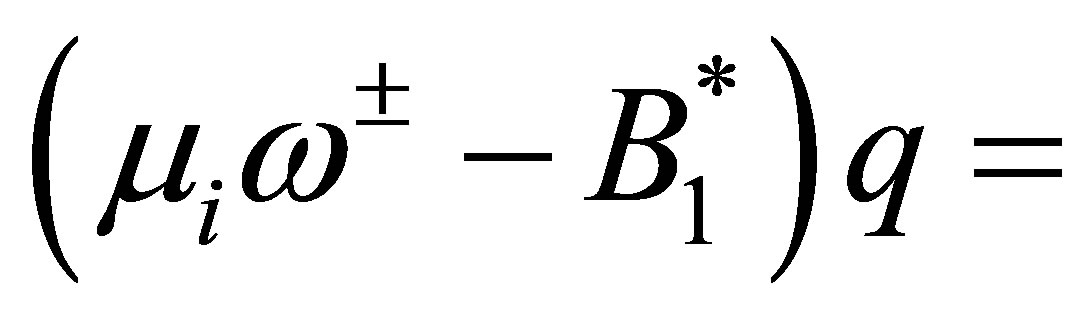
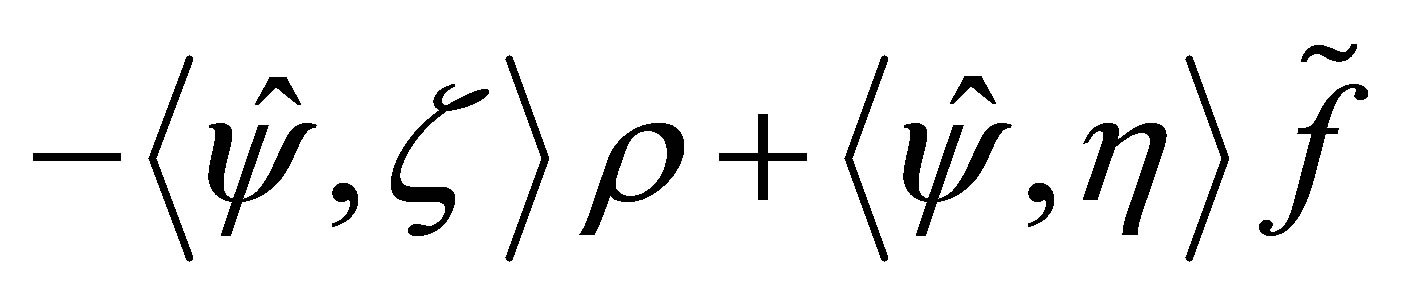 admits a (non-unique) solution
admits a (non-unique) solution  (see the second equation of (58)). By setting
(see the second equation of (58)). By setting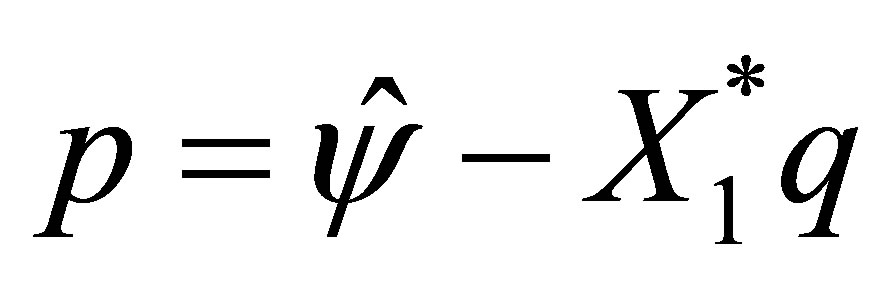 , the vector
, the vector  belongs to the eigenspace of
belongs to the eigenspace of  for
for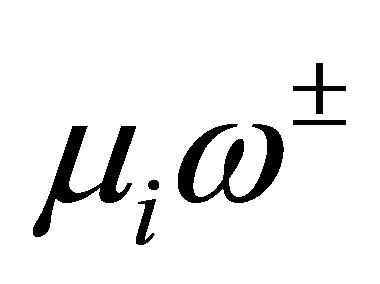 .
.
REFERENCES
- R. F. Curtain, “Finite Dimensional Compensators for Parabolic Distributed Systems with Unbounded Control and Observation,” SIAM Journal on Control and Optimization, Vol. 22, 1984, pp. 255-276. http://dx.doi.org/10.1137/0322018
- T. Nambu, “On Stabilization of Partial Differential Equations of Parabolic Type: Boundary Observation and Feedback,” Funkcialaj Ekvacioj, Vol. 28, No. 3, 1985, pp. 267- 298.
- T. Nambu, “An L2(Ω)-Based Algebraic Approach to Boundary Stabilization for Linear Parabolic Systems,” Quarterly of Applied Mathematics, Vol. 62, No. 4, 2004, pp. 711-748.
- T. Nambu, “A New Algebraic Approach to Stabilization for Boundary Control Systems of Parabolic Type,” Journal of Differential Equations, Vol. 218, No. 1, 2005, pp. 136-158. http://dx.doi.org/10.1016/j.jde.2005.03.013
- T. Nambu, “Alternative Algebraic Approach to Stabilization for Linear Parabolic Boundary Control Systems,” Mathematics of Control, Signals, and Systems, 2013, in Press. http://dx.doi.org/10.1007/s00498-013-0108-4
- Y. Sakawa, “Feedback Stabilization of Linear Diffusion Systems,” SIAM Journal on Control and Optimization, Vol. 21, No. 5, 1983, pp. 667-676. http://dx.doi.org/10.1137/0321040
- S. Itô, “Diffusion Equations,” American Mathematical Society, Providence, 1992.
- S. Agmon, “Lectures on Elliptic Boundary Value Problems,” Van Nostrand, Princeton, 1965.
- A. E. Taylor, “Introduction to Functional Analysis,” John Wiley & Sons, New York, 1958.
- T. Nambu, “Stability Enhancement of Output for a Class of Linear Parabolic Systems,” Proceedings of Royal Society Edinburgh, Section A, Vol. 133A, No. 1, 2003, pp. 157-175.
- T. Nambu, “Stabilization and Decay of Functionals for Linear Parabolic Control Systems,” Proceedings of the Japan Academy, Series A, Vol. 84, No. 2, 2008, pp. 19- 24. http://dx.doi.org/10.3792/pjaa.84.19
- T. Nambu, “On State and Output Stabilization of Linear Parabolic Systems,” Funkcialaj Ekvacioj, Vol. 52, No. 3, 2009, pp. 321-341. http://dx.doi.org/10.1619/fesi.52.321
- T. Nambu, “Stabilization and a Class of Functionals for Linear Parabolic Control Systems,” Proceedings of Royal Society Edinburgh, Section A, Vol. 140, No. 1, 2010, pp. 153-174. http://dx.doi.org/10.1017/S0308210508000978
- G. N. Watson, “A Treatise on the Theory of Bessel Functions,” Cambridge University Press, Cambridge, 1922.
- N. Levinson, “Gap and Density Theorems,” American Mathematical Society Colloquium Publications, New York, 1940.
- E. C. Titchmarsh, “The Theory of Functions,” The Clarendon Press, Oxford, 1939.
- Y. Sakawa and T. Matsushita, “Feedback Stabilization of a Class of Distributed Systems and Construction of a State Estimator,” IEEE Transactions on Automatic Control, Vol. 20, No. 6, 1975, pp. 748-753. http://dx.doi.org/10.1109/TAC.1975.1101095
- R. Courant and D. Hilbert, “Methods of Mathematical Physics, I,” Wiley Interscience, New York, 1953.
NOTES
1For an 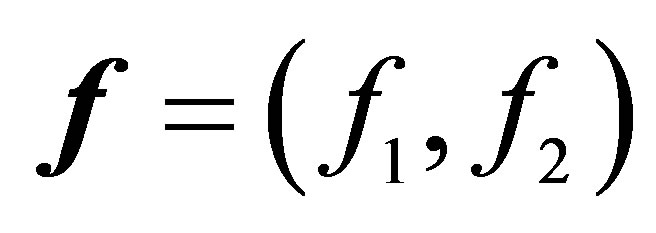 with
with  in a spectral subspace of
in a spectral subspace of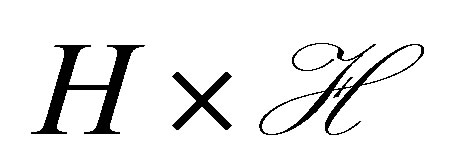 , a faster decay of
, a faster decay of 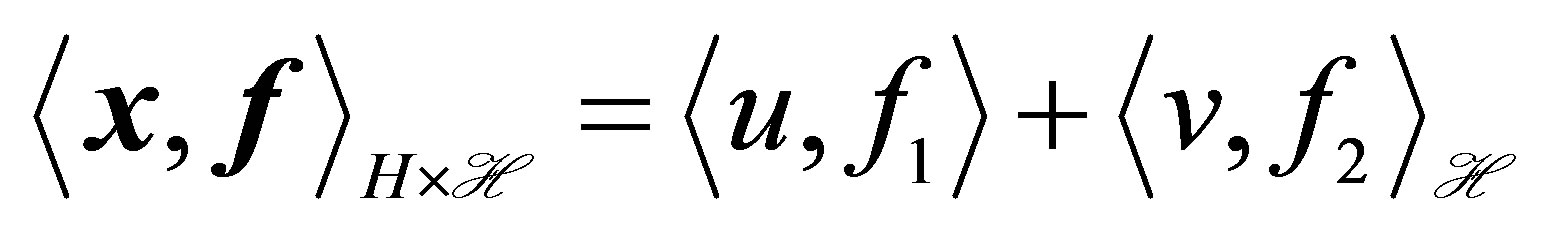 does not ensure the same decay of
does not ensure the same decay of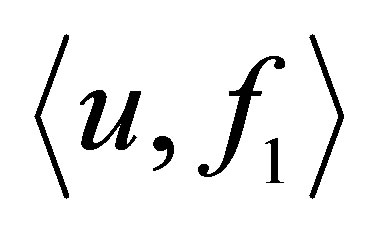 .
.

