Advances in Pure Mathematics
Vol.3 No.7(2013), Article ID:38121,6 pages DOI:10.4236/apm.2013.37082
Permanence and Globally Asymptotic Stability of Cooperative System Incorporating Harvesting
College of Mathematics and Computer Science, Fuzhou University, Fuzhou
Email: weifengying@fzu.edu.cn
Copyright © 2013 Fengying Wei, Cuiying Li. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 5, 2013; revised September 6, 2013; accepted September 28, 2013
Keywords: Cooperative System; Equilibrium; Stability; Asymptotically Periodic Solution
ABSTRACT
The stability of a kind of cooperative models incorporating harvesting is considered in this paper. By analyzing the characteristic roots of the models and constructing suitable Lyapunov functions, we prove that nonnegative equilibrium points of the models are globally asymptotically stable. Further, the corresponding nonautonomous cooperative models have a unique asymptotically periodic solution, which is uniformly asymptotically stable. An example is given to illustrate the effectiveness of our results.
1. Introduction
Permanence, stability and periodic solution for LotkaVolterra models had been extensively investigated by many authors (see [1-8] and the references therein). Jorge Rebaza [1] had discussed the dynamic behaviors of predator-prey model with harvesting and refuge
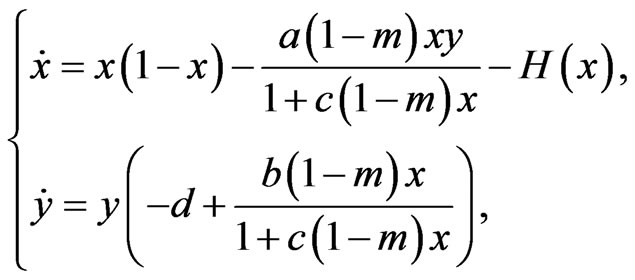 (1)
(1)
he obtained that harvesting and refuge affected the stability of some coexistence equilibrium and periodic solutions of model (1), where  was a continuous threshold policy harvesting function. Motivated by Jorge’s work, we consider the following cooperative system incorporating harvesting
was a continuous threshold policy harvesting function. Motivated by Jorge’s work, we consider the following cooperative system incorporating harvesting
 (2)
(2)
where 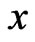 and
and 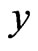 denote the densities of two populations at time
denote the densities of two populations at time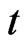 . The parameters
. The parameters 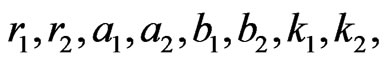
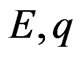 are all positive constants.
are all positive constants.
Definition 1 [2]  is called asymptotically
is called asymptotically 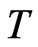 - periodic function, if
- periodic function, if 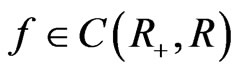 and it satisfies
and it satisfies , where
, where 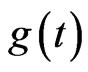 is continuous periodic function with periodic
is continuous periodic function with periodic 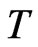 and
and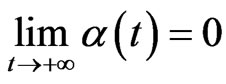 .
.
We will discuss our problems in the region
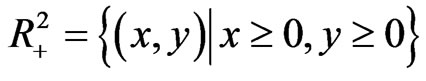 where
where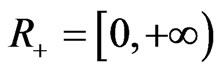 .
.
2. Permanence of System
Definition 2 [2] If there are positive constants  such that each positive solution
such that each positive solution 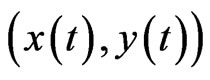 of system (2) satisfies
of system (2) satisfies
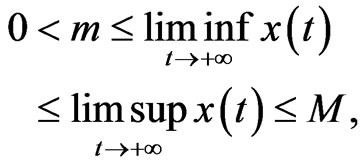

Then system (2) is persistent. If the system is not persistent, then system (2) is called non-persistent.
Lemma 1 If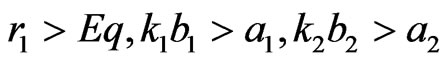 , then system (2) is persistent.
, then system (2) is persistent.
Proof. By the first equation of (2) and the comparison theorem, we get 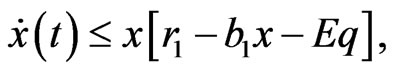 it implies that
it implies that
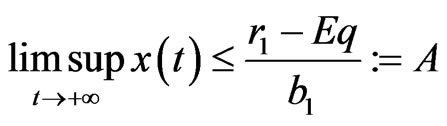 .
.
For any 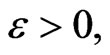
 there exists a
there exists a , as
, as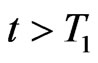 , it then follows
, it then follows
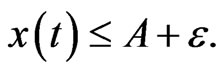
Similarly, we have . By the discussion above, for any
. By the discussion above, for any 
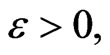 there exists a
there exists a , as
, as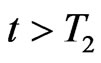 , it yields that
, it yields that 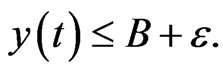
On the other hand, we have
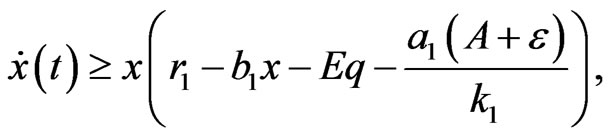
 .
.
By the comparison theorem, and letting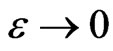 , one gets that
, one gets that

 .
.
By Definition 2, system (2) is persistent. □
3. Equilibrium Points and Stability
If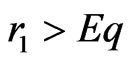 , then the equilibrium points of (2) are
, then the equilibrium points of (2) are
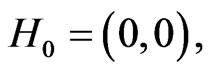
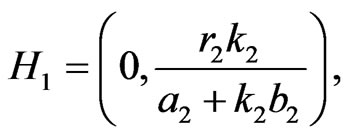
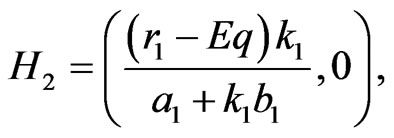
 where
where
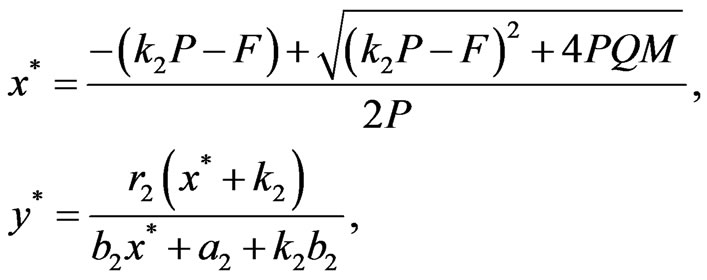 (3)
(3)
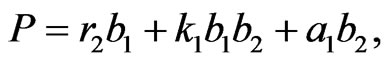
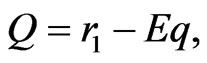

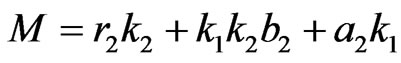 .
.
The general Jacobian matrix of (2) is given by
 .
.
The characteristic equation of system (2) at 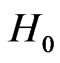 is
is
 , this immediately indicates that
, this immediately indicates that
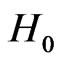 is always unstable.
is always unstable.
The characteristic equation of system (2) at  is
is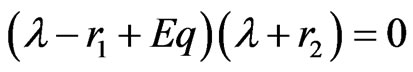 , by the condition
, by the condition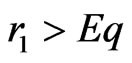 , one then gets that
, one then gets that 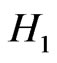 is a saddle point.
is a saddle point.
The characteristic equation of system (2) at  is
is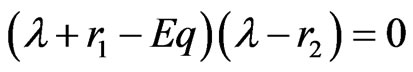 , we derive that
, we derive that  is a saddle point.
is a saddle point.
The characteristic equation of system (2) at  takes the form
takes the form
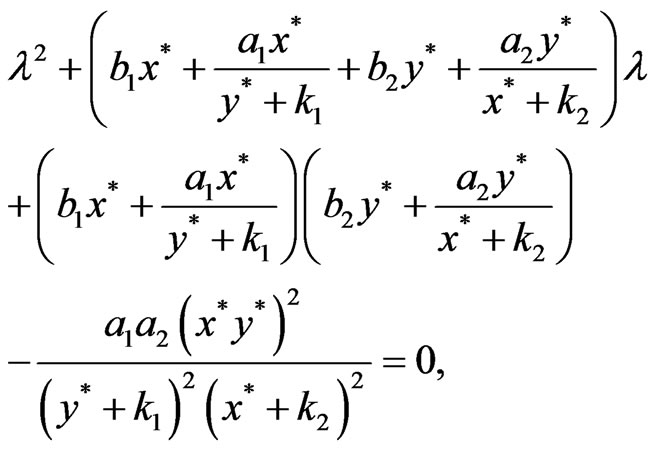
it is easy to check that 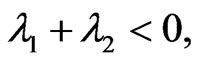
 , then
, then 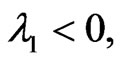
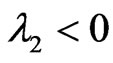 , thus
, thus  is locally asymptotically stable.
is locally asymptotically stable.
Theorem 1 If 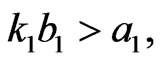

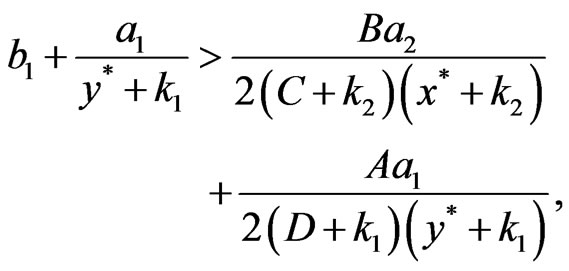
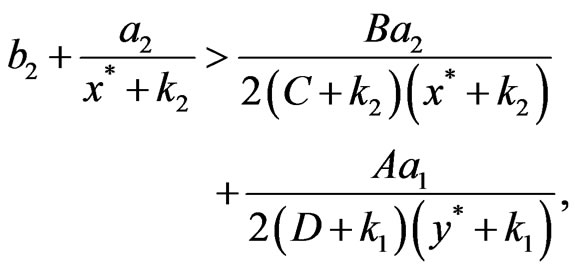
then the positive equilibrium point  of system (2) is globally asymptotically stable, where
of system (2) is globally asymptotically stable, where  can be found in Lemma 1.
can be found in Lemma 1.
Proof. Define a Lyapunov function
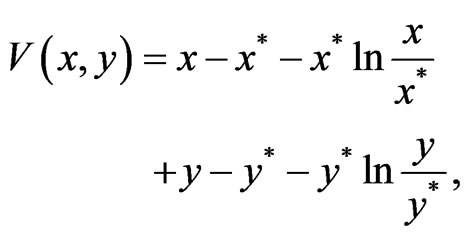
it then yields that

by the conditions of theorem 1, thus,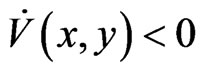 . The positive equilibrium point
. The positive equilibrium point  of system (2) is globally asymptotically stable.
of system (2) is globally asymptotically stable.
4. Existence and Uniqueness of Solutions
Next, we will discuss a nonautonomous system
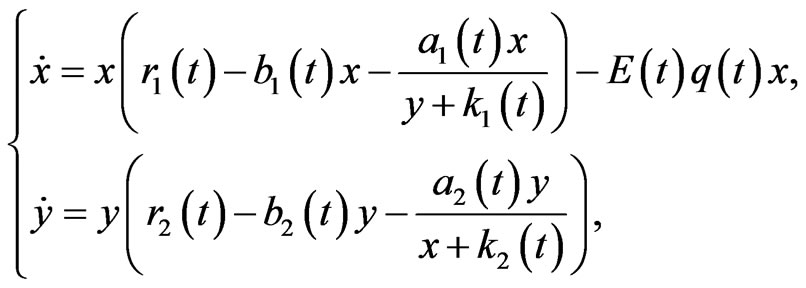 (4)
(4)
where 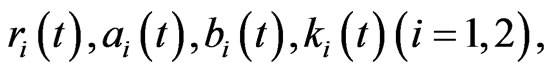
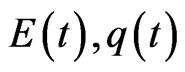 are positive continuous bounded asymptotically periodic functions with period
are positive continuous bounded asymptotically periodic functions with period . The initial data of (4) is given by
. The initial data of (4) is given by
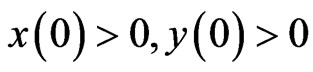 . (5)
. (5)
The solution of (4) with initial data (5) is denoted by
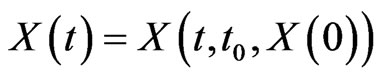 ,
, 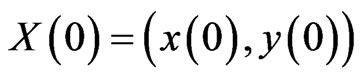 ,
,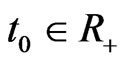 .
.
For a continuous function 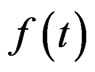 defined on
defined on 
 define
define
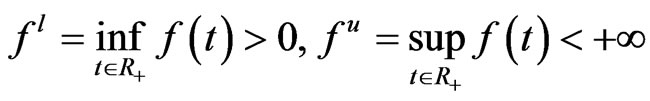 .
.
Definition 3 [2] If there exists a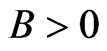 , for any
, for any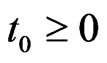 ,
,  , there exists a
, there exists a
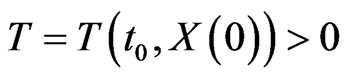
such that  for
for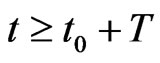 , then the solution
, then the solution
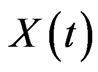 is called ultimately bounded.
is called ultimately bounded.
Let us consider the following asymptotically periodic system
 (6)
(6)
where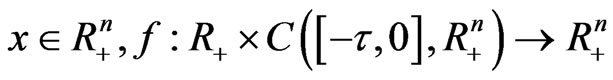 . Set
. Set
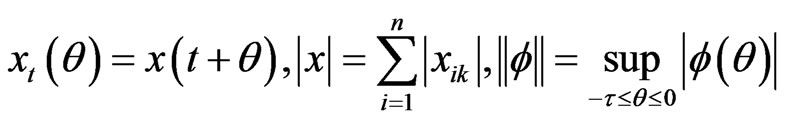 ,
,


In order to discuss the existence and uniqueness of asymptotically periodic solution of system (6), we can consider the adjoint system
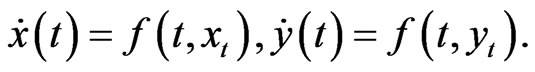 (7)
(7)
Lemma 2 If
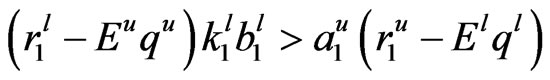
and

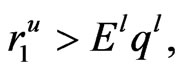
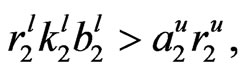
then the solution of system (4) is ultimately boundedness.
Proof. By the first equation of system (4) and the comparison theorem, one gets that
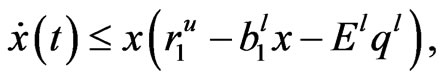
it then implies that
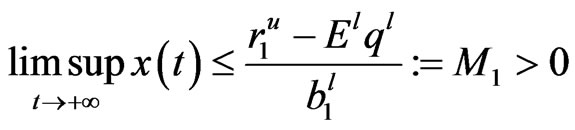 .
.
Similarly, we have
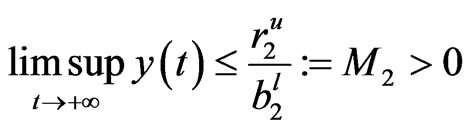 .
.
By the same discussion, one thus gets that
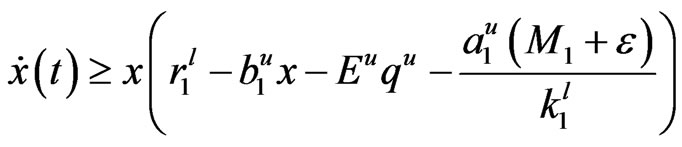 ,
,
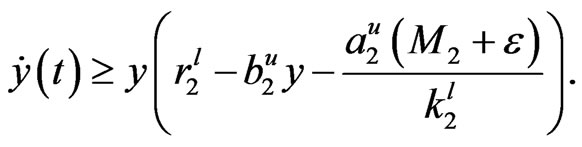
Letting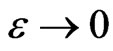 , we have
, we have

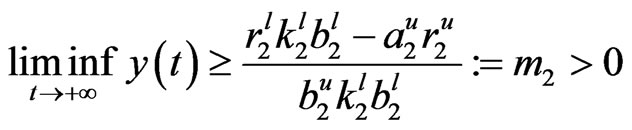 .
.
By the Definition 3, the solution of system (4) is ultimately bounded. □
Lemma 3 [2] If  satisfies the following conditions:
satisfies the following conditions:
1)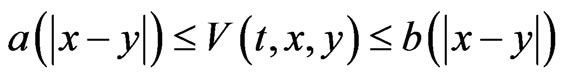 , where
, where 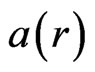 and
and 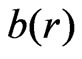 are continuously positively increasing functions;
are continuously positively increasing functions;
2)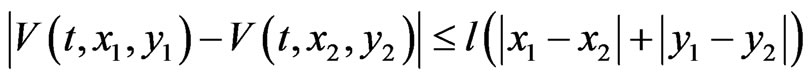 where
where  is a constant;
is a constant;
3) there exists a continuous non-increasing function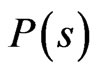 , such that for s > 0,
, such that for s > 0,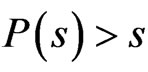 . And as
. And as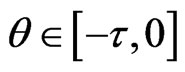 ,
,
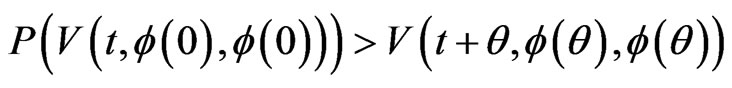 it then follows that
it then follows that
 where
where  is a constant; furthermore, system (6) has a solution
is a constant; furthermore, system (6) has a solution 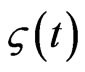 for
for  and satisfies
and satisfies .
.
Then system (6) has a unique asymptotically periodic solution, which is uniformly asymptotically stable.
Theorem 2 If conditions
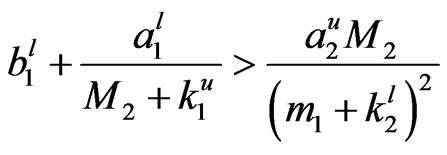
and
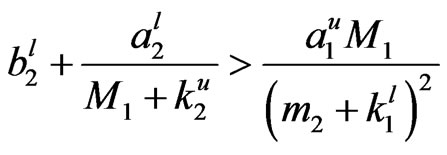
hold, the conditions of Lemma 2 are satisfied, then system (4) has a unique asymptotically periodic solution, which is uniformly asymptotically stable.
Proof. By Lemma 2, the solutions of system (4) is ultimately bounded. We consider the adjoint system
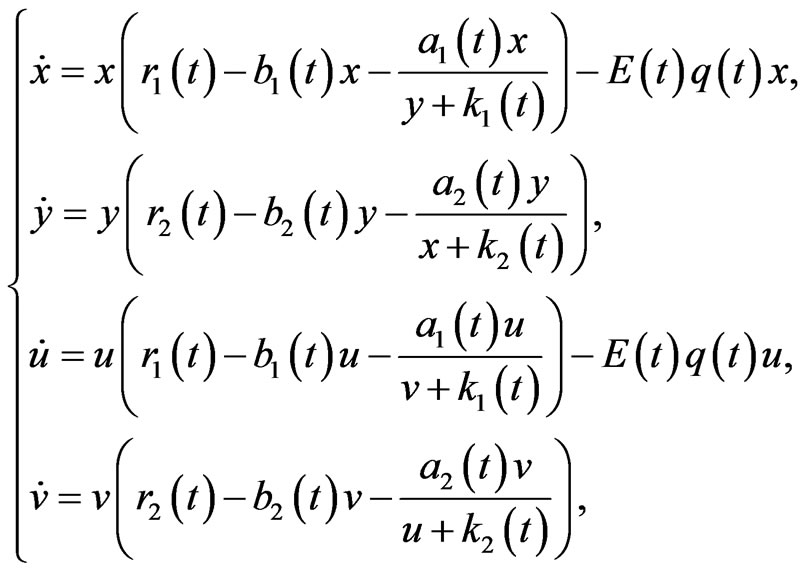 (8)
(8)
Let

and 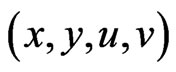 be the solution of (8). By the fact
be the solution of (8). By the fact


where 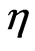 lies between
lies between  and
and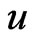 ,
, 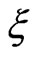 lies between
lies between  and
and , it then follows
, it then follows
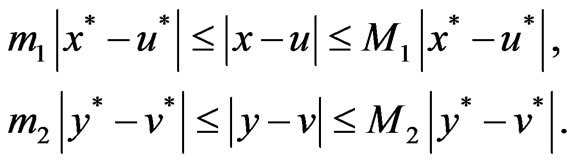 (9)
(9)
Define Lyapunov function , taking
, taking
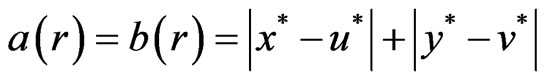 By suing of the inequality
By suing of the inequality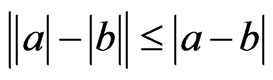 , it is easy to check that 1) and 2) of Lemma 3 are valid. Computing the derivative of
, it is easy to check that 1) and 2) of Lemma 3 are valid. Computing the derivative of 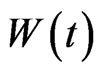 along the solution of system (8), by (9) and
along the solution of system (8), by (9) and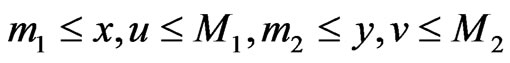 , we get that
, we get that

taking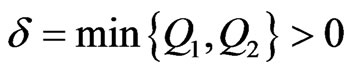 , it yields
, it yields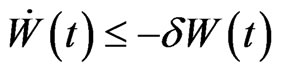 , then, system (4) has a unique positive asymptotically periodic solution, which is uniformly asymptotically stable. □
, then, system (4) has a unique positive asymptotically periodic solution, which is uniformly asymptotically stable. □
5. Examples and Numerical Simulations
Now, let us consider a autonomous cooperative system incorporating harvesting
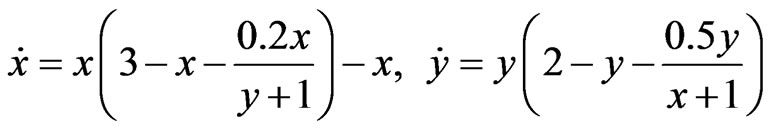 , (10)
, (10)
it is easy to check that
 ,
,
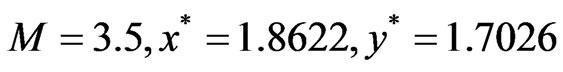 ,
,
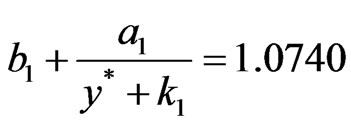 ,
, 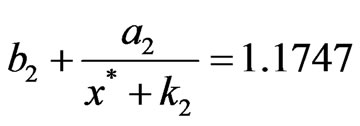 ,
,
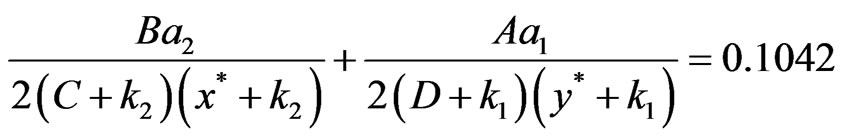 the conditions of Theorem 1 are valid, then the positive equilibrium point
the conditions of Theorem 1 are valid, then the positive equilibrium point 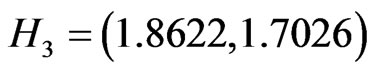 of system (2) is globally asymptotically stable in Figures 1 and 2.
of system (2) is globally asymptotically stable in Figures 1 and 2.
6. Conclusions
By analyzing the characteristic roots of a kind of cooperative models (2) incorporating harvesting, the stability of positive equilibrium point 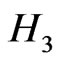 to model (2) is obtained by constructing a suitable Lyapunov function. Our results have shown that the harvesting coefficient
to model (2) is obtained by constructing a suitable Lyapunov function. Our results have shown that the harvesting coefficient 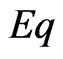 affects the stability and the existence of equilibrium point to model (2).
affects the stability and the existence of equilibrium point to model (2).
The related non-autonomous asymptotically periodic cooperative model (4) has been discussed later. Under some conditions, which also depend on model parameters (see Theorem 2), model (4) has a unique asymptotically periodic solution , which is uniformly
, which is uniformly
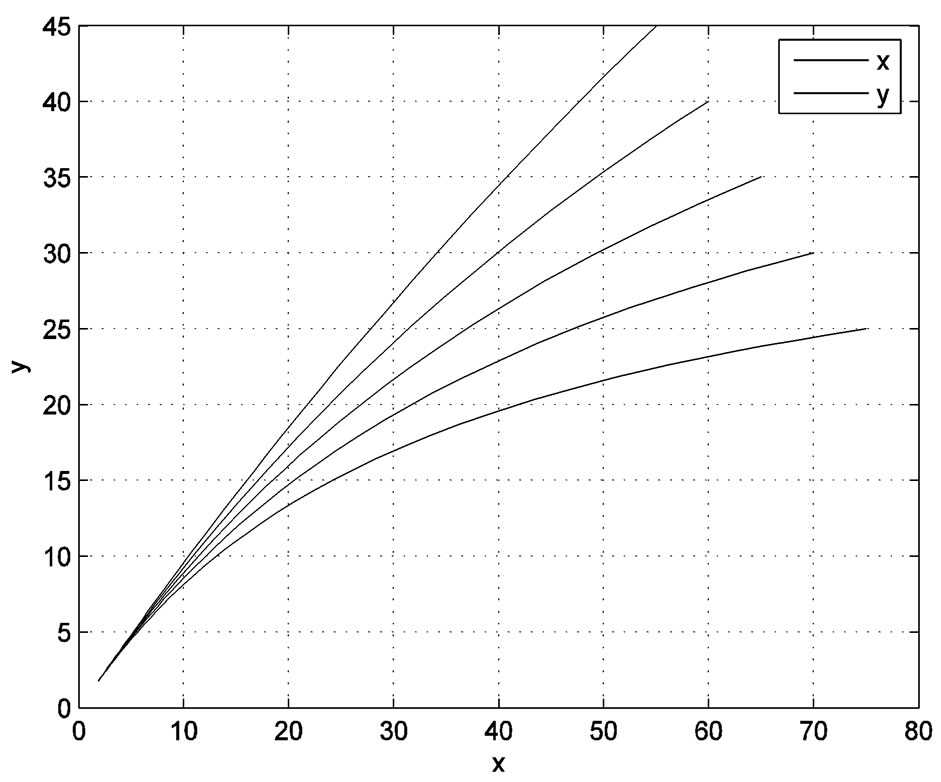
Figure 1. Positive equilibrium point 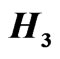 of (2) is globally asymptotically stable.
of (2) is globally asymptotically stable.

Figure 2. Solution of (2) is uniformly asymptotically stable.
asymptotically stable. Example model (10) shows the effectiveness of our results.
7. Acknowledgements
Our work is supported by Natural Science Foundation of China (11201075), the Natural Science Foundation of Fujian Province of China (2010J01005).
REFERENCES
- J. Rebaza, “Dynamics of Prey Threshold Harvesting and Refuge,” Journal of Computational and Applied Mathematics, Vol. 236, No. 7, 2012, pp. 1743-1752. http://dx.doi.org/10.1016/j.cam.2011.10.005
- X. Y. Zhang and K. Wang, “Almost Periodic Solution for n-Species Cooperation System with Time Delay,” Journal of Northeast Normal University (Natural Science Edition), Vol. 34, No. 3, 2002, in Chinese.
- Y. Nakata and Y. Muroya, “Permanence for Nonautonomous Lotka Volterra Cooperative Systems with Delays,” Nonlinear Analysis: Real World Applications, Vol. 11, No. 1, 2010, pp. 528-534. http://dx.doi.org/10.1016/j.nonrwa.2009.01.002
- X. Y. Song and L. S. Chen, “Global Asymptotic Stability of a Two Species Competitive System with Stage Structure and Harvesting,” Communications in Nonlinear Science & Numerical Simulation, Vol. 6, No. 2, 2001, pp. 81-87. http://dx.doi.org/10.1016/S1007-5704(01)90006-1
- T. K. Kar and H. Matsuda, “Global Dynamics and Controllability of a Harvested Prey-Predator System with Holling Type III Functional Response,” Nonlinear Analysis: Hybrid Systems, Vol. 1, No. 1, 2007, pp. 59-67. http://dx.doi.org/10.1016/j.nahs.2006.03.002
- D. W. Hu and Z. Q. Zhang, “Four Positive Periodic Solutions to a Lotka-Volterra Cooperative System with Harvesting Terms,” Nonlinear Analysis: Real World Applications, Vol. 11, No. 2, 2010, pp. 1115-1121. http://dx.doi.org/10.1016/j.nonrwa.2009.02.002
- G. Y. Chen and Z. D. Teng, “On the Stability in a Discrete Two-Species Competition System,” Journal of Applied Mathematics and Computing, Vol. 38, No. 1-2, 2012, pp. 25-39. http://dx.doi.org/10.1007/s12190-010-0460-1
- T. K. Kar and K. Chakraborty, “Effort Dynamics in a Prey-Predator Model with Harvesting,” International Journal of Information and Systems Sciences, Vol. 6, No. 3, 2010, pp. 318-332.

