Advances in Pure Mathematics
Vol.3 No.5(2013), Article ID:35063,3 pages DOI:10.4236/apm.2013.35067
Global Periodic Attractors for a Class of Infinite Dimensional Dissipative Dynamical Systems
College of Management, Shanghai University of Engineering Science, Shanghai, China
Email: lihongyan580@sohu.com
Copyright © 2013 Hongyan Li. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 2, 2013; revised June 10, 2013; accepted July 5, 2013
Keywords: Dissipative Equation; Global Periodic Attractor; One-Dimensional System
ABSTRACT
In this paper we consider the existence of a global periodic attractor for a class of infinite dimensional dissipative equations under homogeneous Dirichlet boundary conditions. It is proved that in a certain parameter, for an arbitrary timeperiodic driving force, the system has a unique periodic solution attracting any bounded set exponentially in the phase space, which implies that the system behaves exactly as a one-dimensional system. We mention, in particular, that the obtained result can be used to prove the existence of the global periodic attractor for abstract parabolic problems.
1. Introduction
In this paper, we consider a class of infinite dimensional dissipative equations with the Dirichlet boundary condition
 (1.1)
(1.1)
where  is a real-valued function on
is a real-valued function on 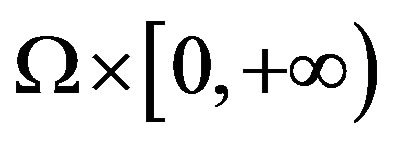 ,
,  is an open bounded set of
is an open bounded set of  with a smooth boundary
with a smooth boundary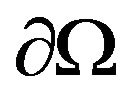 ,
,  takes values in a Hilbert space H, the family
takes values in a Hilbert space H, the family 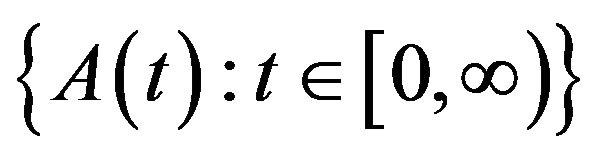 of unbounded linear operators generates a linear evolution operator. The external force term
of unbounded linear operators generates a linear evolution operator. The external force term  is continuous and ω-periodic function in t, where ω is a positive constant. Let
is continuous and ω-periodic function in t, where ω is a positive constant. Let . There exists a nonnegative constant
. There exists a nonnegative constant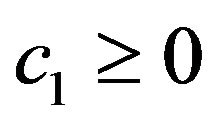 , such that
, such that
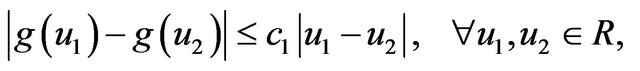 (1.2)
(1.2)
where  denotes the absolute value of the number in R.
denotes the absolute value of the number in R.
There has been an increasing interest in the study of the evolution equations of form (1.1), such as existence and asymptotic behavior of solutions (mild solutions, strong solutions and classical solutions), and existence of global attractors, etc. Especially in physics and mechanics, many important results associated with this problem have been obtained in [1-7]. In [9] and [10], Hernandez and Henriquez have extended the problem studied in [8] to neutral equations and established the corresponding existence results of solutions and periodic solutions. In their work,  , especially,
, especially, 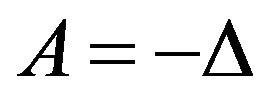 is a negative Laplacian operator, and A generates an analytic semigroup so that the theory of the fractional power has been used effectively there. However, their results clearly cannot apply to Equation (1.1) with
is a negative Laplacian operator, and A generates an analytic semigroup so that the theory of the fractional power has been used effectively there. However, their results clearly cannot apply to Equation (1.1) with  is non-autonomous which is a more general and maybe more important case [11]. So we will use the appropriate assumptions to overcome the difficulty for the non-autonomous operator
is non-autonomous which is a more general and maybe more important case [11]. So we will use the appropriate assumptions to overcome the difficulty for the non-autonomous operator .
.
We arrange this paper as follows. Firstly we present the existence and uniqueness of solutions. Then we obtain a nonstandard estimation under which system (1.1) possesses a global periodic attractor. Finally, for the special case , we discuss the existence of a global periodic attractor for abstract parabolic problems.
, we discuss the existence of a global periodic attractor for abstract parabolic problems.
2. Preliminaries
For the family 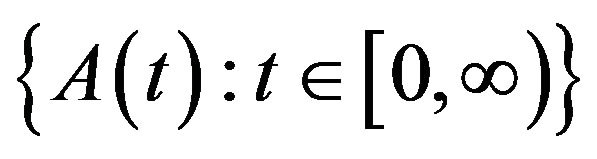 of linear operators, we impose on the following restrictions:
of linear operators, we impose on the following restrictions:
1) The domain 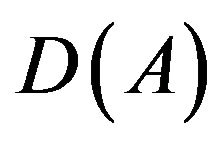 of
of 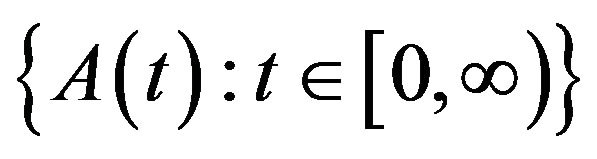 is dense in Hilbert space H and independent of t,
is dense in Hilbert space H and independent of t, 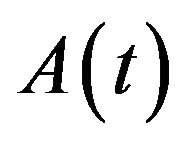 is a closed linear operator;
is a closed linear operator;
2) For each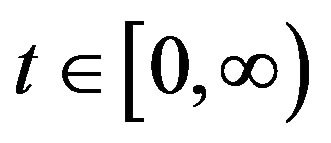 , the resolvent
, the resolvent  exists for all
exists for all![]() , with
, with  and there exists
and there exists 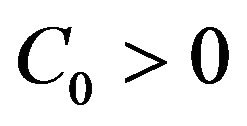 so that
so that ;
;
3) There exists  and
and 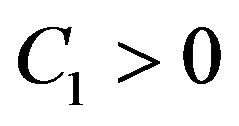 such that
such that
![]()
for all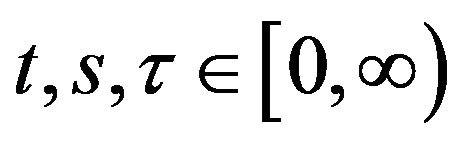 ;
;
4) For each  and some
and some , the resolvent set of
, the resolvent set of , the resolvent
, the resolvent , is a compact operator.
, is a compact operator.
Then the family  generates a unique linear evolution operator
generates a unique linear evolution operator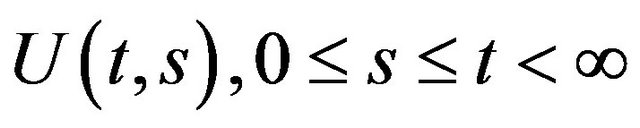 , satisfying the following properties:
, satisfying the following properties:
1) , the space of bounded linear transformations on H, whenever
, the space of bounded linear transformations on H, whenever 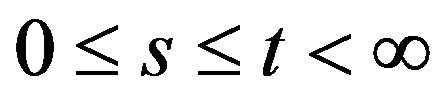 and for each
and for each , the mapping
, the mapping  is continuous;
is continuous;
2) 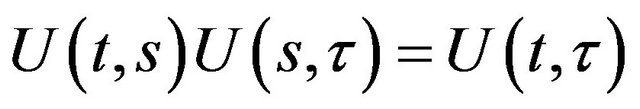 for
for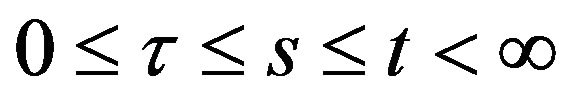 ;
;
3) 
4)  is a compact operator whenever
is a compact operator whenever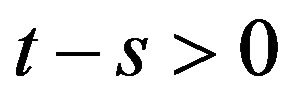 ;
;
5) , for
, for ;
;
6) There is a constant 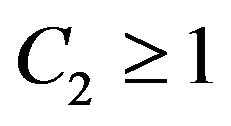 such that
such that ,
,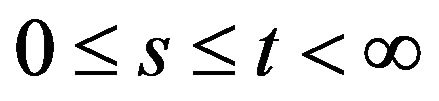 ;
;
7) If 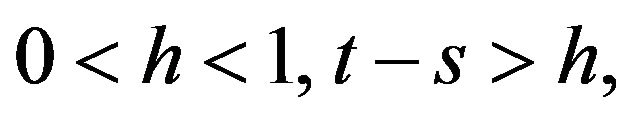 and
and 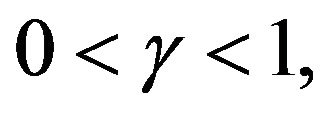 then
then
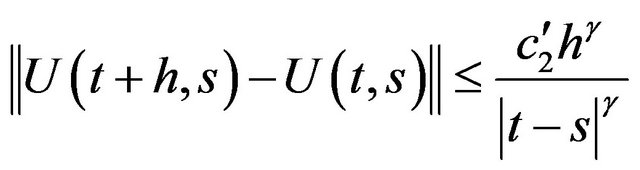
for some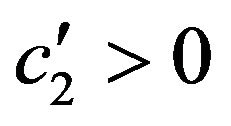 ;
;
8) If  is continuous on
is continuous on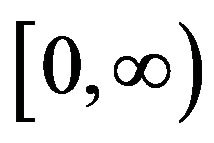 , then the function
, then the function 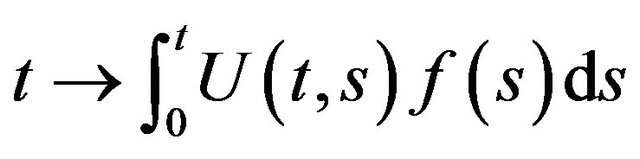 is Holder continuous with any exponent
is Holder continuous with any exponent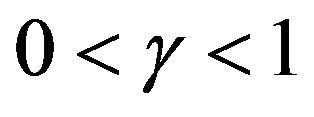 .
.
Condition 4) ensures the generated evolution operator satisfies 4) (see [6], Proposition 2.1).
Proposition 1 (see [11]) The family of operators 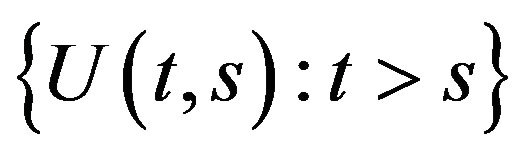 is continuous in t in the uniform operator topology uniformly for s.
is continuous in t in the uniform operator topology uniformly for s.
Lemma 1 (see [11]) Consider the initial value problem (1.1) in E. If 1)-4) hold, then, for any , there exists a unique continuous function
, there exists a unique continuous function 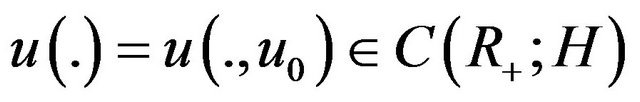 such that
such that 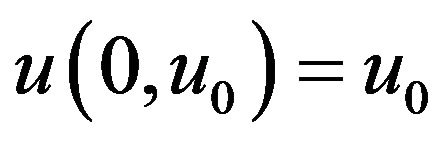 and
and 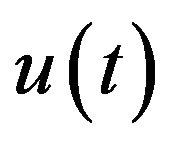 satisfies the integral equation
satisfies the integral equation
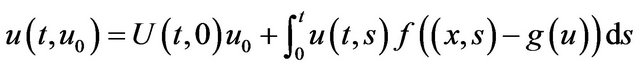 .
.
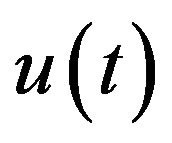 is called a mild solution of (1.1).
is called a mild solution of (1.1).
By Lemma 1, the (mild) solution 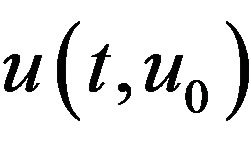 of (1.1) determines a map
of (1.1) determines a map  from H into itself:
from H into itself: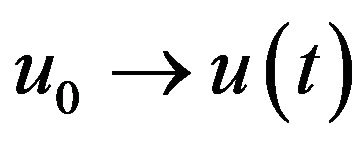 . Obviously,
. Obviously, 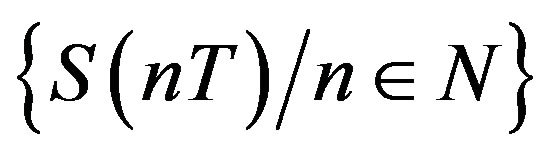 is a discrete semidynamic system in H, since
is a discrete semidynamic system in H, since 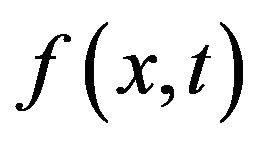 is a ω-periodic function with respect to
is a ω-periodic function with respect to .
.
3. Main Result
Theorem 1 Assume that (1.2), 1)-4) and
 hold, then system (1.1) has a unique continuous ω-periodic solution which attracts any bounded set exponentially. The process
hold, then system (1.1) has a unique continuous ω-periodic solution which attracts any bounded set exponentially. The process  associated with (1.1) possesses a global periodic attractor.
associated with (1.1) possesses a global periodic attractor.
Proof. Let 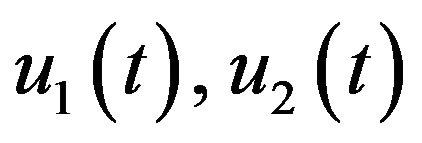 be two solutions of problem (1.1) with initial values
be two solutions of problem (1.1) with initial values , and
, and
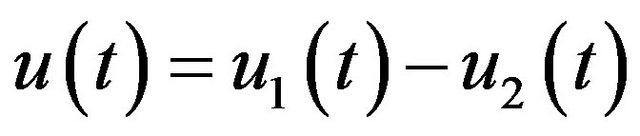 . Then by (1.1), we find
. Then by (1.1), we find
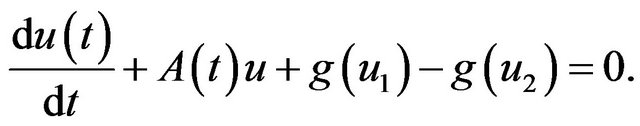 (3.1)
(3.1)
Taking the inner scalar product of each side of (3.1) with 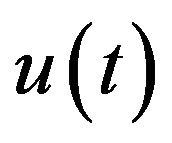 in H, and we see that
in H, and we see that
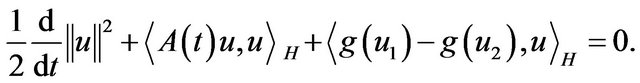 (3.2)
(3.2)
For the third term on the left of (3.2), by (1.2), we have
![]() (3.3)
(3.3)
From (3.1)-(3.3), we find

and if
![]()
we might as well assume
![]() from the Gronwall’s inequality, we have that
from the Gronwall’s inequality, we have that
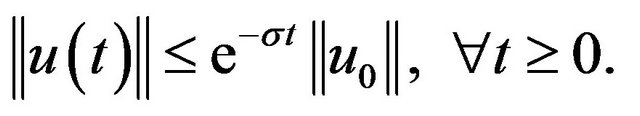 (3.4)
(3.4)
Now considering ω-mapping
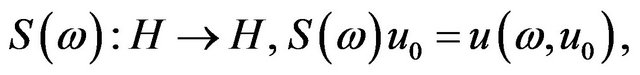
where  is the solution of (1.1),
is the solution of (1.1),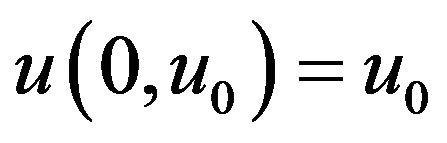 . From (3.4),
. From (3.4),  , we obtain
, we obtain
 .
.
Thus 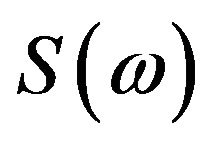 is a contraction mapping. By Banach’s fixed point theorem, there exists a unique fixed point
is a contraction mapping. By Banach’s fixed point theorem, there exists a unique fixed point 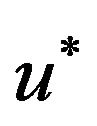 for
for  in H such that
in H such that . At the same time, since
. At the same time, since  is a discrete semidynamic system in H, we can deduce
is a discrete semidynamic system in H, we can deduce

and
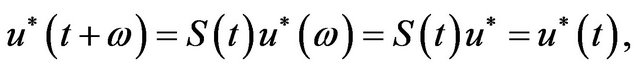
where 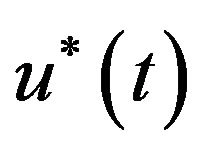 is the solution passing
is the solution passing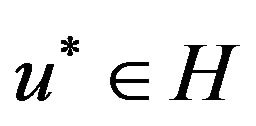 . Thus
. Thus  is a ω-periodic solution of system (1.1). By (3.4),
is a ω-periodic solution of system (1.1). By (3.4), 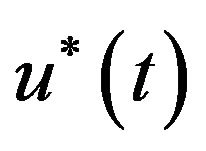 attracts any bounded set exponentially, which is a global periodic attractor of System (1.1). The proof is completed.
attracts any bounded set exponentially, which is a global periodic attractor of System (1.1). The proof is completed.
4. Examples
In this section, as an illustration of the main result in Section 3, we consider one example of System (1.1) and get the corresponding results. We consider an evolution equation (i.e.,  in (1.1)) studied in [2,3]:
in (1.1)) studied in [2,3]:
 (4.1)
(4.1)
and if the function f is continuous ω-periodic in t, we have the following theorem.
Theorem 2 System (4.1) possesses a global ω-periodic attractor which attracts any bounded set exponentially, if  (where
(where 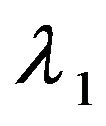 is the first eigenvalue of operator
is the first eigenvalue of operator  that subjects to the homogeneous Dirichlet boundary condition).
that subjects to the homogeneous Dirichlet boundary condition).
5. Acknowledgements
This work is supported by the National Natural Science Foundation of China under Grant 11101265 and 61075115.
REFERENCES
- J. K. Cholewa and T. Dlokto, “Global Attractors in Abstract Parabolic Problem,” Cambridge University Press, Cambridge, 2000. doi:10.1017/CBO9780511526404
- J. K. Hale, “Asymptotic Behavior of Dissipative Systems,” AMS, 1988.
- R. Temam, “Infinite-Dimensional Dynamical Systems in Mechanics and Physics,” Springer-Verlag, New York, 1997.
- M. A. Hussain, “On a Nonlinear Integrodifferential Equation in Banach Space,” Indian Journal of Pure and Applied Mathematics, Vol. 19, 1988, pp. 516-529.
- S. M. Rankin III, “Existence and Asymptotic Behavior of a Functional Differential Equation in Banach Space,” Journal of Mathematical Analysis and Applications, Vol. 88, No. 2, 1982, pp. 531-542. doi:10.1016/0022-247X(82)90211-6
- W. E. Fitzgibbon, “Semilinear Functional Equations in Banach Space,” Journal of Differential Equations, Vol. 29, No. 1, 1978, pp. 1-14. doi:10.1016/0022-0396(78)90037-2
- C. Zhong, C. Sun and M. Niu, “On the Existence of Global Attractor for a Class of Infinite Dimensional Dissipative Nonlinear Dynamical Systems,” Chinese Annals of Mathematics, Vol. 26, No. 3, 2005, pp. 393-400. doi:10.1142/S0252959905000312
- H. R. Henriquez, “Periodic Solutions of Quasi-Linear Partial Functional Differential Equations with Unbounded Delay,” Funkcialaj Ekvacioj, Vol. 37, No. 2, 1994, pp. 329- 343.
- E. Hernandez and H. R. Henriquez, “Existence Results for Partial Neutral Functional Differential Equations with Unbounded Delay,” Journal of Mathematical Analysis and Applications, Vol. 221, No. 2, 1998, pp. 452-475. doi:10.1006/jmaa.1997.5875
- E. Hernandez and H. R. Henriquez, “Existence of Periodic Solutions of Partial Neutral Functional Differential Equations with Unbounded Delay,” Journal of Mathematical Analysis and Applications, Vol. 221, No. 2, 1998, pp. 499-522. doi:10.1006/jmaa.1997.5899
- X. Fu and X. Liu, “Existence of Periodic Solutions for Abstract Neutral Non-Autonomous Equations with Infinite Delay,” Journal of Mathematical Analysis and Applications, Vol. 325, No. 1, 2007, pp. 249-267. doi:10.1016/j.jmaa.2006.01.048

