Advances in Pure Mathematics
Vol.3 No.6(2013), Article ID:37446,8 pages DOI:10.4236/apm.2013.36076
A Modified Wallman Method of Compactification
1Department of Mathematics, Texas A&M University, Kingsville, USA
2University of Texas at San Antonio, San Antonio, USA
Email: hueytzen.wu@tamuk.edu, dd1273@yahoo.com
Copyright © 2013 Hueytzen J. Wu, Wan-Hong Wu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 29, 2012; revised December 28, 2012, accepted January 19, 2013
Keywords: Closed Ãx-Filter; Open and Closed C*D-Filter Bases; Basic Open and Closed C*D-Filters; Compactification; Stone-Čech and Wallman Compactifications
ABSTRACT
Closed Ãx- and basic closed C*D-filters are used in a process similar to Wallman method for compactifications of the topological spaces Y, of which, there is a subset 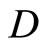 of
of 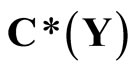 containing a non-constant function, where
containing a non-constant function, where 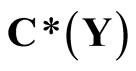 is the set of bounded real continuous functions on Y. An arbitrary Hausdorff compactification
is the set of bounded real continuous functions on Y. An arbitrary Hausdorff compactification 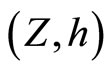 of a Tychonoff space X can be obtained by using basic closed C*D-filters from
of a Tychonoff space X can be obtained by using basic closed C*D-filters from 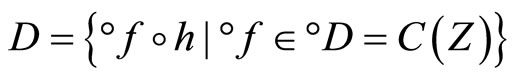 in a similar way, where
in a similar way, where 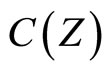 is the set of real continuous functions on Z.
is the set of real continuous functions on Z.
1. Introduction
Throughout this paper,  will denote the collection of all finite subsets of the set
will denote the collection of all finite subsets of the set![]() . For the other notations and the terminologies in general topology which are not explicitly defined in this paper, the readers will be referred to the reference [1].
. For the other notations and the terminologies in general topology which are not explicitly defined in this paper, the readers will be referred to the reference [1].
Let 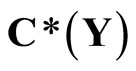 be the set of bounded real continuous functions on a topological space Y. For any subset
be the set of bounded real continuous functions on a topological space Y. For any subset 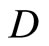 of
of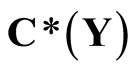 , we will show in Section 2 that there exists a unique rf in
, we will show in Section 2 that there exists a unique rf in 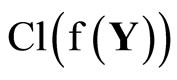 for each f in
for each f in 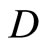 so that for any
so that for any
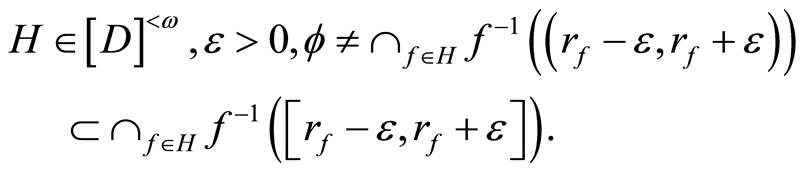
Let K be the set

and let V be the set
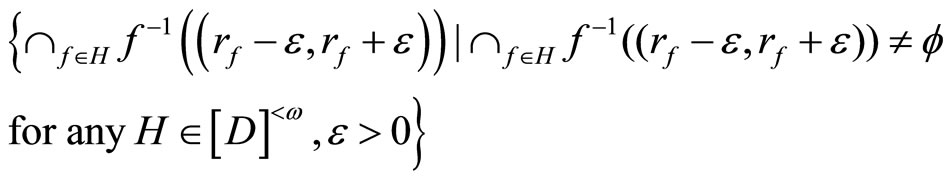
K and V are called a closed C*D-filter base and an open C*D-filter base on Y, respectively. A closed filter (or an open filter) on Y generated by a K (or a V) is called a basic closed C*D-filter (or a basic open C*D- filter), denoted by ℰ (or Å). If 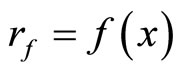 for all f in
for all f in 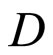 at some x in Y, then K, V, ℰ and Å are denoted by Kx, Vx, ℰx and Åx, respectively. Let Y be a topological space, of which, there is a subset
at some x in Y, then K, V, ℰ and Å are denoted by Kx, Vx, ℰx and Åx, respectively. Let Y be a topological space, of which, there is a subset 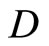 of
of 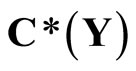 containing a non-constant function. A compactification
containing a non-constant function. A compactification 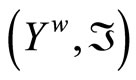 of Y is obtained by using closed Ãx- and basic closed C*D-filters in a process similar to the Wallman method, where
of Y is obtained by using closed Ãx- and basic closed C*D-filters in a process similar to the Wallman method, where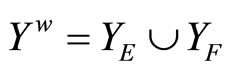 ,
, 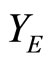 is the set {Nx|Nx is a closed
is the set {Nx|Nx is a closed  -filter, x is in Y},
-filter, x is in Y}, 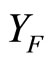 is the set of all basic closed C*D-filter that does not converge in Y,
is the set of all basic closed C*D-filter that does not converge in Y, ![]() is the topology induced by the base τ = {F*|F is a nonempty closed set in Y} for the closed sets of
is the topology induced by the base τ = {F*|F is a nonempty closed set in Y} for the closed sets of 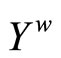 and F* is the set of all ℭ in
and F* is the set of all ℭ in 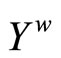 such that
such that 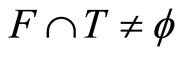 for all
for all ![]() in ℭ. Similarly, an arbitrary Hausdorff compactification
in ℭ. Similarly, an arbitrary Hausdorff compactification 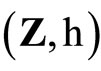 of a Tychonoff space X can be obtained by using the basic closed C*D-filters on X from
of a Tychonoff space X can be obtained by using the basic closed C*D-filters on X from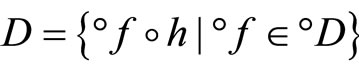 , where
, where 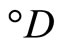 is the set
is the set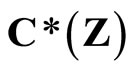 .
.
2. Open and Closed C*D-Filter Bases, Basic Open and Closed C*D-Filters
For an arbitrary topological space Y, let 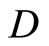 be a subset of
be a subset of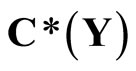 .
.
Theorem 2.1 Let ℱ be a filter on Y. For each f in 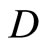 there exists a rf in
there exists a rf in 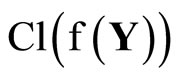 such that
such that

for any 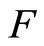 in ℱ and any
in ℱ and any 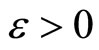 (See Thm. 2.1 in [2, p.1164]).
(See Thm. 2.1 in [2, p.1164]).
Proof. If the conclusion is not true, then there is an f in 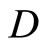 such that for each
such that for each 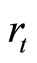 in
in 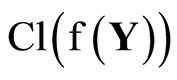 there exist an
there exist an 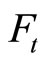 in ℱ and an
in ℱ and an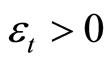 such that
such that

Since 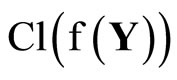 is compact and
is compact and 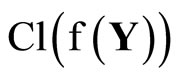 is contained in
is contained in
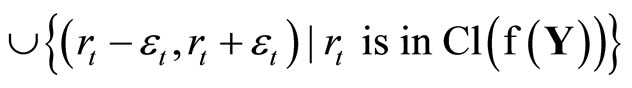 there exist r1,···,rn in
there exist r1,···,rn in  such that Y is contained in
such that Y is contained in
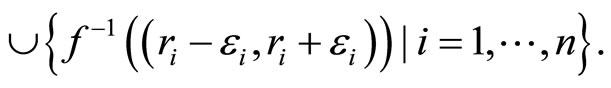
Let 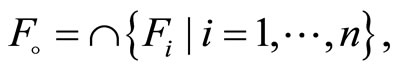 then
then  is in ℱ and
is in ℱ and
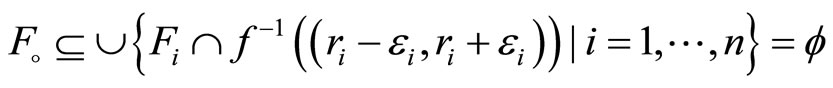 contradicting that f is not in ℱ.
contradicting that f is not in ℱ.
Corollary 2.2 Let ℱ (or Q) be a closed (or an open) ultrafilter on Y. For each f in , there exists a unique
, there exists a unique 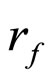 in
in  such that (1) for any
such that (1) for any  any
any 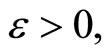
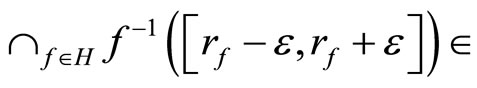 ℱ
ℱ
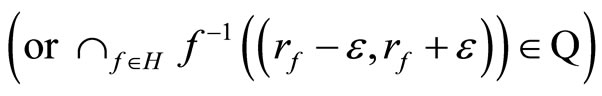
and (2) for any 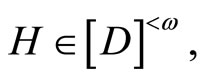 any
any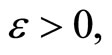
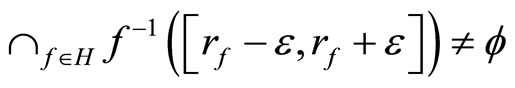
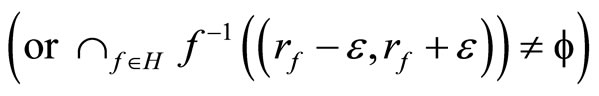 .
.
(See Cor. 2.2 & 2.3 in [2, p.1164].)
Therefore, for a given closed ultrafilter ℱ (or open ultrafilter Q), there exists a unique rf in 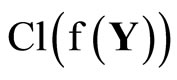 for each f in
for each f in  such that for any
such that for any 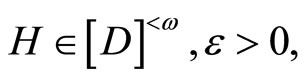
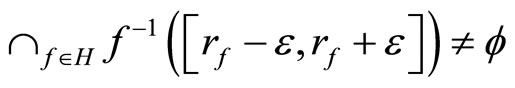

Let K be the set

and let V be the set
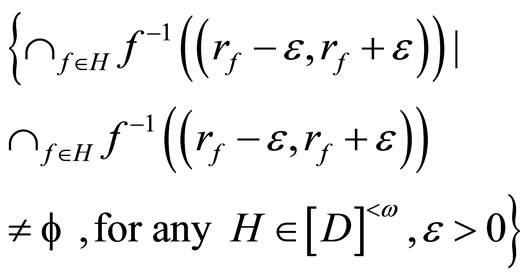
K and V are called a closed and an open C*D-filter bases, respectively. If for all f in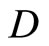 ,
, 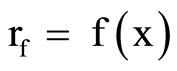 for some x in Y, then K and V are called the closed and open C*D-filter bases at x, denoted by Kx and Vx, respectively. Let ℰ and ℰx (or Å and Åx) be the closed (or open) filters generated by K and Kx (or V and Vx), respectively, then ℰ and ℰx (or Å and Åx) are called a basic closed C*D-filter and the basic closed C*D-filter at x (or a basic open C*D-filter and the basic open C*D-filter at x), respectively.
for some x in Y, then K and V are called the closed and open C*D-filter bases at x, denoted by Kx and Vx, respectively. Let ℰ and ℰx (or Å and Åx) be the closed (or open) filters generated by K and Kx (or V and Vx), respectively, then ℰ and ℰx (or Å and Åx) are called a basic closed C*D-filter and the basic closed C*D-filter at x (or a basic open C*D-filter and the basic open C*D-filter at x), respectively.
Corollary 2.3 Let ℱ and Q be a closed and an open ultrafilters on a topological space Y, respectively. Then there exist a unique basic closed C*D-filter ℰ and a unique basic open C*D-filter Å on Y such that ℰ is contained in ℱ and Å is contained in Q.
3. A Closed (x-Filter and a Modified Wallman Method of Compactification
Let Y be a topological space, of which, there is a subset  of
of 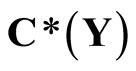 containing a non-constant function. For each x in Y, let Nx be the union of
containing a non-constant function. For each x in Y, let Nx be the union of  and ℰx, if Vx is an open nhood filter base at x; let Nx be the union of
and ℰx, if Vx is an open nhood filter base at x; let Nx be the union of 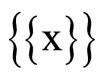 and
and , if Vx is not an open nhood filter base at x. For each x in Y, Nx is a ℘-filter with à being Nx. (See 12E. in [1, p.82] for definition and convergence). Nx is called a closed ℘x-filter. It is clear that Kx is contained in ℰx and ℰx is contained in Nx, Nx converges to x for each x in Y. Let
, if Vx is not an open nhood filter base at x. For each x in Y, Nx is a ℘-filter with à being Nx. (See 12E. in [1, p.82] for definition and convergence). Nx is called a closed ℘x-filter. It is clear that Kx is contained in ℰx and ℰx is contained in Nx, Nx converges to x for each x in Y. Let 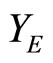 be the set of all Nx, x in Y. Let
be the set of all Nx, x in Y. Let  be the set of all basic closed C*D-filter ℰ that does not converge in Y and let
be the set of all basic closed C*D-filter ℰ that does not converge in Y and let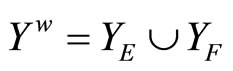 .
.
Definition 3.4 For each nonempty closed set F in Y, let F* be the set of ℭ in  such that the intersection of F and T is not an empty set for all T in ℭ.
such that the intersection of F and T is not an empty set for all T in ℭ.
From the Def. 3.4, the following Cor. 3.5 can be readily proved. We omit its proofs.
Corollary 3.5 For a closed set F in Y, (i) x is in F if Nx is in F*; (ii) F is equal to Y if F* is equal to ; (iii) if F is in ℭ, then ℭ is in F*; (iv) ℭ is in
; (iii) if F is in ℭ, then ℭ is in F*; (iv) ℭ is in 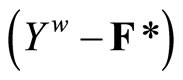 if there is a T in ℭ such that T is contained in Y – F.
if there is a T in ℭ such that T is contained in Y – F.
Lemma 3.6 For any two nonempty closed sets E and F in Y,
(i)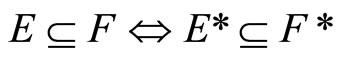 ,
,
(ii)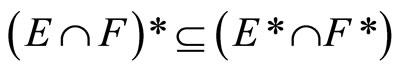 ,
,
(iii)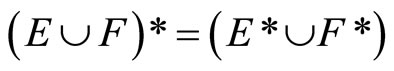 .
.
Proof. (i) For [Ü]: If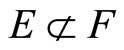 , pick an x in
, pick an x in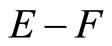 , by Cor. 3.5 (i), Nx is in
, by Cor. 3.5 (i), Nx is in 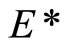 and Nx is not in
and Nx is not in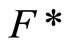 ; i.e.,
; i.e.,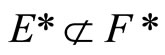 . For (Þ) is obvious. (ii) is clear from (i). (iii) For [Í]: If ℭ belongs to
. For (Þ) is obvious. (ii) is clear from (i). (iii) For [Í]: If ℭ belongs to 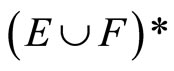 and does not belong
and does not belong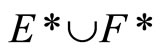 , then pick
, then pick  in ℭ such that
in ℭ such that
 .
.
Since 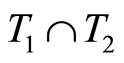 is in ℭ and
is in ℭ and
 .
.
Thus, ℭ does not belong to , contradicting the assumption. For [Ê] is obvious from (i).
, contradicting the assumption. For [Ê] is obvious from (i).
Proposition 3.7 τ = {F*|F is a nonempty closed set in Y} is a base for the closed sets of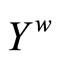 .
.
Proof. Let ℬ be the set 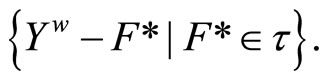 We show that ℬ is a base for
We show that ℬ is a base for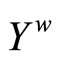 . For (a) of Thm. 5.3 in [1, p.38], if ℭ
. For (a) of Thm. 5.3 in [1, p.38], if ℭ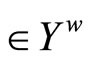 , then there exist an f in
, then there exist an f in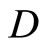 , a
, a 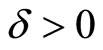 such that
such that
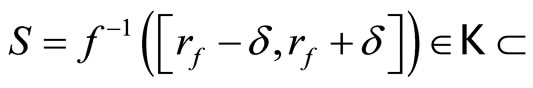 ℰ
ℰ![]()
and
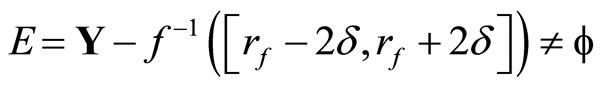 otherwise, if for all f in
otherwise, if for all f in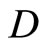 , all d > 0,
, all d > 0, 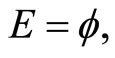 then for all f in
then for all f in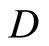 ,
, 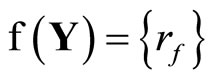 , contradicting that
, contradicting that  contains a non-constant function. Thus
contains a non-constant function. Thus ,
,  is closed,
is closed, ![]() is in ℭ and
is in ℭ and 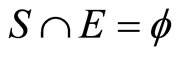 imply that ℭ is in
imply that ℭ is in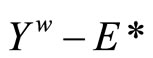 . So,
. So,
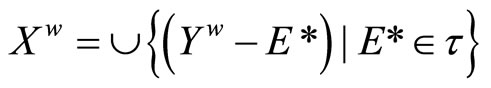 .
.
For (b) of Thm. 5.3, if ℭ belongs to
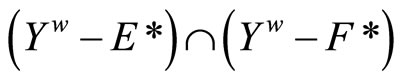 then
then 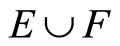 is closed,
is closed,  and
and
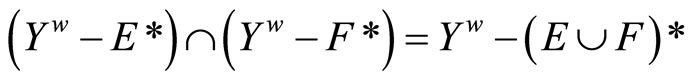
is in ℬ. Thus, ℭ is in
 .
.
Equip 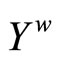 with the topology Á induced by t. For each f Î
with the topology Á induced by t. For each f Î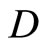 , define f*:
, define f*:  by
by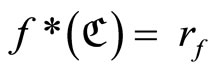 , if
, if
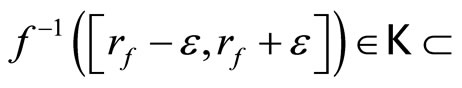 ℰ
ℰ![]()
for all e > 0. Since (i) if ℭ is equal to Nx for some Nx in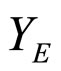 , then
, then
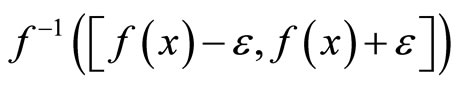
is in Nx for all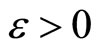 , (ii) if ℭ is ℰ which is in
, (ii) if ℭ is ℰ which is in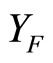 , then
, then
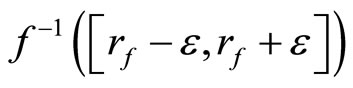
is in ℰ for all  (iii) by Cor. 2.2, the rf is unique for each f in
(iii) by Cor. 2.2, the rf is unique for each f in 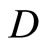 and (iv) the K that is contained in ℭ is unique. Thus, f* is well-defined for each f in
and (iv) the K that is contained in ℭ is unique. Thus, f* is well-defined for each f in . For all f in
. For all f in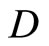 , all x in Y,
, all x in Y,
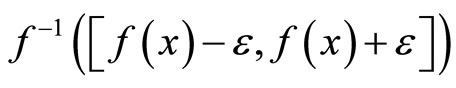
is in Nx for all  thus f*(Nx) is equal to f(x) for all f in
thus f*(Nx) is equal to f(x) for all f in  and all x in Y.
and all x in Y.
Lemma 3.8 For each f in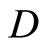 , let r be in
, let r be in , then
, then
(i) 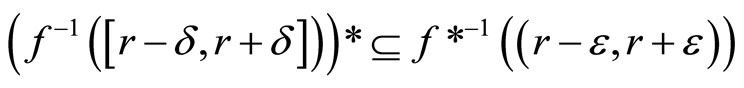
and

Proof. (i): If ℭ is in 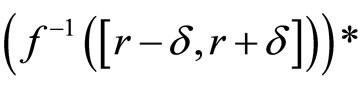 and
and 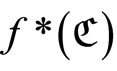 is
is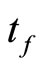 , then
, then
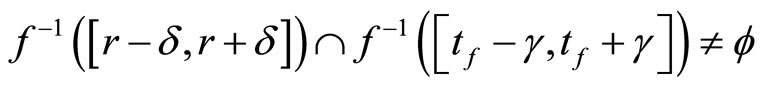
for all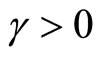 , where
, where 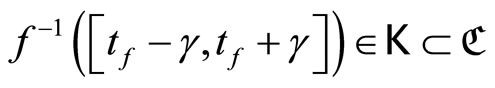 for all
for all . Thus,
. Thus,
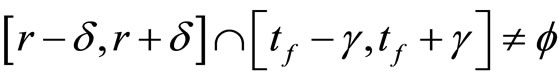
for all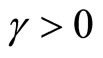 ; i.e.,
; i.e.,  is
is
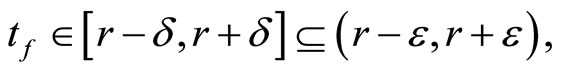
so ℭ is in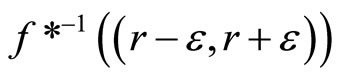 . For (ii): If ℭ is in
. For (ii): If ℭ is in
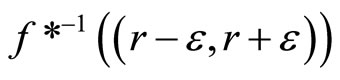 and
and 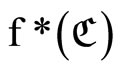 is
is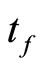 , then
, then
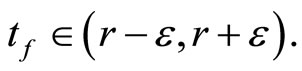
Pick a d > 0 such that
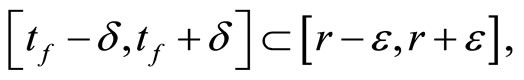
then
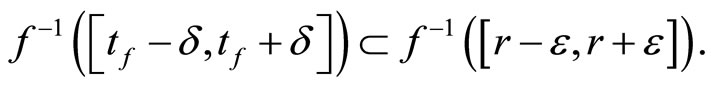
Since
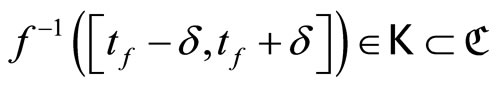 thus
thus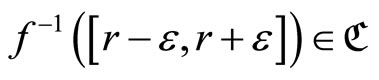 . By Cor. 3.5 (iii), ℭ is in
. By Cor. 3.5 (iii), ℭ is in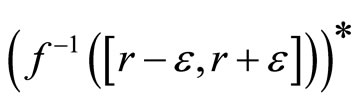 .
.
Proposition 3.9 For each f in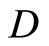 , f* is a bounded real continuous function on
, f* is a bounded real continuous function on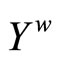 .
.
Proof. For each f in 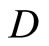 and each ℭ in
and each ℭ in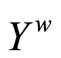 ,
, 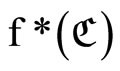 is in
is in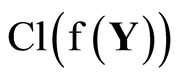 . Thus
. Thus 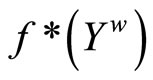 is contained in
is contained in ; i.e., f* is bounded on
; i.e., f* is bounded on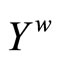 . For the continuity of f*: If ℭ is in
. For the continuity of f*: If ℭ is in 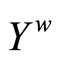 and
and  is tf. We show that for any
is tf. We show that for any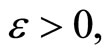 there is a
there is a 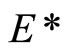 in t such that ℭ is in
in t such that ℭ is in
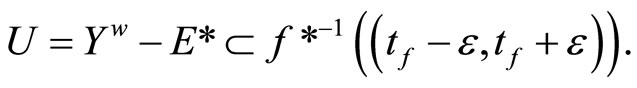
Let
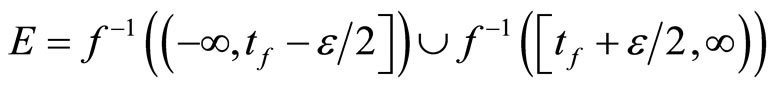
and 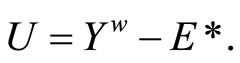 Since
Since
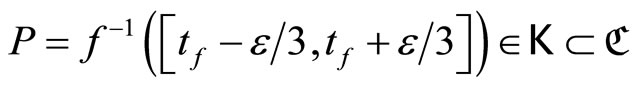
and  by Cor. 3.5 (iv), ℭ
by Cor. 3.5 (iv), ℭ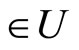 . Next, for any ℭs in
. Next, for any ℭs in , if
, if 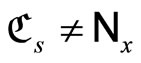 for all x in Y, by Cor. 3.5 (iv), pick a
for all x in Y, by Cor. 3.5 (iv), pick a ![]() in ℭs such that
in ℭs such that
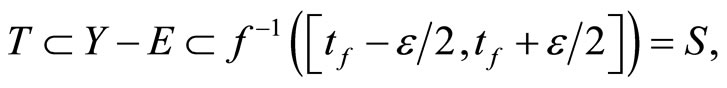
then ![]() is in ℭs. By Cor. 3.5 (iii) and Lemma 3.8 (i), ℭs
is in ℭs. By Cor. 3.5 (iii) and Lemma 3.8 (i), ℭs
is in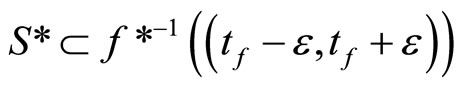 . If ℭs is Nx for some x in Y, by Cor. 3.5 (i), Nx in
. If ℭs is Nx for some x in Y, by Cor. 3.5 (i), Nx in 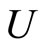 if
if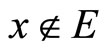 , thus
, thus
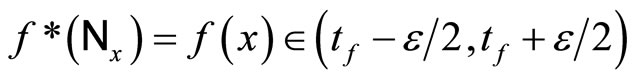 ;
;
i.e., ℭs is Nx which is in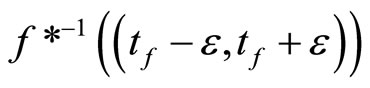 .
.
Lemma 3.10 Let k: 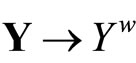 be defined by
be defined by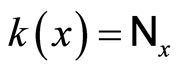 . Then, (i) k is an embedding from Y into
. Then, (i) k is an embedding from Y into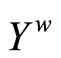 ; (ii) for all f in
; (ii) for all f in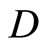 ,
,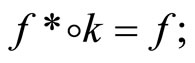 and (iii)
and (iii) 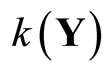 is dense in
is dense in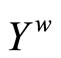 .
.
Proof. (i) By the setting, Nx = Ny if x = y. Thus 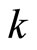 is well-defined and one-one. Let
is well-defined and one-one. Let  be a function from
be a function from
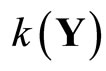 into Y defined by
into Y defined by  To show the continuity of
To show the continuity of 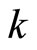 and
and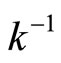 , for any
, for any  in t, (a): x is in
in t, (a): x is in
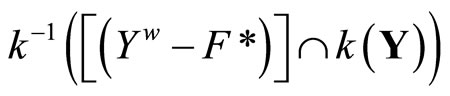
iff (b): 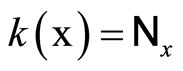 is in
is in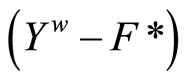 . By Cor. 3.5 (i), (b) iff (c): x is not in
. By Cor. 3.5 (i), (b) iff (c): x is not in . So,
. So,
 ;
;
i.e.,
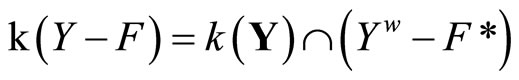 .
.
So, 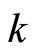 and
and 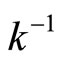 are continuous. (ii) is obvious. (iii) For any
are continuous. (ii) is obvious. (iii) For any 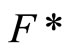 in t such that
in t such that 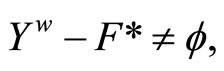 pick a ℭ in
pick a ℭ in 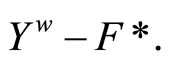 By Cor. 3.5 (iv), there is a
By Cor. 3.5 (iv), there is a ![]() in ℭ such that
in ℭ such that 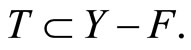 Pick an x in
Pick an x in![]() , by Cor. 3.5 (i),
, by Cor. 3.5 (i), 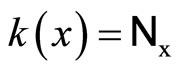 which is not in
which is not in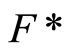 , so
, so 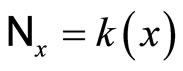 is in both
is in both  and
and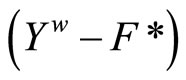 ; i.e.,
; i.e.,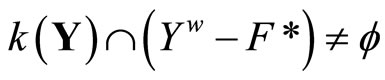 . Thus,
. Thus,  is dense in
is dense in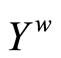 .
.
Let . Then
. Then 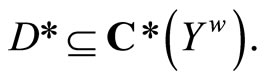 Let
Let

be a closed C*D*-filter base on 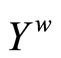 and let ℰ* be the basic closed C*D*-filter on
and let ℰ* be the basic closed C*D*-filter on 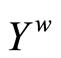 generated by K*. Since
generated by K*. Since 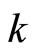 and
and 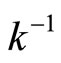 are one-one,
are one-one, 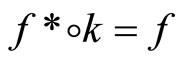 for all
for all 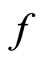 in
in 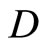 and
and 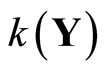 is dense in
is dense in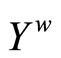 , so
, so
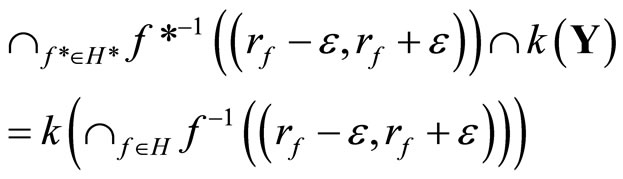
for any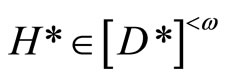 ,
, 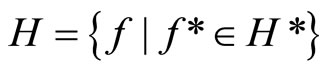 (or any
(or any
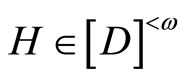 ,
, 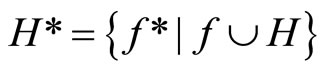 and all
and all 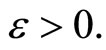 Thus,
Thus,

iff
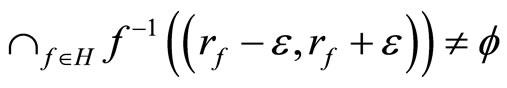
and
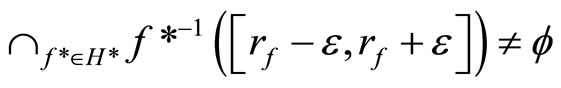
iff

for any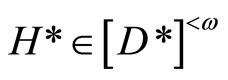 ,
, 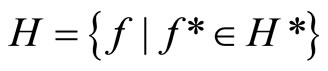 (or any
(or any
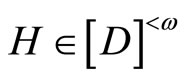 ,
, 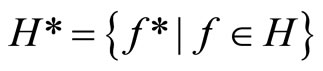 and all e > 0. Therefore, if the K* or ℰ* defined as above is well-defined, so is K or ℰ defined as in Section 2 well-defined and vice versa. If K* or ℰ* is given, then K or ℰ is called the closed C*D-filter base or the basic closed C*D-filter on Y induced by K* or ℰ* and vice versa.
and all e > 0. Therefore, if the K* or ℰ* defined as above is well-defined, so is K or ℰ defined as in Section 2 well-defined and vice versa. If K* or ℰ* is given, then K or ℰ is called the closed C*D-filter base or the basic closed C*D-filter on Y induced by K* or ℰ* and vice versa.
Lemma 3.11 Let ℰ be a basic closed C*D-filter on Y defined as in Section 2. If ℰ converges to a point x in Y, then (i) rf = f(x) for all f in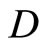 ; i.e. ℰ = ℰx, (ii) Vx is an open nhood base at x in Y and (iii)
; i.e. ℰ = ℰx, (ii) Vx is an open nhood base at x in Y and (iii)
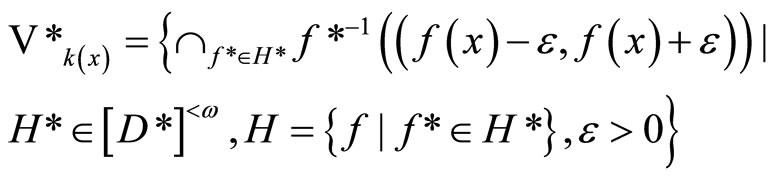
is an open nhood base at k(x) in .
.
Proof. If ℰ converges to![]() in Y, (i): for each
in Y, (i): for each ,
,
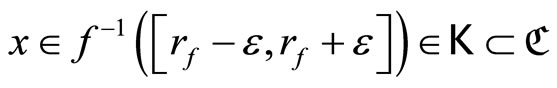
for all  thus
thus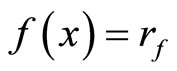 ; i.e., ℰ = ℰx. (ii): Since ℰ converges to x in Y, for any open nhood
; i.e., ℰ = ℰx. (ii): Since ℰ converges to x in Y, for any open nhood  of
of![]() , there is
, there is
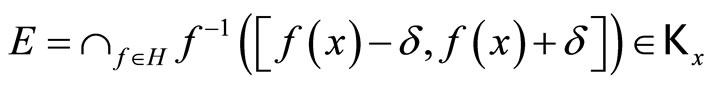
which is contained in ℰx = ℰ for some 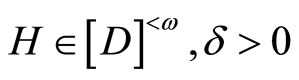 such that
such that 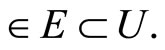 Since x is in
Since x is in
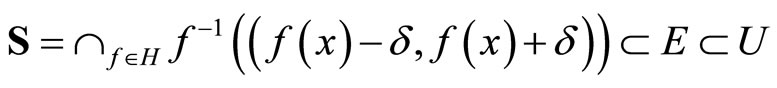
and S is in Vx, thus Vx is an open nhood base at x; (iii): For any  in t such that Nx is not in
in t such that Nx is not in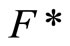 , by Cor. 3.5 (i),
, by Cor. 3.5 (i), ![]() is not in
is not in , and by (ii) of Lemma 3.11 above,
, and by (ii) of Lemma 3.11 above, ![]() is in
is in
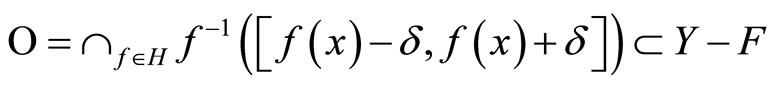
for some 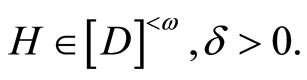 Since
Since
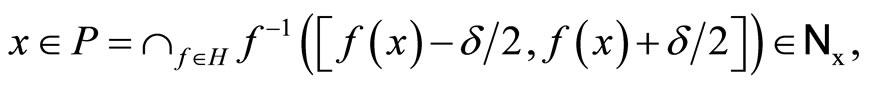
Cor. 3.5 (i), Lemmas 3.6 (ii) and 3.8 (i) imply that
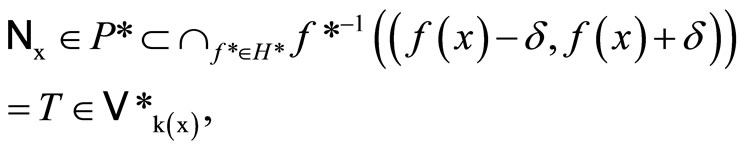
where 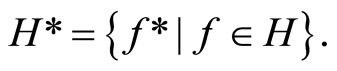 We claim that
We claim that 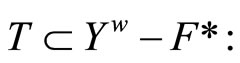
For any ℭs in![]() , if
, if 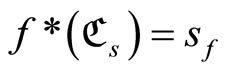 for all f in
for all f in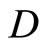 , then sf
, then sf
is in 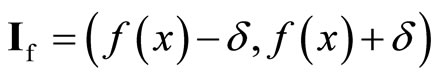 for all f in
for all f in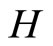 . Pick a
. Pick a
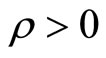 such that
such that 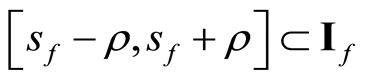 for all f in
for all f in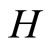 then
then

and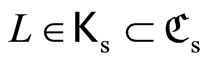 ; i.e.
; i.e. 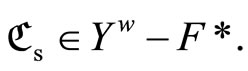 So
So
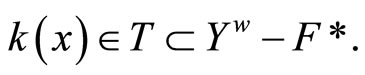
Thus  is an open nhood base at
is an open nhood base at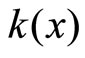 .
.
Lemma 3.12 Let ℰ be a basic C*D-filter on Y defined as in Section 2. If ℰ does not converge in Y,
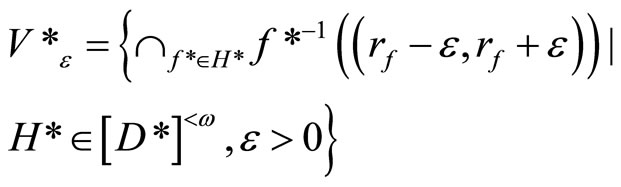
is an open nhood base at ℰ in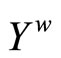 .
.
Proof. If ℰ does not converge in Y, then ℰ is in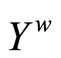 . Since f*(ℰ) = rf for all f* Î D*ℰ
. Since f*(ℰ) = rf for all f* Î D*ℰ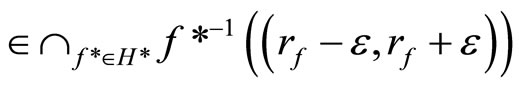
for any 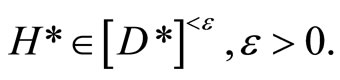 For any
For any 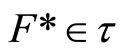 such that ℰ
such that ℰ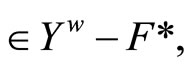 by Cor. 3.5 (iv) there exists a
by Cor. 3.5 (iv) there exists a
 ℰ
ℰ
for some 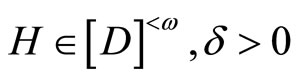 such that E Ì Y – F. For
such that E Ì Y – F. For 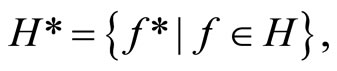 let
let
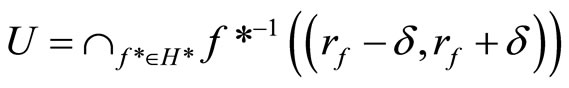 then ℰ
then ℰ
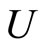
 V*. We claim that
V*. We claim that 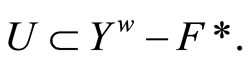 For any ℰt in
For any ℰt in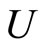 , let f*(ℰt) = tf for each f* in
, let f*(ℰt) = tf for each f* in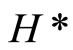 . Then for each f in
. Then for each f in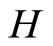 ,
,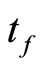 is in
is in
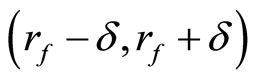 and
and 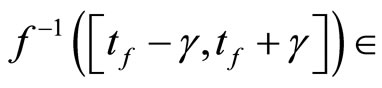 ℰt
ℰt
for all 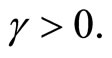 Pick a
Pick a 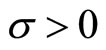 such that
such that
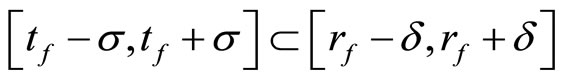
for each f in , then
, then
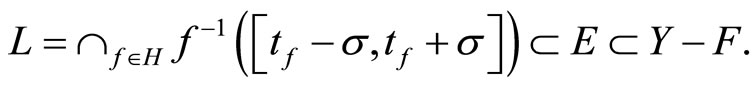
Since 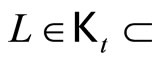 ℰt, so ℰt
ℰt, so ℰt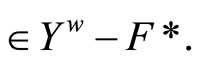 Hence ℰ is in
Hence ℰ is in 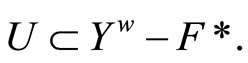 Thus, V*ℰ is an open nhood base at ℰ.
Thus, V*ℰ is an open nhood base at ℰ.
Proposition 3.13 For any basic closed C*D*-filter ℰ* on , ℰ* converges in
, ℰ* converges in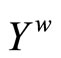 .
.
Proof. For given ℰ*, let K and ℰ be the closed C*D-filter base and the basic closed C*D-filter on Y induced by ℰ*. Case 1: If ℰ converges to an x in Y, then 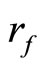 is
is 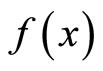 for all f in
for all f in . For any
. For any
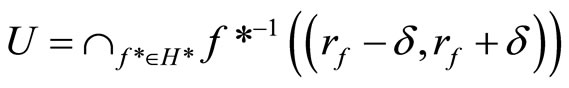
in V*k(x), let
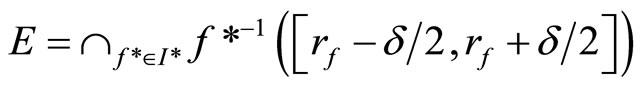 where
where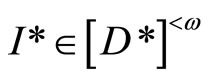 . Then
. Then 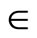
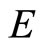 K*
K*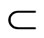 ℰ* and
ℰ* and 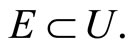
Thus, ℰ* converges to 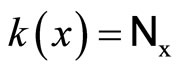 in
in . Case 2: If ℰ does not converge in Y, then ℰ is in
. Case 2: If ℰ does not converge in Y, then ℰ is in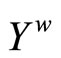 . For any
. For any
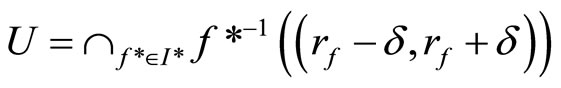
in V*ℰ, let
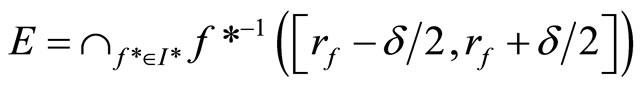 then
then 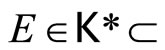 ℰ* and
ℰ* and  Thus, ℰ* converges to ℰ in
Thus, ℰ* converges to ℰ in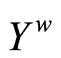 .
.
Theorem 3.14  is a compactification of Y.
is a compactification of Y.
Proof. First, we show that 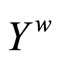 is compact. Let
is compact. Let be a sub-collection of t with the finite intersection property. Let
be a sub-collection of t with the finite intersection property. Let
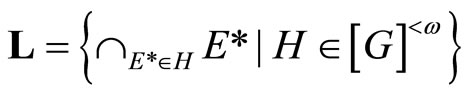 then L is a filter base on
then L is a filter base on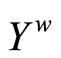 . Let ℱ be a closed ultrafilter on
. Let ℱ be a closed ultrafilter on 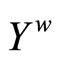 such that L is contained in ℱ. By Cor. 2.3, there is a unique basic closed C*D*-filter ℰ* on
such that L is contained in ℱ. By Cor. 2.3, there is a unique basic closed C*D*-filter ℰ* on  such that ℰ* is contained in ℱ. By Prop. 3.13, ℰ* converges to an ℰo in
such that ℰ* is contained in ℱ. By Prop. 3.13, ℰ* converges to an ℰo in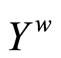 . This implies that ℱ converges to ℰo too. Hence, ℰo is in F for all F in ℱ; i.e., ℰo
. This implies that ℱ converges to ℰo too. Hence, ℰo is in F for all F in ℱ; i.e., ℰo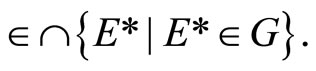 Thm. 17.4 in [1, p.118],
Thm. 17.4 in [1, p.118],  is compact. Thus, by Lemma 3.10 (i) and (iii),
is compact. Thus, by Lemma 3.10 (i) and (iii), 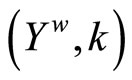 is a compactification of Y.
is a compactification of Y.
4. The Hausdorff Compactification (Xw,k) of X Induced by a Subset D of C*(X)
Let X be a Tychonoff space and let  be a subset of
be a subset of  such that
such that  separates points of X and the topology on X is the weak topology induced by
separates points of X and the topology on X is the weak topology induced by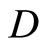 . It is clear that
. It is clear that 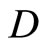 contains a non-constant function. For each x in X, since Vx is an open nhood base at x, it is clear that ℰx converges to x. Let
contains a non-constant function. For each x in X, since Vx is an open nhood base at x, it is clear that ℰx converges to x. Let 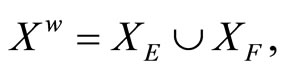 where XE = {ℰx |x
where XE = {ℰx |x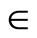 X} and XE = {ℰ|ℰ is a basic closed C*D-filter that does not converge in X}. Similar to what we have done in Section 3, we can get the similar definitions, lemmas, propositions and a theorem in the following:
X} and XE = {ℰ|ℰ is a basic closed C*D-filter that does not converge in X}. Similar to what we have done in Section 3, we can get the similar definitions, lemmas, propositions and a theorem in the following:
(4.15.4) (See Def. 3.4) For a nonempty closed set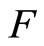 in X,
in X, 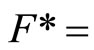 {ℰ
{ℰ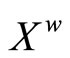
 |
|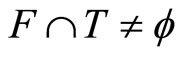 for all
for all ![]() in ℰ}.
in ℰ}.
(4.15.5) (See Cor. 3.5) For a nonempty closed set F in X, (i) x is in F if ℰx is in F*; (ii) F is X if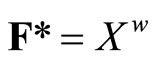 ; (iii) for each ℰ in
; (iii) for each ℰ in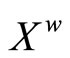 , F is in ℰ implying ℰ is in F*; (iv) ℰ
, F is in ℰ implying ℰ is in F*; (iv) ℰ 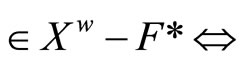 there is a
there is a ![]() in ℰ such that
in ℰ such that 
Proof. (i) (Ü) If ℰx is in , then
, then
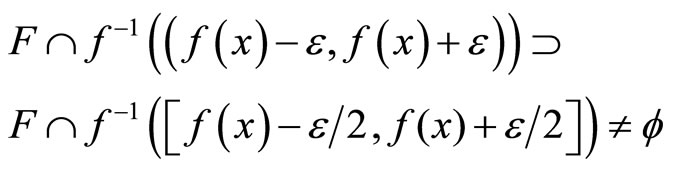
for all f in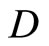 ,
, 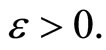 Since Vx is a nhood base at
Since Vx is a nhood base at![]() , thus
, thus ![]() is a cluster point of F, so
is a cluster point of F, so![]() is in F. (i) implying (ii), (iii) and (iv) are obvious.
is in F. (i) implying (ii), (iii) and (iv) are obvious.
(4.15.6) (See Lemma 3.6) For any two nonempty sets 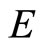 and
and 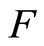 in X,
in X,
(i)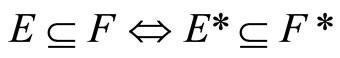 ;
;
(ii) 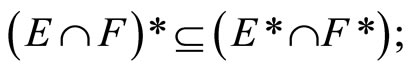
(iii) 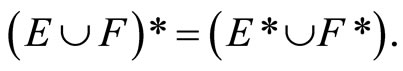
(4.15.7) (See Prop. 3.7) t = {F*|F is a nonempty closed set in X} is a base for the closed sets of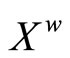 .
.
(4.15.7.1) (See the definitions for the topology Á on 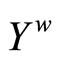 and f* for each f in
and f* for each f in 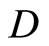 in Section 3.)
in Section 3.)
Equip 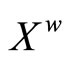 with the topology Á induced by t. For each f in
with the topology Á induced by t. For each f in , define
, define 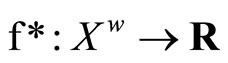 by f*(ℰ) = rf if
by f*(ℰ) = rf if
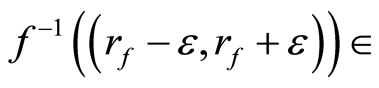 ℰ for all
ℰ for all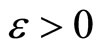 . Then f* is welldefined and f*(ℰx) is f(x) for all f in
. Then f* is welldefined and f*(ℰx) is f(x) for all f in 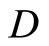 and all x in X.
and all x in X.
(4.15.8) (See Lemma 3.8) For each f in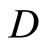 , let r be in
, let r be in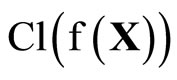 , then
, then
(i) 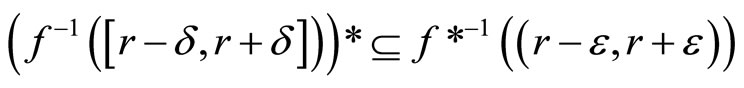
and
(ii) 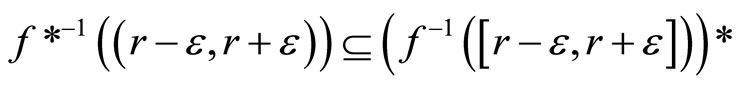
for any 
(4.15.9) (See Prop. 3.9) For each f in , f* is a bounded real continuous function on
, f* is a bounded real continuous function on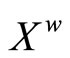 .
.
(4.15.10) (See Lemma 3.10) Let 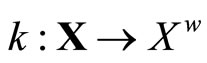 be defined by
be defined by 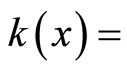 ℰx. Then, (i)
ℰx. Then, (i) 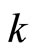 is an embedding from X into
is an embedding from X into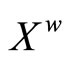 ; (ii)
; (ii) 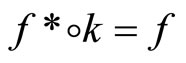 for all f in
for all f in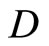 ; and (iii)
; and (iii) 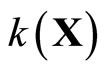 is dense in
is dense in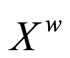 .
.
(4.15.11) (See Lemmas 3.11 and 3.12) For each ℰ in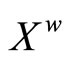 , let
, let
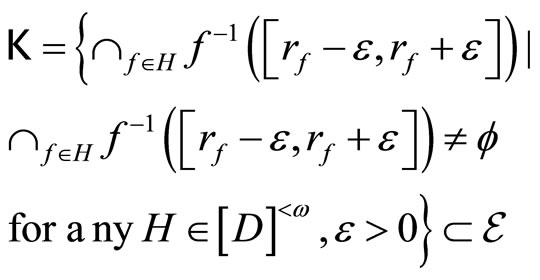
1) If ℰ converges to x, then ℰ is ℰx and V*k(x) is =
V*ℰx =
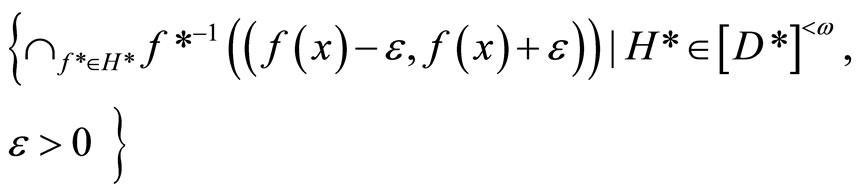
is an open nhood base at ℰx. 2) If ℰ does not converge in X, then ℰ is in  and V*ℰ =
and V*ℰ =
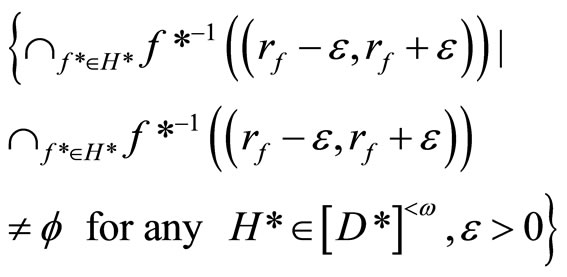
is an open nhood base at ℰ in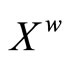 .
.
(4.15.13) (See Prop. 3.13) Each basic closed C*D*- filter ℰ* on 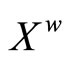 converges to ℰ in
converges to ℰ in .
.
(4.15.14) (See Theorem 3.14)  is a compactification of X.
is a compactification of X.
Lemma 4.16  separates points of
separates points of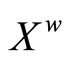 .
.
Proof. For ℰs, ℰt in , let
, let
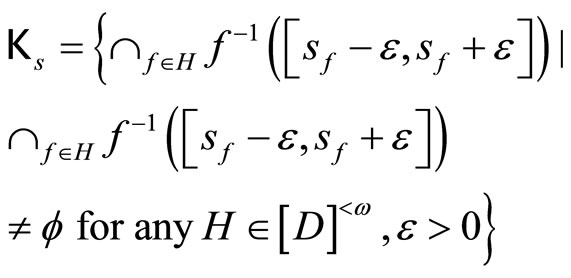
and similarly for Kt. Since ℰs is not equal to ℰt, Ks is not equal to Kt and that 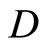 has a g such that
has a g such that 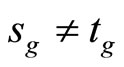 are equivalent, where
are equivalent, where 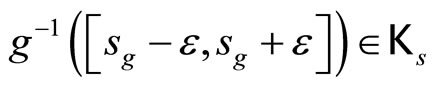 which is contained in ℰs and
which is contained in ℰs and 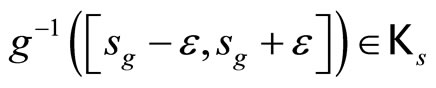 which is contained in ℰt for all
which is contained in ℰt for all 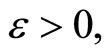 thus by the definition of g*, g*(ℰs)
thus by the definition of g*, g*(ℰs)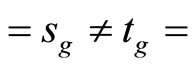 g*(ℰt).
g*(ℰt).
Theorem 4.17 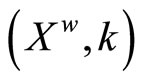 is a Hausdorff compactification of X.
is a Hausdorff compactification of X.
Proof. By 4.15.10 (i) and (iii), 4.15.14 and Lemma 4.16, 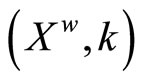 is a Hausdorff compactification of X.
is a Hausdorff compactification of X.
5. The Homeomorphism between (Xw,k) and (Z,h)
Let 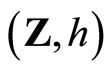 be an arbitrary Hausdorff compactification of X, then X is a Tychonoff space. Let
be an arbitrary Hausdorff compactification of X, then X is a Tychonoff space. Let  denote
denote  which is the family of real continuous functions on Z, and let
which is the family of real continuous functions on Z, and let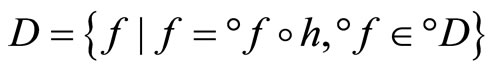 . Then
. Then  is a subset of
is a subset of  such that
such that 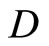 separates points of X, the topology on X is the weak topology induced by
separates points of X, the topology on X is the weak topology induced by 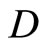 and
and 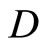 contains a non-constant function.
contains a non-constant function.
Let 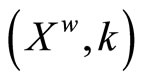 be the Hausdorff compactification of X obtained by the process in Section 4 and
be the Hausdorff compactification of X obtained by the process in Section 4 and 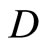 is defined as above. For each basic closed C*D-filter ℰ in
is defined as above. For each basic closed C*D-filter ℰ in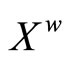 , let ℰ be generated by
, let ℰ be generated by

let °ℰ be the basic closed C*°D-filter on Z generated by

and let h−1 be the function from h(X) to X defined by h−1(h(x)) = x. Since h and h−1 are one-one, f = °f o h and h(X) is dense in Z, similar to the arguments in the paragraphs prior to Lemma 3.11, we have that

iff

for any
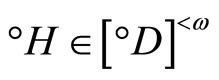 (or any
(or any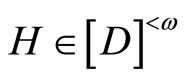 ),
),
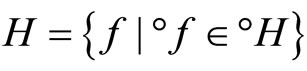 (or
(or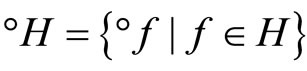 )
)
and all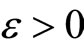 . Thus, if K or ℰ is well-defined, so is °K or °ℰ and vice versa. If K or ℰ is given, °K or °ℰ is called the closed C*°D-filter base or the basic closed C*°D-filter on Z induced by K or ℰ and vice versa. For any z in Z,
. Thus, if K or ℰ is well-defined, so is °K or °ℰ and vice versa. If K or ℰ is given, °K or °ℰ is called the closed C*°D-filter base or the basic closed C*°D-filter on Z induced by K or ℰ and vice versa. For any z in Z,
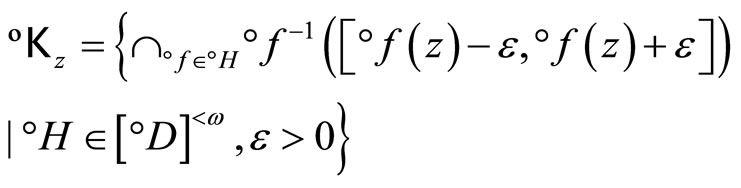
is the closed C*°D-filter base at z. The closed filter °ℰz generated by °Kz is the basic closed C*°D-filter at z. Since Z is compact Hausdorff, each °ℰ on Z converges to a unique point z in Z. So, we define  by
by 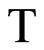 (ℰ) = z, where ℰ is in
(ℰ) = z, where ℰ is in  and z is the unique point in Z such that the basic closed C*°D-filter °ℰ on Z induced by ℰ converges to it. For ℰs, ℰt in
and z is the unique point in Z such that the basic closed C*°D-filter °ℰ on Z induced by ℰ converges to it. For ℰs, ℰt in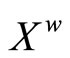 , let
, let
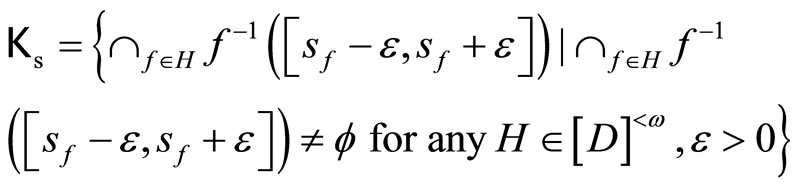
and similarly for Kt such that ℰs and ℰt are generated by Ks and Kt, respectively. Assume that °ℰs and °ℰt converge to zs and zt in Z, respectively. Then ℰs is not equal to ℰt, °ℰs is not equal to °ℰt and zs is not equal to zt are equivalent. Hence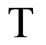 is well-defined and one-one. For each z in Z, let °ℰz be the basic closed C*°D-filter at z, since Z is compact Hausdorff and
is well-defined and one-one. For each z in Z, let °ℰz be the basic closed C*°D-filter at z, since Z is compact Hausdorff and

is an open nhood base at z, thus °ℰz converges to z. Let ℰz be the element in  induced by °ℰz, then,
induced by °ℰz, then, ![]() (ℰz) = z. Hence,
(ℰz) = z. Hence, ![]() is one-one and onto.
is one-one and onto.
Theorem 5.18 (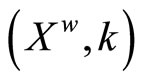 is homeomorphic to
is homeomorphic to 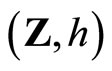 under the mapping
under the mapping ![]() such that
such that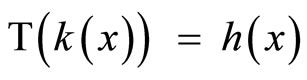 .
.
Proof. We show that  is continuous. For each ℰ in F* which is in t, let °ℰ be the basic closed C*°D-filter on Z induced by ℰ. If °ℰ converges to z in Z,
is continuous. For each ℰ in F* which is in t, let °ℰ be the basic closed C*°D-filter on Z induced by ℰ. If °ℰ converges to z in Z, 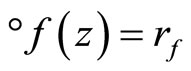 for each f in
for each f in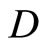 and
and
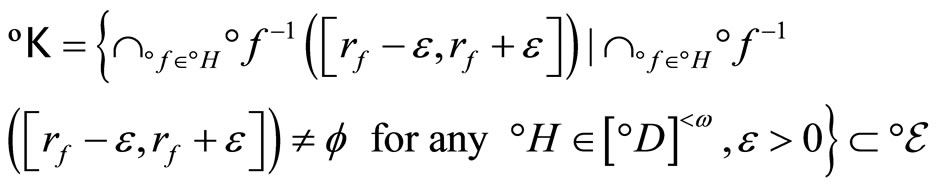
Then (a): ℰ is in F* iff (b):
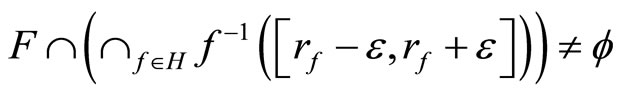
for any  where
where
 ℰ.
ℰ.
Since  is one-one,
is one-one, 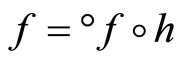 for all f in
for all f in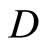 , so (b) iff (c):
, so (b) iff (c):

for any
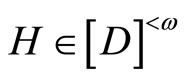 (or
(or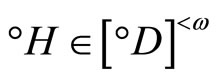 ),
),
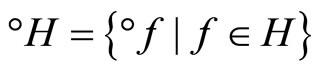 (or
(or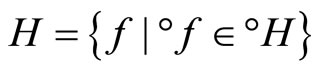 )
)
and any e > 0. Since
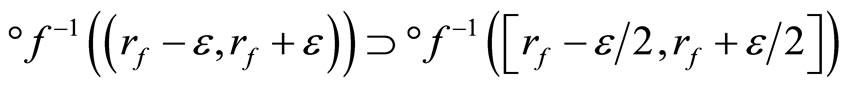
for any °f in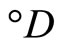 ,
,  (c) iff (d):
(c) iff (d):

for any 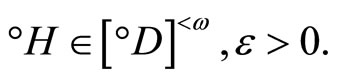 Since
Since
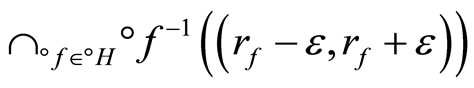
is an arbitrary basic open nhood of z in Z. So, (d) iff z is in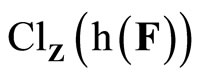 ; i.e., ℰ is in F* if
; i.e., ℰ is in F* if ![]() (ℰ) is equal to z which belongs to
(ℰ) is equal to z which belongs to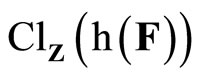 . Hence, T(F*) = ClZ(h(F)) is closed in Z for all F* in t. Thus,
. Hence, T(F*) = ClZ(h(F)) is closed in Z for all F* in t. Thus,  is continuous. Since
is continuous. Since ![]() is one-one, onto and both Z and
is one-one, onto and both Z and 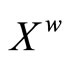 are compact Hausdorff, by Theorem 17.14 in [1, p.123],
are compact Hausdorff, by Theorem 17.14 in [1, p.123], ![]() is a homeomorphism. Finally, from the definitions of
is a homeomorphism. Finally, from the definitions of 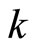 and
and , it is clear that
, it is clear that 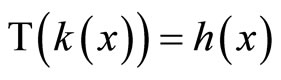 for all x in X.
for all x in X.
Corollary 5.19 Let (bX,![]() ) be the Stone-Čech compactification of a Tychonoff space X,
) be the Stone-Čech compactification of a Tychonoff space X,

and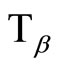 :
: 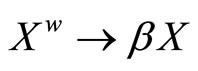 is defined similarly to
is defined similarly to![]() as above. Then (bX,
as above. Then (bX,![]() ) is homeomorphic to
) is homeomorphic to 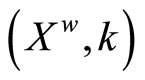 such that
such that
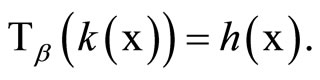
Corollary 5.20 Let (gX,![]() ) be the Wallman compactification of a normal T1-space X,
) be the Wallman compactification of a normal T1-space X,
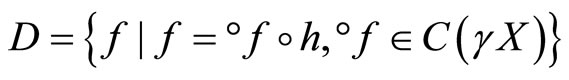
and 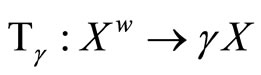 is defined similarly to
is defined similarly to ![]() as above. Then (gX,
as above. Then (gX,![]() ) is homeomorphic to
) is homeomorphic to 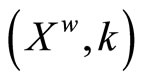 such that
such that
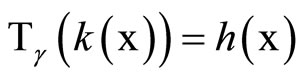 .
.
REFERENCES
- S. Willard, “General Topology,” Addison-Wesley, Reading, 1970.
- H. J. Wu and W. H. Wu, “An Arbitrary Hausdorff Compactification of a Tychonoff Space X Obtained from a C*D-Base by a Modified Wallman Method,” Topology and its Applications, Vol. 155, No. 11, 2008, pp. 1163- 1168. doi:10.1016/j.topol.2007.05.021

