Advances in Pure Mathematics
Vol.2 No.6(2012), Article ID:24367,12 pages DOI:10.4236/apm.2012.26057
Penrose Transform on D-Modules, Moduli Spaces and Field Theory*
Department of Research in Mathematics and Engineering, Technological Institute of High Studies of Chalco, Chalco, Mexico
Email: francisco.bulnes@tesch.edu.mx
Received August 9, 2012; revised September 15, 2012; accepted September 26, 2012
Keywords: Penrose Transform; Coherent D-Modules; Derived Sheaf; Moduli Space; Conformal Classes; Heterotic Strings
ABSTRACT
We consider a generalization of the Radon-Schmid transform on coherent D-modules of sheaves of holomorphic complex bundles inside a moduli space, with the purpose of establishing the equivalences among geometric objects (vector bundles) and algebraic objects as they are the coherent D-modules, these last with the goal of obtaining conformal classes of connections of the holomorphic complex bundles. The class of these equivalences conforms a moduli space on coherent sheaves that define solutions in field theory. Also by this way, and using one generalization of the Penrose transform in the context of coherent D-modules we find conformal classes of the space-time that include the heterotic strings and branes geometry.
1. Introduction
It is opportune to consider a generalization of the RadonSchmid [1], on coherent D-modules [2], of the sheaf of holomorphic bundles into a cohomological context, [3] with the goal of establishing the equivalences between geometrical objects (vector bundles) and algebraic objects as they are the coherent D-modules, these last with the goal of establishing the conformal classes useful to define adequately the differential operators that define the field equations of all the microscopic and macroscopic phenomena of the space-time through the connections or shape operators [4], of the complex holomorphic bundles in gauge theory. The class of these equivalences is precisely in our moduli space, which has in consideration the differential operator that defines the connection of the corresponding vector bundle which establish the relation among dimensions of cohomological conformal classes [5], and the vector bundles corresponding via the differential operators of the equations of shape (connection) of the Riemannian manifold [5].
But studies in algebraic geometry have established that manifolds of Calabi-Yau have the integrals of Penrose type, or at least complex integrals on strings like equivalences of geometrical invariants under the philosophy of the mirror symmetry. From a point of view of coherent D-modules, the conformally comes established in automatic form through the use of Penrose transforms on Dmodules. Of this manner, we come to D-strings and Dbranes corresponding to specific classes of derived sheaves obtained from the appropriate generalized Penrose transform [6].
We define our moduli space as the space of the invariant differential operators of the  -cohomology modulo that are conformally invariants. We determine a cohomology between moduli spaces on the space of differenttial operators that accept a scheme of integral operators cohomology of Penrose type in the context of the coherent D-modules [7], since the scheme of the ireducible unitary representations to these operators are unitary representations of compact components of the group
-cohomology modulo that are conformally invariants. We determine a cohomology between moduli spaces on the space of differenttial operators that accept a scheme of integral operators cohomology of Penrose type in the context of the coherent D-modules [7], since the scheme of the ireducible unitary representations to these operators are unitary representations of compact components of the group 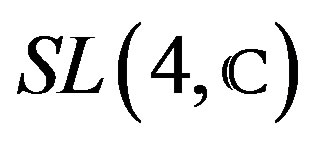 [5].
[5].
2. Conformally Invariant Operators, Penrose Transform and Derived Sheaves
There exists indictions that the class of differential operators that accept an re-interpretation of a integral operators cohomology (as the due for the Penrose transform, the Twistor transform, etc.) is accordingly the class of invariant differential operators, of the fact that the Penrose transform generates these conformal invariants operators [4], and thus we can identify the conformal classes to which they belong [8,9]. Some examples of these differential operators are the existence of the massless field equations (to flat versions and curved of some of their similar ones [10]) and the conformal invariant wave operator given by the map [4]:
 (1)
(1)
or also the Einstein operator [4]:
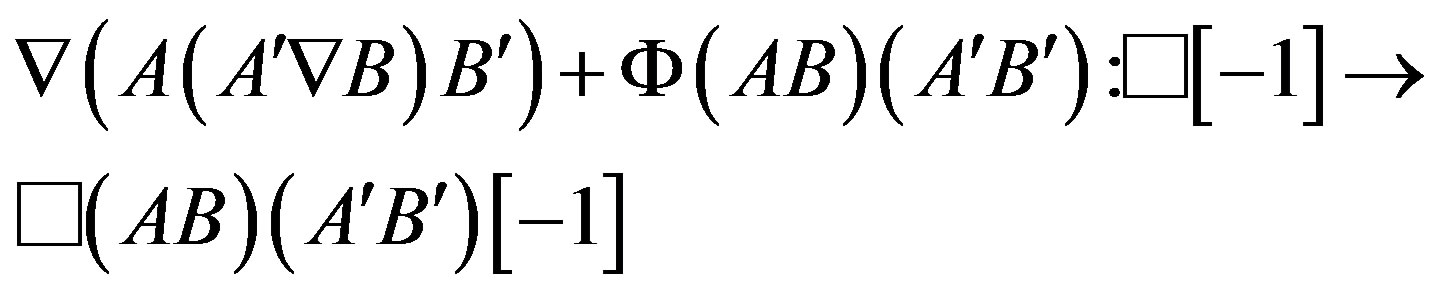 (2)
(2)
or the conformal invariant modification of the square of the wave operator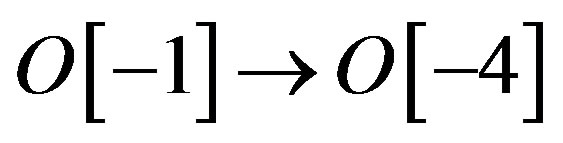 , that is to say; the wave operator who involves terms of the Ricci tensor [4],
, that is to say; the wave operator who involves terms of the Ricci tensor [4],
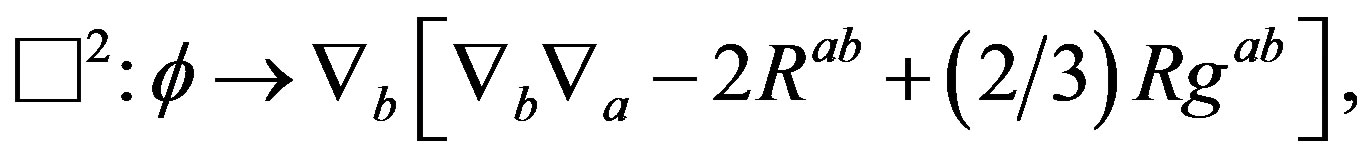 (3)
(3)
Then the integration of the partial differential equations corresponding to these invariant linear differential operators is realized as integrals transform of the Penrose type, because the context of the irreducible unitary representations for these operators are unitary representations of compact components of the group  such as
such as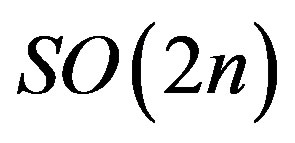 , [7], of the fact that in the flat case the classification of invariant differential operators like those described previously are a problem of representations theory of Lie groups applied to the group of
, [7], of the fact that in the flat case the classification of invariant differential operators like those described previously are a problem of representations theory of Lie groups applied to the group of and its compact subgroups [7]. Then one visualizes these operators through Lie group
and its compact subgroups [7]. Then one visualizes these operators through Lie group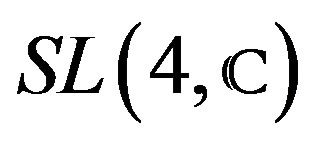 , as equi-variants operators among homogeneous vector bundles on M considering to
, as equi-variants operators among homogeneous vector bundles on M considering to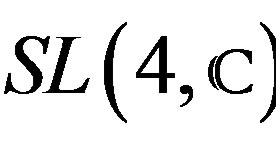 , like homogeneous space [5-11].
, like homogeneous space [5-11].
The integral operators in this case are realizations of these representations and they are orbital integrals of one integral transform from the resolutions to these differential equations which in this concrete case is the Penrose transform.
The problem is solved using the machinery of representations theory and is given in [12], and with more generality in [13]. In after studies, the local twistor connection [14] is used to investigate the questions as to whether these operators have curved analogues i.e. conformally invariant operators in the curved case.
For example, some of these operators that are mentioned in the Equation (2), and the Equation (3) are included in a conformal class that is obtained by the image of the Penrose transform on the corresponding sheaf whose germs are these differential operators in the holomorphic vector bundle given. The Penrose transform generates conformally differential operators.
We consider the Penrose transformation, [15] through the correspondence
 (4)
(4)
where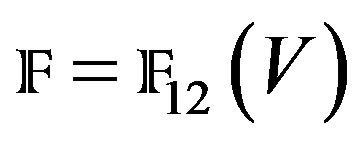 , is the manifold of flags of dimension one and two, associated to 4-dimensional complex vector space V. Let
, is the manifold of flags of dimension one and two, associated to 4-dimensional complex vector space V. Let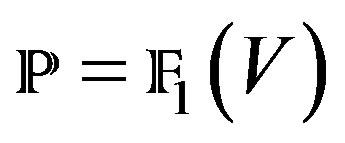 , be such that
, be such that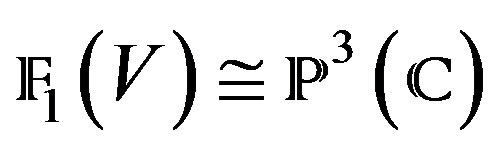 , (complex lines in
, (complex lines in ), and let
), and let , be such that
, be such that 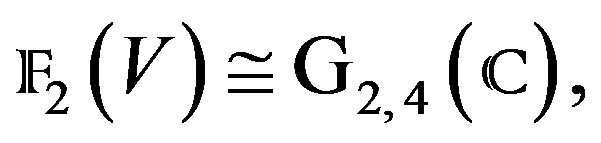 (Grassmannian manifold of 2-dimensional complex subspaces),
(Grassmannian manifold of 2-dimensional complex subspaces), 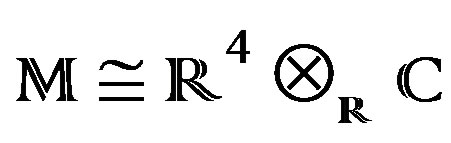 with
with
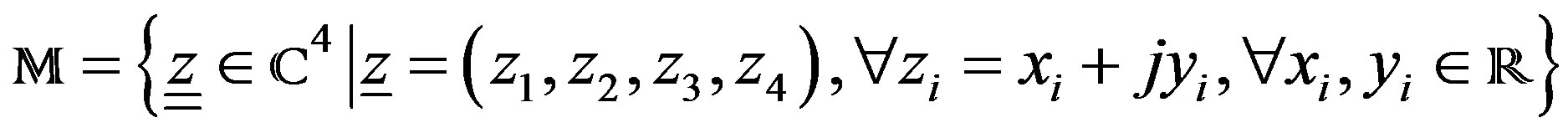 (5)
(5)
is the 4-dimensional complex compactified Minkowski space [16]. The projections of , are given for:
, are given for:
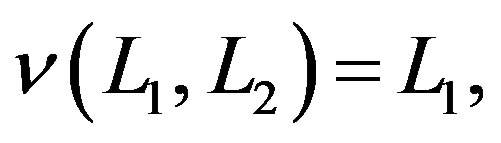 (6)
(6)
and
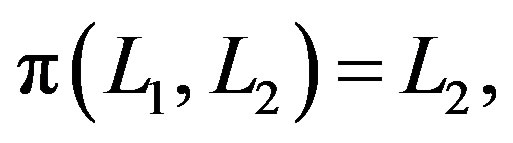 (7)
(7)
where 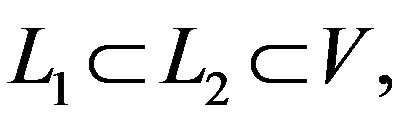 are complex subspaces of dimension one and two, respectively, defined a element
are complex subspaces of dimension one and two, respectively, defined a element 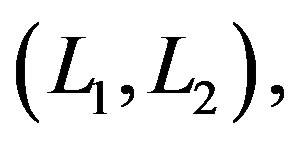 of
of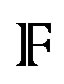 , to know
, to know
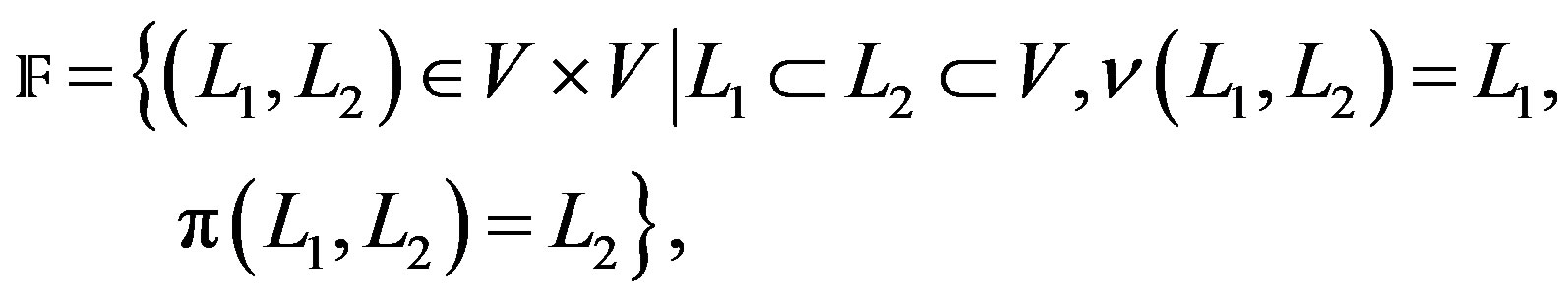 (8)
(8)
If , is compactified Minkowski space [16] then
, is compactified Minkowski space [16] then
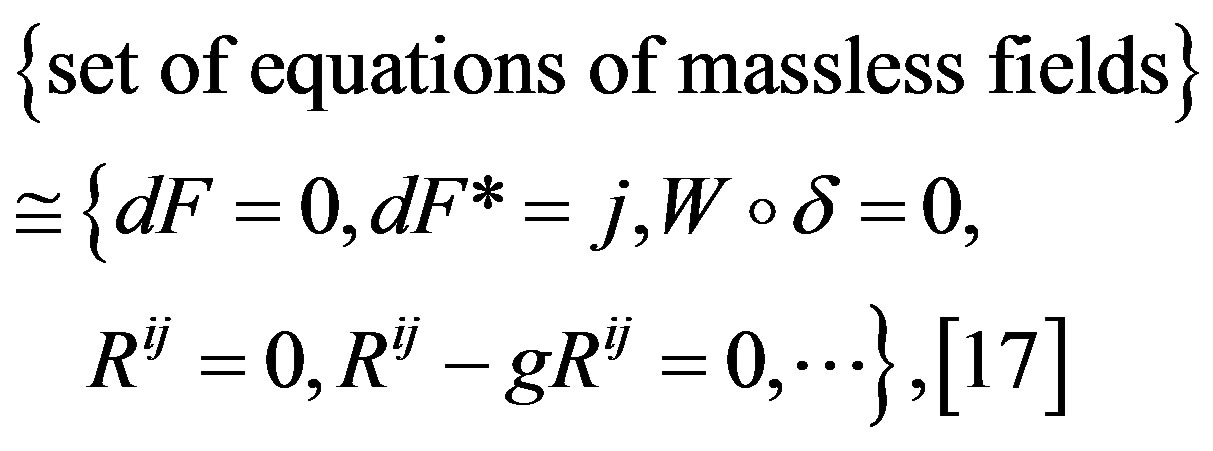 (9)
(9)
that is to say, the spectral resolution of complex sheaves is needed [16], of certain class seated in the projective space , to give solution to the field equations modulo a flat conformally connection [16-18]
, to give solution to the field equations modulo a flat conformally connection [16-18]
 (10)
(10)
Let , be the Penrose transform [16] associated to the double fibration (4), used to represent the holomorphic solutions of the generalized wave equation [16], with parameter of helicity h [17,19]:
, be the Penrose transform [16] associated to the double fibration (4), used to represent the holomorphic solutions of the generalized wave equation [16], with parameter of helicity h [17,19]:
 (11)
(11)
on some open subsets , in terms of cohomological classes of bundles of lines [16], on
, in terms of cohomological classes of bundles of lines [16], on  (
( , is the super-projective space).
, is the super-projective space).
It is necessary to mention that these cohomological classes are the conformal classes that we want to solve the phenomenology of the space-time to diverse interactions studied in gauge theory [20], and can construct a general solution of the general cohomological problem of the space-time.
With major precision, the tensors of the bundle of lines on , are given
, are given , by the kth-tensor power
, by the kth-tensor power , of the tautological bundle [21], (is the bundle that serves to explain in the context of the bundles of lines on
, of the tautological bundle [21], (is the bundle that serves to explain in the context of the bundles of lines on , the general bundle of lines of
, the general bundle of lines of ).
).
Let 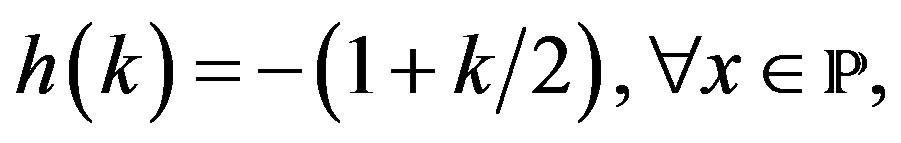 be and let
be and let
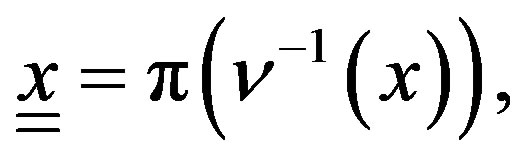 be. Then a result that establishes the equivalences on the cohomological classes of the bundle of lines on
be. Then a result that establishes the equivalences on the cohomological classes of the bundle of lines on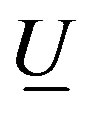 , and the family of solutions of the Equation (9), (equations of the massless fields family on the Minkowski space
, and the family of solutions of the Equation (9), (equations of the massless fields family on the Minkowski space , with helicity h) is given by the following theorem.
, with helicity h) is given by the following theorem.
Theorem 3.1. (Classic Penrose transform) Let , be a open subset such that
, be a open subset such that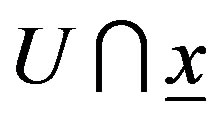 , is connect and simply connect
, is connect and simply connect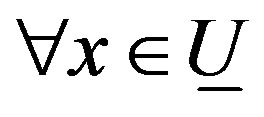 . Then
. Then , the associated morphism to the twistor correspondence (1); which maps a 1-form on
, the associated morphism to the twistor correspondence (1); which maps a 1-form on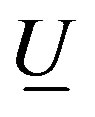 , to the integral along the fibers of
, to the integral along the fibers of , of their inverse image for
, of their inverse image for , induce a isomorphism of cohomological classes:
, induce a isomorphism of cohomological classes:
 (12)
(12)
Proof. [4]. ¡
Which are the classes that are extensions of the space of equivalences of the type Equation (12)? Why are these classes necessary to include more phenomena of the space-time? What version of the Penrose transform will be required?
Part of the object of our research is centered in the extension of the space of equivalences of the type (12), under a more general context given through the language of the D-modules, that is to say, we want to extend our classification of differential operators of the field equations to context of the G-invariant holomorphic bundles and obtain a complete classification of all the differential operators on the curved analogous of the Minkowski space of . Thus our moduli space will be one of the equivalences of the conformal classes given in the equivalence (12), in the language of the algebraic objects D-modules with coefficients in a coherent sheaf [13].
. Thus our moduli space will be one of the equivalences of the conformal classes given in the equivalence (12), in the language of the algebraic objects D-modules with coefficients in a coherent sheaf [13].
A way of answering the first and the second questions is analyzing the origin of the structure of the complexes that define the microscopic physical phenomena. Through this way and in natural form we can establish equivalences (isomorphisms), between derivative categories and categories of physical phenomena, considering a complex as the defined in the succession (10), for the micro-local context in which a regularity theorem subjacent for the Penrose transform on D-Modules is used, that is to say, given a D-Modules complex [13-22]
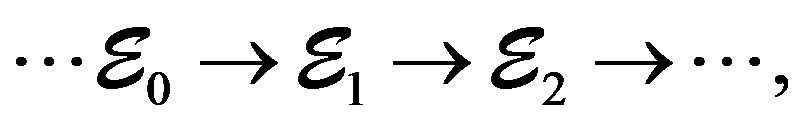 (13)
(13)
we can map this complex to the system of branes/antibranes, in which every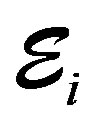 ,
, 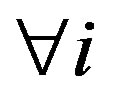 , odd defines branes and other sheaves define anti-branes [22]. Such D-branes and anti-D-branes are defined of equal form in the space-time, although dynamically they annihilates for defining a pair of particle and anti-particle [22].
, odd defines branes and other sheaves define anti-branes [22]. Such D-branes and anti-D-branes are defined of equal form in the space-time, although dynamically they annihilates for defining a pair of particle and anti-particle [22].
This bears to the application of a symplectic context, which also is a consequence of the foliation in Lagrangian submanifolds of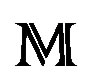 , inside the problem of the uniqueness of the Radon-Penrose transform on the same coherent D-Modules [12].
, inside the problem of the uniqueness of the Radon-Penrose transform on the same coherent D-Modules [12].
3. Resolution on D-Modules
Consider the category of D-modules given by the space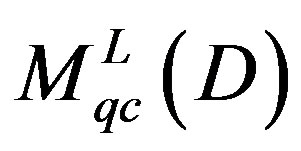 , such that the category of quasi-coherent left D-modules on X, is isomorphic to the category
, such that the category of quasi-coherent left D-modules on X, is isomorphic to the category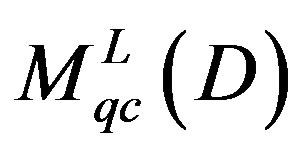 , of quasi-coherent right
, of quasi-coherent right 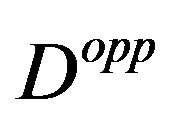 -modules on X. For a category
-modules on X. For a category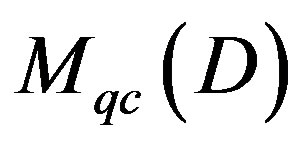 , of D-modules we denote by
, of D-modules we denote by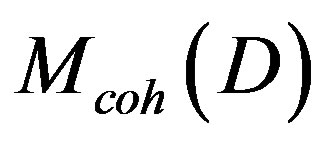 , the corresponding subcategory of coherent D-modules.
, the corresponding subcategory of coherent D-modules.
We consider a correspondence
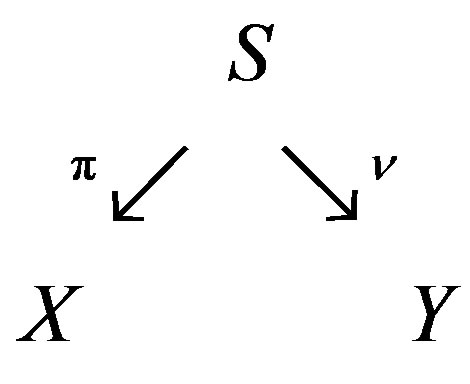 (14)
(14)
where all the manifolds are analytic and complex, 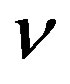 , and
, and , are proper and
, are proper and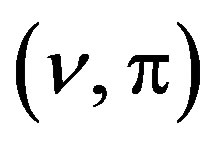 , induce a closed embedment
, induce a closed embedment 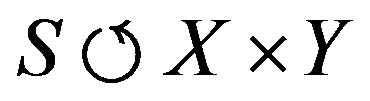 [12]. Be
[12]. Be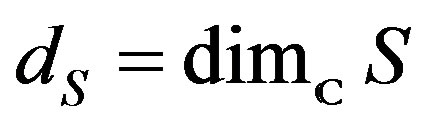 , with
, with 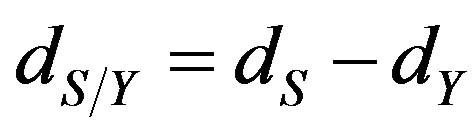 .
.
We define the transform of a sheaf F, on X, (more generally, of an object of the derived category of sheaves) like
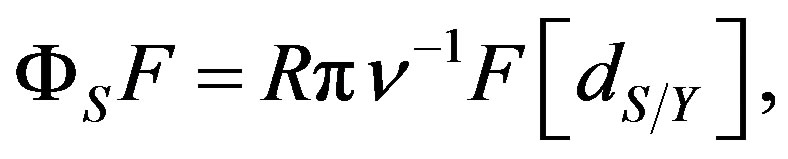 (15)
(15)
and we define the transform of a DX-module , like
, like , where
, where , and
, and  denotes the direct and inverse images of
denotes the direct and inverse images of  and
and  respectively, in the sense of the D-modules1 [2], and we consider also
respectively, in the sense of the D-modules1 [2], and we consider also
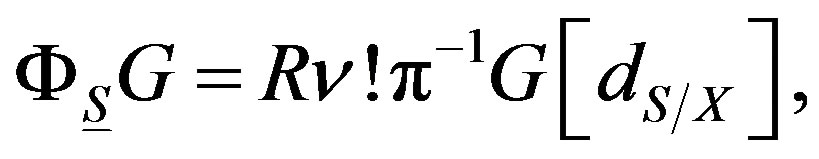 (16)
(16)
to a sheaf , on Y. Then we have the formula
, on Y. Then we have the formula
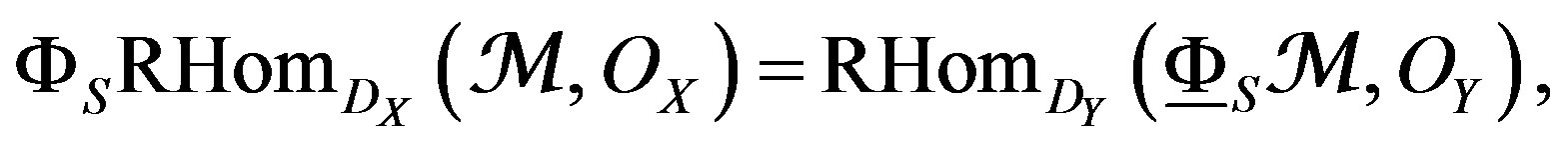 (17)
(17)
of which is deduced the formula, to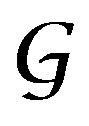 , the sheaf on Y, (coherent sheaf):
, the sheaf on Y, (coherent sheaf):
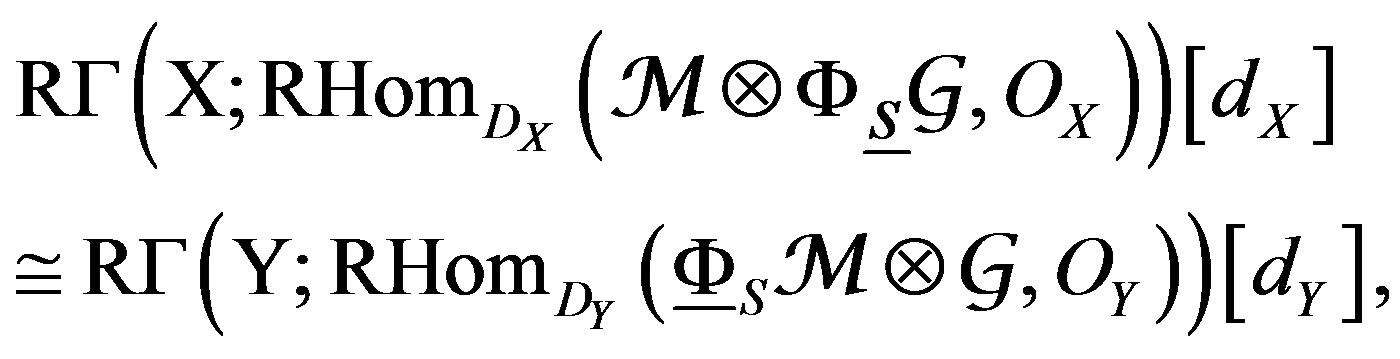 (18)
(18)
This defines a categorical equivalence of the transformation (1), in the context of the right derived D-modules,  , because it is necessary to give an equivalence with a sub-category of the right D-modules that have support in Y, for this way guarantee the inverse image of
, because it is necessary to give an equivalence with a sub-category of the right D-modules that have support in Y, for this way guarantee the inverse image of , and with it, to obtain an image of closed range of the operator
, and with it, to obtain an image of closed range of the operator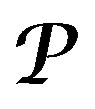 , conforming their uniqueness on the given context [15-21].
, conforming their uniqueness on the given context [15-21].
Theorem of Kashiwara 3.2. Let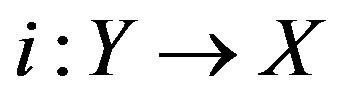 , be the correspondence (14), a closed immersion. Then the direct image functor
, be the correspondence (14), a closed immersion. Then the direct image functor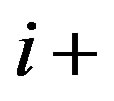 , is an equivalence of
, is an equivalence of , with full sub-category of
, with full sub-category of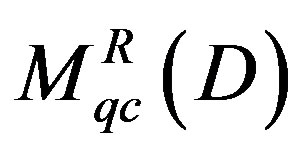 , consisting of modules with support in Y.
, consisting of modules with support in Y.
Proof: [6]. ¡
This equivalence preserves coherency and holonomicity [19]. Then preserves conformability in 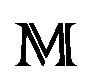 [10-13].
[10-13].
We formulate in the language of the D-modules and their sheaves, like the given in a resolution (10), the correspondence between the space of coherent D-modules and the space of equations of massless fields. It can be established if we can grant the uniqueness of the Penrose transform. But for it is necessary to include a result that it establishes the regularity in the analytical sense of the Riemannian manifold, which shapes the space-time, and that allows the application of the involutive distribution theorem on integral submanifolds as solutions of the corresponding equations of field without mass on sub-manifolds isomorphic in the Kaehlerian model inside of the flat model given on  Of the fact, an analogy in the obtaining of models of space-time (under the same reasoning) must be realized between special Lagrangian submanifolds and m-folds of Calabi-Yau. But to it, we need define the complex micro-local structure that defines all the phenomena of strings and branes in microscopic level, which happens in the 6-dimensional component of the universe (6-dimensional compact Riemannian manifold) with ratio of the order 1033 cm (Max Plank longitude of a string). The Penrose transform is an integral geometric method that interprets elements of various analytic cohomology groups on open subsets of complex projective 3-space as solutions of linear differential equations on the Grassmannian of 2-planes in the 4-space. The motivation for such transform comes from the interpretation of this Grassmannian as the complexification of the conformal compactification of the Minkowski space and their differential equations being the massless field equations of various helicities.
Of the fact, an analogy in the obtaining of models of space-time (under the same reasoning) must be realized between special Lagrangian submanifolds and m-folds of Calabi-Yau. But to it, we need define the complex micro-local structure that defines all the phenomena of strings and branes in microscopic level, which happens in the 6-dimensional component of the universe (6-dimensional compact Riemannian manifold) with ratio of the order 1033 cm (Max Plank longitude of a string). The Penrose transform is an integral geometric method that interprets elements of various analytic cohomology groups on open subsets of complex projective 3-space as solutions of linear differential equations on the Grassmannian of 2-planes in the 4-space. The motivation for such transform comes from the interpretation of this Grassmannian as the complexification of the conformal compactification of the Minkowski space and their differential equations being the massless field equations of various helicities.
By the Kashiwara theorem (Theorem 3.2), and some results of Oshima [20-23], on involutive manifolds [24], we can characterize certain spaces to the regularity of the images of , in D-modules.
, in D-modules.
4. A Micro-Local Analysis and Version of the Penrose Transform
Let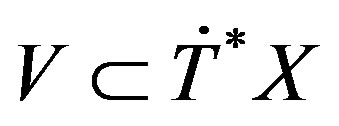 , be a conic regular involutive submanifold. We say that a coherent DX-module
, be a conic regular involutive submanifold. We say that a coherent DX-module , has regular singularities on V, if so we has
, has regular singularities on V, if so we has  (
(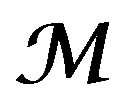 is regular if
is regular if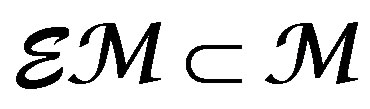 ). We denote by
). We denote by , the thick subcategory of
, the thick subcategory of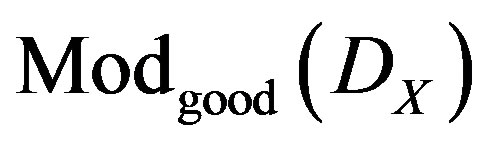 , whose objects have regular singularities on
, whose objects have regular singularities on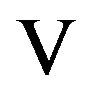 , and by
, and by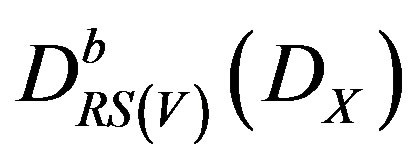 , the full triangulated subcategory of
, the full triangulated subcategory of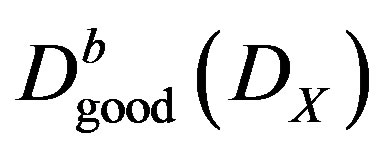 , whose objects have cohomology groups belong to
, whose objects have cohomology groups belong to :
:
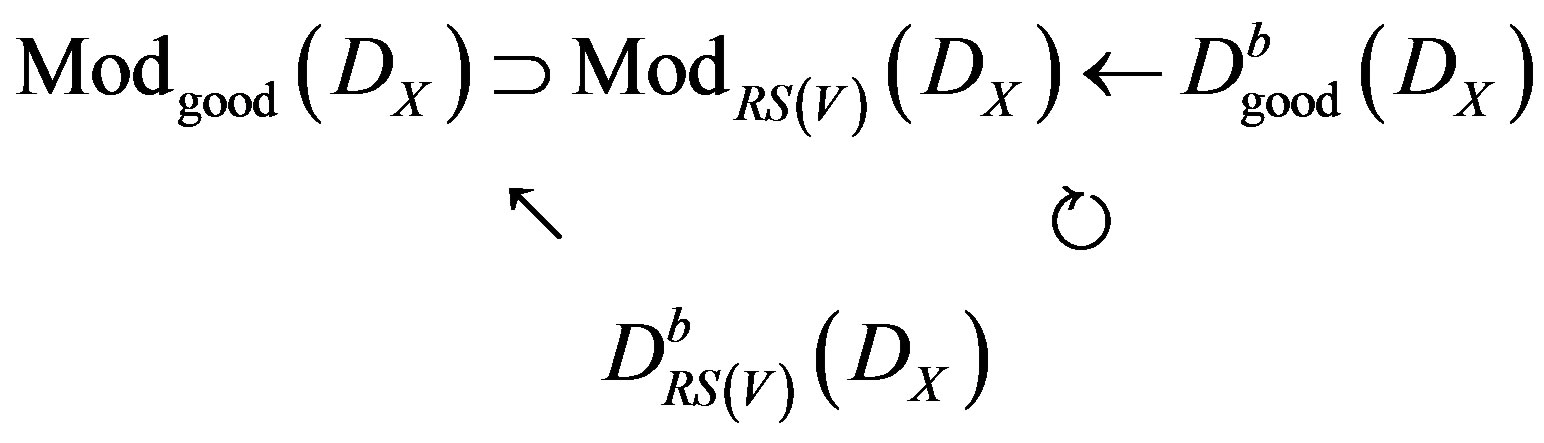
Associated to the correspondence given in (14), we give the microlocal correspondence:
 (19)
(19)
The manifold , being Lagrangian, is well acquaintance that
, being Lagrangian, is well acquaintance that 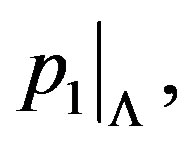 is smooth if and only if
is smooth if and only if 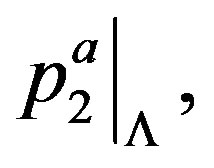 is an immersion. The consequences of this are:
is an immersion. The consequences of this are:
1) 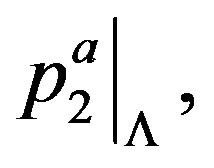 is a closed embedment identifying
is a closed embedment identifying (deep space) to a closed regular involutive manifold
(deep space) to a closed regular involutive manifold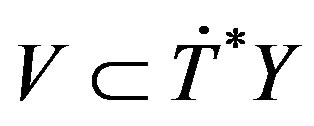 , (foliation) and 2)
, (foliation) and 2) 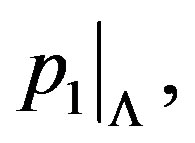 is smooth and surjective on
is smooth and surjective on 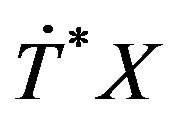 (observables of space-time).
(observables of space-time).
If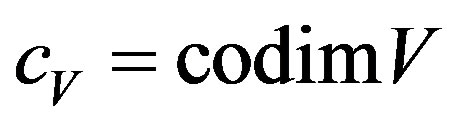 , in
, in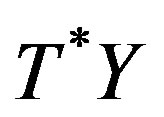 , then we have the following local model of correspondences of (14):
, then we have the following local model of correspondences of (14):
Lemma 4.1. Assume that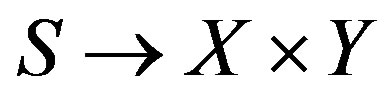 , is a closed embedment and assumptions given by 1), and 2) above. Then, for every
, is a closed embedment and assumptions given by 1), and 2) above. Then, for every , there are open subsets
, there are open subsets ,
, 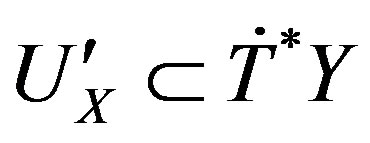 , with
, with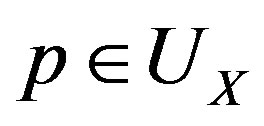 , and
, and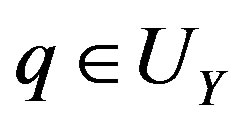 , a complex manifold Z, of dimension
, a complex manifold Z, of dimension , and a contact transformation
, and a contact transformation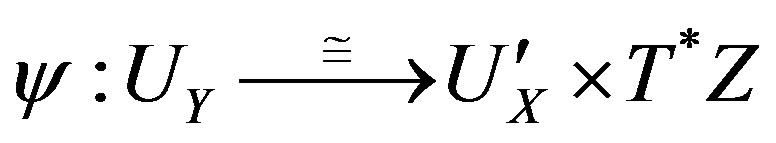 , such that
, such that , induces an isomorphism of correspondences:
, induces an isomorphism of correspondences:
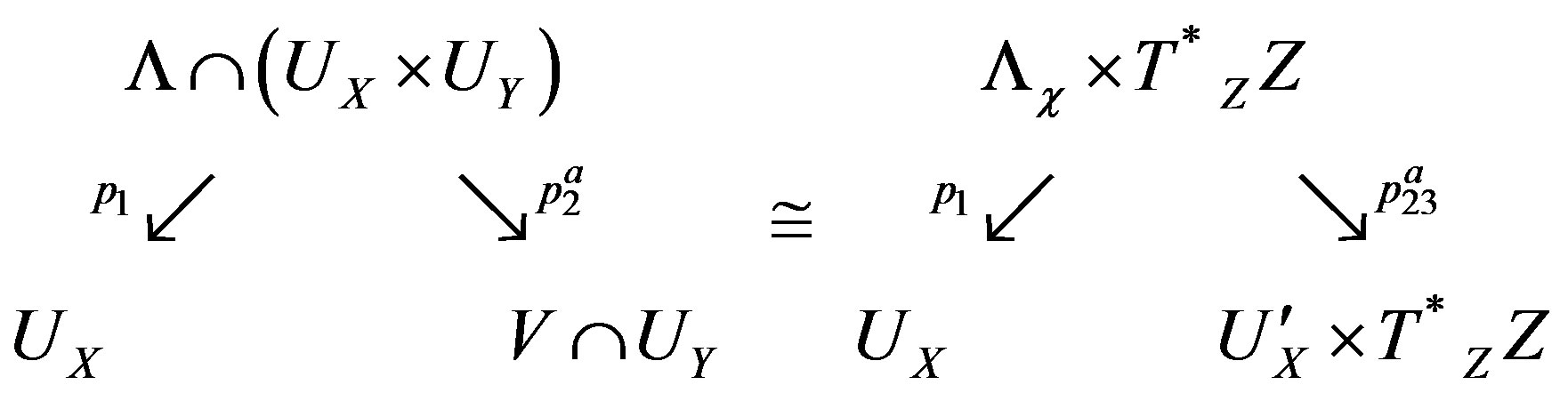 (20)
(20)
where , is the graph of a contact transformation
, is the graph of a contact transformation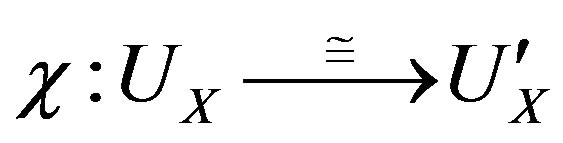 , and
, and , denotes the projection
, denotes the projection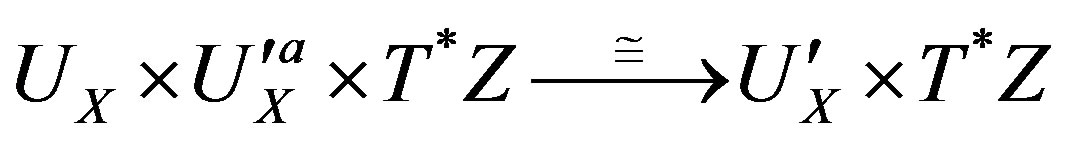 .
.
Proof. [16]. ¡
The construction of characteristic cycles of Kashiwara associates to every object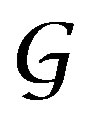 , (coherent sheaf on Y) of this category, a Lagrangian cycle
, (coherent sheaf on Y) of this category, a Lagrangian cycle , into
, into , which is a cone (invariant under recalling of cotangent fibers). If
, which is a cone (invariant under recalling of cotangent fibers). If , is the structure sheaf of closed submanifold like the given by
, is the structure sheaf of closed submanifold like the given by , this cycle is justly the conormal bundle and this tends to be singular. Then we can enounce the Kashiwara Theorem 3.2, also as:
, this cycle is justly the conormal bundle and this tends to be singular. Then we can enounce the Kashiwara Theorem 3.2, also as:
“The construction of a smoothed characteristic cycle gives origin to an full embedment of derived categories 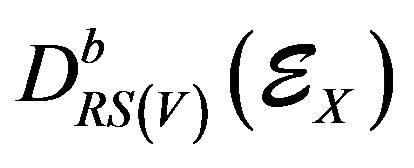 (full subcategory of objects
(full subcategory of objects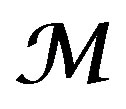 , have cohomology groups with regular singularities along V) into
, have cohomology groups with regular singularities along V) into 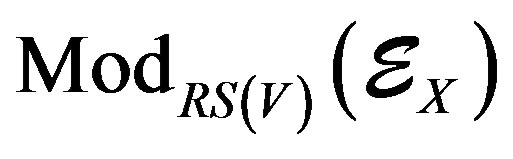 (sheaf of micro-differential formal operators on X)”.
(sheaf of micro-differential formal operators on X)”.
The 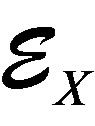 -modules shape a support ring of the DX- modules. A
-modules shape a support ring of the DX- modules. A 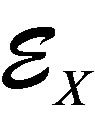 -module is a ring of microdifferential operators of finite order on
-module is a ring of microdifferential operators of finite order on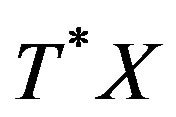 .
.
It is clear that from the lemma 4.1, we can characterize the cycles propitious to determine an embedment full of derived categories that shapes the structure of our sheaves defined in bounded derived category of the full subcategory of sheaves of K-vector spaces comprising complexes with constructible cohomology.
Which are the integral transforms that can obtain the quantized contact transformation?
Definition 4.1. 1) Let V, be a closed conic regular involutive submanifold of , and let
, and let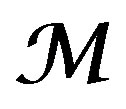 , be a coherent DX-module. We say that
, be a coherent DX-module. We say that , is simple along V, if
, is simple along V, if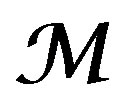 , can be endowed with a good filtration
, can be endowed with a good filtration , such that
, such that , is locally isomorphic to
, is locally isomorphic to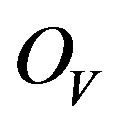 , as an
, as an 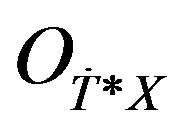 -module. We denote by
-module. We denote by 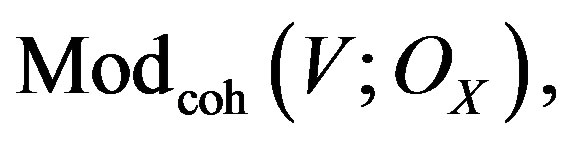 the full subcategory of
the full subcategory of  whose objects are simple along V.
whose objects are simple along V.
Let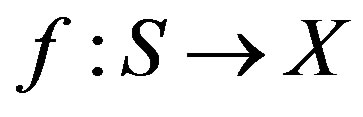 , is a morphism, we denote by
, is a morphism, we denote by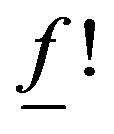 , and
, and 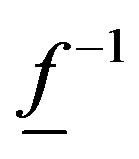 the proper direct image and inverse image for Dmodules, and we denote by
the proper direct image and inverse image for Dmodules, and we denote by , the exterior tensor product. For
, the exterior tensor product. For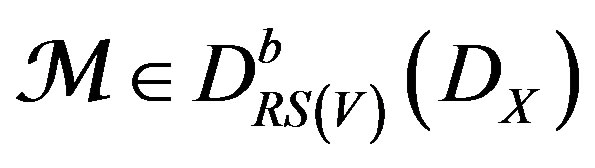 , and using the resolution (13) we associate their dual
, and using the resolution (13) we associate their dual
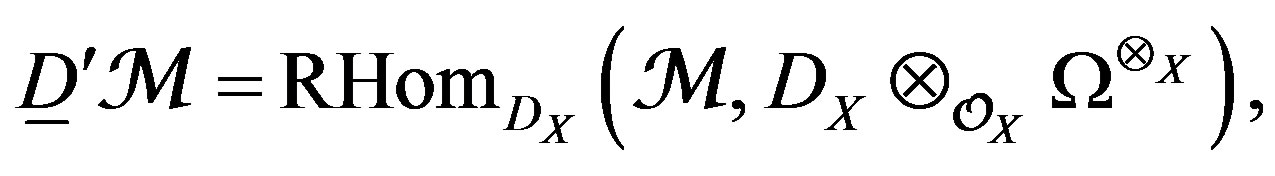 (21)
(21)
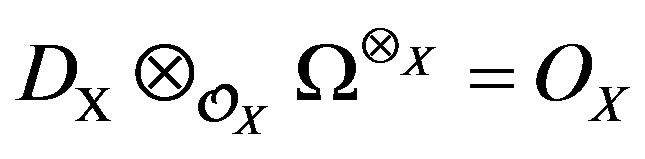 , where
, where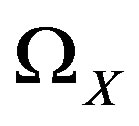 , is the sheaf of holomorphic forms of maximal degree. We also set
, is the sheaf of holomorphic forms of maximal degree. We also set
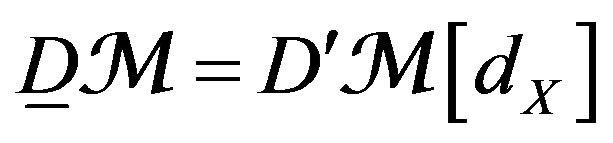 . Thus
. Thus , and
, and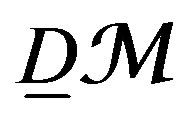 , belong to
, belong to
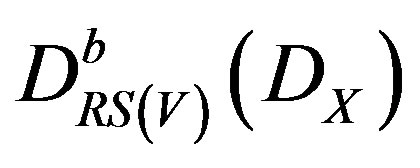 . Let
. Let , be a simple
, be a simple 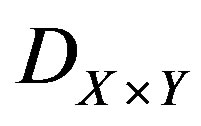 -module along
-module along . In particular
. In particular , is regular holonomic, and hence
, is regular holonomic, and hence , is concentrated in degree zero. For
, is concentrated in degree zero. For
 , and
, and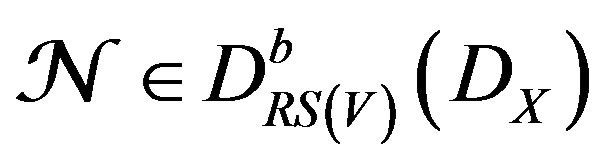 , we set
, we set
 (22)
(22)
where , and
, and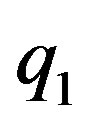 , is defined
, is defined . Also
. Also
 (23)
(23)
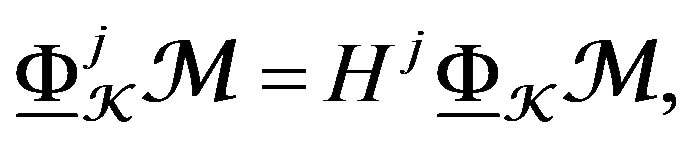 (24)
(24)
 (25)
(25)
Theorem 4.1. Assume that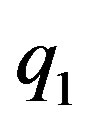 ,
, 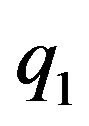 , are proper on
, are proper on , and assume 1), and 2) from (19). Let
, and assume 1), and 2) from (19). Let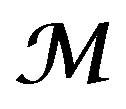 , be a simple DX-module along
, be a simple DX-module along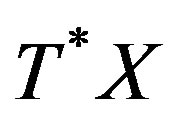 , and let
, and let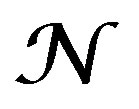 , be a simple DY-module along V. Then 1)
, be a simple DY-module along V. Then 1)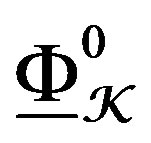 , and
, and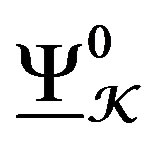 , send isomorphisms (isomorphism modulo flat connections,
, send isomorphisms (isomorphism modulo flat connections,  to isomorphism (isomorphism modulo flat connections
to isomorphism (isomorphism modulo flat connections
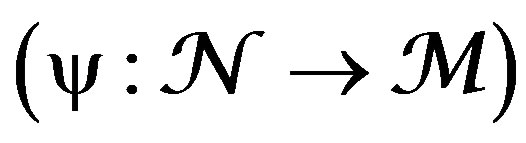 .
.
2)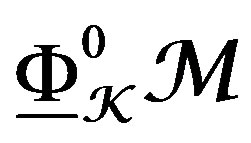 , is simple along V, and
, is simple along V, and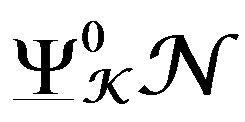 , is simple along
, is simple along . Moreover,
. Moreover, 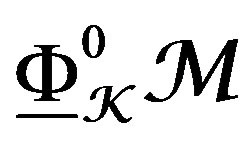 , and
, and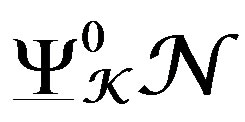 , are flat connections for
, are flat connections for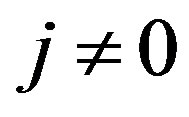 .
.
3) The natural adjunction morphisms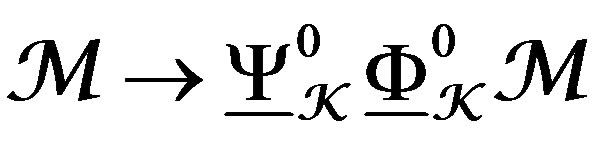 , and
, and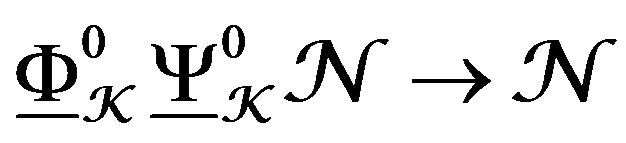 , are isomorphisms modulo flat connections. In particular, the functor
, are isomorphisms modulo flat connections. In particular, the functor
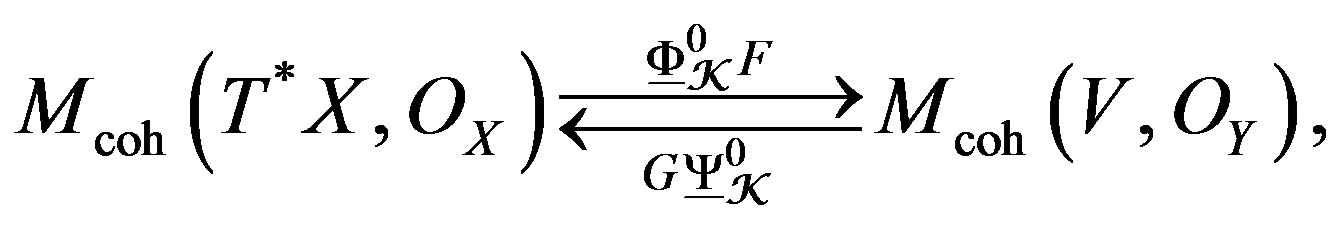
are quasi-inverse to each other, and thus establish the equivalences of categories. In D-modules theory the category given by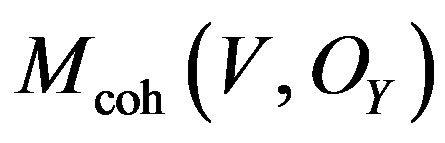 , is of the simple DX- modules to along V. This is due to the support of Radon transform of our Radon-Penrose transform that is required.
, is of the simple DX- modules to along V. This is due to the support of Radon transform of our Radon-Penrose transform that is required.
The following step is to give a result of equivalences between categories that suggest the extension to the before functors to the category of the vector bundle of lines of where it has the classification of differential operators belong to sheaves defined in the Section 2. Indeed.
Theorem 4.2. [12] With the same hypothesis as given by the theorem 4.1, assume also . Then with the notation of the theorem given by the Section 3, then the following correspondence is an equivalence of categories
. Then with the notation of the theorem given by the Section 3, then the following correspondence is an equivalence of categories
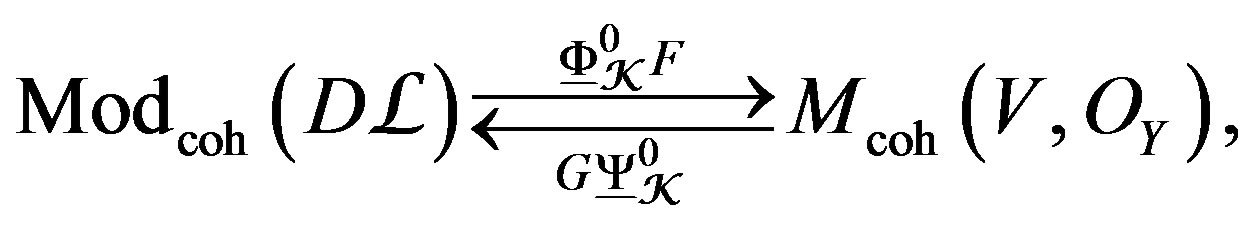
Precisely these equivalences shape a classification of the homogeneous vector bundles of lines [18,19].
As a corollary, using these Penrose transform, which is of Radon type on Lagrangian manifold , we can obtain the complex Minkowski space
, we can obtain the complex Minkowski space , simple
, simple  -modules along the characteristic manifold V, of the wave equations that are classified by (half) integers, so-called helicity
-modules along the characteristic manifold V, of the wave equations that are classified by (half) integers, so-called helicity . The following section establishes these equivalences using geometrical additional hypothesis.
. The following section establishes these equivalences using geometrical additional hypothesis.  , is the full subcategory of
, is the full subcategory of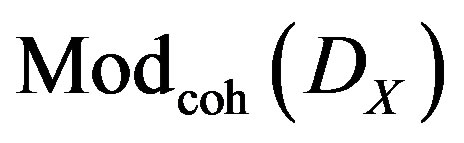 , whose open sets are of the
, whose open sets are of the , type to some bundle of lines
, type to some bundle of lines . In particular, if
. In particular, if , is a simple DY-module along V, there is an unique (up to OX-linear isomorhisms) line bundle
, is a simple DY-module along V, there is an unique (up to OX-linear isomorhisms) line bundle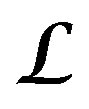 , on X, such that
, on X, such that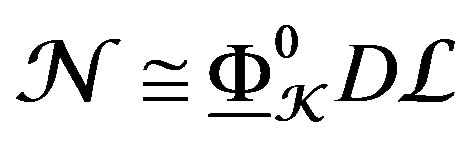 , in
, in 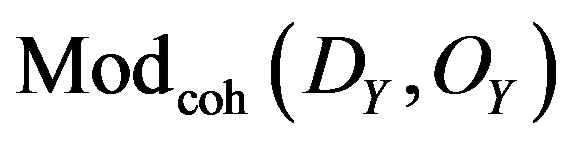 . In other words, the above theorem says that simple DY-modules along V, are classified, up to flat connections, by category of holomorphic vector bundles with flat connections
. In other words, the above theorem says that simple DY-modules along V, are classified, up to flat connections, by category of holomorphic vector bundles with flat connections
 (26)
(26)
The last theorem concludes,
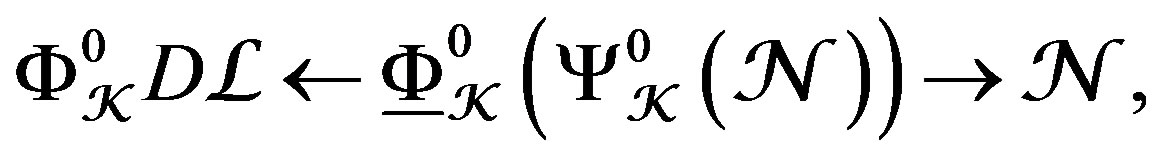 (27)
(27)
However, it is important in calculating explicitly the image of a DX-module associated to a line bundle, one way to do it consists in “quantizing” this equivalence. In the following results we will.
Let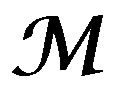 , be a simple DX-module along
, be a simple DX-module along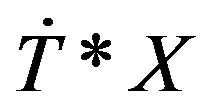 , and let
, and let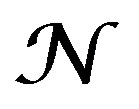 , be a simple DY-module along V. Then
, be a simple DY-module along V. Then , is a simple
, is a simple 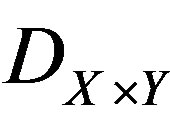 -module along
-module along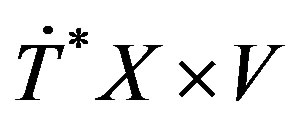 .
.
Definition 4.2. 1) Let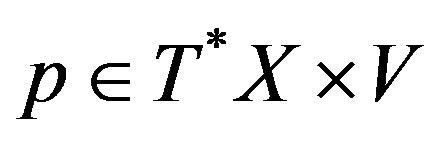 , and let u, be a generator at p, of
, and let u, be a generator at p, of , the
, the  -module associated to
-module associated to . Denote by
. Denote by , the annihilating ideal of u, in
, the annihilating ideal of u, in 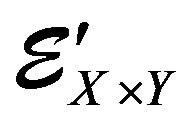 We say that u, is simple if their symbol ideal
We say that u, is simple if their symbol ideal , is reduced, and hence coincide with the defining ideal
, is reduced, and hence coincide with the defining ideal , of
, of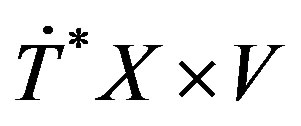 .
.
Continuing with other incises from the theorem 4.1, we have: for 2) Let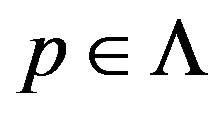 , we say that a section
, we say that a section 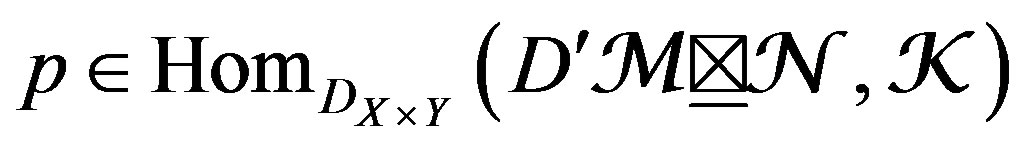 , is non degenerate at p, if for a simple generator u of
, is non degenerate at p, if for a simple generator u of , at p,
, at p, 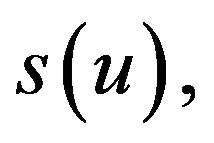 is a non degenerate section of
is a non degenerate section of , at p, in the sense of [7, 25]. (Note that locally simple modules admit simple generators, and one checks immediately that this definition does not depend on the choice of such generators). and for 3) We say that is non-degenerate on
, at p, in the sense of [7, 25]. (Note that locally simple modules admit simple generators, and one checks immediately that this definition does not depend on the choice of such generators). and for 3) We say that is non-degenerate on , if u is nondegenerate of any
, if u is nondegenerate of any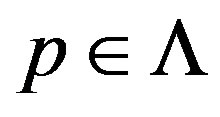 . There is a natural isomorphism
. There is a natural isomorphism
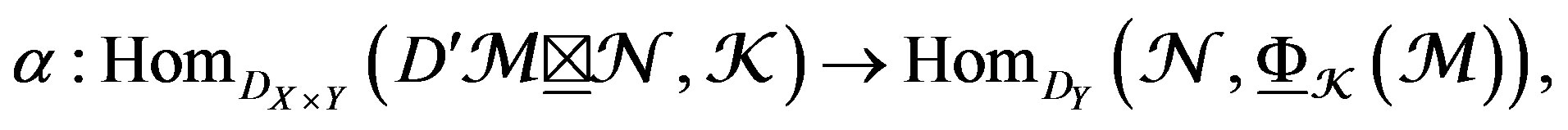 (28)
(28)
Hence, the sections s, defines a DY-linear morphism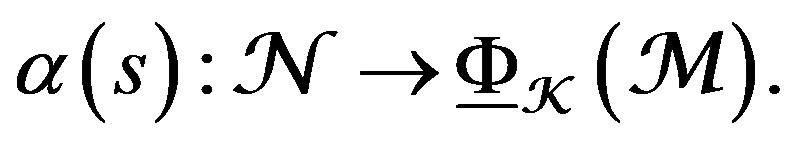
Theorem 4.3. With the above notations, and with s, is non degenerate on , the
, the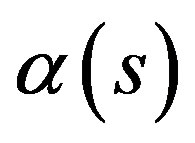 , is an isomorphism modulo flat connections.
, is an isomorphism modulo flat connections.
Proof. [7-25]. ¡
Observe that when , is the graph of a contact transformation (and hence V, is open in
, is the graph of a contact transformation (and hence V, is open in ) the above results reduce to the so-called “quantized contact transformation”, in psedo-differential equations and micro-functions [12].
) the above results reduce to the so-called “quantized contact transformation”, in psedo-differential equations and micro-functions [12].
5. Characteristics Cycles and Equivalences
Now in the context of the generalized D-modules to the use of the Schmid-Radon transform, and finally obtain Radon-Penrose Transform, the functor
 (29)
(29)
establishes an equivalence between the category M(DX- modules/flat connection), and M(DY-modules/Singularities along of the involutive manifold V/flat connection) [12]. Then our moduli space that we construct is the categorization of equivalences:
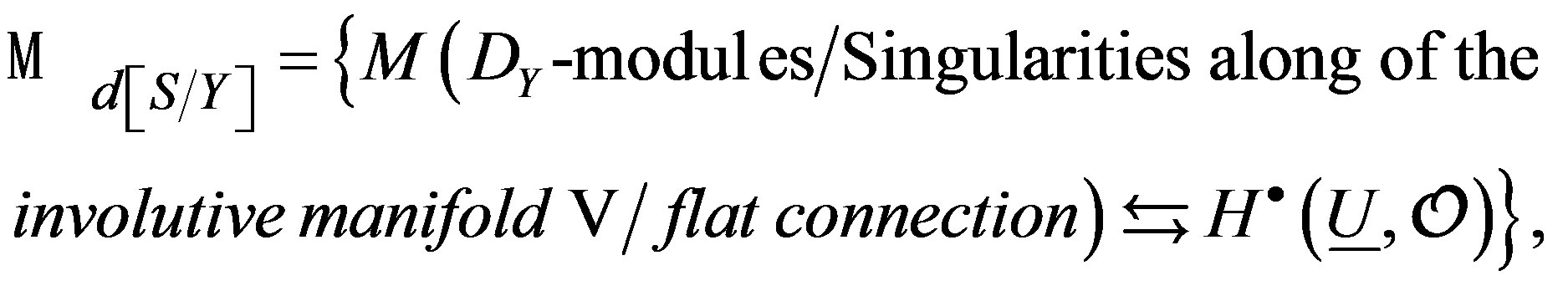 (30)
(30)
considering the moduli space as base [12],
 (31)
(31)
then the cohomology on moduli spaces is the cohomology of the space-time with an equivalence like the given in the equivalence (12), to a more general cohomological group that the given by , and whose dimension of
, and whose dimension of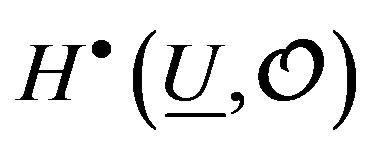 , can be calculated by the intersection methods, to a complex sheaf
, can be calculated by the intersection methods, to a complex sheaf  [13], which is of the type
[13], which is of the type 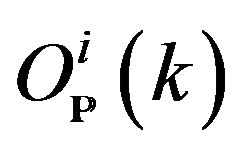 (see examples in Section 6).
(see examples in Section 6).
A version of the theorem 4.1, foreseen in the before section, that establishes the regularity through the transformations realized by the functor , on the categories of derived D-modules adding the corresponding cohomological groups of zero dimension is:
, on the categories of derived D-modules adding the corresponding cohomological groups of zero dimension is:
Theorem 5.1. Let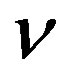 , smooth and
, smooth and , proper. Let
, proper. Let  be a closed embedding.
be a closed embedding.
1) If , then
, then , corresponds to
, corresponds to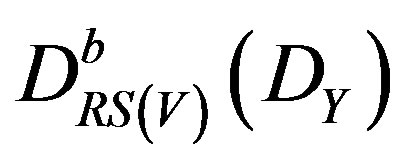 .
.
2) If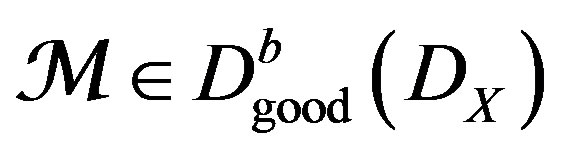 , and
, and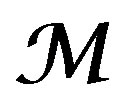 , is locally free and of range one, then
, is locally free and of range one, then , is simple along of V, on
, is simple along of V, on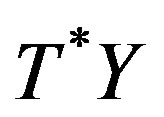 .
.
Proof: [25]. ¡
Our space moduli that we want to characterize is the one that establishes the equivalence induced by the transform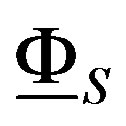 , between the category of coherent D-Modules on X, and the category of coherent D-Modules on Y, with regular singularities on V.
, between the category of coherent D-Modules on X, and the category of coherent D-Modules on Y, with regular singularities on V.
We define the category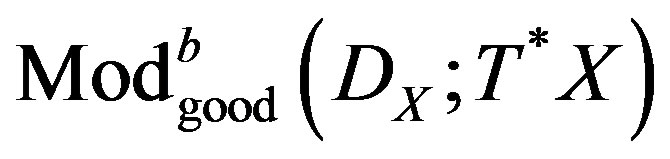 , like the localization of
, like the localization of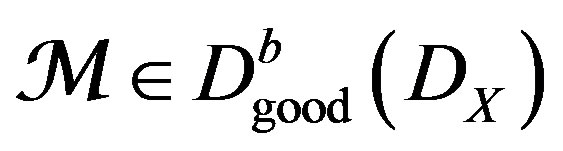 , by the thick sub-category of holomorphic bundles endowed with the flat connection:
, by the thick sub-category of holomorphic bundles endowed with the flat connection:
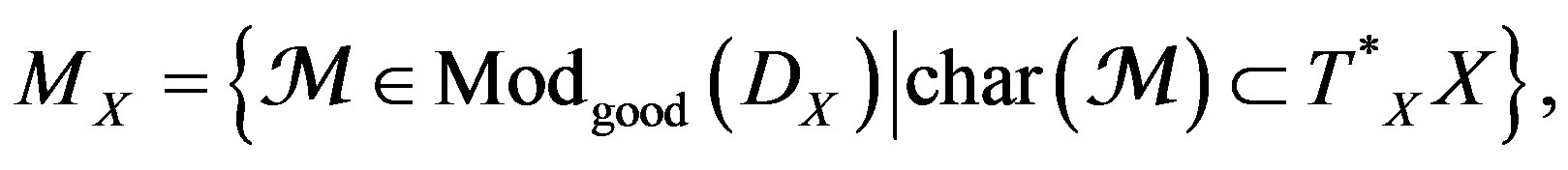 (32)
(32)
In particular, the objects of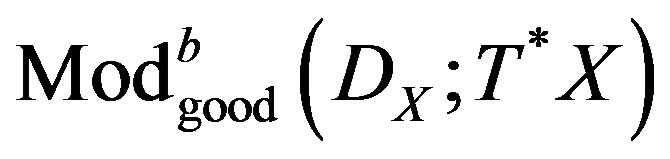 , are the same objects of
, are the same objects of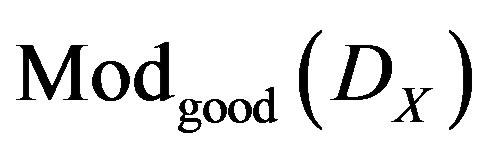 , and a morphism
, and a morphism 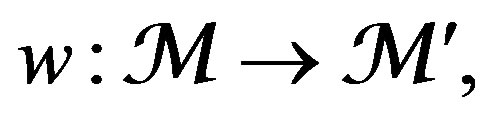 in
in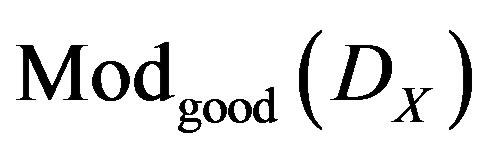 , it turns a isomorphism in
, it turns a isomorphism in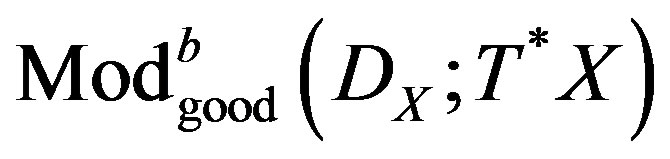 , if w, and coker w, correspond to MX. This is equivalent to say that
, if w, and coker w, correspond to MX. This is equivalent to say that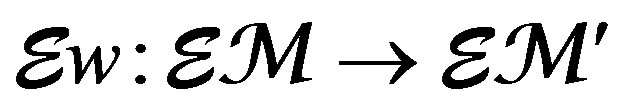 , is an isomorphism on
, is an isomorphism on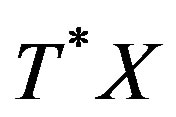 . In similar form we define MY, and the category
. In similar form we define MY, and the category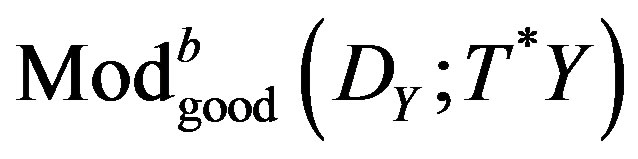 , obtained by localization of
, obtained by localization of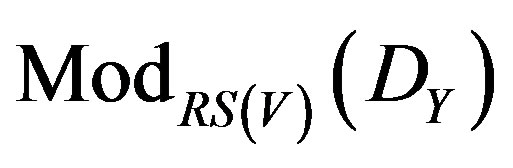 , with respect to MY.
, with respect to MY.
Considering the cohomology groups of zero dimensions of the functors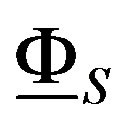 , y
, y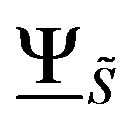 , we give functors that we will be able to denote by
, we give functors that we will be able to denote by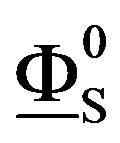 , and
, and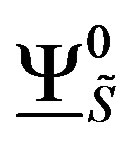 , respectively. In other words we obtain the images:
, respectively. In other words we obtain the images:
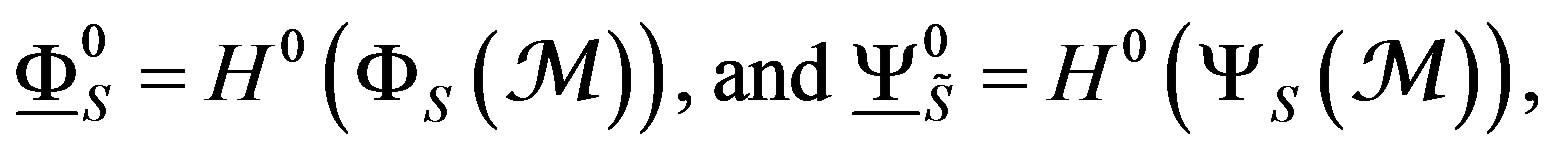 (33)
(33)
from which using the theorem 2.1, (using the local and microlocal analysis of the before sections) the functors are established between categories:
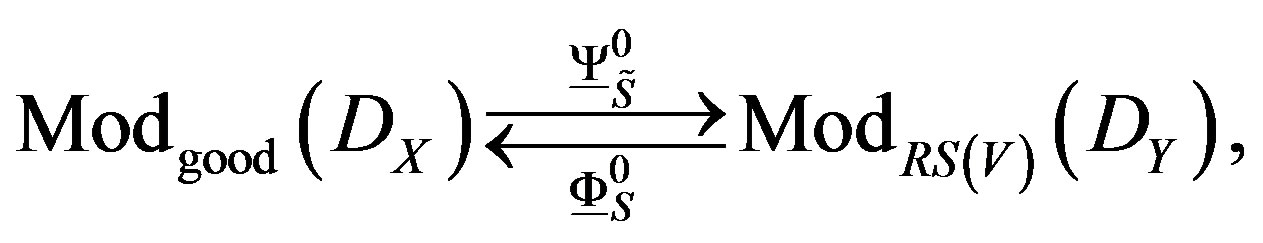 (34)
(34)
For the doble fibration (14), and the moduli spaces (30) and (31), these equivalences shape the moduli space [25]:
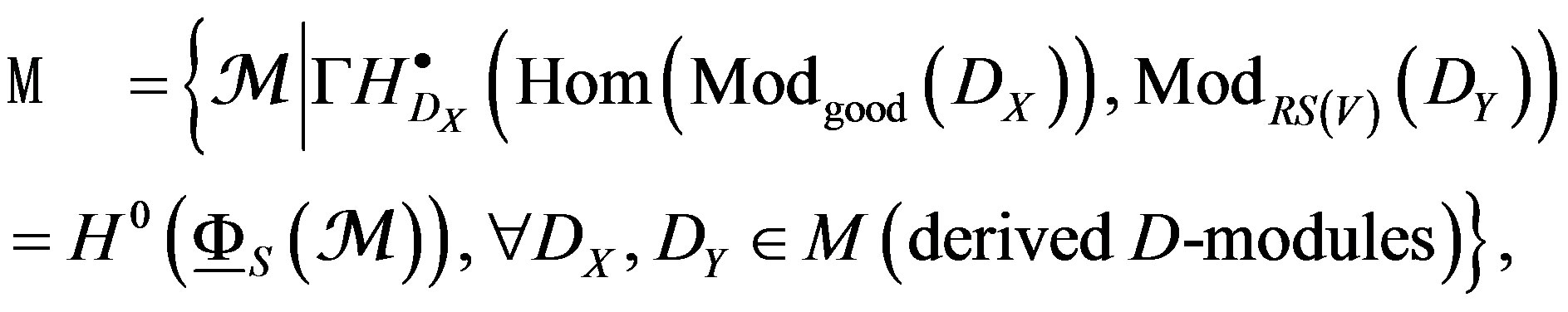 (35)
(35)
The additional geometrical hypothesis in the functor (29), comes established by the geometrical duality of Langlands [26], which says that the derived category of coherent sheaves on a moduli space 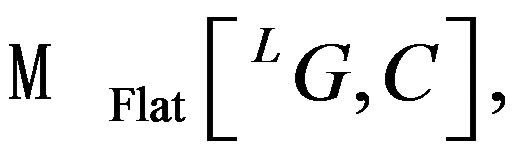 where C, is the complex given by
where C, is the complex given by
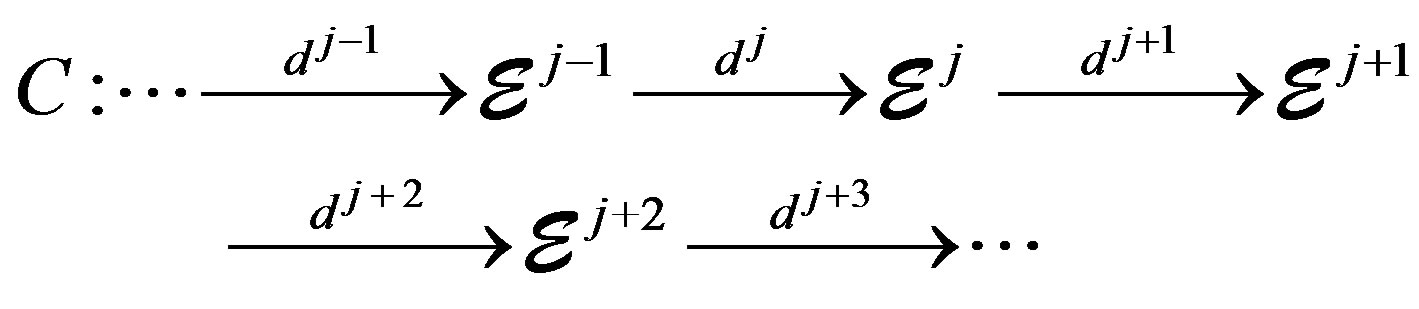 (36)
(36)
is equivalent to the derived category of D-modules on the moduli space of holomorphic vector G-bundles given by  [27]. These equivalences permit to map points of
[27]. These equivalences permit to map points of 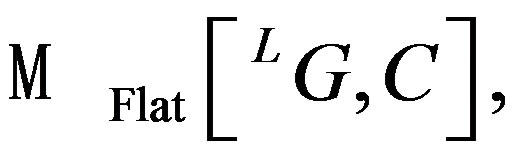 to eigen-sheaf of Hecke given by
to eigen-sheaf of Hecke given by
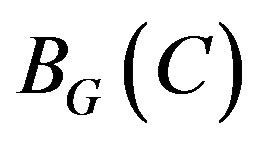 [22].
[22].
6. Results
Theorem 6.1. (F. Bulnes) The moduli space obtained by this way is the moduli space  where
where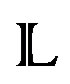 , is the space of Lagrangian submanifolds
, is the space of Lagrangian submanifolds , and defined with C, a complex of certain special sheaf of holomorphic G-bundles (eigensheaf of Hecke).
, and defined with C, a complex of certain special sheaf of holomorphic G-bundles (eigensheaf of Hecke).
Proof. It is necessary to go from the obtained co-cycles for the Radon-Penrose transform on , to the obtained cycles by Penrose on
, to the obtained cycles by Penrose on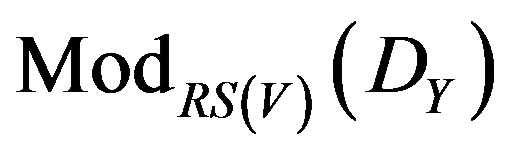 , and viceversa. The equivalence of both spaces of cocycles demonstrates that the functors are the given by
, and viceversa. The equivalence of both spaces of cocycles demonstrates that the functors are the given by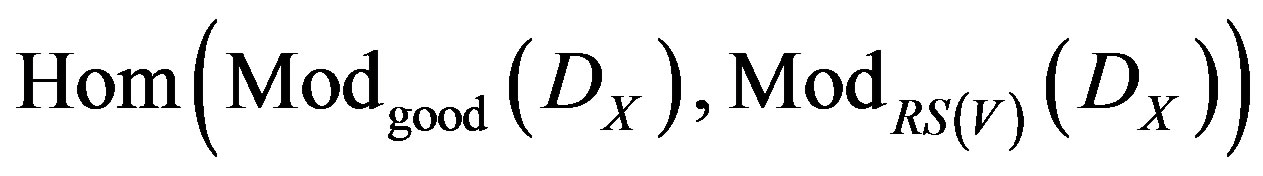 , of the moduli space (35). Then these functors are G-invariants and their image under
, of the moduli space (35). Then these functors are G-invariants and their image under , is recorded in a moduli space of holomorphic bundles
, is recorded in a moduli space of holomorphic bundles 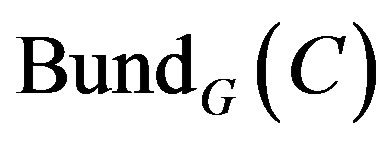 [23], which is an extension of the transformed cycles by the classic Penrose transform [15]. The equivalence under the G-invariance of holomorphic bundles must be demonstrated using a generalized Penrose transform for D-modules that are the composition of an inverse image functor and a direct image functor on the side D-module, which is foreseen by the geometrical duality of Langlands [26,28]. ¡
[23], which is an extension of the transformed cycles by the classic Penrose transform [15]. The equivalence under the G-invariance of holomorphic bundles must be demonstrated using a generalized Penrose transform for D-modules that are the composition of an inverse image functor and a direct image functor on the side D-module, which is foreseen by the geometrical duality of Langlands [26,28]. ¡
In electromagnetic interactions the functors are the objects that characterize the moduli space 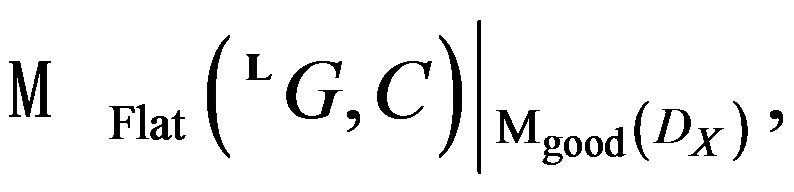 are
are
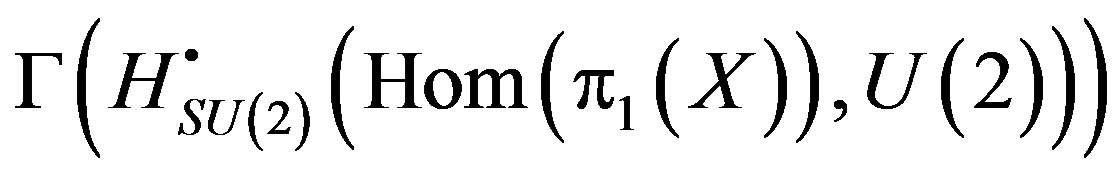 , where
, where , are homotopies on the Riemannian manifold X [9-20].
, are homotopies on the Riemannian manifold X [9-20].
In a more general context and using the flag domains that will be necessary to define the quantum gravity phenomena [28], and equivalences inside of the string theory (for example heterotic strings, D-branes and others phenomena) to give solution a extensions of the wave equation on observables of curvature, boson and fermion equations, Schmid equation [10], and classify their differential operators on the same base of vector bundles, but now through holomorphic vector bundles that are G-invariants.
But this only covers some aspects of brane theory as those given outside of the homogeneous space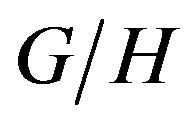 , when
, when .
.
For example, they are acknowledges the cases to heterotic strings that can develop on D-modules that are 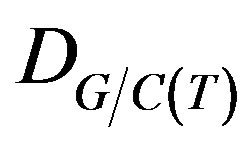 -modules when
-modules when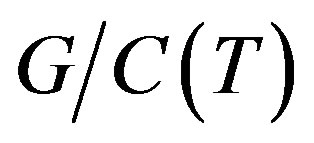 , is a flag manifold [11]. In this case the integral operators cohomology given on such complex submanifolds is also equivalent to the integral operators cohomology on submanifolds of a complex maximum torus. What happen when these flags are complex domains or their equivalents, Lagrangian submanifolds in
, is a flag manifold [11]. In this case the integral operators cohomology given on such complex submanifolds is also equivalent to the integral operators cohomology on submanifolds of a complex maximum torus. What happen when these flags are complex domains or their equivalents, Lagrangian submanifolds in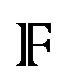 ?
?
To be able to establish a moduli space that could give a resolution for the equations of the mathematical physics given by the set (10) and generalise this resolution for coherent 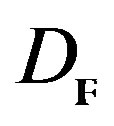 -Modules that are
-Modules that are 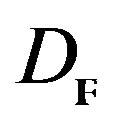 -Modules induced by a bundle of lines
-Modules induced by a bundle of lines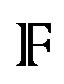 , with complex domains that are integral submanifolds of a Kählerian manifold is necessary to use one generalized Penrose transform with the conformal invariance on the
, with complex domains that are integral submanifolds of a Kählerian manifold is necessary to use one generalized Penrose transform with the conformal invariance on the 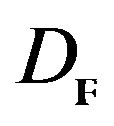 -Modules, and that the differential operators who are not flat might write each one in accordance with similar operators. This last comes reflected when a piecewise linear manifold has a differential structure. This piecewise linear manifold, defines a non-symmetrical component curvature, which reflects their difficult expression by conformal operators of superior degree such as the Laplacian, and Dirac differential operators.
-Modules, and that the differential operators who are not flat might write each one in accordance with similar operators. This last comes reflected when a piecewise linear manifold has a differential structure. This piecewise linear manifold, defines a non-symmetrical component curvature, which reflects their difficult expression by conformal operators of superior degree such as the Laplacian, and Dirac differential operators.
It is necessary consider some conjectures on integral geometry, that shows the construction of the geometrical hypothesis that will conform a version of Penrose transform more useful to generate quasi-conformal operators (quasi D equivariant operators) in an analytic cohomology as the given one by the  -cohomology but in a more generalized context, that it includes the Cĕch-cohomology.
-cohomology but in a more generalized context, that it includes the Cĕch-cohomology.
Conjecture 1. A more generalized Penrose transform is necessary to include differential operators in Hodge representative class to obtain all complete holomorphic cohomological classes.
In other words, there is an isomorphism
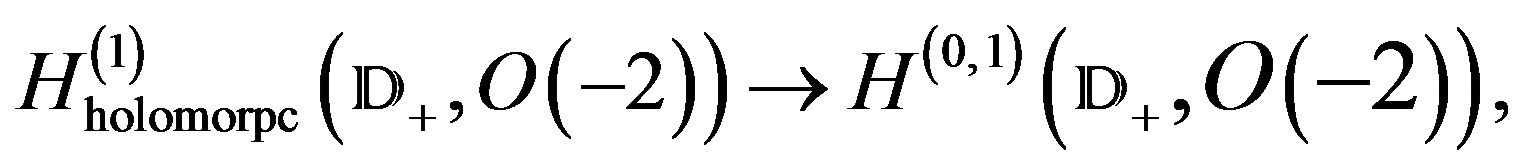 (37)
(37)
where

where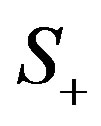 , is the Stein manifold and
, is the Stein manifold and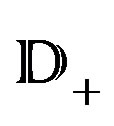 , is a flag domain.
, is a flag domain.
Conjecture 2. The corresponding extended class of differential operator that can be generated like generalized conformal operators are those of the Gelfand-GraevShapiro type [29].
We want to compute the analytic cohomology 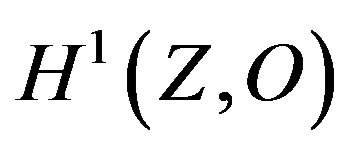 , of a complex manifold Z.
, of a complex manifold Z.
Since solutions of differential equations on manifolds and cohomological classes are part of the bases of this generalized Penrose transform, the theory of sheaf cohomology and D-modules was perfectly considered for their modern study. In [5], we used this theory to generalize and study the Penrose correspondence given by the double fibration (4). More recently the Equation (17), in [1] has studied the generalized Penrose transform between generalized flag manifolds over a complex algebraic group G, using M. The Kashiwara’s corresponddence (see [1-6]) between quasi G equivariant  - modules and some kind of representation spaces which are
- modules and some kind of representation spaces which are  modules (loosely, they are complex vector spaces endowed together with an action of the Lie algebra
modules (loosely, they are complex vector spaces endowed together with an action of the Lie algebra , associated to G, and an action of H, which are compatible in some way) when H, is a closed algebraic subgroup of G.
, associated to G, and an action of H, which are compatible in some way) when H, is a closed algebraic subgroup of G.
Conjecture 3. We have a generalization of Penrose transform on the homogeneous space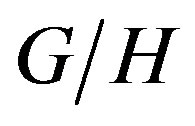 , or a Radon transform on equivariant-D-modules on generalized flag manifolds [10-33].
, or a Radon transform on equivariant-D-modules on generalized flag manifolds [10-33].
Lemma 7.1. (F. Bulnes) We need the version of Radon transform to compute dimensions (transform of dimensions). Their functors with Radon transform will give the equivalences on the generalization mentioned in Conjecture 3.
Proof. See [5,30]. ¡
Theorem 7.1. (F. Bulnes)
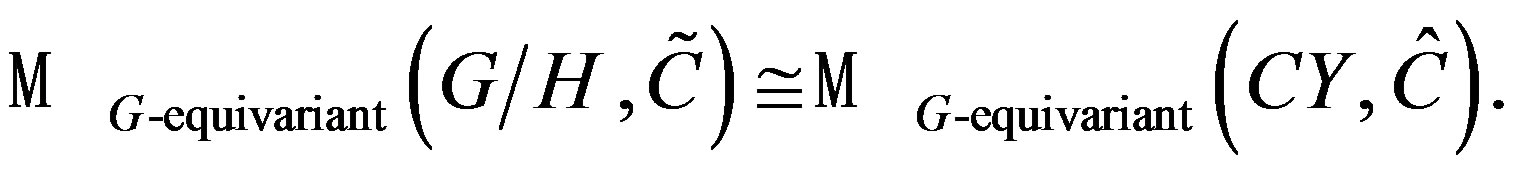
Proof. By the Kashiwara Theorem 3.2, the class given by , is a complex whose sub-class is
, is a complex whose sub-class is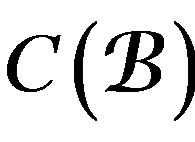 , where
, where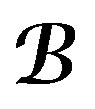 , is a D-brane, that is to say, a D-module
, is a D-brane, that is to say, a D-module
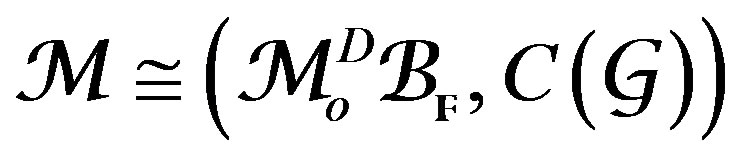 , since, {Massless fields equations}
, since, {Massless fields equations}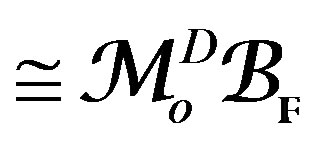 , then all
, then all , that is a complex hypersurface in the space
, that is a complex hypersurface in the space , which is complex parameterized define a Kählerian moduli space
, which is complex parameterized define a Kählerian moduli space , where
, where , is the dimension of the brane space.
, is the dimension of the brane space. , is a D-module which is a
, is a D-module which is a  -module induced by the bundle of lines
-module induced by the bundle of lines . What happens with the orbifolds? It is necessary to consider the D-branes in the orbifolds like D-modules on bundles of lines in
. What happens with the orbifolds? It is necessary to consider the D-branes in the orbifolds like D-modules on bundles of lines in . Of the fact, by the theorem 6.1, we can demonstrate that
. Of the fact, by the theorem 6.1, we can demonstrate that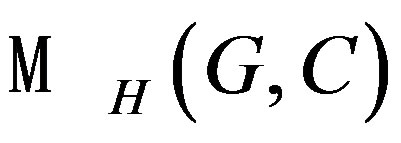 , under certain duality [22], is composed for objects of derived category of D-modules on
, under certain duality [22], is composed for objects of derived category of D-modules on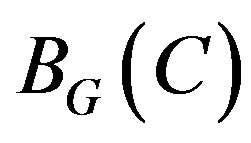 . This vector bundle of lines under the same duality [22], is their wide version which is isomorphic to the moduli space
. This vector bundle of lines under the same duality [22], is their wide version which is isomorphic to the moduli space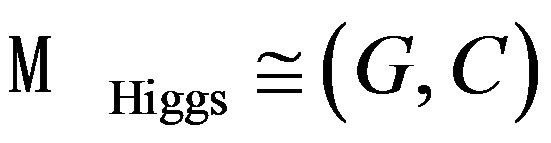 . Using a version of the Penrose transform predicted by Recillas’s conjecture and geometrical duality of Langlands on D-branes, is generated the isomorphism class given by
. Using a version of the Penrose transform predicted by Recillas’s conjecture and geometrical duality of Langlands on D-branes, is generated the isomorphism class given by 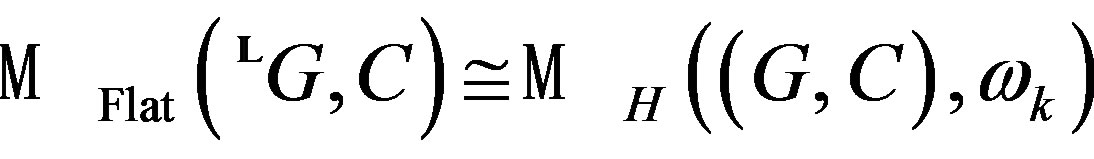 (using Kashiwara theorem between
(using Kashiwara theorem between 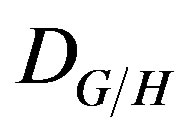 -modules and some
-modules and some 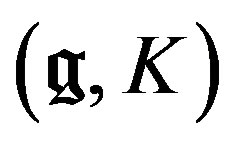 -modules) since equivalence exists between D-modules of
-modules) since equivalence exists between D-modules of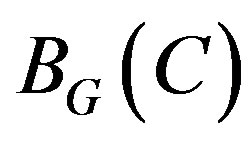 , and some D-branes of
, and some D-branes of . Then by the proposition that says that the scheme Y, is projective [31], that is to say,
. Then by the proposition that says that the scheme Y, is projective [31], that is to say, 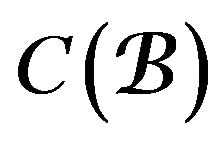 , is a complex whose manifolds Y (that are orbifolds of CY-manifold), are
, is a complex whose manifolds Y (that are orbifolds of CY-manifold), are  -modules. The equivalence between the two moduli spaces is completed with inverse Penrose transform. ¡
-modules. The equivalence between the two moduli spaces is completed with inverse Penrose transform. ¡
Corollary 7.1. (F. Bulnes). Moduli space = {homological relations of the black holes with the distinct cohomological dimensions obtained by lemma 5.1 and lemma 7.1} @ moduli space = {given by theorem 7.1}.
Proof. We use the Radon transform of dimensions [30-32], given by
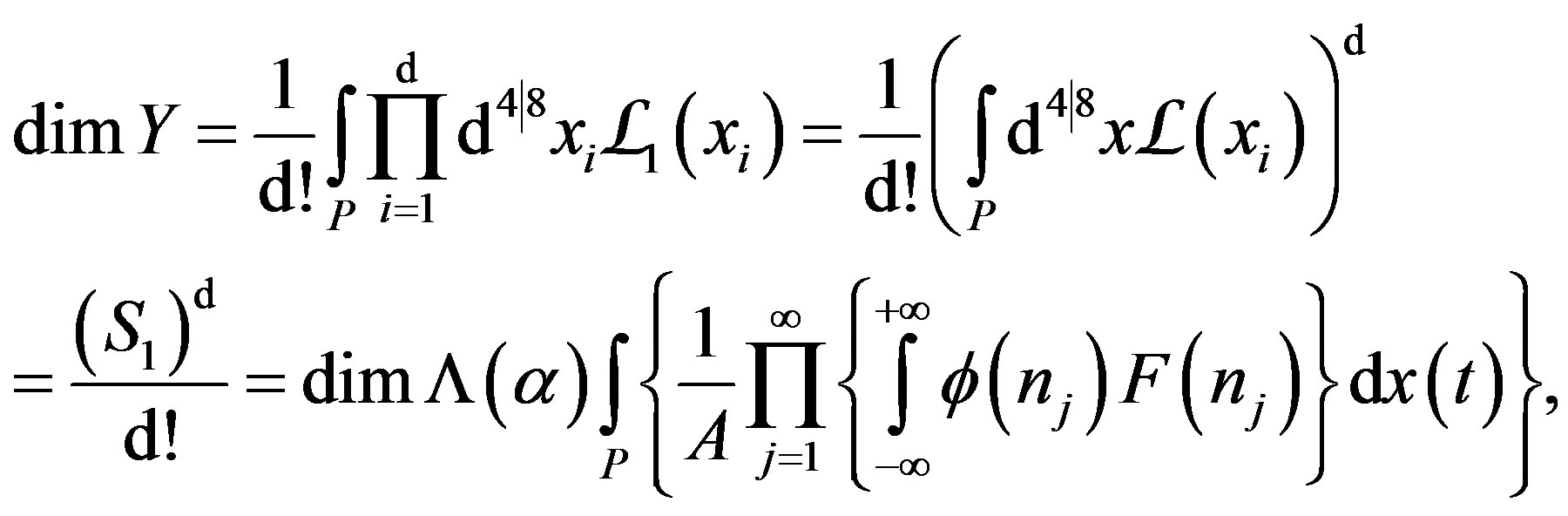
where , are the Lagrangian operators of instantons considered in flat space
, are the Lagrangian operators of instantons considered in flat space , of the corresponding supertwistor space
, of the corresponding supertwistor space  [33]. Then by Theorem 7.1, and using the large resolution
[33]. Then by Theorem 7.1, and using the large resolution

which is a special case of the resolution (36), we obtain the equivalence between the moduli spaces. ¡
The long sequence induced by the coherent D-modules given by the images of Penrose transform in these projective spaces gives the string fabric by heterotic strings [33].
Some consequences and components of the space-time related under the isomorphism discussed in the previous theorem are those that establish the equivalences given by the Equation (12), with the microlocal structure of , and with Floer cohomology group deduced from the cohomology group sketch by the theorem given in the search of the integral operators cohomology that encloses the Penrose transform class.
, and with Floer cohomology group deduced from the cohomology group sketch by the theorem given in the search of the integral operators cohomology that encloses the Penrose transform class.
The corresponding category associated to a CalabiYau threefold X, would be the Fukaya-Floer category of the moduli space of unitary flat bundles over holomorphic curves in X, denote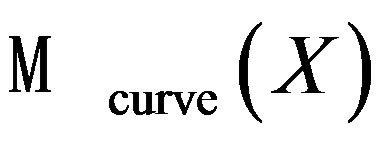 . We summarize these in the following Table 1.
. We summarize these in the following Table 1.
Example 1. The image  + additional geometrical hypothesis, given by the Penrose transform that is a CY-threefold, can be interpreted under the additional geometrical hypothesis, using the Leray-Serre spectral sequence for
+ additional geometrical hypothesis, given by the Penrose transform that is a CY-threefold, can be interpreted under the additional geometrical hypothesis, using the Leray-Serre spectral sequence for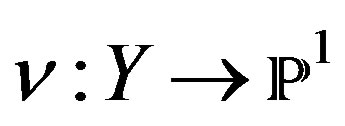 , giving the exact sequence
, giving the exact sequence
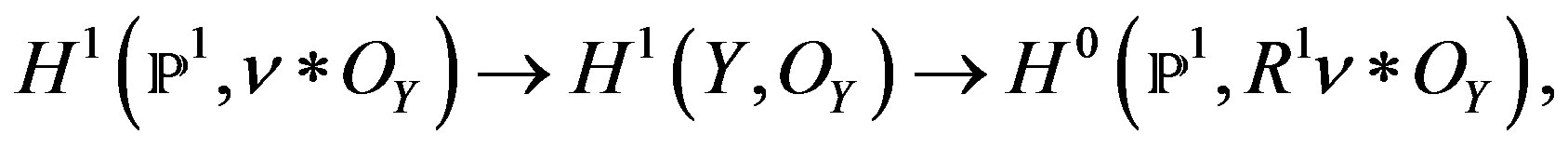
where is the image of right functor on sheaf . Then their corresponding Hodge numbers [33] (corresponding to the cohomology groups in mirror symmetry) are
. Then their corresponding Hodge numbers [33] (corresponding to the cohomology groups in mirror symmetry) are
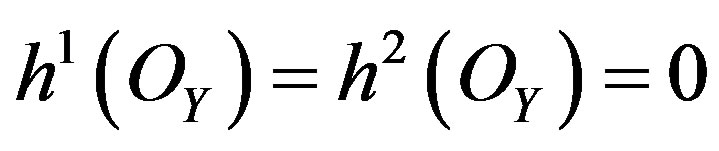 .
.
Example 2. Using a similar correspondence to the double fibration (17) in a twistor context, elements of the cohomology group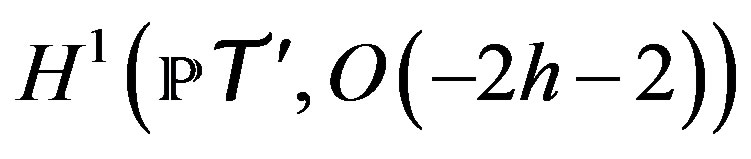 , correspond via the Penrose transform to space-time fields of helicity h, where in particular, a gluon with negative helicity corresponds to a twistor wave function of weight 0.
, correspond via the Penrose transform to space-time fields of helicity h, where in particular, a gluon with negative helicity corresponds to a twistor wave function of weight 0. , is dual orbital corresponding to
, is dual orbital corresponding to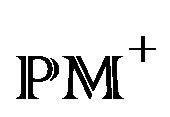 .
.
Example 3. Fix an integer , and an exact sequence
, and an exact sequence
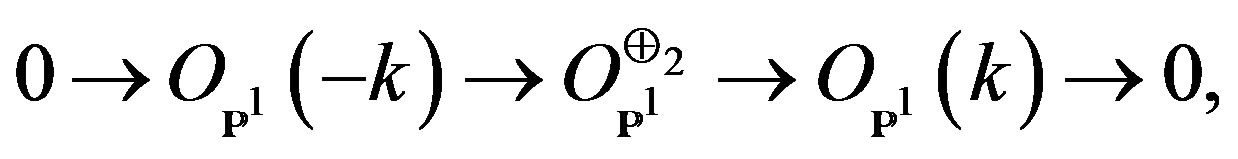
Such extensions correspond to pairs of sections
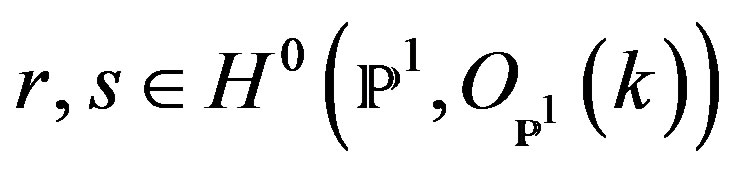 , without common zeros. If
, without common zeros. If
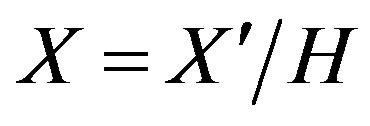 , is a relative Abelian surface on
, is a relative Abelian surface on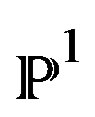 , then their fibers are supersingular surfaces (D-branes of one dimension
, then their fibers are supersingular surfaces (D-branes of one dimension 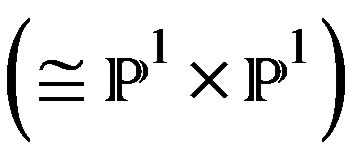 and the inclusion
and the inclusion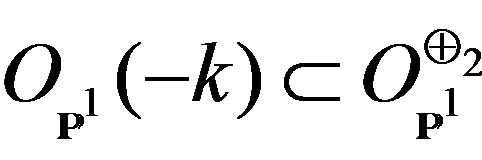 comes from the extension (1). The corresponding solutions are all classes of fields on Calabi-Yau manifold. The
comes from the extension (1). The corresponding solutions are all classes of fields on Calabi-Yau manifold. The , is the space of branes that are included in the Calabi-Yau manifold, in the hole in the 3-dimensional space.
, is the space of branes that are included in the Calabi-Yau manifold, in the hole in the 3-dimensional space.
7. Some Applications and New Research Developments
We base in the scheme on Stein manifolds from Riemannian structure of the space-time [34], and using the generalization by Gindikin conjectures formulated in the Section 7, we obtained a result given in [30] to integral operators cohomologies of Radon-Schmid type:
Teorema 8.1. (F. Bulnes) In the integral operator cohomology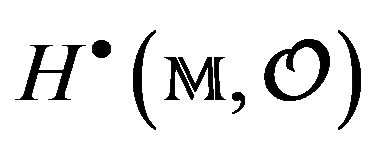 , on complex manifolds (Stein type) the following statements are equivalent:
, on complex manifolds (Stein type) the following statements are equivalent:
1) The open sets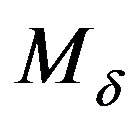 , and
, and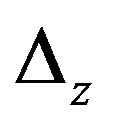 , are G-orbits in X, and their integrals are generalized integrals to
, are G-orbits in X, and their integrals are generalized integrals to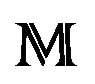 .
.
2) Exist an integral operator T, such that  .
.
3) , and
, and ,
, 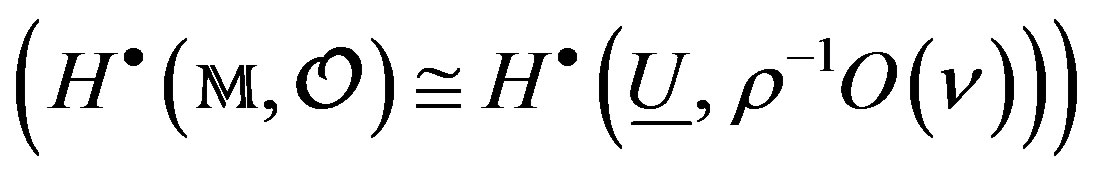 .
.
Proof: [18-30]. ¡
The affirmation 2), and 3), are generalized in the context of the moduli space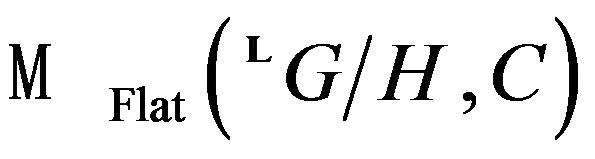 . Using some cohomological classes of geometrical integral transforms that give the equivalences
. Using some cohomological classes of geometrical integral transforms that give the equivalences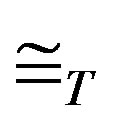 , from the theorem 8.1, with their corresponding identifications in the D-modules context we can give the following Table 2.
, from the theorem 8.1, with their corresponding identifications in the D-modules context we can give the following Table 2.
Other applications and new results obtained recently [22-27], are the relatives to cohomology group classes whose objects have the same metrics in the Kählerian context:
Proposition [27]. The L2-cohomology groups of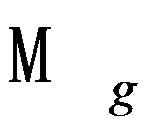 , de complete Kählerians metrics are all the same cohomology groups of D’Rham of
, de complete Kählerians metrics are all the same cohomology groups of D’Rham of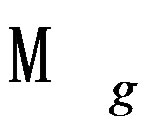 .
.
A concrete application of this result establishes that the moduli space of the relations between hyperbolic waves (horocycles) [35], and the Haar measure of the group action in SU (2.2), on , is the moduli space of the functors
, is the moduli space of the functors
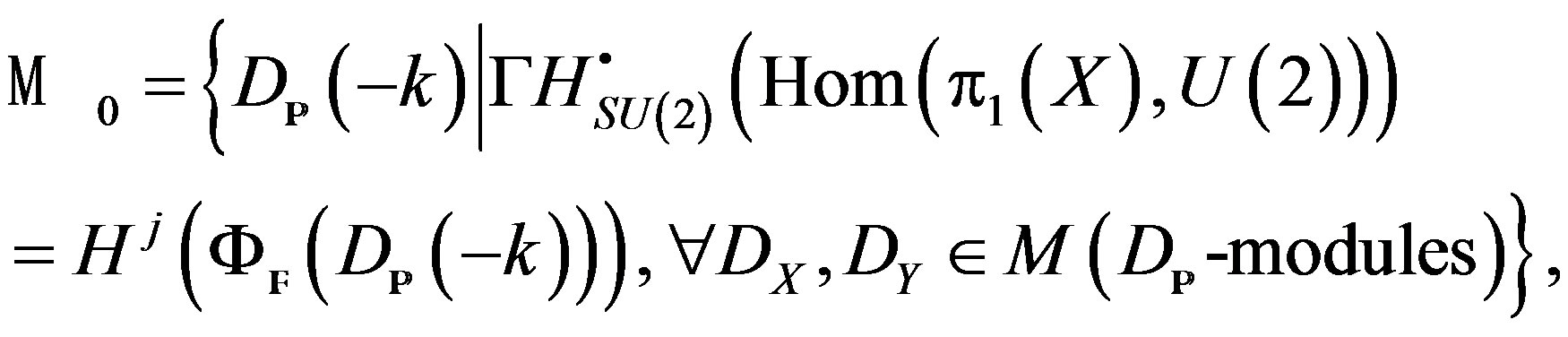
The D-module transform of  is the
is the  -
-

Table 1. Cycles and co-cyles of the Penrose transform on coherent D-modules.

Table 2. Some cohomological classes of geometrical integral transforms and their images inside of the corresponding moduli spaces.
module associated to the wave equation given in the Equation (11), where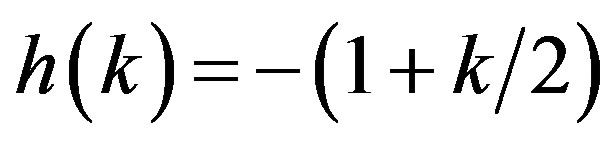 .
.
8. Conclusions
The skills used in this work are the developed maps of coherent sheaves of D-Modules, which establish conformal classes that are useful to realize contexts of the string theory and brane theory inside SUSY theory, for example differential operators that are germs of these sheaves and their corresponding geometric images in the complex holomorphic bundles, who receive sense in the QFT for the particles fields.
These equivalences gives birth to the moduli spaces on the calculated conformal classes that can be useful in the securing of classes of solutions modulo a geometric characteristic of the different equations of field studied in theoretical physics and that an invariant turns out to be geometric of the application of the Penrose transform on classic elements via their classic version.
In this way, departing from some hypotheses obtained by Gindikin on the geometric invariance of cycles in a Kählerian manifold, we can obtain more general versions of the Radon transform, coming to the point of extrapolating these hypotheses to the geometric context of the Penrose transform on the coherent D-Modules in order to use for the generation of the isomorphisms via their double fibration and with it the moduli spaces securing that establish the equivalences of geometric objects that can be re-interpreted algebraically and vice versa. An example of it is the theorem 7.1, and their concrete applications in the description of equivalence of objects happened in the Table 1.
Since the generalized Penrose transform for D-modules is the composition of an inverse image functor and a direct image functor on the side D-module, we first describe the algebraic analogs of these functors. More explicitely, if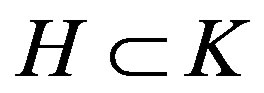 , are two closed algebraic subgroups of a given complex algebraic group G, we enunciate the conjecture based on the result given by Gindikin [10-36] which shows that the D-module inverse image functor associated to the projection
, are two closed algebraic subgroups of a given complex algebraic group G, we enunciate the conjecture based on the result given by Gindikin [10-36] which shows that the D-module inverse image functor associated to the projection  is equivalent to the forgetful functor from the category of
is equivalent to the forgetful functor from the category of 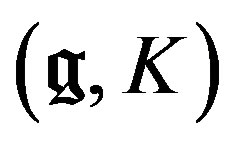 - modules to the category of
- modules to the category of 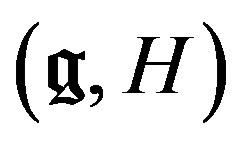 -modules. Gindikin also shows that the derived direct image functor
-modules. Gindikin also shows that the derived direct image functor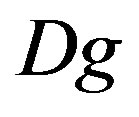 , on the side D-module corresponds (up to a shift) to the algebraic Zuckerman functor
, on the side D-module corresponds (up to a shift) to the algebraic Zuckerman functor , which maps
, which maps 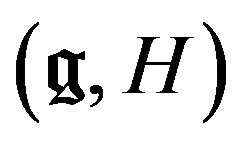 - modules to
- modules to 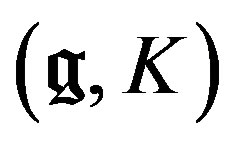 -modules (more precisely, objects of the derived categories). The next step is to obtain an analog of the Bott-Borel-Weil theorem for computing the Zuckerman functor image of “basic objects” of the category of
-modules (more precisely, objects of the derived categories). The next step is to obtain an analog of the Bott-Borel-Weil theorem for computing the Zuckerman functor image of “basic objects” of the category of  -modules [10,26]. In representation theory this is equivalent to computing explicitly the image by the derived Zuckerman functor
-modules [10,26]. In representation theory this is equivalent to computing explicitly the image by the derived Zuckerman functor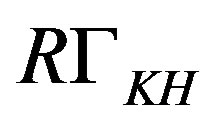 , of generalized Verma modules
, of generalized Verma modules 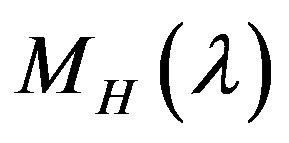 [36], associated to weights
[36], associated to weights , which are integral for
, which are integral for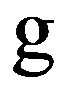 , and dominant for the Lie subalgebra of
, and dominant for the Lie subalgebra of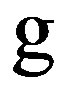 , corresponding to H. Those generalized Verma modules are the objects which correspond via
, corresponding to H. Those generalized Verma modules are the objects which correspond via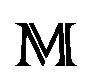 , Kashiwara correspondence to the D-modules which generate the Grothendieck group of the category of quasiG-equivariant
, Kashiwara correspondence to the D-modules which generate the Grothendieck group of the category of quasiG-equivariant  -modules of finite length [23]. In this way, we can also obtain a classification of the differential operators considering extensions of the Verma modules considered [18], and showed to invariance of conformal operators by [4].
-modules of finite length [23]. In this way, we can also obtain a classification of the differential operators considering extensions of the Verma modules considered [18], and showed to invariance of conformal operators by [4].
Nevertheless, from the point of view of the representation theory the demonstration of the theorem 7.1, leaves open questions as soon as to be able to generalize the Radon and Penrose transforms on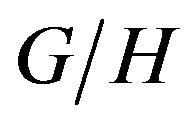 , for not compact case of G, since conditions have not happened to guarantee an operator of this class that is of closed range on these spaces [36,37].
, for not compact case of G, since conditions have not happened to guarantee an operator of this class that is of closed range on these spaces [36,37].
Through the corollary 7.1, we want to establish at least initially in physics, the form in how might there be established the equivalence of the isomorphism obtained by the different Penrose transforms between the dimensions of the singularities, these are seen and shaped by the string theory, and the projective spaces (in the context of the bundles of lines) [18,22,38] that give birth to the conformal classes via the derived sheaves and their stacks in physics, given through the application of the Penrose transform. Likewise, the concrete applications that have been mentioned are studied for the mirror theory in the last advances on field theory.
REFERENCES
- C. Marastoni and T. Tanisaki. “Radon Transforms for Quasi-Equivariant D-Modules on Generalized Flag Manifolds,” Differential Geometry and Its Applications, Vol. 18, No. 2, 2003, pp. 147-176. doi:10.1016/S0926-2245(02)00145-6
- A. Borel, et al., “Algebraic D-Modules,” 2nd Edition, Academic Press, Boston, 1987.
- S. Gindikin and G. Henkin, “Integral Geometry for
 - Cohomology in q-Linear Concave Domains in CPn,” Functional Analysis and Its Applications, Vol. 12, 1978, pp. 247-261.
- Cohomology in q-Linear Concave Domains in CPn,” Functional Analysis and Its Applications, Vol. 12, 1978, pp. 247-261. - R. J. Baston and M. G. Eastwood, “Invariant Operators,” Twistor in Physics, Cambridge, 1981.
- F. Bulnes, “Integral Geometry and Complex Integral Operators Cohomology in Field Theory on Space-Time,” Proceedings of 1st International Congress of Applied Mathematics-UPVT, Government of State of Mexico, Mexico City, 2009, pp. 42-51.
- M. Kashiwara, “Representation Theory and D-Modules on Flag Varieties,” Astérisque, Vol. 173-174, No. 9, 1989, pp. 55-109.
- V. Knapp, “Harish-Chandra Modules and Penrose Transforms,” American Mathematical Society, Mount Holyoke College, 27 June-3 July 1992, pp. 1-17.
- S. Alexakis, “On Conformally Invariant Differential Operators,” In: A. Juhl, Ed., Families of Conformal Covariant Differential Operators, Q-Curvature and Holography, Cornell University, Ithaca, 2007, pp. 1-50.
- C. R. Graham, “Non Existence of Curved Conformally Invariant Operators,” 1980, in Press.
- S. Gindikin, “Penrose Transform at Flag Domains,” The Erwin Schrödinger International Institute for Mathematical Physics, Boltzmanngasse 9, A-1090, Wien, 2011.
- W. Schmid, “Homogeneous Complex Manifolds and Representations of Semisimple Lie Groups,” In: Representation Theory and Harmonic Analysis on Semisimple Lie Groups, American Mathematical Society, Providence, 1989, pp. 223-286.
- A. D’Agnolo and P. Schapira, “Radon-Penrose Transform for D-Modules,” Journal of Functional Analysis, Vol. 139, No. 2, 1996, pp. 349-382. doi:10.1006/jfan.1996.0089
- M. Kashiwara and W. Schmid, “Quasi-Equivariant DModules, Equivariant Derived Category, and Representations of Reductive Lie Groups, in Lie Theory and Geometry,” Birkhäuser, Boston, 1994, pp. 457-488.
- R. Penrose, “Twistor Quantization and Curved SpaceTime,” International Journal of Theoretical Physics, Vol. 1, No. 1, 1968, pp. 61-99. doi:10.1007/BF00668831
- R. J. Baston and M. G. Eastwood, “The Penrose Transform,” The Clarendon Press Oxford University Press, New York, 1989.
- M. G. Eastwood, R. Penrose and R. O. Wells Jr., “Cohomology and Massless Fields,” Communications in Mathematical Physics, Vol. 78, No. 3, 1981, pp. 305-351. doi:10.1007/BF01942327
- R. Penrose, “Solutions of the Zero-Rest-Mass Equations,” Journal of Mathematical Physics, Vol. 10, 1969, pp. 38- 39. doi:10.1063/1.1664756
- F. Bulnes, “Cohomology of Moduli Spaces in Differential Operators Classification to the Field Theory (II),” Proceedings of FSDONA-11 (Function Spaces, Differential Operators and Non-linear Analysis), Tabarz Thur, Vol. 1 No. 12, 2011, pp. 1-22.
- T. N. Bailey and M. G. Eastwood, “Complex Para-Conformal Manifolds Their Differential Geometry and Twistor Theory,” Forum Mathematicum, Vol. 3, 1991, pp. 61- 103. doi:10.1515/form.1991.3.61
- M. F. Atiyah, “Magnetic Monopoles in Hyperbolic Space,” Oxford University Press, Oxford, 1987, pp. 1-34.
- S. Gindikin and G. Henkin, “The Penrose Transforms and Complex Integral Geometry Problems,” VINITI, Moscow, pp. 57-112.
- A. Kapustin, M. Kreuser and K. G. Schlesinger, “Homological Mirror Symmetry: New Developments and Perspectives,” Springer, Berlin, 2009.
- M. Kashiwara and T. Oshima, “Systems of Differential Equations with Regular Singularities and Their Boundary Value Problems,” Annals of Mathematics, Vol. 106, 1977, pp. 145-200. doi:10.2307/1971163
- F. Warner, “Differential Manifolds,” 2nd Edition, SpringerVerlag, Berlin, 1966.
- A. Grothendieck, “Techniques de Construction en Géométrie Analytique. I. Description Axiomatique de l’Espace de Teichmüller et de Ses Variantes,” Séminaire Henri Cartan, Vol. 13, No. 1, 1960, pp. 1-33.
- D. Miličič, “Algebraic D-Modules and Representation Theory of Semi-Simple Lie Groups,” American Mathematical Society, Providence, pp. 133-168.
- L. Kefeng, “Recent Results of Moduli Spaces on Riemann Surfaces,” JDG Conferences, Harvard, 27 June-3 July 2005.
- C. R. LeBrun, “Twistors, Ambitwistors and Conformal Gravity,” Twistor in Physics, Cambridge, 1981.
- S. Gindikin, “The Penrose Transforms of Flags Domains in F(CP2),” Contemporary Mathematical Physics, Vol. 175, No. 2, 1996, pp. 49-56.
- F. Bulnes, and M. Shapiro, “General Theory of Integrals to Analysis and Geometry,” SEPI-IPN, IM-UNAM, Mexico, 2007.
- S. Schröer, “Some Calabi-Yau Threefolds with Obstructed Deformations over the Witt Vectors,” Journal Compositio Mathematica, Vol. 140, No. 6, 2004, pp. 1579- 1592.
- F. Bulnes, “Research on Curvature of Homogeneous Spaces,” Department of Research in Mathematics and Engineering TESCHA, Government of State of Mexico, Mexico,2010. http://tesch.edu.mx/DOC/Investigacion%20Doctor.pdf
- L. Mason and D. Skinner, “Heterotic Twistor-String Theory,” Oxford University, Oxford, 2007. arXiv:0708.2276v1 [hep-th]
- J. A. Wolf, “The Stein Condition for Cycle Spaces of Open Orbits on Complex Flag Manifolds,” Annals of Mathematics, Vol. 136, No. 3, 1992, pp. 541-555. doi:10.2307/2946599
- F. Bulnes, “Design of Measurement and Detection Devices of Curvature through of the Synergic Integral Operators of the Mechanics on Light Waves,” Proceedings of IMECE/ASME on Electronics and Photonics, Vol. 5, 2009, pp. 91-103. doi:10.1115/IMECE2009-10038
- F. Bulnes, “On the Last Progress of Cohomological Induction in the Problem of Classification of Lie Groups Representations,” Proceeding of Masterful Conferences, International Conference of Infinite Dimensional Analysis and Topology, Ivano-Frankivsk, 27 May-1 June 2009, pp. 21-22.
- A. W. Knapp and N. Wallach, “Szegö Kernels Associated with Discrete Series,” Inventiones Mathematicae, Vol. 34, No. 3, 1976, pp. 163-200. doi:10.1007/BF01403066
- S. Helgason, “The Radon Transform,” In: H. Bass, J. Oesterlé, A. Weinstein and Birkhäuser, Eds., Progress in Mathematics, Birkhäuser, Boston Mass, 1980.
Nomenclature and Abbreviations
 —Wave operator. This is a differential operator that composes the wave equation on the space
—Wave operator. This is a differential operator that composes the wave equation on the space , also called D’Alambert operator.
, also called D’Alambert operator.
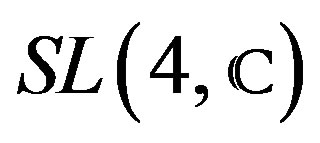 —Special linear group of the complex matrices of rank four. Have the structure of Lie group. This component is necessary to define the linear reductive groups of
—Special linear group of the complex matrices of rank four. Have the structure of Lie group. This component is necessary to define the linear reductive groups of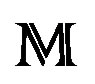 .
.
 —Penrose transform operator.
—Penrose transform operator.
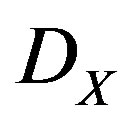 —Sheaf of rings of holomorphic linear differential operators (a D-module).
—Sheaf of rings of holomorphic linear differential operators (a D-module).
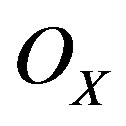 —Sheaf of holomorphic functions on a complex manifold X.
—Sheaf of holomorphic functions on a complex manifold X.
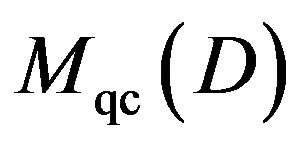 — Category of D-modules.
— Category of D-modules.
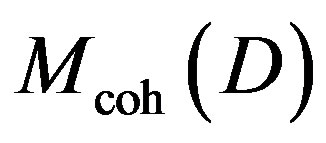 —Category of D-modules that is subcategory of
—Category of D-modules that is subcategory of .
.
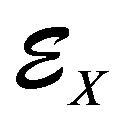 —Ring naturally endowed with a
—Ring naturally endowed with a  -filtration by the degree.
-filtration by the degree.
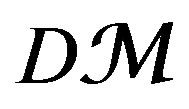 —coherent
—coherent 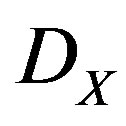 -module. This D-module is the fundamental ingredient of the equivalences of the objects of moduli space.
-module. This D-module is the fundamental ingredient of the equivalences of the objects of moduli space.
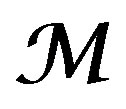 —DX-module object of our research and their category is useful to realize the classification of linear differential operators in field theory. This D-module represents a system of PDE, in mathematical physics to which is necessary to give solution.
—DX-module object of our research and their category is useful to realize the classification of linear differential operators in field theory. This D-module represents a system of PDE, in mathematical physics to which is necessary to give solution.
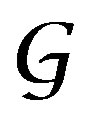 —Coherent Sheaf of the DX-module
—Coherent Sheaf of the DX-module 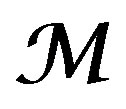 .
.
 — Image of DX-module under Penrose transform.
— Image of DX-module under Penrose transform.
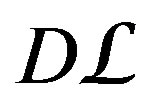 —DX-module of bundles of lines.
—DX-module of bundles of lines.
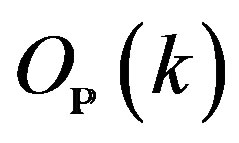 —Coherent Sheaf of D-modules that are
—Coherent Sheaf of D-modules that are 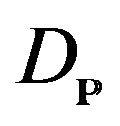 - modules, and that can be induced to
- modules, and that can be induced to 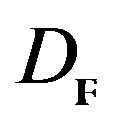 -modules.
-modules.
SUSY Cycles—Supersymmetry Cycles.
QFT—Quantum field theory.
NOTES
*This work was supported for Postdoctoral fellowship by COMECYT, and State Government.
1To define the images of direct functors to D-modules it is have that use derived categories. For it, is simpler defining them for right D-modules. Be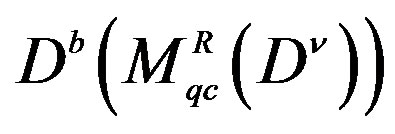 , the derived category bounded for right quasi-coherent
, the derived category bounded for right quasi-coherent  -modules of the form
-modules of the form
 where
where , is the characteristic manifold and R, is the right derived functor following:
, is the characteristic manifold and R, is the right derived functor following:
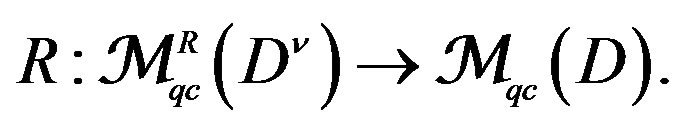
Also  and
and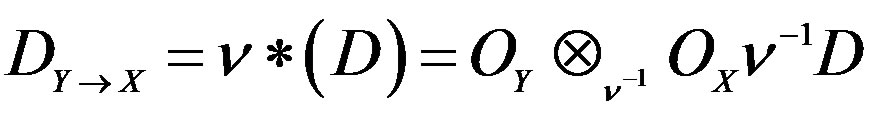 . Then
. Then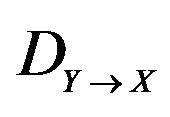 , is a righ
, is a righ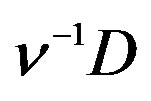 ;-module to the right multiplication in the second functor.
;-module to the right multiplication in the second functor.

