Advances in Pure Mathematics
Vol.2 No.5(2012), Article ID:22799,7 pages DOI:10.4236/apm.2012.25045
Differential Sandwich Theorems for Analytic Functions Defined by an Extended Multiplier Transformation
Department of Mathematics, Faculty of Science, Jazan University, Jazan, KSA
Email: a-e-sh27@hotmail.com
Received March 26, 2012; revised April 28, 2012; accepted May 9, 2012
Keywords: Differential sandwich theorems; Analytic functions; Multiplier transformation
ABSTRACT
In this investigation, we obtain some applications of first order differential subordination and superordination results involving an extended multiplier transformation and other linear operators for certain normalized analytic functions. Some of our results improve previous results.
1. Introduction
Let 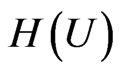 be the class of functions analytic in the open unit disk
be the class of functions analytic in the open unit disk . Let
. Let 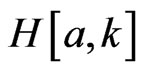 be the subclass of
be the subclass of  consisting of functions of the form:
consisting of functions of the form:
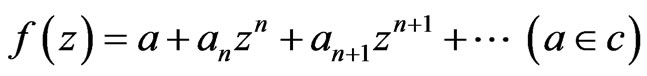 (1.1)
(1.1)
For simplicity, let . Also, let
. Also, let  be the subclass of
be the subclass of  consisting of functions of the form:
consisting of functions of the form:
 (1.2)
(1.2)
If 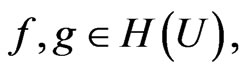 we say that
we say that  is subordinate to
is subordinate to 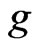 written
written  if there exists Schwarz function
if there exists Schwarz function  which (by definition) is analytic in
which (by definition) is analytic in  with
with  and
and  for all
for all  such that
such that  Furthermore, if the function
Furthermore, if the function  is univalent in
is univalent in  then we have the following equivalence , (cf., e.g. [1,2]; see also [3]):
then we have the following equivalence , (cf., e.g. [1,2]; see also [3]):
We denote this subordination by
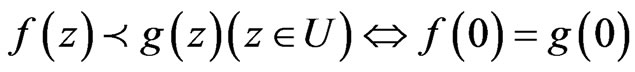
and 
Let 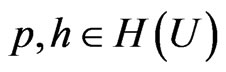 and let
and let . If p and
. If p and 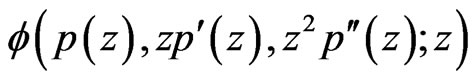 are univalent and if p satisfies the second-order superordination
are univalent and if p satisfies the second-order superordination
 , (1.3)
, (1.3)
then 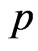 is a solution of the differential superordination (1.3). Note that if
is a solution of the differential superordination (1.3). Note that if  is subordinate to
is subordinate to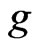 , then
, then  is superordinate to
is superordinate to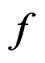 . An analytic function
. An analytic function  is called a subordinant if
is called a subordinant if 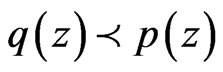 for all
for all  satisfying (1.3). A univalent subordinant
satisfying (1.3). A univalent subordinant 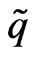 that satisfies
that satisfies 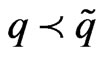 for all subordinants of (1.3) is called the best subordinant. Recently Miller and Mocanu [4] obtained conditions on the functions
for all subordinants of (1.3) is called the best subordinant. Recently Miller and Mocanu [4] obtained conditions on the functions  and
and  for which the following implication holds:
for which the following implication holds:
 (1.4)
(1.4)
Using the results of Miller and Mocanu [4], Bulboaca [5] considered certain classes of first-order differential superordinations as well as superordination-preserving integral operators [6]. Ali et al. [7] have used the results of Bulboaca [5] and obtained sufficient conditions for normalized analytic functions 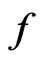 to satisfy:
to satisfy:

where 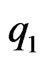 and
and  are given univalent functions in
are given univalent functions in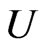 . Also, Tuneski [8] obtained a sufficient condition for starlikeness of
. Also, Tuneski [8] obtained a sufficient condition for starlikeness of 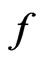 in terms of the quantity
in terms of the quantity .
.
Recently Shanmugam et al. [9] obtained sufficient conditions for a normalized analytic functions 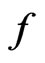 to satisfy
to satisfy

and

Many essentially equivalent definitions of multiplier transformation have been given in literature (see [10-12]. In [13] Catas defined the operator  as follows:
as follows:
Definition 1.1. [13] Let the function . For
. For  where
where 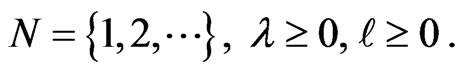 The extended multiplier transformation
The extended multiplier transformation 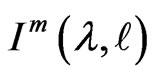 on
on  is defined by the following infinite series:
is defined by the following infinite series:
 (1.5)
(1.5)
It follows form (1.5) that 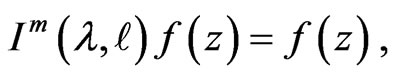
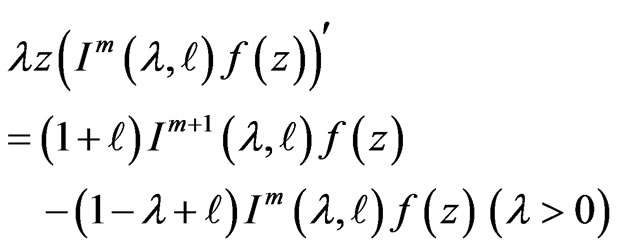 (1.6)
(1.6)
and
 (1.7)
(1.7)
for all integers  and
and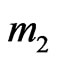 . We note that:
. We note that:
1) 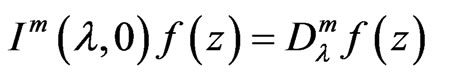 (see [14]);
(see [14]);
2)  (see [15]);
(see [15]);
3)  (see [10,11]);
(see [10,11]);
4)  (see [12]).
(see [12]).
Also if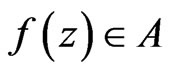 , then we can write
, then we can write

where
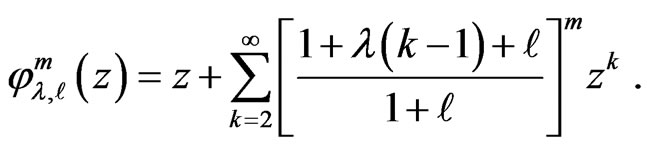
In this paper, we obtain sufficient conditions for the normalized analytic function  defined by using an extended multiplier transformation
defined by using an extended multiplier transformation  to satisfy:
to satisfy:

and

and  and
and  are given univalent functions in
are given univalent functions in .
.
2. Definitions and Preliminaries
In order to prove our results, we shall make use of the following known results.
Definition 2.1. [4]
Denote by  the set of all functions
the set of all functions 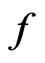 that are analytic and injective on
that are analytic and injective on  where
where
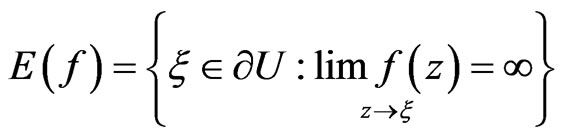
and are such that 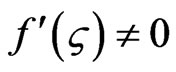 for
for 
Lemma 2.1. [4]
Let the function 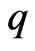 be univalent in the open unit disc
be univalent in the open unit disc  and
and  and
and  be analytic in a domain
be analytic in a domain  containing
containing 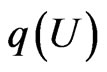 with
with 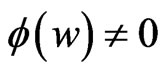 when
when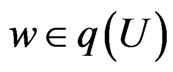 . Set
. Set
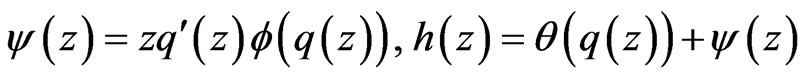 . (2.1)
. (2.1)
Suppose that 1)  is starlike univalent in
is starlike univalent in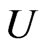 2)
2) 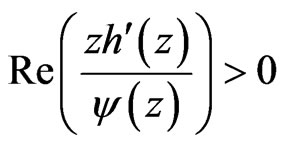 for
for .
.
If  is analytic with
is analytic with 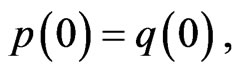
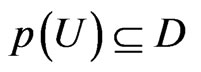 and
and
 (2.2)
(2.2)
then  and
and  is the best dominant. Taking
is the best dominant. Taking 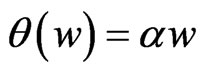 and
and  in lemma 1, Shanmugam et al. [9] obtained the following lemma.
in lemma 1, Shanmugam et al. [9] obtained the following lemma.
Lemma 2.2. [2]
Let  be univalent in
be univalent in  with
with  Let
Let  ;
;  further assume that
further assume that

If  is analytic in
is analytic in , and
, and
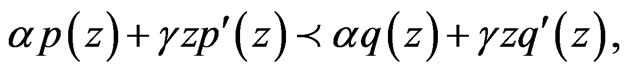
then 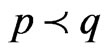 and
and 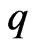 is the best dominant.
is the best dominant.
Lemma 2.3. [5]
Let the function  be univalent in the open unit disc
be univalent in the open unit disc  and
and 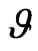 and
and 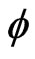 be analytic in a domain
be analytic in a domain  containing
containing 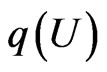 Suppose that 1)
Suppose that 1)  for
for 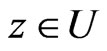 and 2)
and 2)  is starlike univalent in
is starlike univalent in .
.
If  with
with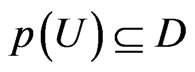 ,
,
 , is univalent in
, is univalent in  and
and
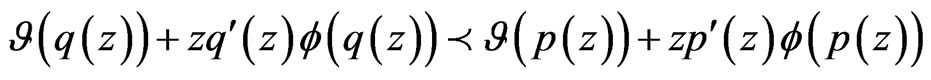 (2.3)
(2.3)
then 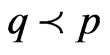 and
and  is the best subordinant.
is the best subordinant.
Taking  and
and 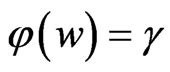 in Lemma 2.3, Shanmugam et al. [9] obtained the following lemma.
in Lemma 2.3, Shanmugam et al. [9] obtained the following lemma.
Lemma 2.4. [2]
Let  be convex univalent in
be convex univalent in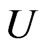 ,
,  Let
Let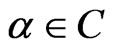 ,
,  and
and  If
If 
 is univalent in
is univalent in 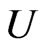 and
and  then
then  and
and 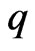 is the best subordinant.
is the best subordinant.
3. Applications to an Extended Multiplier Transformation and Sandwich Theorems
Theorem 3.1.
Let  be convex univalent in
be convex univalent in 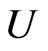 with
with 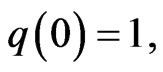
 Further, assume that
Further, assume that
 (3.1)
(3.1)
If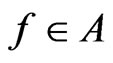 ,
, 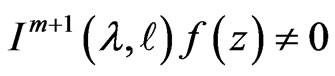 for
for  and
and
 (3.2)
(3.2)
then
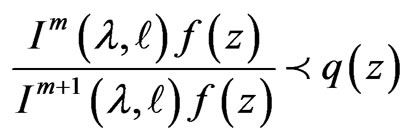
and  is the best dominant.
is the best dominant.
Proof. Define a function  by
by
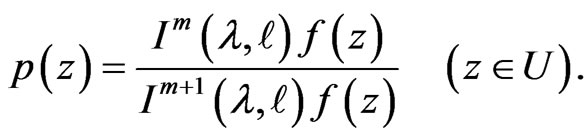 (3.3)
(3.3)
Then the function  is analytic in
is analytic in 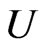 and
and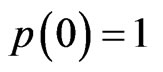 . Therefore, differentiating (3.3) logarithmically with respect to
. Therefore, differentiating (3.3) logarithmically with respect to  and using the identity (1.6) in the resulting equation, we have
and using the identity (1.6) in the resulting equation, we have
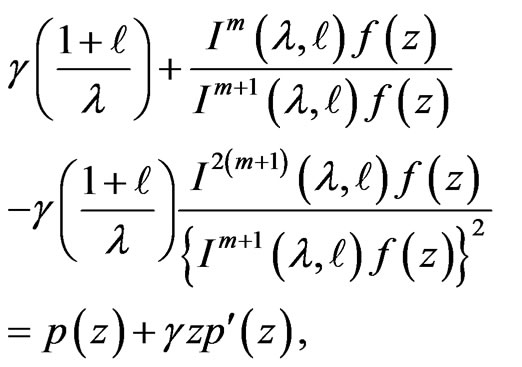
that is,

and therefore, the theorem follows by applying Lemma 2.2.
Putting
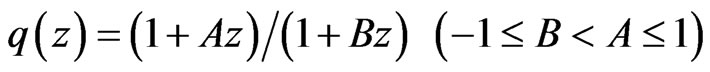
in Theorem 3.1, we have the following corollary.
Corollary 3.1.
If  and
and 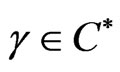 satisfy
satisfy

then
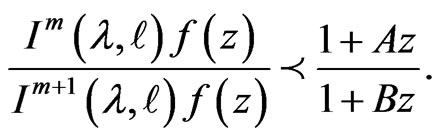
Putting  and
and  in Corollary 3.1, we have
in Corollary 3.1, we have
Corollary 3.2.
If 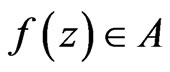 and
and 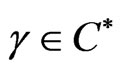 satisfy
satisfy

then
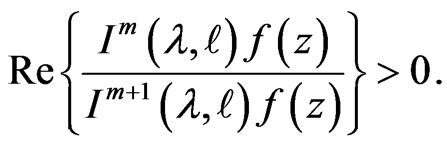
Taking 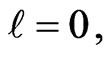 in Theorem 1, we have
in Theorem 1, we have
Corollary 3.3.
Let 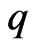 be convex univalent in
be convex univalent in  with
with 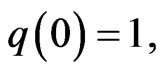
 . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If , and
, and

then

and  is the best dominant.
is the best dominant.
Taking  in Theorem 3.1, we have
in Theorem 3.1, we have
Corollary 3.4.
Let  be convex univalent in
be convex univalent in 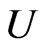 with
with 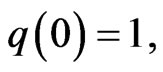
 . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If , and
, and
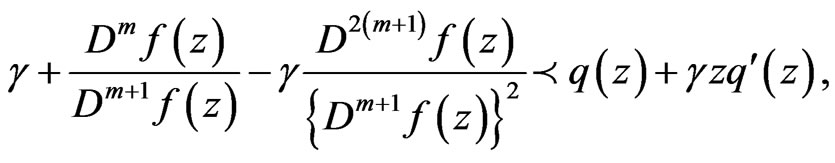
then

and 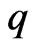 is the best dominant.
is the best dominant.
Taking 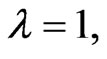 in Theorem 3.1, we have
in Theorem 3.1, we have
Corollary 3.5.
Let 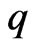 be convex univalent in
be convex univalent in  with
with 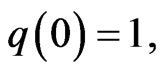
 . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If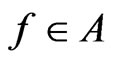 , and
, and

then

and  is the best dominant.
is the best dominant.
Taking 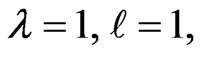 in Theorem 1, we have
in Theorem 1, we have
Corollary 3.6.
Let 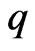 be convex univalent in
be convex univalent in 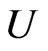 with
with 
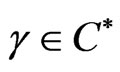 . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If , and
, and
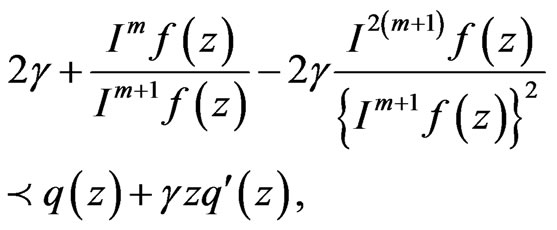
then

and 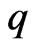 is the best dominant.
is the best dominant.
Now, by appealing to Lemma 2.4 it can be easily prove the following theorem.
Theorem 3.2.
Let 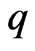 be convex univalent in
be convex univalent in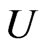 . Let
. Let 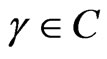 with
with 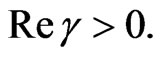
If ,
, 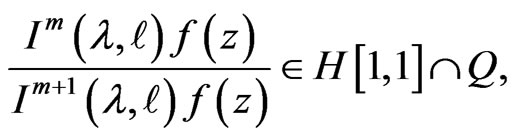
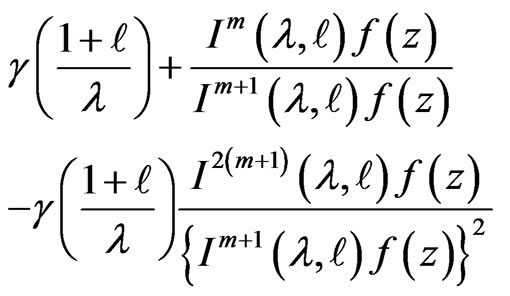
is univalent in , and
, and

then
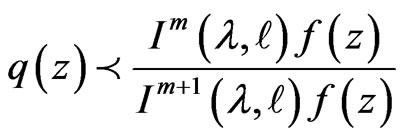
and  is the best subordinant.
is the best subordinant.
Taking , in Theorem 3.2, we have
, in Theorem 3.2, we have
Corollary 3.7.
Let  be convex univalent in
be convex univalent in . Let
. Let  with
with 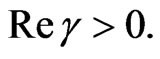
If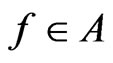 ,
, 

is univalent in , and
, and
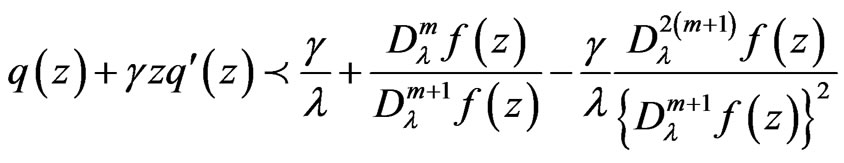 then
then
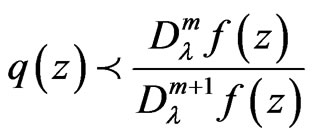
and  is the best subordinant.
is the best subordinant.
Taking  in Theorem 3.2, we have
in Theorem 3.2, we have
Corollary 3.8.
Let  be convex univalent in
be convex univalent in . Let
. Let  with
with 
If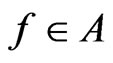 ,
, 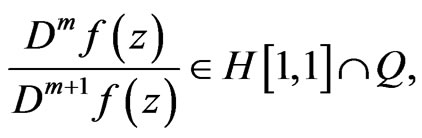
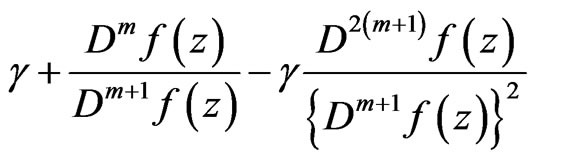
is univalent in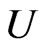 , and
, and
 then
then
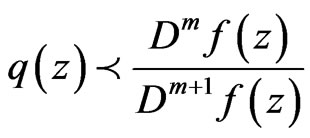
and  is the best subordinant.
is the best subordinant.
Taking 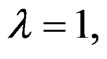 in Theorem 3.2, we have
in Theorem 3.2, we have
Corollary 3.9.
Let 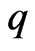 be convex univalent in
be convex univalent in . Let
. Let 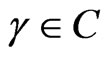 with
with 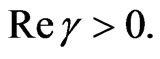
If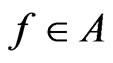 ,
, 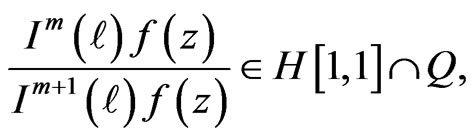
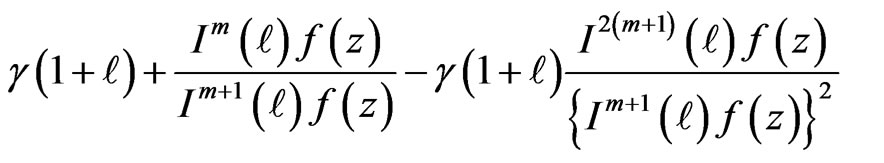
is univalent in , and
, and

then
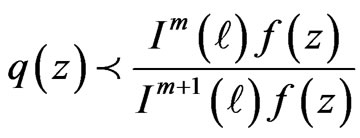
and 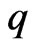 is the best subordinant.
is the best subordinant.
Taking  in Theorem 3.2, we have
in Theorem 3.2, we have
Corollary 3.10.
Let  be convex univalent in
be convex univalent in . Let
. Let  with
with 
If ,
, 
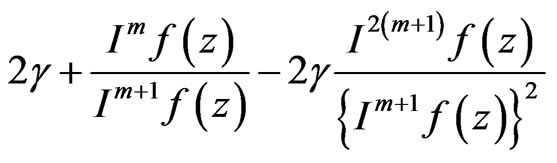
is univalent in , and
, and
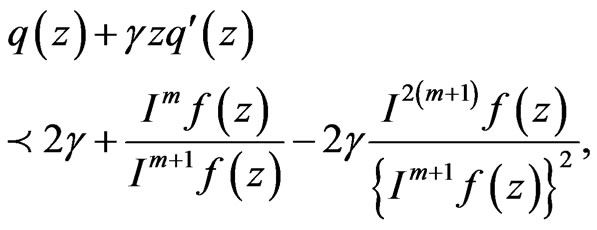
then

and 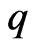 is the best subordinant.
is the best subordinant.
Combining Theorems 3.1 and 3.2, we get the following sandwich theorem.
Theorem 3.3.
Let 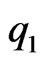 be convex univalent in
be convex univalent in ,
,  with
with 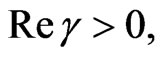
 be univalent in
be univalent in 
 and satisfies (3.1). If
and satisfies (3.1). If 
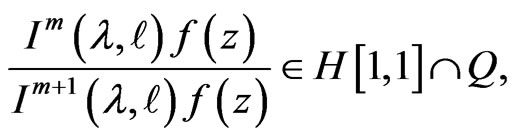

is univalent in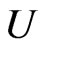 , and
, and

Then
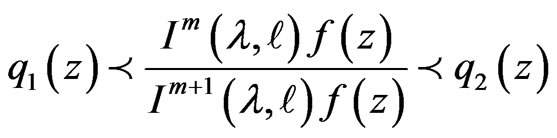
and  and
and 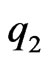 are respectively, the best subordinant and the best dominant.
are respectively, the best subordinant and the best dominant.
4. Remarks
Combining: 1) Corollary 3.3 and Corollary 3.7; 2) Corollary 3.4 and Corollary 3.8; 3) Corollary 3.5 and Corollary 3.9; 4) Corollary 3.6 and Corollary 3.10, we obtain similar sandwich theorems for the corresponding operators.
Theorem 3.4.
Let  be convex univalent in
be convex univalent in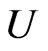 ,
,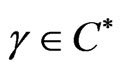 . Further, assume that (3.1) holds.
. Further, assume that (3.1) holds.
If  satisfies
satisfies

then

and q is the best dominant.
Proof. Define the function 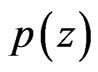 by
by
 .
.
Then, simple computations show that
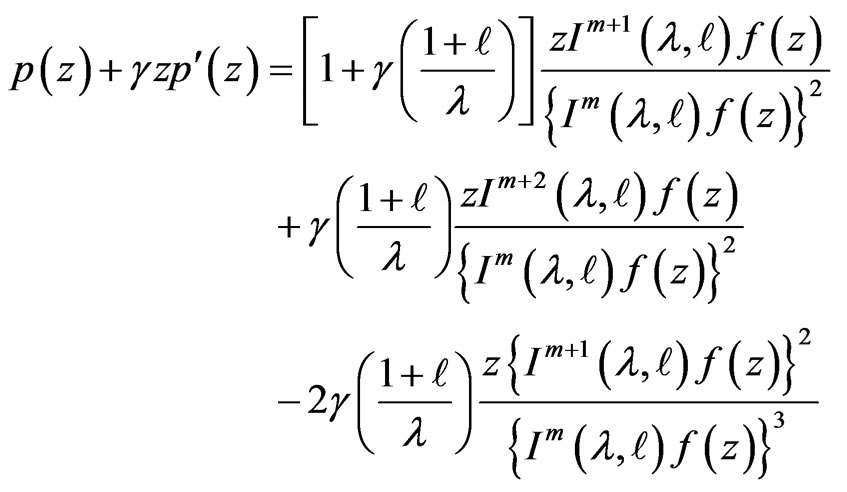
Applying Lemma 2, the theorem follows.
Taking  in Theorem 3.4, we have the following corollary.
in Theorem 3.4, we have the following corollary.
Corollary 3.11.
Let 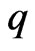 be convex univalent in
be convex univalent in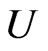 ,
,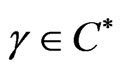 . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If  satisfies
satisfies
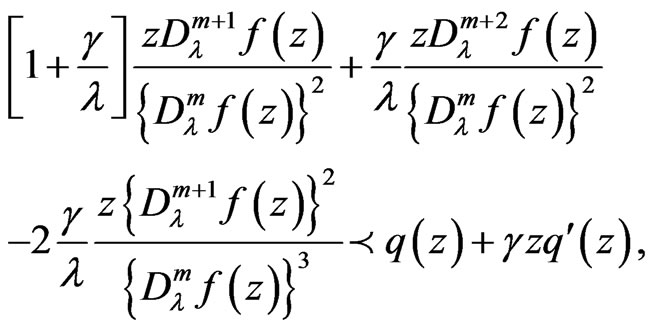
then

and  is the best dominant.
is the best dominant.
Taking  in Theorem 3.4, we have
in Theorem 3.4, we have
Corollary 3.12.
Let 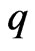 be convex univalent in
be convex univalent in ,
,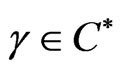 . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If 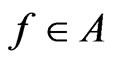 satisfies
satisfies
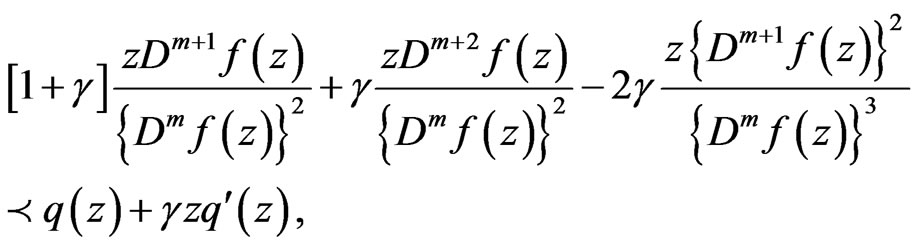
then
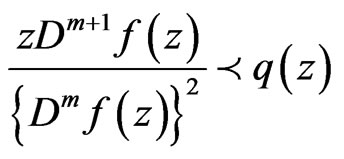
and 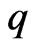 is the best dominant.
is the best dominant.
Taking  in Theorem 3.4, we have
in Theorem 3.4, we have
Corollary 3.13.
Let 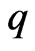 be convex univalent in
be convex univalent in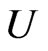 ,
, . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If  satisfies
satisfies

then
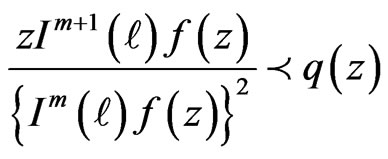
and 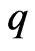 is the best dominant.
is the best dominant.
Taking  in Theorem 3.4, we have
in Theorem 3.4, we have
Corollary 3.14.
Let  be convex univalent in
be convex univalent in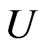 ,
, . Further, assume that (3.1) holds. If
. Further, assume that (3.1) holds. If  satisfies
satisfies
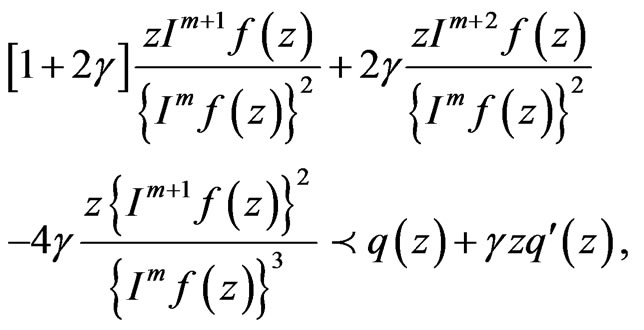
then
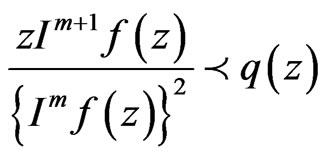
and  is the best dominant.
is the best dominant.
Theorem 3.5.
Let  be convex univalent in
be convex univalent in . Let
. Let  with
with 
If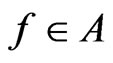 ,
, 

is univalent in 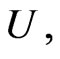 and
and
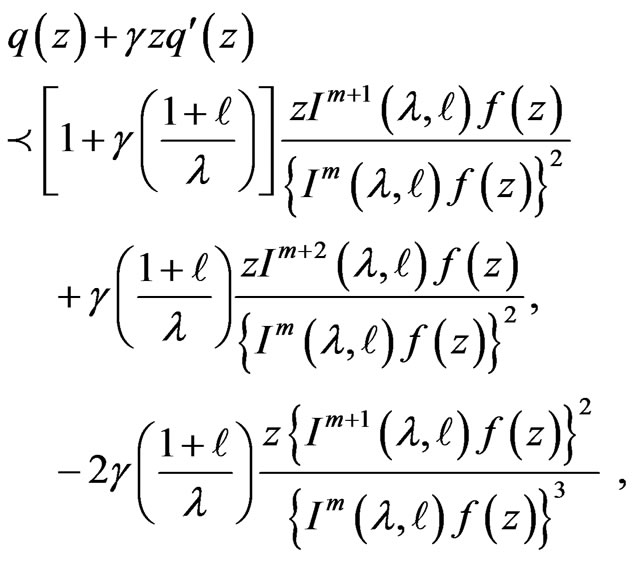
then

and  is the best subordinant.
is the best subordinant.
Proof. The proof follows by applying Lemma 3.4.
Combining Theorems 3.4 and 3.5, we get the following sandwich theorem.
Theorem 3.6.
Let  be convex univalent in
be convex univalent in ,
,  with
with 
 be univalent in
be univalent in 
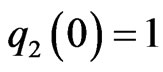 and satisfies (3.1). If
and satisfies (3.1). If ,
, 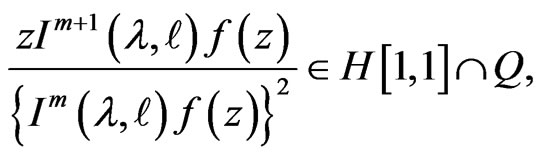

is univalent in  and
and
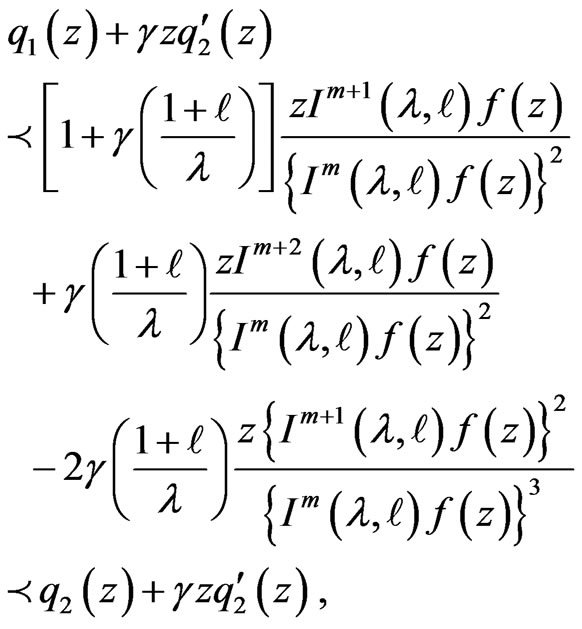
then

and  and
and 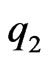 are respectively the best subordinant and the best dominant.
are respectively the best subordinant and the best dominant.
REFERENCES
- T. Bulboaca, “Differential Superordinations and Superordinations,” Recent Results, House of Scientific, Cluj-Napoca.
- S. S. Miller and P. T. Mocanu, “Differential Subordinations and Univalent Functions,” Michigan Math Journal, Vol. 28, No. 2, 1981, pp. 157-171. doi:10.1307/mmj/1029002507
- S. S. Miller and P. T. Mocanu, “Differential Subordinations: Theory and Applications,” Pure and Applied Mathematics No. 225, Marcel Dekker, New York, 2000.
- S. S. Miller and P. T. Mocanu, “Subordinants of Differential Superordinations,” Complex Variables, Vol. 48, No. 10, 2003, pp. 815-826. doi:10.1080/02781070310001599322
- T. Bulboaca, “Classes of First-Order Differential Superordinations,” Demonstratio Mathematica, Vol. 35, No. 2, 2002, pp. 287-292.
- T. Bulboaca, “A Class of Superordination-Preserving Integral Operators,” Indagationes Mathematicae, Vol. 13, No. 3, 2002, pp. 301-311. doi:10.1016/S0019-3577(02)80013-1
- R. M. Ali, V. Ravichandran, M. Hussain Khan and K. G. Subramanian, “Differential Sandwich Theorems for Certain Analytic Functions,” Far East Journal of Mathematical Sciences, Vol. 15, No. 1, 2005, pp. 87-94.
- N. Tuneski, “On Certain Sufficient Conditions for Starlikeness,” International Journal of Mathematics and Mathematical Sciences, Vol. 23, No. 8, 2000, pp. 521-527. doi:10.1155/S0161171200003574
- T. N. Shanmugam, V. Ravichandran and S. Sivasubramanian, “Differential Sandwich Theorems for Some Subclasses of Analytic Functions,” Australian Journal of Mathematical Analysis and Applications, Vol. 3, No. 1, 2006, Article 8, 11.
- N. E. Cho and H. M. Srivastava, “Argument Estimates of Certain Analytic Functions Defined by a Class of Multiplier Transformations,” Mathematical and Computer Modelling, Vol. 37, No. 1-2, 2003, 39-49. doi:10.1016/S0895-7177(03)80004-3
- N. E. Cha and T. H. Kim, “Multiplier Tnsformations and Strongly Close-to-Convex Functions,” Bulletin of the Korean Mathematical Society, Vol. 40, No. 3, 2003, 399- 410. doi:10.4134/BKMS.2003.40.3.399
- B. A. Uralegaddi and C. Somanama, “Certain Classes of Univalent Functions,” In: H. M. Srivastava and S. Owa, Eds., Current Topics in Analytic Function Theory, World Scientific, Publishing Company, Singapore City, 1992, pp. 371-374.
- A. Catas, “A Note on a Certain Subclass of Analytic Functions Defined by Multiplier Transformations,” Proceedings of the Internat, Symposium on Geometric Function Theory and Applications, Istanbul, 20-24 August 2007.
- F. M. Al-Oboudi, “On Univalent Functions de Fined by a Generalized Salagean Operator Internat,” International Journal of Mathematics and Mathematical Sciences, Vol. 27, 2004, pp. 1429-1436. doi:10.1155/S0161171204108090
- G. S. Salagean, “Subclasses of Univalent Functions,” Lecture Notes in Mathematics, Vol. 1013, 1983, pp. 362-372. doi:10.1007/BFb0066543

