World Journal of Vaccines
Vol. 1 No. 4 (2011) , Article ID: 8653 , 6 pages DOI:10.4236/wjv.2011.14016
Impact of Vaccination and Culling on Controlling Foot and Mouth Disease: A Mathematical Modelling Approach
![]()
1Department of Applied Mathematics, National University of Science and Technology, Bulawayo, Zimbabwe; 2Department of Mathematics, University of Zimbabwe, Harare, Zimbabwe.
Email: *steadymushaya@gmail.com
Received July 27th, 2011; revised September 6th, 2011; accepted September 22nd, 2011.
Keywords: Foot and Mouth disease, vaccination, culling, reproductive number, numerical simulations
ABSTRACT
Foot and mouth disease (FMD) is a major threat, not only to countries whose economies rely on agricultural exports, but also to industrialized countries that maintain a healthy domestic livestock industry by eliminating major infectious diseases from their livestock populations. In this paper a simple mathematical model is formulated and comprehensively analyzed to assess the impact of vaccination and culling on controlling FMD. Overally the study demonstrates that vaccination and culling are essential on controlling FMD if they are all implemented. Furthermore the study illustrates that culling latently infected (early detection of infected animals) is extremely important on controlling FMD dynamics.
1. Introduction
Foot-and-mouth disease (FMD) is a highly infectious illness caused by an aphthovirus that affects clovenhoofed animals such as pigs, cattle, and sheep [1,2]. Although not usually fatal, it causes suffering and vastly reduces animals’ commercial value by reducing their weight and milk output. Cattle, swine, sheep, goats, and deer are highly susceptible and can exhibit signs of clinical illness after an incubation period of only 2 to 14 days; however, the incubation period may last longer and, especially in sheep and goats, signs of illness may go undetected altogether [3]. Clinical signs include fever and blister-like lesions followed by erosions on the tongue and lips; in the mouth, muzzle, and snout; on the teats; between the hooves; and around the digits. Excessive salivation, lameness, and decreased feed consumption may also be observed. There are seven different types and more than 60 subtypes of FMD virus, and there is no universal vaccine against the disease. Vaccines for FMD must match to the type and subtype present in the affected area.
Mathematical models have become invaluable management tools for epidemiologists, both shedding light on the mechanisms underlying the observed dynamics as well as making quantitative predictions on the effectiveness of different control measures. The literature and development of mathematical epidemiology is well documented and can be found in [4]. Modeling the transmission dynamics of FMD is an important and interesting topic for a lot of researchers (see, for example [5-11]). Here, we evaluate the impact of vaccination and culling on controlling Foot and mouth Disease.
2. A Mathematical Framework and Approach
Based on epidemiological status, the population of animals is sub-divided into the following subgroups: Susceptible S, vaccinated V, latently infected L and infectious animals I. Thus, the total population is given by N = S + V + L + I. We shall consider the following system of ordinary differential equations
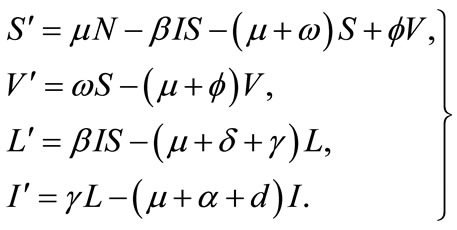 (1)
(1)
Some notable features of the model: the birth rate and the death rate are assumed to be equal (denoted by μ) and in consequence the total population is at an equilibrium; susceptible animals are vaccinated at rate f, and the vaccine wanes off at rate w. Infectious hosts suffer an additional disease-related mortality at rate d, γ denotes the rate of progression from latent stage to infectious stage. Heuristically, 1/g is the mean latent period. The incidence term is of the bilinear mass-action form bIS. Latently infected animals are identified and culled at rate d. Furthermore, infectious animal are culled at rate α. The dynamical transfer of the hosts is depicted in the following figure 1.
For system (1) the first octant in the state space is positively invariant and attracting, that is solutions that start where all the variables are non-negative remain there. Thus, system (1) will be analyzed in a suitable region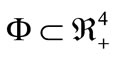 . The region
. The region 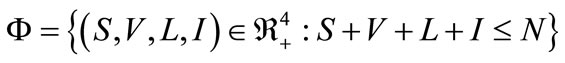 which, is positively invariant and attracting. Existence, a uniqueness and continouation result for system (1) holds in this region.
which, is positively invariant and attracting. Existence, a uniqueness and continouation result for system (1) holds in this region.
3. Analytical Results
3.1. Disease-Free (DFE) Equilibrium
Model system (1) has an evident DFE given by
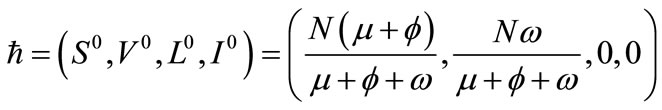
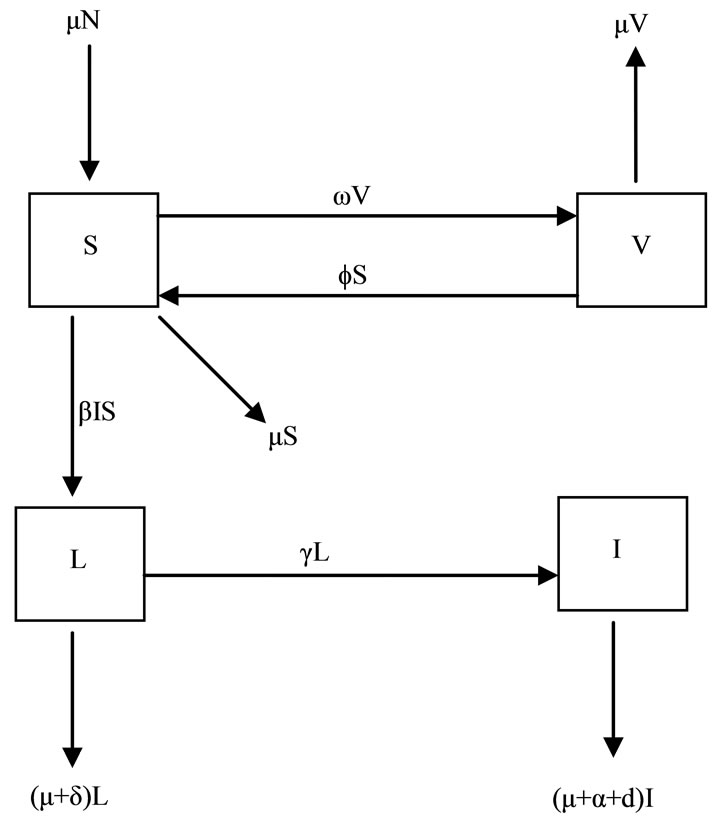
Figure 1. Model flow diagram.
3.2. The Reproductive Number
The linear stability of  is obtained using the next generation matrix [12] for system (1). Using the notation in [12] the non-negative matrix F, and the non-singular matrix V, for the new infection terms and the remaining transfer terms are respectively given (at the disease-free equilibrium) by
is obtained using the next generation matrix [12] for system (1). Using the notation in [12] the non-negative matrix F, and the non-singular matrix V, for the new infection terms and the remaining transfer terms are respectively given (at the disease-free equilibrium) by
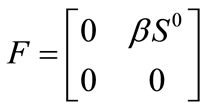
And
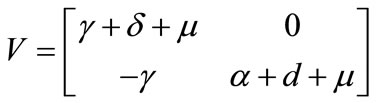
Thus, the basic reproductive number is given by the dimensionless expression:
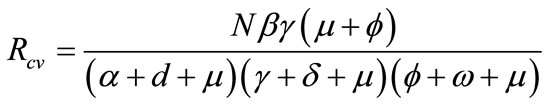 . (2)
. (2)
The threshold quantity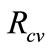 , measures the average number of new secondary FMD cases generated by a single FMD infective introduced in a population where the aforementioned control measures are in place.
, measures the average number of new secondary FMD cases generated by a single FMD infective introduced in a population where the aforementioned control measures are in place.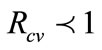 , implies that the epidemic dies out, while
, implies that the epidemic dies out, while 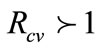 demonstrates the persistence of the epidemic.
demonstrates the persistence of the epidemic.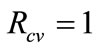 , is the systems change point from the epidemic dying to epidemic persistence.
, is the systems change point from the epidemic dying to epidemic persistence.
3.3. Sensitivity Analysis of the Reproductive Number
We now perform the sensitivity analysis of the reproductive number following Arriola and Hyman [13]:
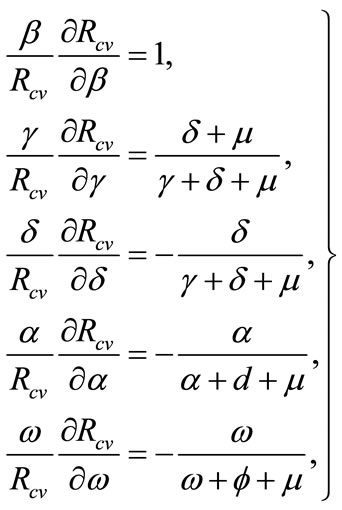 (3)
(3)
Analytical results on (3), demonstrates that parameters; b, g are positively correlated to the reproductive number, while parameters a, d and w are inversely correlated to the reproductive number. According to results on equation (2) it is worth noting that the reproductive number is most sensitive to b, since an increase in b, by any magnitude will result in an increase on the reproductive number by the same magnitude. The effectiveness of intervention strategies (medical or behavioural) is evaluated by the ability of the program to reduce the magnitude of the reproductive number. Ideally, one would like to bring the system to the point where the reproductive number is less than unity. In the absence of vaccination and culling the reproductive number denoted by,  is given by
is given by
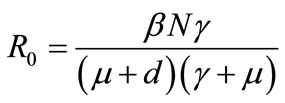 . (4)
. (4)
Using results on equation (4), 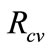 can be rewritten a
can be rewritten a
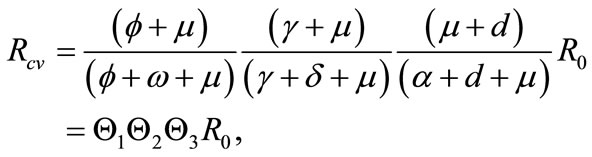 (5)
(5)
where
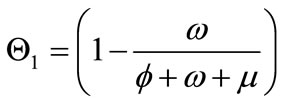 ,
,
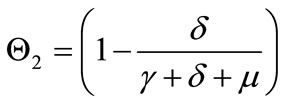 ,
,
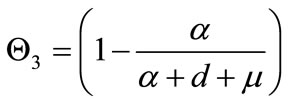 .
.
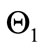 ,
, 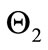 , and
, and  captures the impact of vaccination, culling of latently infected animals and culling of infectious animals, respectively. Since,
captures the impact of vaccination, culling of latently infected animals and culling of infectious animals, respectively. Since, 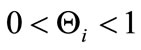 , for
, for 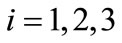 it follows that
it follows that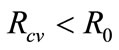 . This shows that the aforementioned FMD intervention strategies have a positive impact on controlling FMD in the community. Furthermore it is worth noting that
. This shows that the aforementioned FMD intervention strategies have a positive impact on controlling FMD in the community. Furthermore it is worth noting that  for
for 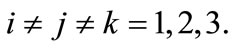 Thus, the combined use of the three intervention strategies have the most positive impact on controlling FMD that the use of either of the two methods or only one intervention strategy. Using Theorem 2 in [12], the following result is established.
Thus, the combined use of the three intervention strategies have the most positive impact on controlling FMD that the use of either of the two methods or only one intervention strategy. Using Theorem 2 in [12], the following result is established.
Theorem 1. The disease-free equilibrium of system (1) is locally-asymptotically stable (LAS) if, 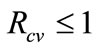 , and unstable otherwise.
, and unstable otherwise.
3.4. Global Stability of the Disease-Free Equilibrium
We now use the Comparison Theorem [13,14] to examine the globally stability of the disease-free. We claim the following results.
Theorem 2. The disease-free equilibrium of system (1) is globally-asymptotically stable (LAS) if, 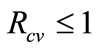 and unstable otherwise.
and unstable otherwise.
Proof: Note that the equations of the infected components in system (1) can be written as
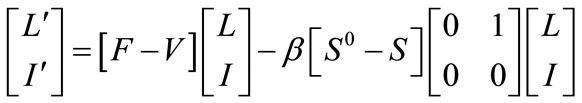
where, 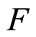 and
and 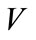 are as defined earlier in (on the computation of the reproductive number). Since,
are as defined earlier in (on the computation of the reproductive number). Since, 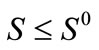 (for all
(for all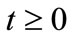 ) in
) in  if follows that
if follows that
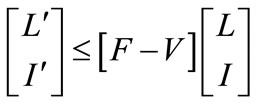 (5)
(5)
Using the fact the eigenvalues of the matrix 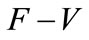 all have negative real parts, it follows that the linearized differential inequality system (5) is stable whenever
all have negative real parts, it follows that the linearized differential inequality system (5) is stable whenever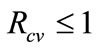 . Consequently,
. Consequently, 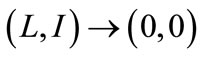 as
as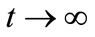 . Thus, by Comparison Theorem [13]
. Thus, by Comparison Theorem [13]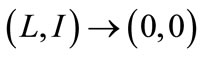 , as
, as 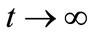 and, evaluating system (1) at
and, evaluating system (1) at 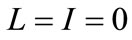 gives,
gives, 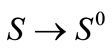 for
for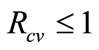 . Hence, the disease-free equilibrium is globally-asymptotically stable for
. Hence, the disease-free equilibrium is globally-asymptotically stable for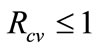 .
.
3.5. Endemic Equilibrium
System (1) has an endemic equilibrium state given by
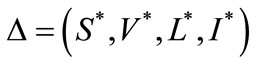 With
With
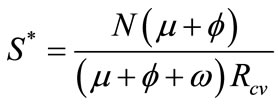 ,
,
 ,
,
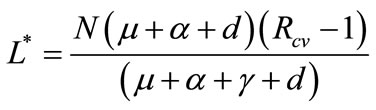 ,
,
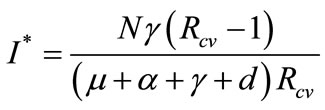 .
.
Thus, System (1) has an endemic equilibrium state which makes biological sense whenever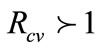 . This leads to Theorem 3 below.
. This leads to Theorem 3 below.
Theorem 3. The endemic equilibrium ( ) of system (1) exists whenever
) of system (1) exists whenever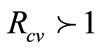 .
.
4. Numerical Simulations
In order to illustrate the results of the foregoing analysis in this study, numerical simulations of system (1) have been carried out, using a set of plausible parameter values given in the Table 1 below.
5. Concluding Remarks
Foot-and-mouth disease (FMD) is a highly infectious animal disease that affects cloven hoofed animals (including cattle, sheep and pigs) and causes acute clinical
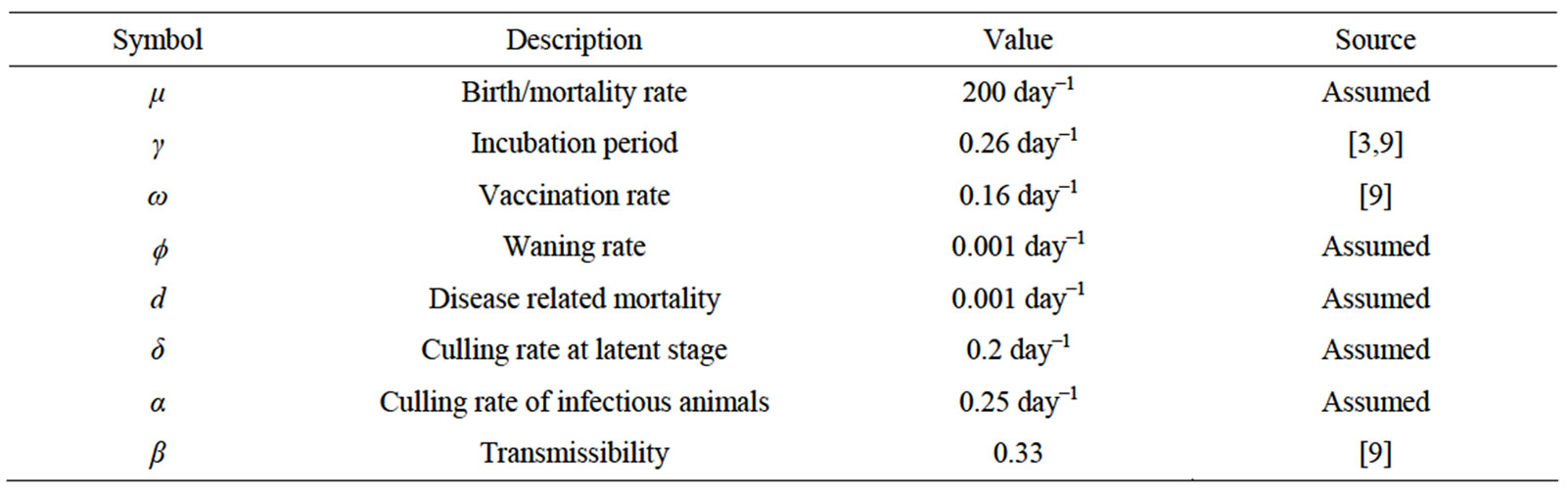
Table 1. Model parameters and their interpretations.
 (a)
(a)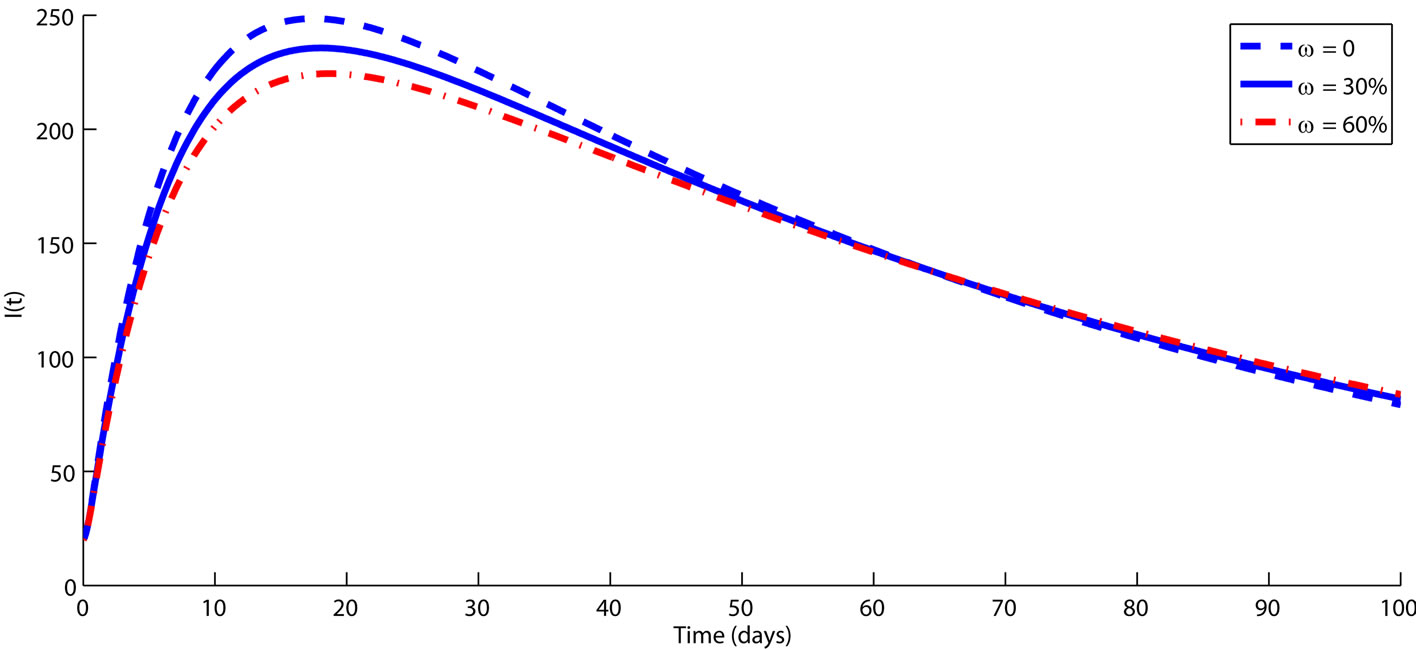 (b)
(b)
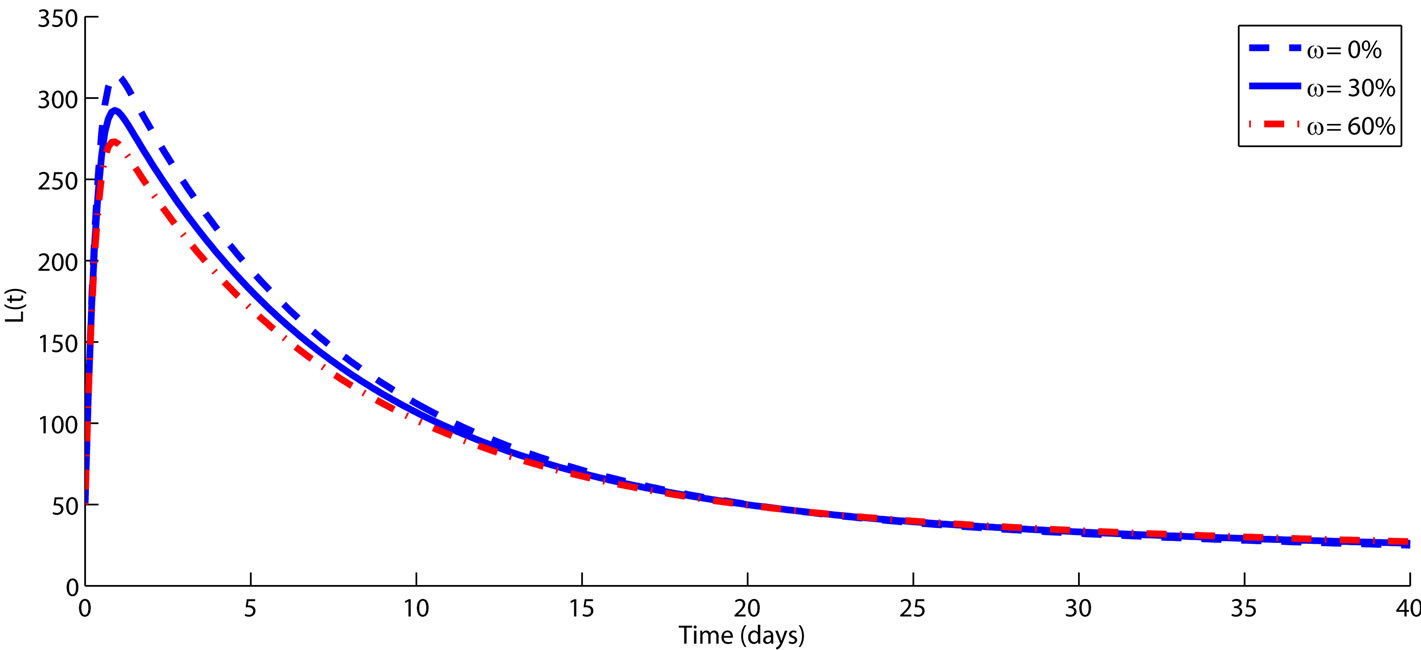
Figure 2. The impact of vaccination on controlling FMD transmission dynamics among animals is demonstrated over a period of time (in days). The rest of the parameters are fixed on their baseline values from Table 1. Simulations clearly shows that when vaccination rate increase, the size of infected subpopulation (L and I) decreases significantly, which leads to a decrease due to the reduction in the risk of exposure to FMD. An intervention which ensures higher rate of animal vaccination may have a positive impact on controlling FMD.
signs such as vesicular lesions in the foot and mouth, lameness, fever and pain; in more severe cases it can lead to death of young livestock. In areas where FMD is endemic, it is considered to be the main threat to animal health and economic development, while an outbreak of FMD in 2001 in the United Kingdom, a disease-free country, resulted in 6.5 million animals being slaughtered and losses of about 6 billion pounds. Persistence of FMD virus (FMDV) occurs in previously infected but apparently recovered animals, in the pharyngeal area, specifically in the dorsal soft palate [1]. In this paper a simple deterministic model to explore the impact of vaccination and culling on controlling foot and mouth epidemic among animals. A dimensionless quantity known as the reproductive number, 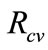 (which measures the average number of new secondary FMD cases generated by a single FMD infective introduced in a population where the aforementioned control measures are in place, that is
(which measures the average number of new secondary FMD cases generated by a single FMD infective introduced in a population where the aforementioned control measures are in place, that is 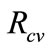 measures the power of a disease to invade a population under conditions that facilitate maximal growth. The higher the reproductive number, the faster the infecting agent runs out of susceptible individuals) has been computed and qualitatively used to explore the condition for FMD control. Comparison Theorem ap-
measures the power of a disease to invade a population under conditions that facilitate maximal growth. The higher the reproductive number, the faster the infecting agent runs out of susceptible individuals) has been computed and qualitatively used to explore the condition for FMD control. Comparison Theorem ap-
 (a)
(a)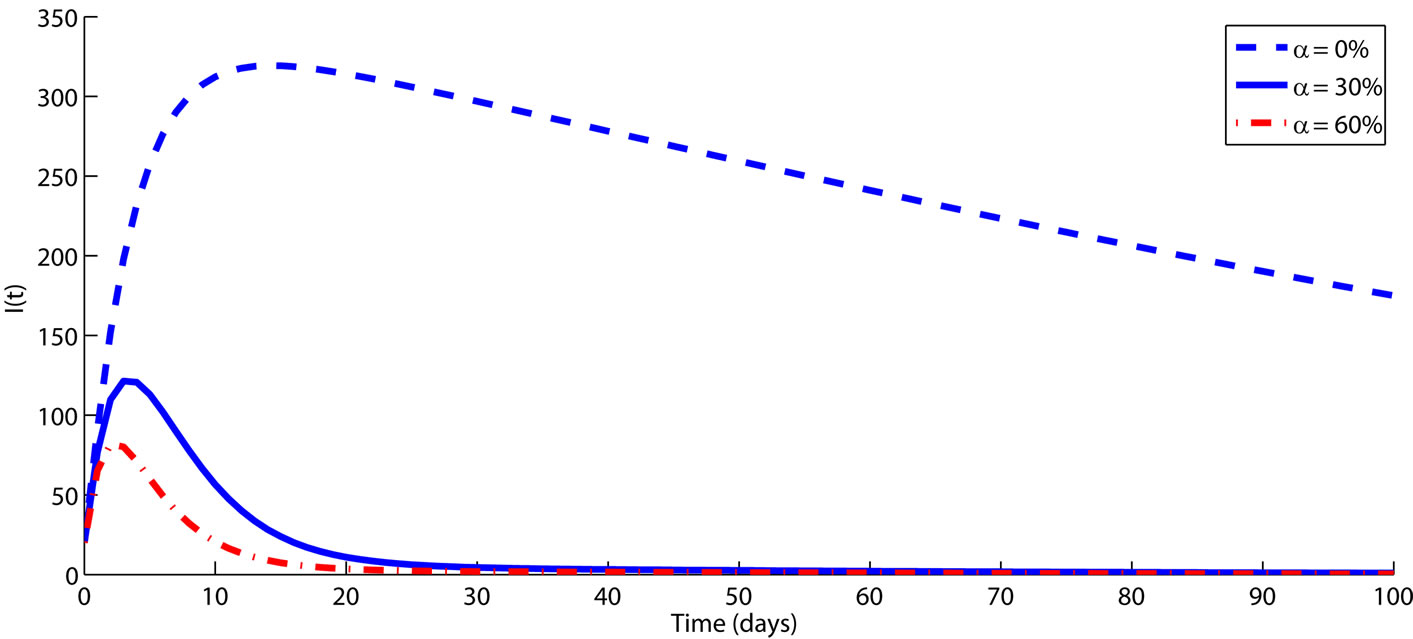 (b)
(b)
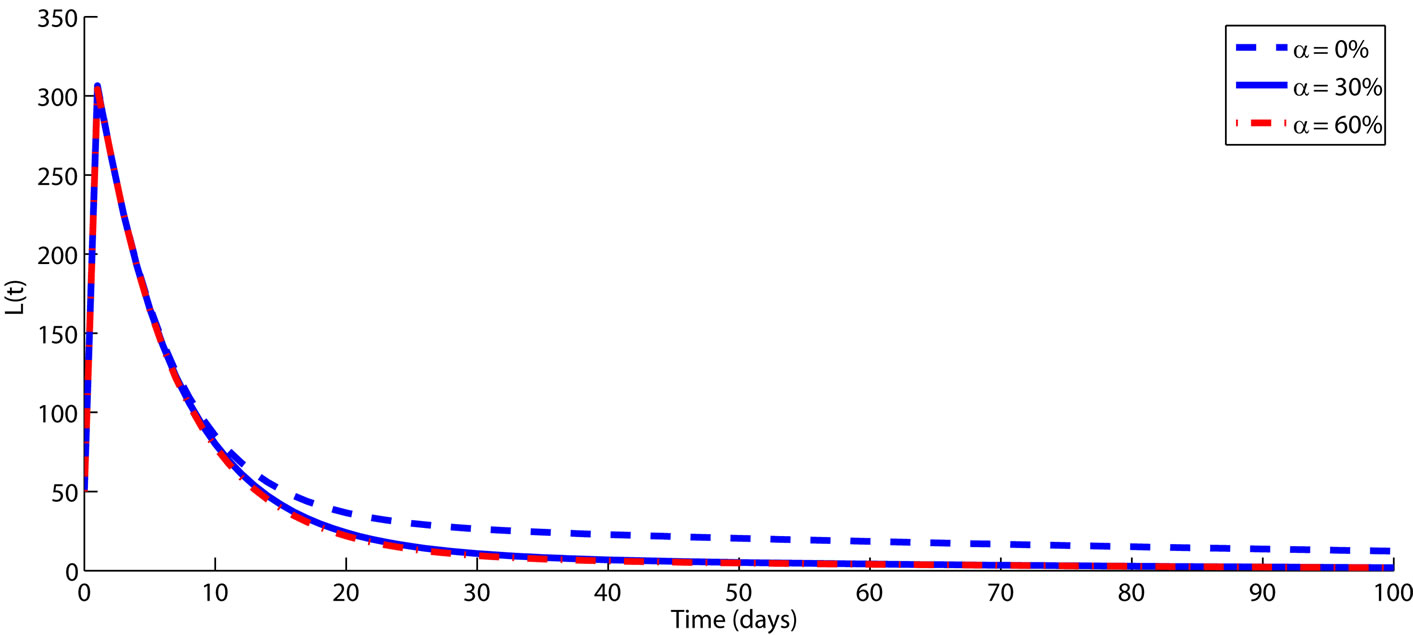
Figure 3. The impact of culling infected animals as an intervention strategy to control FMD transmission among animals is demonstrated over a period of time (in days). The rest of the parameters are fixed on their baseline values from Table 1. Numerical results demonstrate that culling has a positive impact on controlling FMD among animals. It is worth noting that, Figure 3 only demonstrates the role of culling infectious animal, in order to avoid repetition we did not present the numerical results for culling animals at latent since the trend is similar.
proach has been used to show that the model has globally-asymptotically stable disease-free (DFE) whenever the reproductive number is less than unity (epidemic dies out). Robust analysis of the model has shown that the model has an endemic state which exists whenever the reproductive number is greater than unity.
Qualitative analysis of the reproductive number on equation (5) highlights that each of the intervention strategies considered in this paper may be essential on controlling FMD, and this supported by simulation results on Figure 2 (demonstrates that animal vaccination may have a positive impact on controlling FMD) and Figure 3 (demonstrates that culling infectious animals may be an important intervention strategy to control FMD). It is worth noting that the study also highlights that detection and culling of latently infected animals is crucial on FMD control. Over and above, the study demonstrates that FMD may be controlled effectively through implementation of all the aforementioned intervention strategies.
6. Acknowledgements
Authors wish to thank the reviewers and the editor for their valuable comments and suggestions that greatly improved the presentation of this paper.
REFERENCES
- S. Alexandersen, Z. Zhang, A. I. Donaldson and A. J. Garland, “The Pathogenesis and Diagnosis of Foot-andMouth Disease,” Journal of Comparative Pathology, Vol. 129, No. 1, 2003, pp. 1-36. doi:10.1016/S0021-9975(03)00041-0
- R. P. Kitching, A. M. Hutber and M. V. Thrusfield, “A Review of Foot-and-Mouth Disease with Special Consideration for the Clinical and Epidemiological Factors Relevant to Predictive Modelling of the Disease,” The Veterinary Journal, Vol. 169, No. 2, 2005, pp. 197-209. doi:10.1016/j.tvjl.2004.06.001
- USDA/NJDA Foot and Mouth Disease Alert Animal Health Alert, “Foot and Mouth Disease,” March 2001. http://www.state.nj.us/agriculture/footmouth.htm
- R. M. Anderson and R. M. May, “Infectious Diseases of Humans, Dynamics and Control,” Oxford University Press, New York, 1991.
- R. M. Armstrong and E. S. Mathew, “Predicting Herd Protection against Foot-and-Mouth Disease by Testing Individual and Bulk Milk Samples,” Journal of Virological Methods, Vol. 97, No. 1-2, 2001, pp. 87-99. doi:10.1016/S0166-0934(01)00342-1
- S. Alexandersen, M. B. Oleksiewicz and A. I. Donaldson, “The Early Pathogenesis of Foot-and-Mouth Disease in Pigs Infected by Contact: A Quantitative Time-Course Study Using TaqMan RT-PCR,” Journal of General Virology, Vol. 82, 2001, pp. 747-755.
- M. J. Tildesley and M. J. Keeling, “Modelling Foot-andMouth Disease: A Comparison between the UK and Denmark,” Preventive Veterinary Medicine, Vol. 85, No. 1-2, 2008, pp. 107-124. doi:10.1016/j.prevetmed.2008.01.008
- G. Chowell1, A. L. Rivas, N. W. Hengartner, J. M. Hyman and C. Castillo-Chavez, “The Role of Spatial Mixing in the Spread of Foot-and-Mouth Disease,” Preventive Veterinary Medicine, Vol. 73, 2006, pp. 297-314.
- D. Schley, J. Ward and Z. Zhang, “Modelling Foot-andMouth Disease Virus Dynamics in Oral Epithelium to Help Identify the Determinants of Lysis,” Bulletin of Mathematical Biology, Vol. 73, No. 7, 2010, pp. 1503-1528.
- M. J. Keeling, M. E. J. Woolhouse, R. M. May, G. Davies and B. T. Grenfell, “Modelling Vaccination Strategies against Foot-and-Mouth Disease,” Nature, Vol. 421, No. 6919, 2003, pp. 136-142. doi:10.1038/nature01343
- P. Van den Driessche and J. Watmough, “Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission,” Mathematical Biosciences, Vol. 180, 2002 pp. 29-48. doi:10.1016/S0025-5564(02)00108-6
- S. Mushayabasa, J. M. Tchuenche, C. P. Bhunu, E. Gwasira-Ngarakana, “Modeling Gonorrhea and HIV CoInteraction,” BioSystems, Vol. 103, No. 1, 2011, pp. 27- 37. doi:10.1016/j.biosystems.2010.09.008
- L. Arriola and J. Hyman, “Lecture Notes, Forward and Adjoint Sensitivity Analysis: With Applications in Dynamical Systems, Linear Algebra and Optimisation,” Mathematical and Theoretical Biology Institute, 2005.
- V. Lakshmikantham, S. Leela and A. A. Martynyuk, “Stability Analysis of Nonlinear Systems,” Marcel Dekker, New York, 1989.

