World Journal of Mechanics
Vol.2 No.1(2012), Article ID:17684,7 pages DOI:10.4236/wjm.2012.21005
Unsteady Boundary Layer Flow past a Stretching Plate and Heat Transfer with Variable Thermal Conductivity
1Depatment of Applied Sciences, NSIT, New Delhi, India
2Department of Mathematics, Jamia Millia Islamia, New Delhi, India
3Department of Mathematics & Statistics, Faculty of Science, University of Maiduguri, Maiduguri, Nigeria
Email: mamtansit@yahoo.co.in
Received November 10, 2011; revised December 15, 2011; accepted December 25, 2011
Keywords: Unsteady Boundary Layer Flow; Skin Friction Energy Equation; Nusselt Number
ABSTRACT
An unsteady boundary layer flow of viscous incompressible fluid over a stretching plate has been considered to solve heat flow problem with variable thermal conductivity. First, using similarity transformation, the velocity components have been obtained, and then the heat flow problem has been attempted in the following two ways: 1) prescribed stretching surface temperature (PST), and 2) prescribed stretching surface heat flux (PHF) Flow and temperature fields have been analyzed through graphs. The expressions for skin friction and coefficient of convective heat transfer Nusselt number in PST and PHF cases have been derived.
1. Introduction
Due to number of applications in industrial manufacturing process, the problem of boundary layer flow past a stretching plate has attracted considerable attention of researchers during the past few decades. Examples of such technological process are hot rolling, wire drawing, glass-fiber and paper production. In the process of drawing artificial fibers the polymer solution emerges from orifice with a speed which increases from almost zero at the orifice up to a plateau value at which remains constant. The moving fiber, which is of great technical importance, is governed by the rate at which the fiber is cooled and this, in turn affects the final properties of the yarn. A number of works are presently available that follow the pioneering classical work of Sakiadis [1], F. K. Tsou, E. M. Sparrow, R. J. Goldstein [2] and Crane [3]. Table 1 lists some relevant works that pertain to cooling liquids, i.e., heat transfer for stretching surface.
There are liquid metals whose thermal conductivity varies with temperature in an approximately linear manner in the range from 0˚F to 400˚F. In 1996, T. C. Chiam [21] considered heat transfer problem with variable thermal conductivity in stagnation-point flow towards stretching sheet. Naseem Ahmad and Kavita Marwah [22] also studied boundary layer flow of Walters Liquid B Model with heat transfer for linear stretching plate with variable conductivity numerically. In 2010, Ahmad and Mishra investigated unsteady boundary layer flow and heat transfer over a stretching sheet [23].
In almost all the problems of stretching sheet with heat transfer where closed form solution is obtained, the thermal conductivity of liquid has been taken constant. The present paper is the extension of the work done by N. Ahmad and M. Mishra [23] assuming that the thermal conductivity varies in linear manner with temperature. The temperature field has two parts: one mean temperature, other is due to variable thermal conductivity. Both the parts mean temperature and temperature due to variable thermal conductivity have been analyzed thoroughly for some new recommendations.
2. Mathematical Formation and Solution
The problem considered here is the unsteady boundary layer flow due to a stretching flat plate in a quiescent viscous incompressible fluid. The flow is two dimensional where x-axis is along the plane of moving plate and y-axis is normal to it, respectively. We assume that the surface is moving continuously with the velocity
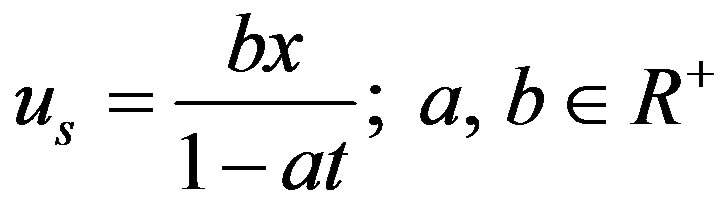 and t < 1/a in the positive x-direction. Under these assumptions, the boundary layer flow along moving plate is governed by the equations
and t < 1/a in the positive x-direction. Under these assumptions, the boundary layer flow along moving plate is governed by the equations
 (2.1)
(2.1)
 (2.2)
(2.2)
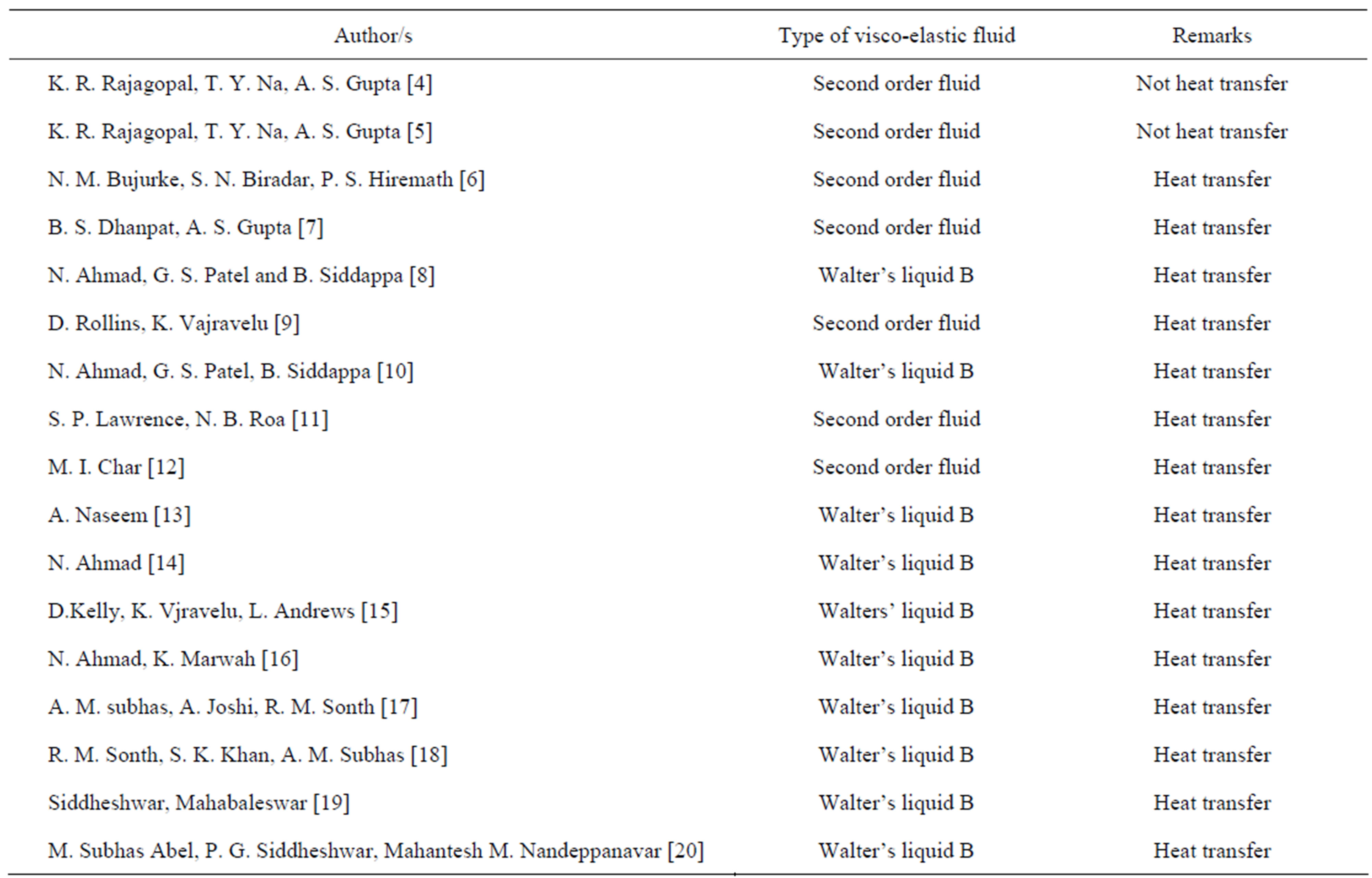
Table 1. Some relevant works that pertain to cooling liquids.
where u, the horizontal velocity component; v, the vertical velocity component;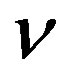 , the kinematic viscosity The relevant boundary conditions are:
, the kinematic viscosity The relevant boundary conditions are:
y = 0, u = us, v = 0 y → ¥, u = 0 Introducing the dimensionless variables
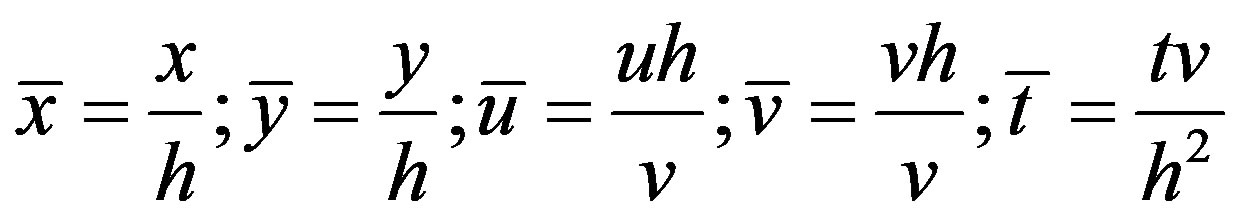
the Equations (2.1) and (2.2) reduce to
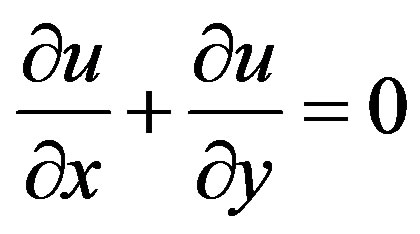 (2.3)
(2.3)
 (2.4)
(2.4)
with boundary conditions
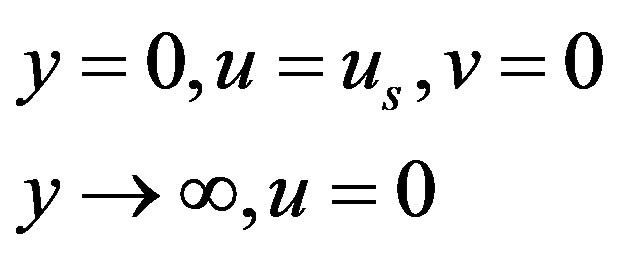 (2.5)
(2.5)
where bar has been dropped for convenience.
Setting the similarity solution of the form
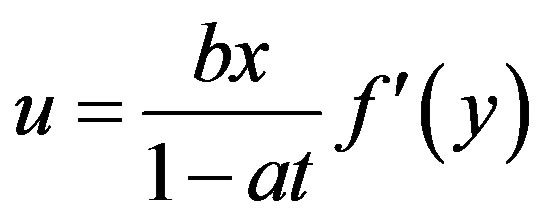 and using continuity equation, we have
and using continuity equation, we have
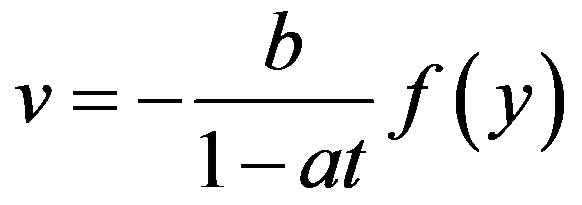 (2.6)
(2.6)
Putting u and v in the Equation (2.4), we have
 (2.7)
(2.7)
and the relevant boundary conditions become
 (2.8)
(2.8)
 (2.9)
(2.9)
Boundary conditions suggest that the velocity function f may be of the form 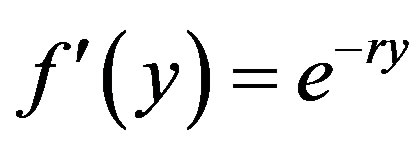
where r is unknown to be determined. Thus
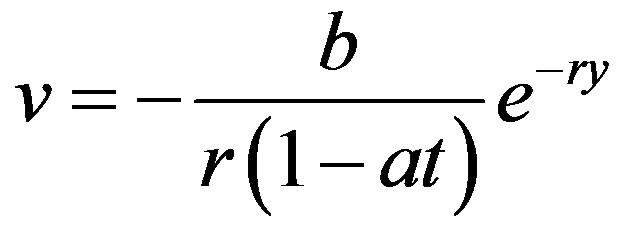
and the Equation (2.7) gives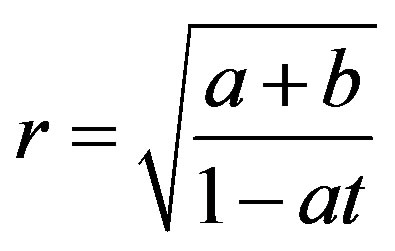 . Therefore, we have the velocity components as follows:
. Therefore, we have the velocity components as follows:
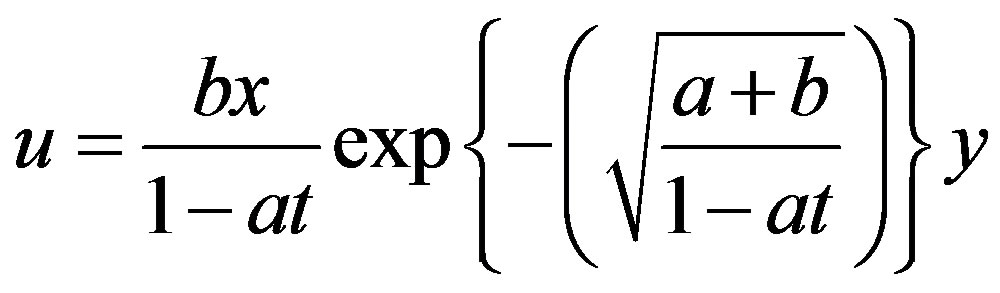
and
 (2.10)
(2.10)
3. Skin Friction
The wall shear stress at the stretching plate is given by


Thus, the skin friction is
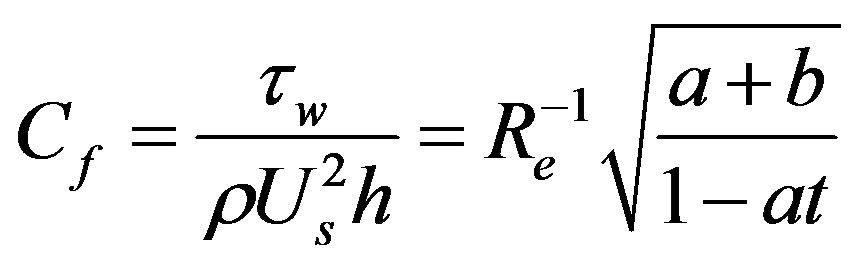 (3.1)
(3.1)
4. Heat Transfer Problem
In absence of viscous dissipation and heat generation, the energy equation for two dimensional heat flow is given b
 (4.1)
(4.1)
subject to boundary conditions
 (4.2)
(4.2)
where TP is plate temperature, T¥ is temperature of surrounding fluid, CP is specific heat at constant pressure and k is thermal conductivity.
4.1. Case A: Prescribed Power Law Surface Temperature (PST)
Let the surface temperature be of the form
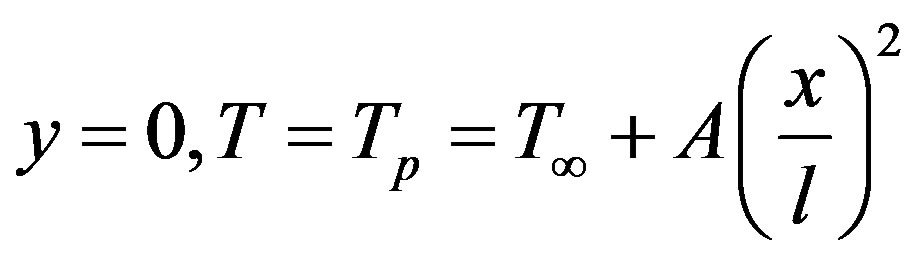
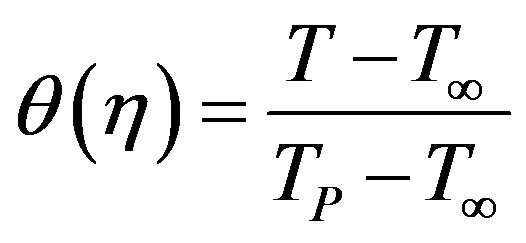
while the temperature outside the dynamic region be . Now, we define the dimensionless temperature by
. Now, we define the dimensionless temperature by 
For liquid metals, it has been found that the thermal conductivity varies with temperature in an approximately linear manner in the range from 0˚F to 400˚F. Thereforewe assume k as 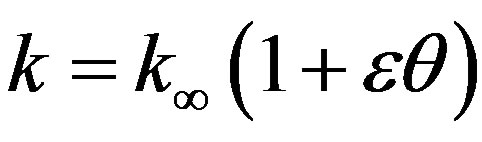 where
where . Nowsubstituting u and v in the Equation (4.1) and changing the independent variable y to
. Nowsubstituting u and v in the Equation (4.1) and changing the independent variable y to , we have
, we have
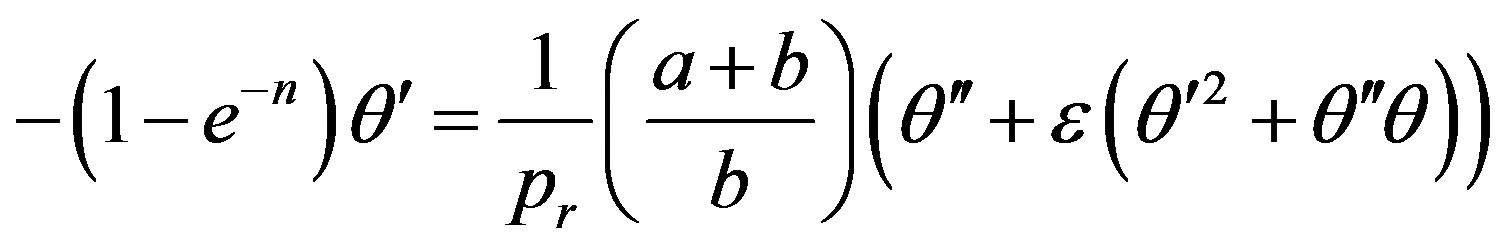 (4.3)
(4.3)
with boundary conditions
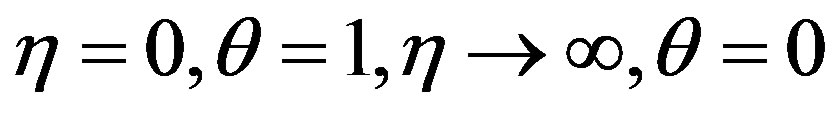 (4.4)
(4.4)
The Equation (4.3) can be rewritten as
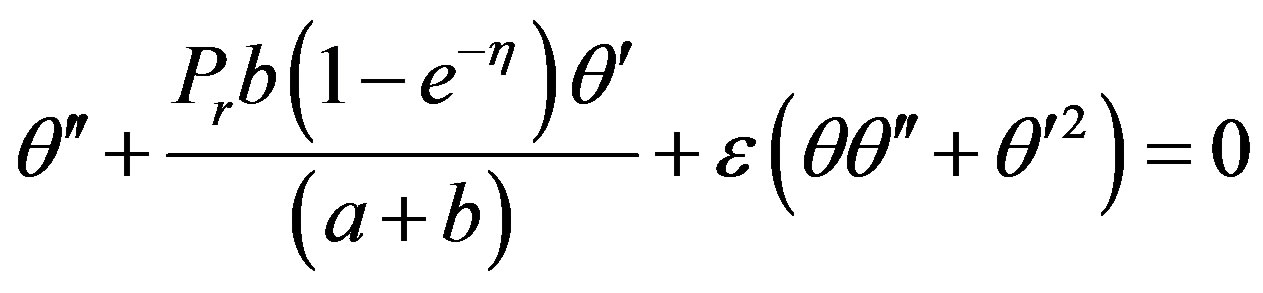 (4.5)
(4.5)
From Equation (4.5), we note that the heat transfer takes place in two parts according to  and
and . If
. If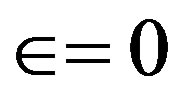 , then we have the main heat transfer due to constant thermal conductivity i.e.
, then we have the main heat transfer due to constant thermal conductivity i.e.
 (4.6)
(4.6)
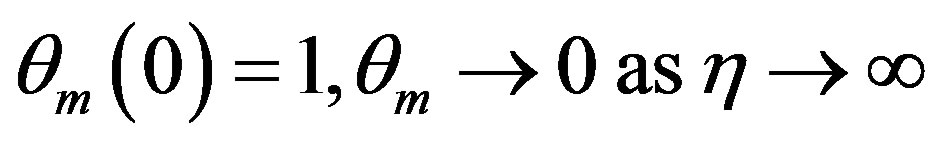 (4.7)
(4.7)
and if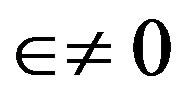 , then we get the first correction equation to main heat transfer as
, then we get the first correction equation to main heat transfer as
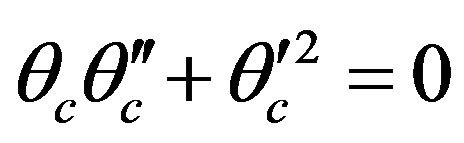 (4.8)
(4.8)
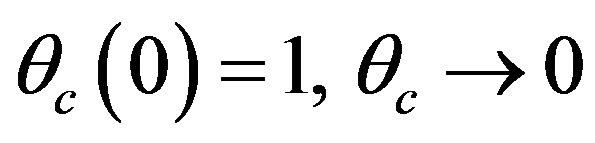 , as
, as
 (4.9)
(4.9)
The solution of the Equation (4.6) is

where
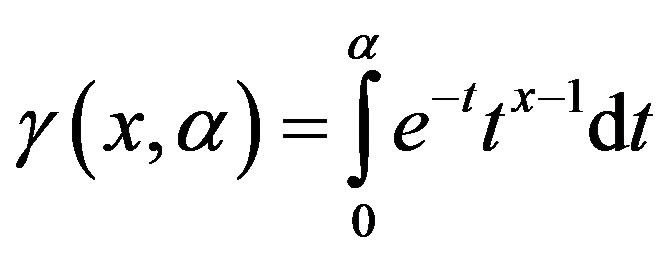
is incomplete gamma function Equation (4.8) is a non linear differential equation of order two. Let the solution of this equation be of the form:
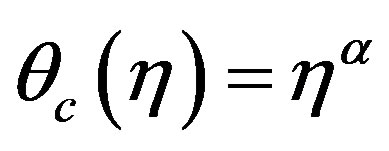
Putting this solution in Equation (4.8) we have
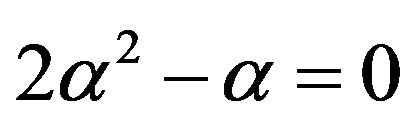 (4.10)
(4.10)
The roots of this equation are 0 and 1/2. Therefore
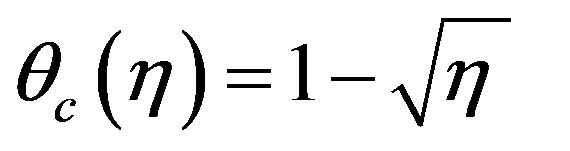 (4.11)
(4.11)
The solution (4.11) of the Equation (4.8) does not satisfy the condition 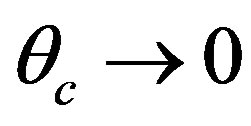 as
as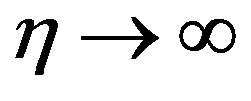 . This condition is met only for
. This condition is met only for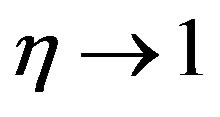 . Therefore, the heat transfer in case
. Therefore, the heat transfer in case  takes place within the dynamic region
takes place within the dynamic region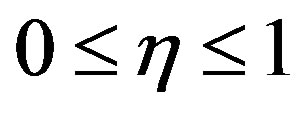 .
.
4.2. Nusselt Number
The coefficient of convective heat transfer is given by
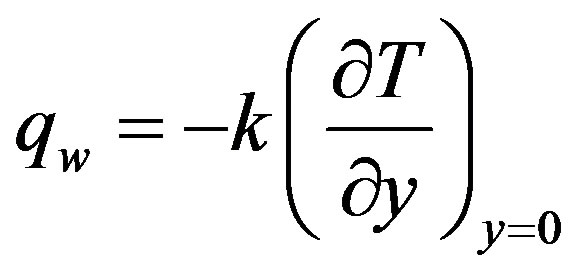 (*)
(*)
Therefore the Nusselt number is (see Table 2):
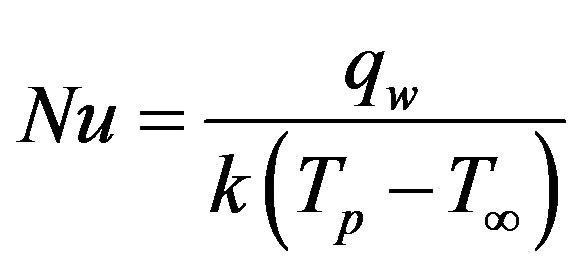
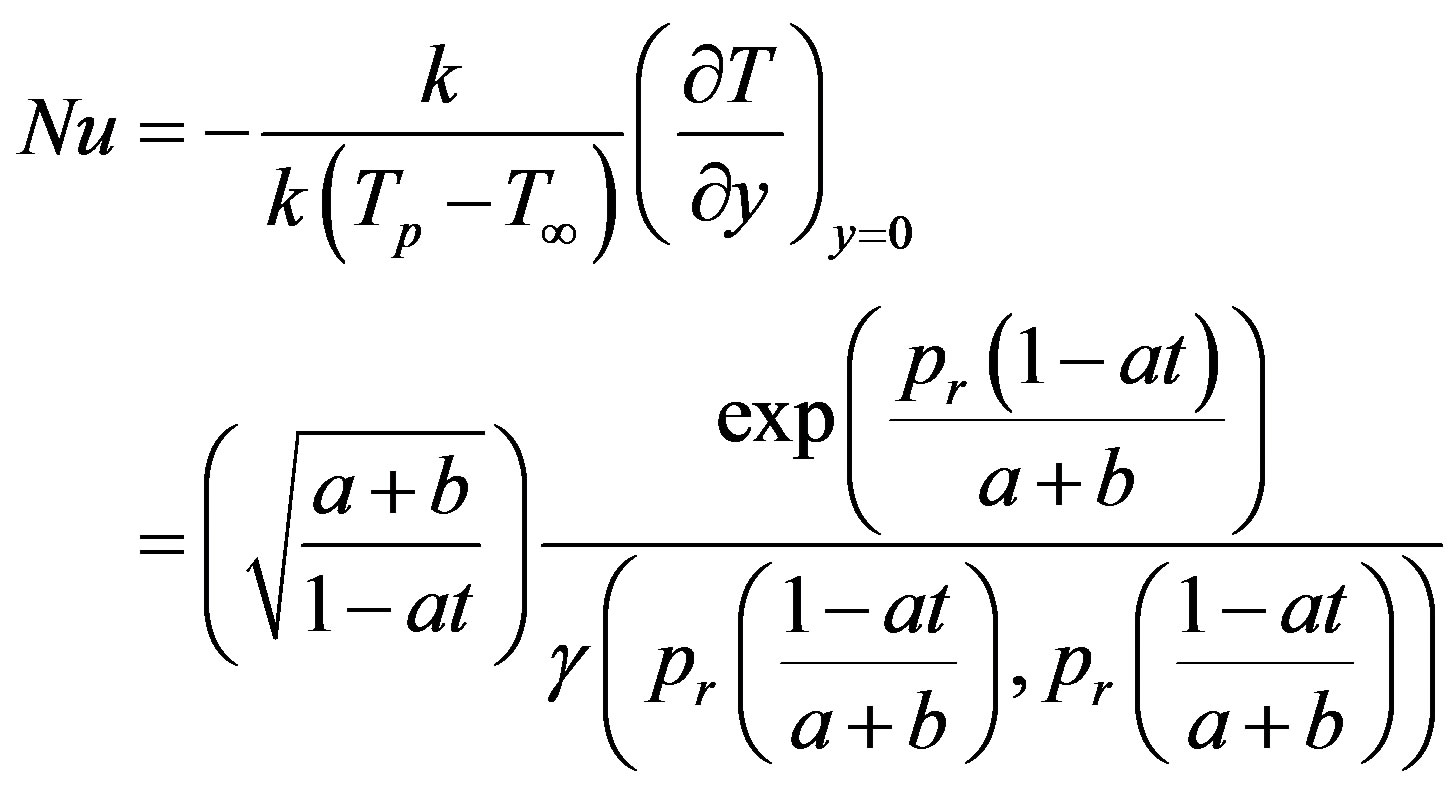 (4.12)
(4.12)
4.3. Case B: Prescribed Power Law Surface Heat Flux (PHF Case)
The power law heat flux on the surface of stretching plate is considered to be a quadratic power of x in the form
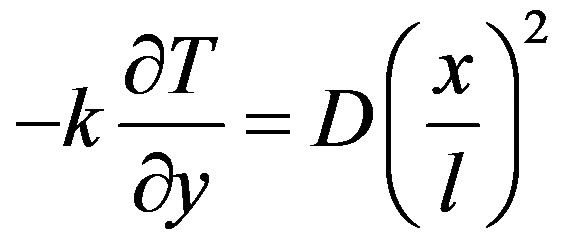 at
at
 (4.13)
(4.13)
 , as
, as
 (4.14)
(4.14)
where D is a constant, k is the thermal conductivity. Now we define dimensionless temperature 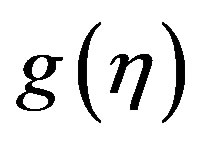 by
by
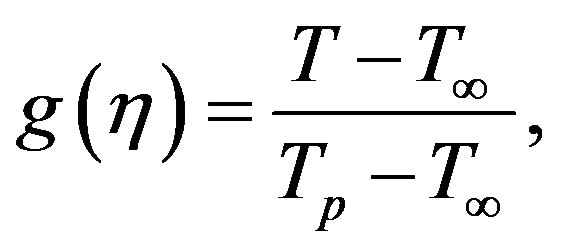 (4.15)
(4.15)
where
 when
when 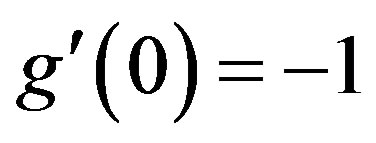
where 
Writing the Equation (4.2) in terms of , we get the following differential equation
, we get the following differential equation
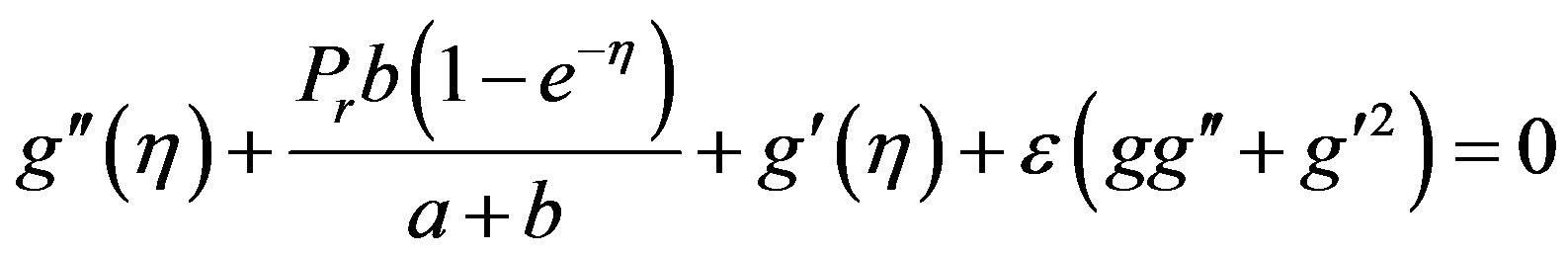 (4.16)
(4.16)
together with boundary conditions:
 (4.17)
(4.17)
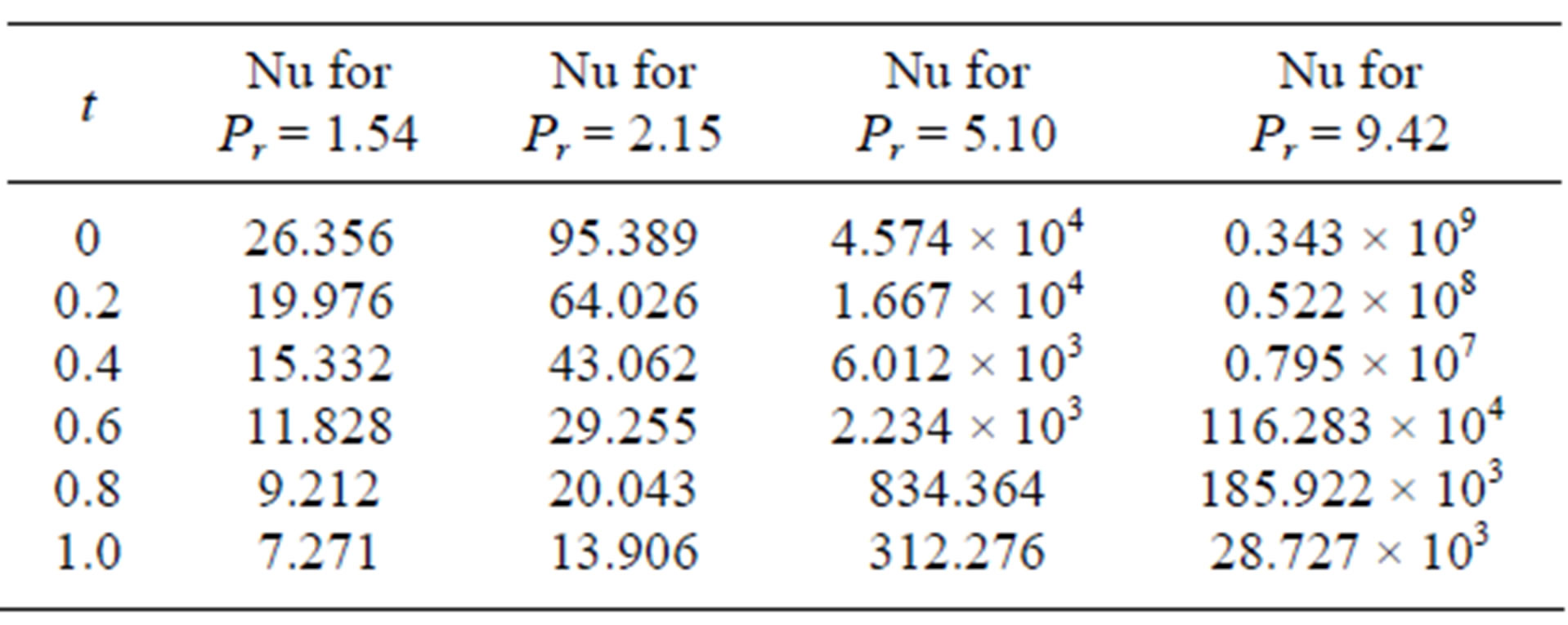
Table 2. Trend of Nusselt number.
Equating the terms independent of and the terms involving from Equation (4.16), we get the following two boundary value problems:
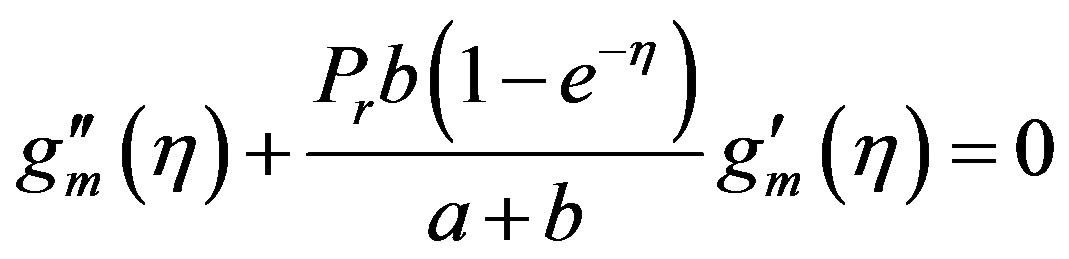 (4.18)
(4.18)
and
 (4.19)
(4.19)
where the nomenclature 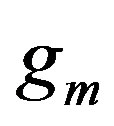 is main heat transfer when thermal conductivity is constant and
is main heat transfer when thermal conductivity is constant and 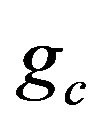 is correction to the heat flow due to variation in thermal conductivity in PHF case. The solution of the Equation (4.18) together with the boundary conditions (4.18) is
is correction to the heat flow due to variation in thermal conductivity in PHF case. The solution of the Equation (4.18) together with the boundary conditions (4.18) is
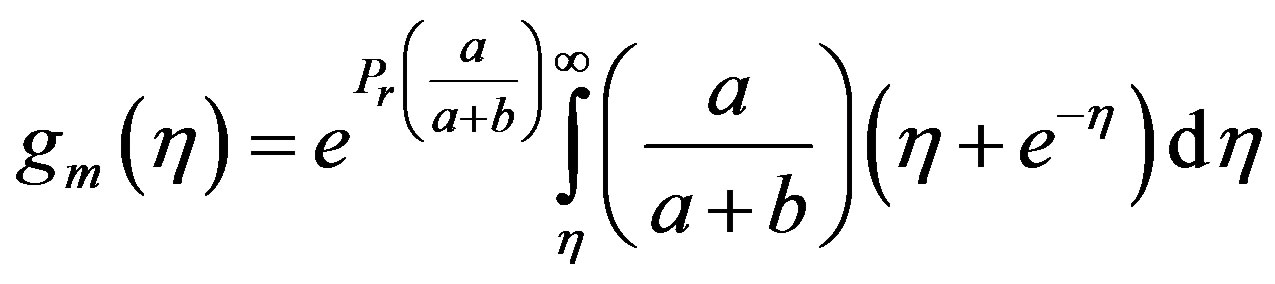 (4.20)
(4.20)
The general solution of the Equation (4.19) is
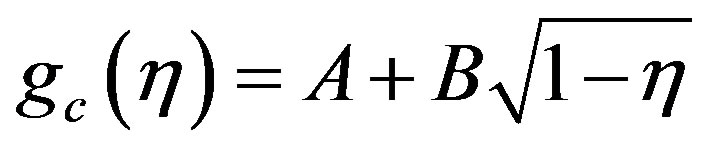 (4.21)
(4.21)
where we again observe that the dynamic region for this temperature field is . Hence, the boundary conditions (4.17) have been modified as
. Hence, the boundary conditions (4.17) have been modified as
 , and
, and 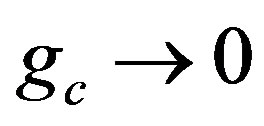 as
as
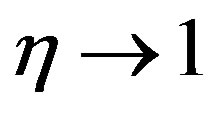 (4.22)
(4.22)
Using boundary conditions (4.22), the solution (4.19) becomes
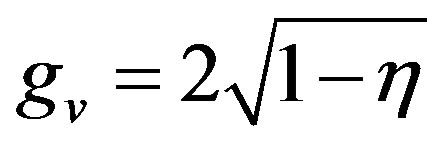
4.4. Nusselt Number (See Table 3)
Recalling (*), we have
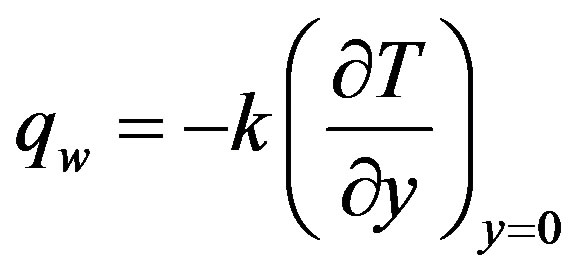

5. Discussion and Results
The problem of unsteady boundary layer flow of viscous
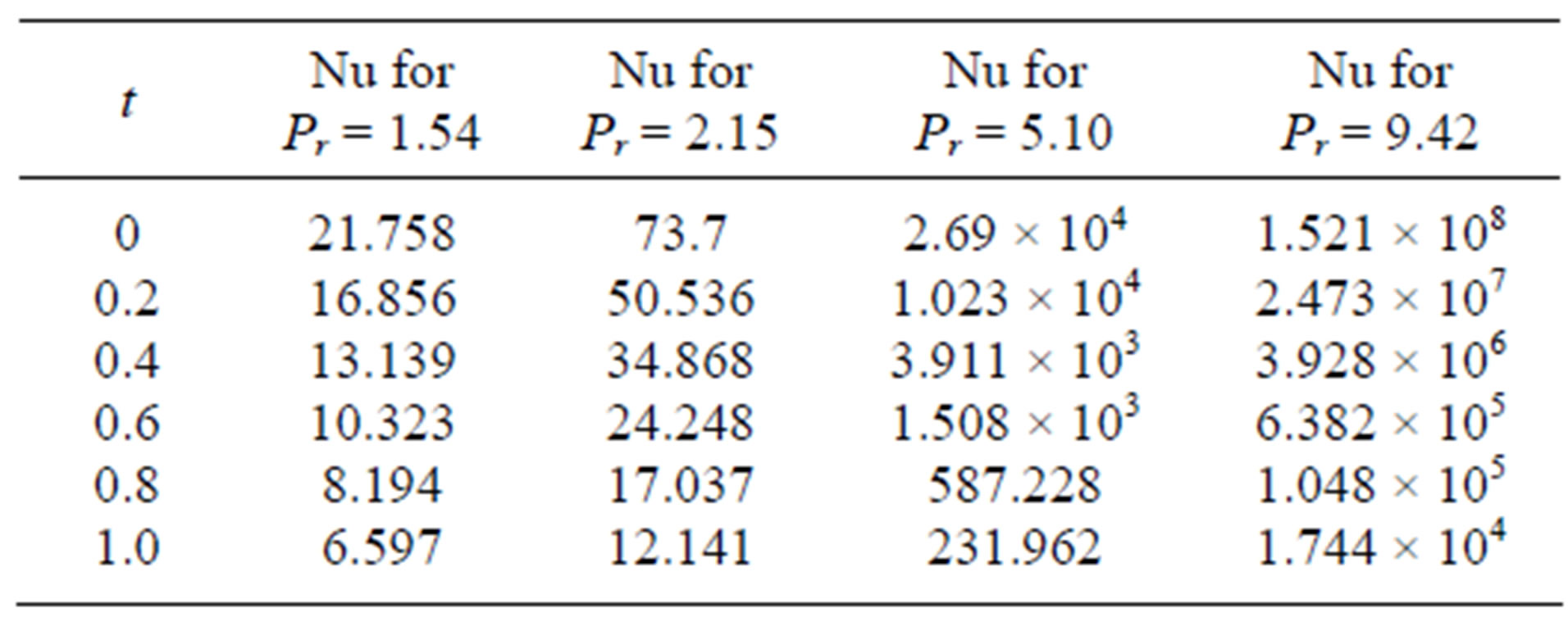
Table 3. Trend of Nusselt number.
incompressible fluid overstretching plate has been analyzed. The velocity field has been obtained by similarity transformation method. Later, the heat flow problem has been studied by considering PST and PHF cases. We summarize the results as in Figure 1 to Figure 6.
Figure 1 shows that horizontal component of velocity u. It increases as time progresses within the dynamical region [0, 1]. We also see that u is maximum in the immediate neighborhood of stretching plate and it starts decreasing as 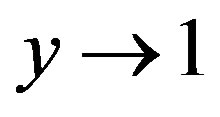 . In fully developed flow, as time goes on progressing, the velocity progresses too.
. In fully developed flow, as time goes on progressing, the velocity progresses too.
Figure 2 is a graph of v versus y for different instant of time. The vertical component v is almost constant within [0, 1] and later it starts increasing. v progresses as we march away from the slit and it also increases as time progresses.
Figure 3 is to study the variation of mean temperature field 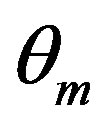 with respect to Prandtl number Pr. We see that as Pr increases,
with respect to Prandtl number Pr. We see that as Pr increases,  decreases within dynamical region
decreases within dynamical region
[0,1] in PST case. As 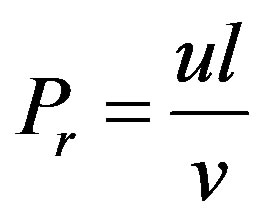 decreases, i.e. kinematic viscosity
decreases, i.e. kinematic viscosity 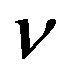 increases in turn viscosity of fluid increases. In case of more viscosity, generally flow of heat becomes slow. It is supported by our study.
increases in turn viscosity of fluid increases. In case of more viscosity, generally flow of heat becomes slow. It is supported by our study.
Figure 4 is expressing the trend of temperature field  due to variable thermal conductivity. We see that the contribution of this temperature is more near the moving plate than as we go away from the plate in PST case.
due to variable thermal conductivity. We see that the contribution of this temperature is more near the moving plate than as we go away from the plate in PST case. 

Figure 1. Velocity field at different instant of time.
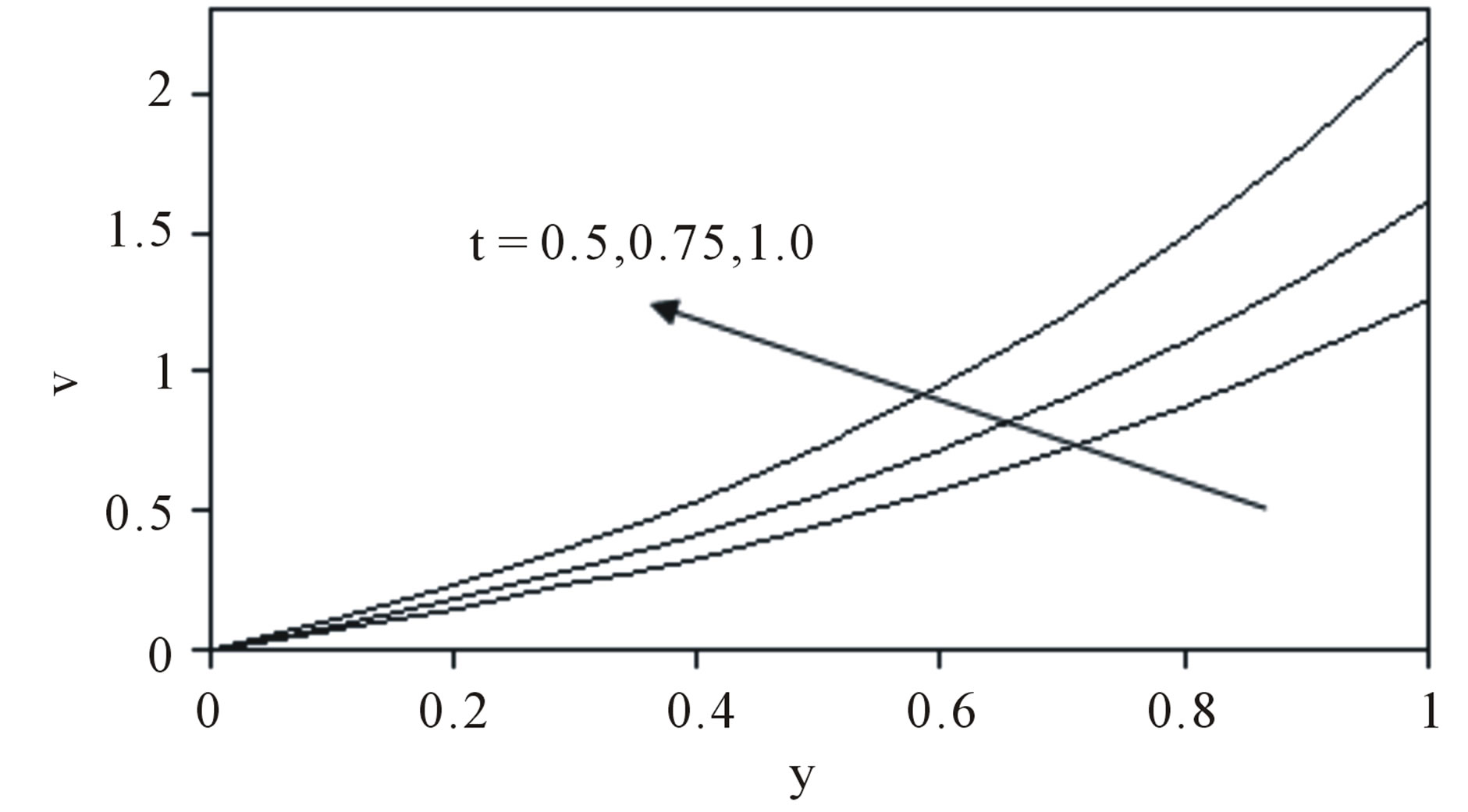
Figure 2. Velocity component v at different instant of time.

Figure 3. Mean temperature field for different values of Prandtl number Pr in PST case.
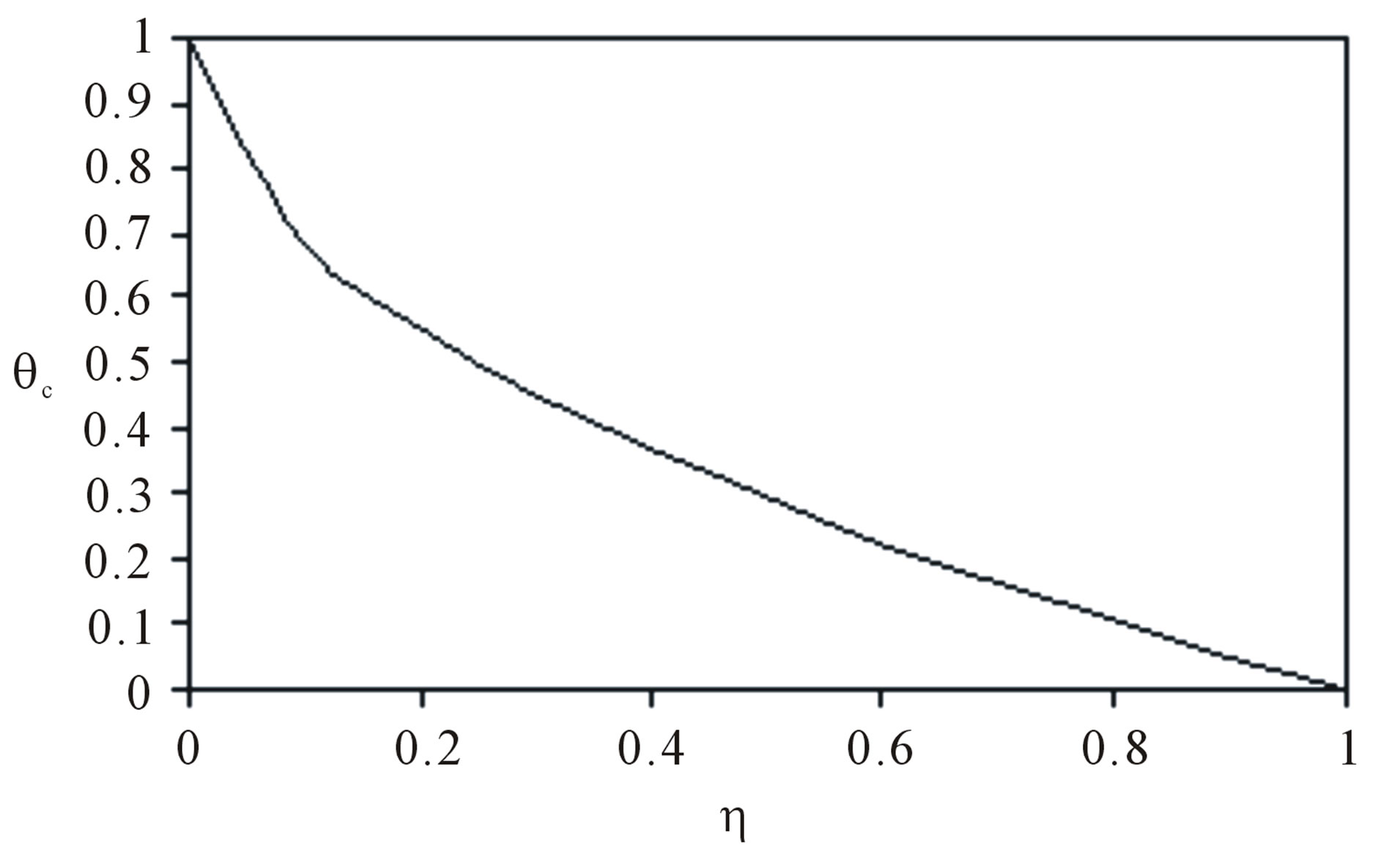
Figure 4. Temperature distribution due to variation in thermal conductivity.

Figure 5. Skin friction with respect to time t.
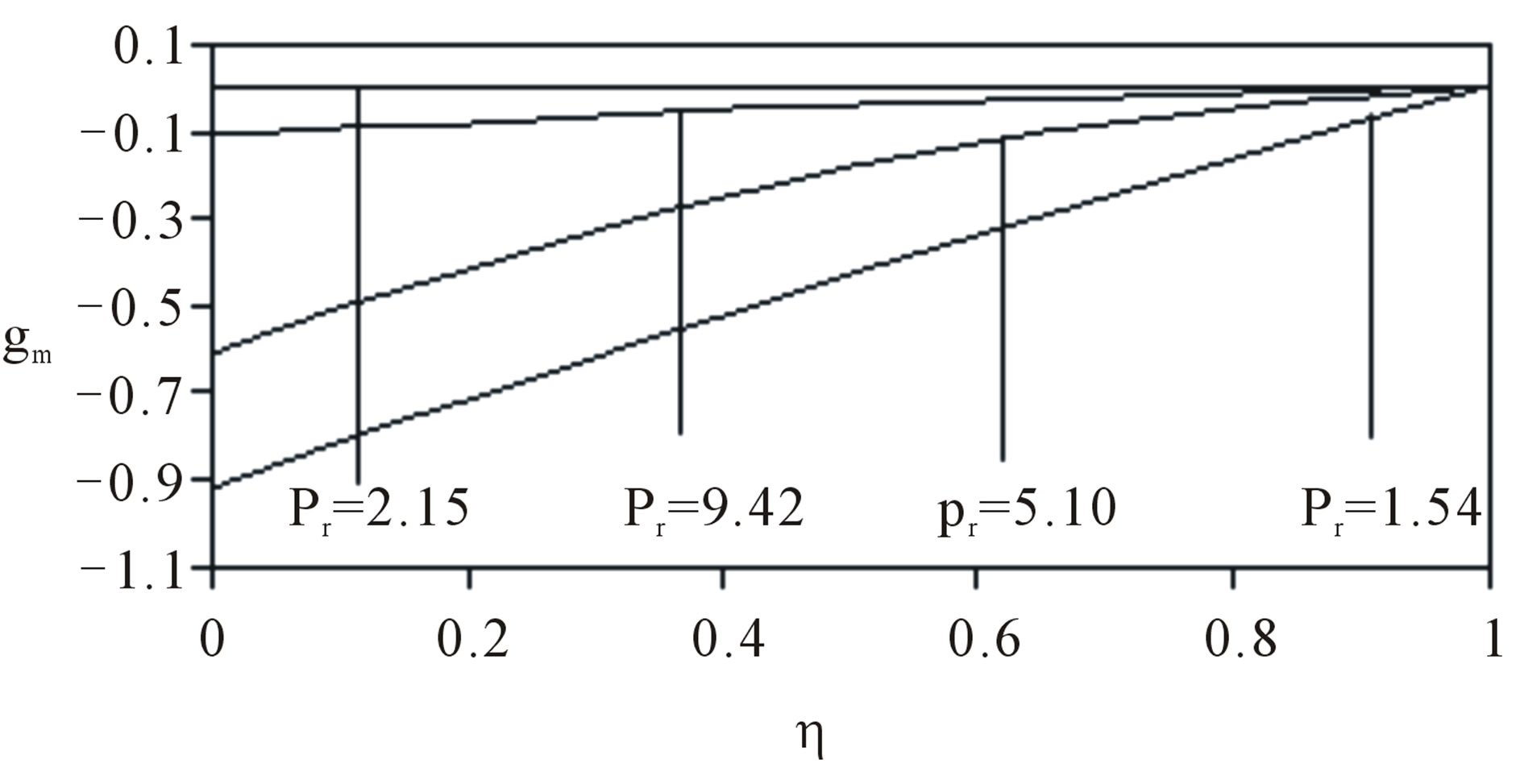
Figure 6. Temperature field for different values of Prandtl number in PHF case.
is independent of Prandtl number Pr.
Figure 5 is the graph of ReCf versus time. We see that as time progresses the skin friction increases .We mean that as time progresses the velocity increases, in turn skin friction increases.
Figure 6 is temperature field in PHF case. We see that it approaches to zero asymptotically.
We see the gm for Pr = 5.10 of liquid oxygen at 56˚K, Pr = 2.15 of para-hydrogen at 14˚K and Pr = 1.54 of liquid ammonia at 10˚C. It has been observed that gm increases absolutely as Pr increases, but for Pr = 9.42 of water at 10˚C, gm behaves in a different way due to its density.
Nusselt number in PST case is given by the Equation (4.12) where we observe referring Table 2 that it depends on Prandtl number and time t as well. From Table 1 we find that as Prandtl number increases the Nusselt number also increases but Nusselt number decreases as time increases.
Referring Table 3 for PHF case, we see the same pattern as in PST case from Table 2.
We have not got Prandtl number from the temperature field due to variation in thermal conductivity.
REFERENCES
- B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces: II Boundary Layer on a Continuous Flat Surface,” AIChE Journal, Vol. 7, No. 2, 1961, pp. 221- 225. doi:10.1002/aic.690070211
- F. K. Tsou, E. M. Sparrow and R. J. Goldstein, “Flow and Heat Transfer in the Boundary Layer on a Continuous Moving Surfaces,” International Journal of Heat and Mass Transfer, Vol. 10, No. 2, 1967, pp. 219-235. doi:10.1016/0017-9310(67)90100-7
- L. J. Crane, “Flow past a Stretching Plate,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 21, No. 4, 1970, pp. 645-647. doi:10.1007/BF01587695
- K. R. Rajagopal, T. Y. Na and A. S. Gupta, “Flow of a Visco-Elastic Fluid over a Stretching Sheet,” Rheologica Acta, Vol. 23, No. 2, 1984, pp. 213-215. doi:10.1007/BF01332078
- K. R. Rajagopal, T. Y. Na and A. S. Gupta, “A Non Similar Boundary Layer on a Stretching Sheet in a Non-Newtonian Fluid with Uniform Free Stream,” Journal of Mathematical Physics, Vol. 21, No. 2, 1987, pp. 189-200.
- N. M. Bujurke, S. N. Biradar and P. S. Hiremath, “Second Order Fluid Flow Past a Stretching Sheet with Heat Transfer,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 38, No. 4, 1987, pp. 890-892. doi:10.1007/BF00946345
- B. S. Dhanpat and A. S. Gupta, “Flow and Heat Transfer in a Visco-Elastic Fluid over a Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 24, No. 3, 1989, pp. 215-219. doi:10.1016/0020-7462(89)90040-1
- N. Ahmad, G. S. Patel and B. Siddappa, “Visco-Elastic Boundary Layer Flow past a Stretching Plate and Heat Transfer,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 41, No. 2, 1990, pp. 294-299. doi:10.1007/BF00945114
- D. Rollins and K. Vajravelu, “Heat Transfer in a Second Order Fluid over a Continuous Stretching Surface,” Acta Mechanica, Vol. 89, No. 1-4, 1991, pp. 167-178. doi:10.1007/BF01171253
- B. Siddappa and M. S. Abel, “Visco-Elastic Boundary Layer Flow past a Stretching Plate with Suction and Heat Transfer,” Rheologica Acta, Vol. 25, No. 3, 1986, pp. 319- 320.
- S. P. Lawrence and N. B. Rao, “Heat Transfer in the Flow of a Visco Elastic Fluid over a Stretching Sheet,” Acta Mechanica, Vol. 93, No. 1-4, 1992, pp. 53-61. doi:10.1007/BF01182572
- M. I. Char, “Heat and Mass Transfer in a Hydromagnetic Flow of Visco-Elastic Fluid over a Stretching Sheet,” Journal of Mathematical Analysis and Applications, Vol. 186, No. 3, 1994, pp. 674-689. doi:10.1006/jmaa.1994.1326
- A. Naseem, “On Temperature Distribution in a No-Participating Medium with Radiation Boundary Condition,” International Journal of Heat and Technology, Vol. 14, No. 1, 1995, pp. 19-28.
- N. Ahmad, “The Stretching Plate with Suction in NonParticipating Medium with Radiation Boundary Condition,” International Journal of Heat and Technology, Vol. 14, No. 1, 1996, pp. 59-66.
- D. Kelly, K. Vjravelu and L. Andrews, “Analysis of Heat Mass Transfer of a Visco-Elastic, Electrically Conducting Fluid past a Continuous Stretching Sheet,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 36, No. 6, 1999, pp. 767-784. doi:10.1016/S0362-546X(98)00128-X
- N. Ahmad and K. Marwah, “Visco Elastic Boundary Layer Flow past a Stretching Plate with Suction and Heat Transfer with Variable Conductivity,” International Journal on Multicultural Societies, Vol. 7, 2000, pp. 54-56.
- A. M. Subhas, A. Joshi and R. M. Sonth, “Heat Transfer in MHD Visco-Elastic Fluid Flow over a Stretching Surface,” Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 81, No. 10, 2001, pp. 691-698. doi:10.1002/1521-4001(200110)81:10<691::AID-ZAMM691>3.0.CO;2-Z
- R. M. Sonth, S. K. Khan, A. M. Subhas and K. V. Prasad, “Heat and Mass Transfer in a Visco-Elastic Fluid Flow over an Accelerating Surface with Heat Source/Sink and Viscous Dissipation,” Heat and Mass Transfer, Vol. 38, No. 3, 2002, pp. 213-220. doi:10.1007/s002310100271
- P. G. Siddheshwar and U. S. Mahabaleswar, “Effects of Radiation and Heat Source on MHD Flow of Viscoelastic Liquid and Heat Transfer over Stretching Sheet,” International Journal of Non-Linear Mechanics, Vol. 40, No. 6, 2005, pp. 807-821. doi:10.1016/j.ijnonlinmec.2004.04.006
- M. S. Abel, P. G. Siddheshwar and M. M. Nandeppanavar, “Heat Transfer in a Visco-Elastic Boundary Layer Flow over a Stretching Sheet with Viscous Dissipation and Non-Uniform Heat Source,” International Journal of Mass and Heat Transfer, Vol. 50, No. 5-6, 2007, pp. 960-966.
- T. C. Chiam, “Heat Transfer with Variable Conductivity in Stagnation—Point Flow towards a Stretching Sheet,” International Communications in Heat and Mass Transfer, Vol. 23, No. 2, 1996, pp. 239-248. doi:10.1016/0735-1933(96)00009-7
- N. Ahmad and K. Marwah, “Visco-Elastic Boundary Layer Flow past a Stretching Plate and Heat Transfer with Variable Conductivity,” Proceedings of 44th Congress ISTAM, 22-25 December 1999, pp. 60-68.
- N. Ahmad and M. Mishra, “Unsteady Boundary Layer Flow and Heat Transfer over a Stretching Sheet,” Proceedings of 28th UIT Heat Transfer Congress, Brescia, 21-23 June 2010, pp. 37-40.

