World Journal of Mechanics
Vol. 1 No. 3 (2011) , Article ID: 5773 , 9 pages DOI:10.4236/wjm.2011.13014
Analysis of Mechanical Behavior of Red Blood Cell Membrane with Malaria Infection
Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee, India
E-mail: vktmafma@rediffmail.com, demeke19@gmail.com
Received March 22, 2011; revised April 20, 2011; accepted April 29, 2011
Keywords: Cell Mechanics, Malaria Infected Red Blood Cell, Mathematical Model, RBC Membrane Elasticity
ABSTRACT
Human red blood cells (RBCs) are responsible to transport oxygen and carbon dioxide for human bodies. The physiological functions of RBCs are greatly influenced by their mechanical properties. When RBC is infected by Malaria parasite called Plasmodium falciparum, it shows progressive changes in mechanical properties and loses its deformability. The infected red blood cells (IRBCs) develop properties of cytoadherence (stickiness) and rosetting (the binding of non-infected RBCs to parasitized RBCs). In this paper to analyze the mechanical properties and deformability of the IRBC, we applied stress-stretch ratio relation of its biomembrane .To express this constitutive relation, we proposed a mathematical model (Neo-Hookean model) based on membrane theory. On this model, we present continuous stress-stretch ratio curves for the relation derived from the model for different intracellular developmental stages of the parasite, to determine the mechanical properties of IRBC. The analytical results obtained from the mathematical model are more closed with the experimental data [1] which demonstrates the validity of the model. By restricting our attention to spherically symmetric deformation in the final schizont stage of parasite development, the pressure-extension ratio relation curve also adapted from the proposed strain energy function. The change in osmotic pressure versus volumetric ratio has been also considered for IRBC before hemolysis.
1. Introduction
The human RBC with a biconcave shape which allows more and more oxygen molecules to come in contact with the cells surface.RBC has an average diameter of about 8µm and a typical life span of 120 days. The physiological functions of RCBs are greatly influenced by their mechanical properties. Studies of the mechanical properties of the human RBC and membrane [2] deformability of RBCs (erythrocytes) has long been a topic of considerable scientific interest and real life significance [3,4].
Particularly, mechanical deformability and biorheology of the human RBC are known to play a vital role in influencing organ function as well as states of overall health and disease system [5]. Healthy red blood cells (HRBCs) are more flexible and highly deformable; they transport oxygen to various parts of the body by squeezing their way through narrow capillaries [6]. In this paper, consequences of alterations of the RBC membrane properties are considered in the context of malaria infectious disease. Malaria induced by plasmodium falciparum parasites is one of the most serious widespread parasitic infectious diseases on earth [1].There are about five hundred million clinical cases with more than two million deaths each year [7]. Invasion and occupation of Plasmodium falciparum in RBCs exercise to change mechanical property. The malaria-infected red blood cells (IRBCs) lose their deformability and develop the properties of cytoadherence (stickiness) and rosetting (the binding of non-infected RBCs to parasitized RBCs) [6,8,9].Membrane stiffness of IRBCs is modified by proteins exported from the parasite to the membrane [10].The export of parasite proteins results in distortion of the cell cytoskeleton and membrane with the multiplication of the parasites within the IRBC,the shape of the IRBC becomes more spherical rather than biconcave shape for the HRBC [6,8]. The RBCs infected by plasmodium falciparum are stiffen considerably with marked increases in their elastic moduli. Profound alterations to the mechanical properties and adhesive response of the infected RBCs cause them to sequester in the microvasculature of major organs [1]. Many researchers have used several techniques to measure the mechanical properties of malaria infected RBCs, micropipette aspiration [10-12], optical tweezers [1,2]. Suresh et al. [1] examined the deformability of IRBCs by employed a stretching experiment using optical tweezers, and revealed that the membrane of the IRBC becomes stiffer when parasites inside of the cell have developed. They clarified that in the final schizont stage, the shear modulus can increase by ten-fold. Changes in the mechanical properties of RBCs have been postulated to link to micro vascular occlusion or poor deformability, particularly in capillary or venules, and subsequently contribute to dysfunction of vital organ [9].Single cell mechanics study [13] had been done to investigate the changes in the structure-property-function relationship of RBCs arising from infection by the malaria parasite plasmodium falciparum. Mauritz et al. [14] used a microfluidic optical cell stretcher by combining the selectivity and sensitivity of single-cell elasticity measurements to measure the elasticity of malaria IRBCs. The measurements confirm an increase in host cell rigidity during the maturation of the parasite Plasmodium falciparum. Imai et al. [8] proposed a numerical model based on a particle method and they employed a two-dimensional spring network of membrane particles to express the deformation of malaria IRBCs.
The functions of RBC are determined by the mechanical properties of its biomembrane. Cell membrane mechanics and the deformation characteristics of human RBCs have received considerable attention [15]. Understanding of the deformability changes is a fundamental requirement for developing new techniques or methods for diagnosis, prediction and treatment of this disease [8].
In this paper we proposed a mathematical model to analyze the mechanical characterization of IRBC membrane arising from malaria infection disease. The model is based on membrane theory and utilizes a hyperelastic material to describe the deformation behavior of RBC biomembrane. Membrane is fundamental structure that strongly influences cell functions.
2. Model Presentation
Blood is a suspension of formed elements (red blood cells, white blood cells and platelets) in plasma. An RBC consists of cytoplasm enclosed by a thin and elastic membrane. Hence, we applied the principle of mechanics regarding to elastic continuum for the present study. To do so, we need to relate the stress in the body to some measure of deformation, which will be accomplished through the introduction of constitutive equations. Because constitutive equations describe stress-strain relations of soft biological tissues require parameters such as the strain energy functions or their derivatives [16].
The spectrin network which underlies the phospholipid bilayer of human RBC membrane is genenerally considered to impart shear induced resistance to the cell membrane although the bilayer itself has little resistance to shear deformation [17]. As Dao et al. [2] reviewed, the human RBC membrane comprises the phospholipid bilayer, the underlying spectrin network and transmembrane proteins. The composite cell membrane structure is commonly modeled as an incompressible effective continuum. Evans [18] and Evans and Skalak [3] suggested that the relationship between the membrane shear stress Ts (expressed in units of force per unit length) and the principal stretch ratios 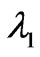 and
and is given by [2].
is given by [2].
 (1a)
(1a)
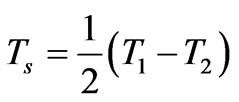 and
and 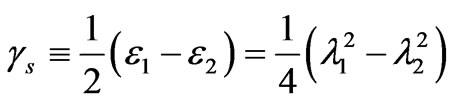 (1b)
(1b)
 (1c)
(1c)
where T1 and T2 are the in-plane principal membrane tensions, 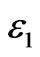 and
and 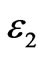 are the in-plane principal Green’s strains components of the membrane, γs is the shear strain and µ the membrane shear modulus (assumed to be constant and expressed in units of force per unit length). Equation (1c) reflects the assumption that the total membrane area is constant during deformation in normal condition. By combining (1a) and (1b) we obtained as,
are the in-plane principal Green’s strains components of the membrane, γs is the shear strain and µ the membrane shear modulus (assumed to be constant and expressed in units of force per unit length). Equation (1c) reflects the assumption that the total membrane area is constant during deformation in normal condition. By combining (1a) and (1b) we obtained as,
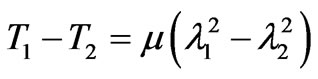 (2)
(2)
For large deformation characteristics of a membrane material, when the biomembrane is assumed to be a three dimensional elastic continuum, the principal tensions T1and T2 can be expressed [19] in the form,
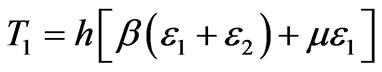 (3a)
(3a)
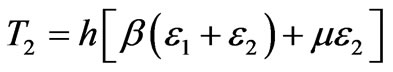 (3b)
(3b)
Where h is the final thickness of the deformed membrane, 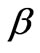 and µ are material properties. The Green (material) strain tensor components can be defined as,
and µ are material properties. The Green (material) strain tensor components can be defined as,
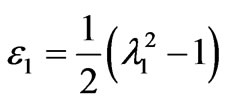 and
and 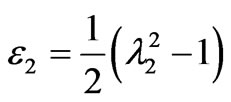 (4)
(4)
Living cells in the human body are constantly subjected to mechanical simulations throughout life. These stresses and strains can arise from both the external environmental and internal physiological conditions. Any deviation in the structural and mechanical properties can result in the breakdown of these physiological functions and may possibly lead to disease [13]. RBC deformability becomes an extremely important determinant of blood flow, as a slight decrease in deformability can result in a sharp decrease in capillary flow rate [20].The changes in deformability and mechanical properties of living cells are also linked strongly to the manner in which the cells respond to structural and molecular alterations induced by the onset and progression of diseases and invasion by foreign organisms such as parasites [1]. For instance, RBCs transport oxygen from lungs to the various parts of human body tissues by deforming their way through blood vessels and small or narrow capillaries. Unfortunately, RBCs are infected by plasmodium falciparum parasite, the result cause malaria [1,8,21].
At the schizont stage the infected red cell is found to exhibit a viscoelastic solid like behavior which is in contrast to the liquid drop behavior demonstrated by healthy RBC and early stage of IRBC [21]. Large deformation response of the RBC has been analyzed using variations of continuum constitutive models. One such approach entails use of hyperelastic effective materials model for capturing the large deformation response of the membrane [17]. Due to the solid like behavior of the late stage of malaria infected cell [21] modeled the deformability of the whole cell using a homogeneous incompressible, standard neo-Hookean solid model. The simplest first order formulation using a one-parameter NeoHookean form where the strain energy potential function U [2] is of the form
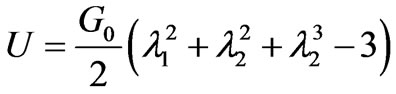 (5)
(5)
where G0 is the initial value of bulk shear modulus, 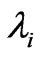 (i = 1,2,3) are the principal stretches. The incompressibility condition implies that
(i = 1,2,3) are the principal stretches. The incompressibility condition implies that .The potential function U, defines the non-linear elastic stress-strain behavior. When the initial membrane thickness is
.The potential function U, defines the non-linear elastic stress-strain behavior. When the initial membrane thickness is , the constitutive description of equation (5) results in the initial in-plane membrane shear modulus
, the constitutive description of equation (5) results in the initial in-plane membrane shear modulus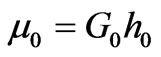 [2]. The Neo-Hookean hyperelastic potential is known to be reasonably accurate when the maximum strains on the order of 100%. For an incompressible isotropic elastic solid materials, the Cauchy principal stress tensors
[2]. The Neo-Hookean hyperelastic potential is known to be reasonably accurate when the maximum strains on the order of 100%. For an incompressible isotropic elastic solid materials, the Cauchy principal stress tensors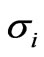 , is given by
, is given by
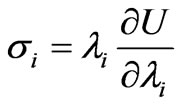 (6)
(6)
where (i = 1,2,3). The principal tensions 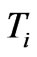 of the cell membrane can be written as
of the cell membrane can be written as
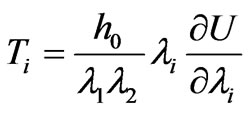 (7)
(7)
The membrane tension resultants from the proposed strain energy potential function are expressed as follows,
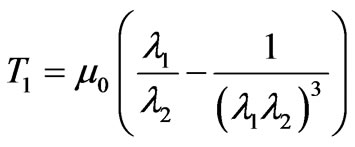 (8)
(8)
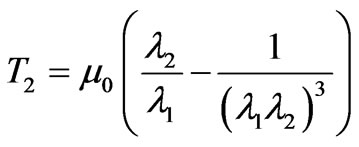 (9)
(9)
If the strain energy density function is supposed to be independent of the second invariant, single test such as a uniaxial tension test is needed for material response [22]. The proposed strain energy potential function of neoHookean form is independent of the second stretch invariant. Hence, for a hyperelastic thin membrane subjected to uniaxial stretch (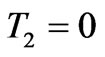 ), the relation between the membrane tension
), the relation between the membrane tension  versus extension ratio from the proposed strain energy potential function U, in uniaxial stretch becomes,
versus extension ratio from the proposed strain energy potential function U, in uniaxial stretch becomes,
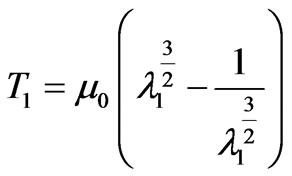 (10)
(10)
Assume D, be diameter of the cell. In the undeformed state this quantity shall have the value D0 taken to be the same as the biconcave model which is approximately 8μm. The principal stretch ratio is defined as λ1 = D/D0, where D is deformed in the axial or transverse direction. By substituting this value in (10), we obtained T1 as a function of diameter as follows.
 (11)
(11)
Since T1 is expressed under uniaxial tension, variations of axial and transverse diameter of the cell are considered. In uniaxial tension (stretch) [1,2,17] the axial diameter of the cell increase and the transverse diameter of the cell becomes reduced. Therefore, (11) presents continuous increasing and decreasing force-deformation curves for the deformation response of the RBC for different developmental stages of the parasite.
The erythrocytic developmental stages of the parasite are broadly classified as the ring stage (pf-R-IRBC), trophozoit stage (pf-T-IRBC) and the schizont stage (pf-S-IRBC). Single cell mechanical property measurements performed using the micropipette aspiration method [12,23] and the laminar shear flow method [24] also show that RBCs parasitized by plasmodium falciparum stiffen considerably with marked increases in the elastic moduli. The elastic properties of bodies are quantitatively characterized by elastic parameters, essentially elastic moduli. Different deformation types are characterized by different elastic moduli. Through the analytical expression (11) using the experimental data, we obtained different shear modulus values corresponding to each developmental stages of the parasite .The different values of the material parameter [25] lead to different forcedeformation curves.
3. Pressure-Volume Relationship of IRBC
As the parasite develops in RBC, the IRBC becomes more spherical with increase in its volume as the parasite multiply within it [1,8]. The possible increased pressure through plasmodium biochemical process, might lead to a higher erythrocyte volume and therefore to the increased erythrocyte fragility [26]. The cytosal is assigned to be a fluid which acts to conserve the inner volume of the RBC during deformation as well as to maintain the even distribution of the internal (hydraulic) fluid pressure on the surface of the inner membrane [2].
One of the factors reduced deformability besides to molecular changes in the cell membrane or cytoplasm among red cells is a purely geometric effect, viz., the decrease in the surface-to-volume ratio of the red cell due to the increased volume resulting from parasite growth [27]. One of the main characteristics of the malaria disease is progressive changes in RBC mechanical properties and geometry. The inflated cylindrical membrane exhibits a critical internal pressure, defined by a maximum limit point along the non linear equilibrium path, after which the internal pressure gradually decrease or remains practically constant [28]. As Canham and Parkinson, [29] suggested that one can calculate the hypothetical hemolytic volume VH and subsequently, PH the osmotic pressure when the cell hemolyzed. This calculation is based on the Van’t Hoff, relation given by
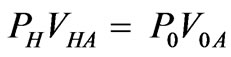 (12)
(12)
where VHA andV0A are the apparently osmotically active volumes of VH and V0 respectively, P0 isotonic osmotic pressure.V0 the isotonic volume of the cell. When the parasite growth in cell membrane, there is a change in osmotic pressure, denoted by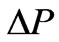 , after the cell become spherical,
, after the cell become spherical,  is given by Canham and Parkinson [29],
is given by Canham and Parkinson [29],
 (13)
(13)
where 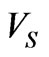 volume of the cell when it first become a sphere, 0.42V0 osmotically inactive fraction of the cell volume in isotonic condition. When the parasite develops and multiplies with in RBC, both the pressure and volume increases in the parasitized cell. According to Magowan et al. [30] the volume of the parasite in the late stage of the parasite development is 30% of the host RBC volume. Therefore, mathematically, volume of the cell when it first become sphere is
volume of the cell when it first become a sphere, 0.42V0 osmotically inactive fraction of the cell volume in isotonic condition. When the parasite develops and multiplies with in RBC, both the pressure and volume increases in the parasitized cell. According to Magowan et al. [30] the volume of the parasite in the late stage of the parasite development is 30% of the host RBC volume. Therefore, mathematically, volume of the cell when it first become sphere is  = Vp + V0 = 0.3V0 + V0, where Vp is volume of the parasite inside the cell membrane. Based on these assumptions (13) can be written as,
= Vp + V0 = 0.3V0 + V0, where Vp is volume of the parasite inside the cell membrane. Based on these assumptions (13) can be written as,
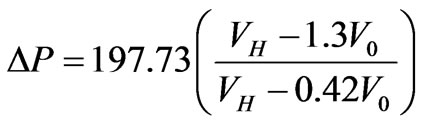 (14)
(14)
The change in osmotic pressure versus volumetric inflation ratio due to the development of parasite inside the cell membrane is the gradient of osmotic pressure which the cell must have either due to stiffness or allowing its membrane to be stretched or by loosing osmotically active solute.
4. Pressure-Extension Ratio Relation
In the schizont stage, the plasmodium falciparum parasite IRBC exhibits a change in shape, which is spherical compared to the biconcave shape of HRBC [1]. We consider this spherical shape of radius (r) and assumed that the HRBC in the undistorted (unstressed) state, this quantities shall have the values (r0). As Skalak, R. et al., [19] restricting to cases in which the deformed shape (as spherical shape of IRBC) is also axisymetric, the principal axes of stress and strain are the meridonal and circumferential directions. So (8) and (9) are sufficient to describe the elastic behavior of the membrane by assuming that the tension T1 acts in the meridonal directions and T2 is the circumferential or hoop stress. The stretches (extension ratios) λ1 and λ2 are obviously given by the ratio (r/r0) of the circumferences of the sphere of the IRBC at any point in the inflated and uninflated state, so that by isotropic tension orientation (T1 = T2), we understood that , therefore, the tension distribution on the sphere is given by
, therefore, the tension distribution on the sphere is given by
 (15)
(15)
The pressure difference in the direction of the outward normal across the spherically deformed cell membrane surface can be calculate from the equation of equilibrium and is written as [19].
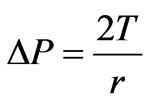 (16)
(16)
Where r is the radius of the spherical shape of IRBC and it can be expressed as .As pressure increases, the value of the stretch ratio increases [19]. By substituting (16) into (15), we obtained the expression
.As pressure increases, the value of the stretch ratio increases [19]. By substituting (16) into (15), we obtained the expression 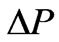 in terms of the extension ratio as
in terms of the extension ratio as
 (17)
(17)
where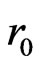 is the initial radius of the cell and μ0 is the parameter in the process of sphering of RBCs for both cases HRBC and IRBC at the final schizont stage of the parasite development.
is the initial radius of the cell and μ0 is the parameter in the process of sphering of RBCs for both cases HRBC and IRBC at the final schizont stage of the parasite development.
5. Result and Discussion
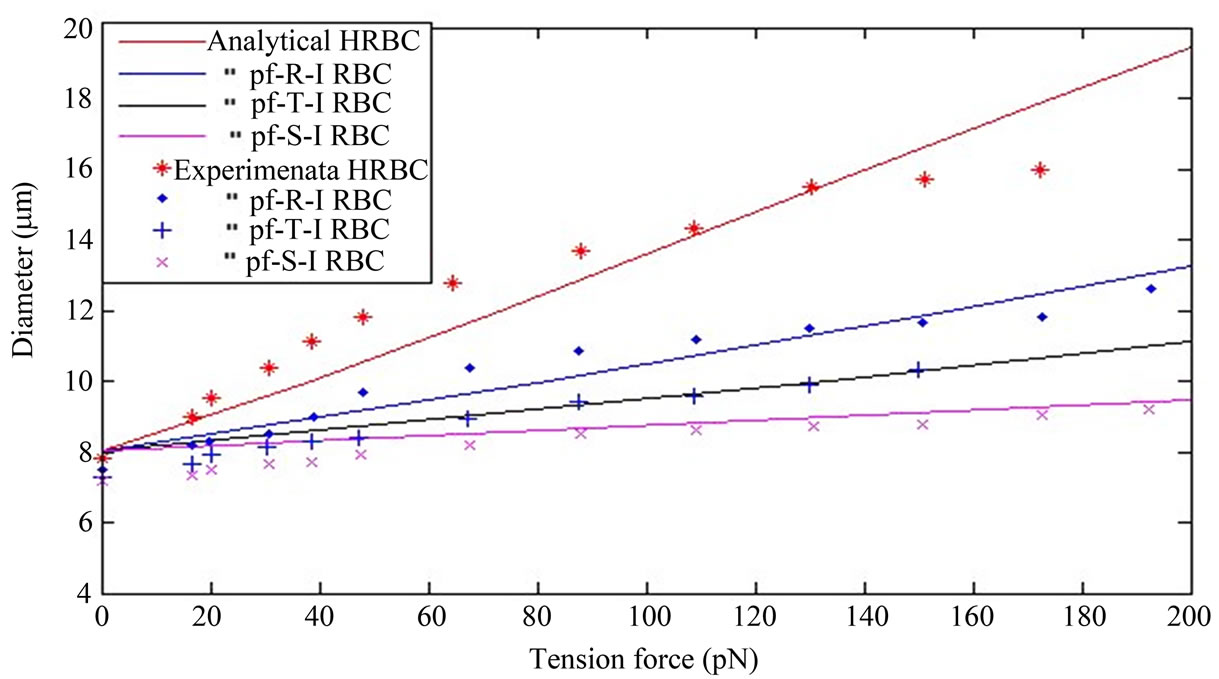
In Figure 1 the solid curves depict the mechanical properties of the cell membrane material regarding to the chosen neo-Hookean first order hyperelastic constitutive model under various developmental stages of plasmodium falciprum parasites in RBC. The curves in Figure 1 present the continuous and stress-strain relations of the cell membrane material as a function of different stages of the parasite development in RBC. As the Figure 1 describes, at a fixed stretching force, the deformability of the parasitized cell is significantly decreased compared to normal conditions. The analytical solution curves geometrically indicate significant stiffening of the RBC with the maturation of parasite from the ring stage to the trophozoite stage to the schizont stage. The increase in axial diameter and the decrease in transverse diameter
 (a)
(a)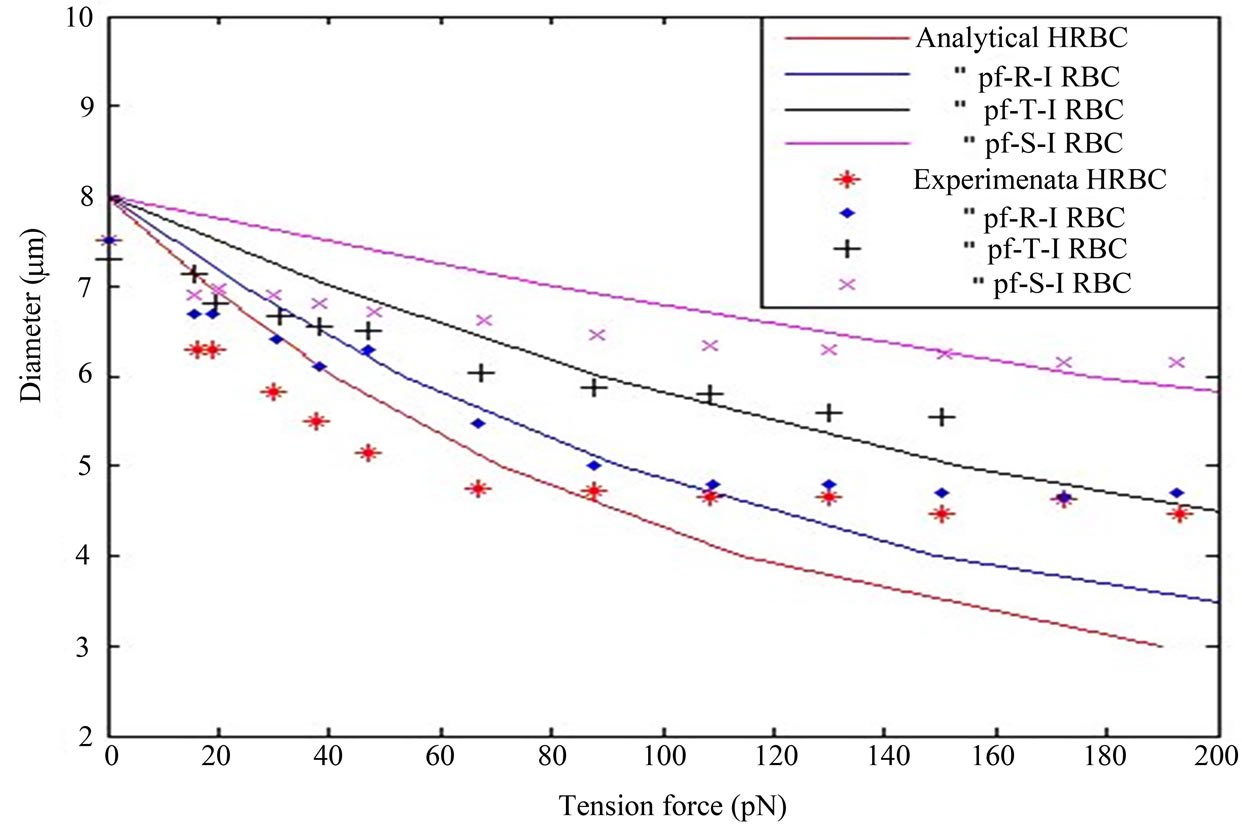 (b)
(b)
Figure 1. The solid curves in the figure represent, that the analytical results of the neo-Hookean model for IRBC at different developmental stages of the plasmodium falciparum parasite in uniaxial stretch test in (11). Also the different point in the figure indicates the experimental results. Consider Diameter in (µm) and Tension force in (pN). (a) Along axial diameter; (b) Along transverse diameter.
with uniaxial stretch progressively reduced in the advanced stages of intracellular parasite compared to the healthy RBC. This is shown in the Figure 1 (a) and (b) as it moves from healthy state to final schizon stages of the parasite development.
The analytical result presents, that the HRBC is easily deformable with low stretch force than the parasitized RBC. Furtherly, the coefficient (shear modulus) of function of IRBC is drastically increased for the period from ring stage to schizont stage. Our analytical solution simulation as shown in Figure 1 is compared to Suresh et al. [1] studied experimentally and presented a continuous force-displacement curves for different erythrocytic developmental stages of the parasite. The matching of experimental data is shown by various colored points in Figure1 (a) and (b) for the different infestation stages of the parasite, with analytical curves of the model in uniaxial extension test. The elasticity modulus (coefficient) of analytical expression was extracted by using the least square objective function from the experimental data. The shear modulus values of HRBC, pf-R-IRBC, pf-T-IRBC, and pf-S-IRBC are 56.7, 120.24, 195.58 and 389.06 pN, respectively. The unit is the same as the unit of the stretching force. The larger the value of the elastic modulus represents the stiffer the late stage. As Dao et al., [2] a higher shear modulus value indicates the red cell as being more rigid, as observed in the reduction in the change in axial diameter.
As can be seen curves from the graph of the proposed mathematical model, through the constitutive relation, the interpretation from the curves leads to different mechanical properties according to different developmental stages of the parasite in RBC. Thus, this study indicates that the proposed mathematical model can be used to predict the deformation characteristics of RBCs during parasite development in RBC and may have potential biomedical applications such as characterizing rheological properties and distinguishing infected cells from normal ones. The membrane tension distribution versus deformation in uniaxial tension is an increasing function of deformation in axial diameter and decreasing function in transverse diameter as shown in Figure 1(a) and (b).
Figure 2 depicts that the nature of the curves of osmotic pressure-volumetirc ratio relationship of RBC infected with plasmodium falciparum parasite from analytical result and the spherical inflation of HRBC during gradual swelling in experimental observation [29]. The curves are nonlinear and they show different mechanical behavior. Malaria IRBCs becomes stiffer and enhance cell rigidity and develop properties of cytoadherence [1, 8]. Due to the parasite matures and multiply within the cell, both the internal pressure and volume of the cell increases until a certain limit point is attained before hemolysis as shown from the curve of the IRBC in the figure. From the figure, at a fixed pressure, we analyze that the HRBC show better flexibility (deformability) than the IRBC. As the assumption of [31] that the red cell membrane cannot tolerate any stretch without hemolysis. Therefore, the curves in the figure shows loss of cell deformability regarding to the cell size (volume) increases before hemolysis. In order for a cell to be deformable, it must have a large membrane area-to-volume ratio [31].
Figure 3 shows that the nature of pressure-extension ratio characteristics of plasmodium falciparum parasite
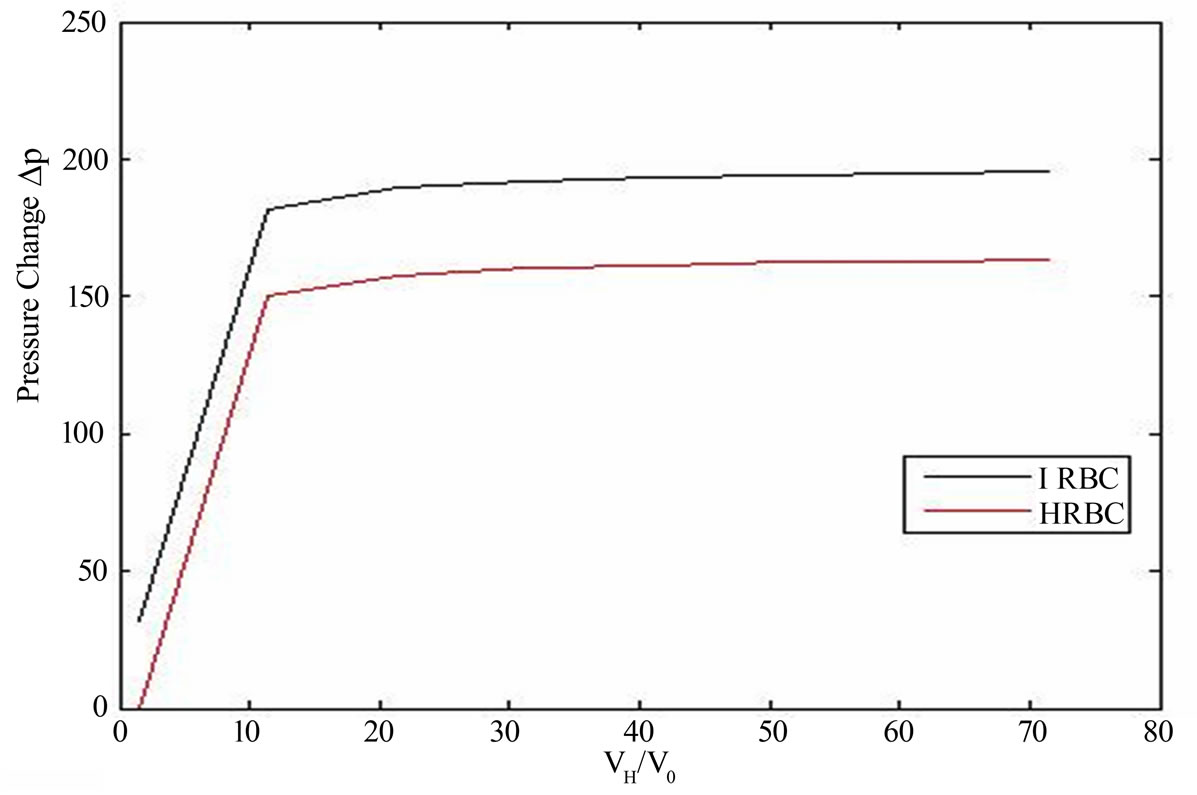
Figure 2. The comparison between the osmotic pressure versus volumetric ratio of IRBC at the schizont stage in (14) and spherically inflated HRBC during gradual swelling observed experimentally [29].
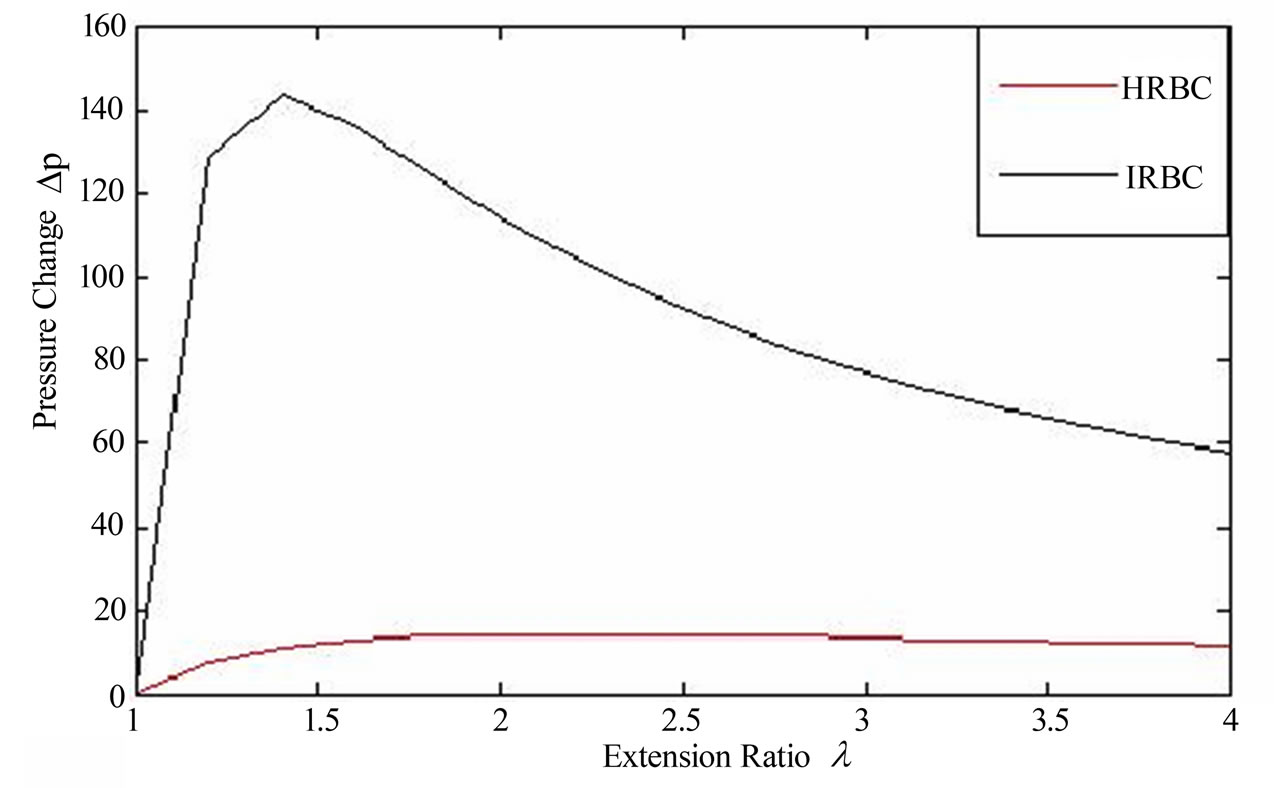
Figure 3. Pressure difference (DP) versus extension ration characteristics of malaria infected red blood cell (IRBC) at the schizont stage (μ0 = 389.06 pN) and HRBC (μ0 = 56.7 pN) from the proposed model as expressed in (17). The parameter values are calculated from experimental observations of Suresh et al. [1].
(IRBC) at the schizont stage and HRBC which is spherical shape with the Neo-Hookean model in an isotropic tension .we obtain a non-monotonic curves with non linear behavior, which have a zero value of course at (λ = 1). The inflated pressure rises steeply with circumferential stretch. At the schizont stage the infected cell exhibits almost solid-like behavior and increased rigidity [21]. Therefore, from the figure the curve of the IRBC shows poor deformability than HRBC even by considering a fixed pressure value before hemolysis. After the pressure has reached a maximum limit point along the non-linear equilibrium path, the internal pressure decreases with increasing radius, which tends to hemolysis.
6. Conclusion
In this study, we proposed a mathematical model to predict the mechanical response or mechanical behavior of the RBC membrane which infected by plasmodium falciparum parasite. Our work is the new method to employ mathematical model regarding to continuum mechanics approach to analyze mathematically and quantify the mechanical behavior of RBC membrane in malaria infection. The model is based on the continuum approach membrane theory to describe the deformation behavior of RBC membrane. Since RBC membrane is a hyperelastic material, it is possible to introduce strain energy function defined with respect to the undeformed state. The unique analytical result (solution) in uniaxial stretch test based on the model makes this study differs from the other previous works on mechanical properties of RBC during the developmental stages of the parasite. With this model, as the curves indicate in Figure 1, we understood that IRBC shows different mechanical properties according to different developmental stages of the parasite.
Moreover, as observed in Figure1 (a) and (b) the analytical result obtained from the mathematical model compared with the experimental results of Suresh et al. [1]. HRBC, along axial diameter, when the stretching force between 20 pN and 100 pN, experimental result shows more deformable, and also between 100 pN and 150 pN both results almost fit, and force greater than 150 pN, the analytical result presents more deformable than experimental result. In the three stages of the parasite development both analytical and experimental results virtually well agree. In transverse diameter, the analytical result shows the rigidity of the three stages of the parasitic development than experimental result. The stretching force less than 100 pN, is HRBC more deformable in experimental than analytical, but greater than 100 pN, it is more deformable in analytical result. The difference may arise from numerical calculation of the parameter shear modulus from the existing data and initial cell diameters. Especially in transverse diameter test, the initial cell diameter is approximately between 7 µm to 7.5 µm. These information demonstrates that our model is valid and can be used to describe the deformation response or the mechanical properties of RBC infected by plasmodium falciparum parasite.
In Figure 2 and 3 generally, the internal pressure which inflates a RBC membrane to a spherical shape and size (volume) increases when the parasites matures and multiply in it, reveals that, there is a change in rheological or mechanical properties.
Since membrane is a constitutive material, we will attempt to study by using other constitutive models, in order to analyze and determine mechanical properties of malaria infected RBCs in our future work.
REFERENCES
- S. Suresh, J. Spatz, J. P. Mills, A. Micoulet, M. Dao, C. T. Lim, M. Biel and T. Seufferlein, “Connection between Single-Cell Biomechanics and Human Disease States: Gastrointestinal Cancer and Malaria,” Acta Biomaterialia, Vol. 1, No. 1, 2005, pp.15-30. doi:10.1016/j.actbio.2004.09.001
- M. Dao, C. T. Lim and S. Suresh, “Mechanics of the Human Red Blood Cell Deformed by Optical Tweezers,” Journal of the Mechanics and Physics Solids, Vol. 51, No. 11-12, 2003, pp. 2259-2280. doi:10.1016/j.jmps.2003.09.019
- E. A. Evans and R. Skalak, “Mechanics and Thermal Dynamics of Biomembranes,” CRC Press, Boca Raton, 1980.
- D. Boal, “Mechanics of the Cell,” Cambridge University Press, Cambridge, 2002.
- S. Suresh, “Mechanical Response of Human Red Blood Cells in Health and Disease: Some Structure-Property-
- Function Relationships,” Journal of Materials Research,
- Vol. 21, No. 8, 2006, pp. 1871-1877. doi:10.1557/jmr.2006.0260
- G. Y. H. Lee and C. T. Lim, “Biomechanics Approaches to Studying Human Diseases,” Trends in Biotechnology, Vol. 25, No. 3, pp. 112-118.
- World Health Organization, “World Malaria Report,” 2008. http://www.who.int/malaria/wmr2008
- Y. Imai, H. Kondo, T. Ishikawa, C. T. Lim and T. Yamaguchi, “Modeling of Hemodynamic Arising from Malaria Infection,” Journal of Biomechanics, Vol. 43, No. 7, pp. 1386-1393. doi:10.1016/j.jbiomech.2010.01.011
- H. Kondo, Y. Imai, T. Ishikawa, K. Tsubota and T. Yamaguchi, “Hemodynamic Analysis of Microcirculation in Malaria Infection,” Annals of Biomedical Engineering, Vol. 37, No. 4, 2009, pp. 702-709. doi:10.1007/s10439-009-9641-1
- F. K. Glenister, R. L. Goppel, A. F. Cowman, N. Mohan das and B. M. Cooke, “Contribution of Parasite Proteins to Altered Mechanical Prop Erties of Malaria-Infected Red Blood Cells,” Blood, Vol. 99, No. 3, 2002, pp. 1060-1063. doi:10.1182/blood.V99.3.1060
- N. B. Nash, E. O’. Brien, E. C. Gorden-Smith and J. A. Dormandy, “Abnormalities in the Mechanical Properties of Red Blood Cells Caused by Plasmodium Falciparum,” Blood, Vol. 74, No. 2, 1989, pp. 855-861.
- M. Paulitschke and G. B. Nash, “Membrane Rigidity of Red Blood Cells Parasitized by Different Strains of Plasmodium Falciparum,” Journal of Laboratory and Clinical Medicine, Vol. 122, No. 5, 1993, pp. 581-589.
- C. T. Lim, “Single Cell Mechanics Study of the Human Disease Malaria,” Journal of Biomechanical Science and Engineering, Vol. 1, No. 1, 2006, pp. 82-92. doi:10.1299/jbse.1.82
- J. M. A. Mauritz, T. Tiffert, R. Seear, F. Lautensclager, A. Esposito, V. L. Lew, J. Guck and C. F. Kaminki, “Detection of Plasmodium Falciparum-Infected Red Blood Cells by Optial Tretching,” Journal of Biomedical Optics, Vol. 15, No. 3, 2010. doi:10.1117/1.3458919
- G. Lenormand, S. Hkenon, A. Richert, S. SimKeon and F. Gallet, “Direct Measurement of the Area Expansion and Shear Moduli of the Human Red Blood Cell Mem Brane Skeleton,” Biophysical Journal, Vol. 81, No. 1, 2001, pp. 43-56. doi:10.1016/S0006-3495(01)75678-0
- K. B. Sahay, “On the Choice of the Strain Energy Function for Mechanical Characterization of Soft Biological Tissues,” Mineral Engineering Processes Ltd., Vol. 13, No. 1, 1984, pp. 11-14.
- J. P. Mills, L. Qie, M. Dao, C. T. Lim and S. Suresh, “Nonlinear Elastic and Viscoelastic Deformation of the Human Red Blood Cell with Optical Tweezers,” Mechanics and Chemistry of Biosystems, Vol. 1, No. 3, 2004, pp. 169-180.
- E. A. Evans, “New Membrane Concept Applied to the Analysis of Fluid Shearand Micropipette-Deformed Red Blood Cells,” Biophysical Journal, Vol. 13, No. 9, 1973, pp. 941-954. doi:10.1016/S0006-3495(73)86036-9
- R. Skalak, “Strain Energy Function of Red Blood Cell Membrane,” Biophysical Journal, Vol.13, No. 3, 1973, pp. 245-264. doi:10.1016/S0006-3495(73)85983-1
- A. M. Dondorp, P. A. Kager, J. Vreeken and N. J. White, “Abnormal Blood Flow and Red Blood Cell Deformability in severe Malaria,” Parasitology Today, Vol. 16, No. 6, 2000, pp. 228-232. doi:10.1016/S0169-4758(00)01666-5
- C. T. Lim, E. H. Zhou and S. T. Quek, “Mechanical Model for Living Cells—A Review,” Journal of Biomechanics, Vol. 39, No. 2, 2006, pp. 195-216. doi:10.1016/j.jbiomech.2004.12.008
- Ali, M. Hosseini and B. B. Sahari, “A Review of Constitutive Models for Rubber-Like Materials,” American Journal of Engineering and Applied Sciences, Vol. 3, No. 1, 2010, pp. 232-239. doi:10.3844/ajeassp.2010.232.239
- H. A. Cranston, C. W. Boylan, G. L. Carroll, S. P. Sutera, J. R. Williamson, I. Y. Gluzman and D. J. Krogstad, “Plasmodium Falciparum Maturation Abolishes Physiologic Red Cell Deformability,” Science, Vol. 223, No. 4634, 1984, pp. 400-403. doi:10.1126/science.6362007
- R. Suwanarusk, B. M. Cooke, A. M. Dondorp, K. Si lamut, J. Sattabongkot, N. J. White and R. Udomsang Petch, “The Deformability of Red Blood Cells Parasitized by Plasma Dium Falciparum and P. Vivax,” Journal of Infectious Diseases, Vol. 189. No. 2004, pp. 190-194.
- Y. Tan, D. Sun and W. Huang, “Mechanical Modeling of Red Blood Cells during Optical Stret Ching,” Journal of Biomechanical Engineering, Vol. 132, No. 4, 2010, pp. 04450(1-5).
- V. Wiwanitkit, “Volume Added, Malarial Infection and Fragility of Red Blood Cell,” Iranian Journal of Medical Hypotheses and Ideas, Vol. 3, No. 4, 2009. http://journals.tums.ac.ir/abs/12485
- S. P. Sutera and D. S. Krogstad, “Reduction of the Surface-Volume Ratio: A Physical Mechanism Contributing to the Loss of Red Cell Deformability in Malaria,” Biorheology, Vol. 28, No. 3-4, 1991, pp. 221-229.
- D. C. Pamplona, P. B. Goncalves and S. X. R. Lopes, “Finite Deformations of Cylindrical Membrane under Internal Pressure,” International Journal of Mechanical Sciences, Vol. 48, No. 6, 2006, pp. 683-696. doi:10.1016/j.ijmecsci.2005.12.007
- P. B. Canham and D. R. Parkinson, “The Area and Volume of Single Human Erythrocytes during Gradual Osmotic Swelling to Hemolysis,” Canadian Journal of Physiology and Pharmacology, Vol. 48, No. 6, 1970, pp. 369-376. doi:10.1139/y70-059
- C. Magowan, J. T. Brown, J. Liang, J. Heck, R. L. Coppel, N. Mohandas, W. Meyer-Ilse, “Intracellular Structures of Normal and aberrant Plasmodium Falciparum Malaria Parasites Imaged by Soft X-Ray Microscopy,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 94, No. 12, 1997, pp. 6222-6227. doi:10.1073/pnas.94.12.6222
- A. W. L. Jay, “Viscoelastic Properties of the Human Red Blood Cell Membrane I, Defromation, Volume Loss, and Rapture of Red Blood Cells in Micropipettes,” Biophysical Journal, Vol. 13, No. 11, 1973, pp. 1166-1182. doi:10.1016/S0006-3495(73)86053-9

