World Journal of Condensed Matter Physics
Vol.06 No.02(2016), Article ID:66498,8 pages
10.4236/wjcmp.2016.62013
Applications of Quantum Physics on Resistivity, Dielectricity, Giant Magneto Resistance, Hall Effect and Conductance
Saleem Iqbal1, Farhana Sarwar1,2, Syed Masood Raza3, Syed Mohsin Raza4
1Department of Mathematics, University of Balochistan, Quetta, Pakistan
2Department of Mathematics, F. G. Girls Degree College, Quetta, Pakistan
3Department of Physics, Federal Urdu University of Arts, Science and Technology, Karachi, Pakistan
4Department of Physics, University of Balochistan, Quetta, Pakistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 February 2016; accepted 14 May 2016; published 17 May 2016
ABSTRACT
Quantum theory with conjecture of fractional charge quantization, eigenfunctions for fractional charge quantization, fractional Fourier transform, Hermite function for fractional charge quantization, and eigenfunction for a twisted and twigged electron quanta is developed and applied to resistivity, dielectricity, giant magneto resistance, Hall effect and conductance. Our theoretical relationship for quantum measurements is in good conformity and in agreement with most of the experimental results. These relationships will pave a new approach to quantum physics for deciphering measurements on single quantum particles without destroying them. Our results are in agreement with 2012 Physics Nobel Prize winning Scientists, Serge Haroche and David J. Wineland.
Keywords:
Quantum Resistivity, Quantum Dielectricity, Giant Magneto Resistance, Quantum Hall Effect and Conductance

1. Introduction
Experimental results in quantum physics since last three decades brought significant changes in our under- standing. The discovery of quantum Hall effect in heteorostructure semiconductors results in the Nobel Prize winning award for the year 1987 to Von Klitzing [1] . With this discovery, the experimental results of quantum conductance are reported by Van Wees et al. [2] in the two dimensional electron gas of a GaAs-AlGaAs heteorostructure. The visible range photons used to illuminate water molecules are studied with absorption and Fourier transform infrared spectroscopies [3] . The biological specimens are also considered for chromotherapy [4] - [7] . A new conjecture of fractional charge quantization with newly developed theory is coined to look into the shape of eigenfunctions, determine the energy eigenvalues and validate the quantum scattering [8] . Mean- while, new experimental results on giant magneto resistance (GMR) to enhance storage capacity with charges are reported. This discovery of GMR led Albert Peter and Paul Gruebber to win the Nobel Prize for the year 2007 [9] . During the last decade (2000-2010), surprising results are noticed on dielectrics and dielectricilty. A new quantum theory, with our conjecture of charge quantization, on dielectricity is presented in which we modify the Clausius Mossotti and Debye equations [10] . The same quantum theory of dielectricity is applied on Faujasite-type molecular sieves and on dolomite [11] [12] , respectively. The quantum theory of dielectrics and dielectricity is further extended and modified by using Hermite function for fractional quantum states and fractional Fourier transform .
Now, we witnessed again new exciting experimental results on individual quantum systems which led the Nobel Prize winning award in physics by Serge Haroche and David J. Wineland in the year 2012. We studied American Institute of Physics (AIP) reports of 2012 prize winning award and all relevant research papers [13] - [21] . Most of the experimental results of physics Nobel Prize winners like Von Klitzing, Albert Peter and P. Gruebber, Haroche and Wineland fit to our “conjecture of fractional charge quantization” and indeed “theory”. A new theory is described “how charge being a constant entity, on anelectron in the momentum space is fractionally quantized while interacting with a photon, with twisting and twigging effects of an electron quanta” [22] [23] . The eigenfunction for an electron quantum wire or string with sub-quanta (twigs) on its lateral surface at different locations namely above its surface, at the surface and within the sub-quanta and the electron string with beaded fractional quantized states for the fractional charges are determined [23] .
2. Results and Discussions
The fractional Fourier transform (FRFT) of order 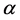 of
of 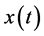 is defined by Almeida [24]
is defined by Almeida [24]
 (1)
(1)
where 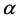 is a rotational angle in the time-frequency plane, and
is a rotational angle in the time-frequency plane, and 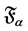 is the FRFT operator. For
is the FRFT operator. For 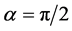 the kernel coincides with the kernel of Fourier transform (FT). Saleem Iqbal et al. developed fractional Fourier integral theorem and fractional Fourier Cosines and Sines transforms [25] . [23] developed Hermite function for the fractional quantum states, i.e.,
the kernel coincides with the kernel of Fourier transform (FT). Saleem Iqbal et al. developed fractional Fourier integral theorem and fractional Fourier Cosines and Sines transforms [25] . [23] developed Hermite function for the fractional quantum states, i.e.,
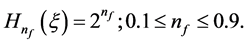 (2)
(2)
Equation (2) is consistent with other definitions of Hermite polynomials. Saleem Iqbal [21] obtained the eigenfunction for a twisted and twigged electron quanta by using Equations (1) and (2), i.e.,
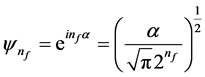 . (3)
. (3)
Equation (3) represents plane wave for a rotation vector alpha (discussed in [21] ) for all corresponding fractional quantum numbers, i.e.,
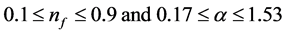 . (4)
. (4)
We shall use Equations (1)-(3) and relation (4) to obtain interesting results for different cases of physics problems.
2.1. Case I―Quantum Resistivity
We know that the electrical resistivity is the inverse of conductivity. The electrical conductivity according to Drude Model (classical) is defined as:
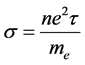 (5)
(5)
where n is the number of charge carriers, e the charge of an electron, 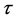 the relaxation time and
the relaxation time and 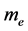 the effective mass of an electron. With the advent of single electron transistors (Spintronics), one could expect quantum conductivity across the interface states. The single electron tunneling will follow a helicon profile with each turn of the helix corresponding to fractional quantum states (charges are fractionally distributed on sub- quanta, i.e., twigs). Changing n with
the effective mass of an electron. With the advent of single electron transistors (Spintronics), one could expect quantum conductivity across the interface states. The single electron tunneling will follow a helicon profile with each turn of the helix corresponding to fractional quantum states (charges are fractionally distributed on sub- quanta, i.e., twigs). Changing n with 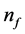 (Equations (2) and (4)), e with
(Equations (2) and (4)), e with 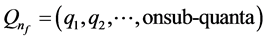 and
and
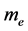 with
with





where 


determined from relative heights of Raman peaks. The helicon profile of an electron is due to spinning or gyroscopic motion. To our conjecture, the dual nature of a quantum particle is a metaphoric states, i.e., it simultaneously behaves as particle and quanta. The fractional quantized state of charge in the momentum space are the manifestations of gyroscopic constant,


Remember that the conductivity is different from conductance.
2.2. Case II―Quantum Dielectricity and Giant Magneto Resistance (GMR)
The mesoscopic fields in a cavity are the manifestations of quantum mechanical dipole moments (fractional charge quantization to a single electron or many electrons systems) due to either molecules, atoms, ions or even the charge, being a constant physical entity, of an electron in the momentum space while interacting with photons. To our conjecture the quantum mechanical dipole moment is a fractional charge quantization, i.e.,

whrer D is the displacement of charge either on an electron or in many electrons system, 

where 







The most attractive quantum electrodynamic potential of an electron or electron quanta (the interior of which is envisaged as a potential well and is defined by the strength of the quantum well)

where 


2.3. Case III―Quantum Hall Effect (QHE)
The megnetoresistance in quantum Hall effect should depend on magnetic field when an electron (charge as a constant physical entity) is fractionally quantized with twisting and twigging of an electron quanta. This is why we are interested in quantum Hall effect on heteorostructure semiconductors by Von Klitzing [1] . The electric
field is fractionally quantized with a gap of quantum Hall resistance, i.e.,
standing, this resistance is a manifestation of twisting and twigging effects of an electron quanta. This is visible
in our Equations (9) and (10), with a gyroscopic constant, 

types, one is longitudinal and the other is transverse. The longitudinal magnetoresistance is associated with magnetic field parallel to the current. The excitonic quantized Hall state at total Landau level filling factor is unity with longitudinal component vanishing and Hall component developing. The Lorentz force, in QHE, for a single electron, is

Changing 

an electron wire or string, 




electron and 



where

quantum numbers, i.e.,


Using eigenfunction 


where 
be solved by considering 




e is changed with





(17). After substitutions and simplifications, Equation (17) is changed in to quantum cyclotron frequency for each of sub-quanta on the lateral surface of electron wire, i.e.,

With resonance Raman Scattering in the fractional regime, 

2.4. Case IV―Quantum Conductance
Quantum conductance was first experimentally observed by Wees et al. [2] . They observed that the
conductance did not increase continuously but rather in quantized steps of
When the electronic mean free path of a wire exceeds the wire length, the wire behaves like an electron wave guide. Each wave guide mode or channel (ballistic conductors) contributes an amount 

where 

effect of Ohemic resistance and dynamic resistances (capacitive reactance and inductive reactance) is called impedance. The inverse of the impedance is termed as admittance. To our opinion, the inverse of the quantum Hall resistance is quantum conductance thus Equation (19) is modified as

We consider the current density j equal to current I,. i.e., 





With our conjecture of fractional charge quantization, change e with



with

where 


where 

3. Conclusion
Formulas for quantum resistivity (Quantum conductivity) and quantum conductance are developed by using fractional Fourier transform. Formulas for quantum behaviour of dielectricity and giant magneto resistance are suggested by using fractional Fourier transform. Formulas for quantum Hall effect following the fractional electric field are suggested. Raman and resonance Raman spectroscopy are suggested for measuring diverse parameters pertaining to quantum behaviour of resistivity, dielectricity, GMR, Hall effect and conductance.
Cite this paper
Saleem Iqbal,Farhana Sarwar,Syed Masood Raza,Syed Mohsin Raza,1 1, (2016) Applications of Quantum Physics on Resistivity, Dielectricity, Giant Magneto Resistance, Hall Effect and Conductance. World Journal of Condensed Matter Physics,06,95-102. doi: 10.4236/wjcmp.2016.62013
References
- 1. Klitzing, V. (1987) Quantum Hall Effect in Heterostructure Semiconductors. American Physical Society News Letter.
- 2. Van Wees, B.J., Van Houten, H., et al. (1988) Quantized Conductance Point Contacts in a Two Dimensional Electron Gas. Physical Review Letters, 60, 848-850.
http://dx.doi.org/10.1103/PhysRevLett.60.848 - 3. Yousaf, S., Raza, S.M., et al. (2008) Absorption of Radiant Energy in Water: A New Conjecture and Theory of Charge Quantization in Chromotized Water Samples. Science International (Lahore), 20, 189-195.
- 4. Yousaf, S., Raza, S.M. and Masoom, Y. (2008) Colours as Catalysts in Enzymatic Reactions. Journal of Acupuncture and Meridian Studies, 1, 139-142.
http://dx.doi.org/10.1016/S2005-2901(09)60034-0 - 5. Yousaf, S., Raza, S.M. and Masoom, Y. (2011) A Case History of Treatment of Cutaneous Leishmaniasis by Chromotherapy. Chinese Medicine, 2, 43-46.
http://dx.doi.org/10.4236/cm.2011.22008 - 6. Yousaf, S., Raza, S., Masoom, Y. and Samad, A. (2009) Effect of Different Wavelenghts on Superoxide Dismutase. Journal of Acupuncture and Meridian Studies, 2, 236-238.
http://dx.doi.org/10.1016/S2005-2901(09)60060-1 - 7. Yousaf, S., Raza, S.M., Masoom, Y., et al. (2011) Effect of Different Colours in the Visible Region on Leishmania Tropic. Advances in Biosciences and Biotechnology, 2, 380-384.
http://dx.doi.org/10.4236/abb.2011.25055 - 8. Yousaf, S., Raza, S.M. and Ahmed, M.A. (2008) Newly Developed Recursive Relationship for Fractional Quantum States and Associated Energy Eigen Values. Science International (Lahore), 20, 255-260.
- 9. Peter, A. and Grubber, P. (2007) Giant Magnetoresistance. APS News Letter, 16, No. 10.
- 10. Rehman, F., Raza, S.M. and Ahmed, M.A. (2009) Quantum Theory of Dielectricity and Its Application to Dolomite. Science International (Lahore), 21, 29-32.
- 11. Jabeen, S., Raza, S.M., et al. (2012) Quantum Mechanical Analysis on Faujasite-Type Molecular Sieves by Using Fermi Dirac Statistics and Quantum Theory of Dielectricity. Journal of the Chemical Society of Pakistan, 34, 251.
- 12. Gormani, M., Rehman, F., et al. (2006) Quantum Behaviour of Dielectric in Dolomite of Balochistan, Pakistan. Journal of the Chemical Society of Pakistan, 28, 414-416.
- 13. Haroche, S., Gilles, N., et al. (2006) Step by Step Engineered Entanglement with Atoms and Photons in a Cavity. AIP Conference Proceedings, 551, 143.
- 14. Haroche, S., Gilles, N., et al. (1995) Manipulating Quantum Fields with a Single Atom in a Cavity. AIP Conference Proceedings, 329, 30.
http://dx.doi.org/10.1063/1.47571 - 15. Britton, J., Liebfried, D., et al. (2009) Scalable Arrays of Paul Traps in Degenerate Silicon. Applied Physics Letters, 95, Article ID: 173102. http://dx.doi.org/10.1063/1.3254188
- 16. Maitre, X., Hagley, X., et al. (1997) Quantum Memory with a Single Photon in a Cavity. Physical Review Letters, 79, 769.
http://dx.doi.org/10.1103/PhysRevLett.79.769 - 17. Derrick, E.B., Haroche, S. and Raimond, M. (1996) Characterising Whispering-Gallery Modes in Microsheres by Direct Observation of the Optical Standing Wave Pattern in the Near Field. Optics Letters, 21, 698.
http://dx.doi.org/10.1364/OL.21.000698 - 18. Knight, J.C., Dubreuil, N., et al. (2000) Single Photons Nondestraction Clarified. Physics Today, 53, 92.
http://dx.doi.org/10.1063/1.1325252 - 19. Haroche, S. and Daniel, K. (1989) Cavity Quantum Electrodynamics. Physics Today, 42, 24-30.
http://dx.doi.org/10.1063/1.881201 - 20. James, C.B., Steven, J.W. and David, R.J. (2001) Time Measurement at the Millanium. Physics Today, 54, 37.
http://dx.doi.org/10.1063/1.1366066 - 21. Iqbal, S., Sarwar, F., Raza, S.M. and Rehman, A. (2015) How Fractional Charge on an Electron in the Momentum Space Is Quantized? ASRJETS, 14, 265-272.
- 22. Iqbal, S. (2012) Analysis and Applications of Fractional Fourier Transform. Unpublished PhD Thesis, University of Balochistan, Quetta, Pakistan.
- 23. Iqbal, S., Sarwar, F. and Raza, S.M. (2016) Eigen Functions for a Quantum Wire on a Single Electron at Its Surface and in the Quantum Well with Beaded Fractional Quantized States for the Fractional Charges. JAMP, 4, 320-327.
http://dx.doi.org/10.4236/jamp.2016.42039 - 24. Almeida, L.B. (1994) The Fractional Fourier Transform and Time-Frequency Representations. IEEE Transactions on Signal Processing, 42, 3084-3091.
http://dx.doi.org/10.1109/78.330368 - 25. Iqbal, S., et al. (2012) Fractional Fourier Integral Theorem and Fractional Fourier Cosine and Sine Transforms. Science International (Lahore), 24, 233-238.
- 26. Lefrant, S., Mulazzi, E. and Mathis, C. (1994) Raman Spectra of n-Doped Transpolyacetylene Systems: Experiments and Theory. Physical Review B-I, 49, 13400-13407.
- 27. Iqbal, S., Jabeen, S., Sarwar, F. and Raza, S.M. (2016) Quantum Theory of Mesoscopic Fractional Electric Fields in a Cavity of Viscous Mediums. WJCMP, 6, 39-44.
http://dx.doi.org/10.4236/wjcmp.2016.61006 - 28. Jabeen, S. and Jabeen, S. (2013) Dielectric Behaviour of Indigenous Rock Materials? PhD Thesis (Supervised by Dr. Syed Mohsin Raza), University of Balochistan, Quetta, Pakistan.


