Received 16 June 2015; accepted 2 August 2015; published 5 August 2015

ABSTRACT

We address the T_c(s) and multiple gaps of La₂CuO₄ (LCO) via generalized BCS equations incorporating chemical potential. Appealing to the structure of the unit cell of LCO, which comprises sub- lattices with LaO and OLa layers and brings into play two Debye temperatures, the concept of itinerancy of electrons, and an insight provided by Tacon et al.’s recent experimental work concerned with YBa₂Cu₃O_6.6 which reveals that very large electron-phonon coupling can occur in a very narrow region of phonon wavelengths, we are enabled to account for all values of its gap-to- T_c ratio (2∆₀/k_BT_c), i.e., 4.3, 7.1, ≈8 and 9.3, which were reported by Bednorz and Müller in their Nobel lecture. Our study predicts carrier concentrations corresponding to these gap values to lie in the range 1.3 × 10²¹ - 5.6 × 10²¹ cm⁻³, and values of 0.27 - 0.29 and 1.12 for the gap-to-T_c ratios of the smaller gaps.

Keywords:

Generalized BCS Equations, Chemical Potential, Two-Phonon Exchange Mechanism, Structure of the Unit Cell of LCO, Gap-to-T_c Ratio, Effective Mass of Electrons, Number Densities of Charge Carriers

1. Introduction

It is well known that La₂CuO₄ (LCO) is an insulator. It becomes superconducting when suitably doped, (La_0.925Sr_0.075)₂CuO₄ being an example which has a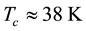. Discovered by Bednorz and Müller [1] , it occupies a unique position among all the high-temperature superconductors (HTSCs) that have been discovered so far for the following reasons:

1) Being the first SC to transcend the BCS barrier of, it heralded the era of high-T_c superconductivity and led to the discovery of YBCO and the Tl-, Bi- and Hg-based SCs―each of them being characterized by a T_c higher than even the liquefaction temperature of nitrogen. This of course is well known.

2) Unlike all the other HTSCs mentioned above, LCO contains predominantly only one species of ions that can give rise to pairing: La (strictly speaking, La_0.925Sr_0.075), which implies that pairing in it is governed by only one interaction parameter. This prima facie poses a problem because application of the generalized BCS equations [2] (GBCSEs) to an SC with a exceeding 23 K and possessing two gaps 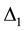and requires two-phonon exchange mechanism (TPEM) for pairing [3] ; by this we mean that phonons are exchanged with two distinct sub-lattice structures. For all the other HTSCs mentioned above, this brings into play two interaction parameters because their sub-lattices contain predominantly two distinct species of ions that can cause electron-phonon interaction to take place, e.g., Y and Ba ions [4] in YBa₂CuO₇ and any two [3] of the Tl, Ba, and Ca ions in Tl₂Ba₂CaCuO₈. This is also the case for the Bi-based [3] and iron-pnictide HTSCs [5] .

3) When the problem mentioned above is addressed―by appealing to the structure of LCO as will be seen below―we find that the input of its T_c alone yields an interaction parameter that enables one to calculate both its gaps. This is in contrast with all the other HTSCs for which the input of two parameters from the set 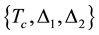is required to calculate the third.

The work reported here is motivated by the need to:

a) Bring the understanding of LCO in the framework of GBCSEs at par with that of all the other HTSCs noted above. This is done in the next section where for any T_c in the range 37 - 40 K, it is shown, in accord with experiment, that 2∆₂₀/k_BT_c = 4.3, where k_B is the Boltzmann constant, and

b) Explain experimental values for the gap-to-T_c ratio other than 4.3, i.e., 7.1, ≈8 and 9.3, attention to which was drawn by Bednorz and Müller [6] in their Nobel lecture. The study of these multiple gap-values is taken up in Section 3 by following an approach that incorporates the chemical potential μ into the equations for the ∆ and T_c of the SC. Such an approach for LCO is based on 1) equations given in two recent papers, one [7] of which sheds light on the BCS-BES crossover physics without appeal to scattering length theory, while the other [8] suggests the possibility of solving a long-standing puzzle posed by and 2) an idea inspired by another recent paper [9] where it has been pointed out that a very large electron-phonon coupling occurs in a very narrow region of phonon wavelengths for an HTSC.

The final section is devoted to a discussion of our findings.

2. LCO Addressed via GBCSEs

2.1. Debye Temperatures of La Ions in LCO

As noted [3] -[5] for all the HTSCs dealt with so far, the first step in their study via GBCSEs is to fix the Debye temperatures of the ions that may be causing pairing. This is done by applying the following equations to each of the sub-lattices of the HTSC comprising layers designated as A_xB_1−x:

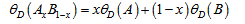(1)

(2)

where is the Debye temperature of the HTSC, and 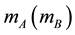is the atomic mass number of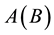. While Equation (1) has been used routinely for binary SCs, Equation (2) has been derived [2] by assuming that the constituents of any sub-lattice simulate the oscillations of a weakly coupled double pendulum. That the constituents of an anisotropic material must have different θ_Ds because their masses are different is an idea that dates back to Born and Karmann [10] .

The observation that 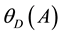and of an HTSC calculated via the above equations depend on the relative positions of A and B in the double pendulum suggests that the structure of the unit cell of the SC should be examined. On doing so we find that it is characterized by layers [11] of LaO, OLa, and CuO₂. This implies that if La is the lower of the two bobs of the double pendulum in the layers that comprise one of the sub-lattices, it is the upper bob in the layers of the other sub-lattice. This feature brings into play two Debye temperatures, in the application of TPEM to LCO as for any of the other HTSCs, but only one interaction parameter because it is the same species of ions in both the sub-lattices that causes pairing.

Applying Equations (1) and (2) to the sub-lattice of LCO comprising OLa layers in which La is the lower of the two bobs, we find that [12] leads to

(3)

where and have been used. The results for the sub-lattice comprising LaO layers are:

(4)

2.2. Dealing with LCO with the Input of Its T_c

For the reason given above, GBCSE for T_c of LCO in the two sub-lattice (two-phonon) scenario, obtained by putting in Equation (4) of [5] , is:

(5)

Note that the equivalent of Equation (5) for YBCO, for example, had two different interaction parameters: and. To determine these, the input of and either or―together with the corresponding θ_Ds―was required. One could then calculate the remaining parameter of the set. Since LCO is characterized by only one interaction parameter, it can be fixed via Equation (5) with the input of T_c alone; we are then enabled to calculate both and.

In writing Equation (5) we have dropped the superscripts of the two θs in the original equation. Solution of this equation with the input of, from Equation (3) and θ₂ = 431.1 K from Equation (4) yields

(6)

This leads to two values for the smaller gap and one for the larger gap via the following equations (Equations (3) and (5) of [5] )

(7)

(8)

In these equations is to be identified with the smaller gap at and with the larger gap at; two values of the former are obtained because θ in Equation (7) can be either 104.8 or 431.1 K. Our results then are:

(9)

Because T_c values of LCO reported in the literature vary from 36 - 40 K, we have given in Table 1 not only the results of the above calculations for T_c = 38 K, but also for four other values.

2.3. Results with a Different Value of Debye Temperature

It was mentioned above that in giving an account of the properties of LCO, Bednorz and Müller in their Nobel lecture [6] had noted that besides 4.3 for the ratio, the following values have also been reported: 7.1, ≈ 8 and 9.3. While our result for this ratio is in agreement with the value 4.3 for any between 37 and 40 K, the problem of explaining the larger values remains. We note in this connection that the value of θ_D (LCO)

employed in our study is 370 K, whereas values both smaller (360 K [12] ) and larger (385 K [13] ) have also been reported in the literature. It therefore seems pertinent to investigate the extent to which the gap-to-T_c ratio changes if one were to adopt the largest of these values, i.e., 385 K. We have carried out this exercise with the following results:

(10)

From these results we conclude that all the different observed values of of LCO cannot be explained on the basis of variation in the Debye temperatures of its different samples.

This study of LCO in the framework of Equations (5) and (8) parallels earlier studies [3] -[5] of various HTSCs in the same framework. Since at the end of it certain observed values of the gap-to-T_c ratio remain unaccounted for, we are led to enlarge the framework employed by incorporating μ in the GBCSEs for ∆ and. This is the task taken up in the next section.

3. LCO Addressed via μ-Incorporated GBCSEs

3.1. μ-Incorporated GBCSEs in the One-Phonon Exchange Mechanism (OPEM) Scenario for a 1-Component SC

It was remarked in [6] that the existence of CPs in LCO is an established experimental fact and that while more than one interaction for pairing may be operative, the phonon mechanism cannot be ruled out. Also reported in this paper is the value of the carrier density in one sample of LCO as being of the order of 10²¹/cm³, which is a parameter that is related to its Fermi energy. We now draw attention to the fact that Fermi energies of HTSCs have of late been attracting considerable interest, partly because their low values are believed [14] to be the cause of high-T_cs and partly because they shed light on the gap-structures of HTSCs. In the context of LCO it seems significant that, on the basis of a thorough theoretical investigation, Jarlborg and Bianconi [15] have recently reported three values for its Fermi energy: 60, 150, and 240 meV. We now recall that both the usual BCS equations and GBCSEs, Equations (5) and (8) above, are derived by assuming

(11)

These considerations strongly suggest the need to study HTSCs in a more general framework of μ-incorpo- rated equations that are not constrained by the above inequality. Some of these equations are already available for studying pairing in the OPEM scenario; as was noted above, they were obtained in studies concerned with crossover physics and the superconductivity of SrTiO₃. In this section we give a complete account of such equations in the OPEM scenario.

In the OPEM scenario, the μ-incorporated GBCSE at for (which is used interchangeably with ∆₁₀ in the equations below) is [7]

(12)

where V₀ is the BCS interaction parameter as in and the chemical potential at, and

Substituting these into Equation (12) and multiplying with, we have

(13)

where

(14)

and

(15)

From the following relations involving the number density of conduction electrons and other relevant parameters

we obtain

(16)

where

(17)

The last step is a consequence of splitting the region of integration into two parts (when): to and to; in the first part whence the expression in the square brackets in the integrand reduces to 2.

From Equations (13) and (16) we obtain

(18)

Equation (18), valid at, is one of our basic equations. Given below from [8] is another basic equation which is valid at:

(19)

where

(20)

(21)

and

(22)

In the above equations μ₁ is the chemical potential and V₁ the value of V in at.

If μ₁ and T_c are known, then we can determine via

(23)

3.2. μ-Incorporated GBCSEs in the Two-Phonon Exchange Mechanism (TPEM) Scenario for a Composite SC

Equations (18) and (19) can be generalized to the TPEM scenario by replacing the “propagator” V used in the former scenario by a “superpropagator” [2] [16] , where for electrons in the energy range to and in the range to; otherwise these interaction parameters have vanishing values. Following then the procedure given in [16] , we obtain for LCO (which we recall involves only one interaction parameter) the following equation as generalization of Equation (18)

(24)

where the superscript (2) of a symbol denotes that it pertains to the TPEM scenario, and

(25)

(26)

In these equations θ₁ and θ₂ are the values of given in Equations (3) and (4), respectively, and the upper limit of the number equation has been taken as the greater of the two Debye temperatures so that pairing can take place due to both the sub-lattices.

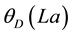
Similarly, we obtain the desired generalization of Equation (19) as

(27)

where

(28)

and

(29)

3.3. An explanation of the Result = 4.27 for LCO on the Basis of Equations (24) and (27) and a Tenet of BCS Theory

While our treatment of the pairing problem in both OPEM and TPEM scenarios has been perfectly general, it has led to an undetermined set of equations. In the latter case we have only two equations, Equations (24) and (27), containing six variables: λ₀, λ₁, μ₀, μ₁, W₂₀, and T_c. Therefore we now assume

(30)

We could have made this assumption at the outset because it is in accord with a tenet of BCS theory. We chose not to do so in order to have readily available a set of equations that might be useful, should it be considered worthwhile to follow up this work with one of greater generality. All calculations in the following are carried out by assuming Equation (30).

Since Equations (24) and (27) are the μ-incorporated versions of Equations (8) and (5), respectively, we need to show that when the constraint embodied in Equation (11) is imposed they yield solutions in agreement with those obtained by solving the latter equations. To this end, we solve Equation (27) for λ with the input of θ₁ = 104.8 K, θ₂ = 431.1 K (see Equations (3) and (4)), T_c = 38 K and different values of μ. We begin with μ = 300 k_Bθ₂, which manifestly satisfies Equation (11), and find that λ = 0.26818, which is the result that we had obtained earlier via Equation (5) and noted in Equation (6). Solution of Equation (24) with μ = 300 k_Bθ₂, and λ = 0.26818 then yields = 6.995 meV, or, which also agrees with the result obtained earlier via Equation (8) and noted in Equation (9). Having thus established that Equations (24) and (27) satisfy the requisite consistency condition, repeating the exercise just carried out by progressively decreasing μ we find that (a) all results quoted for μ = 300 k_Bθ₂ remain unchanged for values of μ up to ≈ 40 meV, and (b) for the limiting value of μ = k_Bθ₂ = 37.15 meV (note that any value lower than this will cause to become complex − see Equation (28)), the results are: λ = 0. 27507, = 6.953 meV, or.

Even after incorporating μ in the equations for T_c and ∆, our considerations so far have succeeded in explaining only one of the observed values of the gap-to-T_c ratio for LCO. Therefore there would seem to be a need for a new idea to explain the other values. It seems to us that the recent findings of Tacon et al. [9] provide precisely such an idea, even though they are based on experiments carried out with another HTSC (YBa₂Cu₃O_6.6). Appealing to it while solving Equations (24) and (27), we present in the next section a complete solution of the problem being addressed.

3.4. An Explanation of the Different Reported Values of for LCO Based on a Treatment of the Number Equations at T = T_c and T = 0 in the Light of the Experimental Findings of Tacon et al. [9]

The work reported in this section is based on an idea inspired by Tacon et al.’s experimental findings about the role of low-energy phonons in YBa₂Cu₃O_6.6 (superconducting transition temperature T_c =  61 K) determined by employing high-resolution inelastic X-ray scattering. These experiments revealed features that were interpreted by the authors as signifying that (a) extremely large superconductivity-induced line-shape renormalizations are caused by phonons in a narrow range of momentum space and (b) the electron-phonon interaction has sufficient strength to generate various anomalies in electronic spectra, but does not contribute significantly to Cooper pairing. Having probed the electron-phonon coupling via their ingenious two-level approach of X-ray scattering, they further noted that “in terms of its amplitude, the coupling is actually by far the biggest ever observed in a superconductor, but it occurs in a very narrow region of phonon wavelengths and at a very low energy of vibration of the atoms”. This statement induces us to review below our earlier treatment of the number equation.

We recall that the limits of the number equation in the previous section―both at T = T_c and T = 0―were taken as −μ and k_Bθ₂. We now call attention to the facts that a) in dealing with an SC that has T_c ≈ 38 K, we need to invoke TPEM, which b) brings into play two Debye temperatures θ₁ and θ₂ > θ₁, and c) if the SC were a 1-component SC characterized by θ₁, the number equation at T = 0 for it would comprise two terms: one corresponding to where = 0 for electrons having energies between −μ and −k_Bθ₁ and the other where ≠ 0 for energies between −k_Bθ₁ and +k_Bθ₁ (see Equation (17)); similarly, if the SC was a 1-component SC characterized by θ₂, the number equation for it at T = 0 would comprise two terms, one corresponding to where = 0 for energies between −μ and −k_Bθ₂ and the other where ≠ 0 for energies between −k_Bθ₂ and +k_Bθ₂. Note that the lower limit in both these cases is −μ. In dealing with a composite SC characterized by two Debye temperatures θ₁ and θ₂ > θ₁, it was then natural to take k_Bθ₂ as the upper limit of the number equation, and this is the choice we had made earlier.

Guided by the insight provided by the findings of Tacon et al. [9] , we now proceed to explore the consequences of narrowing down the range of phonon energies in the problem. If we require that in doing so we should keep intact for both the sub-lattices the region of momentum space for which ≠ 0, then we need to make just one change in our earlier treatment of the number equations: drop the first term in Equation (26). We recall that this term corresponds to the region for which = 0. We now follow up on this idea.

Our procedure above comprised solving Equation (27) for λ with the input of T_c and different values of μ and then using these (λ, μ) values to solve Equation (24) for. We now adopt a variant of this procedure which comprises (a) eliminating λ from Equations (24) and (27) by appealing to Equation (30), (b) solving the resulting equation for μ with the input of T_c = 38 K and with p as a variable, and then (c) determining λ by using either Equation (24) or (27). This is a procedure that enables us to find quickly if sensible solutions for (λ, μ) exist for any particular value of p.

Eliminating λ from Equations (24) and (27) by appealing to Equation (30), we have

(31)

Attempting to solve Equation (31), we find that it has no solution for. The solutions for μ for have been shown in Figure 1. The μ values of this figure are used to calculate the coupling strength λ [with the additional input of θ₁ = 104.8 K, θ₂ = 431.1 K, and T_c = 38 K)] via Equation (24) whence it is found to lie in the range 0.27388 - 0.26843. The resulting plot of λ against p is shown in Figure 2. In Table 2, we have given the (μ, λ) solutions corresponding to the four specific values of p, i.e., 4.3, 7.1, 8, and 9.3, that were mentioned in [6] . These results change insignificantly if T_c is taken as 36 K or 40 K (rather than 38 K) as is seen from the following examples:

4. Predictions of the μ-Incorporated GBCSEs for LCO

4.1. Values of the Smaller Gaps

A review of our procedure so far is as follows. By including μ in GBCSEs as applicable to LCO, appealing to an idea inspired by the work of Tacon et al. [9] and using as input any of the observed values of the gap-to-T_c ratio for 36 ≤ T_c ≤ 40 K, we have been led to solutions for μ and λ that are “sensible”. Sensible because we found a) μ to have a low value―in the meV range (recall that for elemental SCs, μ is in ≈2 - 10 eV range), which is in accord with the assertion made in [14] and the values reported in [15] , and b) λ to be less than 0.5, which is in accord with the Bogoliubov constraint as discussed in [5] .

We now note that the (μ, λ)-values that we have been led to, enable us to calculate and T_c in the OPEM scenario vide Equations (18) and (19), respectively. These results, which constitute predictions of our approach, are also included in Table 2. It thus follows that, in suitably sensitized experimental set-ups, LCO should also exhibit for the gap-to-T_c ratio (with T_c taken as 38 K) the following values: 0.27 - 0.29 (≈3 K) and 1.12 (≈12 K), where the numbers in the parentheses denote the temperatures at which these smaller gaps are predicted to vanish.

4.2. Carrier Concentration

We can calculate the carrier concentration n via the following equation

(32)

which is the second equation after Equation (15), with E_F replaced by μ and the factor of ħ² inserted. However, before we can use this equation we need to find the band effective mass of electrons in LCO. This can be done by using the following expressions for as in

(33)

where we have put the band effective mass as s times the free electron mass m_e, and

(34)

where γ is the experimentally obtained electronic specific heat constant (also known as the Sommerfeld constant) and v the gm-at volume.

From Equations (33) and (34) we obtain

(35)

We now use: γ = 4.5 mJ/mol K² (given in [11] ), = 22.60 cm³ and the values of μ corresponding to p = 4.3 and 9.3 to obtain

(36)

Upon putting m = s times the free electron mass in Equation (32) we obtain

(37)

Since the value of the carrier concentration noted in [6] is “of the order of 10²¹/cm³,” these results support the approach followed in this study.

5. Discussion

1) Strictly speaking, Fermi energy is a term applicable to non-interacting systems. In this note however it has been used interchangeably with the chemical potential, as is usually done in the literature on superconductivity.

2) It is well known that HTSCs are characterized by multiphase and multi-scale complexity and that their Fermi surfaces have highly complex structures comprising many sheets that span different bands. In the light of this observation it would seem that our treatment of LCO based on multiple Debye temperatures and TPEM is rather naive. We are therefore impelled to draw attention to the following:

a) As can be seen in [17] , Fermi surfaces of elemental SCs too have rather complex structures: none of them has the idealized spherical Fermi surface assumed in BCS theory. And yet, with the exception of a few, e.g., Pb and Hg, the mean-field approximation (MFA) employed in the theory works for most of them.

b) It is evident that the values of μ corresponding to different values of ∆₂ and T_c that we have determined reflect the structure of the Fermi surface of the SC. Implicit in our approach is the concept of locally spherical Fermi surfaces (LSFSs), which takes the complexity of the HTSC into account in a rather simple (if not the simplest possible) manner. Such simplicity of approach for the kind of system we are dealing with is a goal every model strives to achieve. We note that LSFSs come into play because of itinerancy of electrons and the adoption of MFA.

c) Itinerancy of electrons in a multi-band SC is a much-invoked concept since at least the time of Suhl et al.’s paper [18] . We give below an analogy to bring out how this concept justifies dropping of the first term in the number equation (26).

d) Consider a convoy on a road passing through a range of mountains. As the road twists and turns through a series of valleys and mountains, the amount of sunlight it receives will vary from a maximum at the highest point of the range to a minimum at a place determined by the topography of the entire range. Itinerant conduction electrons in a solid on a 3-D Fermi surface are akin to such a convoy: there will be places where they can exchange phonons with the A- or the B-ions separately, and a place or places where they can exchange phonons with both of them simultaneously. For the last of these cases, one can then envisage a situation where phonon energies span not the usual range from −μ to k_Bθ₂, but a depleted range from −k_Bθ₂ to k_Bθ₂. The mean value of μ for the electrons under consideration is equivalent to the word “place” used for the convoy.

e) It seems interesting to point out that the concept of LSFSs is similar to the concept of locally inertial coordinate frames employed in the general theory of relativity [19] .

3) In connection with the remark by Tacon et al. [9] that “the electron-phonon interaction has sufficient strength to generate various anomalies in electronic spectra, but does not contribute significantly to Cooper pairing”, we should like to note that this statement is presumably based keeping OPEM in mind, which cannot account for the observed T_c of LCO.

6. Conclusions

Our findings provide a confirmation of the idea that low values of μ play an important role in HTSCs. Besides, we have for the first time given a plausible quantitative explanation of the different values of gap-to-T_c ratio that have been reported for LCO in the literature.

In effect, the approach followed in this note can also be viewed as a new direct method for relating the ∆₀ and T_c of an HTSC with its E_F.

Acknowledgements

G. P. M. acknowledges that his correspondence with Dr. D. M. Eagles and Professor M. de Llano has been invaluable in this study. He thanks Professor G. Szirmai for a perceptive remark during EUROQUAM 2010 on the approach followed herein and Professor D. C. Mattis for encouragement.

Cite this paper

G. P.Malik,V. S.Varma, (2015) A Study of Superconducting La₂CuO₄ via Generalized BCS Equations Incorporating Chemical Potential. World Journal of Condensed Matter Physics,05,148-159. doi: 10.4236/wjcmp.2015.53017

References

NOTES

^*Corresponding author.

^#Present address: B-208 Sushant Lok I, Gurgaon, Haryana, India - 122009.