Received 18 April 2015; accepted 25 May 2015; published 29 May 2015

ABSTRACT

We study the correlation functions of one-dimensional Hubbard model in the presence of external magnetic field through the conformal field method. The long distance behaviour of the correlation functions and their unusual exponents for the model in the presence of a magnetic field are developed by solving the dressed charge matrix equations and setting the number of occupancies 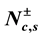to one, as alternative to the usual zero used by authors in literatures. This work shows that the exponent of the correlation functions is a monotonous function of magnetic field and the correlation functions decay as powers of these unusual exponents. As the magnetic field goes to zero, we obtain the exponents as 8.125, 11.125, 17.125, 26.125 and 38.125 at 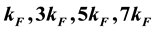and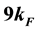. Our analytical results will provide insights into criticality in condensed matter physics.

Keywords:

Correlation Functions, Magnetic Field, Unusual Exponents

1. Introduction

Almost twenty five years ago, Frahm and Korepin introduced the calculation of critical exponents for the one-dimensional (1D) Hubbard model, using the finite size scaling and the principle of conformal field theory (CFT) [1] . This enabled theorists to explore the physics of 1D correlated electron systems. Notwithstanding significant works, the understanding of the behaviour of correlated electron systems is not yet complete. In one dimension, the Hubbard Hamiltonian provides opportunity to study correlation effects in 1D models and the correlation functions decay as power of the distance [2] - [4] . It is the calculation of the critical exponents characterizing this power-law behaviour that have attracted constant theoretical interest. Outstanding results in this field

(with correlation exponents 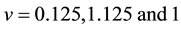for 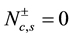at zero magnetic field around the Fermi points

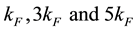) have been obtained from conformal field techniques, perturbation calculations and renormalization group methods in different models [1] [5] -[7] . For our calculation, we obtain the correlation exponents as

8.125, 11.125, 17.125, 26.125 and 38.125 arou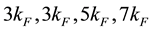nd and 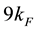by setting the parameter characterizing particle-hole excitation to one 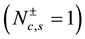as the magnetic field goes to zero, and the unusual expo-

nent of the correlation function changes monotonically with change in magnetic field. The progress made in the understanding of critical phenomena in quantum systems as a result of conformal invariance have provided great insights to the problem of calculation of these critical exponents [8] . Although, interacting 1D quantum systems might carry countless low-energy excitations, with linear dispersion relations, but with different Fermi velocities, so the systems are not Lorentz invariant [9] . When the motions of these excitations are decoupled, one can now apply the CFT [10] . Usually, in the application of the conformal field techniques, the nonnegative integer 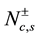characterizing particle-hole excitations is always taken as zero, but in this paper we shall calculate the electron

field correlation function and the density-density correlation function by setting the parameter 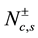to one, and

investigate how this affects the conformal dimensions and critical exponents of the correlation functions. This paper is organized as follows. In Section 2, we review the Bethe Ansatz equations of the Hubbard model and the analytic form of the correlation functions predicted by CFT is given. The dressed charge matrix elements are also calculated with the Wiener-Hopf technique and these elements are used to obtain the magnetic field dependence of the conformal dimensions. The long-distance behaviour of the electron field and density-density correlation functions and their unusual exponents for small magnetic field are calculated in Section 3. The electron field correlation function in momentum space and their Tomonaga-Luttinger (TL) liquid behaviour is examined in Section 4. Finally, Section 5 is devoted to discussion of the properties of the critical exponents for 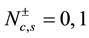and conclusion.

2. The Hubbard Model and the Dressed Charge

The Hubbard model is basically the simplest model describing interacting spin-1/2 fermions in many-body physics. In the presence of magnetic field it is defined by the Hamiltonian [1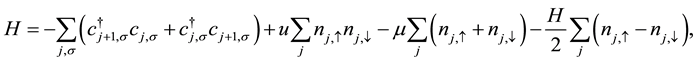1]

(1)

where is the creation (annihilation) operator with electron spin σ at site j and 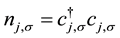is the

number operator. u is the on-site Coulomb repulsion, μ is the chemical potential and H is the external magnetic field. The hopping integral t = 1. Lieb and Wu [2] has solved Equation (1) exactly and obtained the Bethe Ansatz equations

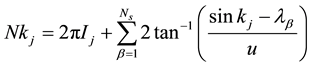(2)

(3)

where the quantum number I_j and J_α are integers or half-odd integer, with N_↑ and N_↓ being the number of electrons with spin up and down, and N_s = N_↓ down spins are characterized by the moment a k_j of holons and rapidities λ_α of spinons.

In the thermodynamic limit, with continuous momentum and rapidity variables, the Lieb-Wu equations become integral equations for the ground state distribution functions of moment a and of rapidities, obeying the equations

(4)

The state corresponding to the solution of Equations (2) and (3) has energy and momentum given by

(5)

(6)

where the conformal dimensions are given by

(7)

(8)

The positive integers, for holon and spinon describes particle-hole excitations, with being the number of occupancies that a particle at the right (left) Fermi level jumps to, represents the

change in the number of electrons (down-spin) with respect to the ground state, represents the number of particles which transfer from one Fermi level of the holon to the other and represents the number of particles which transfer from one Fermi level of the spinon to the other, and both and are either integer or half-odd integer values. Finally, the dressed charge matrix Z describing anomalous behaviour of critical exponents is given by

(9)

and the elements are defined by the solutions of the following coupled integral equations

(10)

(11)

(12)

(13)

where the kernel is defined as

(14)

The values of are fixed by

(15)

(16)

For small magnetic field we solve the dressed charge matrix equations by Wiener-Hopf technique [12] [13] for terms up to order in the strong coupling limit. With Equation (16), we write Equation (13) as

(17)

Fourier transforming Equation (17), we obtain

(18)

where the kernels are given by

(19)

We solve Equation (18) by introducing the function

(20)

and expanding it as

(21)

where are defined as the solutions of the Wiener-Hopf equations

(22)

(23)

The driving terms and the solutions becomes smaller as n increases because is large. Our procedure follows Fabian et al. [11] . Assuming the function and are known. We define

(24)

Where the functions are analytic on the upper and lower planes respectively, with

(25)

Also we assume

(26)

In terms of these functions we express the Fourier transform of Equation (23) as

(27)

where is the Fourier transform of. Now we split Equation (23) into the sum of two parts that are analytical and non-zero in the upper and lower half planes. To obtain this we use the factorization

(28)

(29)

where are analytic and non-zero in the upper and lower half planes respectively and are normalized as

(30)

Useful special function of are

(31)

Using Equations (27) and (28), we obtain

(32)

Decompose the right hand side of Equation (32) into the sum of two functions

(33)

This implies that

(34)

To obtain the solution of Equation (22) for, we set the driving term to be

(35)

We decompose the first term by using

(36)

The second term of Equation (35) is meromorphic function of with simple poles located at

(37)

Note, there is no pole at. The decomposition of the factor gives

(38)

(39)

Using Equation (39) we can express the function, for any function that is analytic and bounded in the lower half-plane as the sum of two functions analytic in the upper/lower half-plane

(40)

(41)

Applying the formula Equations (41) to (35) and Equation (33), we obtain

(42)

(43)

Now,

(44)

Therefore,

(45)

(46)

For

(47)

The functions are obtained by using Equation (34)

(48)

From Equation (23) for, by setting in Equation(48), we obtain

(49)

By definition

(50)

(51)

where is magnetic field, is critical field, strong coupling, magnetic field at zero temperature and corresponds to Fermi points. Combining the result Equation (49) with Equation (50), we obtain the first order contribution to as follows

(52)

As, we use Equations (30) and (31) on Equation (52) to obtain

(53)

Simplifying further, we obtain

(54)

Using Equation (51), we obtain

(55)

Next, the second order contribution to is obtained by taking the Fourier transform of Equation (23) for.

(56)

From Equation (28)

(57)

(58)

From Equation (33),

(59)

We have decomposed into which is analytic in the upper and lower half-planes. is given by

(60)

where is a small positive constant. has a branch cut along the negative imaginary axis and by deforming the contour of integration we rewrite Equation (58) as

(61)

From Equation (29), as

(62)

(63)

Since,

(64)

For the integrand rapidly decrease because, and hence the integral is approximated by expanding the terms other than around. Therefore, we obtain

(65)

From Equation (34), we obtain

(66)

Using

(67)

we obtain

(68)

Using the value of from Equation (51) in Equation (68), we obtain

(69)

Therefore, with Equations (55) and (69), we obtain

(70)

Now to evaluate the dressed charge matrix element we take the Fourier transform of Equations (16) and (18) and obtain

(71)

Applying the same process in the determination of Equation (70), we obtain

(72)

Similarly, with the same process, we obtain the other two elements of the dressed charge matrix as

(73)

and

(74)

From Equation (16) together with the property that for and , the down-spin density is obtained as

(75)

Using Equation (75) on Equations (70) and (72), we obtain the dressed charge matrix equations as

(76)

(77)

(78)

(79)

At half-filling, and by neglecting corrections to order, the elements of the dressed charge become

(80)

(81)

(82)

(83)

To obtain the conformal dimensions in terms of small magnetic field we use Equations (80) to (83) on Equations (7) and (8). Note that,

(84)

Therefore, the magnetic field dependence of the conformal dimensions are given by

(85)

(86)

According to the principles of CFT, the general expression for correlation function contains factors from holons and spinons, given by [11]

(87)

3. Correlation Functions in Magnetic Field

We now use the results obtained in the last section to obtain the magnetic field dependence of the unusual exponents of the electron field correlation function and density-density correlation function by setting the non-

negative integer. First we consider the electron field correlation function with up-spin which originates

from the quantum numbers (D_c, D_s) = (1/2, −1/2), (3/2, −3/2), (5/2, −5/2), (7/2, −7/2), (9/2, −9/2), ΔN_c = 1 and ΔN_s = 0. Therefore, the corresponding conformal dimensions for are

(88)

(89)

(90)

(91)

where the contributions from and terms of order are neglected. Using Equations (89) and (91) on Equation (87), we obtain

(92)

The critical exponent is given by

(93)

This implies that

(94)

and

(95)

Next, we obtain the conformal dimensions for as

(96)

(97)

(98)

(99)

Using Equations (97) and (99) on Equation (87), we obtain

(100)

The critical exponent is given by

(101)

and

(102)

Next, for, we obtain the conformal dimensions as

(103)

(104)

(105)

(106)

Using Equations (104) and (106) on Equation (87), we obtain

(107)

The critical exponent is given by

(108)

and

(109)

For, we obtain the conformal dimensions as

(110)

(111)

(112)

(113)

Using Equations (111) and (113) on Equation (87), we obtain

(114)

The critical exponent is given by

(115)

and

(116)

Finally, for, we obtain the conformal dimensions as

(117)

(118)

(119)

(120)

Using Equations (118) and (120) on Equation (87), we obtain

(121)

The critical exponent is given by

(122)

and

(123)

Combining Equations (92), (100), (107), (114) and (121), we obtain the long-distance asymptotic form of the electron field correlation function with up-spin as

(124)

Lastly, we consider the density-density correlation function which originates from the quantum numbers and. Here the corresponding conformal dimensions for are

(125)

(126)

Again contributions from are neglected. Using Equations (125) and (126) on Equation (87), we obtain

(127)

The critical exponents are given by

(128)

and

(129)

For the conformal dimensions are

(130)

(131)

Using Equations (130) and (131) on Equation (87), we obtain

(132)

The critical exponents are given by

(133)

and

(134)

Next, for the conformal dimensions are

(135)

(136)

Using Equations (135) and (136) on Equation (87), we obtain

(137)

(138)

and

(139)

Finally, for the conformal dimensions are

(140)

(141)

Using Equations (140) and (141) on Equation (87), we obtain

(142)

(143)

and

(144)

4. Correlation Function in Momentum Space

The electron field correlation function Equation (124) has singularities at the Fermi points and respectively. Therefore, at, the momentum distribution is given by

(145)

The critical exponent

(146)

and

(147)

Here we neglect logarithmic field dependence. Equation (145) represents the momentum distribution function around for the electron field correlator. It exhibits a typical power-law behaviour of the TL liquid, with critical exponent given by Equation (146). This unusual exponent as the magnetic field goes to zero.

Another singularity is at. The momentum distribution here is

(148)

with critical exponent

(149)

Equation (148) exhibits a typical power-law singularity of the TL liquid around the Fermi point, and as the magnetic field goes to zero.

Next at, the momentum distribution is given by

(150)

with the unusual exponent

(151)

Also, Equation (150) represents the momentum distribution function around the Fermi point for the electron field correlator, and it exhibits a typical power-law behaviour of the TL liquid with critical exponent given by Equation (151). This unusual exponent as the magnetic field goes to zero.

At, the momentum distribution is

(152)

and

(153)

Equation (152) exhibits a typical power-law behaviour of the TL liquid around, with critical exponent given by Equation (153). This unusual exponent as the magnetic field goes to zero.

Finally, at the momentum distribution takes the form

(154)

with

(155)

and Equation (154) also exhibits typical power-law behaviour of the TL liquid around the Fermi point, with critical exponent as the magnetic field goes to zero.

5. Discussions

In this paper, we have calculated the electron field and density-density correlation functions and their unusual exponents by using the nonnegative integer characterizing particle-hole excitations as 1 in the 1D Hubbard model. Based on the principles of CFT, we obtain expressions for the unusual exponents that describe the long-distance behaviour of the correlation functions in coordinate and momentum space. The unusual behaviour of the exponents depend on the magnetic field. The zero magnetic field exponents at and for in the strong-coupling limit has been obtained before [1] [3] [14] -[16] . At zero magnetic field is a monotonous function of the coupling constant u. In our calculation, we have used and obtain the exponents at and respectively, and observe that is a monotonous function of the magnetic field. The part arises

from the excitation of, the part from , the part from, the part from, and part from . This implies both holon and spinon excitations are responsible for and oscillation parts respectively.

In conclusion, the electron field correlation function and the unusual exponents has been obtained around the Fermi points and respectively, and the density-density correlation function around and is also obtained for. These results show that the correlation function clearly exhibits power-law behaviour of TL liquids as the exponent changes monotonically with change in magnetic field. Setting indicates presence of particle-hole excitations in the asymptotics. Therefore, the results obtained here are contributions from both particle-hole excitations and collective modes (holons and spinons).

References