World Journal of Condensed Matter Physics
Vol.05 No.01(2015), Article ID:54295,5 pages
10.4236/wjcmp.2015.51005
Effective Mass of Acoustic Polaron in Quantum Dots
Hao Li, Junhua Hou, Xiaofeng Duan
College of Physics and Information Engineering, Shanxi Normal University, Linfen, China
Email: jhhou@126.com, sxnuxf@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 February 2015; accepted 24 February 2015; published 27 February 2015
ABSTRACT
The variational effective mass with respect to the e-p coupling constant for different values of cutoff wave vector is performed in quantum dot. The self-trapping transition of acoustic polaron in quantum dot is reconsidered by character of the effective mass curve varying with the e-p coupling. The holes are determined to be self-trapped in AlN quantum dot systems.
Keywords:
Quantum Dot, Effective Mass, Acoustic Polaron, Self-Trapping

1. Introduction
The luminous property of the photoelectric materials has been explored by the trapping electrons for a long time [1] - [17] . As is well-known, an electron interacts with the acoustic and optical modes of the QD, but the abrupt change of the polaron states from the quasi-free to the self-tripping is usually caused by the electron-longitudinal acoustic-phonon (e-LA-p) interaction [6] . The problems of acoustic polaron have been studied by many scientists in the past decades. For weak electron-phonon (e-p), one expects that the electron behaves as a quasi-free particle (free polaron) and should be de-localized over all sites, whereas for very strong coupling it is conceivable that the electron is self-trapped by phonons [7] . Peeters had studied the question of trapping polaron in 3D structures and pointed out that the electron in most of semiconductors cannot be trapped [11] . In addition, the interactions between electron and phonon are enhanced in confined structures, such as quantum wires and quantum dots [8] [9] [12] . So that the self-trapping transition of the electron in low dimension is easier to be realized.
It is well-known that the effective mass is corresponding to the carrier mobility, and has more experimental comparability. So that it will be an effective method to count the traps of electron by measuring the effective mass of the acoustic polaron. Effective mass theory had been used for years in several branches of modern physics like nuclear physics or solid-state physics. This theory is a useful tool for studying the motion of carriers in pure crystals and also for the virtual-crystal approximation to the treatment of homogeneous alloys (where the actual one-electron potential is approximated by a periodic potential), as well as of graded mixed semiconductors.
In this paper, we study the interaction of e-LA-p in quantum dots by using a Huybrechts-like variational approach [18] . The numerical calculation for the effective mass of the polarons will be performed and used to discuss the characters of self-trapping of the acoustic polarons in quantum dots.
2. The Ground State of the Acoustic Plaron
Considering the acoustic plaron in nanoscale spherical is confined in three dimensional boxes. The e-LA-p system Hamiltonian in the nanoscale spherical had been written as the following form in our previous work:
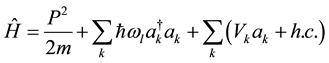 (1)
(1)
where  denotes the kinetic energy of the electron. The acoustic phonon contribution is given by
denotes the kinetic energy of the electron. The acoustic phonon contribution is given by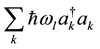 .
.
In case of breathing mode, the e-p coupling function can be given by
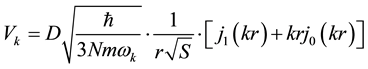 (2)
(2)
where j0 is correspondingly the spherical Bessel function of order zero, 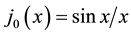 , and j1 is the spherical Bessel function of order one,
, and j1 is the spherical Bessel function of order one,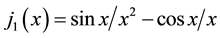 . The N is the number of the unit cells and D is the dimensionless e-p coupling constant. The S is presented as
. The N is the number of the unit cells and D is the dimensionless e-p coupling constant. The S is presented as
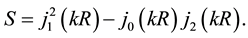 (3)
(3)
The j2 in above equation is the spherical Bessel function of order two and can be presented as 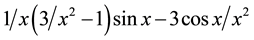 . R is the radius of the quantum dot.
. R is the radius of the quantum dot.
Firstly, we carry out two unitary transformations to Equation (1)
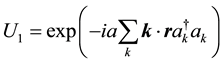 (4a)
(4a)
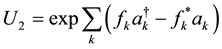 (4b)
(4b)
where a in above is the variational parameter, which will tend to 0 in the strong coupling limit and 1 in weak coupling limit. 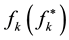 is a physical description decided by coupling strength.
is a physical description decided by coupling strength.
Then let us introduce the linear combination operators of the position and momentum of the electron by the following relations.
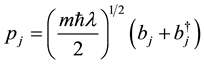 (5a)
(5a)
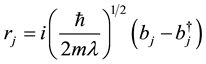 (5b)
(5b)
where 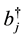 and
and 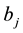 are respectively the creation and annihilation operators.
are respectively the creation and annihilation operators. 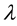 is another variational parameter.
is another variational parameter.
The Hamiltonian finally transforms to the following form:

Then the ground-state of the acoustic polaron can be calculated by averaging Hamiltonian (6) over the zero- phonon state |0ñ, for which we have

3. Strong and Weak-Coupling Limit
3.1. Strong-Coupling Limit
In Unitary transformation U1, a → 0 is corresponding to the strong-coupling limit. Using (6) and (7), by some treatments, the ground-state energy in spherical QD can be obtained as:

Making a variation to a

One can obtain the following equation

And the ratio of effective mass to band mass can be presented as [11]

3.2. Weak-Coupling Limit
In Unitary transformation U1, a → 1 is corresponding to the weak-coupling limit, the ground state energy of the polar on can be obtained as follows:

Then make a variation to a:


The ratio of effective mass to band mass is [11]

4. Results and Discussions
For purpose of comparison facility, we have expressed the energy in units of mc2 and the phonon vector in units of mc/ħ in the calculations. As can be seen in Figure 1 and Figure 2, the effective mass of the acoustic polarons as the function of the e-p coupling constant in quantum dot with a fixed radius 0.1 are performed in weak- coupling limit and strong-coupling limit, respectively.
Figure 1. Effective mass of the weak-coupling acoustic polarons in quantum dot with the radius R = 0.1 as a function of the e-p coupling constant a for k0 = 5, 10 and 20, respectively.
Figure 2. Effective mass of the strong-coupling acoustic polarons in quantum dot with the radius R = 0.1 as a function of the e-p coupling constant a for k0 = 5, 10 and 20, respectively.
Comparative observation on the numerical effective mass results of the Figure 1 and Figure 2, one can find in Figure 2 the obvious nonlinearity of the increasing effective mass with the enhanced couping of the electron and acoustic phonon in quantum dot. Which we thought the self-trapping transition of the electron is coming up induced by the acoustic phonon interaction. In Figure 1, the fuction curve of the effective mass varies linearly as the e-p coupling. So that the self-trapping transtion can not be realized in case of the weaking coupling limit of the electron and acoustic phonon interaction.
As can be seen in Figure 2 a knee in the effective mass curve with respect to α at αc ≈ 0.320, for k0 = 5, which is called the “phase transition” critical point, where the polaron state transforms from the quasi-free to the self- trapped [6] [7] [9] [10] . When k0 = 10 and 20, the critical points are at αc ≈ 0.111 and 0.062, respectively. It is obviously that the critical point αc shifts toward the weaker e-p coupling with increasing the cutoff wave-vector k0. The character of the critical coupling constant varying with the cutoff wave-vector k0 is corresponding to the previous papers [6] [7] [10] .
The αck0 had been used as a criterion for the self-trapping transition of the acoustic polaron. Acoustic polaron can be self-trapped if the material’s αk0 larger than the αck0. In this work the αck0 are close to 1.6, 1.1 and 1.2 for k0 = 5, 10 and 20, respectively. The AlN has the αk0 closed to 1.16 and 2.79 for light and heavy holes, respectively [10] . So that the self-trapping transition of the holes might be realized in the AlN quantum dot with the radius of 0.1.
5. Summary
The trapped electron influences luminescence properties of photoelectric material. The self-trapping transition of acoustic polaron in quantum dot has been reconsidered by calculating the effective mass of the acoustic polaron. It can be concluded that the holes in AlN are expected to have the self-trapping transition in quantum dot systems. Some criterion values (αck0) of the acoustic polaron in spherical QD systems are smaller than those in 3D and 2D systems. Therefore, the self-trapping transition of the acoustic polaron in spherical QD is easier to be realized than that in 3D and 2D systems. The conclusion meets the general sense that the e-p coupling effects will be substantially enhanced in confined quantum structures.
Acknowledgements
This work is supported under Grant No. 11147159 from the National Natural Science Foundation of China.
References
- Wittmer, J.P., Tanguy, A., Barrat, J.-L. and Lewis, L. (2002) Vibrations of Amorphous, Nanometric Structures: When Does Continuum Theory Apply? Europhysics Letters, 57, 423. http://iopscience.iop.org/0295-5075/57/3/423/fulltext/ http://dx.doi.org/10.1209/epl/i2002-00471-9
- Murray, D.B. and Saviot, L. (2004) Phonons in Inhomogeneous Continuum: Vibrations of an Embedded Nanoparticle. Physical Review B, 69, Article ID: 094305. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.69.094305#fulltext http://dx.doi.org/10.1103/PhysRevB.69.094305
- Andrievski, R.A. and Glezer, A.M. (2001) Size Effects in Properties of Nanomaterials. Scripta Materialia, 44, 1621- 1624. http://www.sciencedirect.com/science/article/pii/S1359646201007862?np=y http://dx.doi.org/10.1016/S1359-6462(01)00786-2
- Rolo, A.G. and Vasilevskiy, M.I. (2007) Raman Spectroscopy of Optical Phonons Confined in Semiconductor Quan- tum Dots and Nanocrystals. Journal of Raman Spectroscopy, 38, 618-633. http://onlinelibrary.wiley.com/doi/10.1002/jrs.1746/abstract http://dx.doi.org/10.1002/jrs.1746
- Sternitzke, M. (1997) Structural Ceramic Nanocomposites. Journal of the European Ceramic Society, 17, 1061-1082. http://www.sciencedirect.com/science/article/pii/S0955221996002221# http://dx.doi.org/10.1016/S0955-2219(96)00222-1
- Peeters, F.M. and Devreese, J.T. (1985) Acoustical Polaron in Three Dimensions: The Ground-State Energy and the Self-Trapping Transition. Physical Review B, 32, 3515-3521. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.32.3515 http://dx.doi.org/10.1103/PhysRevB.32.3515
- Hou, J.H. and Liang, X.X. (2007) On the Possibility of Self-Trapping Transition of Acoustic Polarons in Two Dimen- sions. Chinese Physics, 16, 3059-3066. http://iopscience.iop.org/1009-1963/16/10/040 http://dx.doi.org/10.1088/1009-1963/16/10/040
- Manka, R. and Suffczynski, M. (1980) The Large Polaron First-Order Phase Transition. Journal of Physics C: Solid State Physics, 13, 6369-6379. http://iopscience.iop.org/0022-3719/13/34/007 http://dx.doi.org/10.1088/0022-3719/13/34/007
- Shoji, H. and Tokuda, N. (1981) Phase-Transition-Like Behaviour in the Problems of Different Types of Polaron. Journal of Physics C: Solid State Physics, 14, 1231-1242. http://iopscience.iop.org/0022-3719/14/9/010 http://dx.doi.org/10.1088/0022-3719/14/9/010
- Hou, J.H. and Liang, X.X. (2007) Self-Trapping of Acoustic Polaron in One Dimension. Chinese Physics Letters, 24, 3222-3224. http://cpl.iphy.ac.cn/EN/abstract/abstract35961.shtml http://dx.doi.org/10.1088/0256-307X/24/11/055
- Peeters, F.M. and Devreese, J.T. (1985) Acoustical Polaron in Three Dimensions: The Ground-State Energy and the Self-Trapping Transition. Physical Review B, 32, 3515-3521. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.32.3515 http://dx.doi.org/10.1103/PhysRevB.32.3515
- Farias, G.A., da Costaw, W.B. and Peeters, F.M. (1996) Acoustical Polarons and Bipolarons in Two Dimension. Physical Review B, 54, 12835-12840. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.54.12835#fulltext http://dx.doi.org/10.1103/PhysRevB.54.12835
- Xiao, J.L., Eerdun, C. and Zhang, P. (1999) Properties of Surface Magnetopolaron in CdF2 Semiconductor. Chinese Journal of Semiconductors, 20, 411-447. http://www.jos.ac.cn/bdtxben/ch/reader/view_abstract.aspx?file_no=200592656361205&flag=1
- Liang, X.X. and Gu, S.W. (1984) The Polarons and the Third Layers in Semi-Infinite Polar Crystals. Solid State Communications, 50, 505-508. http://www.sciencedirect.com/science/article/pii/003810988490317X
- Sun, J.P., Teng, H.B., Haddad, G.I. and Stroscio, M.A. (1998) Electron-Interface Phonon Interaction in Multiple Quan- tum Well Structures. Semiconductor Science and Technology, 13, A147. http://iopscience.iop.org/0268-1242/13/8A/042?fromSearchPage=true http://dx.doi.org/10.1088/0268-1242/13/8A/042
- Mori, N. and Ando, T. (1989) Electron-Optical-Phonon Interaction in Single and Double Heterostructures. Physical Review B, 6175. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.40.6175#fulltext http://dx.doi.org/10.1103/PhysRevB.40.6175
- Meyer, R., Lewis, L.J., Prakash, S. and Entel, P. (2003) Vibrational Properties of Nanoscale Materials: From Nanoparticles to Nanocrystalline Materials. Physical Review B, 68, Article ID: 104303. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.68.104303#fulltext http://dx.doi.org/10.1103/PhysRevB.68.104303
- Huybrechs, W.J. (1977) Internal Excited State of the Optical Polaron. Journal of Physics C: Solid State Physics, 10, 3761-3768. http://iopscience.iop.org/0022-3719/10/19/012 http://dx.doi.org/10.1088/0022-3719/10/19/012



