World Journal of Condensed Matter Physics
Vol.05 No.04(2015), Article ID:61400,7 pages
10.4236/wjcmp.2015.54030
High-Frequency Electric Field Induced Nonlinear Electron Transport in Chiral Carbon Nanotubes
Sulemana S. Abukari1, Samuel Y. Mensah1, Musah Rabiu2, Kofi W. Adu3,4*, Natalia G. Mensah5, Anthony Twum1, Alfred Owusu1, Kwadwo A. Dompreh1, Patrick Mensah-Amoah1, Matthew Amekpewu2
1Department of Physics, Laser and Fibre Optics Centre, University of Cape Coast, Cape Coast, Ghana
2Department of Applied Physics, University for Development Studies, Navorongo, Ghana
3Department of Physics, The Pennsylvania State University-Altoona, Altoona, USA
4Materials Research Institute, The Pennsylvania State University, University Park, USA
5Department of Mathematics, University of Cape Coast, Cape Coast, Ghana

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 5 November 2014; accepted 21 November 2015; published 24 November 2015

ABSTRACT
We investigate theoretically the high frequency complex conductivity in carbon nanotubes that are stimulated axially by a strong inhomogeneous electric field of the form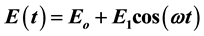 . Using the kinetic approach based on Boltzmann’s transport equation with constant relaxation time approximation and the energy spectrum of the electron in the tight-binding approximation, together with Bhatnagar-Gross-Krook collision integral, we predict high-frequency nonlinear effects along the axial and the circumferential directions of the carbon nanotubes that may be useful for the generation of high frequency radiation in the carbon nanotubes.
. Using the kinetic approach based on Boltzmann’s transport equation with constant relaxation time approximation and the energy spectrum of the electron in the tight-binding approximation, together with Bhatnagar-Gross-Krook collision integral, we predict high-frequency nonlinear effects along the axial and the circumferential directions of the carbon nanotubes that may be useful for the generation of high frequency radiation in the carbon nanotubes.
Keywords:
Carbon Nanotubes, High Frequency Electric Field, Electric Current Density, Complex Conductivity

1. Introduction
Carbon nanotube (CNT) is an allotrope of carbon with nanometers size diameter and an aspect ratio as high as ~107. In 1952, images of 50 nanometer diameter tubes of carbon were reported by Radushkevich and Lukyanovich [1] . Using the vapor-growth technique, Orberlin and coworkers [2] reported observation of hollow carbon fibers of nanometer size diameters. Other reports also published similar observation of tubular carbon nanostructures [3] . However, the credit for the discovery of CNTs goes to S. Iijima [4] . This one-atom thick sheet of graphene rolled up into a seamless cylinder has since attracted a great deal of interest, mainly due to their unique thermal, chemical and physical properties [5] [6] . These properties depend on the fundamental indices (n,m) of the CNTs. The indices (n,m) determine the diameter and the chiral angle of the CNTs. As n and m vary, the conduction ranges from metallic to semiconducting [7] , with an inverse diameter dependent band gap of ≤ 1 eV [7] .
The electron transport properties of the CNTs continue to be the subject of intense research. CNTs have been shown to exhibit ballistic transport [8] -[10] , Coulomb-blockade [11] -[13] , Luttinger Liquid [14] [15] and superconductivity [16] [17] . The unique architectural, structural and physicochemical properties have made CNT a promising candidate for application in new generation of nanoelectronics [18] -[21] , sensors [22] [23] , electrochemical capacitors [24] -[26] , Li-ion batteries [27] -[29] and terahertz (THz) generation and amplification [30] - [34] , just to mention a few. Furthermore, negative differential conductivity properties of CNTs have been reported [6] [35] [36] , while phenomena like rectification of electromagnetic waves, domain suppression in negative differential conductivity region, high-frequency (hf) conductivity, high order harmonic generation and many others have also been considered [37] -[40] .
In this work, we report on a high frequency (hf) complex conductivity 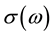 in CNTs using the standard linear electrodynamical approach [15] -[17] . We use the kinetic approach based on Boltzmann’s transport equation with constant relaxation time approximation and the energy spectrum of the electron in the tight-binding approximation, together with Bhatnagar-Gross-Krook (BGK) collision integral. This approach permits adequate allowance for the particle-number conservation law for scattering inhomogeneous field as well as the influence on the electron spectrum by both resonance effects due to Bloch oscillations of the electrons and by the effects connected with the carrier drift and diffusion under conditions of strong spatial dispersions.
in CNTs using the standard linear electrodynamical approach [15] -[17] . We use the kinetic approach based on Boltzmann’s transport equation with constant relaxation time approximation and the energy spectrum of the electron in the tight-binding approximation, together with Bhatnagar-Gross-Krook (BGK) collision integral. This approach permits adequate allowance for the particle-number conservation law for scattering inhomogeneous field as well as the influence on the electron spectrum by both resonance effects due to Bloch oscillations of the electrons and by the effects connected with the carrier drift and diffusion under conditions of strong spatial dispersions.
2. Theory
Using the simple model of the tight-binding approximation, we describe the energy spectrum of the CNTs as [39]
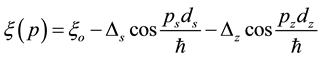 , (1)
, (1)
where the indices s and z correspond to the circumferential and axial directions, respectively.  is the energy of an outer-shell electron in an isolated carbon atom, Dz and Ds are the real overlapping integrals for jumps along the respective coordinates,
is the energy of an outer-shell electron in an isolated carbon atom, Dz and Ds are the real overlapping integrals for jumps along the respective coordinates,  and
and 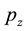 are the components of momentum tangential to the base helix and along the nanotube axis, respectively.
are the components of momentum tangential to the base helix and along the nanotube axis, respectively. 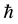 is Planck’s constant, and dz and ds are the distances along the CNT axis and helix, respectively.
is Planck’s constant, and dz and ds are the distances along the CNT axis and helix, respectively.
We consider the Boltzmann transport equation with constant relaxation time together with Bhatnagar-Gross- Krook (BGK), which account for the spatial effects due to the conservation of the number of scattered particles [41] [42] ,
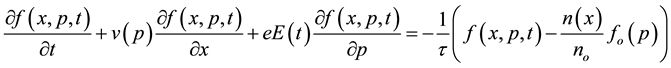 . (2)
. (2)
The distribution function 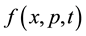 and the equilibrium distribution function
and the equilibrium distribution function  are periodic and can be written in Fourier series as in Equations (3) and (4), respectively.
are periodic and can be written in Fourier series as in Equations (3) and (4), respectively.
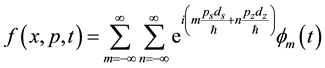 (3)
(3)
and
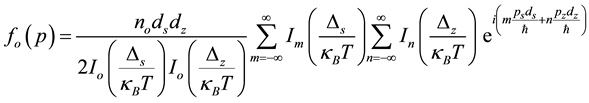 (4)
(4)
where no is the equilibrium carrier density, n(x) is the electron density at position x, v(p) is the electron velocity, p
is the electron dynamical momentum, t is elapsed time, τ is the electron relaxation time, e is the electron charge, E(t) is the external electric field,  is the Boltzmann’s constant and T is the temperature. The collision integral is taken in the relaxation time τ approximation and further assumed to be constant.
is the Boltzmann’s constant and T is the temperature. The collision integral is taken in the relaxation time τ approximation and further assumed to be constant. 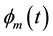 is the factor by which the Fourier transform of the nonequilibrium distribution function differs from its equilibrium distribution counterpart. Im (In) is the modified Bessel function of the order m(n) and Io is the modified Bessel function of the zeroth order.
is the factor by which the Fourier transform of the nonequilibrium distribution function differs from its equilibrium distribution counterpart. Im (In) is the modified Bessel function of the order m(n) and Io is the modified Bessel function of the zeroth order.
In addition to Equation (2), we employ the Poisson equation that will allow for continuous current, i.e., 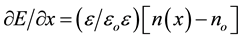 , where ε is the lattice dielectric constant. For a constant homogeneous electric field
, where ε is the lattice dielectric constant. For a constant homogeneous electric field

where 


neous perturbations with frequency w and wave-vector k of the following form:


tion (2)), we obtained [41] -[43] ,

where




where the integration is done over the first Brillouin zone. Using Equation (7) together with the solution of Equation (6) we obtain the following expressions:


Defining the axial 




and

Using 



and

3. Results and Discussions
Using the solution to the Boltzmann’s transport equation with constant relaxation time together with Bhatnagar- Gross-Krook collision integral, we obtained the expressions for the complex conductivities along the axial and circumferential directions of the CNTs. We analyzed the effects of the high frequency electric field by considering the dependence of the complex conductivity 



Figure 1. The real (red solid curve) and the imaginary (blue solid curve) parts of the normalized complex conductivity s/so as a function of normalized frequency w/W along the circumferential (top) and axial (bottom) directions of CNT.
circumferential [Figure 1(b)] directions. The red and the blue curves represent the real and the imaginary parts of the conductivity, respectively. The complex conductivity along both directions exhibits similar characteristics. The dimensionless complex conductivity 

4. Conclusion
In summary, we have obtained the nonlinear high frequency conductivity in CNTs that are stimulated axial with a strong inhomogeneous electric field by using the Boltzmann’s equation with constant relaxation time approximation together with the Bhatnagar-Gross-Krook collision integral. We predict this high-frequency nonlinear effect along the axial and the circumferential directions of the carbon nanotubes may be useful for the generation of a high frequency radiation in the carbon nanotubes.
Cite this paper
Sulemana S.Abukari,Samuel Y.Mensah,MusahRabiu,Kofi W.Adu,11,Natalia G.Mensah,AnthonyTwum,AlfredOwusu,Kwadwo A.Dompreh,PatrickMensah-Amoah,MatthewAmekpewu, (2015) High-Frequency Electric Field Induced Nonlinear Electron Transport in Chiral Carbon Nanotubes. World Journal of Condensed Matter Physics,05,294-300. doi: 10.4236/wjcmp.2015.54030
References
- 1. Radushkevich, L.V. and Lukyanovich, V.M. (1952) The Structure of Carbon Forming in Thermal Decomposition of Carbon Monoxide on an Iron Catalyst. Russian Journal of Physical Chemistry, 26, 88-95. (In Russian)
- 2. Oberlin, A., Endo, M. and Koyana, T. (1976) Filamentous Growth of Carbon through Benzene Decomposition. Journal of Crystal Growth, 32, 335-349.
http://dx.doi.org/10.1016/0022-0248(76)90115-9 - 3. Abrahamson, J., Wiles, P.G. and Rhodes, B. (1999) Structure of Carbon Fibres Found on Carbon Arc Anodes. Carbon, 37, 1873-1875. http://dx.doi.org/10.1016/S0008-6223(99)00199-2
- 4. Iijima, S. (1991) Helical Microtubules of Graphitic Carbon. Nature, 354, 56-58.
http://dx.doi.org/10.1038/354056a0 - 5. Maksimenko, A.S. and Slepyan, G.Y. (2000) Negative Differential Conductivity in Carbon Nanotubes. Physical Review Letters, 84, 362.
http://dx.doi.org/10.1103/PhysRevLett.84.362 - 6. Pennington, G. and Goldsman, N. (2003) Semiclassical Transport and Phonon Scattering of Electrons in Semiconducting Carbon Nanotubes. Physical Review B, 68, Article ID: 045426.
http://dx.doi.org/10.1103/PhysRevB.68.045426 - 7. Saito, R., Dresselhaus, G. and Dresselhaus, M.S. (1998) Physical Properties of Carbon Nanotubes. Imperial College Press, London.
- 8. Li, H.J., et al. (2005) Multichannel Ballistic Transport in Multiwall Carbon Nanotubes. Physical Review Letters, 95, Article ID: 086601.
http://dx.doi.org/10.1103/PhysRevLett.95.086601 - 9. Kajiura, H., et al. (2005) Quasi-Ballistic Electron Transport in As-Produced and Annealed Multiwall Carbon Nanotubes. Carbon, 43, 1317-1319.
http://dx.doi.org/10.1016/j.carbon.2004.12.004 - 10. Kajiura, H., et al. (2004) Quasi-Ballistic Electron Transport in Double-Wall Carbon Nanotubes. Chemical Physics Letters, 398, 476-479.
http://dx.doi.org/10.1016/j.cplett.2004.09.115 - 11. Bezryadin, A., Verschueren, A.R.M., Tans, S.J. and Dekker, C. (1998) Multiprobe Transport Experiments on Individual Single-Wall Carbon Nanotubes. Physical Review Letters, 80, 4036-4039.
http://dx.doi.org/10.1103/PhysRevLett.80.4036 - 12. Hsiou, Y.F., Yang, Y.J., Chen, C.D. and Chan, C.H. (2006) Coulomb Blockade Behavior in Individual Multiwalled Carbon Nanotubes. Journal of Vacuum Science & Technology B, 24, 143.
http://dx.doi.org/10.1116/1.2151216 - 13. Haruyama, J., Takesue, I. and Sato, Y. (2000) Coulomb Blockade in a Single Tunnel Junction Directly Connected to a Multiwalled Carbon Nanotube. Applied Physics Letters, 77, 2891.
http://dx.doi.org/10.1063/1.1312254 - 14. McEuen, P.L., Bockrath, M., Cobden, D.H., et al. (1999) Luttinger-Liquid Behaviour in Carbon Nanotubes. Nature, 397, 598-601.
http://dx.doi.org/10.1038/17569 - 15. Shiraishi, M. and Ata, M. (2003) Tomonaga—Luttinger-Liquid Behavior in Single-Walled Carbon Nanotube Networks. Solid State Communications, 127, 215-218.
http://dx.doi.org/10.1016/S0038-1098(03)00417-4 - 16. Kociak, M., Kasumov, A.Y., Guéron, S., Reulet, B., et al. (2001) Superconductivity in Ropes of Single-Walled Carbon Nanotubes. Physical Review Letters, 86, 2416-2419.
http://dx.doi.org/10.1103/PhysRevLett.86.2416 - 17. Southard, A., Sangwan, V., Cheng, J., et al. (2009) Solution-Processed Single Walled Carbon Nanotube Electrodes for Organic Thin-Film Transistors. Organic Electronics, 10, 1556-1561.
http://dx.doi.org/10.1016/j.orgel.2009.09.001 - 18. Hong, K., Nam, S., Yang, C., et al. (2009) Solution-Processed Organic Field-Effect Transistors Composed of Poly(4-styrene sulfonate) Wrapped Multiwalled Carbon Nanotube Source/Drain Electrodes. Organic Electronics, 10, 363-367.
http://dx.doi.org/10.1016/j.orgel.2008.11.008 - 19. Aguirre, C.M., Ternon, C., Paillet, M., Desjardins, P. and Martel, R. (2009) Carbon Nanotubes as Injection Electrodes for Organic Thin Film Transistors. Nano Letters, 9, 1457-1461.
http://dx.doi.org/10.1021/nl8033152 - 20. Novak, J.P., Snow, E.S., Houser, E.J., Park, D., Stepnowski, J.L. and McGill, R.A. (2009) Nerve Agent Detection Using Networks of Single-Walled Carbon Nanotubes. Applied Physics Letters, 83, 4026-4028.
http://dx.doi.org/10.1063/1.1626265 - 21. Kong, J., Franklin, N.R., Zhou, C.W., et al. (2000) Nanotube Molecular Wires as Chemical Sensors. Science, 287, 622- 625.
http://dx.doi.org/10.1126/science.287.5453.622 - 22. Robinson, J.A., Snow, E.S., Badescu, S.C., Reinecke, T.L. and Perkins, F.K. (2006) Role of Defects in Single-Walled Carbon Nanotube Chemical Sensors. Nano Letters, 6, 1747-1751.
http://dx.doi.org/10.1021/nl0612289 - 23. Signorelli, R., Ku, D.C., Kassakian, J.G. and Schindall, J.E. (2009) Electrochemical Double-Layer Capacitors Using Carbon Nanotube Electrode Structures. Proceedings of the IEEE, 97, 1837-1847.
http://dx.doi.org/10.1109/JPROC.2009.2030240 - 24. Du, C.S. and Pan, N. (2006) High Power Density Supercapacitor Electrodes of Carbon Nanotube Films by Electrophoretic Deposition. Nanotechnology, 17, 5314-5318.
http://dx.doi.org/10.1088/0957-4484/17/21/005 - 25. Du, C.S. and Pan, N. (2006) Supercapacitors Using Carbon Nanotubes Films by Electrophoretic Deposition. Journal of Power Sources, 160, 1487-1494.
http://dx.doi.org/10.1016/j.jpowsour.2006.02.092 - 26. Zhao, J.J., Buldum, A., Han, J. and Lu, J.P. (2000) First-Principles Study of Li-Intercalated Carbon Nanotube Ropes. Physical Review Letters, 85, 1706-1709.
http://dx.doi.org/10.1103/PhysRevLett.85.1706 - 27. Udomvech, A., Kerdcharoen, T. and Osotchan, T. (2005) First Principles Study of Li and Li+ Adsorbed on Carbon Nanotube: Variation of Tubule Diameter and Length. Chemical Physics Letters, 406, 161-166.
http://dx.doi.org/10.1016/j.cplett.2005.02.084 - 28. Chen, J., Liu, Y., Minett, A.I., et al. (2007) Flexible, Aligned Carbon Nanotube/Conducting Polymer Electrodes for a Lithium-Ion Battery. Chemistry of Materials, 19, 3595-3597.
http://dx.doi.org/10.1021/cm070991g - 29. Tang, Z.K., Zhang, L.Y., Wang, N., et al. (2001) Superconductivity in 4 Angstrom Single-Walled Carbon Nanotubes. Science, 292, 2462-2465.
http://dx.doi.org/10.1126/science.1060470 - 30. Slepyan, G.Y., Maksimenko, S.A., Kalosha, V.P., et al. (1999) Highly Efficient High-Order Harmonic Generation by Metallic Carbon Nanotubes. Physical Review A, 60, R777-R780.
http://dx.doi.org/10.1103/PhysRevA.60.R777 - 31. Ferguson, B. and Zhang, X.C. (2002) Materials for Terahertz Science and Technology. Nature Materials, 1, 26-33.
http://dx.doi.org/10.1038/nmat708 - 32. Slepyan, G.Y., Maksimenko, S.A., Kalosha, V.P., Gusakov, A.V. and Herrmann, J. (2001) High-Order Harmonic Generation by Conduction Electrons in Carbon Nanotube Ropes. Physical Review A, 63, Article ID: 053808.
http://dx.doi.org/10.1103/PhysRevA.63.053808 - 33. Dragoman, D. and Dragoman, M. (2005) Terahertz Continuous Wave Amplification in Semiconductor Carbon Nanotubes. Physica E, 25, 492-496.
http://dx.doi.org/10.1016/j.physe.2004.08.001 - 34. Dragoman, M., Cismaru, A., Hartnagel, H. and Plana, R. (2006) Reversible Metal-Semiconductor Transitions for Microwave Switching Applications. Applied Physics Letters, 88, Article ID: 073503.
http://dx.doi.org/10.1063/1.2177369 - 35. Farajian, A.A., Estarjani, K. and Kawazoe, Y. (1999) Nonlinear Coherent Transport through Doped Nanotube Junctions. Physical Review Letters, 82, 5084-5087.
http://dx.doi.org/10.1103/PhysRevLett.82.5084 - 36. Abukari, S.S., Adu, K.W., Mensah, S.Y., et al. (2013) Rectification Due to Harmonic Mixing of Two Coherent Electromagnetic Waves with Commensurate Frequencies in Carbon Nanotubes. The European Physical Journal B, 86, 106.
http://dx.doi.org/10.1140/epjb/e2013-30011-3 - 37. Abukari, S.S., Mensah, S.Y., Adu, K.W., et al. (2012) Domain Suppression in the Negative Differential Conductivity Region of Carbon Nanotubes by Applied AC Electric Field. World Journal of Condensed Matter Physics, 2, 274-277.
http://dx.doi.org/10.4236/wjcmp.2012.24045 - 38. Abukari, S.S., Mensah, S.Y., Mensah, N.G., Adu, K.A., Rabiu, M. and Twum, A. (2012) High Frequency Conductivity in Carbon Nanotubes. AIP Advances, 2, Article ID: 042178.
http://dx.doi.org/10.1063/1.4771677 - 39. Slepyan, G.Y., Maksimenko, S.A., Lakhtakia, A., et al. (1998) Electronic and Electromagnetic Properties of Nanotubes. Physical Review B, 57, 9485-9497.
http://dx.doi.org/10.1103/PhysRevB.57.9485 - 40. Slepyanet, G.Y., Maksimenko, S.A., Lakhtakia, A., Yevtushenko, O. and Gusakov, A.V. (1999) Electrodynamics of Carbon Nanotubes: Dynamic Conductivity, Impedance Boundary Conditions, and Surface Wave Propagation. Physical Review B, 60, 17136-17149.
- 41. Ignatov, A.A. and Shashkin, V.I. (1987) Bloch Oscillations of Electrons and Instability of Space-Charge Waves in Semiconductor Superlattices. Soviet Physics—JETP, 66, 526-530.
- 42. Ryndyk, D.A., Demarina, N.V., Keller, J. and Schomburg, E. (2003) Superlattice with Hot Electron Injection: An Approach to a Bloch Oscillator. Physical Review B, 67, Article ID: 033305.
http://dx.doi.org/10.1103/PhysRevB.67.033305 - 43. Bass, F.G. and Tetervov, A.P. (1986) High-Frequency Phenomena in Semiconductor Superlattices. North-Holland, Amsterdam.
- 44. Ktitorov, S., Simin, G. and Sindalovskii, V. (1972) Bragg Reflections and the High-Frequency Conductivity of an Electronic Solid-State Plasma. Soviet Physics—Solid State, 13, 1872.
NOTES
*Corresponding author.


