World Journal of Condensed Matter Physics
Vol.4 No.2(2014), Article ID:45830,6 pages DOI:10.4236/wjcmp.2014.42012
On the Validity of Janak’s Theorem and Ground State Energies of Ensembles of Interacting Quantum N-Particle Systems
Antonios Gonis
Physical and Life Sciences, Lawrence Livermore National Laboratory, Livermore, USA
Email: gonis1@llnl.gov
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 6 February 2014; revised 19 March 2014; accepted 2 April 2014
ABSTRACT
It is established that for finite number of electrons, 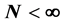 , and in the limit
, and in the limit![]() , the line of reasoning leading to the proof of Janak’s theorem is flawed, based on the incorrect treatment of a mixed state as a pure state. The derivative discontinuity at integral values of
, the line of reasoning leading to the proof of Janak’s theorem is flawed, based on the incorrect treatment of a mixed state as a pure state. The derivative discontinuity at integral values of 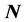 of the total ground state energy,
of the total ground state energy, 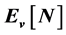 , of an interacting N-particle system under an external single-particle potential,
, of an interacting N-particle system under an external single-particle potential, 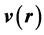 , is shown to follow from general quantum principles governing the behavior of ensembles of systems with varying particle number, and its presence is shown to be independent of the particular approximation used in determining the total ground-state energy of an ensemble.
, is shown to follow from general quantum principles governing the behavior of ensembles of systems with varying particle number, and its presence is shown to be independent of the particular approximation used in determining the total ground-state energy of an ensemble.
Keywords:Janak’s Theorem, Slater Transition State

1. Introduction
In 1978, Janak published [1] a seemingly remarkable paper. It purported to show that “the variation of the total energy, as constructed in the density-functional theory, with respect to an orbital occupation, is equal to the orbital and independent eigenvalue of the detailed form of the exchange-correlation functional.” He further went on to propose that “this leads to a rigorous connection between the ground-state energies of N− and (N + 1)- particle systems, which is useful in the calculation of certain excitation energies.”
Janak’s theorem has provided the foundation of a number of formal developments [2] -[8] , notably that of density functional theory for open systems [2] [3] , related concepts such as the derivative discontinuity [4] of the exchange-correlation potential at integral values of electrons, as well as the study of physical properties [5] [8] of materials. At the same time, some difficulties are indicated by numerical studies [5] that show deviations from the linear behavior predicted by the theory (see Equation (1.6) below).
These difficulties can be traced to the fundamental level. Unfortunately, and in spite of the applications just cited (and many others, too numerous to mention here), Janak’s proof of the theorem turns out to be invalid. This does not negate the theorem per se, but does point to the need of an alternative proof. As shown below, the lack of validity results from the incorrect treatment of a fractionally normalized charge as associated with a pure state (and an antisymmetric wave function) that, by the foundational postulates of quantum mechanics, must be normalized to unity and lead to densities with integral normalization. No potential acts instantaneously on a fractional number of electrons and no Schrödinger equation describes the evolution of such a system. Hence, no pure state (or wave function) exists for non-integral charges.
2. Analysis of the Theorem
The two opening sentences in the paper by Janak [1] imply the existence of a general theorem on total energies whose validity in a special case (that of ground states of systems with an integral number of electrons) was established by the theorems of Hohenberg and Kohn [9] . The statement is then interpreted mathematically in the form of a functional expression,
 (1.1)
(1.1)
where  is the external single-particle potential acting on the system,
is the external single-particle potential acting on the system,  is the kinetic energy of a noninteracting electron system with the same density,
is the kinetic energy of a noninteracting electron system with the same density, 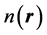 ,
, 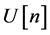 is the classical Coulomb energy for a charge density, n, and
is the classical Coulomb energy for a charge density, n, and 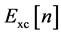 is the exchange and correlation functional [10] . Then, as summarized in the paper, in the theorems of Hohenberg and Kohn, the density, n, is that of the ground state of an interacting N-particle system, and is hence normalized to N,
is the exchange and correlation functional [10] . Then, as summarized in the paper, in the theorems of Hohenberg and Kohn, the density, n, is that of the ground state of an interacting N-particle system, and is hence normalized to N,
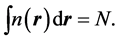 (1.2)
(1.2)
This density is also given within the Kohn-Sham formalism [10] in terms of a Slater determinant constructed out of the lowest-in-energy eigenfunctions, 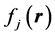 , of a single-particle in an effective field, thus taking the form,
, of a single-particle in an effective field, thus taking the form,
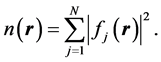 (1.3)
(1.3)
The generalization attempted by Janak is an extension of Slater’s transition state [11] to the formalism of density functional theory (DFT). It is based on the use of the expression in (1.1) but interpreted in terms of a function of a charge density (an expression in which the charge density occurs as a parameter) that is normalized to a fractional number by including the fractional occupation of the next state higher in energy of a noninteracting N-particle system, taking the form, ![]() ,
,
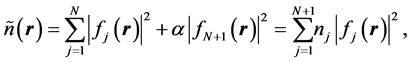 (1.4)
(1.4)
where ![]() denotes the occupancy of the state (orbital),
denotes the occupancy of the state (orbital),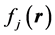 . With the orbitals normalized to unity, we have,
. With the orbitals normalized to unity, we have,
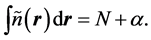 (1.5)
(1.5)
In a result that ostensibly bridges the application of ground-state DFT to excited states as well as the passage from the ground state energy of a system of ![]() particles to that of
particles to that of ![]() particles under the same external potential, Janak purports to establish the central result of the paper, Janak’s Theorem,
particles under the same external potential, Janak purports to establish the central result of the paper, Janak’s Theorem,
 (1.6)
(1.6)
where 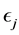 is the single-particle eigenvalue corresponding to
is the single-particle eigenvalue corresponding to  in the potential,
in the potential, .
.
It is now shown that in the limit of finite number of particles (electrons) at the zero of temperature, the formalism in the paper by Janak is invalid because it fails to distinguish between pure and mixed states.
In quantum mechanics, the study of physical systems defined in terms of a fixed number, ![]() , of mutually interacting particles is carried out on the basis of pure states (Solutions of a Schrödinger equation, say). Such a system is described by quantum states,
, of mutually interacting particles is carried out on the basis of pure states (Solutions of a Schrödinger equation, say). Such a system is described by quantum states, 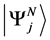 , that are elements of an abstract Hilbert space and obey the normalization condition,
, that are elements of an abstract Hilbert space and obey the normalization condition, 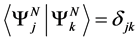 (see also (1.7) below). The projection of a state onto a coordinate point in
(see also (1.7) below). The projection of a state onto a coordinate point in ![]() -dimensional space,
-dimensional space, 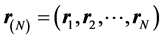 , gives rise to a wave function (dropping the subscripts),
, gives rise to a wave function (dropping the subscripts), 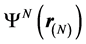 , whose modulus squared gives the classical probability of encountering the system in the configuration described by the positions of the particles in
, whose modulus squared gives the classical probability of encountering the system in the configuration described by the positions of the particles in![]() . For Fermions, wave functions are antisymmetric with respect to interchange of single-particle coordinates (and spins for electrons). Because of the requirement that the sum of probabilities must equal unity, every state in N-particle Hilbert space satisfies the normalization condition,
. For Fermions, wave functions are antisymmetric with respect to interchange of single-particle coordinates (and spins for electrons). Because of the requirement that the sum of probabilities must equal unity, every state in N-particle Hilbert space satisfies the normalization condition,
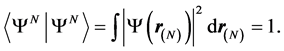 (1.7)
(1.7)
The single-particle (charge) density, the probability of finding a particle at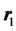 , is defined by the integral over all but one coordinate of the modulus squared of the wave function, (with the electronic charge set equal to one),
, is defined by the integral over all but one coordinate of the modulus squared of the wave function, (with the electronic charge set equal to one),
 (1.8)
(1.8)
while the pair density, the probability of finding simultaneously a particle at 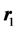 and one at
and one at , is given by the expression,
, is given by the expression,
 (1.9)
(1.9)
Finally, the Hamiltonian of a many-particle interacting system takes the form,
 (1.10)
(1.10)
where the operators, 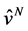 ,
,  and
and 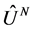 correspond to the external potential, the kinetic energy and interparticle potential of the N-particle system. Hilbert spaces are identified by the number of particles and the potential, so that different numbers of particles define different and mutually disjoint Hilbert spaces, even if the potentials acting on the separate systems are identical.
correspond to the external potential, the kinetic energy and interparticle potential of the N-particle system. Hilbert spaces are identified by the number of particles and the potential, so that different numbers of particles define different and mutually disjoint Hilbert spaces, even if the potentials acting on the separate systems are identical.
Therefore, the last three expressions are sensible if and only if ![]() is an integer.
is an integer.
Because of (1.7), a density must be normalized to an integer number, a condition fulfilled in (1.2). The requirement clearly fails in (1.5). Furthermore, energies are given as expectation values of Hamiltonians, ![]() , with respect to quantum states in the Hilbert space of
, with respect to quantum states in the Hilbert space of ![]() particles, so that energies (expectation values) are restricted by the dimensionality of the system to correspond to densities with integral normalization. Therefore, the expression for the energy in (1.1) when interpreted in terms of a density, such as that in (1.4), cannot possibly correspond to an expectation value of a Hamiltonian with respect to a wave function in any Hilbert space.
particles, so that energies (expectation values) are restricted by the dimensionality of the system to correspond to densities with integral normalization. Therefore, the expression for the energy in (1.1) when interpreted in terms of a density, such as that in (1.4), cannot possibly correspond to an expectation value of a Hamiltonian with respect to a wave function in any Hilbert space.
The formalism in the paper by Janak overlooks the true character of the density in (1.5) as that associated with an ensemble, or mixed state. Mixed states, in the form of reduced density matrices (RDMs) encode the statistics of measurement outcomes of a system described by the states in a particular RDM. In the case of, say (1.4), it denotes the fact that a strictly single-particle system is found in one and only one of the states,  , without the knowledge of which state is occupied. The expression can only give the classical probability,
, without the knowledge of which state is occupied. The expression can only give the classical probability, 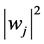 , of finding the system in the state
, of finding the system in the state . This classical expression (describing the results of measurement on a singleparticle system) has no bearing on the question of the single-particle occupation of a state in an otherwise interacting many-particle system.
. This classical expression (describing the results of measurement on a singleparticle system) has no bearing on the question of the single-particle occupation of a state in an otherwise interacting many-particle system.
Let 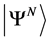 and
and 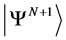 denote the ground states of two systems, one with
denote the ground states of two systems, one with ![]() and the other with
and the other with ![]() particles, both under the same external potential. Then the density matrix describing an ensemble of the two systems consisting of the N-particle system occurring in the ensemble with likelihood
particles, both under the same external potential. Then the density matrix describing an ensemble of the two systems consisting of the N-particle system occurring in the ensemble with likelihood , while that of the
, while that of the ![]() particles with likelihood
particles with likelihood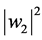 , with
, with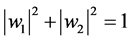 , can be written in the Fock-space representation in the form,
, can be written in the Fock-space representation in the form,
 (1.11)
(1.11)
Projecting each state on a point in its multi-particle coordinate space, and integrating over all coordinates but one, we obtain,
 (1.12)
(1.12)
where superscripts denote normalization. With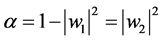 , one gains the normalization in (1.5).
, one gains the normalization in (1.5).
Consistent with the classical nature of the mixed state density, the lowest energy of the state corresponding to the density,  , is given exactly by the ensemble average of the ground-state energies of the separate systems in
, is given exactly by the ensemble average of the ground-state energies of the separate systems in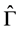 ,
,
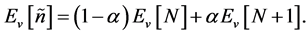 (1.13)
(1.13)
For an ensemble density of the form,
 (1.14)
(1.14)
the result in (1.13) is immediately generalizable to the expression,
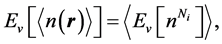 (1.15)
(1.15)
meaning that the ground state energy of the ensemble density is the ensemble of the ground state energies associated with individual densities. This expression is both intuitively obvious and exact.
The fractionally normalized density, 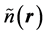 , is characteristic of an open system, one that is allowed to interact with a reservoir (or its environment) and can exchange particles with it. The Hohenberg and Kohn theorems, on the other hand, are formulated for the ground states of isolated systems characterized by a fixed number of particles.
, is characteristic of an open system, one that is allowed to interact with a reservoir (or its environment) and can exchange particles with it. The Hohenberg and Kohn theorems, on the other hand, are formulated for the ground states of isolated systems characterized by a fixed number of particles.
As an explicit example, consider ![]() and
and ![]() to be associated with the lowest in energy of
to be associated with the lowest in energy of ![]() and
and ![]() non-interacting systems of particles under the same potential,
non-interacting systems of particles under the same potential,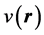 . The densities then take the form of (1.3) in terms of single-particle eigenstates of
. The densities then take the form of (1.3) in terms of single-particle eigenstates of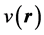 , with the
, with the ![]() orbitals for the N-partickle system coinciding with the
orbitals for the N-partickle system coinciding with the ![]() lowest in energy orbitals of the
lowest in energy orbitals of the 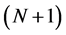 -particle system. From the expression in (1.3), the expression in (1.4) follows. But the two systems are separate and distinct blocking the formation of a single system, described by a pure state in either the space of the
-particle system. From the expression in (1.3), the expression in (1.4) follows. But the two systems are separate and distinct blocking the formation of a single system, described by a pure state in either the space of the ![]() or
or ![]() particles, that gives rise to an averaged density with non-integral normalization.
particles, that gives rise to an averaged density with non-integral normalization.
The expression in (1.15) is the central result of this paper to whose analysis we now proceed.
From (1.13), a special case of (1.15), the variation of the ensemble energy with respect to 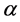 takes the form,
takes the form,
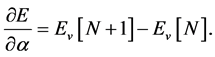 (1.16)
(1.16)
The last expression replaces that in (1.6). It signifies that the energy can be taken to vary linearly with respect to occupation of a many-particle state, rather than the occupation of single-particle orbitals. It is consistent with the classical character of the ensemble density that describes the results of measuring the energy of systems with varying numbers of particles. It shows that the energy vs particle number curve varies linearly between ![]() and
and ![]() with a derivative discontinuity at all integer
with a derivative discontinuity at all integer![]() . Indeed, given that
. Indeed, given that ![]() -particle interacting quantum systems are described in terms of
-particle interacting quantum systems are described in terms of ![]() -particle states, not single-particle orbitals, the expression in Janak’s theorem is devoid of manifest meaning. Because no state bridges the Hilbert spaces of
-particle states, not single-particle orbitals, the expression in Janak’s theorem is devoid of manifest meaning. Because no state bridges the Hilbert spaces of ![]() and
and ![]() particles, the suggestion upon which the proof of Janak’s theorem is based, that a single implementation of the Kohn-Sham formalism can yield the set of orbitals forming a fractionally charged density, is equally without foundation.
particles, the suggestion upon which the proof of Janak’s theorem is based, that a single implementation of the Kohn-Sham formalism can yield the set of orbitals forming a fractionally charged density, is equally without foundation.
The expression in (1.16) is also consistent with the definition of the ionization potential of an atom as the difference in the ground state energies of the atom and the ion. Formally, the difference in orbital energies carry no information about ionization potentials contrary to the implications of Janak’s theorem. The expression in (1.16) also indicates that the expectation values of the external potential, the kinetic energy and the interparticle potential are ensemble averages of the values for the individual many-particle states, thus free of unphysical features of fractions of electrons interacting with fractions of electrons. Specifically, in the case of (1.4), we have,
 (1.17)
(1.17)
Also, the correct quantum expression for the Coulomb energy is given in terms of the pair densities of the states in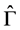 ,
,
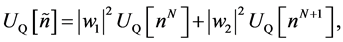 (1.18)
(1.18)
where for a state with ![]() particles, the Coulomb energy is given in terms of the pair density,
particles, the Coulomb energy is given in terms of the pair density,
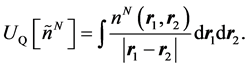 (1.19)
(1.19)
No quantum mechanically correct expressions for the Coulomb energy can be constructed on the basis of pure states describing physical systems in either of the Hilbert spaces of ![]() or
or ![]() particles and leading to a fractionally normalized density,
particles and leading to a fractionally normalized density, .
.
Furthermore, the formalism provides no connection between the excited states of a system of ![]() -particles, all of which are associated with densities normalized to
-particles, all of which are associated with densities normalized to![]() , and the ground state of
, and the ground state of 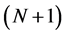 -particle systems, with densities normalized to
-particle systems, with densities normalized to![]() . There exists no transition state, which is a pure state and connects the excited states of a system of
. There exists no transition state, which is a pure state and connects the excited states of a system of ![]() particles to the ground state of a system of
particles to the ground state of a system of  particles. Slater’s transition state and Janak’s theorem depend on considerations of parameter spaces defined by the occupation numbers,
particles. Slater’s transition state and Janak’s theorem depend on considerations of parameter spaces defined by the occupation numbers,  , that effectively mix Hilbert spaces corresponding to different numbers of particles. As such they have no standing as pure states in the quantum realm of either system: Hilbert spaces are not fuzzy.
, that effectively mix Hilbert spaces corresponding to different numbers of particles. As such they have no standing as pure states in the quantum realm of either system: Hilbert spaces are not fuzzy.
Finally, the formal expressions in (1.15) and (1.16) are a result of quantum considerations and independent of the method used to calculate ground state energies (which affects accuracy and the magnitude of the difference in energy but not fundamental relations), or of the functional form of the curve describing the variation of the energy with particle number.
As suggested above, although Janak’s proof is not valid, it does not preclude the possibility that the theorem itself, i.e., Equation (1.6), may still hold under certain conditions. Physical systems can be identified whose energetics satisfy (approximately, to be sure, the expression in (1.6)). Within the context of Fermi-Liquid theory [12] -[16] (and references therein), in the limit of strictly infinite number of particles and elevated temperatures, the energy of a small number of quasi-excitations relative to the ground state is given by the superposition, (suppressing spin),
 (1.20)
(1.20)
where 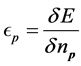 is the single-quasiparticle energy that, for rotationally invariant systems depends only on
is the single-quasiparticle energy that, for rotationally invariant systems depends only on
 , although
, although![]() , and
, and  (the temperature-dependent occupation number) denotes the Fermi distribution function at
(the temperature-dependent occupation number) denotes the Fermi distribution function at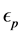 .
.
3. Summary
To summarize: At ![]() and a finite number of electrons, the rate of change of the energies of ensembles of systems with varying number of particles is to be determined with respect to occupation probabilities of many-particle states rather than the probabilities of single-particle orbitals. The ramifications of this result to further developments in density functional theory are currently under consideration.
and a finite number of electrons, the rate of change of the energies of ensembles of systems with varying number of particles is to be determined with respect to occupation probabilities of many-particle states rather than the probabilities of single-particle orbitals. The ramifications of this result to further developments in density functional theory are currently under consideration.
Acknowledgements
Comments and guidance by Henk Monkhorst improved the paper. Paul Ziesche pointed out a number of recent works in this area. Discussions with Chris Billman are also gratefully acknowledged. Work at LLNL was performed under the auspices of the US Department of Energy under Contract DE-AC52-07NA27344 with LLNS, LLC.
References
- Janak, J.F. (1978) Proof That
 in Density-Functional Theory. Physical Review B, 18, 7165-7168. http://dx.doi.org/10.1103/PhysRevB.18.7165
in Density-Functional Theory. Physical Review B, 18, 7165-7168. http://dx.doi.org/10.1103/PhysRevB.18.7165 - Perdew, J.P., Parr, R.G., Levy, M. and Balduz, J.L. (1982) Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy. Physical Review Letters, 49, 1691-1694. http://dx.doi.org/10.1103/PhysRevLett.49.1691
- Perdew, J.P. and Levy, M. (1983) Physical Content of the Exact Kohn-Sham Orbital Energies: Band Gaps and Derivative Discontinuities. Physical Review Letters, 51, 1884-1887. http://dx.doi.org/10.1103/PhysRevLett.51.1884
- Zheng, X., Cohen, A.J., Mori-Sánchez, P., Hu, X.Q. and Yang, W. (2011) Improving Band Gap Prediction in Density Functional Theory from Molecules to Solids. Physical Review Letters, 107, Article ID: 026403. http://dx.doi.org/10.1103/PhysRevLett.51.1884
- Göransson, C., Olovsson, W. and Abrikosov, I.A. (2005) Numerical Investigation of the Validity of the Slater-Janak Transition-State Model in Metallic Systems. Physical Review B, 72, Article ID: 134203. http://dx.doi.org/10.1103/PhysRevB.72.134203
- Sanna, S., Frauenheim, T. and Gerstmann, U. (2008) Validity of the Slater-Janak Transition-State Model within the
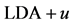 Approach. Physical Review B, 78, Article ID: 085201. http://dx.doi.org/10.1103/PhysRevB.78.085201
Approach. Physical Review B, 78, Article ID: 085201. http://dx.doi.org/10.1103/PhysRevB.78.085201 - Elkind, P.D. and Staroverov, V.N. (2012) Energy Expressions for Kohn-Sham Potentials and Their Relation to the Slater-Janak Theorem. The Journal of Chemical Physics, 136, Article ID: 124115. http://dx.doi.org/10.1063/1.3695372
- Chakrabarty, A. and Patterson, C.H. (2012) Transition Levels of Defects in Zno: Total Energy and Janak’s Theorem Methods. The Journal of Chemical Physics, 137, Article ID: 054709. http://dx.doi.org/10.1063/1.4739316
- Hohenberg, P. and Kohn, W. (1964) Inhomogeneous Electron Gas. Physical Review, 136, B864-B871. http://dx.doi.org/10.1103/PhysRev.136.B864
- Kohn, W. and Sham, L.J. (1965) Self-Consistent Equations Including Exchange and Correlation Effects. Physical Review, 140, A1133-A1138. http://dx.doi.org/10.1103/PhysRev.140.A1133
- Slater, J.C. (1972) Statistical Exchange-Correlation in the Self-Consistent Field. Volume 6 of Advances in Quantum Chemistry, Academic Press, 1-92.
- Pitaevskii, L.P. and Lifshitz, E.M. (1981) Statistical Physics. Part 2. Butterworth-Heinemann, Oxford.
- Gorkov, A.A., Dzyaloshinskii, L.P. and Abrikosov, I.Y. (1965) Quantum Field Theoretical Methods in Statistical Physics. Pergamon Press, New York.
- Phillips, P. (2008) Advanced Solid State Physics. Perseus Books.
- Monkhorst, H.J., Harris, F.E. and Freeman, F.E. (1992) Algebraic and Diagrammatic Methods in Many-Fermion Theory. Oxford University Press, Oxford.
- http://www.pma.caltech.edu/mcc/Ph127/c/Lecture9.pdf

