World Journal of Condensed Matter Physics
Vol.1 No.4(2011), Article ID:8771,4 pages DOI:10.4236/wjcmp.2011.14022
Transport Properties of the Layer Manganite La1.5Ca1.5Mn2-xFexO7
![]()
1Department of Pure & Applied Physics, Guru Ghasidas Vishwavidyalaya, Bilaspur, India; 2Department of Physics, University of Rajasthan, Jaipur, India.
Email: mps.phy@gmail.com
Received June 20th, 2011; revised August 9th, 2011; accepted August 20th, 2011.
Keywords: Layered perovskite, M-I transition, GMR
ABSTRACT
Layered perovskite manganite ceramics with a nominal chemistry La1.5Ca1.5Mn2−xFexO7 (x = 0.0, 0.05, 0.1, 0.3, 0.5) were prepared using sol-gel method. The manganese ions are highly mixed states of Mn3+ and Mn4+. It is found that the Mn3+/Mn4+ ratio decreases with the Fe doping content increasing. The conductivity and magnetoresistance (MR) were studied. The sample of x = 0.05 shows metal insulator transition (MIT) at 135 K. The MIT peak temperature (Tp) shifts towards higher temperature with increasing applied magnetic field. All the samples can be well fitted to the variable-range hopping (VRH) model. The maximum value of MR (%) [ρ(0) − ρ(H)]/ρ(0) × 100 for x = 0.05 is 34% (105 K, 7 kOe).
1. Introduction
The hole-doped ABO3-type perovskite manganites (Ln, M)MnO3 (Ln is lanthanide ion, and M is divalent cation) have attracted much attention owing to the colossal magnetoresistance (CMR) exhibited by them [e.g., 1-3]. Substitution of M2+ ions for Ln3+ leads to ferromagnetism and also metallic conduction. This has been explained as arising due to double exchange (DE) interaction and electron hopping between Mn3+ and Mn4+ cations (Mn4+ arising due to replacement of Ln3+ by M2+) via Mn-O-Mn path [4,5]. In the three dimensional perovskites, the Mn3+/ Mn4+ ratio and the microstructure of the Mn–O network are two key parameters controlling the DE interaction, and magnetic properties. La3Mn2O7 like bi-layer manganites also exhibit magneto-resistive behaviour [6] but these are much less studied. In the present paper, the result of temperature and field dependent resistivity measurements on substituting Fe ion for Mn site in calcium substituted bi-layer system La1.5Ca1.5Mn2O7.
2. Experimental Details
Polycrystalline samples of La1.5Ca1.5Mn2-xFexO7 (x = 0.0, 0.05, 0.1, 0.3, 0.5) were prepared by sol-gel method. The method consisted of adequate citric acid and stoichiometric amounts of the starting materials La(NO3)2·6H2O, Ca(NO3)2·6H2O, Mn(NO3)2·4H2O and Fe(NO3)3·6H2Owhich were dissolved in distilled water, and the pH was adjusted to about 3 to 4 with ammonia solution. First it was heated at 80˚C until a forming the powder. The powder was pressed into thin plates and calcined in air at 1200˚C for 24 h and 1350˚C for 24 h with intermediate grindings between each heating step. To characterize the samples, X-ray diffraction (XRD) measurements were carried [7]. The electrical resistivity was measured at zero field and 7 kOe field by a standard four-point technique. The magnetoresistance (MR) ratio is defined here as Δρ/ρ(0) = [ρ(0) − ρ(H)]/ρ(0), where ρ(0) and ρ(H) denote resistivity at zero field and an applied field, respecttively.
3. Results and Discussion
Figure 1 shows resistivity versus temperature plots for the La1.5Ca1.5Mn2−xFexO7 (x = 0.0, 0.05, 0.1, 0.3 and 0.5) samples at zero field. It is clear from the plots that resistivity enhances with increasing x. It is due to the Mn3+/ Mn4+ ratio reducing with increasing x. This results in the eg electrons decreasing, which in turn weakens doubleexchange mechanism.
For the samples of x = 0.0 and 0.05, resistivity first rises with increase in temperature, and then exhibits peak around the metal-insulator transition (MIT) temperature denoted by Tp, with the peak temperature Tp about 150 K and 140 K respectively.
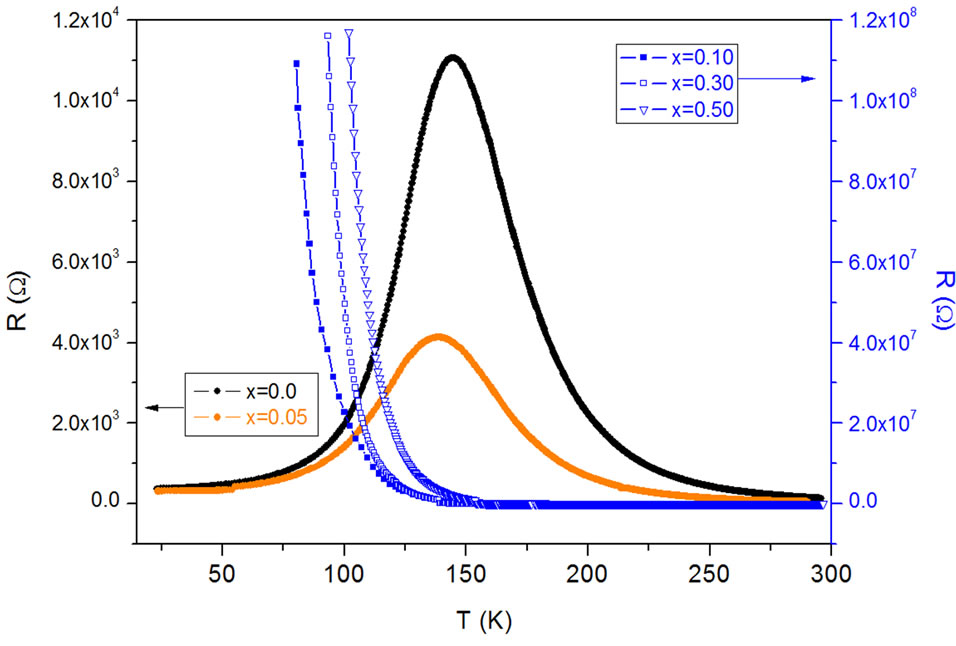
Figure 1. Temperature dependence of resistance for the La1.5Ca1.5Mn2-xFexO7 (x = 0.0, 0.05, 0.10, 0.30, 0.50).
For T > Tp, resistivity decreases with increase of temperature. Concentrating on the behavior of temperature dependent resistivity curve, it is noted that dρ/dT < 0 for T > Tp, which is a characteristic of semiconducting behavior. However for T < Tp, the sample showed metallic character with dρ/dT > 0. For higher values of x, the samples show semiconducting behavior and no metalinsulator transition is observed. Usually, the conduction behavior can be described by the a band-gap model, variable range hopping (VRH) mechanism [8-11], or can be described by the adiabatic nearest neighbor hopping model of small polaron conduction (NSPH) [12-14]. An Arrhenius law 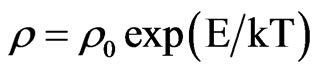 is used to account for thermal activation process due to a band gap or a mobility edge. In Mott’s VRH model, the resistivity is expressed in the form of
is used to account for thermal activation process due to a band gap or a mobility edge. In Mott’s VRH model, the resistivity is expressed in the form of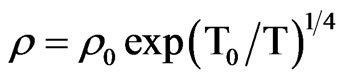 , where ρ0 is the pre-factor and T0 represents the characteristic temperature. In the nearest-neighbor hopping model of small polaron conduction (NSPH), the resistivity of the sample is given by
, where ρ0 is the pre-factor and T0 represents the characteristic temperature. In the nearest-neighbor hopping model of small polaron conduction (NSPH), the resistivity of the sample is given by , where E is the characteristic energy of small polaron hopping. To understand the nature of electronic conduction in the samples, we tried to fit the resistivity to all the three samples. The increasing size disorder with increasing x produces random spin and Coulombic potential fluctuations. So, the carriers find some potential difference beyond the Mn–O distances to hop at farther distances and hence conduct through the Mott’s type of Variable Range Hopping. The T0 occurring in the VRH relation can be related to the carrier localization length by the expression kT0 = 24/ L3pN(E), where k is the Boltzmann constant, L the carrier localization length and N(E) is the density of states [8,15]. The values of the localization length should be comparable to Mn-O distances for the VRH type of conduction, here L = 10−10 m [16].
, where E is the characteristic energy of small polaron hopping. To understand the nature of electronic conduction in the samples, we tried to fit the resistivity to all the three samples. The increasing size disorder with increasing x produces random spin and Coulombic potential fluctuations. So, the carriers find some potential difference beyond the Mn–O distances to hop at farther distances and hence conduct through the Mott’s type of Variable Range Hopping. The T0 occurring in the VRH relation can be related to the carrier localization length by the expression kT0 = 24/ L3pN(E), where k is the Boltzmann constant, L the carrier localization length and N(E) is the density of states [8,15]. The values of the localization length should be comparable to Mn-O distances for the VRH type of conduction, here L = 10−10 m [16].
Figure 2 displays the fitting results using the three different functions, a band-gap model, nearest-neighbor hopping model of small polaron conduction (NSPH) and variable-range hopping (VRH) respectively. It can be seen that the fitting results of VRH are better than the other two models i.e. band-gap model and NSPH. This leads us to conclude that the VRH process dominates the conduction mechanism at T > 170 K in these layered manganites. We show the fitting results of VRH model in figure 3. The fitting parameters T0, N(E) and chi-square are given in Table 1.
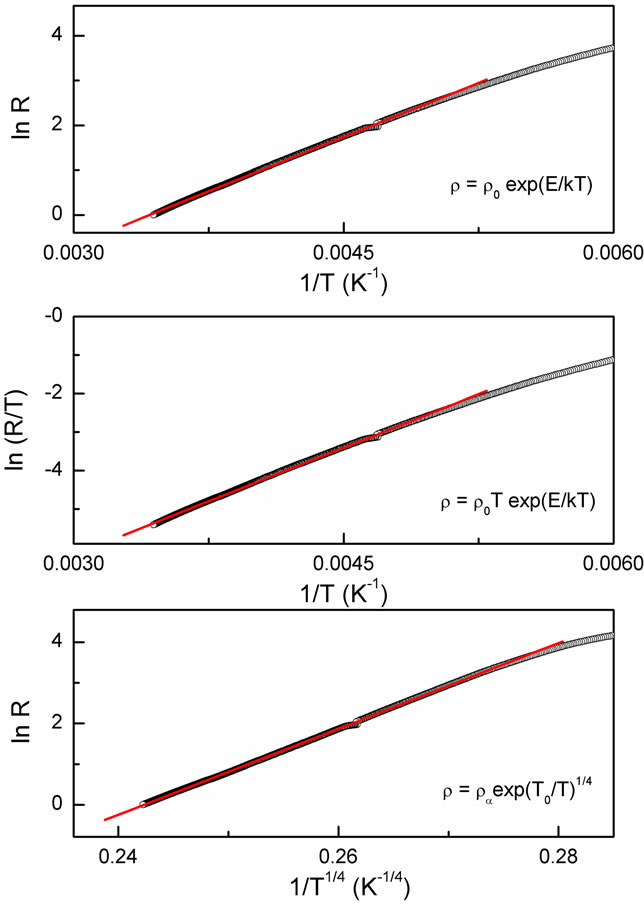
Figure 2. Fitting of three different functions in R-T data for La1.5Ca1.5Mn1.95Fe0.05O7.
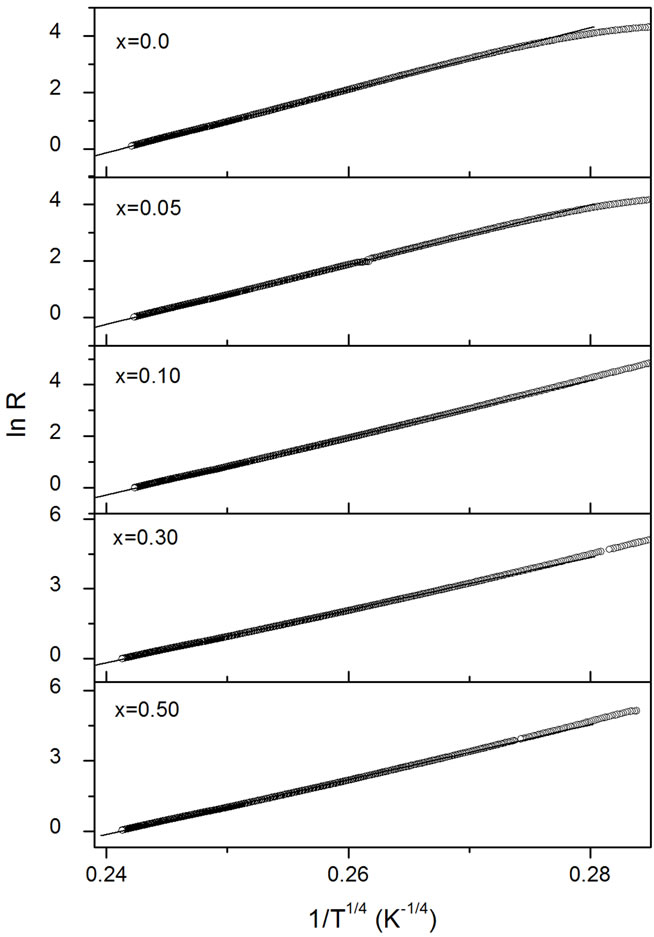
Figure 3. ln(R) shown as a function of 1/T1/4 for La1.5Ca1.5Mn2−xFexO7 (x = 0, 0.05, 0.1, 0.3, 0.5). Solid line show Mott’s VRH model fitting.
From table 1 one finds that the value of N(E) decreases with the x increasing, which indicates that the capacity to conduct reduces with the Fe ion doping. N(E) is also two orders of magnitude higher in these manganites than those of usual oxide semiconductors. Such a higher value of N(E) also estimated by other researchers [8,17], is due to the higher conductivity of these oxides than those of the usual transition-metal-oxide semiconductors [18] and this large value of N(E) is also an indication of adiabatic hopping behavior of the carriers in these manganites as pointed out by Jung [17]. For the NSPH model, the value of EP augments with the x increasing. It is based on that the amount of eg electrons reduces with the Fe ion increasing. This results in the resistivity increasing and accordingly the hopping energy increases.
From figure 4 one finds that for the samples of x = 0.05, the resistivity decreases but Tp shifts to higher temperature with the application of magnetic field. This is due to charge carrier delocalization is induced by the magnetic field, which suppresses the resistivity. The application of the magnetic field, also causes the local ordering of magnetic spin and due to this ordering, the ferromagnetic metallic (FMM) state suppresses the paramagnetic insulating (PMI) state. So, the peak temperature (Tp) shifts to the high temperature regime with application of magnetic field.
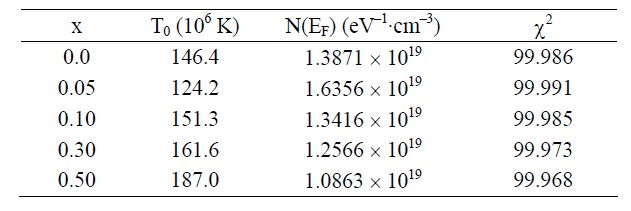
Table 1. Values of T0, density of states at Fermi energies and chi-square obtained from fitted of resistivity-temperature data of the samples in the series La1.5Ca1.5Mn2−xFexO7.

Figure 4. The temperature dependence resistance and MR for La1.5Ca1.5Mn1.95Fe0.05O7.

Figure 5. The field dependence of MR for La1.5Ca1.5Mn1.95Fe0.05O7 at 20 K.
We discuss below, about magnetoresistance (MR) of the samples of our present investigation. Figure 4 indicates the thermal variation of MR (ρ/ρ(0) (%) = ρ(0) − ρ(H)/ρ(0) × 100, where ρ(H) = resistance in a field of 7 kOe, ρ(0) = resistance at zero field) of two samples. The maximum value of MR for x = 0.05 is 34% (105 K, 7 kOe). The pronounced MR ratio for x = 0.0 and 0.05 is stable in a wide temperature region below Tp. This low temperature MR effect is popular in many n = 2 layered perovskites [6]. Figure 5 show the field variation of MR at 20 K for x = 0.05. As for the heavily doped samples with x = 0.1, 0.3 and 0.5, they present the other kind of ρ-T curves, which are quite different from those of the lightly doped samples.
4. Conclusions
Single-phase rare-earth manganites La1.5Ca1.5Mn2-xFexO7 (x = 0.0, 0.05, 0.1, 0.3 and 0.5) were prepared to study the effect of doping content on the metal-insulator transition and electrical resistivity. It is found that the ratio of Mn3+/Mn4+ reduces with the x increasing. The metalinsulator transition is observed with the lower values of x (x = 0.0, 0.05) and the Tp shifts to higher temperature with the application of magnetic field. The conductivity also depends on the Fe concentration and shows obvious decrease with the increase of Fe content in the samples. It is due to the eg electrons decrease which in turn weakens double-exchange mechanism. All the ρ-T curves in T > 170 K are fitted quite well in the VRH mechanism. The density of states N(E) is two orders of magnitude higher than those of many transition-metal-oxide semiconductors. The value of N(E) decreases with the x increase, which indicates that the capacity to conduct reduces with the Fe ion doping.
5. Acknowledgements
MPS thanks to Council of Scientific and Industrial Research (CSIR), New Delhi, for the award of fellowship.
REFERENCES
- R. Mahendiran, S. K. Tiwary, A. K. Raychaudhuri and T. V. Ramakrishnan, “Structure, Electron-Transport Properties, and Giant Magnetoresistance of Hole-Doped LaMnO3 Systems,” Physical Review B, Vol. 53, No. 6, 1996, pp. 3348-3385. doi:10.1103/PhysRevB.53.3348
- P. Mandal and B. Ghosh, “Transport, Magnetic, and Structural Properties of La1-xMxMnO3 (M = Ba, Sr, Ca) for 0 £ x £ 0.20,” Physical Review B, Vol. 68, No. 1, 2003, pp. 014422(1-8). doi:10.1103/PhysRevB.68.014422
- K. H. Ahn, X. W. Wu, K. Liu and C. L. Chien, “Magnetic Properties and Colossal Magnetoresistance of La(Ca)MnO3 Materials Doped with Fe,” Physical Review B, Vol. 54, No. 21, 1996, pp. 15299-15302. doi:10.1103/PhysRevB.54.15299
- C. Zener, “Interaction between the d-Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure,” Physical Review, Vol. 82, No. 3, 1960, pp. 403-405. doi:10.1103/PhysRev.82.403
- P.-G. de Gennes, “Effects of Double Exchange in Magnetic Crystals,” Physical Review, Vol. 118, No. 1, 1960, pp. 141-154. doi:10.1103/PhysRev.118.141
- H. Asano, J. Hayakawa and M. Matsui, “Giant Magnetoresistance of a Two-Dimensional Ferromagnet La2−2xCa1+2xMn2O7,” Applied Physics Letters, Vol. 68, No. 25, 1996, pp. 3638-3640. doi:10.1063/1.115755
- M. P. Sharma, A. Krishnamurthy and B. K. Srivastava, “Magnetization and Mössbauer Study of Double Layer Perovskites La1.5Ca1.5FexMn2-xO7 Prepared by Sol-Gel Method,” Hyperfine Interaction, Vol. 184, No. 1-3, 2008, pp. 201-206. doi:10.1007/978-3-540-78697-9_83
- M. Viret, L. Ranno and J. M. D. Coey, “Magnetic Localization in Mixed-Valence Manganites,” Physical Review B, Vol. 55, No. 13, 1997, pp. 8067-8070. doi:10.1103/PhysRevB.55.8067
- J. M. D. Coey, M. Viret, L. Ranno and K. Ounadjela, “Electron Localization in Mixed-Valence Manganites,” Applied Physics Letters, Vol. 75, No. 21, 1995, pp. 3910-3913. doi:10.1103/PhysRevLett.75.3910
- M. Viret, L. Ranno and J. M. D. Coey, “Colossal Magnetoresistance of the Variable Range Hopping Regime in the Manganites,” Journal of Applied Physics, Vol. 81, No. 8, 1997, pp. 4964-4971. doi:10.1063/1.365013
- Y. Sun, X. Xu and Y. Zhang, “Variable-Range Hopping of Small Polarons in Mixed-Valence Manganites,” Journal of Physics: Condensed Matter, Vol. 12, No. 50, 2000, pp. 10475-10481. doi:10.1088/0953-8984/12/50/309
- D. Emin and T. Holstein, “Adiabatic Theory of an Electron in a Deformable Continuum,” Physical Review Letters, Vol. 36, No. 6, 1976, pp. 323-326. doi:10.1103/PhysRevLett.36.323
- M. Ziese and C. Srinitiwarawong, “Polaronic Effects on the Resistivity of Manganite Thin Films,” Physical Review B, Vol. 58, No. 17, 1998, pp. 11519-11525. doi:10.1103/PhysRevB.58.11519
- A. Banerjee, S. Pal and B. K. Chaudhuri, “Nature of Small-Polaron Hopping Conduction and the Effect of Cr Doping on the Transport Properties of Rare-Earth Manganite La0.5Pb0.5Mn1−xCrxO3,” Journal of Chemical Physics, Vol. 115, No. 3, 1998, pp. 1550-1558. doi:10.1063/1.1378018
- D. S. Rana, C. M. Thaker, K. R. Mavani, D. G. Kuberkar, D. C. Kundaliya and S. K. Malik, “Magnetic and Transport Properties of (La0.7−2xEux)(Ca0.3Srx)MnO3: Effect of Simultaneous Size Disorder and Carrier Density,” Journal of Applied Physics, Vol. 95, No. 9, 2004, pp. 4934- 4940. doi:10.1063/1.1667258
- H. Zhu, X. J. Xu, L. Pi and Y. H. Zheng, “Two-Dimensional Magnetic Correlation and Transport Behavior of Layered Manganite La1.4Sr1.6Mn2-xCuxO7,” Physical Review B, Vol. 62, No. 10, 2002, pp. 6754-6760. doi:10.1103/PhysRevB.62.6754
- W. H. Jung, “Evaluation of Mott’s Parameters for Hopping Conduction in La0.67Ca0.33MnO3 above Tc,” Journal of Materials Science Letters, Vol. 17, No. 15, 1998, pp. 1317- 1319. doi:10.1023/A:1006665200481
- J. W. Liu, G. Chen, Z. H. Li, W. W. An and Z. G. Zhang, “X-Ray Photoemission Spectra and the Electro-Transport Properties Studies on the Layered Manganites Sm2−2xSr1+2xMn2O7,” Journal of Alloys and Compounds, Vol. 431, No. 1-2, 2007, pp. 1-5. doi:10.1016/j.jallcom.2006.05.038

