World Journal of Condensed Matter Physics
Vol.1 No.3(2011), Article ID:6931,8 pages DOI:10.4236/wjcmp.2011.13014
Noise-Dependent Stability of the Synchronized State in a Coupled System of Active Rotators
![]()
1Department of Physics, Campus Box 1105, Washington University, St. Louis, USA; 2Universität Duisburg-Essen, Campus
Duisburg, Fachbereich Physik, Duisburg, Germany.
Email: {sbrandt, rw}@physics.wustl.edu, axel.pelster@uni-duisburg-essen.de
Received March 26th, 2011; revised April 15th, 2011; accepted April 26th, 2011.
Keywords: Stochastic Analysis Methods, Synchronization, Coupled Oscillators
ABSTRACT
We consider a Kuramoto model for the dynamics of an excitable system consisting of two coupled active rotators. Depending on both the coupling strength and the noise, the two rotators can be in a synchronized or desynchronized state. The synchronized state of the system is most stable for intermediate noise intensity in the sense that the coupling strength required to desynchronize the system is maximal at this noise level. We evaluate the phase boundary between synchronized and desynchronized states through numerical and analytical calculations.
1. Introduction
Networks of coupled nonlinear oscillators provide useful model systems for the study of a variety of phenomena in physics and biology [1]. Among many others, examples from physics include solid-state lasers [2] and coupled Josephson junctions [3,4]. In biology, the central nervous system can be described as a complex network of oscillators [5], and cultured networks of heart cells are examples of biological structures with strong nearest-neighbor coupling [6]. In particular, the emergence of synchrony in such networks [7,8] has received increased attention in recent years.
Disorder and noise in physical systems usually tend to destroy spatial and temporal regularity. However, in nonlinear systems, often the opposite effect is found and intrinsically noisy processes, such as thermal fluctuations or mechanically randomized scattering, lead to surprisingly ordered patterns [9]. For instance, arrays of coupled oscillators can be synchronized by randomizing the phases of their driving forces [10,11]. Synchronization in these systems is caused by the interactions between the elements and results in the emergence of collective modes. It has been shown to be a fundamental mechanism of self-organization and structure formation in systems of coupled oscillators [12]. Biological systems of neurons are subject to different sources of noise, such as synaptic noise [13] or channel noise [14]. In particular, sensory neurons are notoriously noisy. Therefore, the question arises how stochastic influences affect the functioning of biological systems. Especially interesting are scenarios in which noise enhances performance. In the case of stochastic resonance [15], e.g., noise can improve the ability of a system to transfer information reliably, and the presence of this phenomenon in neural systems has been investigated [16,17]. Furthermore, numerous studies have addressed the effect of noise on the dynamics of limit cycle systems [18-23].
Small neural circuits composed of two or three neurons form the basic feedback mechanisms involved in the regulation of neural activity [24]. They can display oscillatory activity [25,26] and serve as central pattern generators involved in motor control [27]. Here, we consider a system of two limit cycle oscillators with repulsive coupling. We investigate the influence of the noise and the coupling strength on the dynamics of the system. We distinguish between two different classes of dynamics, a synchronized state, in which the joint probability density of the oscillator phases is characterized by a single-hump shape, and a desynchronized state. The single-hump shaped distribution of the oscillator phases has been modeled by a Gaussian distribution [28,12], and systems consisting of a large number of oscillators were analyzed by examining the resulting dynamics for the mean of the oscillator phases [20]. In contrast, the simplicity of our two oscillator system allows us to obtain the stationary probability density function for the full system both numerically and analytically. We show that the probability distribution of the oscillator phases has the single-hump shape only for weak coupling, whereas it deviates from this shape for strong coupling. We evaluate the coupling strength at which the transition between the two forms of the probability distribution occurs as a function of the noise intensity.
In Section 2, we introduce the Kuramoto model for excitable systems. Under the influence of noise, the dynamics of the limit cycle oscillators are described by a stochastic differential equation (SDE), and we state the Fokker-Planck equation for the system. In Section 3, we consider a single active rotator driven by noise and derive its mean angular frequency from the stationary solution to the Fokker-Planck equation. We compare our analytical results with Monte-Carlo simulations of the corresponding SDE. In Section 4, we consider two coupled deterministic rotators and perform a bifurcation analysis of the system. We show that the system possesses a fixed point that is stable for small coupling strengths but loses its stability when the coupling is increased. For some range of the coupling strength, the stable fixed point and a stable limit cycle coexist. In Section 5, we consider two coupled active rotators under uncorrelated stochastic influences. In Section 5.1, we solve the Fokker-Planck equation of the system numerically and show that the shape of the probability distribution undergoes a characteristic change, corresponding to the transition from a synchronized to a desynchronized state, as coupling is increased. We evaluate the boundary between the synchronous and the asynchronous regime through a Fourier expansion approach in Section 5.2. A summary concludes the paper in Section 6.
2. Excitable Systems and the Kuramoto Model
Neurons can display a wide range of behavior to different stimuli and numerous models exist to describe neuronal dynamics. A common feature of both biological and model neurons is that sufficiently strong input causes them to fire periodically; the neuron displays oscillatory activity. For subthreshold inputs, on the other hand, the neuron is quiescent. When a subthreshold input is combined with a noisy input, however, the neuron will be pushed above threshold from time to time and fire spikes in a stochastic manner. In this regime, the neuron acts as an excitable element. In general, an excitable system possesses a stable equilibrium point from which it can temporarily depart by a large excursion through its phase space when it receives a stimulus of sufficient strength [22]. Besides neurons, chemical reactions, lasers, models of blood clotting, and cardiac tissues all display excitable dynamics [29-33]. Pulse propagation, spiral waves, spatial and temporal chaos, and synchronization have been studied in these systems [34-37].
The phase dynamics of an active rotator without interaction and random forces can be described by the model developed by Kuramoto and coworkers [38,39]:
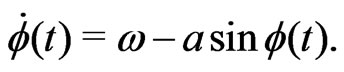 (1)
(1)
To obtain the case of the excitable system with one stationary point, one chooses the parameter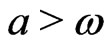 . When we have n coupled identical oscillators, subject to stochastic influences, the model is described by the Langevin Equation [23]
. When we have n coupled identical oscillators, subject to stochastic influences, the model is described by the Langevin Equation [23]
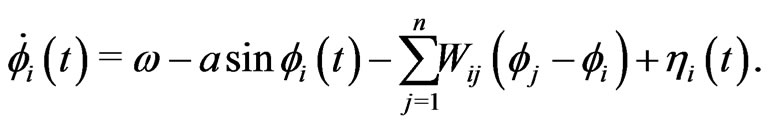 (2)
(2)
Here, we take the 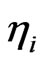 to be uncorrelated Gaussian white noise, i.e.
to be uncorrelated Gaussian white noise, i.e.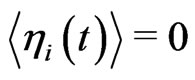 ,
,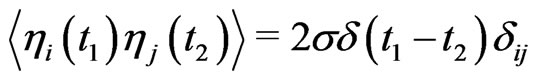 . We will concentrate on the simplest case, namely that the coupling functions
. We will concentrate on the simplest case, namely that the coupling functions  are sin-functions multiplied by a coupling constant
are sin-functions multiplied by a coupling constant , i.e.,
, i.e., . Then, the dynamical evolution of the system's probability density function
. Then, the dynamical evolution of the system's probability density function 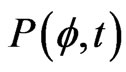 is described by the Fokker-Planck equation
is described by the Fokker-Planck equation
 (3)
(3)
where in our case the drift terms read
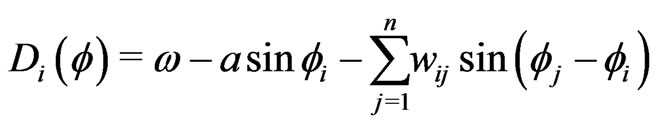 (4)
(4)
and the diffusion terms are given by
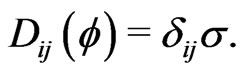 (5)
(5)
Since the angle variables 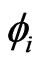 describe the phases of the oscillators, the probability density function must satisfy the periodic boundary conditions
describe the phases of the oscillators, the probability density function must satisfy the periodic boundary conditions
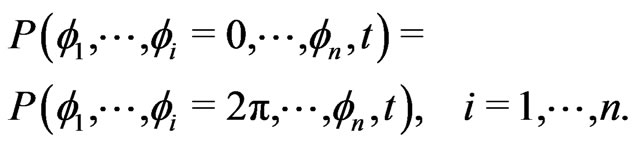 (6)
(6)
Furthermore, the normalization condition for the probability density reads
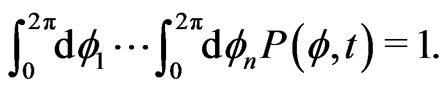 (7)
(7)
3. Single-Rotator System
We first exam a single rotator subject to a noisy input and, following Ref. [40], calculate the mean frequency of oscillations as a function of the noise level. In this case, the Fokker-Planck Equation (3) reads
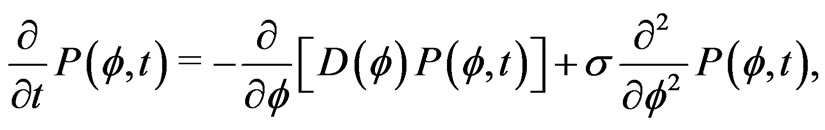 (8)
(8)
with
 (9)
(9)
We can thus write the drift term as the negative gradient of a potential, 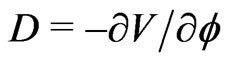 , with the potential given by
, with the potential given by
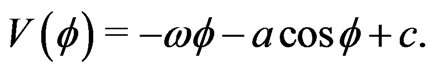 (10)
(10)
Introducing the probability current
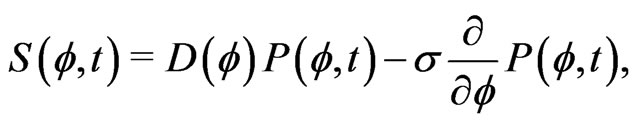 (11)
(11)
the Fokker-Planck equation takes the form of a continuity equation,
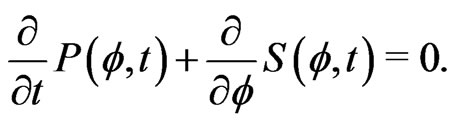 (12)
(12)
We now look for a stationary solution of the form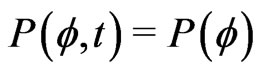 ,
,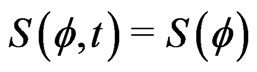 . In this case, we conclude from (12) that the derivative of the probability current with respect to
. In this case, we conclude from (12) that the derivative of the probability current with respect to 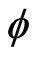 must vanish, and we have to solve
must vanish, and we have to solve
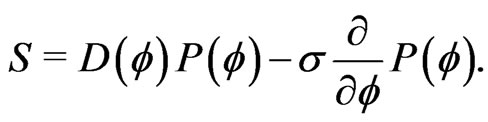 (13)
(13)
The constant probability current S is related to the mean drift velocity, i.e., the mean angular frequency of the active rotator system according to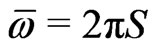 . The solution to the ordinary differential Equation (13) is given by
. The solution to the ordinary differential Equation (13) is given by
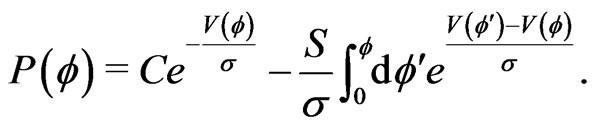 (14)
(14)
The integration constant in (10) can thus be absorbed into the constant C in (14), and the two free constants S and C are determined by the periodicity and normalization conditions (6) and (7). These two conditions can be written in matrix form as
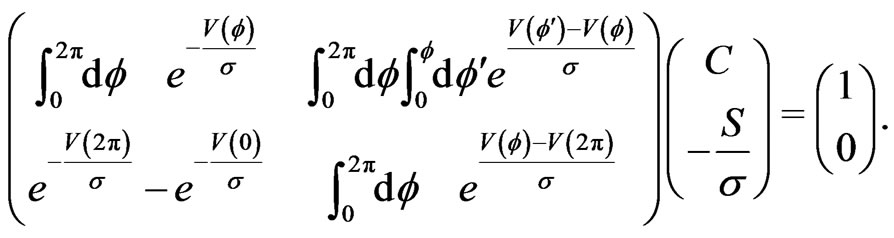 (15)
(15)
Denoting the determinant of the 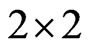 matrix in the last expression as det, the constants C and S are given by
matrix in the last expression as det, the constants C and S are given by
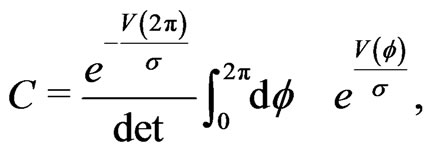 (16)
(16)
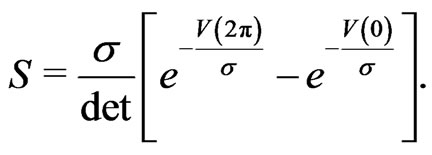 (17)
(17)
Specializing to the potential of the active rotator (10), we obtain
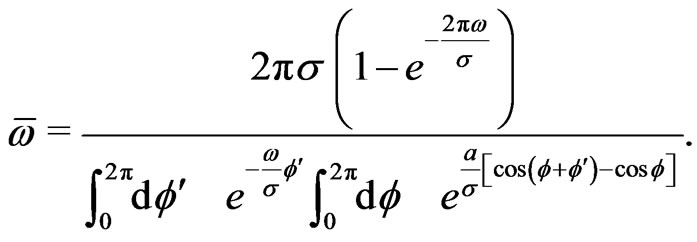 (18)
(18)
Note that in the limit 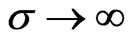 the integrand in the denominator approaches one, and
the integrand in the denominator approaches one, and 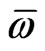 converges to
converges to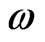 . To obtain the leading order behavior of
. To obtain the leading order behavior of 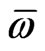 in the limit of small noise, we approximate the denominator using Laplace's method described in Ref. [41]. According to Laplace's method the asymptotic behavior of the integral
in the limit of small noise, we approximate the denominator using Laplace's method described in Ref. [41]. According to Laplace's method the asymptotic behavior of the integral
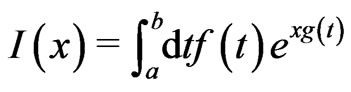 (19)
(19)
as  is given by
is given by
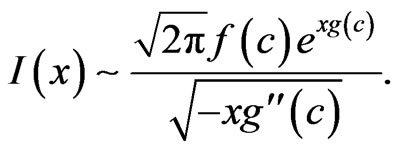 (20)
(20)
Here, it is assumed that 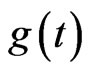 has a maximum at
has a maximum at 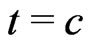 with
with 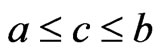 and that
and that 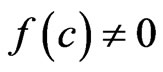 and
and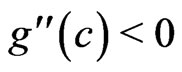 . We first apply Laplace's method to the inner integral in the denominator of (18), which we denote as
. We first apply Laplace's method to the inner integral in the denominator of (18), which we denote as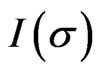 . The function
. The function 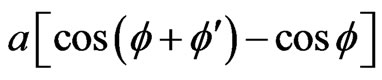 has a maximum inside the interval
has a maximum inside the interval 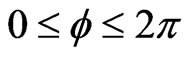 at
at
 (21)
(21)
Using (20) we thus obtain for 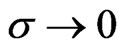
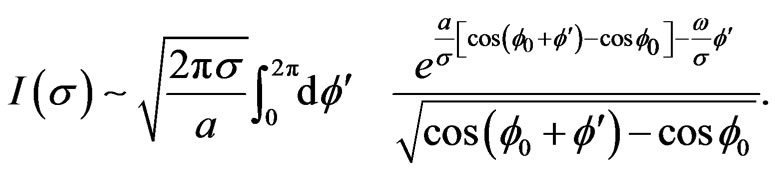 (22)
(22)
The argument of the exponential function in the last identity can be simplified to
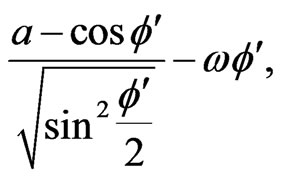 (23)
(23)
whose maximum within the interval 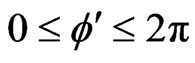 is at
is at
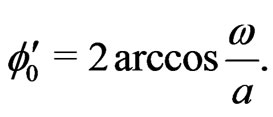 (24)
(24)
Using this and applying (20) to the intermediate result (22), we obtain
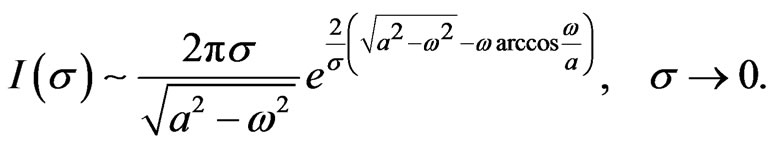 (25)
(25)
The leading asymptotic behavior of 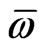 as
as 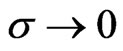 is then given by
is then given by
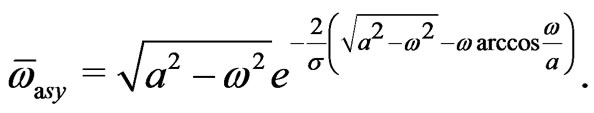 (26)
(26)
Figure 1 shows the mean angular frequency 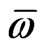 as a function of the noise level
as a function of the noise level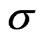 . The evaluation of the analytical expression (18) yields results that are in good agreement with Monte-Carlo simulations of the Langevin Equation (2). Furthermore, the asymptotic expansion (26) is in excellent agreement with numerical evaluations of (18) for small noise.
. The evaluation of the analytical expression (18) yields results that are in good agreement with Monte-Carlo simulations of the Langevin Equation (2). Furthermore, the asymptotic expansion (26) is in excellent agreement with numerical evaluations of (18) for small noise.
4. Deterministic Two-Rotator System
We next turn to a system of two coupled active rotators, where we first consider the deterministic case, i.e.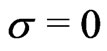 . In particular, we are interested in rotators with repulsive coupling, i.e. we consider the case
. In particular, we are interested in rotators with repulsive coupling, i.e. we consider the case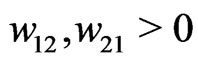 . Introducing the center of mass and difference coordinates
. Introducing the center of mass and difference coordinates 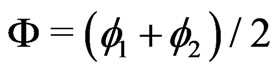 and
and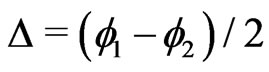 , the set of Equations (2) takes the form
, the set of Equations (2) takes the form
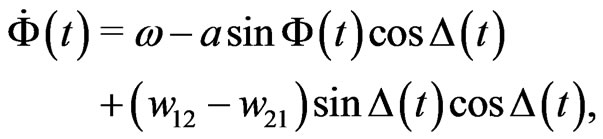
 (27)
(27)
The system has a trivial stationary point at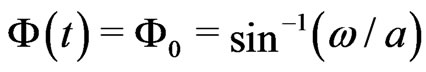 ,
, 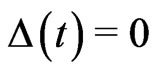 , whose stability we analyze by linearizing the system (27). Writing
, whose stability we analyze by linearizing the system (27). Writing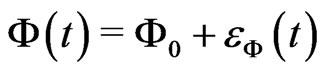 ,
, 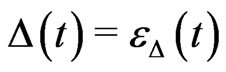 we obtain to first order
we obtain to first order
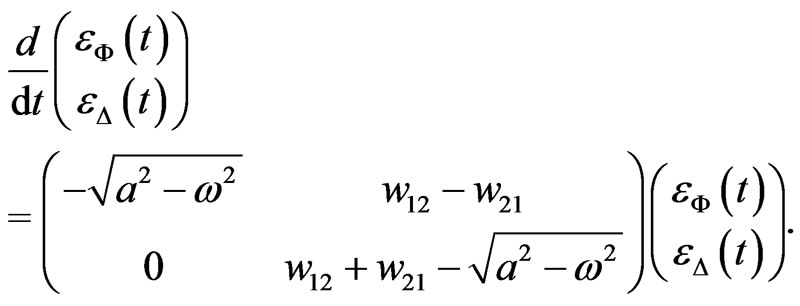 (28)
(28)
The real parts of the eigenvalues of the 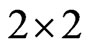 matrix on the right-hand side of the last identity determine the stability of the fixed point
matrix on the right-hand side of the last identity determine the stability of the fixed point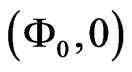 . Under the assumption
. Under the assumption 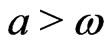 the first eigenvalue
the first eigenvalue  is always real and negative. The second eigenvalue
is always real and negative. The second eigenvalue 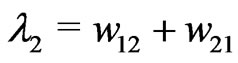
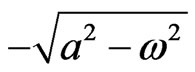 is also always real; for small coupling it is negative, but when the sum of the coupling strengths
is also always real; for small coupling it is negative, but when the sum of the coupling strengths 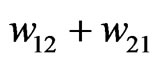 increases it becomes positive and the fixed point
increases it becomes positive and the fixed point  loses its stability in, as it turns out, a subcritical pitchfork bifurcation. Further fixed points of the system can be determined and turn out to be unstable for all values of the coupling strengths. In the case
loses its stability in, as it turns out, a subcritical pitchfork bifurcation. Further fixed points of the system can be determined and turn out to be unstable for all values of the coupling strengths. In the case 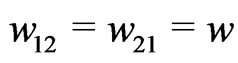 they are given by
they are given by
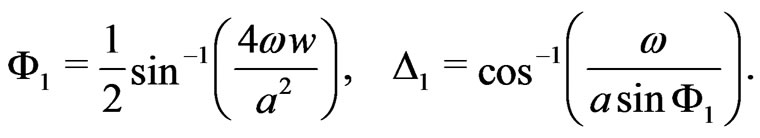 (29)
(29)
Figure 2(a) shows a bifurcation diagram of the system. For small coupling strength, the system does not display oscillatory behavior. When the coupling strength is increased above a critical value, a stable limit cycle emerges
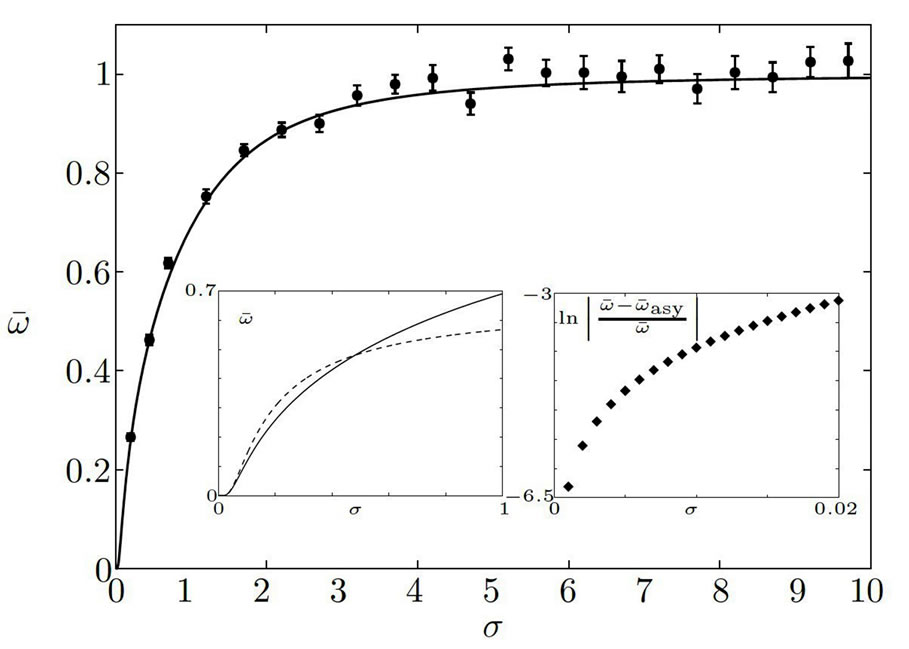
Figure 1. Average angular frequency of the single-rotator as a function of the noise intensity. The solid line shows the result (18). The dots represent results from Monte-Carlo simulations (mean  standard error of the mean) of the Langevin Equation (2). For each value of the noise intensity, forty runs where simulated up to
standard error of the mean) of the Langevin Equation (2). For each value of the noise intensity, forty runs where simulated up to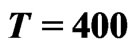 . The first inset shows a comparison between the asymptotic expansion (26, dashed line) and numerical evaluations of the expression (18, solid lines) for small noise. The diamonds in the second inset show the logarithm of the relative deviation between the result (18) and its asymptotic approximation (26). Parameters are:
. The first inset shows a comparison between the asymptotic expansion (26, dashed line) and numerical evaluations of the expression (18, solid lines) for small noise. The diamonds in the second inset show the logarithm of the relative deviation between the result (18) and its asymptotic approximation (26). Parameters are: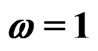 ,
,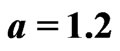 .
.
from a homoclinic orbit. For a small range of coupling strengths, the stable fixed point coexists with the stable limit cycle. In this case, it depends on the initial conditions whether the system will converge toward the fixed point 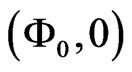 or the limit cycle. Figure 2(b) shows the attractors for fixed point and limit cycle dynamics in the
or the limit cycle. Figure 2(b) shows the attractors for fixed point and limit cycle dynamics in the 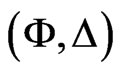 -plane for
-plane for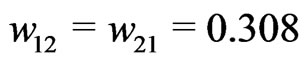 . In the strong-coupling limit, the minimum and maximum of
. In the strong-coupling limit, the minimum and maximum of 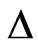 in Figure 2(a) both converge toward
in Figure 2(a) both converge toward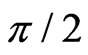 . Thus, the system approaches antisynchronous oscillatory dynamics, where
. Thus, the system approaches antisynchronous oscillatory dynamics, where  and
and 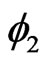 are phase shifted by
are phase shifted by 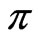 while their sum increases constantly.
while their sum increases constantly.
5. Stochastic Two-Rotator System
We now consider the coupled two-rotator system in the case where both rotators receive uncorrelated stochastic driving. The temporal evolution of the probability density of this system is given by the Fokker-Planck Equation (3) with the drift and diffusion coefficients (4) and (5).
5.1. Numerical Results
First, we investigate the stationary solution to the Fokker-Planck equation numerically. To this end, we numerically solve the partial differential Equation (3) under the periodic boundary conditions (6) for the homogeneous initial condition 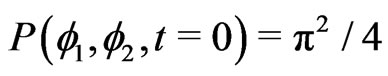 and observe that the solution converges to the stationary solu-
and observe that the solution converges to the stationary solu-
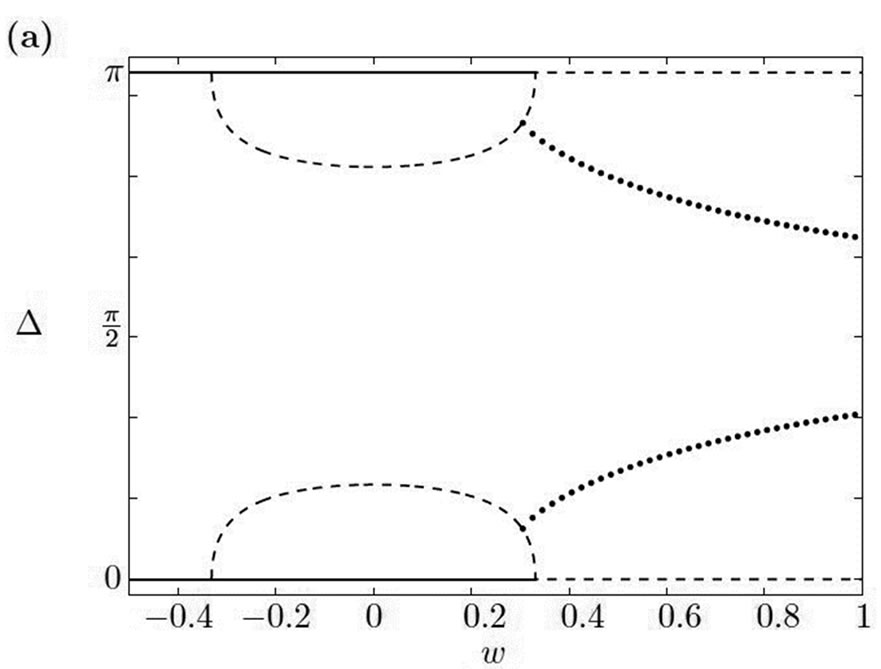
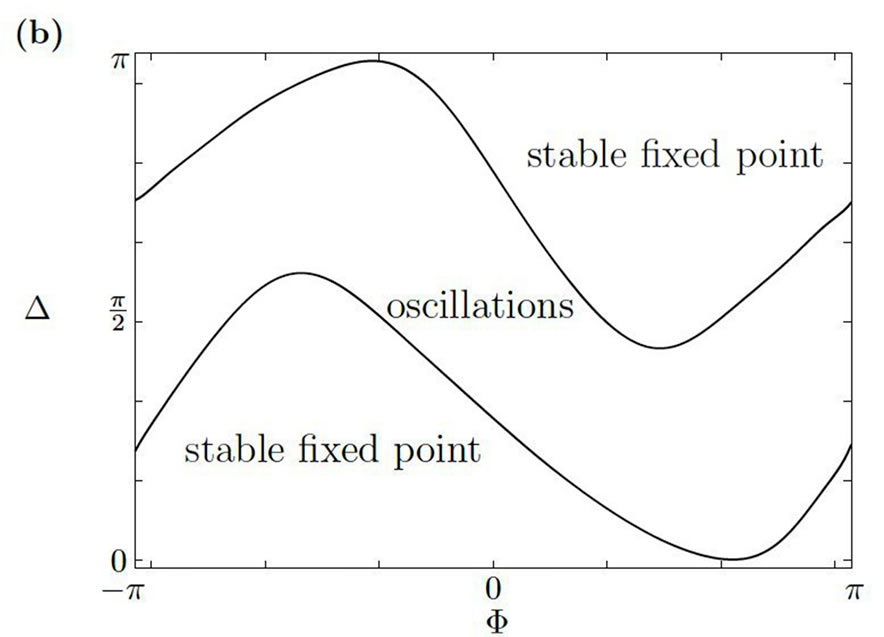
Figure 2. Stable and unstable fixed points and oscillations in the deterministic two-rotator system. (a) shows the bifurcation diagram with stable (solid lines) and unstable (dashed lines) fixed points of the system (27) for the choice of parameters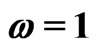 ,
, 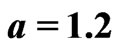 ,
,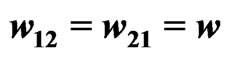 . Dots indicate the minimum and maximum values of oscillations in the value of
. Dots indicate the minimum and maximum values of oscillations in the value of  that result for the initial conditions
that result for the initial conditions ,
,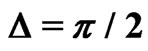 . (b) depicts for
. (b) depicts for 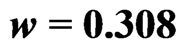 the boundaries between the regions in the space of initial conditions for which the system converges to the limit cycle or the stable fixed point.
the boundaries between the regions in the space of initial conditions for which the system converges to the limit cycle or the stable fixed point.
tion after some time. Figure 3 shows the stationary solution in the coordinates 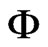 and
and 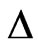 for two different values of the coupling strength. We find that, depending on the strength of the noise and coupling, two different characteristic forms of the stationary solution exist. In the case shown in Figure 3(a) the probability density is peaked around the stable fixed point of the deterministic two-rotator system
for two different values of the coupling strength. We find that, depending on the strength of the noise and coupling, two different characteristic forms of the stationary solution exist. In the case shown in Figure 3(a) the probability density is peaked around the stable fixed point of the deterministic two-rotator system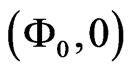 . In Figure 3(b), the peak at the fixed point
. In Figure 3(b), the peak at the fixed point 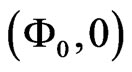 is much less pronounced. Furthermore, if we consider the probability distribution for
is much less pronounced. Furthermore, if we consider the probability distribution for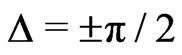 , i.e., at the edge of the region shown in Figure 3, we see that the probability distribution is not given by one central hump anymore. In order to distinguish between the two different scenarios in a quantitative way, we consider the marginal stationary probability density
, i.e., at the edge of the region shown in Figure 3, we see that the probability distribution is not given by one central hump anymore. In order to distinguish between the two different scenarios in a quantitative way, we consider the marginal stationary probability density
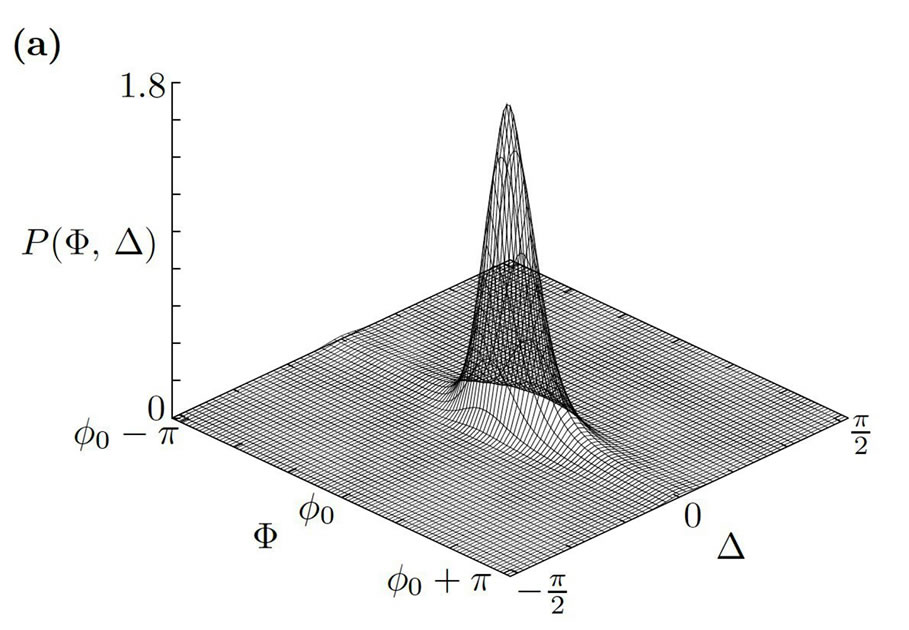
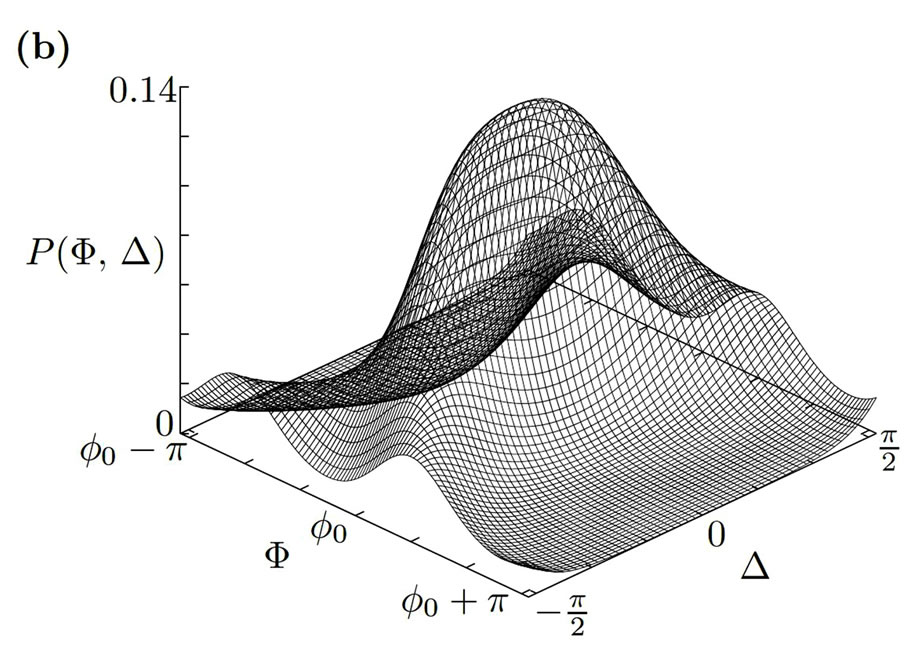
Figure 3. Synchronized and desynchronized modes in the stochastic two-rotator system. The stationary solution to the Fokker-Planck Equation (3) is shown for different values of the coupling strength. In both (a) and (b), we have 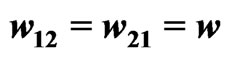 and
and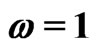 ,
, 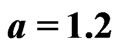 ,
, . In (a) the coupling strength is
. In (a) the coupling strength is 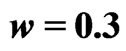 and the rotators are in a synchronized state; in (b) the coupling is increased to
and the rotators are in a synchronized state; in (b) the coupling is increased to 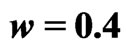 and the two rotators desynchronize.
and the two rotators desynchronize.
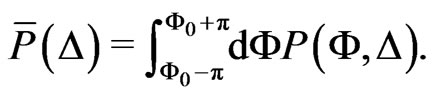 (30)
(30)
Figure 4 shows this quantity for one level of the noise intensity 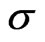 and for different coupling strengths. For weak coupling,
and for different coupling strengths. For weak coupling, 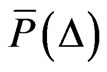 has a pronounced maximum at
has a pronounced maximum at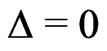 . For increasing coupling strengths, this maximum decreases and eventually turns into a minimum. We can thus classify the system dynamics as synchronized or desynchronized according to the sign of the second derivative of
. For increasing coupling strengths, this maximum decreases and eventually turns into a minimum. We can thus classify the system dynamics as synchronized or desynchronized according to the sign of the second derivative of 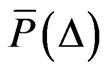 at the origin and can label the
at the origin and can label the 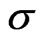 -w plane accordingly. In the next section, we calculate the phase boundary between the synchronized and desynchronized regime through a Fourier expansion approach.
-w plane accordingly. In the next section, we calculate the phase boundary between the synchronized and desynchronized regime through a Fourier expansion approach.
5.2. Fourier Expansion Results
The probability density 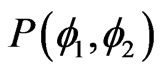 is periodic in
is periodic in  and
and , so we expand it as
, so we expand it as
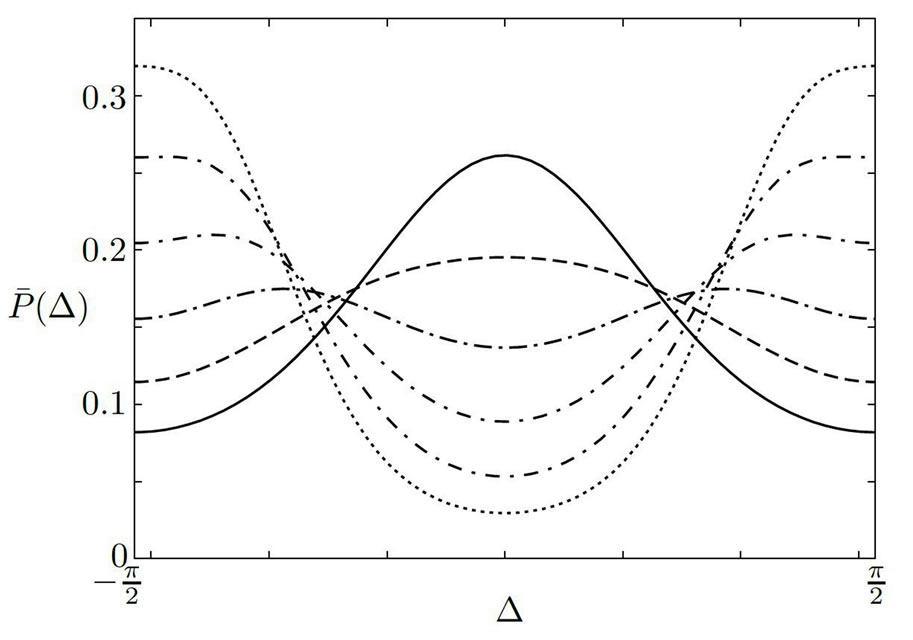
Figure 4. Marginal probability density for different values of the coupling strength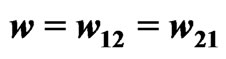 . The coupling strength for the curve with the highest value at
. The coupling strength for the curve with the highest value at 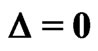 (solid line) is
(solid line) is  and increases from curve to curve in increments of
and increases from curve to curve in increments of 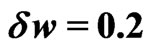 to the maximum value
to the maximum value 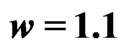 (dotted line). Other parameters are:
(dotted line). Other parameters are: ,
, 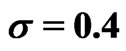 ,
,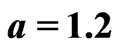 .
.
 (31)
(31)
Inserting this approach into the right-hand side of (3) yields together with (4) and (5)
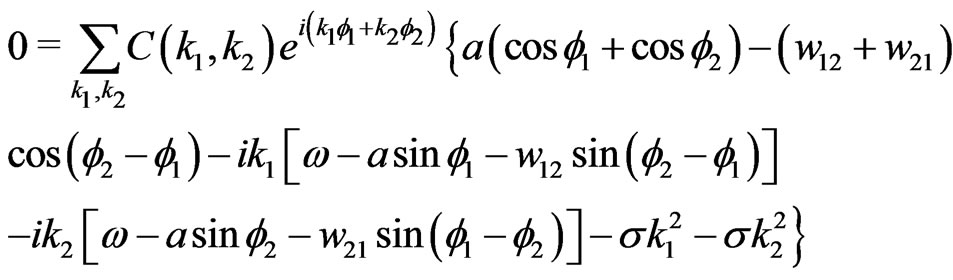 (32)
(32)
The term inside the curly brackets on the right-handside of the last identity is itself periodic in 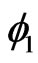 and
and 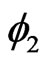 and can also be expanded as a Fourier series
and can also be expanded as a Fourier series
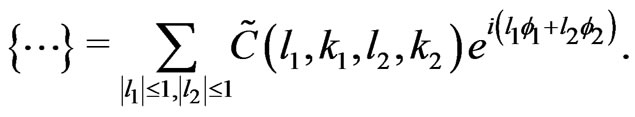 (33)
(33)
Here, the coefficients 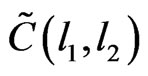 read
read
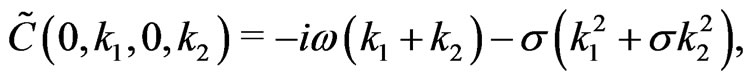
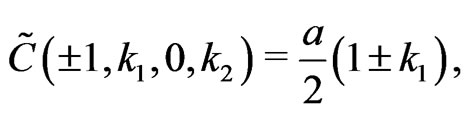
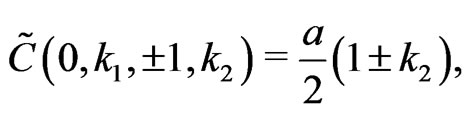
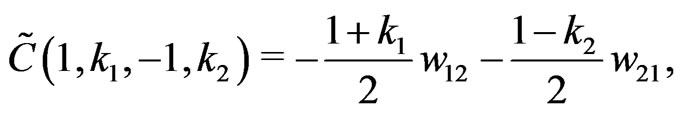
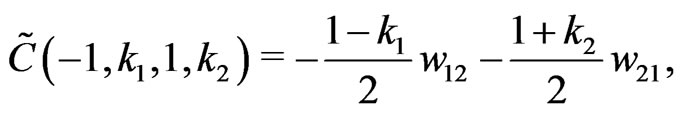
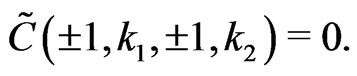 (34)
(34)
We can then rewrite (32) as
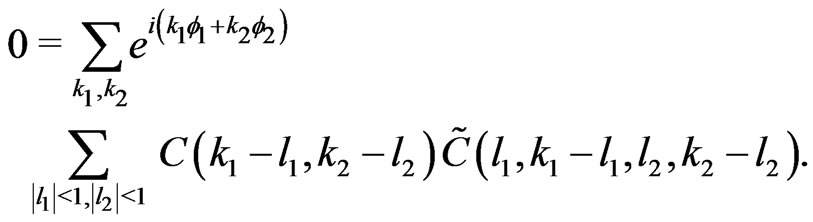 (35)
(35)
Setting the inner sum to zero, we obtain an infinite system of algebraic equations. In order to obtain the N th Fourier order approximation we truncate the outer sum such that we set 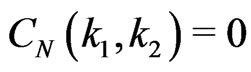 for
for 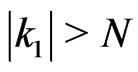 or
or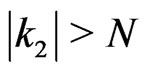 . Then, we have to solve a system of
. Then, we have to solve a system of 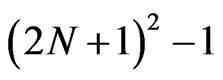 algebraic equations in order to obtain the expansion coefficients to N th order
algebraic equations in order to obtain the expansion coefficients to N th order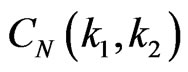 , where the additional index N indicates the approximation order. Finally, the coefficient
, where the additional index N indicates the approximation order. Finally, the coefficient  is determined from the normalization condition as
is determined from the normalization condition as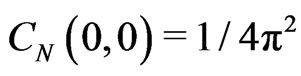 .
.
As an illustrative example we now consider the first order in the Fourier expansion for the case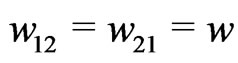 . The system of algebraic equations we need to solve then reads
. The system of algebraic equations we need to solve then reads
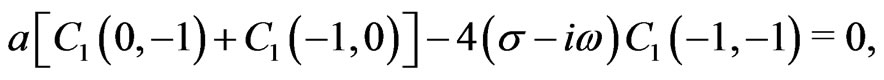
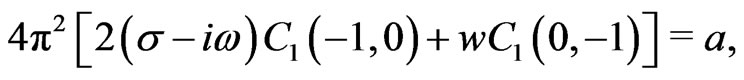
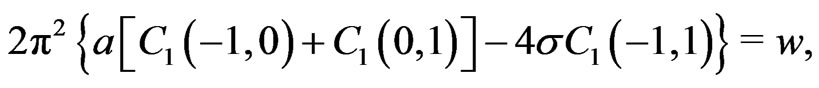
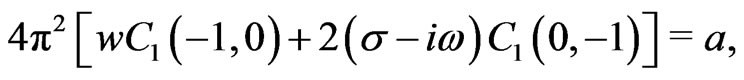

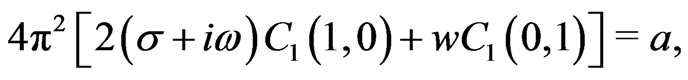
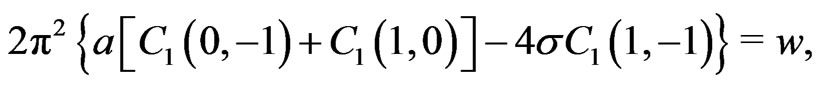
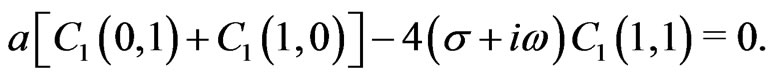
From this we obtain the first order approximation
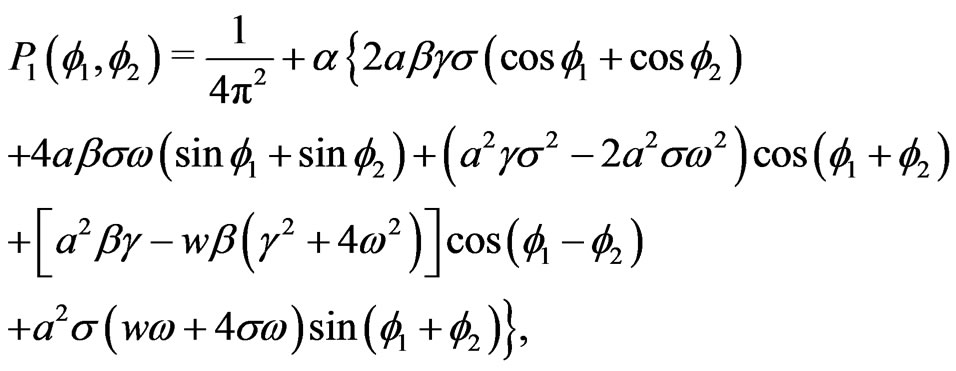 (36)
(36)
with the abbreviations
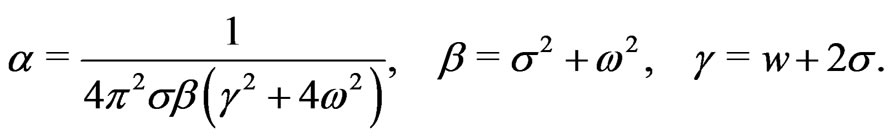 (37)
(37)
Substituting the coordinates 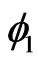 and
and 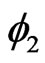 according to
according to 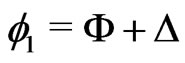 and
and 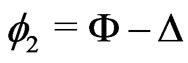 and integrating with respect to
and integrating with respect to 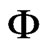 we obtain the marginal probability density
we obtain the marginal probability density
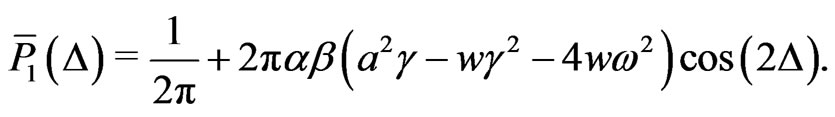 (38)
(38)
Setting its second derivative to zero, we obtain the equation
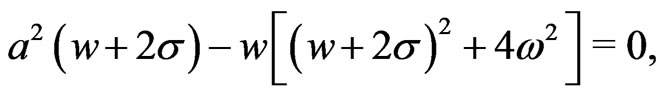 (39)
(39)
which we can solve in w or in . Eventually, we want to obtain w as a function of
. Eventually, we want to obtain w as a function of . However, since we have a cubic equation in w and only a quadratic equation in
. However, since we have a cubic equation in w and only a quadratic equation in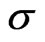 , for convenience we express
, for convenience we express 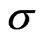 as a function of
as a function of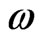 :
:
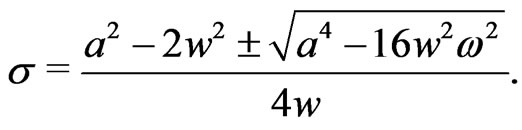 (40)
(40)
This procedure can easily be generalized to higher orders. Figure 5 shows the resulting phase diagram obtained from solving the Fokker-Planck equation numerically and from the Fourier expansion. The accuracy of the Fourier expansion results improves with increasing strength of the noise. This can be seen, for instance, in the second inset of Figure 5, where even the first expansion order yields very accurate results for strong noise. In general, even relatively low orders in the expansion give a good estimate for the phase boundary for a wide range of noise strengths, as can be seen from the results for the fourth expansion order in Figure 5. However, for very small noise levels the Fourier expansion diverges, as is exemplified in the first inset in Figure 5 for the fourth
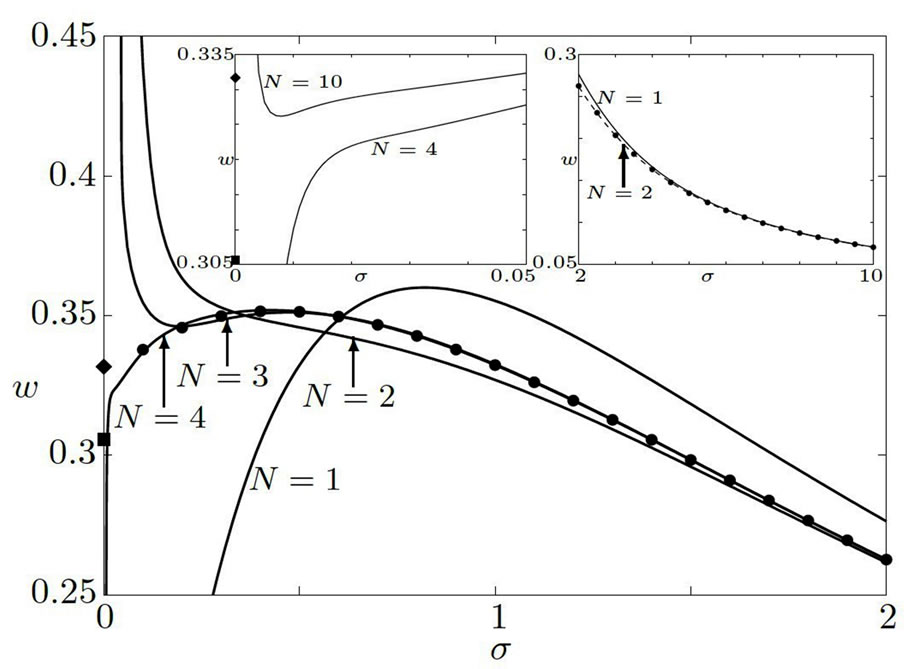
Figure 5. Regimes of synchronized and desynchronized dynamics. The phase boundary between the synchronized and desynchronized regimes is shown as a function of the noise strength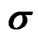 . Areas below the curves correspond to the synchronized, areas above the curve to the desynchronized regime. The solid lines show the results of the first four Fourier orders, the dots represent numerical results. The diamond represents the coupling strengths for which the fixed point
. Areas below the curves correspond to the synchronized, areas above the curve to the desynchronized regime. The solid lines show the results of the first four Fourier orders, the dots represent numerical results. The diamond represents the coupling strengths for which the fixed point 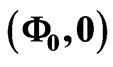 of the deterministic system becomes unstable; the square indicates the value of w at which the stable limit cycle is first observed. The insets show results for small and for large noise. In the first inset (small noise) the results from the fourth and tenth Fourier orders are shown. The second inset (large noise) shows the results from the first (solid line) and second (dashed line) Fourier orders. Parameters are
of the deterministic system becomes unstable; the square indicates the value of w at which the stable limit cycle is first observed. The insets show results for small and for large noise. In the first inset (small noise) the results from the fourth and tenth Fourier orders are shown. The second inset (large noise) shows the results from the first (solid line) and second (dashed line) Fourier orders. Parameters are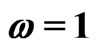 ,
,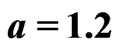 .
.
and tenth expansion orders. Considering the first inset in Figure 5, we conclude that in the limit  the results from the Fourier expansion approach a value of the coupling strength for which the stable fixed point coexists with the limit cycle in the deterministic system. Therefore, neither the existence of the stable limit cycle nor the stability of the fixed point can be used exclusively to determine the zero-noise limit of the phase transition between the synchronized and desynchronized states. Strong noise has a desynchronizing effect on the system, as the minimal coupling for desynchronization vanishes in the limit of
the results from the Fourier expansion approach a value of the coupling strength for which the stable fixed point coexists with the limit cycle in the deterministic system. Therefore, neither the existence of the stable limit cycle nor the stability of the fixed point can be used exclusively to determine the zero-noise limit of the phase transition between the synchronized and desynchronized states. Strong noise has a desynchronizing effect on the system, as the minimal coupling for desynchronization vanishes in the limit of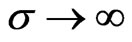 . If the noise is weak, however, it stabilizes the synchronized state, as is indicated by the initially upward slope of the phase boundary in Figure 5. In conclusion, the synchronized state of the system is most stable for intermediate noise.
. If the noise is weak, however, it stabilizes the synchronized state, as is indicated by the initially upward slope of the phase boundary in Figure 5. In conclusion, the synchronized state of the system is most stable for intermediate noise.
6. Summary
We have investigated the transition from synchronized to desynchronized behavior in a system of two-coupled active rotators under stochastic influences. The two regimes are distinguished by the sign of the second derivative of the marginal probability density at vanishing phase difference. We have evaluated the phase boundary between the two states in the (coupling strength) - (noise intensity) plane. Finally, we have shown that the synchronized state is most stable, in the sense that the coupling strength required to desynchronize the system is maximal for nonvanishing noise intensity.
7. Acknowledgements
We thank Janet Best, Anders Carlsson, John Clark, and John Rinzel for fruitful discussions. This work was supported in part by NIH-EY 15678.
REFERENCES
- J. F. Heagy, T. L. Carroll and L. M. Pecora, “Synchronous Chaos in Coupled Oscillator Systems,” Physical Review E, Vol. 50, No. 3, 1994, pp. 1874-1885. doi:10.1103/PhysRevE.50.1874
- R. Roy and K. S. Thornburg Jr., “Experimental Synchronization of Chaotic Lasers,” Physical Review Letters, Vol. 72, No. 13, 1994, pp. 2009-2012. doi:10.1103/PhysRevLett.72.2009
- A. V. Ustinov, M. Cirillo and B. A. Malomed, “Fluxon Dynamics in One-Dimensional Josephson-Junction Arrays,” Physical Review B, Vol. 47, No. 13, 1993, pp. 8357-8360. doi:10.1103/PhysRevB.47.8357
- K. Wiesenfeld, P. Colet and S. H. Strogatz, “Synchronization Transitions in a Disordered Josephson Series Array,” Physical Review Letters, Vol. 76, No. 3, 1996, pp. 404-407. doi:10.1103/PhysRevLett.76.404
- J. Hertz, A. Krogh and R. Palmer, “Introduction to the Theory of Neural Computation,” Addison-Wesley, Redwood City, 1991.
- Y. Soen, N. Cohen, D. Lipson and E. Braun, “Emergence of Spontaneous Rhythm Disorders in Self-Assembled Networks of Heart Cells,” Physical Review Letters, Vol. 82, No. 17, 1999, pp. 3556-3559. doi:10.1103/PhysRevLett.82.3556
- A. Pikovsky, M. Rosenblum and J. Kurths, “Synchronization: A Universal Concept in Nonlinear Sciences,” Cambridge University Press, Cambridge, 2003.
- S. Strogatz, “Sync: The Emerging Science of Spontaneous Order,” Hyperion, New York, 2003.
- T. Shinbrot and F. J. Muzzio, “Review Article Noise to Order,” Nature, Vol. 410, 2001, pp. 251-258. doi:10.1038/35065689
- S. F. Brandt, B. K. Dellen and R. Wessel, “Synchronization from Disordered Driving Forces in Arrays of Coupled Oscillators,” Physical Review Letters, Vol. 96, No. 3, 2006, pp. 034104-034107. doi:10.1103/PhysRevLett.96.034104
- R. Chaon and P. J. Martínez, “Controlling Chaotic Solitons in Frenkel-Kontorova Chains by Disordered Driving Forces,” Physical Review Letters, Vol. 98, No. 22, 2007, pp. 224102-224105. doi:10.1103/PhysRevLett.98.224102
- M. A. Zaks, A. B. Neiman, S. Feistel and L. Schimansky-Geier, “Noise-Controlled Oscillations and Their Bifurcations in Coupled Phase Oscillators,” Physical Review E, Vol. 68, No. 6, 2003, pp. 066206-066214. doi:10.1103/PhysRevE.68.066206
- W. H. Calvin and C. F. Stevens, “Synaptic Noise and Other Sources of Randomness in Motoneuron Interspike Intervals,” Journal of Neurophysiology, Vol. 31, 1968, pp. 574-587.
- J. A. White, J. T. Rubinstein and A. R. Kay, “Channel Noise in Neurons,” Trends in Neurosciences, Vol. 23, No. 3, 2000, pp. 131-137. doi:10.1016/S0166-2236(99)01521-0
- L. Gammaitoni, P. Hänggi, P. Jung and F. Marchesoni, “Stochastic Resonance,” Reviews of Modern Physics, Vol. 70, No. 1, 1998, pp. 223-287. doi:10.1103/RevModPhys.70.223
- J. K. Douglass, L. Wilkens, E. Pantazelou and F. Moss, “Noise Enhancement of Information Transfer in Crayfish Mechanoreceptors by Stochastic Resonance,” Nature, Vol. 365, 1993, pp. 337-340. doi:10.1038/365337a0
- K. Wiesenfeld and F. Moss, “Stochastic Resonance and the Benefits of Noise: From Ice Ages to Crayfish and SQUIDs,” Nature, Vol. 373, 1995, pp. 33-36. doi:10.1038/373033a0
- H. Treutlein and K. Schulten, Ber. Bunsenges. Phys. Chem. 89, 710 (1985).
- C. Kurrer and K. Schulten, “Effect of Noise and Perturbations on Limit Cycle Systems,” Physica D: Nonlinear Phenomena, Vol. 50, No. 3, 1991, pp. 311-320. doi:10.1016/0167-2789(91)90001-P
- C. Kurrer and K. Schulten, “Noise-Induced Synchronous Neuronal Oscillations,” Physical Review E, Vol. 51, No. 6, 1995, pp. 6213-6218. doi:10.1103/PhysRevE.51.6213
- C. Kurrer and K. Schulten, “Neuronal Oscillations and Stochastic Limit Cycles,” International Journal of Neural Systems, Vol. 7, No. 4, 1996, pp. 399-402. doi:10.1142/S0129065796000373
- M. A. Zaks, X. Sailer, L. Schimansky-Geier and A. B. Neiman, “Noise Induced Complexity: From Subthreshold Oscillations to Spiking in Coupled Excitable Systems,” Chaos, Vol. 15, No. 2, 2005, p. 026117. doi:10.1063/1.1886386
- B. Lindner, J. García-Ojalvo, A. Neiman and L. Schminasky-Geier, “Effects of Noise in Excitable Systems,” Physics Reports, Vol. 392, No. 6, 2004, pp. 321-424. doi:10.1016/j.physrep.2003.10.015
- J. Milton, “Dynamics of Small Neural Populations,” American Mathematical Society (AMS), Providence, 1996.
- S. F. Brandt, A. Pelster and R. Wessel, “Variational Calculation of the Limit Cycle and Its Frequency in a Two-Neuron Model with Delay,” Physical Review E, Vol. 74, No. 3, 2006, pp. 0362010-0362014. doi:10.1103/PhysRevE.74.036201
- S. F. Brandt, A. Pelster and R. Wessel, “Synchronization in a Neuronal Feedback Loop through Asymmetric Temporal Delays,” Europhysics Letters, Vol. 79, No. 3, 2007, pp. 38001/1-5. doi:10.1209/0295-5075/79/38001
- M. Rabinovich, A. Selverston, L. Rubchinsky and R. Huerta, “Dynamics and Kinematics of Simple Neural Systems,” Chaos, Vol. 6, 1996, p. 288. doi:10.1063/1.166176
- N. G. van Kampen, “Stochastic Processes in Physics and Chemistry,” 2nd Edition, North Holland, Amsterdam, 1992.
- T. Sakurai, E. Mihaliuk, F. Chirila and K. Showalter, Science, Vol. 14, 2002, p. 296.
- H. J. Wünsche, O. Brox, M. Radziunas and F. Henneberger, “Excitability of a Semiconductor Laser by a TwoMode Homoclinic Bifurcation,” Physical Review Letters, Vol. 88, No. 3, 2001, pp. 023901-023904. doi:10.1103/PhysRevLett.88.023901
- E. S. Lobanova, E. E. Shnol and F. I. Ataullakhanov, “Complex Dynamics of the Formation of Spatially Localized Standing Structures in the Vicinity of Saddle-Node Bifurcations of Waves in the Reaction-Diffusion Model of Blood Clotting,” Physical Review E, Vol. 70, No. 3, 2004, pp. 032903-032906. doi:10.1103/PhysRevE.70.032903
- A. V. Panfilov, S. C. Müller, V. S. Zykov and J. P. Keener, “Elimination of Spiral Waves in Cardiac Tissue by Multiple Electrical Shocks,” Physical Review E, Vol. 61, No. 4, 2000, pp. 4644-4647. doi:10.1103/PhysRevE.61.4644
- C. Koch, “Biophysics of Computation: Information Processing in Single Neurons,” Oxford University Press, New York, 1999.
- J. D. Murray, “Mathematical Biology,” 2nd Edition, Springer, New York, 1993. doi:10.1007/b98869
- A. S. Mikhailov, “Foundations of Synergetics I,” 2nd Edtion, Springer-Verlag, Berlin, 1994.
- T. R. Chay and J. Rinzel, “Bursting, Beating, and Chaos in an Excitable Membrane Model,” Biophysical Journal, Vol. 47, No. 3, 1985, pp. 357-366. doi:10.1016/S0006-3495(85)83926-6
- B. Hu and C. Zhou, “Synchronization Regimes in Coupled Noisy Excitable Systemsphys,” Physical Review E, Vol. 63, No. 2, 2001, pp. 026201-026206. doi:10.1103/PhysRevE.63.026201
- S. Shinomoto and Y. Kuramoto, “Phase Transitions in Active Rotator Systems,” Progress of Theoretical Physics, Vol. 75, No. 5, 1986, pp. 1105-1110. doi:10.1143/PTP.75.1105
- H. Sakaguchi, S. Shinomoto and Y. Kuramoto, “Phase Transitions and Their Bifurcation Analysis in a Large Population of Active Rotators with Mean-Field Coupling,” Progress of Theoretical Physics, Vol. 79, No. 3, 1988, pp. 600-607. doi:10.1143/PTP.79.600
- H. Risken, “The Fokker-Planck Equation. Methods of Solution and Applications,” Springer-Verlag, Berlin, 1984.
- C. M. Bender and S. A. Orszag, “Advanced Mathematical Methods for Scientists and Engineers,” Springer, New York, 1999.

