Atmospheric and Climate Sciences
Vol.07 No.01(2017), Article ID:73503,17 pages
10.4236/acs.2017.71005
Historical Phase-Locked El Niño Episodes
David H. Douglass1, Robert S. Knox1, Scott Curtis2*, Benjamin S. Giese3, Sulagna Ray4
1Department of Physics and Astronomy, University of Rochester, Rochester, NY, USA
2Department of Geography, Planning, and Environment, East Carolina University, Greenville, NC, USA
3Department of Oceanography, Texas A&M University, College Station, TX, USA
4Atmospheric and Ocean Sciences Program, Princeton University, Princeton, NJ, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 21, 2016; Accepted: January 13, 2017; Published: January 16, 2017
ABSTRACT
Using a newly reported Pacific sea surface temperature data set, we extend a prior study that assigned El Niño episodes to distinct sequences. Within these sequences the episodes are phase-locked to subharmonics of the annual solar irradiance cycle having two- or three-year periodicity. There are 40 El Niño episodes occurring since 1872, each found within one of eighteen such sequences. Our list includes all prev- iously reported events. Three El Niño episodes have already been observed in boreal winters of 2009, 2012 and 2015, illustrating a sequence of 3-year intervals that began in 2008. If the climate system remains in this state, the next El Niño is likely to occur in boreal winter of 2018.
Keywords:
Climate, Climatology, Solar Forcing, Seasonal Effects, El Niño, Phase Locking

1. Introduction
In a paper “El Niño occurrences in the past four and a half centuries,” Quinn, Neal and Mayolo [1] catalogue such events based upon published accounts of changes in wind, currents, physical damage, rainfall, flooding. They give the dates and magnitudes of about a hundred historic El Niño episodes. The present era of quantitative characterizations of the El Niño/La Niña phenomena has led to studying changes in the sea surface temperature (SST) of the equatorial Pacific Ocean. Positive variations in SST are called El Niño episodes and negative variations are called La Niña episodes.
Where in the tropical Pacific are the El Niño phenomena to be found? By finding the location in the tropical Pacific with the strongest correlation with related phenomena, Barnston, Chelliah and Goldenberg [2] determined that a particular sea surface temperature (SST) area (latitude: 5˚S to 5˚N; longitude: 120˚W to 170˚W) that overlaps previously defined Area3 and Area4 was best. This area, to be called A34, has an average SST over A34 ranging between 24˚C and 30˚C, and the data set is named SST3.4. Although SST areas with different names are also defined and studied, SST3.4 is the most commonly used proxy for analysis of the El Niño/La Niña phenomena.
The importance of area A34 to El Niño /La Niña studies is apparent in that of SST by Giese and Ray [3] in equatorial Pacific latitude band ±5˚. These authors give a list of El Niño episodes by date, magnitude, area, longitude and latitude. The longitude distribution was centered at 139˚W with a standard deviation of 12.8˚ and the average latitude was found to be ?0.12˚ ± 0.29˚ [4] . Thus, the location of these events is in the “center” of area A34. This is dramatic confirmation of the wisdom of the creation of area A34 and the corresponding index SST3.4 by Barnston, Chelliah and Goldenberg.
1.1. Classification
Independent events. Many studies have proposed classification schemes of El Niño episodes with the assumption that they were independent events. Categories based upon geographic location and similar criteria have been proposed by many authors. This effort resulted in a flurry of papers in which many different kinds of El Niño episodes having names such as EP, CP, Mixed, Modoki, etc. were proposed [5] - [11] . Johnson [12] summed up the state of this approach when he asked: “How many ENSO flavors can we distinguish?” The answer was nine!
Classification based on phase-locked states. Perhaps the first scientific report of phase locking was by Bjerknes [13] . He studied SST and the wind velocities at Canton Island (Equatorial mid-Pacific) for the period 1962-1967 and reported
“… sequence of rhythmic changes of temperature of approximately 2-year periodicity. … The main maxima of SST in late 1963 and late 1965 coincide with the main minima of the [annual] easterly wind component.”
Thus, he showed phase locking at the second subharmonic of the annual frequency. A generalization of the second sentence in this quoted text provides a definition of phase locking-regular coincidence of relative phases―not limited to any particular harmonic or subharmonic of the reference signal. Bjerknes’s observation is identified in the text below as occurring during phase-locked segment #5. Rasmusson and Carpenter [14] showed that the maximum SST anomalies in the central tropical Pacific near 170˚W occurred at the end of the calendar year―again indicating phase locking to the annual cycle. Later, Rasmusson, Wang and Ropelewski [15] identified a biennial mode in SST data that was phase locked with the annual cycle. They describe the period 1960-1970 as a “well-organized biennial regime.”
Gu and Philander [16] identified the annual cycle with the Sun:
“… The seasonal cycle, the forced response of the earth’s climate to the periodic change in the solar radiation.”
In a study of SST3.4 from 1856 to 2010 Douglass [17] (ref. [17] to be called D2011a) reported distinct time segments that had periodicities of two or three years. These segments were shown to be phase locked to the annual cycle. In a later paper four other Pacific climate indices were shown also to have the nearly the same phase-locked states [18] showing that phase locking is not confined to area A34.
In a statistical study of SST3.4, Douglass [19] gave an ordered list of the 20 largest magnitude El Niño episodes since 1856. He reported that SST3.4 contains two com- ponents: a low frequency component that exhibits the familiar El Niño/La Niña phenomenon and a signal of frequency 1.0 cycle/year and its harmonics. Both of these components are phase-locked to the annual variation in solar irradiation. It was reported that the first component (aSST3.4) contained at least 10 distinct time segments since 1856 that were phase locked to either the second or third subharmonic of the annual forcing frequency of 1.0 cycles/year. In that study, identification of phase-locked states was done by visual observation such as the four maxima of spacing three years between 1895 and 1905 followed by application of the autocorrelation method to this time segment resulting in phase-locked segment #2. What Douglass [17] failed to do was a systematic search of the entire time series with the same care where there was no obvious similar pattern. This paper corrects this failing and will report seven new phase-locked segments.
Douglass and Knox [20] [21] reported an eleventh phase-locked segment that began in 2008.
1.2. Models
Several attempts toward a realistic first-principles theory of ENSO have been published. Cane and Zebiak [22] (CZ) proposed a coupled tropical ocean-atmosphere model of El Niño Southern Oscillation that has been used by later investigators. In 1994/95 three papers based upon CZ were published nearly simultaneously [23] [24] [25] . These will be referred to as the JTC models. These later models had both an external forcing at 1.0 cycle/year and nonlinear coupling terms. The nonlinearities considered involved such variables as westerly winds and poleward transport of heat. These models all yielded some form of chaotic solutions that manifested in the appearance of stable subharmonics for certain values of adjustable nonlinear parameters. The nonlinearities in these models are all different and none vary the nonlinear terms that corresponded to the available observations. Chang et al. [25] , in fact, found that when they varied the amplitude of the “heat flux” parameter in their model, subharmonics at two- and three- year periods appeared within certain heat flux values. None of these models corresponded to our case. The data available to these groups at that time were not good enough to compare to their models. Additional comments on models are below.
In Section 2, data and methods are described. The analysis is done in Section 3. Discussion and concluding remarks are in Section 4.
2. Data and Methods
A new sea surface temperature data set, SODA 2.2.4, has recently been introduced [26] . It contains monthly values beginning in January 1871 and ending on December 2008. These data are called here SSTs. The average value of SSTs over area A34 (5˚S to 5˚N; 120˚W to 170˚W) is computed and is called SST3.4s. An earlier (beginning in 1859) SST data set [27] is denoted by SSTk, from which the similar average SST3.4k is calculated for area A34. The values of SST3.4k and an anomaly index Nino3.4k created by the “climatology scheme” since 1950 exists [28] . Values are added every month. The newer SST3.4s data have been used by Giese and Ray [3] , who showed that differences with SST3.4k are important in the latter part of the nineteenth century, but that the two data sets are nearly the same in the latter part of the twentieth century. We have compared the two data sets explicitly and verify that the differences are very small in the region of overlap (1950 to 2008). In this paper we use SST3.4s from 1871 to the end (2008) and SST3.4k after 2008.
The methods used in this study are the same as those described in detail in D2011a and by Douglass and Knox [20] , are summarized in the Appendix, and sketched here.
It is well known through its deleterious effects on local climate that El Niños are phenomena that recur after at least two years; in all the SST data sets, annual effects exist that cannot be associated with El Niños. When these are cleanly removed by a centered 12-month filter (see Part 1 of the Appendix), the resulting data sets, expressed as anomalies and called here aSST3.4s and aSST3.4k, show definite regularities. Peaks occur in clusters or “segments” with regular inter-peak spacings of two or three years; moreover, the beginnings and ends of these segments are strongly associated with independently-determined climate shifts [29] [30] .
Quantitative studies reviewed and extended here make use of autocorrelations of the data sets to establish the characteristic periodicities and the end points of the El Niño segments. It is found that the events are phase-locked to the solar irradiance cycle and have only one of two observed periodicities, either two or three years, which correspond to subharmonics of that cycle. Phase-locking and the method of analysis, including a description of a test of its validity (Douglass and Knox [20] , Appendix A), are described in Part 2 of the Appendix.
Finally, it has been determined that greater quantitative regularities exist, in that two more discrete parameters can be associated with each segment (parity p and substates). The complete state of a segment is specified by these parameters along with the subharmonic number n. Details are given in Part 3 of the Appendix.
3. Analysis of SST3.4s and SST3.4k
The index SST3.4s is shown in Figure 1(a) as a thin black line. It ranges from 24˚C to 30˚C and has a trend of ?0.0061˚C/decade. Also shown is the filtered index FSST3.4s (see Appendix) in red. Figure 1(b) shows the anomaly index aSST3.4s (red); five of the 18 phase-locked segments are indicated by blue rectangles. The 18 phase-locked segments are enumerated and discussed in the next section.
Notation. In D2011a, ten phase-locked segments in SST3.4k were identified by the autocorrelation method. In a later paper, Douglass and Knox [21] confirmed #9 and #10 and reported a new phase-locked segment (#11). These segments were labeled by 1 through 11. In this study of SST3.4s seven additional phase-locked segments are found. In order to preserve chronological order with the first eleven (and the original numbering) they have been labeled 0, 3a, 4a, 4b, 4c, 4d, and 4e, and are inserted at the appropriate place in the chronological list.
3.1. Eighteen Phase-Locked Segments
All eighteen phase locked segments are shown in Figures 2(a)-(q) and Figure 3. Their properties are given in Table 1. The three discrete state indices mentioned above are
Figure 1. (a) Original data SST3.4s from 1870 to 2010. SST3.4s (black), trend (dotted black) and filtered data FSST3.4s (red). (b) Anomaly aSST3.4s (red). Also shown by shaded rectangles are phase-locked segments #0, 1, 2, 4b and 9 discussed in the text. In both (a) and (b), the slope of the trend line is −0.06˚C/century.
listed. Also listed are the algebraic sign of the value and slope of aSST3.4 at the end of the phase-locked segment.
Some of the more interesting results are:
・ Fifteen of these phase-locked segments have ortho parity―i.e., the principal maxima occur in boreal winter and three have para parity―i.e., the principal maxima occur in boreal summer.
・ Of the 18 segments, six have period 2 years and twelve have period 3 years.
・ Importance of sub-index s. In D2011a, segments 6 and 7, separated by only a few months, had the same parity (ortho) and period (n = 3), but were clearly distinguished from each other by the autocorrelation method because they had different sub-indices (s = 0 and 2).
・ Segment #11 of period three years and ortho parity (Figure 3) was ongoing in November 2016, showing a third El Niño episode whose maximum occurred during November 2015. It may continue in this state and show a fourth episode in boreal winter of 2018.
Figure 2. Seventeen phase-locked segments of aSST3.4s. Full descriptions of the segments shown in (a)-(q) are found in Table 2. Segment 2, (c) is the most dramatic of the period-3-year segments. The first four of the El Niño episodes are among the largest events listed by Quinn et al. [1] , Douglass [19] , and Giese and Ray [3] . Episodes 24 and 25 in segment 5 (l) are mentioned by Bjerknes [13] .
3.2. Phase-Locked States: Three Examples in Detail
The autocorrelation vs. delay of a pure sinusoid is a pure cosine. Its value is 1.0 at delay
Figure 3. The eighteenth phase-locked segment, now using aSST3.4k; see the last line of Table 2. In order to extend beyond 2008, data from ERSST (Nino3.4), black curve, is included.
Table 1. List of El Niño segments and their properties.
zero and is 1.0 again when the delay equals the period. For data in which one expects the period to be close to a sinusoid of period two or three years, and in the presence of some noise, one would expect the second maximum to be less than 1.0. We call such a plot “cosine-like.” This behavior was in fact reproduced in a test with an artificial data set (see Appendix, Section 2).
The first example is phase-locked segment #2. Figure 2(c) shows the values of aSST3.4s from 1895 to 1909. One sees four prominent maxima whose separations appear to be three years and a fifth only two years from the fourth. These numbered maxima will be defined later in this paper as El Niño episodes. (The numbers 6 through 10 are their sequence in the enumeration of episodes.) The autocorrelation method from above was used to examine the time series in this range. A candidate time segment spanning these four maxima was selected and studied by the autocorrelation method described above. Data points were added and subtracted. When the beginning date was January 1896 and the end date was June 1908 the “cosine” signature was found in the autocorrelation plot with period 36 months as shown in Figure 4. These dates have an uncertainty of several months. Note that the maximum labeled #10 is included in this phase-locked segment despite a separation of less than 3 years from #9, which is an illustration of the primacy of the autocorrelation method for determining the nature of the segments. This phase-locked segment is designated with the discrete subharmonic index n = 3.
The second example is phase-locked segment #10. Figure 2(q) shows the values of aSST3.4s from 2001 to 2009. One sees three prominent maxima whose separation appear to be two years. A candidate time segment spanning these three maxima was selected and studied by the autocorrelation method. The candidate time segment the resulting autocorrelation plot in Figure 4 shows clearly the “cosine” signature with period 24 months when the beginning date was June 2001 and the end date was March 2008. This phase-locked segment is designated with the discrete subharmonic index n = 2. This confirms the findings of Douglass and Knox [20] , who decisively demonstrated n = 2 for this segment by showing that its Lissajous plot is a closed curve with two loops.
Figure 4. Autocorrelation of segments 2, 4c, and 10. Segment 2 (blue, open triangles) and 4c (blue, filled diamonds) are seen to have period three years and segment 10 (red) has period two years.
The third example is phase-locked segment 4e shown in Figure 2(k), much different from the first two in that there is no guidance from multiple maxima in aSST3.4. There is only a single maximum at about 1958. We were guided by the fact that both Quinn et al. [1] and Giese and Ray [3] had reported an El Niño episode near this date. We began by choosing a candidate segment that included this maximum and added data points to each end. When the beginning date was September 1956 and the end date was October 1962, we obtained the autocorrelation plot shown in Figure 4. The phase-locked signal was found to have period three years. This emphasizes again that the nature of a state is determined by the autocorrelation function and not solely by the separation of maxima in aSST3.4.
We propose the following: An El Niño episode is defined by a positive maximum in aSST3.4 and is identified by its date. Although maxima at negative values of aSST3.4 contribute to the definition of the duration of a phase-locked state, they are not by this definition considered as El Niño episodes. The largest magnitude episodes are frequently given names, such as the “El Niño of 1997/98”.
Among the 40 El Niño episodes from 1871 to January 2016, every one occurs within a phase-locked segment-i.e., there are no El Niño episodes that are not in a phase- locked segment. Every phase-locked segment has at least one El Niño episode while 14 have more than one (segment #2 has four).
4. Discussion
4.1. Comparisons to Other Lists of El Niño Episodes
There are five prior publications that list El Niño episodes.
1) Quinn et al. [1] give a list of 25 historical El Niño occurrences by magnitude and date range in the time period of overlap. Our study finds all these episodes. See Table 1. However, Our El Niño episodes #3, 5, 10, 19, and 29 are not in their list.
2) Giese and Ray [3] introduce a new index CHI that is the weighted average of SST3.4s anomalies calculated within a strip from 120˚E to the coast of South America and from 5˚S and 5˚N. CHI measures the strength, longitude, latitude and area. Their definition of an El Niño episode is that the CHI strength must exceed a threshold of 0.5 C. They list 35 El Niño episodes chronologically. Our study lists 37 episodes over their date range, two of which are below their threshold. It appears that the CHI index and our definition based upon a positive maximum of aSST3.4s are equally good at finding El Niño episodes (Table 2).
3) NOAA/CPC defines an Ocean Niño Index (ONI) based upon ERSSTv4 data [28] . An El Niño episode begins when the three month running mean of ONI exceeds a threshold of 0.5˚C for five successive months. La Niñas are similarly defined with a threshold of −0.5˚C. Their list begins in 1950. See Table 2. We find all of their El Niño episodes. However, the NOAA/CPC list also contains spurious―by our definition―El Niño episodes (October 1958 to February 1959, August 1969 to January 1970 and September 1977 January 1978). These events follow a real El Niño episode by one year. NOAA/CPC describes these “pairs” as “double El Niños.” Spurious La Niña episodes are also reported, such as the event from Aug 2011 to Mar 2012―this event along with the real La Niña event one year earlier have been described as a “double-dip” La Niña
Table 2. List of 40 El Niño episodes and their characteristics. Note A. Segment 11 may contain more El Niño episodes. There is no indication of its termination as of November 2016. Note B. Giese and Ray [3] did not list episodes 3, 5, 10, 19 and 29 because these events did not rise above their threshold.
episodes. These spurious episodes arise from the annual SST3.4 signal, which was not completely removed by the climatology scheme [20] [21] .
4) Yu et al. [5] classified El Nino episodes from 1870 to 2010 as either Central Pacific (CP), Eastern Pacific (EP), or mixed. We did not find a link between periodicity of the phase-locked segment (2 or 3 years) and predominance of El Niño type.
5) Douglass [19] gave a list of the 20 largest El Niño episodes by date and magnitude since 1856. All are found in this study except his #18 (1866), which is outside the date range of aSST3.4s. See Table 2.
4.2. Is the List of 40 El Niño Episodes Complete?
Are there episodes in aSST3.4 that we did not find? First, there are no El Niño episodes listed by others that we did not find. Missing episodes would have to occur between phase-locked segments. There are 17 such intervals totaling 26 years (out of 144 years in the aSST3.4 record). The interval average is 1.5 years with a few exceeding three years. Those have been reexamined. We believe our list of 40 El Niño episodes is complete.
4.3. Unanswered Questions
New models are needed. The JTC models of some 20 years ago were promising. These nonlinear models yielded solutions that were subharmonics of an annual forcing in agreement with our results. However, the observational data available at that time were not suitable to test these models. Should this problem be revisited, the study of the chaotic properties of the SST3.4 data by Douglass [31] should be considered.
Cause of abrupt beginning and end of phase-locked states. This question has been discussed by Douglass [18] . Volcanoes and large El Niño events are ruled out. It seems likely that the explanation of the abrupt changes will be similar to that in the solutions of the one-dimensional nonlinear oscillator problem [32] . For that case the subharmonic oscillations are stable only between an upper and lower limit of a parameter p that depends on the nonlinearity, the amplitudes and other quantities. If during a subharmonic oscillation the conditions change such that the value of p moves outside of these limits, then the oscillations will end abruptly. In the JTC models subharmonic solutions were found between ranges of the nonlinear parameter. This range had an upper and a lower bound. When these limits were exceeded the subharmonic oscillation ceased and the system went into a new state, which could be a state of a different subharmonic or a “chaotic” state.
In recent studies, Stein et al. [33] [34] have found model evidence for the synchronization of certain subharmonics of two-year period with the annual forcing. Also, Wang et al. [35] find that climate shifts may be initiated through the nonlinear interaction of the North Atlantic Oscillation with many others including ENSO. It is hoped that our new El Niño classification will be of assistance in analyzing the overall climate shift phenomenon.
It is interesting to note that the transition from Phase-locked segment 9 to 10 and 10 to 11 involved a change in the spatial pattern of El Niño SST anomalies [5] . In phase 9, El Niños 32 and 33 were CP-type, but 34, which was the last in the segment was an EP-type. Likewise, in phase 10, El Niños 35 and 36 were CP-type and 37, which was the last in the segment showed mixed signals. Thus, a shift in location of maximum warming may point to nonlinear forcings transitioning the system into a new state. This requires further study.
5. Conclusions
As Quinn et al. [1] showed in 1987, El Niño episodes have been recurring events for at least four and a half centuries. This paper shows that this phenomenon continues to the present day and one would expect the future to be the same.
The scheme sketched out here does not provide absolute predictivity of El Niño behavior. In particular, the precise beginning month of the segments is determined only post hoc, by an autocorrelation method. The end month may be indicated by a breakdown of the autocorrelation method. Nonetheless, the existence of these periodic segments points toward the probable existence of specific nonlinear dynamical atmospheric-oceanic mechanisms. It also provides a further physical attribute that might be correlated with other climate phenomena in an identification of these mechanisms.
The climate system is currently in an n = 3, ortho state. Three maxima have already been observed. As the amplitude decreases from that maximum we predict that one of two possibilities will happen in early 2017. 1) This state will terminate, or 2) this state will continue to the next maximum in boreal winter of 2018 and the same question will arise again. The existence of a fourth El Niño within an n = 3 segment has a precedent (segment 2).
Cite this paper
Douglass, D.H., Knox, R.S., Curtis, S., Giese, B.S. and Ray, S. (2017) Historical Phase-Locked El Niño Episodes. Atmospheric and Climate Scien- ces, 7, 48-64. http://dx.doi.org/10.4236/acs.2017.71005
References
- 1. Quinn, W.H., Neal, V.T. and Antonez de Mayolo, S.E. (1987) El Niño Occurrences over the Past Four and a Half Centuries. Journal of Geophysical Research, 92, 14449–14461.
https://doi.org/10.1029/JC092iC13p14449 - 2. Barnston, A.C., Chelliah, M. and Goldenberg, S.B. (1997) Documentation of a Highly ENSO-Related SST Region in the Equatorial Pacific. Atmosphere-Ocean, 35, 367-383.
https://doi.org/10.1080/07055900.1997.9649597 - 3. Giese, B. and Ray, S. (2011) El Niño Variability in Simple Ocean Assimilation (SODA) 1871-2008. Journal of Geophysical Research, 116, C02024.
- 4. Ray, S. (2011) El Niño Southern Oscillation Variability from 1871-2009. Doctoral Thesis, Texas A&M University.
- 5. Yu, J.-Y. and Kim, S.T. (2013) Identifying the Types of Major El Niño Events since 1870. International Journal of Climatology, 33, 2105-2112.
https://doi.org/10.1002/joc.3575 - 6. Stein, K.A., Timmermann, A. and Schneider, N. (2011) Phase Synchronization of the El Niño-Southern Oscillation with the Annual Cycle. Physical Review Letters, 107, 128501.
https://doi.org/10.1103/PhysRevLett.107.128501 - 7. Newman, M., Shin, S.-I. and Alexander, M.A. (2011) Natural Variation in ENSO Flavors. Geophysical Research Letters, 38, L14705.
https://doi.org/10.1029/2011gl047658 - 8. Kao, H.-Y. and Yu, J.-Y. (2009) Contrasting Eastern-Pacific and Central-Pacific Types of ENSO. Journal of Climate, 22, 615-632.
https://doi.org/10.1175/2008JCLI2309.1 - 9. Kug, J.-S., Jin, F.-F. and An, S.-I. (2009) Two Types of El Niño Events: Cold Tongue El Niño and Warm Pool El Niño. Journal of Climate, 22, 1499-1514.
https://doi.org/10.1175/2008JCLI2624.1 - 10. Ashok, K., Behera, S.K., Rao, S.A., Weng, H. and Yamagata, T. (2007) El Niño Modoki and Its Possible Teleconnections. Journal of Geophysical Research, 112, C11007.
https://doi.org/10.1029/2006JC003798 - 11. Trenberth, K.E. and Stepaniak, D.P. (2001) Indices of El Niño Evolution. Journal of Climate, 14, 1697-1701.
https://doi.org/10.1175/1520-0442(2001)014<1697:LIOENO>2.0.CO;2 - 12. Johnson, N.C. (2013) How Many ENSO Flavors Can We Distinguish? Journal of Climate, 26, 4816-4827.
https://doi.org/10.1175/JCLI-D-12-00649.1 - 13. Bjerknes, J.A.B. (1969) Analysis of the Rhythmic Variations of the Hadley Circulation over the Pacific during 1963-67. Technical Report, ONR Contract No. N0014-69-A-0200-4044 NR 083-287.
- 14. Rasmusson, E.M. and Carpenter, T.H. (1982) Variations in Tropical Sea Surface Temperature and Wind Associated with the Southern Oscillation/El Niño. Monthly Weather Review, 110, 354-384.
https://doi.org/10.1175/1520-0493(1982)110<0354:VITSST>2.0.CO;2 - 15. Rasmusson, E.M., Wang, X. and Ropelewski, C. (1990) The Biennial Component of ENSO Variability. Journal of Marine Systems, 1, 71-96.
https://doi.org/10.1016/0924-7963(90)90153-2 - 16. Gu, D. and Philander, S.G.H. (1995) Secular Changes of Annual and Interannual Variability in the Tropics during the Past Century. Journal of Climate, 8, 864-876.
https://doi.org/10.1175/1520-0442(1995)008<0864:SCOAAI>2.0.CO;2 - 17. Douglass, D.H. (2011) The Pacific Sea Surface Temperature. Physics Letters A, 376, 128-135.
https://doi.org/10.1016/j.physleta.2011.10.042 - 18. Douglass, D.H. (2013) Phase-Locked States and Abrupt Shifts in Pacific Climate Indices. Physics Letters A, 377, 1749-1755.
https://doi.org/10.1016/j.physleta.2013.04.053 - 19. Douglass, D.H. (2010) El Niño-Southern Oscillation: Magnitudes and Asymmetry. Journal of Geophysical Research, 115, D15111.
https://doi.org/10.1029/2009JD013508 - 20. Douglass, D.H. and Knox, R.S. (2015) The Sun Is the Climate Pacemaker I. Equatorial Pacific Ocean Temperatures. Physics Letters A, 379, 823-829.
https://doi.org/10.1016/j.physleta.2014.10.057 - 21. Douglass, D.H. and Knox, R.S. (2015) The Sun Is the Climate Pacemaker II. Global Ocean Temperatures. Physics Letters A, 379, 830-834.
https://doi.org/10.1016/j.physleta.2014.10.058 - 22. Cane, M.A. and Zebiak, S.E. (1985) A Theory for El Niño and the Southern Oscillation. Science, 228, 1085-1087.
https://doi.org/10.1126/science.228.4703.1085 - 23. Jin, F.-F., Neelin, J.D. and Ghil, M. (1994) ENSO on the Devil’s Staircase: Annual Subharmonic Steps to Chaos. Science, 264, 70-72.
https://doi.org/10.1126/science.264.5155.70 - 24. Tziperman, E., Stone, L., Cane, M.A. and Jarosh, H. (1994) El Niño Chaos: Overlapping of Resonances between the Seasonal Cycle and the Pacific Ocean-Atmosphere Oscillator. Science, 264, 72-74.
https://doi.org/10.1126/science.264.5155.72 - 25. Chang, P., Ji, L., Wang, B. and Li, T. (1995) Interactions between the Seasonal Cycle and El Niño-Southern Oscillation in an Intermediate Coupled Ocean-Atmosphere Model. Journal of the Atmospheric Sciences, 52, 2353-2372.
https://doi.org/10.1175/1520-0469(1995)052<2353:IBTSCA>2.0.CO;2 - 26. SODA: SST Data.
http://iridl.ldeo.columbia.edu/SOURCES/.CARTON-GIESE/.SODA/.v2p2p4/.temp/?Set-Language=en - 27. Kaplan, A. SST3.4 Data.
http://iridl.ldeo.columbia.edu/SOURCES/.Indices/.nino/.KAPLAN/.NINO34/ - 28. NOAA/CPC. SST3.4. http://www.cpc.ncep.noaa.gov/data/indices/
- 29. Douglass, D.H. (2010) Topology of Earth’s Climate Indices and Phase-Locked States. Physics Letters A, 374, 4164-4168.
https://doi.org/10.1016/j.physleta.2010.08.025 - 30. Towsley, A., Pakianathan, J. and Douglass, D.H. (2011) Correlation Angles and Inner Products: Application to a Problem from Physics. ISRN Applied Mathematics, 2011, Article ID: 323864.
https://doi.org/10.5402/2011/323864 - 31. Douglass, D.H. (2011) Separation of a Signal of Interest from the Seasonal Effect in Geophysical Data: I. The El Niño/La Niña Phenomenon. International Journal of Geosciences, 2, 414-419.
https://doi.org/10.4236/ijg.2011.24045 - 32. Stoker, J.J. (1950) Nonlinear Vibrations. Interscience Publishers, New York.
- 33. Stein, K., Timmermann, A. and Schneider, N. (2011) Phase Synchronization of the El Niño-Southern Oscillation with the Annual Cycle. Physical Review Letters, 107, Article ID: 128501.
https://doi.org/10.1103/PhysRevLett.107.128501 - 34. Stein, K., Timmermann, A., Schneider, N., Jin, F.-F. and Stuecker, M.F. (2014) ENSO Seasonal Synchronization Theory. Journal of Climate, 27, 5285-5310.
https://doi.org/10.1175/JCLI-D-13-00525.1 - 35. Wang, G., Swanson, K.L. and Tsonis, A.A. (2009) The Pacemaker of Major Climate Shifts. Geophysical Research Letters, 36, L07708.
https://doi.org/10.1029/2008gl036874
Appendix
1. Removing the Annual Signal
For signals relating to El Niño effects, one first wants to remove the annual signal. Two schemes relate to the present work.
a) The “climatology” method. This scheme attempts to do two things: removal of the annual term and creation of an anomaly signal (Nino3.4) from SST3.4. In D2011a and references within, it is shown that the annual term is never completely removed by this scheme. In some cases false signals are introduced into the anomaly index Nino3.4. Nevertheless, this index is useful in attempts to predict the future because there is very little time delay with SST3.4.
b) The 12-month moving average method. In this scheme the data are subjected to a 12-month centrally located moving average filter F. In D2011a and prior papers it is pointed out that this filter completely removes signals whose frequencies are exactly 1.0 cycle/year and its harmonics. The resulting filtered data is named FSST3.4. Note: In this scheme, in contrast to the climatology scheme, removal of the annual effect has been done before creating an anomaly. In D2011a (text ref. 17) the anomaly is created by subtracting the average of FSST3.4 over the range of the data. Thus,
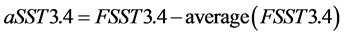 . (1)
. (1)
A “high frequency” index is defined by
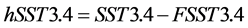 . (2)
. (2)
The disadvantage is that aSST3.4 is a lagging (6 months) index that has little short- term predictive value. Both indices Nino3.4 and aSST3.4 will be used in this study.
Equations (1) and (2) apply, mutatis mutandis, to the data sets SST3.4s and SST3.4k.
Quinn et al. [1] showed in 1987, El Niño episodes have been recurring events for at least four and a half centuries. This paper shows that this phenomenon continues to the present day and one would expect the future to be the same.
2. Identifying Phase-Locked Time Segments in aSST3.4
Phase locking occurs when a signal of frequency f1 from a system has a fixed phase with respect to that of a second signal from the same system of frequency f2 = (n/m) f1, where n and m are integers. The relationship is usually a result of a non-linear mechanism within that system. A familiar example of phase-locked phenomena is that of a child “pumping” on a swing to sustain the oscillating motion. The oscillation frequency is at the second subharmonic of the “pump” frequency.
The phenomenon of phase locking is well known in the field of non-linear dynamics. Stoker31 considers the 1-D nonlinear oscillator of intrinsic frequency ω0 driven by a forcing F at frequency ωF. There is a direct response at ωF. In addition, there can be a phase-locked response at the subharmonics of ωF (note-this is not ω0). If certain conditions involving the nonlinear coupling are met, there is a region of stability in parameter space that has upper and lower bounds. If the parameters change and take the system out of this region the subharmonic behavior will abruptly cease. It is asserted that the forcing FS in the climate system is due to the 1.0 cycles/year variation in solar irradiation and that the “high frequency” signal hSST3.4 at 1.0 cycle/year is in response to this forcing. In addition, FS also may cause a second response aSST3.4 at the second or third subharmonic of FS.
Phase-locked segments of SST3.4 are found by calculating the autocorrelation function of a candidate segment. If that segment contains a component whose period is a multiple of one year then the autocorrelation function vs. delay τ will be a cosine-like function with a minimum at τ/2 and a maximum at τ. The value of τ will be a multiple of one year. The extent of such a segment in time is determined by adding or subtracting beginning- and end-date data points from a candidate segment until a cosine-like pattern appears. The segments for the case of aSST3.4 have been shown to be phase- locked to the above-mentioned annual forcing [20] . The subharmonic number n in years and the range of the phase-locked segment are defined by the autocorrelation calculation.
Since we deal with finite data sets, autocorrelation values are increasingly less precise with the increase of time. Each month one data point is lost. We consider only 70% of the time range of a sequence to be significant, and the plots here cover only this range.
Our application of the autocorrelation method itself can be tested. This was done in an earlier paper (Douglass and Knox [20] , Appendix A) by constructing a noisy time series consisting of an annual signal, an artificial signal of interest (one containing two- and three-year segments), and random noise. The method clearly extracted the artificial signal and showed that in the presence of noise the cosine-like autocorrelation function resembles that of the displacement of a damped oscillator.
3. Characterizing the Phase-Locked State Requires Three Discrete Indices
Some of the various subharmonic segments observed in the extended study of SST3.4 had maxima only in October through January (called boreal winter) or April through July (boreal summer). These two possibilities are called parity states. The first possibility is called “ortho” parity and the second “para” parity. A complete classification of a phase-locked segment is given by three discrete indices:
Subharmonic number n. n is the period, in years, of one oscillation of aSST3.4 within a phase-locked segment.
Parity p. The parity ortho is assigned if the maxima occur during boreal winter and para if they occur during boreal summer.
Sub-state index s. Consider two similar segments having the same subharmonic number and parity, separated by Y years as measured between the first maxima of the segments. Since Y is not necessarily a multiple of n, a third descriptor s is defined by s = Y(mod n), whose values are 0, 1, ・・・ , n − 1. Thus, a segment with period 3 years has three possible equivalent “sub-states” indexed by 0, 1, and 2. Since the sub-state index depends on the choice of a reference year, for which it is defined as 0, it is relative, used only in comparing segments of the same n and parity. For example, phase-locked state #9 is assigned sub-state index 0 and all other phase-locked segments have sub-state values relative to segment #9. See Douglass and Knox [20] [21] .







