Atmospheric and Climate Sciences
Vol.04 No.05(2014), Article ID:51584,12 pages
10.4236/acs.2014.45073
Dynamic Interactions in the Atmosphere
Gabriel Barceló
Advanced Dynamics S.A., Madrid, Spain
Email: gestor@advanceddynamics.net
Academic Editor: Mohammad Valipour, University of Tehran, Iran
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 September 2014; revised 28 October 2014; accepted 14 November 2014
ABSTRACT
Even today, with the great progress that has been made in the scientific, technological and com- putational fields, we are still stunned by the devastating effects brought about by atmospheric phenomena. This paper aims to propose new hypotheses in the field of dynamics to enhance our understanding of the behaviour of atmospheric disturbances caused by rotating winds. I believe that the criteria of classical dynamics that are applied to vortex systems in the atmosphere should be rigorously reviewed. I propose to establish new hypotheses in the field of dynamics, in order to better interpret rotation in nature. These hypotheses have been structured into a new theory that has been tested experimentally by both ourselves and third parties, with positive results. I pro- pose to use the Theory of Dynamic Interactions (TDI) to interpret the behaviour of systems under- going successive rotations around different axes—which we will refer to as non-coaxial rotations. I hold that this theory applies to air masses and groups of particles in suspension that are accele- rated by rotations. Accordingly, it should be used to interpret the behaviour of tornadoes, cyclones and hurricanes. I believe that this proposal could enhance our understanding of these atmospheric phenomena and improve predictions about them.
Keywords:
Atmospheric Vortex, Rotational Dynamics, Non-Coaxial Spins, Velocity Fields, Dynamic Interactions, Theory of Dynamic Interactions

1. Background
The devastating effects of atmospheric vortex phenomena have been the subject of a great deal of research; our understanding of them is still, however, imperfect.
Every year, the catastrophic consequences of tornadoes, typhoons and cyclones cause loss of life and substan- tial economic losses. In all these cases, we are dealing with a circular flow or rotating turbulence, rotating to form a spiral or around an axis, with changing paths. In structural terms, these are enormous vertical thermal machines maintained by the combination of atmospheric mechanics and the Earth’s gravity, which generate ro- tating cloud, wind and/or storm systems.
In the case of tropical cyclones, the process begins with the Sun’s heat causing seawater to evaporate. This water vapour condenses at great heights, releasing the heat of condensation, and thus generates a powerful and devastating primary source of energy. A small fraction of the energy released is turned into mechanical energy, giving rise to strong winds. Heavy rain and lightning are also generated. Dust particles act as nucleation centers, leading to the formation of clouds and raindrops. Indeed, they can even cause storm surges in coastal areas.
On the other hand, tornadoes normally form over large plains in mid-latitude areas, when a hot and humid mass of air meets one that is much colder and dryer.
Hurricane-generated winds are mostly horizontal and not vertical. It is thought that it is vertical motion that favours the production of electric charges and contributes to causing lightning. For example, charges can be ge- nerated when a hurricane comes up against a high mountain range and then has to move upwards to get over the mountain. This is why there are more electrical storms in mountain areas.
Within thunderclouds, vertical winds cause ice crystals and water droplets (called “hydrometeors”) to bump together. This “rubbing” causes the hydrometeors to become charged... Winds and gravity separate the charged hydrometeors, producing an enormous electric field within the storm [1] .
On the other hand, hurricanes that form at sea are not normally accompanied by thunder and lightning. In 1998, however, during the CAMEX-3 project [2] , lightning was detected in the eye of Hurricane Georges over the Caribbean island of Hispaniola.
In all of these cases, ions were generated when bonds were broken, mainly due to friction. Thus, when study- ing these processes, we must not only apply the laws of fluid dynamics for particles in suspension, but also the laws of electrodynamics.
In all cases, these phenomena are manifestations of nature’s water and energy cycles [3] (see Figure 1), which act as the mechanism driving global atmospheric circulation, which in turn maintains the balance of the troposphere and the homogeneity of the Earth’s temperature.
In recent years, substantial investments have been poured into researching these atmospheric phenomena with the aim of determining the forces involved and to make predictions that alleviate their impact. We know a wide typology of atmospheric phenomena with rotation (see Figure 2). There are numerous data capture systems that use sensors, some on planes or geosynchronous satellites. There are also powerful computers with logic and si- mulation software for designing models to predict the paths and effects of these phenomena.
To forecast the track and intensity of tropical cyclones, the National Hurricane Centre (NHC-USA) uses sev- eral different mathematical computer models that represent the tropical cyclone and its environment in a greatly simplified manner [5] . These models are used to make predictions concerning both the intensity and path of a tropical cyclone.
The joint missions of the National Oceanic and Atmospheric Administration (NOAA) and the National Aero- nautics and Space Administration (NASA) have also involved considerable investments, such as that in the Geostationary Operational Environmental Satellite—R Series (GOES-R) [6] .
The fact that hurricanes obey a power law, as do other natural phenomena involving very large amounts of energy (such as earthquakes), makes it difficult to predict changes in their intensity. Despite this, the reliability of predictions is on the rise. Forecasts are becoming increasingly more accurate, although we are still not fully satisfied with the results of predicting hurricane intensity or behaviour. Perhaps we do not fully understand these phenomena because there is something missing in our knowledge of the underlying science and of the factors that affect how they are created and how they change over time.
Indeed, predicting their intensity continues to be one of the goals of atmospheric physics, given that the dis- aster warning and prevention systems for inhabited areas act on the basis of this information. It is thought that there is a mathematical-statistical relationship between the number of hurricanes that take place in a certain area of the planet and the energy they release [8] . Within a certain range, the number of hurricanes is inversely pro- portional to the energy released [9] .
These phenomena can follow complex geometrical models. The simplest is that of the torus seen in the to- roidal vortices in the atmosphere. In all cases, there is a low-pressure area with air masses rotating around it. Nevertheless, spiral cloud-rain bands (SCRB) are some of the most distinguishing features inherent in satellite and radar images of tropical cyclones (TC) [10] . The reason why a hurricane has spiral bands is a subject of
Figure 1. Example of a cyclonic mass. OAR/ERL/National Severe Storms Laboratory (NSSL)/NOAA [4] .
Figure 2. Tornadic waterspout at Sant Lluís, Menorca, Balearic Isles, Spain, 24 September 2014 [7] .
study and debate [11] [12] , but most hurricanes and tropical storms have both these spiral arms (see Figure 3), and approximately resemble a logarithmic spiral, or even a golden spiral, when the phenomenon is of smaller magnitude.
It must be pointed out that many galaxies, as well as storms, cyclones and cyclonic hurricanes, are in the shape of spectacular, logarithmic spirals, as does any natural phenomenon in which rotation is combined with expansion or contraction. Indeed, in making this comparative analysis, we should emphasize the fact that galax- ies are assumed to have a large central mass that results in a centripetal force, and there is no corresponding source of a centripetal force in cyclones. All we have is air rotating in accordance with the Coriolis effect, and the paths we observe are caused by dynamic interactions.
Against this background of study and constant progress in unravelling the physical behaviour of nature, we suggest that the criteria of dynamics that have been applied to date in atmospheric science should be reviewed, given that we believe that the principles of classical rotational dynamics may well be inappropriately interpreted.
2. Theory of Dynamic Interactions
We define the concept of Dynamic Interaction as the reciprocal action of bodies in motion and the resultant effect
Figure 3. Hurricane Catarina on 26 March 2004, as seen from the Moderate Resolution Imaging Spectroradiometer (MODIS) on board the Terra satellite [13] (Credit NASA).
due to the dynamic and inertial reactions generated by the mass. This capacity to interact, or to exert an interac- tion, is shown by bodies or particles having mass when they undergo successive rotations, whether caused by the action of external forces, or by internal reactions to collisions, or reactions of some other type, that involve no ex- ternal input.
We also base our theory on the concept of intrinsic angular momentum, which is equivalent to the concept of spin in quantum mechanics. In accordance with the principle of conservation of angular momentum, when a mass of atmospheric air moves, the initial rotation speed originally created by the Coriolis acceleration increases as the mass becomes more concentrated on entering the zone bordering the area of low pressure.
Based on these concepts, the Theory of Dynamic Interactions (TDI) studies the behaviour of mass when it is exposed to successive accelerations due to rotation, and further analyses the couplings of the dynamic fields that act on a rigid body or on each particle in suspension in a fluid, or on a portion of the mass of air, specifically when the body or particle experiences successive and different rotations around different axes. The distinguish- ing hypothesis of this theory of dynamics is not to accept, as does classical mechanics, the different rotations that are acting on the mass are coupled or algebraically added together. The theory we defend does not accept that these rotations must be coupled into a single resulting rotation. We start from the hypothesis that each ex- ternal action acts separately, in such a way that the initial rotation is maintained constant due to rotational iner- tia, whereas the resulting translational velocity of the action of a new moment couples to the linear translational velocity. In this way, and in accordance with the hypotheses we are putting forward, the path of the centre of mass of each particle in suspension changes from linear to curvilinear—i.e. it becomes curved. Moreover, if the moments of force acting remain constant and the initial translational velocity is likewise constant, the path will be closed, like that of a boomerang. If the initial speed were accelerated or decelerated, each particle would fol- low a spiral path.
According to the hypotheses we are proposing, the true coupling of the fields of the translational velocities and the field generated by the second moment, allows the vectors representing them to be algebraically added together. These fields are vector fields and the sum of velocities resulting from their coupling can be vectorially represented as the sum of the vectors. Nonetheless, we believe that this conceptual structure does not apply to pseudo-vectors or axial vectors. It does not apply to vectors that represent intrinsic rotations.
Classical mechanics holds that, for a solid body in space, with a constant initial velocity V(0) and intrinsic angular momentum, which is exposed to a new, external non-coaxial torque, the centre of gravity of this body will follow a straight line, with the constant initial velocity V(0), and the body will begin a different rotation around its own centre of gravity as a result of the coupling or superimposition of the initial rotation and the one caused by the new torque. This prediction is deduced from the mathematical result of the procedures for calcula- tions that have been established within the context of classical mechanics. However, this conventional position employs analogy, and consequently should not be taken to be rigorously proven, but rather should be accurately confirmed.
Furthermore, if we look closely at nature, we can confirm that it does not in fact act in accordance with the prediction calculated using the formula applied in classical mechanics.
After conducting the first experimental tests, we showed that, paradoxically, nature’s true behaviour is not in keeping with this supposed result: a body in translational movement that is exposed to moments that are not coaxial with its intrinsic rotation does not maintain its linear path. This claim can be confirmed by numerous examples, as exemplified by the spinning top or boomerang [14] .
We have proven experimentally that the assumptions on which all the algorithms of classical mechanics are based do not, in our opinion, correspond to how nature actually behaves:
(1) It is assumed that the movement of the centre of gravity and the body’s rotary movement decouple.
(2) It is assumed that the existing angular momentum and the one generated by the new torque will couple.
(3) It is assumed that the equations of rotational dynamics are based on vector algebra.
As a result, these baseline hypotheses of classical mechanics must be revised. Mathematical calculations need to incorporate operators that reflect the true inertial behaviour of nature. These operators will, in turn, enable us to formulate a true mathematical representation of the phenomenon being studied. Moreover, the hypotheses on the coupling of velocities that actually occurs need to be incorporated into the mathematical formulae.
Under these circumstances, we understand the principles and theorems of classical mechanics to remain valid. Nevertheless, they receive a distinct and different interpretation in the case of a body having intrinsic angular momentum, given that, for such bodies, we feel that the following hypotheses should be applied:
The rotational movements cannot be added together in accordance with vector algebra.
The principle of proportionality between forces and accelerations is not met.
Magnitudes of rotation, made up of the angle and its derivatives, are not added together algebraically.
Neither does the commutative law of vectors apply.
Discrete coupling occurs between the translational movement and that generated by the second torque.
Rotary inertia prevents the initial intrinsic angular momentum from coupling with that which arises from other, later actions.
There is no need to use reference systems external to the body.
The resulting mathematical equations will hold for a particular state of excitation, and may change, depending on later actions on the body.
The dynamic state of a single body can be determined by logical sequences, which can be represented by computer programmes.
These hypotheses must be taken into account when designing any alternative mathematical-physical model to represent bodies having angular momentum in general, whenever disturbed by new non-coinciding torques. They should also be borne in mind when it comes to modelling cyclones, tornadoes and any other atmospheric phenomena that involve rotation.
I wish to reiterate that, after our studies on the inertia of bodies in rotation [15] , I have come to the conclusion that, under certain circumstances, the rotation of a body on an axis prevents the addition of rotations in such a way that, if a new moment with an axis non-coincident with the existing one acts, the latter will persist and the body will react by changing its path, adding an orbital movement in space to the initial rotation, as if it were ex- posed to a central force, although this central force does not actually exist, given that this is a case of dynamic interaction.
Based on our analysis, we suggest that the dynamic behaviour of solid bodies follows a logical sequence that can be represented by a computer programme, but not by a single, universally applicable equation.
Instead of equations—which are the norm in classical mechanics—the dynamic state of a system can be iden- tified bi-univocally by means of a logical model, which can be represented as a logical sequence.
A mathematical model has been designed, and the paths were calculated for different simulations. The outcomes of these simulations were in accordance with the results obtained in our experimental tests.
Figure 4 shows the path obtained for a particle moving with variable tangential velocity, under the following simulation conditions:
-Variable tangential velocity in accordance with the following law V = 5 + 0.2 × t (m/s)
-Constant torque, perpendicular to the tangential velocity vector at all times
It should be pointed out that the resulting path is not closed, but is a planar orbit like that of a spiral.
The resemblance between the spirals obtained in our simulation and the shapes of the arms of storms, tornadoes and cyclones, which are given as examples in Figure 2 and Figure 3 above, is notable. This shows us that, in accordance with the Theory of Dynamic Interactions, the nature of these arms could be that of air masses that are moving with acceleration and have angular momentum which are subjected to dynamic interactions, either due to external moments, or, indeed, due to the internal collision of their particles in suspension.
Having analysed the behaviour of bodies that have intrinsic angular momentum, we can now put forward a paradox:
A body… having intrinsic rotation, when subject to a new non-coaxial torque, instead of rotating around the axis of the new torque, reacts inertially by rotating on an axis perpendicular to this torque.
If the body has translational velocity at its centre of mass, the axis of this new rotation will be at a point external to the body, situated at a distance proportional to the translational velocity. If this is zero, the axis is situated above the body’s centre of mass and the body acquires a new rotation on a new axis.
All of the foregoing is due to the coupling that occurs between the field of translational velocities, determined by the centre of mass, and that resulting from the new torque, in such a way that the total translational velocity will not be equal for all the body’s particles, thus generating the orbital movement [16] .
Therefore, in the light of the above, and in accordance with the TDI, we suggest that the arms or spiral cloud- rain bands (SCRB) of these atmospheric phenomena are in fact accelerating masses of air subject to dynamic interactions. Their specific rotational dynamics generate the spiral path shown in Figure 4.
3. Equations of Rotational Dynamics
Over the last thirty years, we have been analysing the behaviour of bodies subject to accelerations by non- coaxial rotations. We propose a new interpretation of the dynamic behaviour of the boomerang and, in general, of the rigid bodies exposed to simultaneous non-coaxial rotations. We have developed a new hypothesis of rotational non-inertial dynamics, which can be applied to understand both the flight of the boomerang and celestial mechanics [17] .
As indicated above, we can identify curvilinear path masses of air in all of the atmospheric phenomena under study due to the so-called Coriolis effect, generated by Earth’s rotation. If we accept that, at the same time, the particles in suspension in these air masses have their own rotational movement, they are bodies that are subject to simultaneous non-coaxial accelerations, which are in keeping with the hypotheses provided for in the Theory of Dynamic Interactions.
When stating the TDI laws, and throughout this paper, we have avoided making use of the concept of inertial force, given that it is not possible to infer the existence of these forces from the behaviour of the matter observed. On the basis of our observations, we have deduced that these circumstances result in non-homogeneous velocity distributions (see Figure 5). The derivatives of these velocities generate a field of accelerations that is also not homogeneous, but which can be interpreted to be a field of inertial forces.
These non-homogeneous velocity fields are generated in air masses and in their particles in suspension when- ever they are subject to successive rotary accelerations and it is these fields that cause the behaviour we pointed out above. These are called Dynamic Interactions.
In accordance with the Theory of Dynamic Interactions: The anisotropic distribution of the velocities (Vc) generated by the torque shall be compounded with the initial linear velocity (VT), causing a curved path… The velocity VR = (vx, vy, vz) of the new path of its centre of mass will be defined by the matrix multiplication of the
rotating operator
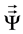 by the velocity vector V0 = (0, V0, 0) [19] :
by the velocity vector V0 = (0, V0, 0) [19] :
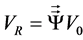 (1)
(1)
This is the equation for movement that we have deduced for mass systems with intrinsic rotation and translation when they are subjected to moments that are non-coaxial with their rotation. In our opinion, this applies to
Figure 4. Path of the centre of mass of a moving object, in the hypothetical case that the applied moment is constant, but the translational linear speed of the moving object is variable. This was obtained via computer simulation, based on the mathe- matical model of dynamic interactions. Variable tangential velocity in accordance with S = 5 + 0.2 t (m/s). Constant torque, perpendicular to the tangential velocity vector at all times. Projections of the trajectory obtained on three planes of reference.
Figure 5. Non-homogeneous velocity distribution in a disc with angular velocity ω around its main axis when the body is subject to a non-coaxial angular velocity Ω [18] .
any object with mass, but we also suggest that it would make it possible to define the path of each particle of a mass of air, as long as the baseline hypotheses that have been established are met.
The rotational operator is a function of the torque and of the particle’s initial angular momentum. Indeed, there is a clear relationship between the orbital angular velocity and the initial intrinsic angular velocity. We therefore have a simple mathematical relationship between each particle’s angular velocity and its translational velocity. This relationship indicates that, in such circumstances, there may be a transfer of rotational energy to translational energy, or vice versa.
The above allows us to propose certain general laws [20] that govern the behaviour of bodies having angular momentum.
We have referred to those interactions that are caused by applying successive, non-coaxial torques or external moments, but other cases without any external input could arise. A specific case of interaction is that resulting from the elastic collision between two body masses m1 and m2 with velocities V1 and V2. This would be the case, for example, of two billiard balls or two particles in suspension. The elastic forces that arise at the moment of collision are governed by Newton’s third law of motion:
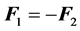 (2)
(2)
This relationship can also be described according to the amount of movement of each ball:
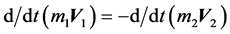
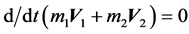
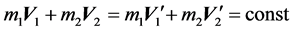 (3)
(3)
where
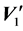 and
and
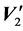 refer to the speeds of the bodies after collision.
refer to the speeds of the bodies after collision.
Equation (3) represents the law of the conservation of momentum of a system of bodies in elastic collision.
The elastic collision of bodies in classical mechanics, without slipping and with rotation, is based on the hy- pothesis of the conservation of the angular momentum, which can be conceived of as an application of Newton’s third law of motion, determining that the moment of action M1 is equal to the moment of the reaction M2
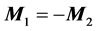 (4)
(4)
Nevertheless, angular momentum is an axial vector and as such its vector algebra differs from that of polar vectors.
On analysing the elastic collision of two rotating balls without slipping and with R1 and R2 radii, m1 and m2 masses and inertial momenta I1 and I2, we can make the initial assumptions that the rotary angular velocities’ vectors ω1 and ω2 are parallel and that the linear speeds of the centers of mass V1 and V2 are contained on a perpendicular plane to the angular velocities’ vectors and that they pass through their centers of mass (Figure 6).
In the collision, the system undergoes an exchange of linear momenta, but we also cannot leave out a possible interchange of angular momenta. The system has two axes of rotation located at the centers of mass of each ball, which we can also assume to be initially perpendicular to the plane of the diagram. The angular momentum L1 of the first body is made up of the angular momentum I1ω1 in relation to its own axis of rotation and of the or- bital momentum
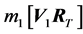 in relation to the axis of rotation of the second body
in relation to the axis of rotation of the second body
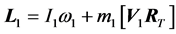 (5)
(5)
The square brackets [] indicate the vector product of V1 and RT. The position vector RT is plotted here from point 01 to point 02. Its absolute value is:

Likewise, we get the angular momentum of the second ball:

where
Assuming that on colliding the law (4) is fulfilled, we get

We can formulate this law of conservation of angular momentum in accordance with the above equations, on the basis that the sum of the angular momenta before the collision will be equal to the sum of the angular mo- menta after the collision:

where



If we break down velocity V1 along the x axis and along the y1 auxiliary axis (see Figure 6) and velocity V2 along the x axis and along the y2 auxiliary axis, the law of conservation (9) is then divided into two laws: the law of conservation for the linear momentum for the x-components of the linear velocity
Figure 6. Elastic collision without slipping of two ball-shaped bodies. The vectors of the angular or rotation velocities of the bodies are perpendicular to the plane of the diagram.

and the law of conservation for the rotational momentum:

The orbital angular velocities


Nevertheless, if the impact is at the centre, there will then be no value for the components on the Y axes:

and in accordance with the law of conservation of rotational momentum (11) we get

This is the conclusion that is normally accepted by classical mechanics, under which it is assumed that there is no other interchange apart from the linear one. Nevertheless, if we generalise our deduction, there is nothing to prevent us assuming a more extensive interchange of momenta.
If we assume an oblique impact, the linear velocities V1 and V2 of the bodies do not take place along the line 0102 that connects the centers of mass, the equality (12) is not fulfilled and, therefore, in the law of conservation (11), in the case of elastic collision with no slipping, a dynamic interaction can arise that causes the angular and orbital momenta themselves to be redistributed.
From the structure of the orbital momenta it can be deduced that the changes in them after the collision, can modify the V¹y and V²y vectors, which in turn modify the V1 and V2 linear velocities of the bodies and, therefore, that the law of conservation enables us to deduce a connection between the translational movement and the rota- tional one, thus making the transfer of translational kinetic energy into rotational kinetic energy possible, and vice versa. It also enables us to deduce that an interchange between translational and rotational momenta can modify the momentum of the centre of mass of an isolated mechanical system, without any need for an external force [21] .
In our opinion, the above can also be applied to particles of any geometrical shape in suspension in a mass of air that have intrinsic angular momentum, whenever they collide with other particles or even against a flat ob- stacle. Such a collision can immediately create a new non-coaxial rotation, thus giving rise to a dynamic interac- tion due to the coupling of the non-homogeneous distribution of velocities generated by the new rotation with the moving object's field of translational velocities. In these circumstances, a transformation of translational ki- netic energy into rotational kinetic energy would take place in the particle having a new rotation.
The dynamic interactions caused by collision mean that we have to find a more extensive explanation of the dynamic behaviour of nature, even at non-relativistic speeds.
We propose a profound revision of the classical mechanics of rotation and put forward a new dynamic model for air in which the different velocities and accelerations acting on each particle are taken into account. We sug- gest that the dynamics of the TDI be studied, since this would give us a better understanding of the dynamics of air masses and the main constituents of the atmospheric phenomena being studied.
We hold that the theoretical principles of the dynamics of mass exposed to multiple accelerations by non- coaxial rotations can be applied in general to all bodies or particles with mass. We therefore reiterate our sug- gestion that the theory of the classical mechanics of rotation be rigorously tested and verified. We recommend that cases of the dynamics of rotating bodies, such as the boomerang, the mechanics of galaxies and the beha- viour of cyclones and tornadoes, be studied. The analogies and similarities displayed should be studied and checked.
4. Experimental Tests
We have conducted several experimental tests on the theory under proposal, e.g. moving objects with intrinsic rotation on their main axis semi-submerged in water and subject to a righting torque, consisting of the weight and force of floatation, the relative positions of which do not coincide. This righting torque was not coaxial with the intrinsic rotation. The moving object was, therefore, subject to two non-coaxial rotations, as is the case with the boomerang, but we noticed that the rotation caused by the righting torque did not generate any new moving rotations, but rather was transformed into a change of path of the centre of mass [22] . Experiments were also conducted on terra firma [23] , which can also be seen in the video [24] [25] .
In accordance with the theory being put forward, and as it can be appreciated in Figure 6, we suggest that each particle, instead of following a linear path, as would be expected from the classical mechanics equations of Newton-Euler (Trajectory I on Figure 7), would follow a curvilinear path, as we have indicated above, due to the coupling of the resultant fields of velocities cause at every point of each particle (Trajectory II on Figure 7).
The question can be summed up as follows: If we apply this dynamic theory to a mass of air, every particle in suspension that has intrinsic rotation will follow a curvilinear path when it experiences a momentum that is non-coaxial with its intrinsic angular momentum. The path will be closed if the forces and torques on the par- ticle remain constant; otherwise, if the forces and torques are variable, an open path will be observed. For exam- ple, if the mass of air is accelerated, the result is a spiral that grows outwards. This same dynamic behaviour, as we have already deduced, can be caused by the collision of particles in suspension in a mass of air.
Consequently, there are several authors [23] [26] who share these same hypotheses with a view to under- standing the dynamic behaviour of bodies or particles in those circumstances in which they have translational velocity, intrinsic rotation and are simultaneously subjected to a non-coaxial momentum with its own rotation [27] .
Nevertheless, it must be remembered that, in our hypothesis and based on a possible analogy, we are extrapo- lating the behaviour observed in macroscopic moving objects to the particles in a mass of air.
It must be pointed out that, in our research, as we have already stated, we have reached a rational deduction to the effect that, in such circumstances, the translational kinetic energy can be transformed into rotational kinetic energy, and vice versa, and in general, energy transfers can occur at the core of particles with intrinsic angular momentum: …kinetic energy can be transferred, increasing its rotation velocity, its linear velocity or modifying its state of potential… [28] .
This dynamic capacity to transfer energy that underpins the TDI could make it possible to explain the conse- quences of these phenomena-which are generally disastrous, especially when they pass through inhabited areas- given that the translational velocities of these air masses are not sufficient on their own to explain the damage and havoc caused by these phenomena.
5. Electrodynamics
We referred above to the need to apply the laws of electrodynamics to these processes and to consider the electric charges that may manifest themselves in such phenomena. Given the presence of electric charges, we should also study the effect of the Lorentz force on the atmospheric phenomena under study. This force arises when an elec- tric charge moves in a magnetic field. In our opinion, the origin of this force is analogous to that of the inertial reactions that occur in the circumstances to which TDI applies and which cause particles to follow curvilinear paths. We understand that the Lorentz force can also explain the behaviour of these atmospheric phenomena.
Figure 7. Classical trajectory and trajectory predicted with the Theory of Dynamic Interactions (TDI). The position of the centre of mass changes as a result of the coupling between the field of the linear velocity and the velocity field caused by the non-coaxial torque [27] .
Both the ideas being proposed should, I feel, be further explored and, where appropriate, confirmed experi- mentally; on the one hand, that the Lorentz force is analogous to an inertial dynamic force, similar to TDI ones, and on the other hand, that this theory be applied to the study of atmospheric dynamics.
I insist that, while it is necessary to include the classical factors, such as viscosity, system scale, specific speed and density in the study of a fluid’s field of movement, the Lorentz force and the TDI hypotheses put forward in this paper must also be taken into account.
6. Conclusions
We still do not know in sufficient detail or with sufficient accuracy the dynamic behaviour of the masses of air that form part of rotating atmospheric phenomena.
I propose a profound revision of the principles of classical rotational mechanics, especially as regards par- ticles subjected to accelerations by simultaneous and non-coaxial rotations. After conducting our research, we put forward certain specific, alternative dynamic hypotheses grounded in a conceptual framework, namely, the Theory of Dynamic Interactions (TDI).
These new dynamic hypotheses we are putting forward and which we believe to be applicable to particle sys- tems accelerated by rotation can, in our opinion, be used in interpreting these phenomena and in the design of more accurate models for making predictions in atmospheric physics.
I therefore believe that the TDI could also constitute a complementary theoretical tool that would make it possible to design more effective models for making predictions about those atmospheric phenomena that in- volve vorticity.
In this paper, I claim that the TDI provides a better explanation of how spiral cloud-rain bands (SCRB) are produced. It also explains that the damage and havoc caused by these atmospheric phenomena is due to the fact that translational energy can be transformed into rotational energy and vice-versa.
The equation of motion that I are proposing in the Theory of Dynamic Interactions for these non-inertial situ- ations is very simple (1)... it becomes possible to determine the path of… [29] particles in translation, when these particles are endowed with intrinsic rotation and are subjected to torques around other, different axis [30] .
The Theory of Dynamic Interactions on which this proposal is based is fully described in different texts and articles. These sources explain how this theory has far-reaching effects on the basic principles of dynamics [31] , not to mention astrophysics [32] , cosmology [33] [34] , atomic physics and technology. An analysis of this theory reveals its capacity to provide answer to many unanswered questions on dynamics and celestial mechan- ics and, moreover, explains the behaviour of rotating bodies… [31] .
Consequently, I insist that the ideas expounded in this paper with respect to the origin of the Lorentz force and the true, dynamic nature of air masses in a cyclone or a tornado be explored, based on the fact that they hold in suspension intrinsically rotating particles that have mass, and which are subject to new non-coaxial moments.
The scientific development of the Theory of Dynamic Interactions would enable a greater understanding of all phenomena which involve both intrinsic rotation and spatial changes in angular momentum and, thus, its appli- cation to numerous areas of physics, particularly astrophysics, atomic physics and dynamics [35] .
This is especially true in the fields of atmospheric physics and the study of fluids. I therefore propose a new approach to the analysis of atmospheric circulation systems, particularly when it comes to analysing the move- ments of the air masses that cause hurricanes, tornadoes and cyclones, and further propose that new methods should be found for calculating predictions.
References
- Internet Science Portal at NASA (2006) The NASA/Marshall Space Flight Center Directory of Science. http://science.nasa.gov/
- https://cloud1.arc.nasa.gov/camex3/
http://data.eol.ucar.edu/codiac/projs?CAMEX3 - Water and Energy Cycle. http://science.nasa.gov/earth-science/focus-areas/water-and-energy-cycle/
- (2014) OAR/ERL/National Severe Storms Laboratory (NSSL)/NOAA and Center for Disaster & Extreme Event Preparedness (DEEP Center). www.deep.med.miami.edu/x472.xml
- (2014) National Hurricane Center: Hurricane Computer Models. http://www.nhc.noaa.gov/aboutmodels.shtml
- http://www.goes-r.gov/
- Cap de fibló 24 Sep 2014 Sant Lluís, Menorca, Balearic Isles, Spain. Send by J. Drake. http://menorca.info/menorca/local/2014/485818/cap-fiblo-invade-redes-sociales.html
- (2010) Energía de los huracanes. Investigación y Ciencia (Scientific American).
- Corral, Á., Ossó, A. and Llebot, J.E. (2010) Scaling of Tropical-Cyclone Dissipation. Nature Physics, 6, 693-696. http://www.nature.com/nphys/journal/v6/n9/full/nphys1725.html http://dx.doi.org/10.1038/nphys1725
- Yurchak, B.S. (2008) Formula for Spiral Cloud-Rain Bands of a Tropical Cyclone. 28th Conference on Hurricanes and Tropical Meteorology, 1 May 2008.
- Malkus, J.S. and Riehl, H. (1960) On the Dynamics and Energy Transformations in Steady-State Hurricanes. Tellus, 12, 1-20. http://dx.doi.org/10.1111/j.2153-3490.1960.tb01279.x
- Willoughby, H.E. (1978) A Possible Mechanism for the Formation of Hurricane Rainbands. Journal of Atmospheric Sciences, 35, 838-848. http://dx.doi.org/10.1175/1520-0469(1978)035<0838:APMFTF>2.0.CO;2
- Science@NASA, 2 April 2004. http://science.nasa.gov/
- Theory of Dynamic Interactions. http://www.youtube.com/watch?v=P9hGgoL5ZGk&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=XzTrGEtJGXU&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=dtMqGSU9gV4&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=qK5mW2j2nzU&list=PL3E50CF6AEBEED47B
- Barceló, G. (2008) Un mundo en rotación (A Rotating World). Editorial Marcombo, Barcelona, 92. http://www.dinamicafundacion.com/
- Barceló, G. (2008) Un mundo en rotación (A Rotating World). Editorial Marcombo, Barcelona, 259. http://www.dinamicafundacion.com/
- Barceló, G. (2014) Theory of Dynamic Interactions: The Flight of the Boomerang. Journal of Applied Mathematics and Physics, 2, 569-580. http://dx.doi.org/10.4236/jamp.2014.27063
- Barceló, G. (2012) Analysis of Dynamics Fields in Noninertial Systems. World Journal of Mechanics, 2, 175-180. http://www.scirp.org/journal/wjm http://dx.doi.org/10.4236/wjm.2012.23021
- Barceló, G. (2005) El vuelo del boomerang (The Flight of the Boomerang). Ed. Marcombo, Barcelona. http://www.dinamicafundacion.com/
- Barceló, G. (2013) Theory of Dynamic Interactions: Laws of Motion. World Journal of Mechanics, 3, 328-338. http://dx.doi.org/10.4236/wjm.2013.39036
- Barceló, G. (2008) Un mundo en rotación (A Rotating World). Editorial Marcombo, Barcelona, 263. http://www.dinamicafundacion.com/
- Barceló, G. (2011) Analysis of Dynamics Field Systems Accelerated by Rotation. Dynamics of Non-Inertial Systems. DeMSET-2011 Congress, Miami. http://www.coiim.es/forocientifico/FORO%20CIENTFICO/Documentos/DeMSET_2011_GBarcelo.pdf
- Pérez, L. (2013) New Evidence on Rotational Dynamics. World Journal of Mechanics, 3, 174-177. http://dx.doi.org/10.4236/wjm.2013.33016
- Pérez, L.A. (2013) Reflecting New Evidence on Rotational Dynamics. http://vimeo.com/68763196
- Bauluz, E. (2012) New Dynamic Hypotheses. This Video Showed the Experimental Tests Carried out by Advanced Dynamics S. A. to Prove and Justify the Theory of Dynamic Interactions.
- Dorado González, M. (2013) Dinámica de sistemas con spin: Un nuevo enfoque. Fundamentos y aplicaciones. ADI Ser, Ed., Madrid.
- Dorado González, M. (2006) Equation of Motion of Systems with Internal Angular Momentum—II. arXiv:physics/0603207
- Barceló, G. (2013) Technological Applications of the New Theory of Dynamic Interactions. Global Journal of Researches in Engineering: Mechanical and Mechanics Engineering-G, 13, Version 1.0. https://globaljournals.org/GJRE_Volume13/E-Journal_GJRE_(G)_Vol_13_Issue_5.pdf
- Barceló, G. (2014) Dynamic Interaction Confinement. World Journal of Nuclear Science and Technology. http://www.scirp.org/journal/wjnst http://dx.doi.org/10.4236/wjnst.2014.44031
- Barceló, G. (2008) Un mundo en rotación (A Rotating World). Editorial Marcombo, Barcelona. http://www.dinamicafundacion.com/
- Barceló, G. (2010) On the Equivalence Principle. 61st International Astronautical Congress, American Institute of Aero- nautics and Astronautics, Prague, CZ. http://www.coiim.es/forocientifico/FORO%20CIENTFICO/Documentos/ON_THE_EQUIVALENCE_PRINCIPLE.pdf
- Barceló, G. (2013) Proposal of New Criteria for Celestial Mechanics. International Journal of Astronomy and Astrophysics, 3, 385-391. http://dx.doi.org/10.4236/ijaa.2013.34044
- Barceló, G. (2013) Imago Universi: A Story of the Human Conception of the Cosmos. Ed. Arpegio, Barcelona. http://www.editorialarpegio.com/
- Sanchez Boyer, J. (2013) Video Imago Universi. http://imagouniversi.com/ http://vimeo.com/62247544
- Barceló, G. (2008) Un mundo en rotación (A Rotating World). Editorial Marcombo, Barcelona, 409. http://www.dinamicafundacion.com/











