Atmospheric and Climate Sciences
Vol. 3 No. 3 (2013) , Article ID: 33891 , 12 pages DOI:10.4236/acs.2013.33032
Calculated and Experimental Regularities of Cloud Microstructure Formation and Evolution
Institute of Experimental Meteorology, FBSI RPA “Typhoon”, Obninsk, Russia
Email: vernik@typhoon.obninsk.ru
Copyright © 2013 Nikolai Romanov, Vasiliy Erankov. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 2, 2013; revised May 4, 2013; accepted May 11, 2013
Keywords: Clouds; Fogs; Cloud Microstructure; Spectra Approximation
ABSTRACT
Based on the model of regular condensation it was found that at low concentrations of CN (LC mode) at a height of about 10 m from the condensation level narrow spectra of cloud drop are formed. Their dispersion quickly decreases with increasing height. For high concentrations (HC mode) broad spectra are formed immediately due to the absence of separation into growing drops and CN covered with water. The process of spectra evolution at a constant height results, in all the cases, in the appearance of asymptotic spectra with a relative width rb ≥ 0.215. To approximate these calculated asymptotic spectra, the modified gamma-distribution with the fixed parameter α = 3 and a variable parameter γ are most suitable. For the intermediate spectra applicable are the simpler mirror-transformed known distributions. The comparison of the above distributions with the experimental spectra of a fog artificially formed in the Big Aerosol Chamber (BAC) of RPA “Typhoon” and the spectra of the morning fog and super cooled stratiform clouds demonstrated their good agreement. The phenomenon of multimodal spectra formation at a sharp rise of stratiform clouds with the velocity more than 0.1 - 0.3 m/s was theoretically shown and experimentally confirmed. The effect of CN high concentrations, evolution processes and sharp fluctuations of vertical velocities on the formation of cloud spectra observed in nature is discussed.
1. Introduction
This Studying of the processes of cloud and fog microstructure formation during their initiation plays an important role in the understanding of the mechanisms of the microstructure formation and interaction of the drops formed with the environmental pollutants. The connection of a cloud microstructure with atmospheric aerosol composition influences the climate forming conditions. Of importance is also the problem of precipitation enhancement at cloud modification with hygroscopic agents. But up to the present, there is no generally accepted mechanism of experimentally observed in natural conditions rather broad cloud spectra [1], because the mechanism of regular condensation does not explain this aspect. In the monograph [2] devoted to the initial stage of condensation it is shown that within the frameworks of the theory of regular condensation at a constant rate of updraft the drop spectrum becomes narrower with altitude. In the same way, by analyzing dominant estimations for the Junge condensation nuclei (CN) the regularities of cloud drop spectra were obtained. These are the exponential function of maximum oversaturation and the concentration of the drops formed unambiguously connected with it on the velocity of updraft and CN concentration. Corresponding expressions for the exponents are given. In [3] broad drop spectra, formed due to evaporation of fine drops, were obtained for high concentrations of CN. But this result has not been analyzed from the physical viewpoint and was not considered later on. In the recently published work [4] with the use of a numerical model of regular condensation confirmed is the dependence, obtained in [2] of drop concentration on the velocity of air mass updraft, and its corrected dependence on CN concentration is given. The dependence of drop concentration on air mass temperature and pressure is given as well. But the author limited himself by the case of small concentrations at which the cloud drop concentration formed at the initial moment remained constant at a further updraft Analytical solutions were used [5] to study the dependences of integral values of cloud spectra on environmental parameters and the velocity of air mass updraft for a lognormal distribution of CN. The proposal to use some new parameters of drop spectra was made in [6]. But a comprehensive understanding of cloud spectra can be obtained only with the development of an adequate model of processes involved in the formation of cloud spectra.
The attempts to find an answer in solving this problem, including the problem of broad spectra, are described in detail in the review [7]. It is emphasized in this review that the model of regular condensation with a constant velocity of air mass updraft results in narrowing with the increasing updraft height cloud spectra in contrast to the broad and even miltimodal spectra observed in nature. In the works considered by them earlier, where an answer to this question was sought, most frequently proposed were the mechanisms of shifting of several cloud portions with different drop spectra, including those with pure air. Special attention is paid at the situation when the spectra of separate cells are mixed—these spectra are formed at different velocities of updrafts at the cloud base. In more detail this situation is analyzed in [8] where the situation with increasing updraft velocities from zero to 1.5 m/s is considered.
A possibility of bimodal spectra formation in the cells of a low velocity at the cloud base and its strong increase in the middle section are considered in [7]. But for this case there exist doubts in the sufficiency of the amounts of condensation nuclei left after the formation of an initial cloud drop spectrum for the formation of additional drops. These doubts are especially enhanced after the analysis of the aerosol-cloud system [9], where it is concluded that at the formation of cloud drops almost 80% of aerosol go into the drops.
When searching analytic approximations of cloud spectra [7] was thinking that at a modern level of computer technologies more adequate for studies of cloud processes is the direct computation of cloud drop spectra. Numerous researchers are likely to support the same position. Therefore, at present a three-parametric modified gamma-distribution, introduced in the monograph [10], is used (in particular) [11] to analyze optical properties of clouds. Because of a great number of parameters in this distribution, an unambiguous choice of the latter for concrete cloud structures presents difficulties.
To remove the above-mentioned gaps in the present paper a series of studies on the cloud microstructure formation at the stage of air mass updraft and its further evolution at a constant height based on the numerical model of regular condensation constructed by the authors is presented. As a result, a qualitative difference of cloud spectra formation at low and high concentrations of condensation nuclei (the LC and HC) has been found. The formation of spectra with a negative asymmetry was also found both at the updraft and evolution, that required the search of new approximation relationships for them. Qualitative and quantitative regularities of cloud drop concentration formation, relative spectrum widths and other characteristics depending on CN concentrations and also the updraft velocity and environmental temperature were obtained.
The calculated regularities were compared with the observed ones during the process modeling in the cloud chamber and also with the stratified clouds and morning fogs spectra measured by the authors. As a result of such studies, an identification of processes occurring in real clouds leading to broad and even multi-modal spectra is given. A recommendation is given for an analytic description of cloud spectra with the use of the known mirror symmetric distributions and a modified gamma-distribution with the parameter α = 3.
2. Calculated Regularities of Cloud Spectra Formation
2.1. Basic Relationships and General Pattern of Calculation Spectra Formation
First, For studying calculated regularities of cloud spectra formation we shall limit ourselves by a two-parametric inverse power distribution of the condensation nuclei over their equivalent radii rc.
 (1)
(1)
where Cc determines the number of particles with rc > rc,0 per 1 mg of air. This distribution is transformed at a 100% humidity into an equilibrium distribution over the radii rw of CN covered with water being droplets of a salt particles dissolved in water [2]
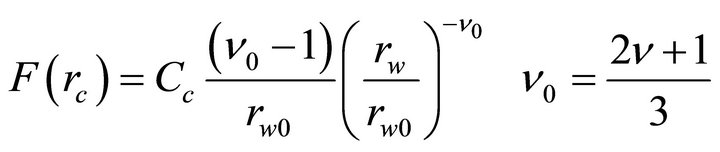 (2)
(2)
Under an approximation of the equality of the surface tension σw and the solution density ρ with the corresponding characteristics of pure water, the value of rw is determined by the number of salt molecules nc multiplied by the Van’t-Hoff factor ic with the relationship [12].
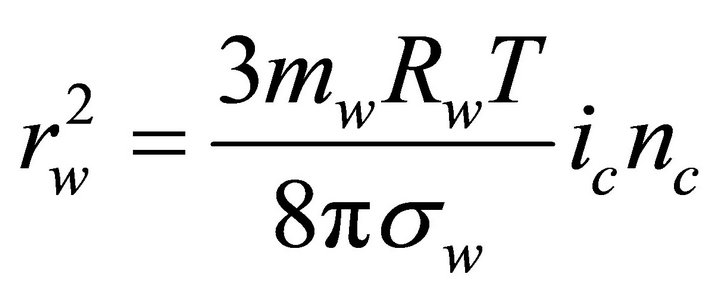 (3)
(3)
Here mw is the mass of a water molecule, T is temperature, Rn is the gas constant of water vapor.
The use of distribution (3) makes it possible to avoid the numerical procedure of studying the process of dry CN transformation at increasing relative humidity of air. For calculating the processes of drop formation the CN interval chosen is separated into n channels with an equal number of CCN in them, that is not necessarily to be an integer. At a growth of a drop the number of salt molecules in it remains constant, and its growth depends on the precipitation of the number of water molecules at increasing relative humidity f. The Van’t-Hoff factor is considered constant, the distribution of salt is homogeneous. The formulae for drop growth are taken from [2]. The value of vapor molecules accommodation is taken equal to 0.98.
At the first stage during the time interval Dt is determined by the variation of thermodynamic parameters due to the air mass updraft. At the second stage an increment of mass that occurred during this time is calculated for every nucleus. Then, the value of f is corrected for the total growth of mass on drops. It has been stated experimentally that stable results of calculations were obtained at Dh ≤ 1 cm and n ≥ 100. For the drop spectrum formation the condensation nuclei from Equation (2) were included, the radii of which were greater than rwb. Its value was chosen from the condition that there would stay about 5% of nuclei cowered with water after the drop spectrum formation. At varying CN concentration it appeared that during the air mass updraft two different modes of cloud spectra formation (that will be named the modes of low (LC) and high (HC) concentrations) may be realized The difference of these regimes is illustrated by the curves in Figure 1, where for the process of air mass updraft with the velocity of 1 m/s to the height of 30 m and at its further evolution at a ceased updraft are the trajectories of drop growth at the separation of the whole spectrum into 100 channels (the upper figures). In the lower figures present the trend of the integral values: asymmetry coefficients kas, relative breadth rb, drop concentration Cd, oversaturation ε = lnf and um = max (u = r/
The vertical lines in the upper figures denote the moments of updraft stopping at t = 30 s, and the numbers at the trajectories correspond to the serial number of the channels. From Figure 1(a) the process of growing drops separation from the CN covered with water at the moment when maximum oversaturation occurred at the 10- th second is distinctly seen. For the case presented in Figure 1(b) the concept of a drop is already smeared because in the spectrum different from the stationary spectra of CN covered with water there exist both the growing and evaporating drops. Therefore, all the drops covered with water with non-stationary sizes or those exceeding any size (in the given case—0.4 micrometer) can be considered drops.
From the figures presented it is seen that under the regime of a constant temperature fine drops are evaporating and large drops are growing. Such a process takes place at an air mass updraft at small velocities and high concentrations of CN. The distribution function formed in this case has a negative asymmetry coefficient and a maximum shifted to the right relatively to an average value.
2.2. Approximation of Calculated Spectra
The well-studied and frequently used for the representation of cloud spectra two-parameter gamma-distribution, as is seen from the supplement, has positive values of kas
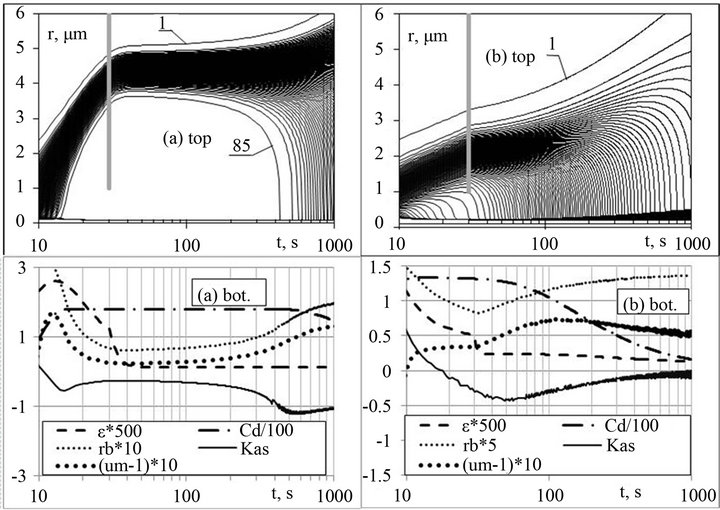
Figure 1. Trajectories of drop growth (the top figures) and the course of ε, Cd, rb, kas and um values with multipliers indicated in the legend (the bottom figures). (a) In the mode of LC, Cc = 102 mg−1; (b) In the mode of HC, Cc = 104 mg−1 (n = 5, Т = 20˚C, n = 100).
and a maximum shifted to the left. The same peculiarities belong to the log-normal distribution and to that proposed in [13]. Therefore, they in principle are inapplicable for the approximation of the calculated evolution spectra. The selection of expressions in the form of the power law with the exponent from 2.6 to 3 in the left and the inverse power law with the exponent from 8 to 10 in the right wings and parabolic in the spectrum center has demonstrated that such an approach can satisfactorily describe calculation spectra but is practically inconvenient. The for-parameter modified gamma-distribution at a certain combination of the parameters α and γ used in it may lead to negative values of kas. But it should be mentioned that the above-mentioned dimensions are not physically substantiated.
The only one known to us asymptotic distribution [14] flif, obtained at solving the differential equations describing the growth and evolution of crystals in an oversaturated solution without external crystallization centers. In work [15] was physically substantiated the similarity of these processes with the evolution processes of cloud drop spectra not containing salt. This normalized by unity solution with the use of a relative drop radius u = r/
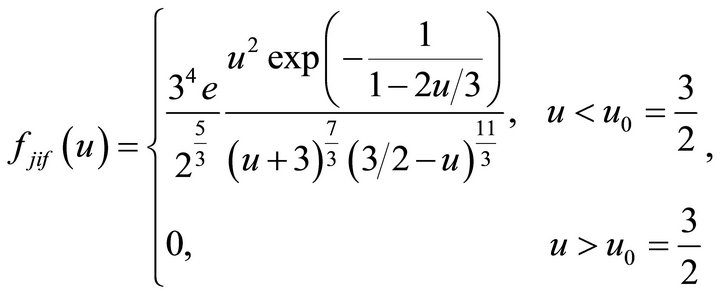 (4)
(4)
The main parameters of this distribution have the following values: rb = 0.215, kas = −0.92, um = 1.135, f(um) = 2.135. It coincides qualitatively with the above properties of numerical calculations, i.e. it gives broad asymptotic spectra with negative asymmetry. The attempts to introduce into this distribution additional parameters, that could lead to a possibility to parameterize the calculated spectra formed on CN, failed.
From the expression it is seen that the value of u operates in the asymptotic solution as an algebraic combination with several constants. The introduction of such combinations in the above-mentioned distributions can be made by the method of their mirror transformations with the use of
 (5)
(5)
where ub is similar to u0 in Equation (4) and determines the boundary of the non-zero value of the function.
For the value of γ and S-distribution characteristics of which are given in the Supplement the mirror functions (fγm(u) and fSm(u)) normalized by unity are written in the form of
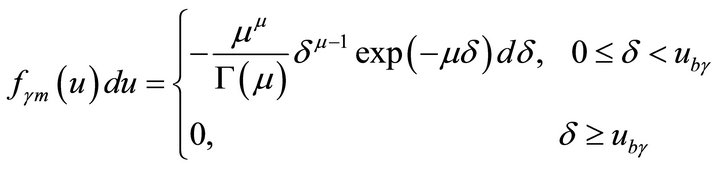 (6a)
(6a)
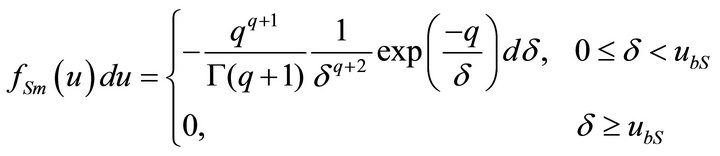 (6b)
(6b)
In spectra (6a and b) the locations of maxima for the value of δ are correspondingly equal to
 ;
;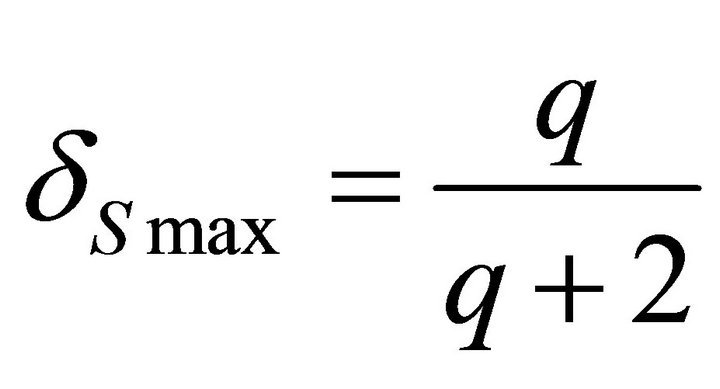 (6c)
(6c)
For the locations of maximum values of functions (6a and b) for the approximated spectra to have the values of um the condition of
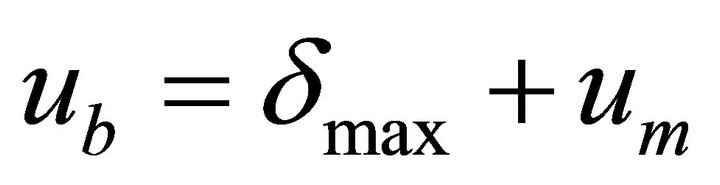 (6d)
(6d)
should be fulfilled.
The substitution of expressions (6c) into (6a and b) give the expressions for maximal values maxf of the function:
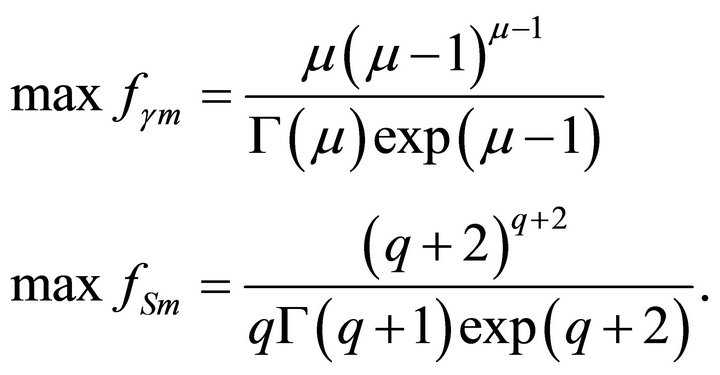 (6e)
(6e)
The problem of choosing the parameters of these distributions is set in the following way. First the location of maximum um and the value of maxf for a calculated (experimental) spectrum are determined. After this the values of μ and q can be determined by solving the equation of the direct dependence (6e) with one variable. As far as the inverse dependence in these relationships does not have exact analytic expressions, the approximation relationships giving an error of no more than unity of the second sign after the point at the values of q ≥ 10 were obtained. They have the form of
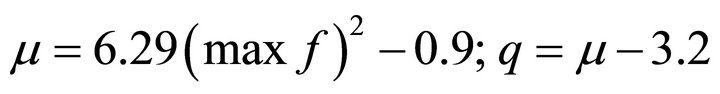 (6f)
(6f)
After the substitution of the obtained from Equation (6f) values μ or q into Equations (6c) and (6d) the corresponding value of ub is determined. Thus the problem of finding both parameters of the approximation functions (6a) and (6b) is solved.
Both distributions are the two-parametric ones that turn to zero at the boundary value of u = ub and do not turn to zero at u = 0. The latter obstacle should not embarrass one, because physics of cloud spectra formation points to the presence of the lower boundary of cloud spectra determined by the maximal equilibrium radius of the remaining CN covered with water. The moments of these functions may (with a certain error) be expresses by the moments of the main functions at the substitution of the ub value by ∞ in the relationship
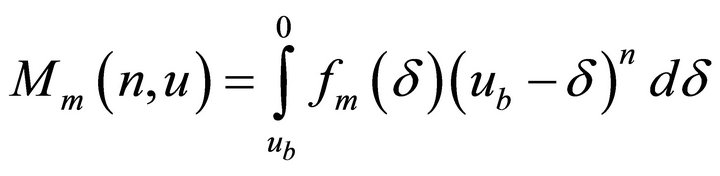 (7)
(7)
For narrow distributions this substitution will not result in a great error. Therefore, below we give the formulae for expressing the first two moments and the relationships for rb obtained with them.
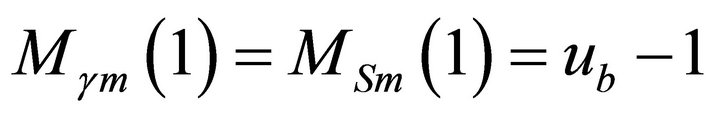 ; (8a)
; (8a)
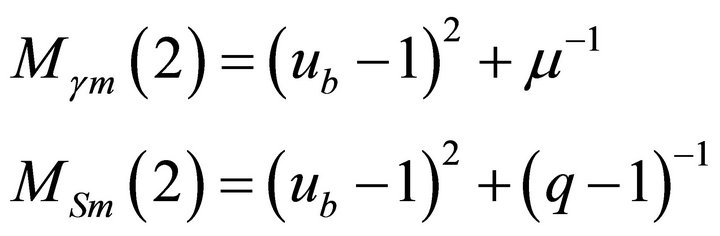 ; (8b)
; (8b)
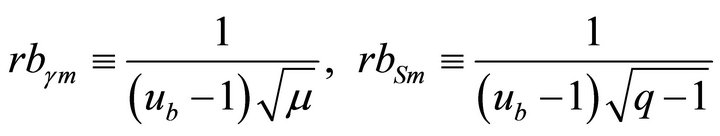 . (8c)
. (8c)
With the use of (relationships) correlations 8(c) and (6c) and (6d) an iteration scheme for determining the parameters of distributions (6a) and (6b) can be constructed on the basis of the known parameters um and rb. Such a procedure may be useful for a description of experimenttal spectra for which due to their cut-up character the definition of maxf presents difficulties.
It has been mentioned earlier that a more complex tree-parametric modified gamma-distribution fmγ(u) with the parameters α and γ, the general form of which is given in the Supplement, has also the regions (at γ > 3) with negative kas values. When studying the problem of choosing the appropriate parameters of this distribution to approximate the calculation spectra it appeared that for all the spectra with maxf(u) within the limits from 2.3 to 1.5 the calculation spectra at the evolution stage at a constant height are well approximated by the function fmγ(u) with the parameter α = 3 at the known value of um. As a result, the case with the distribution fmγ(u) written as
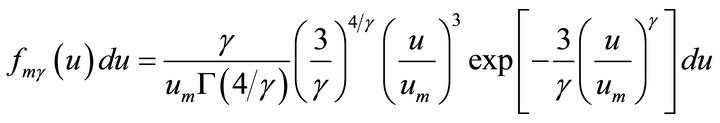 (9)
(9)
So this distribution is reduced to the two-parametric one as well. In particular, its form coincides with the spectrum (4) at the substitution of um = 1.1345 and γ = 16.3. The maximum of function (9) occurs at u = um. It is expressed by a rather complex dependence on the parameter γ not having an exact analytic expression for the inverse function. That is why it is not given here. The approximation expression for the inverse function was obtained in the form having an error no more than unity of the first sign after the point at 2 < γ < 20
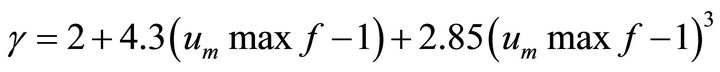 (9a)
(9a)
The approximation expression between rb and γ with account for the asymptotic value from the Supplement for rb for high values of γ was obtained in the form of
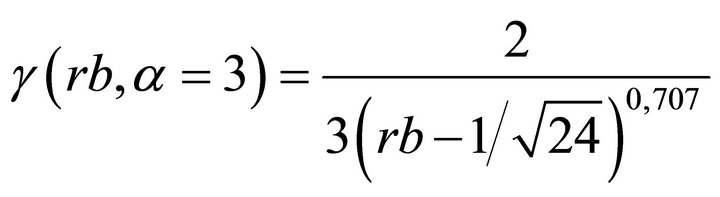 (9b)
(9b)
Relationship (9b) can be applied directly for determining the parameter γ at approximating experimental spectra by distribution (9).
2.3. Results of Calculated and Approximated Spectra Comparison
The results of calculated and approximated spectra comparison for updraft beginning and ceasing of evolution process at a constant temperature are given in Figures 2(a) and (b). For convenience of formation of the figure here and later on the Greek γ is substituted by the Latin g.
From this figure it is seen that the set of distributions fmg, fgm and fSm makes it possible to adequately reproduce the shape of the calculation spectra during the whole process of formation and evolution of cloud drop spectra. From comparison at other updraft heights, CN concentrations and other parameters it appeared that at all the regimes studied the set of three functions fmg, fgm and fSm describes rather well the calculated spectra in the range of 0.3 < u < 1.4. In a general case it is possible to recommend after the definition of parameters for these distributions to choose out of three the best coincidence kas of the approximation spectrum. The existing difference at u > 1.4 can be removed by applying the inverse power law to this part.
2.4. Approximation Relationships for Integral Parameters of the Initial Stage of Condensation for Regime of LC
The studies of maximum oversaturation εm and other parameters effect on the updraft velocity V, CN concentration Cc, the index ν, air mass temperature T and pressure p were performed at the subdivision into 1000 intervals. Studied were the ranges of V = 0.1 ÷ 10 m/s, Cc = 102 ÷ 104 (1/mg) at rw,0 = 0.1 μm, n from 4 to 8, Tc = −10÷ +30˚C and p = 0.8÷ 1.25 atm. In the relationships presented below the measurement units are valid.
As a result, it appeared that at LC εm can be approximated via the following relationships:
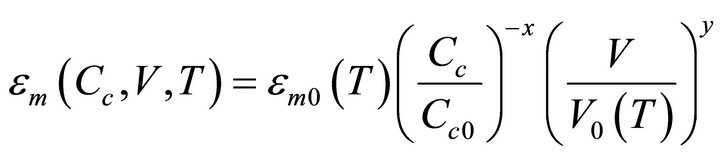
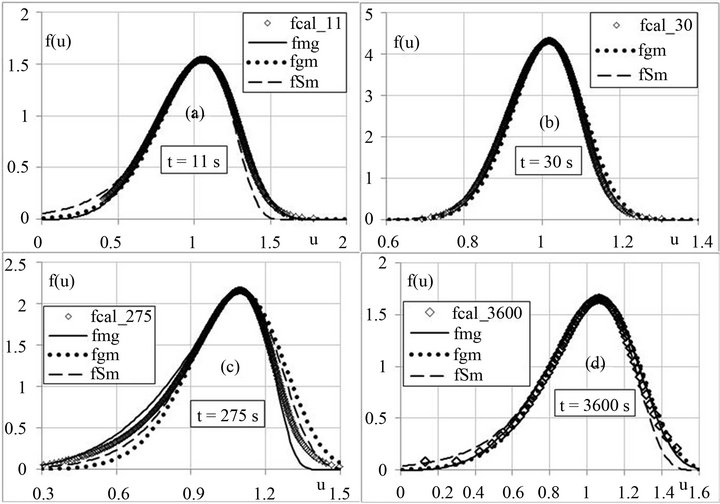
Figure 2. Comparison of calculated fcal and the approximation spectra for the time moments (a) 11 s, (b) 30 s (termination of updraft), (c) 275 s (the moment of reaching rb = 0.215) and (d) 3600 s after the beginning of the process.
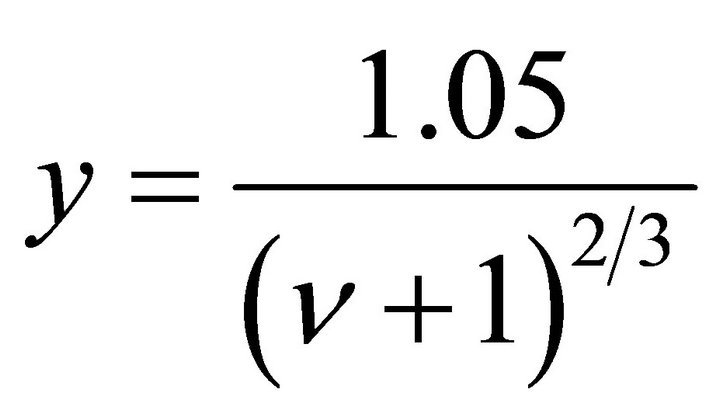 ;
; 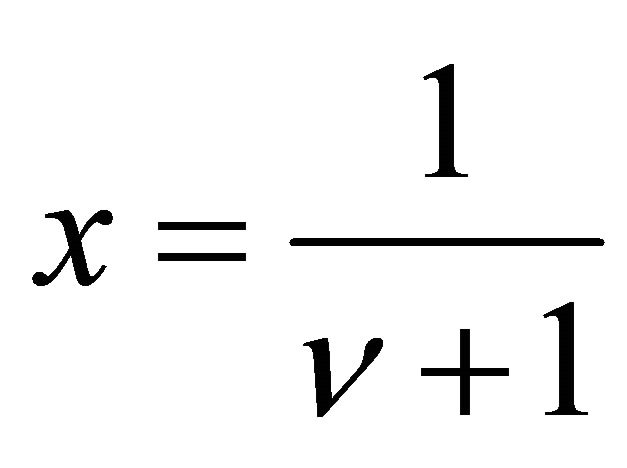
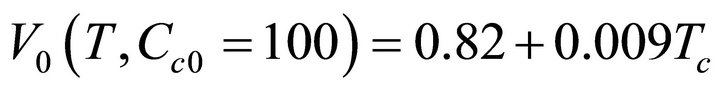
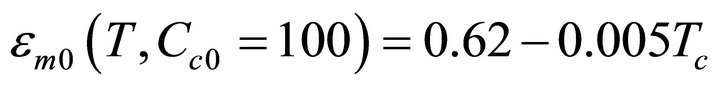 . (10)
. (10)
The height of the updraft hm at which εm is attained is practically proportional to εm and is determined by the relationship similar to (10). Let us write this relationship in the form of
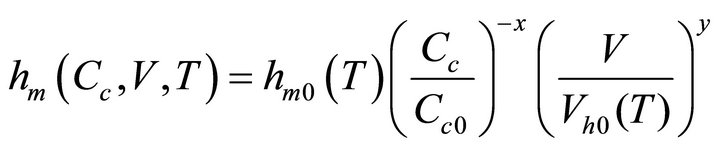 (11)
(11)
where the exponents x and y are determined by formulae (10) and the values of hm0 (20˚C) = 10 m and Vh0 (20˚C) = 0.42 m/s at Cc0 = 100 mg−1.
At the heights h = 2hm and 3hm the drop liquid content makes 80% and 90% as compared with the thermodynamic one, correspondingly. Note that for the mode of LC an approximation error (11) does not exceed the units of percent.
The analytic regularities for the drop concentration Cd (1/mg) for the mode of LC can be obtained by integration over ε from 0 to εm of the nucleus distribution function over oversaturation (10). But for the errors from there not to be included here, an approximation for the drop concentration was obtained on the basis of its own calculations. It has the form of:
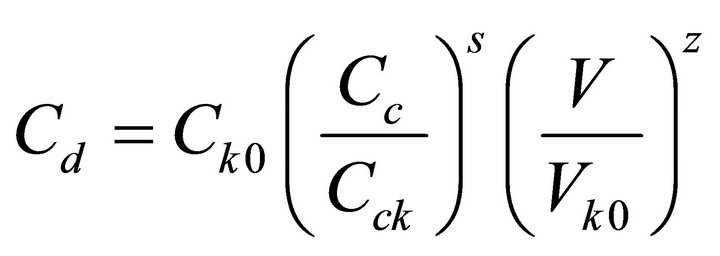


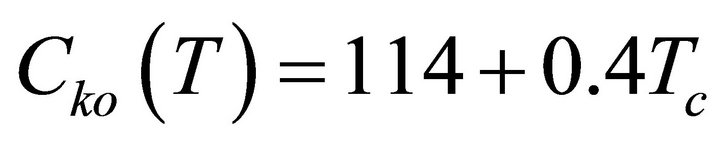

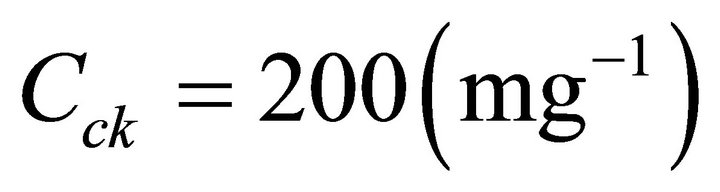 . (12)
. (12)
We shall note that in our calculations the dependence relation (10)-(12) on p has not been found.
The comparison of the above-mentioned relationships for the indices x, y, s and z with the corresponding values [2] has shown an extremely good numerical agreement (despite the difference in expressions) for the values of q and y obtained without corrections for hygroscopicity, the jumps of vapor concentration and temperature. The values of x and especially of s are noticeably different from our results. The relationship presented in [4] for the parameter z coincides with [2] and for the parameter s it numerically corresponds to our relationships with a difference in the analytic expression.
The condition of LC, at which relations (10)-(12) are valid, can be expressed by the following rather approximate relationship of drop concentration dependence on air mass updraft velocity (m/s) and temperature (˚C).
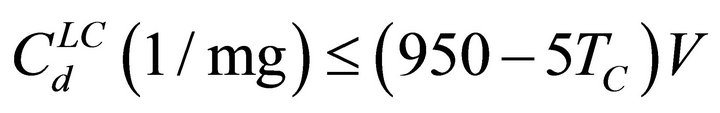 (13)
(13)
2.5. Evolution of Cloud Parameters at a Constant Height
A calculated character of integral parameters behavior at a constant temperature depending on the conditions of their formation at an ascending air mass is illustrated in Figures 3(a)-(c).
From the data presented in these figures and calculation for other conditions it follows that under evolution at a constant temperature a relative dispersion increase with time and tends to the theoretical limit rb = 0.215 at low concentrations of CN (Cc = 102 in Figure 4(b)) and high liquid water content (h = 100 m in Figure 4(a)). At increasing СCN the asymptotic limit rb grows.
From the figures it is also seen that in some time after the air mass ascent ceased depending on the value of h, the growth of the drop average mass starts to acquire a
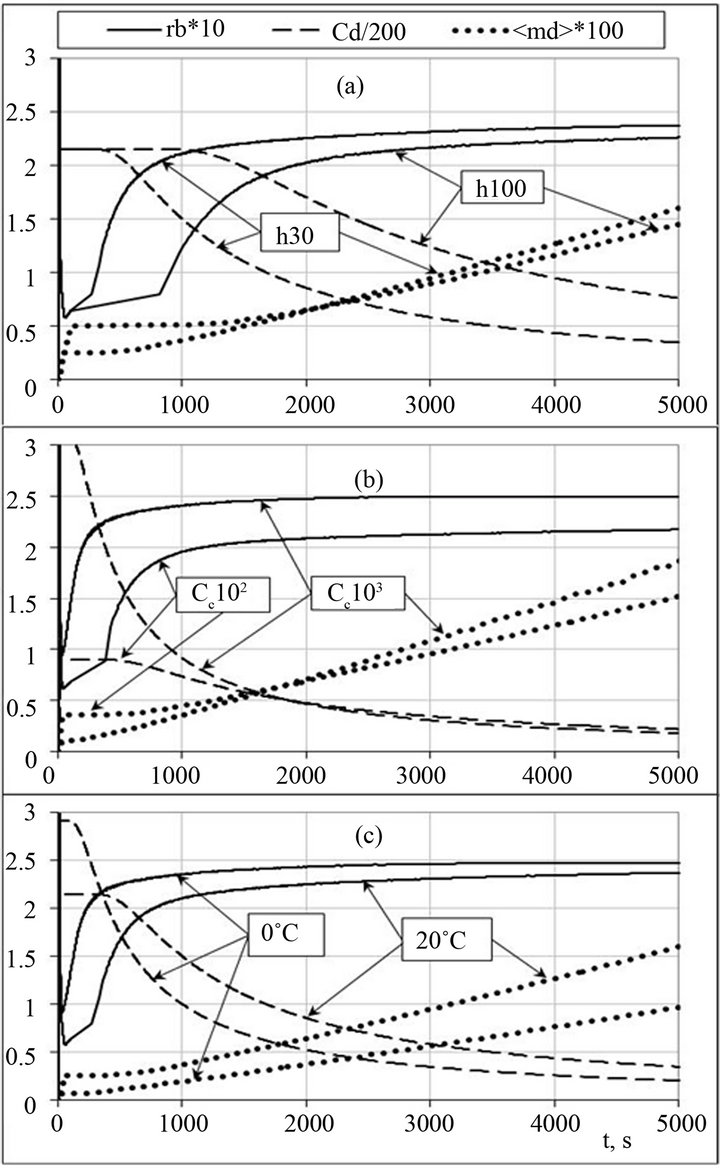
Figure 3. Dependence (V = 1 m/s) of an average drop mass <md> (10−10 g), Cd (mg−1) and relative breadth rb on time at different: (a) Updraft heights (Cc = 500, T = 20˚C); (b) CN concentrations (h = 30 m, T = 20˚C) and (c) Temperatures (h = 30 m, Cc = 500). The data are multiplied by the coefficients from the legend.
linear regularity determined in [14] with time counted from the moment t0. The coefficient a of this dependence weakly depends on the updraft height (drop liquid content) and increases insignificantly with a growing CN concentration and becomes especially noticeable at a temperature increase. Considering only the dependence on temperature and taking into consideration the range of the value of a changes at varying h and Cc, this dependence can be written in the form of
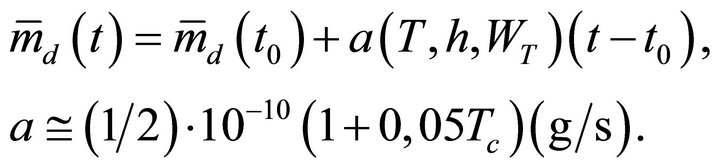 (14)
(14)
The moment when the regularity comes into action t0 strongly depends on the initial breadth of spectra and may last several hours at rb ≈ 0.01. We shall not analyze these dependences in detail in this work.
2.6. Formation of Multi-Modal Drop Spectra
A fast growth of updraft velocity can result in the appearance in the spectrum the drops of the second kind. An illustration of such a condition is given in Figure 4, where for two CN concentrations given are the trajectories of particle sizes at an increase of updraft velocity by 5 times.
From the results of calculations for the parameters, given in p. 2.3, it appeared that the condition for the appearance of the second mode V2 ≥ 5V1 does not practically depend on the Cc and the velocity V1. For a cloud medium remaining for some time at a constant height, the appearance of the second mode is possible at the updraft velocities of V ≈ 0.2 m/s.
3. Experimental Studies of Cloud Microstructure Formation Processes in the Chamber and Natural Conditions
3.1. Description and Results of Experiments in Chamber
Experimental studies of regularities of cloud spectra formation and transformation were performed in the BAC (Big Aerosol Chamber) of RPA “Typhoon” [16] (cylinder of the height of 18 and diameter of 15 m), where an air mass updraft was simulated by dropping excessive pressure created earlier. The Chamber is equipped with the temperature and humidity sensors with the use of standard instrumentation and a photo-electric counter of water drops FIROK operating in the range of cloud drop radii from 0.5 to 50 micrometer [17].
A change of updraft equivalent velocity is ensured by the change of a corresponding pressure dropping rate. The conditions of isothermality were ensured by a termination of the process of pressure dropping at equal temperature in the Chamber and the temperature of its walls.
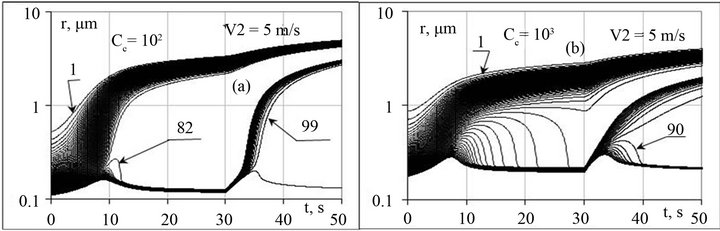
Figure 4. Trajectories of particles at a strong growth of updraft velocity at moment t = 30 s (V1 = 1 m/s, T = 20˚C, n = 5).
The composition of CN was determined by their content in the environmental air. CN spectra and composition was not controlled, but the stability of their characteristics was checked by the reproducibility of characteristics of cloud drop spectra formed under similar conditions of pressure dropping. Some experimental results obtained with the use of the BAC were reported at the 13-th Conference on Cloud Physics [18] without a comparison with the calculation data. The present paper gives new results with a corresponding comparison.
At the first stage studied was a dependence of cloud drop concentration on the equivalent velocity of air mass updraft. It appeared that the experimental points coincide best of all with the calculated ones at n = 5, Cc = 104 (1/mg). Such high concentrations of condensation nuclei are explained by the fact that the air is pumped into the chamber from the height of only 20 m. The formation of spectra at such CN concentration occurs in the HC mode. Therefore, in the experiments in the BAC no narrow spectra were observed. Their form is stabilized in some time. The dependence of cloud parameters on time connected with drop spectra is shown in Figure 5, where for an updraft cycle to 200 m with the velocity of 1 m/s (after which the air temperature in the chamber becomes equal to the wall temperature) shown is the curve of an average drop mass, and their concentration and a relative width of spectra depending on time.
From the figure it is seen that the relative spectrum width changes little during the whole process, the average drop mass grows linearly just after the updraft termination with the growth coefficient, that is almost twice as that in the calculated relationship (14). The observation of spectra form made during the process showed its sufficient stability.
A comparison of spectra obtained in two different experiments (without and with cleaning of the air from aerosols) is shown in Figure 6.
From the comparison it is seen that for the approximation of the experimental spectra most reasonable is the function fsm. Without taking into consideration the differences in the range of small values of u, we shall note that at u > 1.4 the experimental spectra are a little greater than the approximation ones. They are higher for the spectrum a) than for the spectrum b). Such an excess was noted for the calculated spectra as well. The experiments with the formation of the second mode demonstrated that for the updraft velocities V1 = 0.3 - 1 m/s the appearance of the second mode was noted at V2 = (4.5 - 5)V1, that corresponds to the calculated values of this relationship. For cloud spectra after 10 min of evolution at a constant temperature the appearance of the second mode was noted at V = 0.2 m/s, that qualitatively agrees with the calculated results obtained. Figure 7 is an illustration of spectra formation and transformation.
From this figure it is seen that already at the 20-th second of the updraft beginning a fine-drop spectrum fraction is formed. Before the 260-th second the spectrum becomes a bimodal one. Later both modes merge.
3.2. Comparison with Field Measurements of Cloud and Fog Drop Spectra
Headings Measurements of natural fog drop spectra were made by one of the authors [19,20]. In [19] appearance of two-modal spectra over the hill-like risings of the fog upper boundary level was noted. In view of the conditions of the second mode formation created above at small updraft velocities in stationary clouds we have now an explanation of the appearance of this mode. It is the presence of a convective updraft causing a local increase of the fog upper boundary. Due to a low resolution of the drop spectrum counter, the spectra shown are not reliably comparable with the approximation relationships. The registration of twoand even of three-modal spectra in China was mentioned in the review [21].
In [20] the results of measurements of drop spectra of a warm fog formed as a result of morning dew evaporation into the cold morning humid air are presented. During these measurements an improved instrumentation described in this paper was used. But because of the absence of an adequate model no approximation was made. The next figure gives the comparison of one of this fog spectrum with the approximations proposed above.
The measurements of stratiform super cooled cloud drop spectra were carried out from a helicopter in 2000
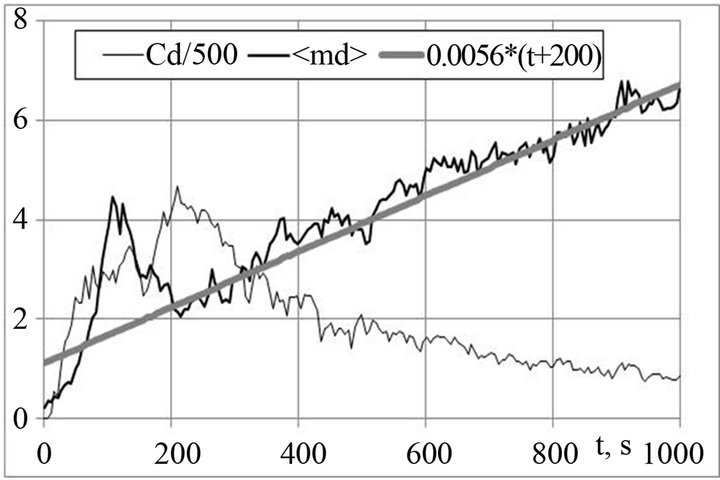
Figure 5. Dependence of Cd (cm−3),
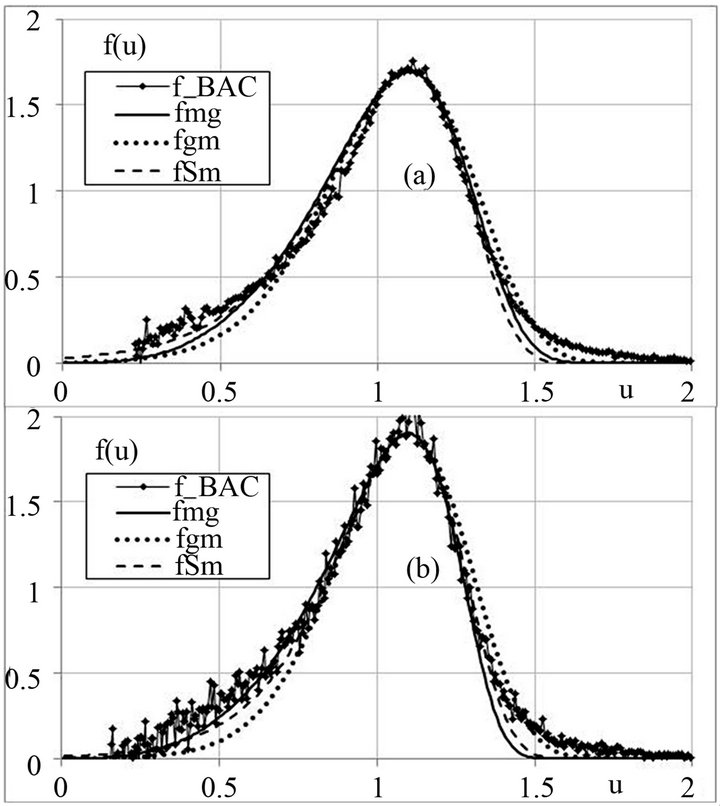
Figure 6. Comparison of an experimental in BAC and approximation spectra with um = 1.1 for the conditions: (a) without cleaning (
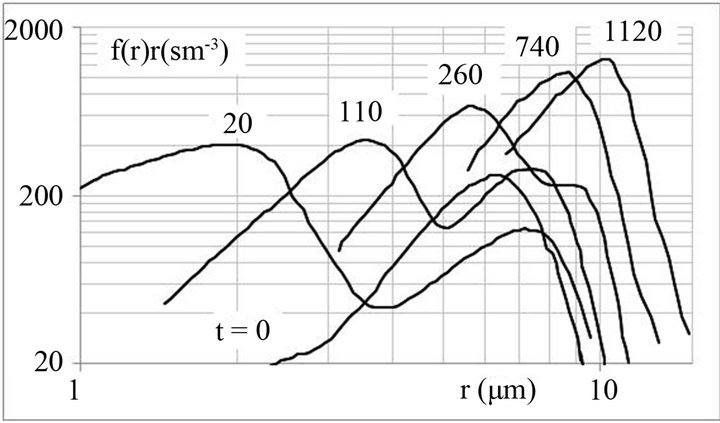
Figure 7. Formation of the second mode at the updraft velocity of 0.2 m/s after fog evolution at a constant height (temperature). The numbers at the curves indicate time in seconds from the updraft beginning.
in the Northern Caucasus Mountains. An average cloud thickness was 250 - 300 with the upper level boundary of 1300 m. The cloud medium temperature was about minus 10˚C at the lower level; it decreased with height by about 0.5 degree with the inversion at the upper boundary (UB) with about 2 degrees. An average drop radius increased with height and reached the value of 3.0 - 3.5 μm near the UB. The results of these measurements have not been published because the differences connected with their analytic description. A comparison of two spectra measured near the UB with the approximation ones is shown in Figure 8.
The spectra a and b differ only in the time of their measurements at the same heights. The jagged form of spectrum lines is explained by a short time of spectrum sampling (5 s at the helicopter horizontal flight velocity of about 50 m/s). One can note a plateau in the left-hand portion of experimental spectra. For its description it is possible to use the spectrum of CN covered with water (2), but for a reliable determination the number of measurements of small sizes is insufficient. Therefore, we shall only make a conclusion on an adequate description of the drop fraction of the investigated cloud spectra with the distributions like fmg and fSm.
4. Main Results and Conclusions
A On the basis of the calculations made with the model of cloud spectra formation and evolution it has been found that the formation processes differ qualitatively depending on CN concentrations. At small CN concentrations (the mode of LC) narrow spectra of cloud drops
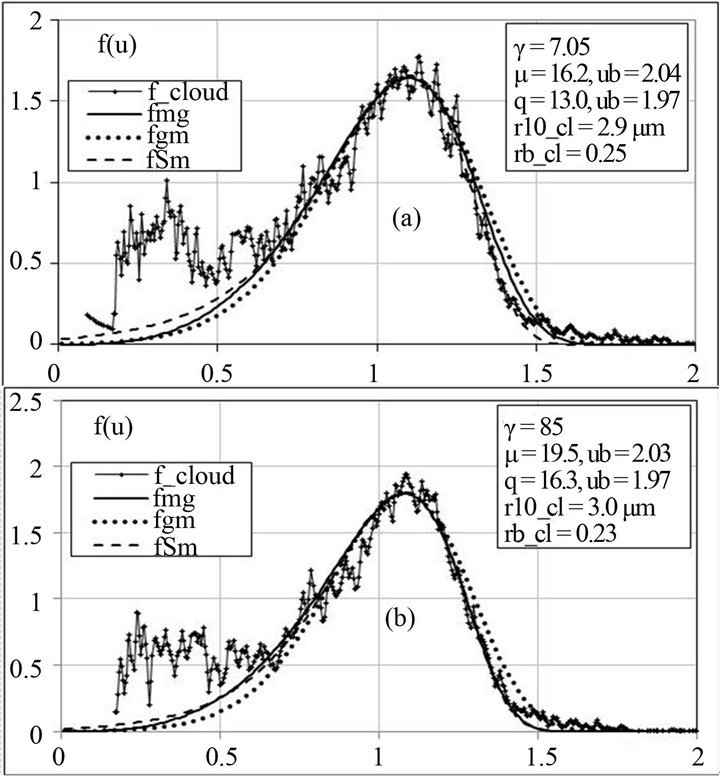
Figure 8. A drop spectrum of a super cooled stratiform cloud and its approximation.
are formed already at the height of about 10 meters from the condensation level, a relative drop dispersion of which quickly decreases with increasing height. For high concentrations (the mode of HC) no distinct separation of growing drops and CN covered with water is observed due to the immediately beginning evaporation of the drops. The boundary of separation of these modes in view of cloud drop concentrations is almost proportional to the air mass updraft velocity with the coefficient, decreasing with increasing temperature. But when the updraft is terminated, the evolution of spectra both in the first and the second case leads to the appearance of asymptotic spectra, a relative dispersion of which depends generally only on the condensation nuclei concentration and changes from the theoretical value of rb = 0.215 for the spectra at very low to rb = 0.25 ÷ 0.28 at high CN concentrations At all the stages of formation and evolution, the calculation spectra have the negative asymmetry coefficient and a shifted from the mean value (towards high positive values) location of maxima. At the results of analysis of analytical relations it is assumed that for the mirror functions fmg the well-known gamma distributions and lessknown Smirnov’s formulae fSm and also а modified gamma-spectrum fgm with the fixed parameter α = 3 are applicable. The reconstruction of the parameters of the above-mentioned distributions is made with the use of location and amplitude of the spectrum maximum. The choice of a most-applicable from those mentioned above (and also of other possible mirror distributions) can be made with the use of best coincidence of asymmetry coefficients. Here, most reasonable for us is the use in the numerator of expression (3s) of the value um instead of u10.
The dependences of integral parameters (drop concentration, maximum supersaturation, etc.) on the updraft velocity, CN concentration and temperature given in this paper make the results obtained previously more accurate and broad. It is shown that the conditions of appearance of additional modes in drop spectra during updraft at an excess of additional increase of updraft velocity by 4.5 - 5
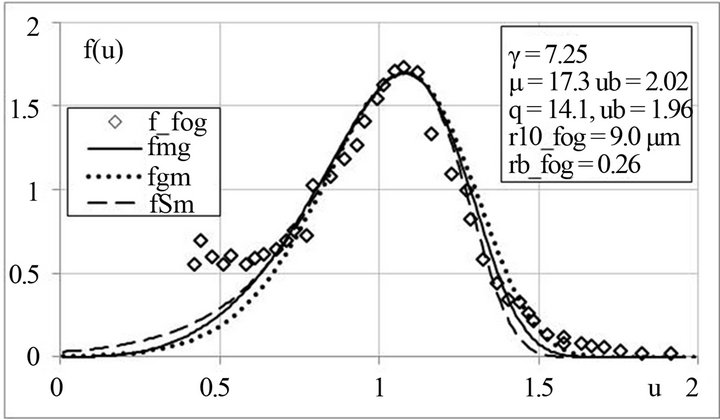
Figure 9. Approximation of the morning fog drop spectrum mentioned in [20].
times are studied. During spectra evolution at a constant height the process of additional mode formation can occur at updraft velocities of 0.1 - 0.2 m/s. This conclusion was confirmed by the experiment in the BAC.
Experimental spectra obtained in the Big Aerosol Chamber of FSBI RPA “Typhoon” and the natural fog and supercooled stratiform cloud spectra obtained by the authors are well approximated by Smirnov’s distribution fSm. The modified gamma-distribution fmg in the frameworks of uncertainties in the experimental spectra can be considered applicable as well.
One can draw the following conclusions on the peculiarities of natural cloud spectra formation with the use of the results obtained:
• Broad spectra in natural cloud spectra can be explained both by a great CN concentration and evolution of cloud microstructure under steady meteorological conditions;
• The first argument can be supported by the following consideration: drop concentrations of 300 - 800 cm−3 existing in continental stratiform clouds at equivalent velocities of cloud clusters and fog formation of 0.1 m/s and less, according to the condition of (13), can be formed only in the mode of HC;
• An effect of cloud drop spectrum broadening under evolution, with the exception of the evident case of stratiform cloud formation, can be possible also in cumulus clouds (especially at their upper boundary) in the presence in them of regions with zero and even negative air mass updraft velocities [7,8];
• The multimodality of natural spectra is likely to be caused by the fluctuation of air mass vertical motions. This conclusion is supported by the bimodal spectra observed in the hilly formations at the fog upper boundary [19]. The formation of an additional mode at vertical fluctuations of a cloud layer even at the velocities of several tenths of m/s may lead in reality to a considerable drop spectrum broadening and to stimulation of coagulation processes in clouds. They may serve as a trigger mechanism for precipitation formation from warm clouds;
• The spectra of natural fogs and stratified clouds (see Figures 8 and 9) have the form described by Smirnov’s mirror distribution and the modified gammadistribution with the parameter α = 3. The spectra of various forms of natural objects are likely to be presented by these analytic expressions.
REFERENCES
- P. Mazin and V. M. Merkulovich, “Stochastic Condensation and Its Possible Role in the Formation of Cloud Drop Microstructure (Review). Some Problems of Cloud Physics,” In: Collected Papers: “Memorial Issue Dedicated to Prof. Solomon M. Shmeter”, Moscow, 2008, pp. 217-267 (in Russian).
- Yu. S. Sedunov, “Physics of Liquid-Drop Phase Formation in the Atmosphere,” Leningrad, Gidrometeoizdat, 1972 (in Russian).
- E. L. Alexandrov, N. V. Klepikova and Yu. S. Sedunov, “Some Results of Cloud Drop Spectra Formation,” Parts I and II. Trudy IEM, Gidrometeoizdat, Moscow, 1976, p. 19.
- A. S. Drofa, “Formation of Cloud Microstructure during Hygroscopic Seeding,” Izvestiya, Atmospheric and Oceanic Physics, Vol. 42, No. 3, 2006, pp. 326-336. doi:10.1134/S0001433806030066
- V. I. Khvorostyanov and J. A. Curry, “Kinetics of Cloud Drop Formation and Its Parameterizationfor Cloud and Models,” Journal of the Atmospheric Sciences, Vol. 65, No. 9, 2008, pp. 2784-2802. doi:10.1175/2008JAS2606.1
- N. Kivekas, V.-M. Kerminen, T. Anttila, H. Korhonen, H. Lihavainen, M. Komppula and M. Kulmala, “Parameterization of Cloud Droplet Activation Using a Simplified Treatment of the Aerosol Number Size Distribution,” Journal of Geophysical Research, Vol. 113, No. D15, 2008. doi:10.1029/2007JD009485
- A. Khain, M. Ovchinnikov, M. Pinsky, A. Pokrovsky and H. Kruglak, “Notes o State-of-the-Art Numerical Modeling of Cloud Microphysics,” Atmospheric Research, Vol. 55, No. 3-4, 2000, pp. 159-224.
- C. Erlick, A. Khain, M. Pinsky and Y. Segal, “The Effect of Wind Velocity Fluctuations of Drop Spectrum Broadening in Stratocumulus Clouds,” Atmospheric Research, Vol. 75, No. 1-2, 2005, pp. 15-45.
- A. I. Flossmann and W. Wobrock, “A Review of Our Understanding of the Aerosol-Cloud Interaction from the Perspective of a Bin Resolved Cloud Scale Modeling,” Atmospheric Research, Vol. 97, No. 4, 2010, pp. 478- 497. doi:10.1016/j.atmosres.2010.05.008
- D. Deirmenjian, “Electromagnetic Scattering on Spherical Polydispersion,” Amerikan Elsevier Publishing Company, New York, 1969.
- S. M. Prigarin, K. B. Bazarov and U. G. Oppel, “Looking for a Glory in A-Water Clouds,” Atmospheric and Oceanic Optics, Vol. 25, No. 4, 2012, pp. 256-262. doi:10.1134/S1024856012040124
- N. P. Romanov, “Analytic Representation of Van’-Hoff’s Factor for Aqueous Solutions of Strong Electrolytes,” Izvestiya, Atmospheric and Oceanic Physics, Vol. 41, No. 5, 2005, pp. 641-651.
- V. I. Smirnov, “About of the Approximation of Empirical Distributions on a Size Clouds Drops and Other Aerosol Particles,” Izvestiya, Atmospheric and Oceanic Physics, Vol. 9, No. 1, 1973, pp. 54-65.
- I. M. Lifshitz and V. V. Slyosov, “On the Kinetics of Oversaturated Solid Solution Diffusion Decay,” ZETF, Vol. 35, No. 2, 1958, pp. 479-492 (in Russian).
- A. S. Kabanov, “Kinetics of Condensation Growth of a Drops at Late Stage of Adiabatic Process,” Izvestiya, Atmospheric and Oceanic Physics, Vol. 8, No. 12, 1972, pp. 1279-1288.
- N. P. Romanov and G. P. Zhukov, “Thermodynamic Relationships for the Fog Chamber,” Russian Meteorology and Hydrology, No. 10, 2000, pp. 37-52.
- A. S. Drofa, V. N. Ivanov, D. Rosenfeld and A. G. Shilin, “Studying an Effect of Salt Powder Seeding Used for Precipitation Enhancement from Convective Clouds,” Atmospheric Chemistry and Physics, Vol. 10, No. 16, 2010, pp. 8011-8023. doi:10.5194/acp-10-8011-2010
- N. P. Romanov, “Experimental Investigation of the Processes of Formation and Evolution of Natural and Artificial Fogs Microstructure,” 13th International Conference on Clouds and Precipitation, Reno Area, 14-18 August 2000.
- N. P. Romanov, “Some Characteristics of Fog in the Center of European Territory of Russia in October 1987,” Soviet Meteorology and hydrology, No. 4. 1990, pp. 49-55.
- N. P. Romanov, “Evolution of Morning Fogs Microstructure,” Meteorologiya i gidrologiya, No. 2, 2001, pp. 36- 45 (in Russian).
- S. J. Niu, C. S. Lu, H. Y. Yu, L. J. Zhao and J. J. Lu, “Fog Research in China: A Review,” Advances in Atmospheric Sciences, Vol. 27, No. 3, 2010, pp. 639-661. doi:10.1007/s00376-009-8174-8
- I. P. Mazin and S. M. Smeter, “Clouds, Their Structure and Formation,” Gidrometeoizdat, Leningrad, 1983 (in Russian).
Supplement
Moments of the n-th order
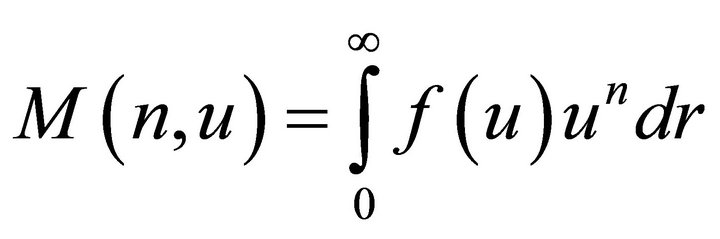 ;
;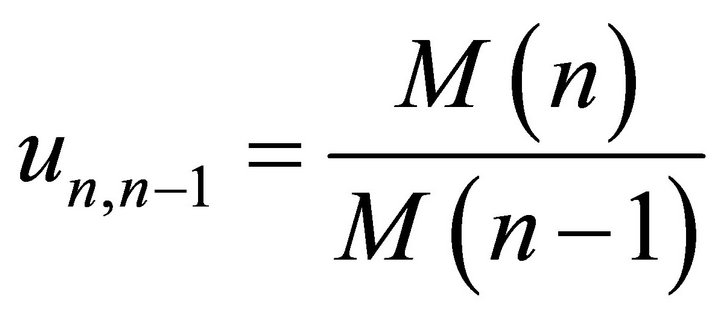 . (1s)
. (1s)
Relative Breadth
 (2s)
(2s)
Asymmetry coefficients
 . (3s)
. (3s)
Gamma-distribution described, in particular, in [22].
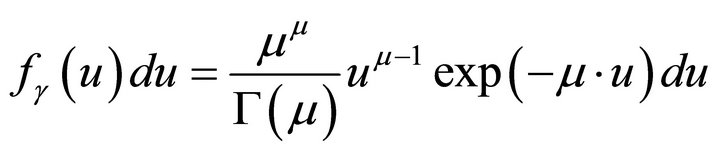 ; (4s)
; (4s)
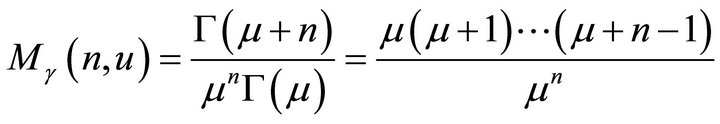 ; (4sa)
; (4sa)
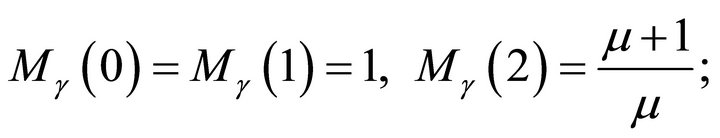 (4sb)
(4sb)
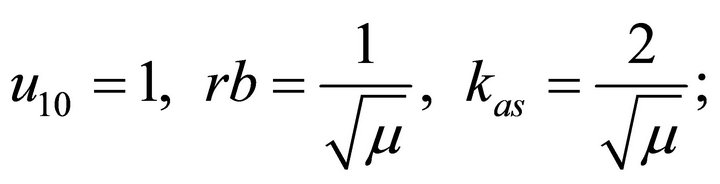 (4sc)
(4sc)
 (4sd)
(4sd)
Distribution proposed in [13] at s = 1:
 ; (5s)
; (5s)
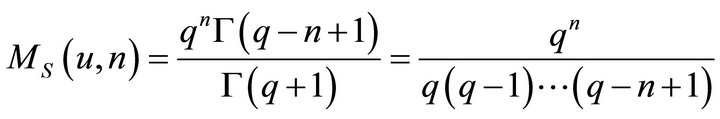 ; (5sa)
; (5sa)
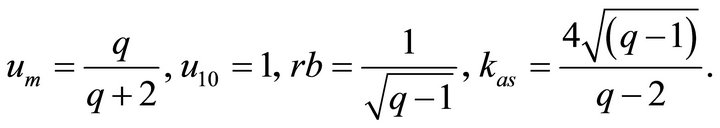 (5sb)
(5sb)
Modified gamma-distribution fmγ:
 ; (6s)
; (6s)
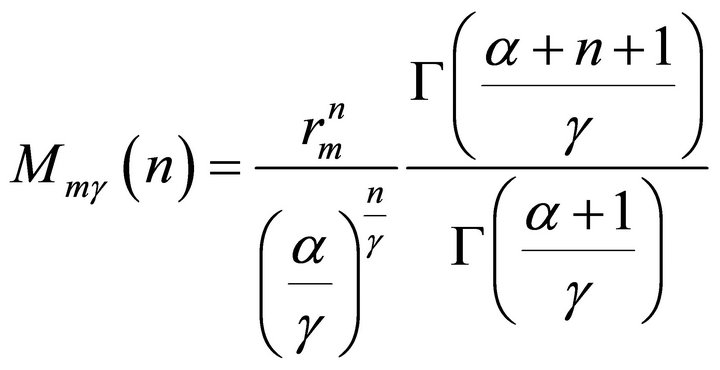 . (6sa)
. (6sa)
Direct expressions for rb and kas for this distribution are rather complex and therefore it would be better simply to calculate them with the use of moments (6sa) and expressions (2s) and (3s), correspondingly.
Let us note only two limited cases. i.e. at γ = 1 distribution (6s) reduce to similar (4s) with μ = α + 1. When γ >> α with the account for the tendency of the functions Γ(z) ≈ 1/z at z→0 for rb we obtain the following asymptotic relationship
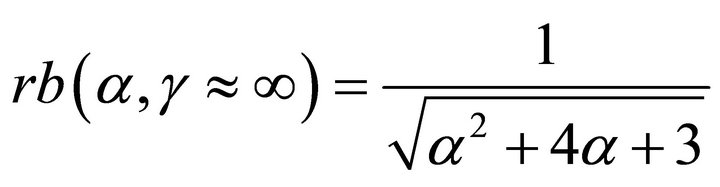 . (6sb)
. (6sb)

