International Journal of Astronomy and Astrophysics
Vol.07 No.02(2017), Article ID:77049,12 pages
10.4236/ijaa.2017.72009
The Light Curve and the Orbital Period Variations of Binary System TT Andromedae
Davood Manzoori1,2, Salar Abbasvand1, Vahid Abbasvand3,4
1Department of Physics, University of Mohaghegh Ardabili, Ardabil, Iran
2Imam Khomeini International University of Qazvin, Qazvin, Iran
3Astrophysics Department, Faculty of Physics, University of Tabriz, Tabriz, Iran
4Research Institute for Astronomy and Astrophysics of Maragha, Maragha, Iran

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 24, 2017; Accepted: June 18, 2017; Published: June 21, 2017
ABSTRACT
The first photoelectric light curve analysis of the TT And system in a broad band filter (400 - 700 nm) was carried out using the PHOEBE program. The absolute dimensions of the system are determined and its evolution is discussed. The most distinct feature of the system is a comparatively very low mass of the cooler component i.e. M2 = 0.26M⊙. Moreover, using the Observed-minus-Calculated data, the period changes of the system are studied, which reveal the presence of a third body orbiting the system with a period P3 = 63.89 yr, superimposed on which is a secular period increase, which is ascribed to mass transfer with a rate −7.60 × 10−12 M⊙ yr−1 from the cooler secondary component.
Keywords:
Binaries: Eclipsing, Stars: Evolution, Stars: Individual (TT And)

1. Introduction
The regular Algol-type (also called semi-detached) binaries are stars whose less massive component (secondary) fills its Roche lobe. One of their main characteristics is mass transfer from the Roche lobe filling secondary to the primary forming a circumprimary rotating accretion disk, due to transfer of high angular momentum material by the donor star. The magnetic activities of the secondary, X-ray flares, and variations of light, are the phenomena which make the Algols an interesting field for researchers. The mass transfer is due to the Roche lobe filling of one or both components in a binary system. In a close binary system the more massive star expands during its evolution and at some moment fills up its Roche lobe. Then a rapid mass transfer takes place on the thermal time scale [1] . The rapid mass transfer stops when the thermal equilibrium of the mass losing star is restored. The mass ratio is then more than reversed. If further evolution is such that the primary (which is now the less massive component) still fills its Roche lobe, we obtain a typical semidetached system (also called Algol-type system).
Close binary systems usually show orbital period variations in different ways. The apparent sinusoidal variations in the period are because of the presence of additional third or fourth bodies or the precession of the binary orbit due to tidal and rotational effects in its own plane. Another cause of alternating changes in rapidly rotating and possessing outer large convection zone is exchange and distribution of angular momentum between the star’s rotation and their mutual orbit [2] , so called magnetic activity cycle through Apllegate (1992) mechanism [3] . Also mass transfer/loss processes can cause none-periodic changes in orbital period. Complex variations of orbital periods of the eclipsing binaries are made by magnetic activity cycles. Hence, investigating the orbital period of eclipsing binaries based on minima times makes unprecedented information on the evolution of close binary systems.
TT And (GSC 3623.02323, RA = 23h13min23sec, Dec = 46˚08'48") is a typical short period semi detached (Algol-type) eclipsing binary composed of A0-A2 + [G7IV] stars with orbital period of 2.675d. The system was discovered in 1907, its variability was announced by Ceraski in 1913 [4] . First photographic light-curve and observations of the system was made by Nijland at the Utrecht Observatory [5] . Shapley (1913) prepared a catalogue for orbital elements of 87 binary systems including TT And [6] . The fundamental parameters of the system reported were: The orbital period, maximum magnitude, and orbital inclination angle 2.765 days, 11.30, and 85.18 degrees respectively. Then, Fetlaar (1930) analysed Nijlands unpublished light curves and reported some orbital and physical elements for 15 binary stars including TT And system [7] . Several authors ( [8] [9] [10] ) have observed the times of minima, as the minima show changes in orbital period. Wood and Forbes (1963) asserted that the orbital period of the system is changing with time [11] . To our knowledge, there exist no radial velocity curve of the system.
Erdem et al 2007 have studied period variations in five eclipsing binaries i.e. TT And, V342 Aql, RW Cap, BZ Cas and TW Lac [12] . Physical parameters of these eclipsing binaries were taken from the Catalogue of Algol-Type binary stars of Budding et al. (2004) [2] and the Catalogue of Approximate Photometric and Absolute Elements of Eclipsing Variable Stars Svechnikov and Kuznetsova (1990) [13] and are listed for TT And in their Table 1. They reported a sinusoidal variation superimposed on a parabolic form for TT And system. By deeming that the most likely cause of the sinusoidal variation could be an unseen third star in the system. The quadratic term in their results exhibits a slow rate of increasing of the orbital period at about 0.072 ± 0.007 sec per year. In addition by considering TT And as a hypothetical three-body, their computations suggest that the eclipsing pair TT And orbits around the center of mass of a three-body system with a long period of 78 ± 2 yr. In this system, the mass center of eclipsing pair lies at distance of 8.5 ± 0.7 AU from mass center of triple system. These values lead to a large mass function of f (M3) = 0.101 ± 0.021M⊙. The semi-ma- jor axis of the third-body orbit around the mass center would be accreted, when relative orbital inclination of the three-body system is equal to the orbital inclination of TT And. This increment shows that the third body revolves far beyond the outer Lagrangian points of TT And, and its orbit should be stable [12] .
The rest of the present paper is organized as follows. The analysis of light curve of TT And is described in section 2 and the analysis of O-C curve is presented in section 3. In section 4 we summarize our findings and discuss evolutionary status of the system their implications.
2. Light Curve Analysis
In the previous section, we pointed out that studies of the TT And system don’t cover all important details. So we purpose to study the properties of this system by using available photometric data. The photometric data used in this study were obtained from the Super WASP (Wide Angle Search for Planets) project which ran between 2006-2008 in a broadband filter with a passband of 400 - 700 nm (for details see [14] ). These data were reduced to phase magnitude system using the following Ephemeris from Kholopov [15] .
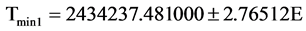 (1)
(1)
More than 5800 data points were used, few of them were omitted due to large scattering. However to carry on the LC analysis since the spectral type was reported to be A0-A2 ( [16] ) therefore we fixed the primary temperature at T1 = 9900K, and the appropriate gravity darkening (gi) and Bolometric Albedo (Ai) coefficients are selected according to the spectral types of the primary and Algol-type binaries, i.e., g1 = 1.0, A1 = 1.0 and g2 = 0.32, A2 = 0.5. The limb darkening coefficients are read from Van Hamme (1993) tables automatically by the PHOEBE program [17] . Furthermore since no spectroscopic mass ratio was available, we performed a q-search method to obtain the mass ratio (q = M2/M1). For this purpose a grid of q values (0.1, 0.2, ...) were selected, then for each value of the q the main parameters of the system i.e. Ω1 the non-dimensional surface potential of the primary, T2 effective temperature of the secondary star, i, inclination of the orbital plan, were adjusted so that to minimize the χ2 value and best fit of synthetic to observed points via visual inspections. Then we have plotted χ2/q in Figure 1, and selected the value of q corresponding to minimum χ2 as the best estimate of q = 0.110 value and used this as initial q-value. This value of q is well agreed with the value of q obtained from the empirical relation: q = 10(logL1−logL2)/3.664.
Moreover, to estimate the absolute dimensions of the system we have taken the value of the semi-major axis i.e. a = 11.6R⊙ from Erdem et al. (2007) [12] . To obtain the LC solution we used PHOEBE (PHysic of Eclipsing BinariEs) tool version 0.31a ( [18] ), which is a tool based on the Wilson and Devinney ( [19]
Figure 1. The relation between q and χ2 for TT And.
[20] ) code, for modeling of eclipsing binary stars by using photometric and spectroscopic data. Using the q and T1 as fixed parameters, the other binary main parameters Ω1, T2, i, eccentricity e, and L1, the monochromatic luminosity of the primary component were set as free parameters. Since the period analysis of the system indicated a third body orbiting around the system, therefore, in addition to the free parameters just mentioned, l3, the luminosity of the third component was also taken as a free parameter. The free parameters were adjusted sequentially by trail and error method so that to minimize the χ2 and reduce corrections to the parameters errors. Also best fit of the observatioal points to theoretical LC was inspected visually for each run of the program. We have illustrated the results of analysis in Table 1 and observed and fitted synthetic LC in Figure 2 and the residuals between the synthetic and observed LC in Figure 3. In Table 2 we have tabulated the absolute dimensions of the system obtained in this work.
3. Period Analysis
In order to study period variations of the system, the observed minus calculated (O-C) values were collected from different sources mainly from the updated O-C web page of Czech Astronomical Society. Then with help of the following linear Ephemeris all the O-C points were converted to a common Epoch.
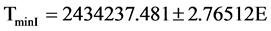 (2)
(2)
Then we have plotted the O-C residuals against Epoch cycles (E) in the Figure 4. As evident from the Figure overall trend of the O-C normal points display a distorted parabolic behavior. Hence we have fitted an upward curved parabola described by the equation: y = a + bx + cx2 through least squares method, where, a = −0.0024 ± 0.006, b = −1.08557 × 10−5 ± 6.19475 × 10−7, c = 2.47595 × 10−9 ± 2.31675 × 10−10.
Table 1. Physical and orbital parameters of TT And obtained by the LC analysis using the HOEBE code.
Figure 2. Synthetic light curve (continuous curve) and observed light curve (open circles), based on the calculated parameters in Table 1.
Figure 3. Residuals between the synthetic LC (continuous curve) and the observed SWAP data for TT And.
Table 2. Absolute physical and orbital parameters of the TT And system obtained by the LC analysis.
The residuals between the fitted parabola (i.e. continuous curve) and O-C normal points are displayed in Figure 5. However these residuals display a significant sinusoidal variations which may be fitted by a sine curve via non-linear least square fitting described by the following Eq.:
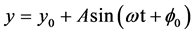 (3)
(3)
where, y0 = 0.015 ± 0.004 d, A = 0.050 ± 0.004 d, ω = 0.00024π ± 0.00001 d−1, ϕ0 = 1.476 ± 0.111 rad, and corresponding period P3 = 63.89 yr and illustrated in the Figure 5 by a continuous sine curve (see the section 4.2 for discussions and interpretations of these results).
Figure 4. Representation of the (O-C) residuals (filled squares) and its description by a upward curved parabola (continuous curve) for TT And.
Figure 5. Representation of the residuals between O-C normal point with fitted parabolic curve and their description by a sine curve for TT And.
4. Results and Discussions
4.1. Light Curve
From the light curve, the physical situation can be directly deduced. The EA light curves meaningfully divided in two groups, EAD and EAS. The EAS light curve, with its deep eclipse of an early type star, normally provides a clear indication of Algol evolution.
Reference to Figure 2 the LC of TT And system displays a typical Algol-type curve. The cooler component of the system is a low mass evolved star. Figure 6 displays Roche configuration of the system, this Fig. also confirm semidetached nature of the system the low mass secondary component has filled its Roche critical surface and is losing mass from Lagrangian L1 point. Using the Equation
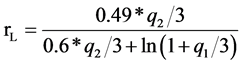 from Eggleton (1983) [21] to calculate the Roche
from Eggleton (1983) [21] to calculate the Roche
critical radius the fill out factor of secondary comes to be ~100%., however, the hotter A star has partially filled its Roche lobe. Low mass of the secondary and high temperature of the primary A-type star may suggest that the system is at the case B mass transfer evolutionary state. In the Figures 7-9 we have determined the positions of the individual components on the H-R, M-R and M-L diagrams.
Figure 6. Representation of the Roche geometry of TT And (for ϕ = 0.75) based on potentials given in Table 1.
Figure 7. H-R diagram and positions of both components of TT And.
Figure 8. M-R diagram and positions of both components of TT And.
Figure 9. M-L diagram and positions of both components of TT And.
As evident from these Figs. both of the components are evolved away from the Main Sequence (MS). This situation for the secondary (cooler component) is expected, however the hot primary shows a bit more evolved on the H-R and M-L diagrams, this may be due to inaccuracies in mass determination of the individual component. Therefore spectroscopic mass determination is need and the masses determined should be used with due caution.
The position of the secondary low mass on the M-R diagram is typical for low mass star and consistent with the departure of low mass stars from the mass radius relation.
4.2. Orbital Period Variations
Referring to Figure 4 section 3, as mentioned there is a parabolic change in the O-C diagram which implies a continuous secular increase in the orbital period of the system with a rate of dP/dt = 0.057 ± 0.005 sec/yr. This secular increase in period may be attributed to the mass transfer from the secondary to the primary with a rate of dm/dt = 7.6 × 10−12 M⊙/yr (assuming conservative mass transfer). After subtraction of the mass transfer effect (i.e. parabolic change) there is still a significant sinusoidal variation in the residual points. These residuals were depicted in the Figure 5 and best fitted by a sine curve as pointed out in section 3. Such an alternating variation in the orbital period can be attributed to the Light Travel Time Effect (LTTE) because of approaching and receding of a third mass to the eclipsing pair with a period of P3 = 63.89 yr, the mass and orbital radius of the third body can be estimated as follow: Assuming a third body with circular orbit and coplanar with the system, then we may estimate the radius of the orbit and a lower limit to the mass of the possible third body using the equations 4 below, by putting the orbital inclination of the presumed third body i3 = 90◦ and using the amplitude (A), from the Equation (3), we get (see Mayer 1990) [22] , a12 sini3 = A × c
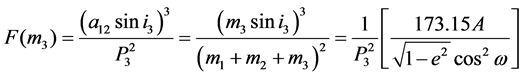 (4)
(4)
where the quantities
m1 = 2.476 M⊙, mass of the hotter component (primary), m2 = 0.272 M⊙, mass of the cooler component (secondary) e = 0, orbital eccentricity of the third body orbit based on these values the estimated mass of the possible third body m3 ≃ 1.39 ± 0.50 M⊙ and its orbital radius a3 ≃ 8.69 ± 0.54 AU.
The mass and period of the presumed third body found are in rough agreement with those of Erdem et al. (2007) [12] , i.e. 78.0 yr and 1.16 ± 2.99 M⊙.
5. Conclusion
TT And is an Algol type system. The eclipsing pair consists of a hot A-type star as primary and the cool secondary is a low mass K-type subgiant star. The period analysis reveals a mass transfer with a rate of dm/dt = 7.6 × 10−12 M⊙/yr and a third body orbiting the system with period P3 = 63.89 yr and mass m3 = 1.4 M⊙. Hence the system is a triplet system.
Acknowledgements
We have used data from the WASP public archive in this research. The WASP consortium comprises of the University of Cambridge, Keele University, University of Leicester, The Open University, The Queens University Belfast, St. Andrews University and the Isaac Newton Group. Funding for WASP comes from the consortium universities and from the UKs Science and Technology Facilities Council.
Cite this paper
Manzoori, D., Abbasvand, S. and Abbasvand, V. (2017) The Light Curve and the Orbital Period Variations of Binary System TT Andromedae. International Journal of Astronomy and Astrophysics, 7, 112-123. https://doi.org/10.4236/ijaa.2017.72009
References
- 1. Morton, D.C. (1960) Evolutionary Mass Exchange in Close Binary Systems. The Astrophysical Journal, 132, 146.
https://doi.org/10.1086/146908 - 2. Budding, E. and Demircan, O. (2007) Introduction to Astronomical Photometry. 2nd Edition, Cambridge University Press, Cambridge.
- 3. Applegate, J.H. (1992) A Mechanism for Orbital Period Modulation in Close Binaries. The Astrophysical Journal, 385, 621.
https://doi.org/10.1086/170967 - 4. Ceraski, W. (1913) Mosc. Ann. (2), 5, Kartenserie 3, GSC22. The Guide Star Catalogue, Version 2.2.01, Space Telescope Science Institute (STScI) and OsservatorioAstronomico di Torino (2001).
- 5. Nijland, A.A. (1930) The Light Curves and Orbital Elements of Fifteen Eclipsing Binary. Bulletin of the Astronomical Institutes of the Netherlands: Communications from the Observatory at Leiden, Utrecht, 6, 29.
- 6. Shapley, H. (1913) The Orbits of Eighty-Seven Eclipsing Binaries—A Summary. Astrophysical Journal, 38, 158.
https://doi.org/10.1086/142018 - 7. Fetlaar, J. (1930) Light-Curves and Orbital Elements of Fifteen Eclipsing Binaries. IBID, 6, 29.
- 8. Szafraniec, R. (1958) Minima of Eclipsing Variables Observed in 1957. Acta Astronomica, 8, 189.
- 9. Whitney, I. (1959) Minima and Periods of Eclipsing Stars. The Astronomical Journal, 64, 258.
https://doi.org/10.1086/107930 - 10. Kordylewski, K. (1963) Observed Minima of Eclipsing Variables. IBVS, 35, 1.
- 11. Wood, B.D. and Forbes, J.E. (1963) Ephemerides of Eclipsing Stars. The Astronomical Journal, 68, 257.
https://doi.org/10.1086/108949 - 12. Erdem, A., et al. (2007) First Period Analyses of Five Neglected Algol-Type Eclipsing Binaries: TT and, V342 Aql, RW Cap, BZ Cas and TW Lac. New Astronomy, 12, 613-621.
- 13. Svechnikov, M.A. and Kuznetsova, E.F. (1990) Catalogue of Approximate. Izd-vo Ural’skogo universiteta.
- 14. Butters, O.W., et al. (2010) The First WASP Public Data Release. Astronomy and Astrophysics, 520L, 10.
https://doi.org/10.1051/0004-6361/201015655 - 15. Kholopov, P.N. (1985) General Catalogue of Variable Stars. 3 Volumes, Nauka Publishing House, Moscow.
- 16. Budding, E., Erdem, A., Cicek, C., Bulut, I., Soydugan, F. and Soydugan, E. (2004) Catalogue of Algol Type Binary Stars. Astronomy and Astrophysics, 417, 263B.
https://doi.org/10.1051/0004-6361:20034135 - 17. Van Hamme, W. (1993) New Limb-Darkening Coefficients for Modeling Binary Star Light Curves. The Astronomical Journal, 106, 2096.
https://doi.org/10.1086/116788 - 18. Prsa, A. and Zwitter, T. (2005) A Computational Guide to Physics of Eclipsing Binaries. I. Demonstrations and Perspectives. The Astrophysical Journal, 628, 426.
https://doi.org/10.1086/430591 - 19. Wilson, R.E. and Devinny, E.J. (1971) Realization of Accurate Close-Binary Light Curves: Application to MR Cygni. The Astrophysical Journal, 166, 605.
https://doi.org/10.1086/150986 - 20. Van Hamme, W. and Wilson, R.E. (2003) ASP Conf. Ser. 298, GAIA.
- 21. Eggleton, P.P. (1983) Approximations to the Radii of Roche Lobes. The Astrophysical Journal, 268, 368.
https://doi.org/10.1086/160960 - 22. Mayer, P. (1990) Eclipsing Binaries with Light-Time Effect. Astronomical Institutes of Czechoslovakia, Bulletin, 41, 231-236.











