International Journal of Astronomy and Astrophysics
Vol.06 No.04(2016), Article ID:72801,15 pages
10.4236/ijaa.2016.64033
Special Relativity in Three-Dimensional Space-Time Frames
Tower Chen1, Zeon Chen2
1Retiree from Unit of Mathematical Sciences, College of Natural and Applied Sciences, University of Guam, UOG Station, Mangilao, Guam, USA
2Independent Researcher, Berkeley, California, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 5, 2016; Accepted: December 13, 2016; Published: December 16, 2016
ABSTRACT
In
Keywords:
Four-Dimensional Space-Time Frame, Three-Dimensional Space-Time, Time Contraction, Length Contraction, Lorenz Transformation, Big Bang, Multiple Big Bangs, Quantum Entanglement

1. Introduction
In order to describe the position of a static object, Descartes constructed three axes perpendicular to one another in the space using  coordinate to represent the position of this static object along x-axis, y-axis, and z-axis. The coordinate is called Cartesian frame.
coordinate to represent the position of this static object along x-axis, y-axis, and z-axis. The coordinate is called Cartesian frame.
In order to describe the position of a moving object, Galileo constructed an time axis which is perpendicular to three axes in the space, which using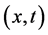 ,
,  , and
, and 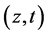 coordinate to represent the position of this moving object along x-axis, y-axis, and z-axis. Galileo combined these coordinates into the
coordinate to represent the position of this moving object along x-axis, y-axis, and z-axis. Galileo combined these coordinates into the  coordinate. This coordinate is called Galileo’s frame.
coordinate. This coordinate is called Galileo’s frame.
In order to describe the position of a moving object in Special Relativity, Minkowski constructed a time axis, ct, which is perpendicular to three axes in the space simultaneously. First, he treated space and time independently, then added a constraint:  in order to make space and time dependent. He used the
in order to make space and time dependent. He used the 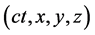 coordinate to represent the position of this moving object along x-axis, y-axis, and z-axis. This coordinate is called Minkowski’s frame.
coordinate to represent the position of this moving object along x-axis, y-axis, and z-axis. This coordinate is called Minkowski’s frame.
In order to describe the position of a moving object in Special Relativity, we construct polar coordinate for time on  plane,
plane, 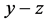 plane, and
plane, and 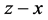 plane, because space and time are dependent. We use the
plane, because space and time are dependent. We use the 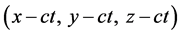 coordinate to represent the position of this moving object along x-axis, y-axis, and z-axis. The unit for the radius of polar coordinate is light-sec or period T, the unit for x-axis, y-axis, and z-axis in space is light-sec or wavelength,
coordinate to represent the position of this moving object along x-axis, y-axis, and z-axis. The unit for the radius of polar coordinate is light-sec or period T, the unit for x-axis, y-axis, and z-axis in space is light-sec or wavelength,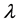 . We embed time into space directly by the velocity of light, c, which is equal to
. We embed time into space directly by the velocity of light, c, which is equal to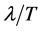 . It shows that space and time are dependent. This coordinate is called 3-d s-t frame.
. It shows that space and time are dependent. This coordinate is called 3-d s-t frame.
Theory of one Big Bang creating the universe is based on 4-d s-t frame. There are many unsolved paradoxes in this theory: Hubble’s constant should be a fixed value, but having wide range; There are two different methods to measure the distance of a quasar, but results are very different; In order to raise up the density of the universe keeping present status, there is need of dark matter; In order to explain the observation of acceleration of the universe, there is need of dark energy. The paper of “The Shell Model of the Universe: a universe generated from multiple big bangs” [1] , which is based 3-d s-t frame, was published in Research on Gravitation, Astrophysics and Cosmology Journal of Modern Physics in July 2016. This paper solves the problems raised from the standard model of the universe generated from Big Bang based on 4-d s-t frame.
Any particle’s motion in space can be described by choosing a 3-d s-t frame with the proper velocity of a medium [2] . In Special Relativity, time dilation and length contraction can be geometrically derived using two 3-d s-t inertial frames having a constant relative velocity by choosing the velocity of light as a medium. In addition, the Lorentz transformation can also be straightforwardly obtained from the result of time dilation and length contraction in 3-d s-t frames.
In order to describe the motion of micro quanta, there is uncertainty relation between its momentum and its position. When the motion of a macro object or a micro quantum is observed, the only difference between a macro object and a micro quantum is that one is visible and the other is invisible while interacting with measurement equipment. There are two uncertain measurements related to this measuring: the probability of hitting different spots which is inversely proportional to mass and velocity, and the probability of hitting either the front or the rear of the wave of the photon wave which is proportional to the wave length. The matter wavelength can be explained as the probability of uncertainty in measuring a quantum with the unit of length. The second beam of photon may hit a different spot from the first one because of the rotation of the particle. To verify the assumptions made previously, the Heisenberg uncertainty relationship can be derived by multiplying these two independent probabilities (matter wavelength of an object and light wavelength of measuring medium) [3] .
For quantum entanglement, there is a medium affecting each of a pair of particles with a velocity much faster than light, and it might be with an infinity velocity. It is against the main assumption of Special Relativity: the velocity of light is the upper limit of particle in the universe. If we locate a particle on the platform and the other particle at any distance from the platform, then the medium can be treated as the moving train. If the moving train travels with the velocity of light, the observers on the train will reach the other particle at any distance from the platform with zero second. It means that the medium will affect both particles instantly and the distance between both particles is also zero meter measured by observers. It can apply to any force between two objects including gravitational force, as long as the medium between two objects traveling with velocity of light. The proposed 3-d s-t frame shows the advantage of 3-d s-t frame [4] .
2. Construction of a 3-d s-t Frame
The motion of any particle in space can be decomposed into its x, y, and z directions. In order to describe the motion of an object in 3-dimensional space along the locations of x-axis, y-axis, and z-axis, we can construct a new space-time frame. Spheres with different radius representing different outgoing time, polar coordinates will be formed from circles of intersections between spheres and x-y plane, y-z plane, and z-x plane [4] . We are able to use the red polar coordinates of x-y plane, the blue polar coordinates of y-z plane, and the gray polar coordinates of z-x plane to describe the locations of a moving object moving along x-axis, y-axis, and z-axis. The construction of a 3-d s-t frame is shown in Figure 1. This kind of new coordinate frame embedding time axis into space axes is called three-dimensional space-time frame which saves one dimension. We won’t be puzzled by being not able to visualize four-dimensional space-time frame.
Its component along the x-axis can be described as a function of time, which is represented by the time circles created from the intersections between the x-y plane and the concentric time spheres. If the velocity of an appropriate medium is , then the radius of the sphere is
, then the radius of the sphere is 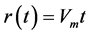 at time t. The point with the properties,
at time t. The point with the properties,
 and
and , on the x-y plane can represent the location of the particle moving along the x-axis at time t. The component of motion along the y-axis can similarly be described as a function of time, which is represented by the time circles created from the intersection between the y-z plane and the concentric time spheres. The point with the properties,
, on the x-y plane can represent the location of the particle moving along the x-axis at time t. The component of motion along the y-axis can similarly be described as a function of time, which is represented by the time circles created from the intersection between the y-z plane and the concentric time spheres. The point with the properties, 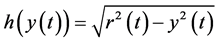 and
and

Figure 1. The construction of a 3-d s-t frame. h(x(t)) = (r2 − x2)1/2 and cosα = x/r on the x-y plane represent the location of the particle along the x-axis. h(y(t)) = (r2 − y2)1/2 and cosα = y/r on the y-z plane represent the location of the particle along the y-axis. h(z(t)) = (r2 − z2)1/2 and cosα = z/r on the z-x plane represent the location of the particle along the z-axis.
intersection between the z-x plane and the concentric time spheres The point with the properties, 

If messages are relayed by sound of Vm = 350 m/sec then the radius of the sphere representing one second is equivalent to (Vm)(1 sec) = 350 m; the radius of the sphere representing two seconds is equivalent to (Vm)(2 sec) = 700 m; …; and the radius of the sphere representing n seconds is equivalent to (Vm)(n sec) = n(350) m.
If the message is transmitted by light of Vm ~3(108) m/sec, then the radius of the sphere representing one second is equivalent to (Vm)(1 sec) = 3(108) m; the radius of the sphere representing two second is equivalent to (Vm)(2 sec) = 6(108) m; …; and the radius of the sphere representing n seconds is equivalent to (Vm)(n sec) = 3n(108) m. Since the velocity of light is the limiting velocity, all possible motions of a particle can be described using this 3-d s-t frame.
In cosmology, the expansion velocity of the universe is very high, as the recession velocities of some galaxies away from the earth are nearly 90% of the velocity of light [1] . Because all galaxies are far away from us, the interval of 1 sec would be too small to meaningfully describe their motion. The unit of time can be scaled up by choosing the light year. Hence, the radius of the sphere representing one year is equivalent to (Vm)(1 year) = 9.46(1015) m = 1ly; the radius of the sphere representing two years is equivalent to (Vm)(2 year) = 1.89(1016) m = 2ly; …; and the radius of the sphere representing n years is equivalent to (Vm)(n year) = 9.46n(1015) m = nly.
In high energy physics, if a particle’s velocity approaches the velocity of light, the interval of 1 sec would be too large to meaningfully describe its motion. The units can be scaled down by choosing the period 










The proposed new coordinate frame can also be used to describe the motion of the object moving along the x-axis in various trajectories and at different speeds using the methods described above. In Figure 2, OA represents an object remaining stationary at O; OB represents an object moving with a relatively slow, constant velocity; OC represents an object moving with a relatively fast, constant velocity; OD represents an object moving with a constant acceleration; OE represents an object moving with a constant deceleration; and FG represents an object remaining stationary at F.
A 3-d s-t frame, created by embedding time into space directly, reveals the dependency of space and time. Although the space coordinates are bi-directional, time cannot be given a negative value thus, because it only has one outgoing direction in this 3-d s-t frame.
3. Time Dilation and Length Contraction
Before describing time dilation and length contraction, we will first define some terms. If two frames have a constant relative velocity between them, two frames are called a pair of inertial frames which are inertial to each other [7] . For this discussion, we will have a train passing by a station platform at constant velocity. Theoretically, we are allowed to choose any one frame of the two frames to be the stationary (inertial) frame and the other frame to be the moving (inertial) frame. For convenience, we construct a stationary frame S on the platform and a moving frame S’ on the train.
In Figure 3, a rod is laid along the side of the station platform. There is an observer on the platform and another observer on the train and both measure the rod’s length
Figure 2. The object stays still at O by OA and at F by FG, moves with a constant slow velocity by OB, a constant fast velocity by OC, a constant acceleration by OD, a constant deceleration by OE along x-axis.
Figure 3. A stationary rod is measured by a moving train. It is laid along the side of the platform.
using a sensor attached to the front of the train, i.e. the origin O’ of the moving frame S’. The length of the rod as measured by an observer in the stationary frame S, is defined as proper length, 





At the same time the sensor touches the left end of the rod, the observer in the moving frame S’ sends a pulse of light towards the ceiling of the car, where a mirror is placed. To the observer in the moving frame S’, the light travels vertically up towards the ceiling and is then reflected vertically down. The ceiling height of the boxcar is adjustable, such that the pulse of light reaches the ceiling at the same time that the sensor reaches the right end of the rod. In Figure 4, if it takes the time 



From Figure 4, we can derived the following property for θ, where

From the previous discussion, we know that 
Figure 4.The height of the ceiling is adjustable. The pulse of light reaches the ceiling at the same time as the sensor touches the right side of the rod.







4. Geometric Lines Representing Time Dilation and Length Contraction
When an observer on the train moves to the right with velocity 
The two equations,

and

are derived from Figure 5, which imply that

The event where the sensor attached to the observer on the train moves from the left of the rod to the right of the rod can be described by two the different observers. To the observer at the origin of the moving frame S’, the event occurred at the same location, and the duration of the event is called the proper time, 




Since






5. Lorentz Transformation
In the next discussion, we designate the occurrence of an event at the coordinate x on the x-axis of a stationary frame S, by laying a rod on the x-axis from 0 to x. The proper length 
Figure 5. The geometric meaning of time dilation and the length contraction. The origin O’ moves to the right with the velocity v with respect to the origin O. l = l0 = OO’ = vt, l' = OO” = vt' = 

Figure 6. If the event happens in the coordinate x on the x-axis on the stationary frame S, then we can assume there is a rod laid on the x-axis from 0 to x.
equal to 

In order to check that the time 



on the clock on the wall at x'. When the light reaches the wall at x', the time 


both walls on the moving frame S’. In the moving frame S’, if

then the time 




on the wall at x'. When the light reaches the wall at x', the time 
be theoretically recorded on the clock on the wall at 0 because it takes extra time



recorded on the clock on the wall at x'. To observers in the stationary frame S, if

Figure 7. If the event happens in the coordinate x' on the x'-axis on the moving frame S’, then we can assume there is a box laid on the x'-axis from 0 to x'.
then the time 


in the moving frame S’. This means that the proper time is adjusted by 
the coordinate x' when the proper time is 

by 
two coordinates is

Combining all relationships between coordinates of the stationary frame S and the moving frame S’ forms the following Lorentz transformation:




In order to derive the reverse Lorentz transformation, we can construct a stationary frame S’ on the moving train, and a moving frame S on the platform which is moving to the left with respect to the train with the constant velocity 


Figure 8. If the event happens in the coordinate x' on the x'-axis on the stationary frame S’, then we can assume there is a rod laid on the x'-axis from 0 to x'.
in the moving frame S is equal to 

In order to check that the time 




on the clock on the wall at x. When the light reaches the wall at x, the time 


both walls on the moving frame S. In the moving frame S, if

then the time 




x'. When the light reaches the wall at x, the time 



the wall at x. To observers in the stationary frame S’, if

Figure 9. If the event happens in the coordinate x on the x-axis on the moving frame S, then we can assume there is a box laid on the x-axis from 0 to x.
then the time 


in the moving frame S. This means that the proper time is adjusted by 
the coordinate x when the proper time is 

by 
two coordinates is

Combining all relationships between coordinates of the moving frame S and the stationary frame S’ forms the following reverse Lorentz transformation:




6. An Example of Length Contraction and Time Dilation
Length contraction and time dilation between two inertial frames was discussed in the section IV. In the following example, we particularly select a blue light as the median to transmit message with wavelength

as the unit of length and period

as the unit of time to construct 3-d s-t frames [9] .
For a rod of length 



by length contraction.
In order to draw length into graph, we can change the unit of length from m to

and

These values with new units satisfies the formula of length contraction

It takes regular time

for the origin O’ of the moving frame S’ to pass from the left to the right ends of the rod measured by observers on the stationary frame S, thus the proper time measured from
observers on the moving frame S’ is 

formula. We can calculate the proper time

In order to draw time into graph, we change the unit of time from sec to T. Because

then

and

then

These values with new units also satisfy the length contraction equation

From Figure 10, it also shows that

then

and

Figure 10. A 3-d s-t stationary frame and a 3-d s-t moving frame λ = 5(10−7) m as the unit of length and T = 1.667(10−15) sec as the unit of time.
then

This example shows that the actual value of time dilation and the actual value of length contraction can be measured simultaneously in this 3-d s-t frame by selecting 

7. Conclusions
In classical physics, time and space are treated independently. Einstein demonstrated the inseparability of time and space. The realistic difference between time and space is the single direction of time and the two directions of space. In the proposed 3-d s-t frame, time is represented by spheres of different radii with the origin of the space axes as their center and time can only have a single direction.
In Special Relativity, two 3-d s-t inertial frames can be constructed by choosing light as a medium for transmitting messages. The geometric meaning of time dilation of an event occurring at the same location in the moving frame for an observer in the stationary frame and length contraction of a rod lying still in the stationary frame for an observer in the moving frame can be clearly illustrated in this 3-d s-t. The Lorenz transformation can also be derived from graphs of time dilation and length contraction. The universe generated from multiple big bangs based on a 3-d s-t frame solves the problems which are unsolved by the universe generated from Big Bang. Time contraction and length contraction on the moving train helps us explain quantum entanglement. These demonstrate the value of 3-d s-t frames.
Acknowledgements
We would like to thank Elizabeth Chen, Min Chou, Zen-Fu Chow, Angel Garciel, Li-Shing Hsu, Bo Liu, Yaijei Sun, Chu-Tak Tseng, Chun-Zin Wu, Lin Wu, Wan-Zin Zhaw, Yousuo Zou for their support, encouragement, suggestions.
Cite this paper
Chen, T. and Chen, Z. (2016) Special Relativity in Three- Dimensional Space-Time Frames. International Journal of Astronomy and Astrophysics, 6, 410-424. http://dx.doi.org/10.4236/ijaa.2016.64033
References
- 1. Chen, T. and Chen, Z. (2016) The Shell Model of the Universe: A Universe Generated from Multiple Big Bangs. Journal of Modern Physics, 7, 611-626.
https://doi.org/10.4236/jmp.2016.77062 - 2. Chen, T. and Chen, Z. (2005) Motions of Particles Described in a Three-Dimensional Space-Time Frame. The Proceeding of the Tenth Asian Technology Conference in Mathematics, Korea, 15-20 December 2005.
http://epatcm.any2any.us/EP/EP2005/2005P163/fullpaper.pdf - 3. Chen, T. (2006) The Heisenberg Uncertainty Relation Derived by Multiplying Matter Wavelength and Light Wavelength. Concepts of Physics, III.
http://merlin.fic.uni.lodz.pl/concepts/2006_1/2006_1_1.pdf - 4. Chen, T. and Chen, Z. (2012) The Advantage of Three-Dimensional Space-Time Frames. Frontiers in Sciences of Sciences, 2, 18-23.
http://www.sapub.org/journal/archive.aspx?journalid=1015&issueid=337 - 5. Chen, T. and Chen, Z. (2016) Time, Length, Mass Are Derived Quantities. Journal of Modern Physics, 7, No. 10.
https://doi.org/10.4236/jmp.2016.710108 - 6. Chen, T. and Chen, Z. (2016) A Bridge Connecting Classical Physics and Modern Physics. Journal of Modern Physics, 7, 1378-1387.
https://doi.org/10.4236/jmp.2016.711125 - 7. Chen, T. and Chen, Z. (2008) A Pair of Inertial Frames versus an Inertial Frame. Concepts of Physics, V, No. 3.
http://merlin.fic.uni.lodz.pl/concepts/www/V_3/523.pdf - 8. Chen, T. and Chen, Z. (2008) The Paradox of Twins Described in a Three-Dimensional Space-Time Frame. The Proceeding of the Tenth Asian Technology Conference in Mathematics, Bangkok, Thailand, 15 December 2008.
http://atcm.mathandtech.org/EP2008/papers_full/2412008_15023.pdf - 9. Chen, T. and Chen, Z. (2009) Time Dilation and Length Contraction Shown in Three-Dimensional Space-Time Frames. Concepts of Physics, VI, No. 2.
http://merlin.phys.uni.lodz.pl/concepts/www/VI_2/221.pdf











