International Journal of Astronomy and Astrophysics
Vol.05 No.04(2015), Article ID:62159,16 pages
10.4236/ijaa.2015.54031
Effect of Perturbations in Coriolis and Centrifugal Forces on the Non-Linear Stability of L4 in the Photogravitational Restricted Three Body Problem
Kavita Chauhan1, S. N. Rai2, Rajiv Aggarwal3
1Department of P. G. Department of Mathematics, V.K.S. University, Ara, India
2Department of Department of Mathematics, S.B. College, Ara, India
3Department of Mathematics, Sri Aurobindo College, University of Delhi, Delhi, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 July 2015; accepted 21 December 2015; published 24 December 2015
ABSTRACT
Effect of perturbations in Coriolis and centrifugal forces on the non-linear stability of the libration point
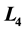 in the restricted three body problem is studied when both the primaries are axis symmetric bodies (triaxial rigid bodies) and the bigger primary is a source of radiation. Moser’s conditions are utilized in this study by employing the iterative scheme of Henrard for transforming the Hamiltonian to the Birkhoff’s normal form with the help of double D’Alembert’s series. It is found that
in the restricted three body problem is studied when both the primaries are axis symmetric bodies (triaxial rigid bodies) and the bigger primary is a source of radiation. Moser’s conditions are utilized in this study by employing the iterative scheme of Henrard for transforming the Hamiltonian to the Birkhoff’s normal form with the help of double D’Alembert’s series. It is found that
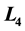 is stable for all mass ratios in the range of linear stability except for the three mass ratios
is stable for all mass ratios in the range of linear stability except for the three mass ratios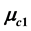 ,
,
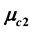 and
and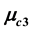 , which depend upon the perturbations
, which depend upon the perturbations
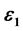 and
and
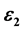 in the Coriolis and centrifugal forces respectively and the parameters
in the Coriolis and centrifugal forces respectively and the parameters
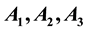 and
and
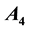 which depend upon the semi-axes
which depend upon the semi-axes
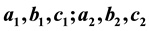 of the triaxial rigid bodies and p, the radiation parameter.
of the triaxial rigid bodies and p, the radiation parameter.
Keywords:
Restricted Three Body Problem, Axis Symmetric Bodies; Non-Linear Stability, Libration Point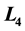 , Double D’Alembert’s Series Method
, Double D’Alembert’s Series Method

1. Introduction
We propose to study the effect of perturbations in Coriolis (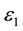 ) and centrifugal forces (
) and centrifugal forces (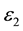 ) on the non-linear stability of libration point (
) on the non-linear stability of libration point (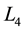 ) when both the primaries are axis symmetric bodies and the bigger primary is a source of radiation. We use Moser’s conditions by employing the iterative scheme of Henrard (Deprit and Deprit-Bartholome [1] ), for transforming the involved Hamiltonian to the Birkhoff’s normal form with the help of double D’Alembert’s series. In the year 1983, Bhatnagar and Hallan [2] investigated the perturbation effects in Coriolis and centrifugal forces in the non-linear aspect of stability of
) when both the primaries are axis symmetric bodies and the bigger primary is a source of radiation. We use Moser’s conditions by employing the iterative scheme of Henrard (Deprit and Deprit-Bartholome [1] ), for transforming the involved Hamiltonian to the Birkhoff’s normal form with the help of double D’Alembert’s series. In the year 1983, Bhatnagar and Hallan [2] investigated the perturbation effects in Coriolis and centrifugal forces in the non-linear aspect of stability of . Rajiv Aggarwal et al. [3] studied the non-linear stability of
. Rajiv Aggarwal et al. [3] studied the non-linear stability of


2. Equations of Motions and Linear Stability
We shall use dimensionless variables and adopt the notation and terminology of Szebehely [7] . The equations of motion of the infinitesimal mass


where













We adopt the method used by Bhatnagar and Hallan [2] and give perturbation in Coriolis and centrifugal forces with the help of the parameters


where
Equations of motion of mass


where
Figure 1. Configuration of the photogravitational restricted problem with both the primaries axis symmetric bodies and the bigger primary is source of radiation.
3. Location of Libration Point of L4
At
On solving above equations, we get

The Lagrangian (L) of the system of equations (1) is
Shift the origin to


where
Hamiltonian function H corresponding to above Lagrangian is given by:

where




and
To investigate the linear stability of the motion, as in Whittaker [8] , we consider the following set of linear equations in the variables x and y

where
The Equation (5) has a nonzero solution if and only if

Let the discriminant of the characteristic Equation (6) be denoted by D.
If




Let the roots of characteristic Equation (6) be

Here


We may write

by taking perturbations in the Coriolis and centrifugal forces. Here

where
4. Determination of the Normal Co-Ordinates
To express

We use the canonical transformations from the phase space (



where
Following the procedure of Bhatnagar and Hallan [2] , we get the normal form of the Hamiltonian
Taking

Equations of motion
become
The general solution of the equations of the motion is



5. Second Order Normalization
Now, to perform Birkhoff’s normalization, the coordinates (

where


The double summation over the indices i and j is such that:
1) i runs over those integers in the interval

2) j runs over those integers in the interval




where


According to Deprit and Deprit Bartholome [1] , the canonical character of the transformation will be ensured formally by requesting that the double D’Alembert series satisfy the identities
Where the left hand members stand for the Poisson’s brackets with respect to the phase variables




The values of

Proceeding as in Deprit and Deprit-Bartholome [1] , it is observed that the second order components


where


Now
where
The values of all


6. Third-Order Terms in H
Following the procedure of Bhatnagar and Hallan [2] , Hamiltonian H given by Equation (4) transforms to the Hamiltonian in which the 3rd order term in


7. Second Order Coefficient in the Frequencies
Following the iterative procedure of Henrard, the third order homogeneous components


where
The values of

The partial derivatives in the last two equations have been obtained by substituting




We find that
After simplification the values of A, B and C are given by:

The values of


8. Stability
While evaluating





We note that the inequalities (13) are violated when

Case (i)
We get
Putting these values in second of Equations (8), we get
Putting




Case (ii)
Proceeding as in case (i), we get

Hence for the value


where

Now after simplification, the determinant D occurring in condition (ii) of Moser’s theorem is given by:
That is
Substituting the values of








where
9. Conclusions
The abscissa of




With the increase of perturbation in Coriolis force, the range of linear stability increases whereas if we increase perturbation in centrifugal force, the range of stability decreases (Equation (7)).
Values of second order coefficients (







Values of


It may be observed that values of


Moser’s second condition is violated for unperturbed problem (i.e. for

It may also be observed that value of




By taking both the primaries as axis symmetric bodies and the bigger mass as a source of radiation, the triangular point

The results of Jagadish Singh [6] can be deduced by taking


All the results of Bhatnagar and Hallan [2] can be deduced by taking

Cite this paper
KavitaChauhan,S. N.Rai,RajivAggarwal, (2015) Effect of Perturbations in Coriolis and Centrifugal Forces on the Non-Linear Stability of L4 in the Photogravitational Restricted Three Body Problem. International Journal of Astronomy and Astrophysics,05,275-290. doi: 10.4236/ijaa.2015.54031
References
- 1. Deprit, A. and Deprit-Bartholome, A. (1967) Stability of the Triangular Lagrangian Points. Astronomical Journal, 72, 173-179.
http://dx.doi.org/10.1086/110213 - 2. Bhatnagar, K.B. and Hallan, P.P. (1983) The Effect of Perturbation in Coriolis and Centrifugal Forces on the Nonlinear Stability of Equilibrium Points in the Restricted Problem of Three Bodies. Celestial Mechanics, 30, 97-114.
http://dx.doi.org/10.1007/BF01231105 - 3. Aggarwal, R., Taqvi, Z.A. and Ahmad, I. (2006) Non-Linear Stability of in the Restricted Three Body Problem for radiated Axes Symmetric Primaries with Resonances. Bulletin of Astronomical Society of India, 34, 327-356.
- 4. Jain, M. and Aggarwal, R. (2015) A Study of Non-Collinear Libration Points in Restricted Three Body Problem with Stokes Drag Effect when Smaller Primary Is an Oblate Spheroid. Astrophysics and Space Science, 358, 51.
http://dx.doi.org/10.1007/s10509-015-2457-6 - 5. Kaur, B. and Aggarwal, R. (2013) Robe’s restricted Problem of 2+2 Bodies when the Bigger Primary Is a Roche Ellipsoid. Acta Astronautica, 89, 31-37.
http://dx.doi.org/10.1016/j.actaastro.2013.03.022 - 6. Singh, J. (2011) Combined Effects of Perturbations, Radiation and Oblateness on the Non-Linear Stability of Triangular Points in the R3BP. Astrophysics and Space Science, 332, 331-339.
http://dx.doi.org/10.1007/s10509-010-0546-0 - 7. Szebehely, V. (1967) Theory of Orbits. Academic Press, New York, 242-264.
- 8. Whittaker, E.T. (1965) A Treatise on the Analytical Dynamics of Particles and Rigid Bodies. Cambridge University Press, London, 427-430.
- 9. Moser, J. (1953) Periodische Losungen des restringierten Dreikorperproblems, die sich erst nach vielen umlaufen schliessen. Mathematische Annalen, 126, 325-335.
http://dx.doi.org/10.1007/BF01343166
Appendix









Values of


Values of























































































