Received 16 March 2015; accepted 8 June 2015; published 11 June 2015

ABSTRACT

The existence and stability of stationary solutions of the restricted three body problem under the effect of the dissipative force, Stokes drag, are investigated. It is observed that there exist two non collinear stationary solutions. Further, it is also found that these stationary solutions are unstable for all values of the parameters.

Keywords:

Restricted Three Body Problem, Libration Points, Linear Stability, Dissipative Forces, Stokes Drag

1. Introduction

Two finite masses, called primaries, are moving in circular orbits around their common centre of mass, and an infinitesimal mass is moving in the plane of motion of the primaries. To study the motion of the infinitesimal mass is called the restricted three body problem. [1] proved that there existed five points of equilibrium, or points of libration (often denoted by L₁, ….. L₅), which were the stationary solutions of the restricted problem. Out of them, three are collinear and two are non collinear. The collinear libration points are unstable for all values of mass parameter 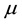and the triangular libration points are stable for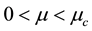, where 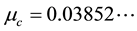is a critical value of mass parameter [2] .

As we know, dissipative forces are those where there is a loss of energy such as friction and one of the most important mechanisms of dissipation is the Stokes drag which is a force experienced by a particle moving in a gas, due to the collisions of the particle with the molecules of the gas.

[3] has determined some results on the global dynamics of the regularized restricted three body problem with dissipative forces. Their investigations have motivated us to study the motion of the restricted three body problem under dissipative forces such as Stokes drag. In the synodic frame, Stokes drag force is defined by [4] :

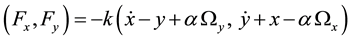
where 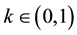is the dissipative constant, depending on several physical parameters like the viscosity of the gas, the radius and mass of the particle. Here

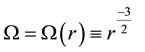
is the keplerian angular velocity at distance 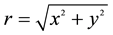from the origin of the synodic frame and 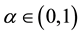is the ratio between the gas and keplerian velocities.

A number of authors have investigated the location and stability of the equilibrium point in the presence of specific dissipative forces. [5] has used the Jacobi constant to investigate the effect of an external drag force proportional to the velocity in the rotating frame and has concluded that L₄ and L₅ are unstable to this type of drag force. In their studies of the motion of dust particles in the vicinity of the Earth, [6] has analyzed the stability of the equilibrium points in the presence of radiation pressure which includes the Poynting Robertson drag terms. They have shown that the libration points are unstable to such a drag force. The effects of radiation pressure and Poynting Robertson light drag on the classical equilibrium points are analyzed by [7] and [8] . [9] has systematically discussed the dynamical effect of general drag in the planar circular restricted three body problem and has found that L₄ and L₅ are asymptotically stable with this kind of dissipation. It has been shown by [10] , [11] , [12] and [13] that, in the case of Stokes drags, exterior resonances may compensate the decrease of the semi major axis and that stationary solutions still exist. A numerical analysis of 1:1 resonance, taking into account the effect of the inclination and the eccentricity, has been studied by [14] . An analytical study of the linearised stability of L₄ and L₅ is provided in [4] .

Furthermore, [15] has examined the linear stability of triangular equilibrium points in the generalized photo gravitational restricted three body problem with Poynting Robertson drag. They have considered the smaller primary as an oblate body and bigger one as radiating and they have concluded that the triangular equilibrium points are unstable in linear sense. [16] has discussed the nonlinear stability in the generalized restricted three body problem with Poynting Robertson drag considering smaller primary as an oblate body and bigger one radiating. They have proved that the triangular points are stable in nonlinear sense. [17] has discussed the stability of triangular equilibrium points in photo gravitational circular restricted three body problem with Poynting Robertson drag and a smaller triaxial primary. They proved that the parameters involved in the problem (radiation pressure, oblateness and Poynting Robertson drag) influenced the position and linear stability of triangular points. In the presence of Poynting Robertson drag, triangular points are unstable, and in the absence of Poynting Robertson drag, these points are conditionally stable. In a series of papers, [18] has performed an analysis in the restricted three body problem with Poynting Robertson drag effect. They found that there existed two noncollinear stationary solutions which were linearly unstable.

In the present paper, we study the same problem but with the effects of stokes drag instead Poynting Robertson drag on noncollinear libration points L₄ and L₅ in the restricted three body problem.

2. Equations of Motion

Suppose 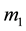and 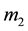are the primaries revolving with angular velocity n in circular orbits about their centre of mass O, an infinitesimal mass 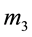is moving in the plane of motion of 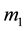and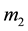. The line joining 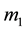and 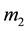is taken as X-axis and “O” their center of mass as origin and the line passing through O and perpendicular to OX and lying in the plane of motion of 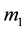and is the Y-axis. We consider a synodic system of coordinates O (xyz); initially coincident with the inertial system O (XYZ), rotating with the angular velocity n about Z-axis; (the z-axis is coincident with Z-axis) (Figure 1).

In the synodic axes the equation of motion of in the restricted three body problem with Stokes drag S is

(1)

where

= Gravitational Force acting on due to

= Gravitational Force acting on due to

= Stokes drags Force acting on due to along.

Its components along the synodic axes (x, y) are and

where

Angular velocity of the axes = const.

The equations of motion of in Cartesian coordinates (x, y) are

,

where

n = Mean motion, G = Gravitational constant,

and = coordinates of A and B in the synodic system.

Using [2] terminology, the distance between primaries is unchanged and same is taken equal to one; the sum of the masses of the primaries is also taken as one. The unit of time is chosen so as to make the gravitational constant unity. The equations of motion of the infinitesimal mass in the synodic coordinate system (x, y) and dimensionless variables are

(2)

(3)

where

(4)

(5)

The Stokes drag effect is of the order of (generally and as stated in the introduction).

3. Stationary Solutions (Libration Points)

The solutions (x, y) of Equations (2) and (3) with are given by

(6)

and

. (7)

Here, if we take, then it will be the classical case of the restricted three body problem and the solutions of these equations are just the five classical Lagrangian equilibrium points L_i (i = 1, 2, 3, 4, 5). The L_i (i = 1, 2, 3) are three collinear libration points which lie along the x-axis and L_i (i = 4, 5) are the two non collinear libration points which make the equilateral triangles with the primaries. Due to the presence of the Stokes drag force, it is clear from Equations (6) and (7) that collinear equilibrium solution does not exist. Since there is a possibility of non collinear libration points under the effect of drag forces, so we restrict our analysis to these points. Their locations when, are (see, e.g., [19] )

.

Now, we suppose that the solution of Equations (6) and (7) when and are given by

Making the above substitutions in Equations (6) and (7), and applying Taylors series expansion around the libration points by using that is a solution of these equations when, we can get a linear set of equations.

(8)

and

(9)

After substituting the values of the constants and in the above equations and rejecting the second and higher order terms in and, we get the values of and as

Hence, putting the values of and, the displaced equilibrium points are given by

(10)

Here, the shifts in L₄ and L₅ are of. If we calculate numerically, taking for different values of, we find that while using Stokes drag, as far as the values of increase corresponding values decrease and the values increase.

4. Stability of L_{4, 5}

We write the variational equations by putting and, , , in the equations of motion (2) and (3), where are the coordinates of the libration point. Therefore, expanding and by Taylors Theorem, we get

(11)

(12)

Let us consider the trial solution of Equations (11) and (12),

where and are constants and is a complex constant. Then we have

(13)

(14)

Now, from Equations (13) and (14), we derive the following simultaneous linear equations

(15)

and

(16)

The simultaneous linear Equations (15) and (16) can be written as

(17)

(18)

where

(19)

(20)

(21)

(22)

and

(23)

Neglecting terms of, the condition for the determinant of the linear equations defined by the Equations (17) and (18) to be zero is

(24)

This quadratic Equation (24) has the general form

(25)

where

Here, and can be derived by evaluating e, f, g and h defined earlier. The value of the coefficient in the zero drag case is denoted by adding additional subscript 0. If we neglect product of powers of with any of the constants defined in Equation (23), we obtain

(26)

By assuming to be small, we investigate the stability of the non zero drag case. We can use the classical solutions of the zero drag case (i.e. when k = 0). Equation (25) reduces to

(27)

The four classical solutions for L₄ and L₅ to are given by the pair of values

(28)

Since we are primarily interested in the stability of L₄ and L₅ under the effects of a drag force, we restrict our analysis to these points. The four roots of the classical characteristic equation can be written as

(29)

where

(30)

is a real quantity for L₄ and L₅. Using the values of and given in Equations (26) we have

(31)

With the introduction of drag we assume a solution of the form

(32)

where and are small real quantities. To lowest order we have

(33)

(34)

(35)

Substituting these in Equation (25), and neglecting products of or with, and solving the real and imaginary parts of the resulting simultaneous equations for or we get

(36)

(37)

(i) The stability of

For, we have

(38)

(39)

On putting the values of, in Equations (38) and (39) from Equation (26) and also taking, , we have

Now, putting these values of and in Equation (35), and neglecting the terms of, we get the characteristic equation as

whose roots are

Also on taking in Equations (38) and (39) from Equation (26), we get the characteristic equation as

whose roots are

If

According to [9] , the resulting motion of a particle is asymptotically stable only when all the real parts of are negative and the condition for asymptotically stable under the arbitrary drag force is given by

(40)

where and are defined in Equation (26). But we see that the linear stability of triangular equilibrium points does not depend on the value of and. Therefore the condition can only be satisfied when k is positive and the drag force is a function of and.

But here in our case of Stokes drag and therefore and hence L₄ is not asymptotically stable. Further one of the roots of i.e. has positive real root. Therefore L₄ is not stable. Thus we conclude that L₄ is neither stable nor asymptotically stable and hence linearly unstable.

Similarly, we conclude that is neither stable nor asymptotically stable and hence linearly unstable.

5. Conclusions

We have studied the existence of the triangular libration points and their linear stability by using Stokes drag. We have shown that there exist two noncollinear stationary points and (Equation (10)). If we put, these results agree with the classical restricted three body problem.

In the classical case i.e. when, we observe that as the value of increases, the abscissa of decreases and the ordinate of remains constant, while in our case (i.e. Stokes drag), when, we observe that the abscissa of decreases and the ordinate of changes slightly. In our previous paper ( [18] ) i.e. in the case of Poynting Robertson drag, the abscissa and the ordinate decrease with. As regards, the stability of in both the cases (Poynting Robertson drag and Stokes drag) is always unstable for all values of. The result of stability is quite different when we compare with the classical case. In the classical case, is stable for, whereas in the case of drag forces, motion is unstable for all values of.

In the case of Stokes drag, we have derived a set of linear equations in terms of and (Equations (17) and (18)), which involve the components of the Stokes drag force evaluated at the libration points (Equations (19)-(23)). From these, we derive a characteristic equation having the general form (Equation (25)).

Further, we have derived the approximate expressions for and occurring in the above characteristic equation. These expressions are given in terms of the partial derivatives of the Stokes drag, evaluated at the libration points.

Using the [9] terminology, in the case of drag force, we assume a solution of the form (Equation (32)), where and are small real quantities and

is a real quantity for L₄ and L₅ in the classical case. After substituting the values of, , and in the characteristic equation, we get the values of and (Equations (36) and (37)).

Further to investigate the stability of the shifted points, by using [9] terminology, the resulting motion of a particle is asymptotically stable only when all the real parts of are negative. Also, the condition for asymptotical stability under the drag force is given by Equation (40).

The condition can only be satisfied when k > 0. In the case of Stokes drag and, Equation (40) is not satisfied. Therefore, L₄ and L₅ are not asymptotically stable. Further, we have seen that one of the roots of i.e. has positive real root; thus, L₄ and L₅ are not stable. Hence, due to Stokes drag, L₄ and L₅ are neither stable nor asymptotically stable but unstable whereas in the classical case L₄ and L₅ are stable for the mass ratio [19] .

References