International Journal of Astronomy and Astrophysics
Vol.05 No.01(2015), Article ID:54871,9 pages
10.4236/ijaa.2015.51005
Diurnal Variations and Spikes by the Torsind Registered and Their Impact on the Accuracy of G Measurement
A. F. Pugach
Main Astronomical Observatory of the NASU, Kiev, Ukraine
Email: pugach@yandex.ru, pugach@mao.kiev.ua
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 March 2015; accepted 17 March 2015; published 20 March 2015
ABSTRACT
The article reports on the results of an analysis of the torsind behavior long-term observations. The torsind is a species of ultralight disc torsion balance. The data analysis showed that the signal recorded contains the 24-hour periodic component presumably associated with the Sun. More- over, unpredictable strong impacts, forcing torsind disk to rotate in one or another direction, were revealed. Presumably the reason of these effects is the Sun. This indicates the existence of an unknown radiation that bears a torque which may impact on the mechanical systems dynamics. This fact leads to the need to measure the gravitational constant G overnight and during periods of minimum of the solar activity, provided that the G measurements are carried out using a torsion balance.
Keywords:
Torsion Indicator, Torsind Measurements, Gravitational Constant G

1. Introduction
American scientists E. Saxl and M. Allen were observing diurnal variations of the period of a massive torsion pendulum over the 16-day interval starting on September 20, 1979 and terminating on October 5, 1979 [1] . The pendulum regularly speeded up by approximately 1 part in 6000 shortly before or after local noon. That process was quite regular, implying a connection with the circadian rhythm of the Sun.
Since the observation lasted 15 days, the length of a resulting series of the measurements was large enough to get a statistically significant conclusion about the reality of the periodic variations. Minimum of the readings always come near to noon, from which it was concluded that the 24-hour variability of the signal exists.
This finding has long remained unknown to the general physical community, despite the fact that the measurements were done by well-known experts, and the measurements themselves were carried out methodically correctly (for details, see [2] pp. 127-137).
It is fair to say that E. Saxl and M. Allen were not the first in this issue. Similar diurnal variations were studied in the first half of the twentieth century yet. The French astronomer of Russian origin N.M. Stoyko tracked diurnal oscillations of a vertical pendulum and published his results in [3] .
However, even these studies can not be considered as pioneering ones, since long before that the daily fluctuations of a torsion pendulum were first reported by N.P. Myshkin―a professor of the Novo Alexandria Institute. For many years he had been studying an effect of heat and light on rotation of a horizontally suspended mica disk. In 1898 he came to the conclusion that “the fluctuations are in some connection with the position of the Sun relative to horizon” [4] . After that he was trying to find out “whether these vibrations of the system have not only daily, but the annual periodicity?” [4] .
Thus, the history of study of the diurnal variations of a torsion pendulum has more than a century. However, the very small amplitude of these oscillations and significant impact on the behavior of pendulums both the researcher and environmental conditions made it difficult to study. Therefore, these works had more reconnaissance rather than deep exploratory mode.
New possibilities for the study of this delicate phenomenon appeared recently in connection with the use of the torsind [5] and appropriate methods of analysis.
2. Brief Description of the Torsind and Methods of Observation
The torsind―torsion indicator―is a specific type of torsion balance that uses a very light metal or paper disc instead of the linear beam of a classical unit, suspended from a monofilament made from natural silk, instead of quartz or a rigid suspension [5] . A specific feature of this thread allows the device disk to make a lot of revolutions on its axis without accumulation of reverse torque in the thread itself. In other words, if the torsind disc, being influenced with an external torque, slowly makes several revolutions then after the termination of the torque it retains at the last position having no backspin. This surprising property of a silk thread is due to its specific molecular structure. The basis of a thread are fibroin protein molecules, substances even stronger than Kevlar. Repetitive amino acid sequences of this protein form antiparallel pleated β-layers which are connected to each other by hydrogen bonds. These bonds are not very strong and allow for moderate mechanical offsetting of the layers. This explains the fact that under slow (necessarily slow!) rotation the layers can slide relative to each other. Moreover, it does not reduce the mechanical strength of the thread. The housing of the torsind is made from a quartz cylinder.
A web-camera monitors the disc rotation. The webcam is mounted above the upper face of the cylinder and is connected to a computer.
The design of such a balance makes it insensitive to variations in gravitational potential and ensures that it is unaffected by gravitational (tidal) influences from any direction
The instrument can not measure a force, but indicates the direction of the applied torque only. The low weight of the suspended unit (the aluminum disk mass does not exceed 100 mg) provide high sensitivity of the device. The device is clearly responds to a torque:
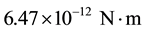
It should be added that the torsind is equipped with an automatic registration system and its continuous ope- ration does not require the presence of an operator. Since mid-2009 the torsind has been sited at the Main Astronomical Observatory (Kiev, Ukraine) in an isolated, shaded room with tightly closed doors and windows, the entrance being barred to outsiders.
A detailed description of the instrument and its properties, identified for several years of our examination, is published in [5] .
From this description it follows that the torsind does not respond to changes in:
・ gravitation potential;
・ temperature of the device itself;
・ meteorological parameters (pressure, humidity);
・ static electric field during a thunderstorm;
・ moderate magnetic field;
・ degree of ionization of the ionosphere;
・ operation of electromechanical units;
・ change in the load on the torsind thread;
・ possible microvibration of the floor;
・ sound waves of moderate intensity;
・ radio waves and cell phones.
Possible weak convective air movement inside the torsind housing can also not be a source of significant interference.
On the other hand, torsind responds to some astronomical phenomena under such unusual circumstances, when other astrophysical instruments are powerless. For example, torsind “sees” a solar eclipse, which occurs on the opposite side of the globe [6] [7] . Moreover, torsind reacts to some syzygy effects, being underground at a depth of 40 meters [8] .
The torsind ability to respond to some planetary configuration is truly surprising. For example, in June 2012, there was the transit of the planet Venus across the sun’s disk. This phenomenon has been recorded with two devices shown qualitatively similar picture (see [5] , Figure 10). It should be noted here that at the time of the transit the Venus was at a distance of 42 million km from the Earth. This fact has been reliably recorded, but it lacks any solid explanation. Thus, the torsind disk rotation seems to have a much deeper cause than the osten- sible reasons (changes in temperature, pressure, etc.).
The measurement accuracy defined 13.02.2013 under a stable space weather is characterized by the standard error (se) of a single measurement of:
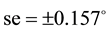 .
.
Thus, the torsind as a unique instrument simultaneously combines two qualitatively opposite features. On the one hand, the torsind operation is not influenced by many external circumstances which seem to be strong noise- producing factors for many other scientific instruments. On the other hand, torsind can register some events, not be observed with other devices.
Using this specific torsind’s features allowed us for several years to observe periodic changes in signals registered that we previously called “the diurnal variations”.
3. Observational Material
We did not plan to observe the diurnal variations as an independent scientific task. It is a specific “by product” of our long-term monitoring of the torsind reactions. All discussed observations were performed using the torsind WEB_1. These observations contained some fragments where repeatable mode of records was present.
One of the most spectacular manifestation of the diurnal variations was registered in June, 2013 (see Figure 1). That short fragment clearly shows the daily periodicity.
The followings are the observations when stable periodic oscillations were present in their “pure” form with- out significant interference for a long time. Thus, Figure 2 shows a record of relatively stable oscillations, when the torsind counts at night time during 8 days almost did not change, however during daytime counts increased by about 14 - 25 degrees.
Figure 3 shows the diurnal changes which are superimposed on variable background substrate. Moreover, the amplitude of the variations varies by almost an order. These data prompted us to more thoroughly analyze all the available observations in order to confirm the reality of diurnal variations and determine their exact period. The autocorrelation analysis method was used as an adequate one for this task.
4. Determination of the Period of the Diurnal Variation
We have analyzed the least noisy series of observations where the varying signal was more regular in appea- rance, including the short sequences shown on the above figures. That is, the most plain observations were chosen, including no other processes with large amplitudes.
That fact that torsind registers diurnal fluctuations is not in doubt. The question remains open: is it solar or sidereal day. The autocorrelation analysis (ACA) method was used to accurately determine the period of the diurnal variation. Several observations which were made at the moments of quiet space weather, when there
Figure 1. One of the results with the records of the diurnal variations.
Figure 2. Sustained diurnal variations in February 2009.
Figure 3. Periodic variations of alternating amplitude with a marked trend in 2010.
were no spikes, significant astro-space phenomena or other strong influences, were chosen for the analysis. In these periods of the observation the most significant signals were the same daily fluctuations. All autocorrelation functions obtained for these series have a form similar to that shown in Figure 4.
The average values of the periods were drawn from the first six partitive maxima for each individual obser- vation series. The resulting values of the periods (in minutes) are presented in the last column of Table 1. For all of these data the general average value of the period 1440.24 ± 2.69 minutes was obtained.
Figure 4. The partitive maxima of the autocorrelation function follow by exactly 1 day.
Table 1. Observational series used and result.
N―quantity of individual counts in a series.
Thus, the results of ACA clearly indicate that the daily variations are modulated by the Sun, rather than the other sources (the galaxy core, the Moon, star sources, planets, etc.).
5. The So-Called “T-Momentum”
As a result of the analysis performed, it was found that in almost all cases there is the periodic signal which is close to 24 hours. This conclusion is valid in cases when it was possible to carry out the long-term continuous monitoring in quiet space weather conditions. What does “non-quiet” space weather mean will be mentioned further down.
On the basis of our visual assessment and taking into account the results of the preliminary analysis, we estimate the amplitude of the periodic component in range of 20 - 50 degrees. It is important to note that the 24-hour periodic component manifests itself in different seasons of the year, which is likely to indicate its constant presence.
We do not consider a reason which forces the torsind disk to rotate. At the present stage of research this problem seems to be premature, since a carrier that transmits torque on the unit is not known yet. A purpose of this publication is to draw the attention of researchers on the fact of the periodic rotation of the torsind disk in different directions. This fact indicates the presence of an unknown torque, affecting the state of the mechanical system. Let’s call it conditionally “Torsind-momentum” or “T-momentum”.
The detection of periodic torsind oscillations proposes a certain scientific interest because it indicates a new, unexplained phenomenon. But that’s not all. We are clear aware that intermittent heteropolar torque can affect the readings of torsion balances, which are still used in the determination of the Newtonian gravitational con- stant G. According to small statistics given by S. Shlamminger [9] -[11] about two-thirds of all works on measur- ing of G are based on the use of torsion balances. This means that two-thirds of all measurement results have been in some extend distorted by the presence of the unaccounted T-momentum.
This circumstance may perhaps explain why universal constant G is measured so far with a rather large error, and the accuracy of its determination is by several orders of magnitude lower than the accuracy of the deter- mination of other universal constants. At the moment there is no possibility to calculate the impact of the T-momentum very accurate. However, if we look at Figure 2, Figure 3 and Figure 4 it becomes clear that extreme perturbing effect manifests itself in the middle of the day, close to local noon.
In reading the recent history of the G measurement the apparent contradiction between the increased measure- ment accuracy and the decrease in the accuracy of the final result becomes obvious. For example we refer to recent measurements of G performed by two teams: the Franco-British [12] and Chinese [13] . Having reached the accuracy of the G determination in each of its methods at 26 - 27 ppm, they have, nevertheless, got results that differed by an amount that was almost an order of magnitude higher than the standard error of each method. We can offer an explanation for this discrepancy based on our long-term torsind observations.
6. Spikes
The fact that the torsind responds well to syzygies [7] , solar and lunar eclipses [6] [8] [14] , Venus’ transit [5] and other astronomical phenomena has been defined reliably. However besides the torsind very often registers strong bursts, responding to some unknown astro-space phenomena. At these moments the torsind disk can make 5, 10, 20 or more revolutions in a row. Such a sharp reaction of the torsind we will conventionally call SPIKE.
Figure 5 shows one spike recorded by the torsind on 2-3 of May, 2013. Within 18 hours the torsind disk made 6 revolutions clockwise, and then it began to rotate in the opposite direction, making 8 full revolutions more.
Apparently, at this time a strong rotational momentum has sprung up, carrying a right- and then a left-screw torques. Evidently, a G measurement, being performed elsewhere in any other laboratory with a torsion balance at the same time, could be distorted by the additional torque. And besides, the sign of the perturbation would depend on what a branch of the spike (ascending or descending) was active during the measurement process. Of course, this statement is true under the assumption that the sphere of the spike action covers the entire Earth. The fact that torsind feels syzygy effects, even when deep underground, is the basis for this assumption [7] [8] .
A double spike―is a spike when the disc rotation in one direction is immediately replaced by rotation in the opposite direction. They are relatively rare. More often there are cases when the torsind disc turns round several hundreds or thousands of degrees then ceases its rotation and stops.
Figure 5. The double strong spike recorded on 2-3 May 2013.
Figure 6 shows the torsind reaction in the summer of 2010. Here there are weak double negative spike recorded on July 15 and a small single positive spike at night on July 2-3, and a small single negative spike on July 27. It should be noted that in this case the amplitudes of the spikes were rather small, so the diurnal variations of low amplitude are readily traced throughout the curve.
The nature and the mode of the spike appearances were not understood yet, but it was noted that the spikes began to appear more and more frequently in recent years. This was established as follows.
The regular torsind observations were conducting over the last several years. Each series of daily measure- ments was considered as a random sequence, and the standard deviations SD were calculated for it. Figure 7 illustrates how the value of SD changed over time.
We believe that the large SD values are conditioned namely by the spikes so far as the diurnal variations and the syzygy effects have not large amplitudes.
It should be noted that the Figure 7 shows the statistical parameter D only, rather than the amplitudes of the spike. But even this parameter as we see clearly reflects the increased spike activity.
7. Discussion
Based on the foregoing, it follows that the processing of the G measurement results must take into account the
Figure 6. The result of the continuous observations in June-August 2010.
Figure 7. Change in the parameter SD over time.
possible influence of the diurnal variations, and especially of the spikes.
More than 20 years ago in the publication [15] dedicated to finding the cause of significant variation of the measured values of G, the following was stated.
“Analysis of measurement results of the gravitational constant shows that they are associated with a variety of space and geophysical phenomena. It is reasonable to assume that this analysis reveals some unrecorded by researchers factors that directly or indirectly affect the measurement results rather than the change in the physical parameter―the gravitational constant G. The perennial search for these factors ... has not been successful”.
We believe that we have managed to identify one of the possible factors that is periodically or randomly affecting the beam position of a torsion balance, which is used for the measuring of G.
It is effect of the above mentioned T-momentum. The nature of its effect is not known, but it is obvious that it can be considered as an unknown field or pulse carrying a torque that can influence the dynamic of a mechanical system. The torque of such exposure is extremely small.
The torsind disc, with a sensitivity at least of 6.47 × 10−12 N∙m rotates with an angular velocity of no more than 0.01˚ per second in the most cases. But even such a low impact must be considered. Especially it is necessary to take into account the effect of strong spikes when the angular velocity of the disk rotation reaches 1˚/s. According to our preliminary estimates the T-momentum imparts to the torsind disk the left-screw rotation in the most cases.
We propose an idea of the key experiment to verify our hypothesis. If the suspected T-momentum does have an impact on the behavior of the torsion balance, then instrumentation counts should deviate compared to the true (unperturbed) readings during spike-activity. Sign of the deviation depends on the direction of torque (left- or right-handed).
In Table 2, we present the complete list of all spikes recorded in early 2012, when the spike activity was very high (see Figure 7). The table shows the precise times of start and end of the spikes, their amplitude and direction of the T-momentum―a right-handed (+) or left-handed (−).
If measurements of G have been somewhere conducted in January 2012, the staff of that laboratory may use the data in Table 2 for adequate analysis in order to assess whether there were large deviations in the results of their measurements. This key experiment should clearly answer the question whether there is the influence of spikes on the measurement result.
For the full understanding we give a graph of the continuous torsind record made in January 2012 (Figure 8). The graph helps to understand at what time and in what direction the T-momentum was. The spikes listed in Table 2 can be easily detected in this graph.
Table 2. Spike activity within January, 2012.
Figure 8. Continuous recording in January, 2012.
8. Conclusions
We hope that clarification of the G value will be significantly improved if the gravimetric measurements should be conducted at night time provided there is no spike activity. Since the spike activity increases with the increas- ing of the solar activity [10] , then for the reliable measurements of G, some quiet periods at minimum 11-year solar cycle should be chosen.
And the most important, the gravilaboratories where the measurements of G are carrying out must be equipped with sensitive instruments like the torsion indicator.
Such instruments should allow conducting continuous monitoring of the environment situation for the selec- tion of suitable working hours, when there is no spike activity.
Cite this paper
A. F.Pugach, (2015) Diurnal Variations and Spikes by the Torsind Registered and Their Impact on the Accuracy of G Measurement。 International Journal of Astronomy and Astrophysics,05,28-37. doi: 10.4236/ijaa.2015.51005
References
- 1. Saxl, E.J. and Allen, M. (1971) 1970 Solar Eclipse as “Seen” by a Torsion Pendulum. Physical Review D, 3, 823-825.
http://dx.doi.org/10.1103/PhysRevD.3.823 - 2. Munera, H.A. (Ed.) (2011) Should the Laws of Gravitation Be Reconsidered? Apeiron, Montreal, 448 p.
- 3. Stoyko, N.M. (1947) Sur la variation jouraliere de la marche des pendules et de la deviation de la verticale. Acad. Sci. Comptes, Rendus., Paris, 224, 1440-1441.
- 4. Myshkin, N.P. (1906) The Movement of a Body in the Flow of Radiant Energy. Russian Journal of Physical and Chemical Society, 3, 151-184. (In Russian)
- 5. Pugach, A.F. (2013) The Torsind—A Device Based on a New Principle for Non-Conventional Astronomical Observations. International Journal of Astronomy and Astrophysics, 3, 33-38.
http://dx.doi.org/10.4236/ijaa.2013.32A006 - 6. Pugach, A.F. (2009) Observations of the Astronomical Phenomena by Torsion Balances. Physics of Consciousness and Life, Cosmology and Astrophysics, 9, 30-51.
- 7. Olenici, D., Pugach, A.F., Cosovanu, I., Lesanu1, C., Deloly, J.-B., Vorobyov, D., Delets, A. and Olenici-Craciunescu, S.-B. (2014) Syzygy Effects Studies Performed Simultaneously with Foucault Pendulums and Torsinds during the Solar Eclipses of 13 November 2012 and 10 May 2013. International Journal of Astronomy and Astrophysics, 4, 39-53.
http://dx.doi.org/10.4236/ijaa.2014.41006 - 8. Olenici, D. and Pugach, A.F. (2012) Precise Underground Observations of the Partial Solar Eclipse of 1 June 2011 Using a Foucault Pendulum and a Very Light Torsion Balance. International Journal of Astronomy and Astrophysics, 2, 204-209.
http://dx.doi.org/10.4236/ijaa.2012.24026 - 9. Pugach, A.F. (2011) Is the Maurice Аllais’s Effect Exclusively Gravitational in Nature? In: Munera, H., Ed., Should the Laws of Gravitation Be Reconsidered? Apeiron, Montreal, 257-264.
- 10. Pugach, A.F. (2013) Torsind as a Recorder of a Possibly New Energy. Thermal Energy and Power Engineering, 2, 129-133.
www.vkingpub.com/tepe - 11. Schlamminger, S. (2013) The Measurement of Newton’s Constant of Gravitation.
http://www.schlammi.com/ri_g.html - 12. Quinn, T., Parks, H, Speake, C. and Davis, R. (2013) Improved Determination of G Using Two Methods. Physical Review Letters, 111, Article ID: 101102.
http://dx.doi.org/10.1103/PhysRevLett.111.101102 - 13. Luo, J., Liu, Q., Tu, L.-C., et al. (2009) Determination of the Newtonian Gravitational Constant G with Time-of-Swing Method. Physical Review Letters, 102, Article ID: 240801.
http://dx.doi.org/10.1103/PhysRevLett.102.240801 - 14. Pugach, A.F. and Olenici, D. (2012) Observations of Correlated Behavior of Two Light Torsion Balances and a Paraconical Pendulum in Separate Locations during the Solar Eclipse of January 26th, 2009. Advances in Astronomy, 2012, Article ID: 263818.
http://dx.doi.org/10.1155/2012/263818 - 15. Izmailov, V.P., Karagioz, O.V., Kuznetsov, V.A., et al. (1993) Temporal and Spatial Variations of the Measured Values of the Gravitational Constant. Measurement Techniques, 36, 1065-1069.
http://dx.doi.org/10.1007/BF00979446










