International Journal of Astronomy and Astrophysics
Vol.4 No.2(2014), Article ID:46306,6 pages DOI:10.4236/ijaa.2014.42030
The Relativistic Three-Dimensional Evolution of SN 1987A
Lorenzo Zaninetti
Dipartimento di Fisica, Turin, Italy
Email: zaninetti@ph.unito.it
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 11 April 2014; revised 10 May 2014; accepted 17 May 2014
ABSTRACT
The high velocities observed in supernovae require a relativistic treatment for the equation of motion in the presence of gradients in the density of the interstellar medium. The adopted theory is that of the thin layer approximation. The chosen medium is auto-gravitating with respect to an equatorial plane. The differential equation which governs the relativistic conservation of momentum is solved numerically and by recursion. The asymmetric field of relativistic velocities as well the time dilation is plotted at the age of 1 yr for SN 1987A.
Keywords:Supernovae, General Supernovae, Individual (SN 1987A) ISM, Supernova Remnants

1. Introduction
The expansion velocities in supernovae (SN) are quite high and, for example, a time series of eight spectra in SN 2009ig reported that the velocity at the CA II line, decreased from 32,000 km∙s−1 to 21,500 km∙s−1, in 12 days, see Figure 9 in [1] . Another example is given by SN 2009bb in which the velocity of expansion has been evaluated to be ≈255,000 km∙s−1, see [2] .
We briefly recall that the corrections in special relativity (SR) for stable atomic clocks in satellites of the Global Positioning System (GPS) are applied to satellites which are moving at a velocity of ≈3.87 km∙s−1. The problem of the aspherical SN, such as SN 1987A, is to find an acceptable model which can reproduce the observed complex morphology of the aspherical SN 1987A and this was done in a classical framework by [3] . In this paper, we shall discuss a relativistic treatment of the thin layer approximation in the presence of an autogravitating medium.
2. Relativistic Conservation of Momentum
The chosen auto-gravitating profile is
 (1)
(1)
where ![]() is the density in the equatorial plane (
is the density in the equatorial plane (![]() ),
),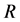 is the radius of the advancing shell,
is the radius of the advancing shell, ![]() is the latitude angle (
is the latitude angle (![]() at the equator and
at the equator and ![]() at the two poles) and
at the two poles) and  is a parameter which characterizes the gradient. The chosen symmetry imposes that the motion is independent of the azimuthal angle in spherical coordinates but depends only on the latitude angle and the time. The classical conservation of momentum in the presence of an auto-gravitating medium was treated in [3] and therefore we will not duplicate the results already obtained. The relativistic conservation of momentum, see [4] -[6] , is formulated as
is a parameter which characterizes the gradient. The chosen symmetry imposes that the motion is independent of the azimuthal angle in spherical coordinates but depends only on the latitude angle and the time. The classical conservation of momentum in the presence of an auto-gravitating medium was treated in [3] and therefore we will not duplicate the results already obtained. The relativistic conservation of momentum, see [4] -[6] , is formulated as
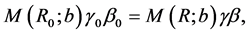 (2)
(2)
with
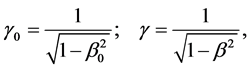 (3)
(3)
and
 (4)
(4)
 being the velocity of light, here
being the velocity of light, here 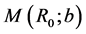 is a first mass between 0 and
is a first mass between 0 and 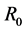 and
and 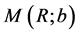 is a second mass between 0 and
is a second mass between 0 and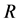 . We know already that
. We know already that 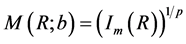 where the integral
where the integral 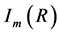 has been defined in Equation (15) of [3] and
has been defined in Equation (15) of [3] and ![]() is a parameter to be found. The fundamental Equation (2) can be first solved for
is a parameter to be found. The fundamental Equation (2) can be first solved for 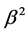
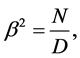 (5)
(5)
where
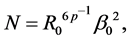
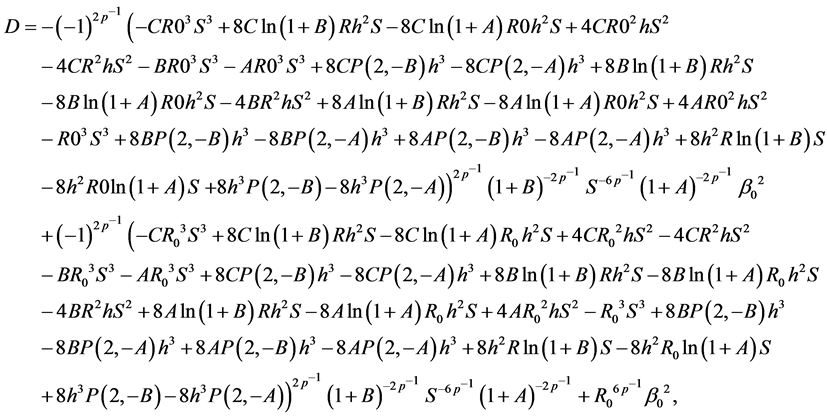
with
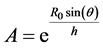


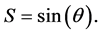
and 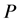 the polylog operator, which is defined by
the polylog operator, which is defined by
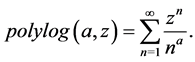 (6)
(6)
The value of  is
is
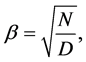 (7)
(7)
or
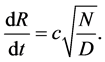 (8)
(8)
This first order differential equation can be solved with the Runge-Kutta method, see FORTRAN SUBROUTINE RK4 in [7] . Another approach separates the variables
 (9)
(9)
The previous integral does not have an analytical solution and we treat the previous result as a non-linear equation to be solved with the FORTRAN SUBROUTINE ZRIDDR in [7] . The presence of an analytical expression for  as given by Equation (8) allows setting up the recursive solution
as given by Equation (8) allows setting up the recursive solution
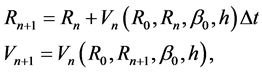 (10)
(10)
where ,
, ![]() ,
, ![]() are the temporary radius, the relativistic velocity, and the interval of time, respectively. An interesting application of SR is the time delay: given an interval of time,
are the temporary radius, the relativistic velocity, and the interval of time, respectively. An interesting application of SR is the time delay: given an interval of time, ![]() , in the laboratory frame the interval of time,
, in the laboratory frame the interval of time,  , in a frame that that is moving with velocity
, in a frame that that is moving with velocity 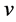 in the x-direction is
in the x-direction is
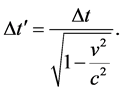 (11)
(11)
We can therefore introduce the following ratio
 (12)
(12)
which measures the time dilation, and lies between 0 and 1.
3. Astrophysical Application
We numerically solved the non-linear equation, Equation (9) even if the same results can be obtained by solving the differential Equation (8) or implementing the recursive relationship as given by Equation (10), see Table 1 for the adopted data.
The complicated structure of SN 1987A is due to the great variety of shapes obtained when the point of view of the observer changes. One way to parametrize the point of view of the observer is the introduction of the Euler angles , as an example, Figure 1 shows the 3D advancing shell after 23 years.
, as an example, Figure 1 shows the 3D advancing shell after 23 years.
In order to avoid complicated changes of framework for the field of velocity we limit ourselves to the non-rotated image. This choice is already widely used by astronomers in order to reduce the data of ![]() -Carinae, see Figure 4 in [8] . The progressive increase of the asymmetry is clearly outlined in Figure 2, in which sections of the expansion are drawn at time steps of 1 yr.
-Carinae, see Figure 4 in [8] . The progressive increase of the asymmetry is clearly outlined in Figure 2, in which sections of the expansion are drawn at time steps of 1 yr.
The difference in velocity between the polar direction and equatorial direction are oulined in Figure 3.
Table 1. The numerical values of the parameters of the relativistic simulation for SN 1987A.
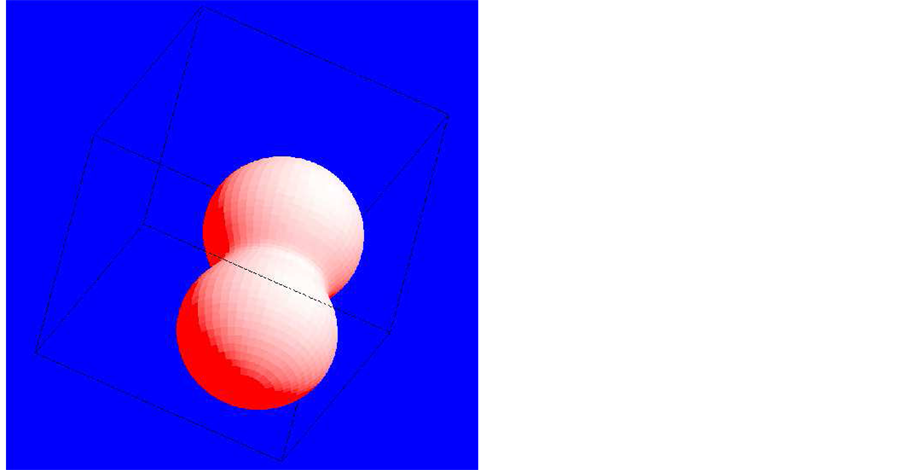
Figure 1. Continuous three-dimensional surface of SN 1987A after 23 yr: the three Eulerian angles characterizing the point of view are Φ = 105˚, Θ = 55˚ and Ψ = −165˚. Physical parameters as in Table 1.
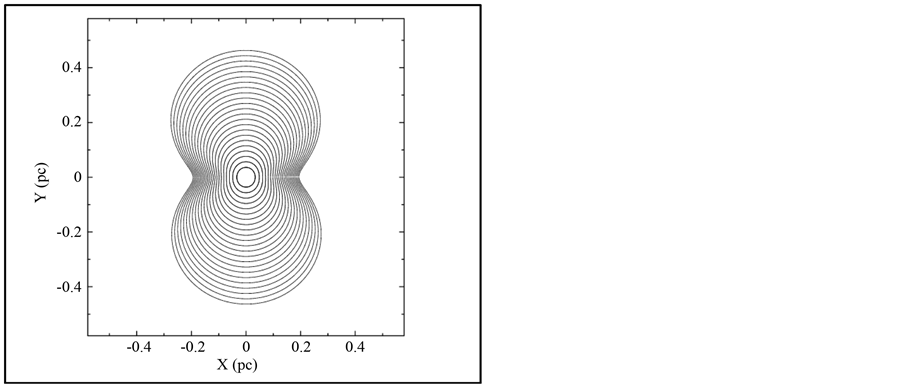
Figure 2. Sections of SN 1987A in the X-Z plane at time steps of 1 yr. Physical parameters as in Table 1. This is a non-rotated image and the three Euler angles characterizing the orientation are Φ =180˚, Θ = 90˚ and Ψ = 0˚.

Figure 3. Velocity in the equatorial direction (full line) and in the polar direction (dashed line) in the first 50 days.

Figure 4. Map of the relativistic velocity as a function of the latitude for SN 1987A at the age 1 yr.
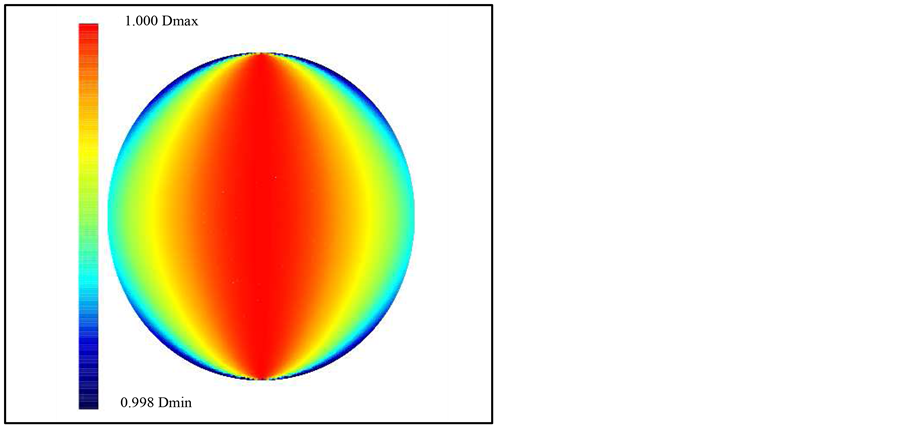
Figure 5. Map of the relativistic time dilation D, see Equation (12), for velocity of SN 1987A in the direction perpendicular to the observer at the age 1 yr at time intervals of 1 s in the laboratory frame.
The relativistic field of velocity in the various points of SN 1987A after 1 yr was shown in Figure 4.
The relativistic time dilation is mapped in Figure 5 where the velocity of expansion perpendicular to the observer (x-direction) is considered.
4. Conclusion
We have covered the evolution of a SN in an auto-gravitating medium in a relativistic framework. The initial shape is represented by a sphere of radius 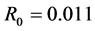 pc. After 1 yr, the asymmetry between the radius in the equatorial plane and the radius in the polar direction is well defined and Figure 4 summarizes both the asymmetrical shape and the anisotropic field of velocity. The time dilation at 1 yr as represented by the parameter
pc. After 1 yr, the asymmetry between the radius in the equatorial plane and the radius in the polar direction is well defined and Figure 4 summarizes both the asymmetrical shape and the anisotropic field of velocity. The time dilation at 1 yr as represented by the parameter ![]() varies between a minimum of 0.9975 and a maximum of 1.
varies between a minimum of 0.9975 and a maximum of 1.
References
- Marion, G.H., Vinko, J. and Wheeler, J.C. (2013) High-Velocity Line Forming Regions in the Type Ia Supernova 2009ig. The Astrophysical Journal (ApJ), 777, 40.
- Soderberg, A.M., Chakraborti, S. and Pignata, G. (2010) A Relativistic Type Ibc Supernova without a Detected
 - Ray Burst. Nature, 463, 513. http://dx.doi.org/10.1038/nature08714
- Ray Burst. Nature, 463, 513. http://dx.doi.org/10.1038/nature08714 - Zaninetti, L. (2013) Three-Dimensional Evolution of SN 1987a in a Self-Gravitating Disk. International Journal of Astronomy and Astrophysics, 3, 93.
- French, A.P. (1968) Special Relativity. CRC. New York.
- Zhang, Y. (1997) Special Relativity and Its Experimental Foundations. World Scientific, Singapore City.
- Guéry-Odelin, D. and Lahaye, T. (2010) Classical Mechanics Illustrated by Modern Physics: 42 Problems with Solutions. Imperial College Press, London. http://dx.doi.org/10.1142/p679
- Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (1992) Numerical Recipes in FORTRAN. The Art of Scientific Computing. Cambridge University Press, Cambridge.
- Smith, N. (2006) The Structure of the Homunculus. I. Shape and Latitude Dependence from H2 and Fe II Velocity Maps of eta Carinae. The Astrophysical Journal (ApJ), 644, 1151.


