International Journal of Astronomy and Astrophysics
Vol.3 No.4(2013), Article ID:39347,3 pages DOI:10.4236/ijaa.2013.34045
Redefining the Event Horizon
Kashipur, Samastipur, Bihar, India
Email: aryan.coip@gmail.com
Copyright © 2013 Shiv Raj Aryan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 4, 2013; revised October 2, 2013; accepted October 9, 2013
Keywords: Event Horizon; Black Hole; Lorentz Transformation; Relativity
ABSTRACT
Presented herein is a new and independent derivation of equation for the radius of Black Holes, i.e. the event horizon of black holes. The equation has been derived by formulating the relativistic equation of escape velocity derived from the relativistic equations for gravitational potential and kinetic energy. Based upon that, it is now shown that the actual size of a black hole, as determined by its event horizon, is exactly half the value predicted by the escape velocity equation used in the Newtonian mechanics. It proves that the actual radius of a black hole is exactly one half of the Schwarzschild radius.
1. Introduction
This work shows that the principles introduced by Einstein in his paper published in 1911 on the influence of gravitation on light propagation [1], when properly interpreted lead to a relativistic form of the escape velocity equation in addition to a relativistic form of the gravitational potential energy equation. It is now shown in this present work that the relativistic form of the escape velocity equation leads to a relativistic value for the event horizon of black holes that is exactly half the distance determined by using the Newtonian form of the escape velocity equation. As stated in the abstract, this means that the actual radius of a black hole is exactly one half of the Newtonian based Schwarzschild radius.
2. Review of the Newtonian Principles
The standard Newtonian derivation of the escape velocity equation is as follows: First we are given the equation for the potential energy of a mass m at any radius R from the centre of a celestial body of mass M as stated by
 (1)
(1)
Gravitational Potential Energy, where PE is the gravitational potential energy [2]. Then we are given the Newtonian kinetic energy equation in the form
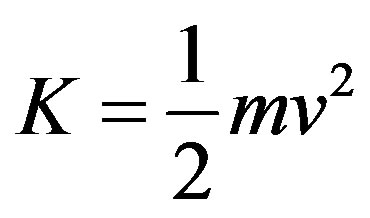 (2)
(2)
Newtonian Kinetic Energy, where K is kinetic energy of a mass m moving at speed v [2]. Next we are given the relationship
 (3)
(3)
Minimum Escape Energy that gives the minimum energy required for mass m to escape the gravity of the celestial body of mass M [2]. Solving this equation for v then gives
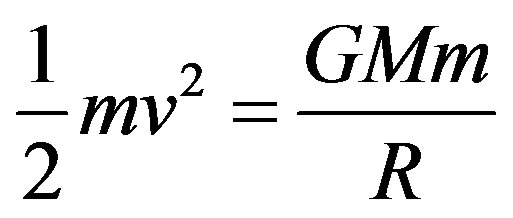 (4)
(4)
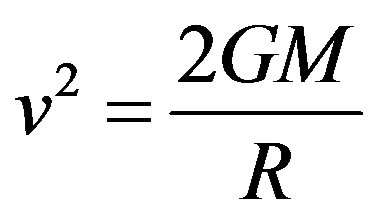 (5)
(5)
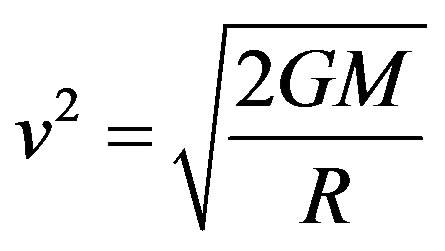 (6)
(6)
Newtonian Escape Velocity where v of the final equation is the Newtonian escape velocity. This is considered the minimum speed in a radial direction that an isolated body would have to be moving at when it reaches radial distance R from the centre of mass in order to escape the gravity of a celestial body of mass M. Since it is given that
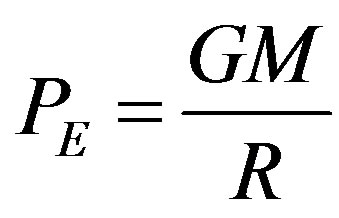 (7)
(7)
Gravitational Potential where PE is the gravitational potential [2], and by substituting it into Equation (6) we obtain
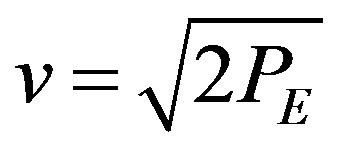 (8)
(8)
Newtonian Escape Velocity as the final form of the Newtonian equation for escape velocity. (Only now, as will be shown next in Section 3, is it known for certain that Equation (1) gives the Newtonian value for gravitational potential energy PE and not the relativistic value.)
3. Relativistic Escape Velocity
To begin the relativistic derivation process, first we need to convert the equation for gravitational potential energy PE to its relativistic form. We do this by simply factoring it with the Lorentz transformation factor [3]. This gives
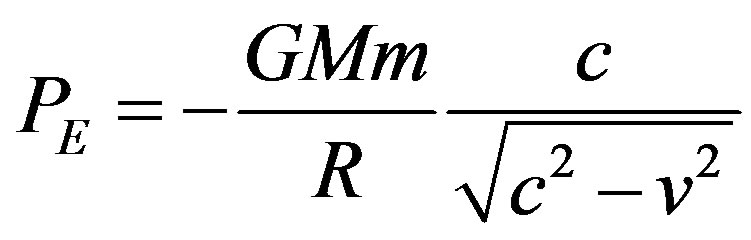 (9)
(9)
where the term to the far right is an exact version of the Lorentz factor commonly referred to as gamma, and represented by the Greek symbol “γ” [3]. Simplification of Equation (9) then gives
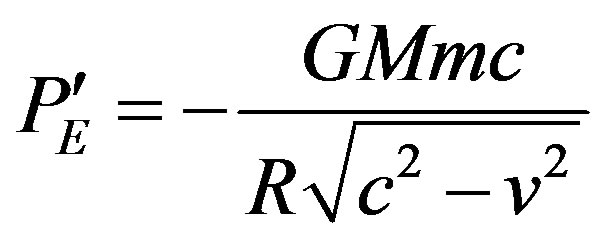 (10)
(10)
Relativistic Potential Energy Where  is the relativistic potential energy for the relationships defined. This conversion is justified by the evidence supported observations of the asymptotic increase in energy needed to accelerate an object to speed v. An object at a given potential then by definition contains the amount of potential energy given by Equation (10) and not the amount given by Equation (1).
is the relativistic potential energy for the relationships defined. This conversion is justified by the evidence supported observations of the asymptotic increase in energy needed to accelerate an object to speed v. An object at a given potential then by definition contains the amount of potential energy given by Equation (10) and not the amount given by Equation (1).
For our next step in the derivation process we employ the relativistic kinetic energy
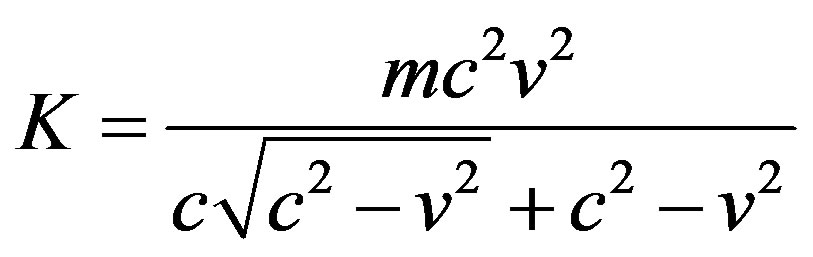 (11)
(11)
Relativistic Kinetic Energy, where K now gives the correct value for kinetic energy at all speeds of v from 0 to c. This equation has previously been acknowledged as a correct equation for relativistic kinetic energy by scientific authorities. To continue the derivation process we now simply follow the same procedure used in the previous Newtonian derivation beginning with
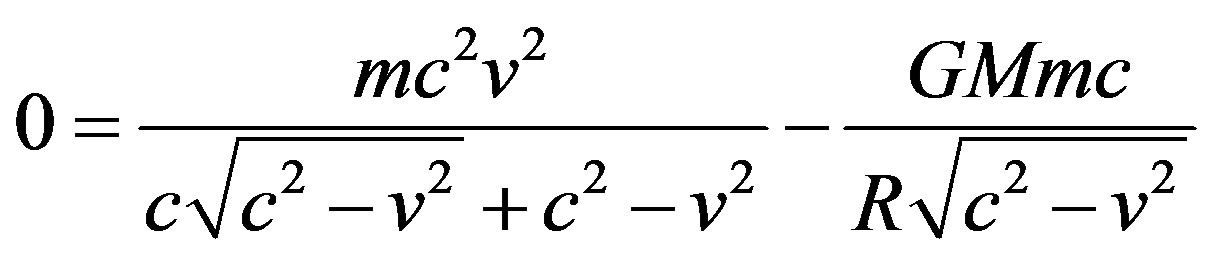 (12)
(12)
Minimum Escape Energy, where now we show the minimum relativistic escape energy and not the minimum Newtonian escape energy needed to overcome the gravitational force of celestial body M. This then gives
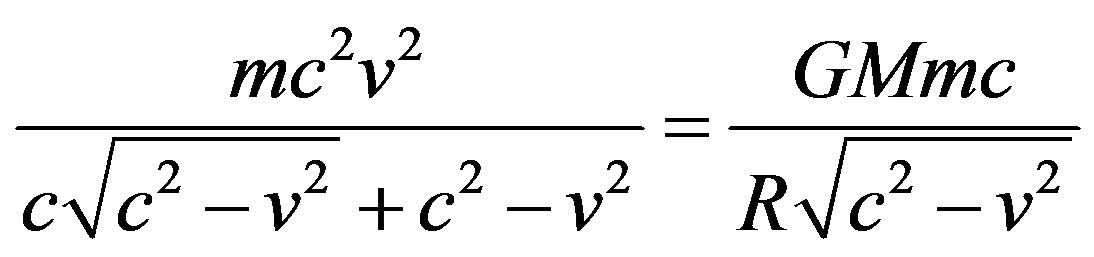 (13)
(13)
that when solved for v gives
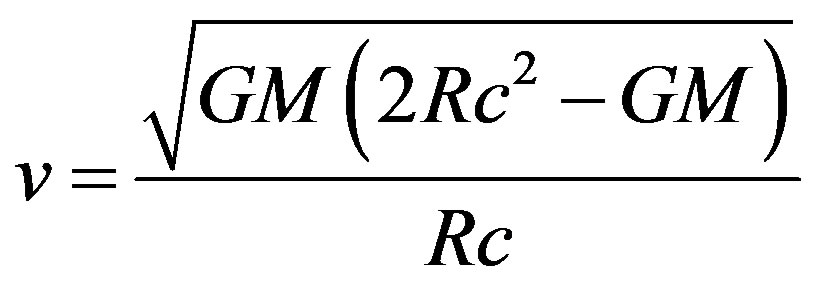 (14)
(14)
that simplifies to
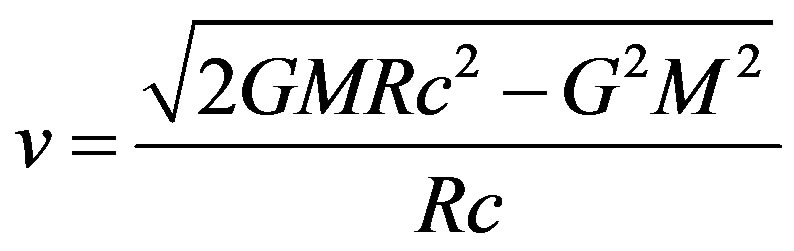 (15)
(15)
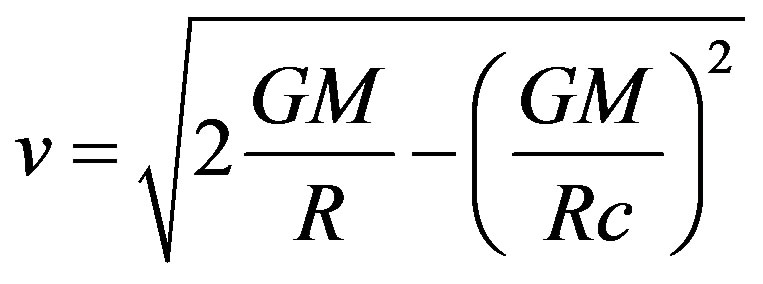 (16)
(16)
and since
 (7)
(7)
Gravitational Potential, we obtain
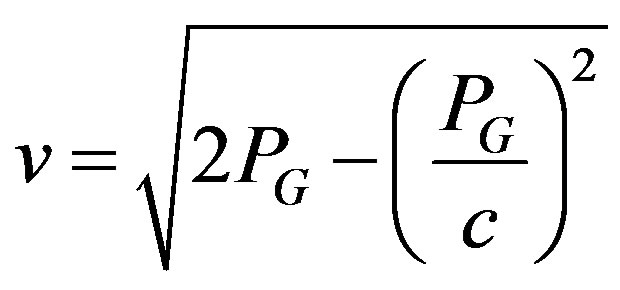 (17)
(17)
Relativistic Escape Velocity for the relativistic version of the escape velocity equation. It gives virtually the same results for v as the Newtonian version of the Equation, Equation (8), except for gravitational potential PE values that approach c2. At that potential the escape velocity v takes on the value of v = c, as a quick visual inspection of Equation (17) will indicated. At the same potential the Newtonian Equation (8) will give a value of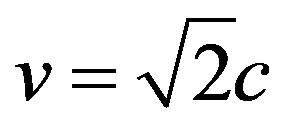 , or v =1.414c as a quick visual inspection of the equation will show.
, or v =1.414c as a quick visual inspection of the equation will show.
4. Deriving the Relativistic Event Horizon Radius
Similarly Equation (17) when solve for PG at gives
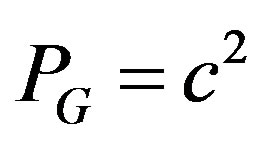 (18)
(18)
from which by way of substitution with Equation (7) we obtain
 (19)
(19)
that when solved for radial distance R gives
 (20)
(20)
Relativistic Event Horizon, where R is the radius of the black hole, or the distance from its centre to the event horizon. This equation gives exactly half the value as that of the standard Newtonian equation (Schwarzschild radius)
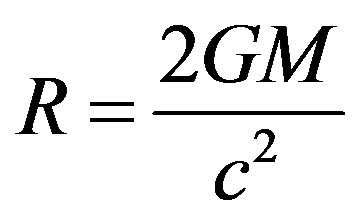 (21)
(21)
Schwarzschild Radius, as is readily seen by comparison of the two.
5. Conclusion
In consideration of the fact that the independent mathematical derivation presented in this work gives an identical result to that of the previous derivations that used completely different principles of general relativity, it seems more than reasonable to conclude that the result must be valid. Based upon several independent analyses, the Schwarzschild radius is twice the distance from the centre of a black hole to its event horizon. It then directly follows that black holes are only half as large as previously believed. This finding, however, affects more than just back holes; it affects our entire understanding of the universe right out to its very edge and it also affects the interaction of all of the matter it contains.
REFERENCES
- A. Einstein, “On the Influence of Gravitation on the Propagation of Light,” Annalen der Physik, Vol. 340, No. 10, 1911, pp. 898-908. http://dx.doi.org/10.1002/andp.19113401005
- I. Newton, “The Principia: Mathematical Principles of Natural Philosophy,” University of California Press, Berkeley, 1999.
- H. A. Lorentz, “Electromagnetic Phenomena in a System Moving with Any Velocity Smaller than That of Light,” Proceedings of the Royal Netherlands Academy of Arts and Sciences, Vol. 6, 1904, pp. 809-831.

