ABSTRACT

One of the main problems of contemporary physics is to find a quantum description of gravity. This present approach attempts to remedy the problem through the quantization of a finite but large flat Minkowski space-time by means of Fourier expansion of the displacement four vector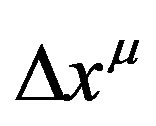. By applying second quantization techniques, space-time emerges as a superposition of space-time eigen states or lattices of quantized space-time vibrations also known as gravitons. Each lattice element four vector is a graviton and traces out an elementary four volume (lattice cell). The stress-momentum tensor of each graviton defines its curvature and also the curvature of the associated lattice as described by General Relativity. The eigen states of space-time are found to be separated by a quantum of energy equal to the product of the Hubble constant and the Planck constant. The highest energy state is at Planck energies. This paper also shows that gravitons can be absorbed and emitted by the space-time lattice changing the volume of its primitive cells and that particles of observable matter are associated with a graviton whose frequency is equal to the particle’s Compton frequency which the lattice can absorb producing a perturbation in the lattice. The space-time lattice is found to be unstable and decays by radiating low energy gravitons of energy equal to the product of the Hubble constant and the Planck constant. This decay causes the space-time superstructure to expand. The graviton is seen a composite spin 2 particle made from a combination of spin half components of the displacement four vector elements. The spin symmetry of its constituent elements can breakdown to give rise to other vector or scalar bosons. Dark Matter is seen as a consequence of Bose-Einstein statistics of gravitons which results in some regions of the lattice having more energy than others.

1. Introduction

Currently, observed phenomena can be explained either by invoking the explanatory power of Quantum Mechanics or General Relativity. The microworld of elementary particles and molecules is elegantly described by the Quantum Theory. General Relativity on the other hand, explains the physics of the macro cosmos in terms of the geometry of space-time itself. Physics seeks to discover the nexus of these two fundamental ideas either by incorporating one theory into the other or by rendering the other obsolete. The impetus is currently on deriving a quantum theory of gravity and not a geometric theory of the microworld. There seems to be a knowledge gap on the properties of space-time at infinitesimal distances and time intervals characteristic of the microworld and this gap prevents a clear understanding of the role of gravity in the quantum world. Clearly the concepts of physical space and time need to be re-examined. Thus a quantum theory that seeks to incorporate General Relativity must first probe into the very fabric of space-time itself in search of its quantum behavior which at the classical limit reduces into a smooth, connected Lorentzian manifold.

The advantages of a quantized space-time are twofold. First it eliminates the need of points in space-time that are the source of many divergences in the current theory of elementary particles in which particles are considered as point like dimensionless particles. These divergences first manifested as early as in classical electromagnetic field theory, in which there occurs a Coulomb divergence. Here an infinitely large value for the energy of the Coulomb field of a charged point particle is calculated, since at very small distances r from a particle (r → 0) the field increases without limit. Secondly, establishing a theory of gravitation on a correctly quantized manifold will inevitably lead to a quantum theory of gravity which includes General Relativity.

Limitations of Current Quantum Gravity Theories

There exist a number of quantum gravity theories [1,2] attempting to bring a quantum aspect to gravity but most physicists agree that there are only two major contenders: Loop Quantum Gravity (LQG) and String Theory. LQG approaches quantum gravity in the spirit of General Relativity by viewing gravity as a manifestation of a property of space-time itself. The protagonists (namely C. Revolli, L. Smolin et al.) [3-5] of this approach posit that the fabric of space-time is granular in nature consisting of loops which are quantum excitations of the gravitational field. While there has been some notable success by the theory in terms of black hole entropy calculations, there are however issues. Like the other contender, String Theory, whose strong advocates include among others L. Susskind, Ed Witten [6-8], it has not been verified experimentally [9,10] and does not explain recent discoveries in cosmology such as dark matter and dark energy. Furthermore String theory has 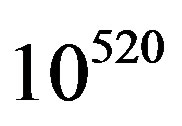possible solutions which to some physicist such as L. Kraus, P. Woit [10-12] shows lack of uniqueness of predictions. The approach that is presented in this paper agrees with LQG in as far as that the very fabric of space-time is responsible for manifesting gravity and that time evolution progresses in quantized steps as well as in the existence of quantized volume elements. This current paper further explains dark matter and the root causes of the expansion of spacetime. For any semblance of a real quantum theory of gravity to emerge, General Relativity must be seamlessly integrated into that theory. This aspect is intrinsic in this present approach to Quantum Gravity.

2. Space-Time Quantization

In attempting to reconcile these two fundamental theories, it is sometimes postulated that the space-time manifold should be quantized at the very smallest scales. In this current approach however, the intention is to quantize the displacement four vector, 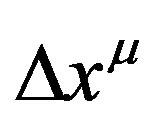, of dimensions equal to the radius of the Hubble sphere. The length of this fourvector can be found from its inner product:

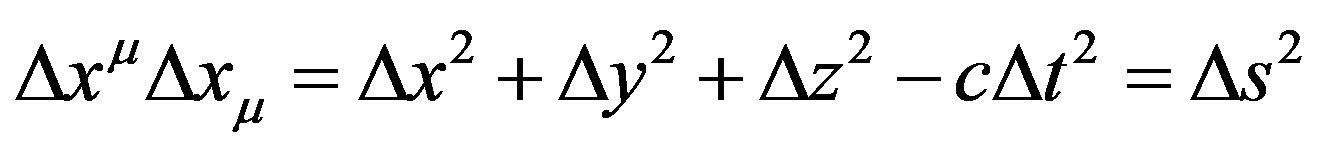(1)

We will apply a Fourier series expansion in a manner analogous to the quantization of the electromagnetic field for the quantization process. To this end we express the above expression in the form

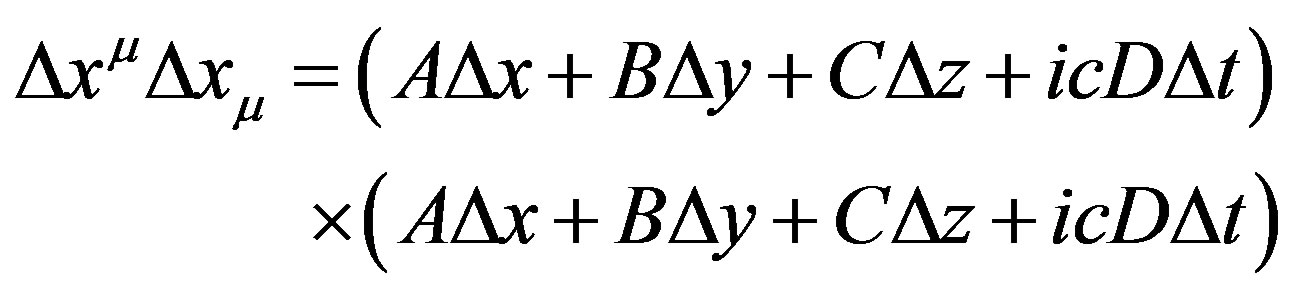(2)

On multiplying out the right side we see that, to get all the cross-terms such as to vanish, we must assume

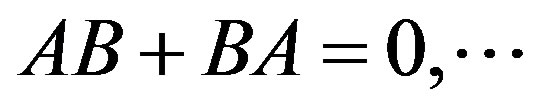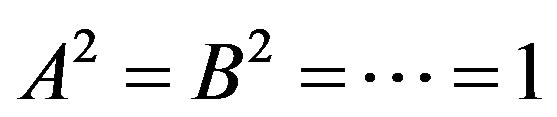  and           (3)

Applying the same technique as Dirac [13,14] we find that A, B, C and D are matrices. With 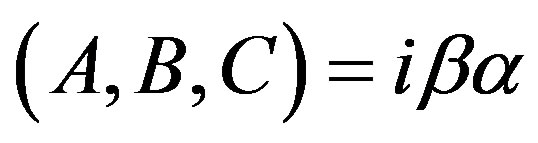and 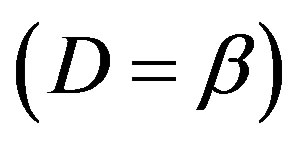which can be expressed as the following Dirac matrices:

, (4)

where

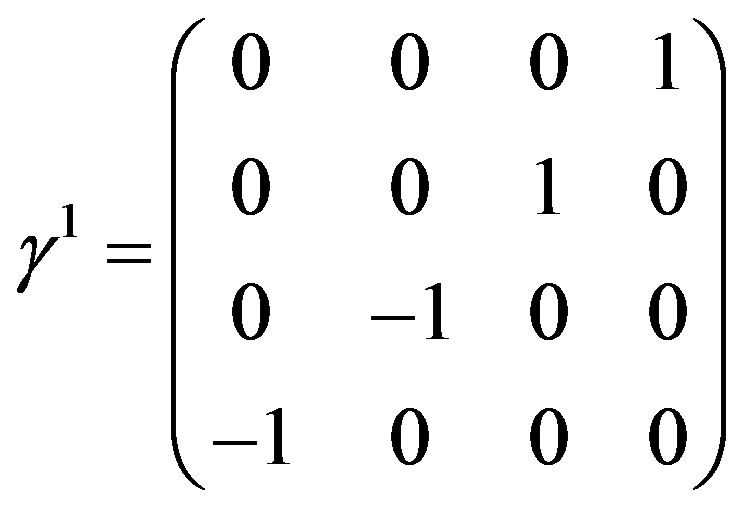
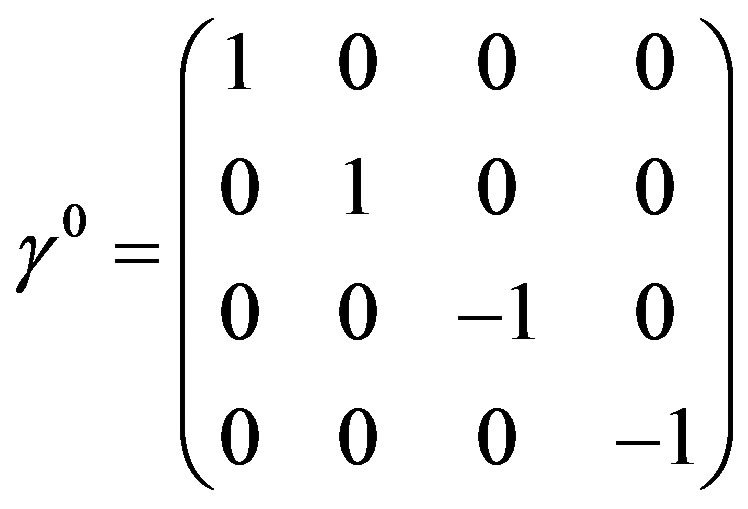
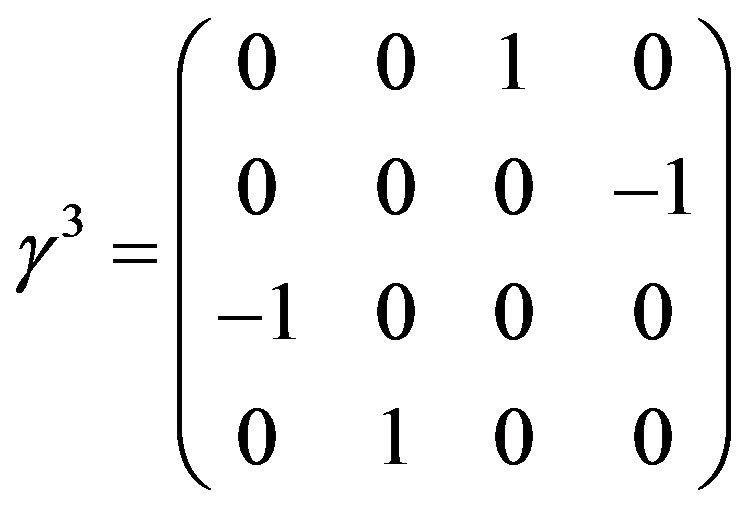
(5)

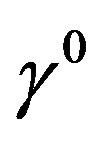is Hermitian, and the 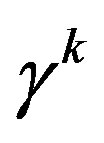are anti-Hermitian.

The gammas may be summarized using the Minkowski metric on space-time in the form

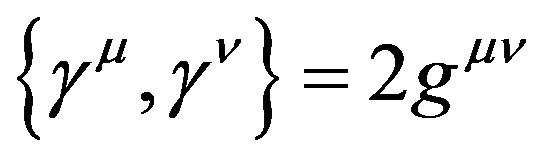(6)

Thus the displacement four vector 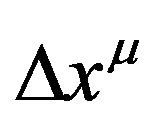can now be expressed in the form

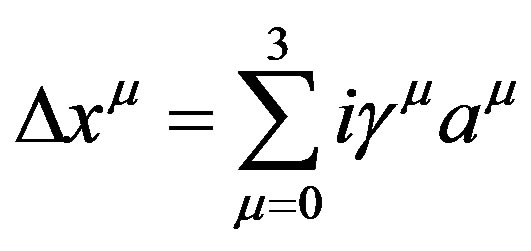(7)

A Fourier expansion of 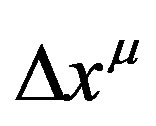leads to the following expression

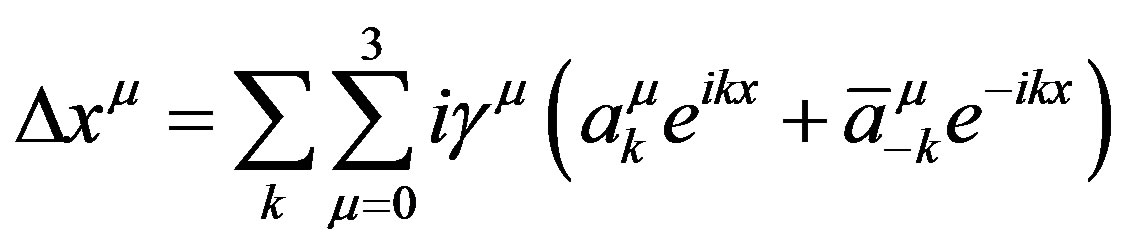(8)

where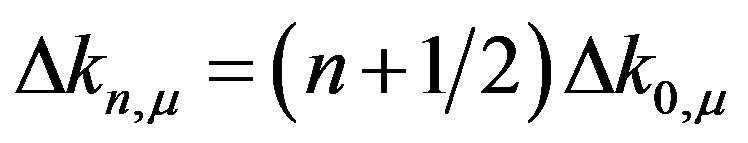and The components of the vector  have discrete values a consequence of the finite length of the four vector. Clearly, the (discrete) set of Fourier coefficients 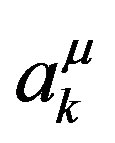and 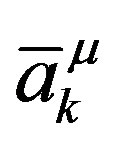define the vector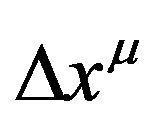. If we promote them to annihilation and creation operators we obtain:

(9)

therefore the four-vector 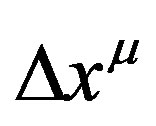can be seen as a superposition of elementary four vectors in Minkowski space that are appearing and disappearing in constant flux at intervals defined by the norm of the eigen vectors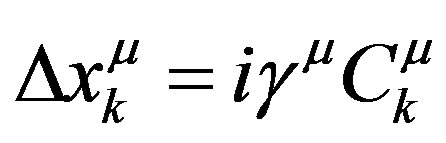. Also for any given the vectors define a periodic lattice structure along the entire length of the four vector and the norm of each eigen vector is a radius of an elementary four-volume sphere.

These eigen four-vectors defined by annihilation and creation operators are associated with four momentum vectors

(10)

Thus space-time is made from a superposition of spacetime world line elementary oscillations. We picture a constituent particle of the quantum vacuum being associated with a world line element. This is a consequence of the uncertainty principle. The presence of a vacuum particle of four momentum is associated with a perturbation in position 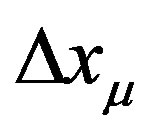via the relation

(11)

The uncertainty in position can be seen as an elementary excitation of the world line. Hence a virtual particle is inextricably associated with an elementary excitation of the world line via the uncertainty principle. We then picture space-time and the quantum vacuum as a crystal lattice that can assume different eigen states.

2.1. The Graviton

Each component of the displacement four vector

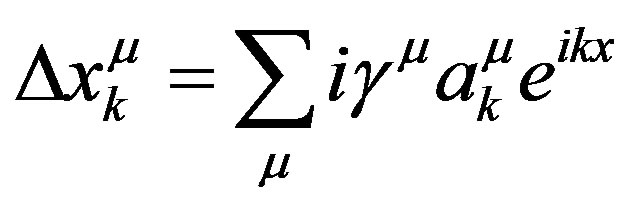(12)

transforms according to the law [15]

(13)

where ω_µν is an antisymmetric 4 × 4 matrix parameterizing the transformation Therefore, each component of the four vector has a spin half. If we add up all the four half spins, they give us a total spin of 2 for each elementary displacement four vector.

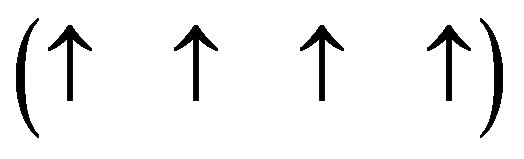
This makes each elementary displacement four vector a vibrating spin 2 particle. This elementary spin 2 excitation of space-time must be a graviton. Consequently, spacetime is a superposition of gravitons just as the Electromagnetic field is a superposition of photons. Therefore the energy of the vibrating four vectors or graviton gives rise to a stress momentum tensor as in Einstein’s field equations which give a rotational distortion to the four vectors. The stress energy tensor of each graviton defines its curvature as described by Einstein’s field Equations [10]

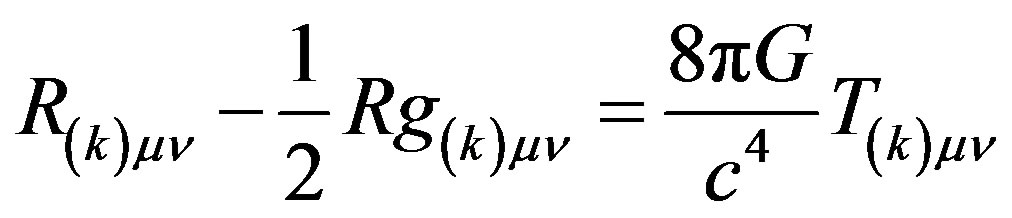(14)

where and R are the Ricci curvature tensor and the scalar curvature respectively, 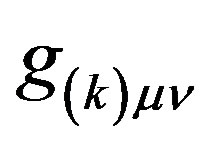the metric tensor for a given elementary world line of four wave vector k, c the speed of light and G is the Newtonian gravitational constant. 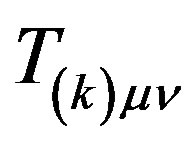is the stress momentum tensor for the elementary world line excitation.

2.2. Graviton Energies

We seek to find the energy of the most energetic graviton or space-time element. This world line element will have a curvature identical to that of an event horizon.

From the uncertainty relation

(15)

We multiply each term by c the speed of light to obtain

or

(16)

At the event horizon

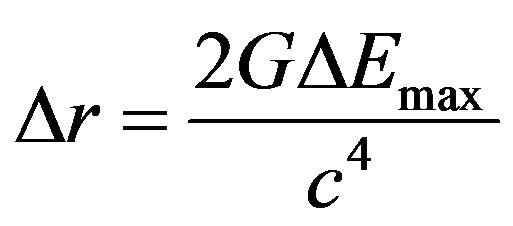(17a)

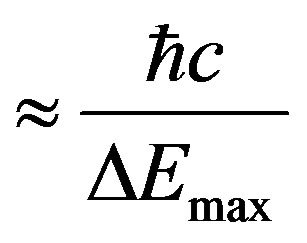(17b)

Thus

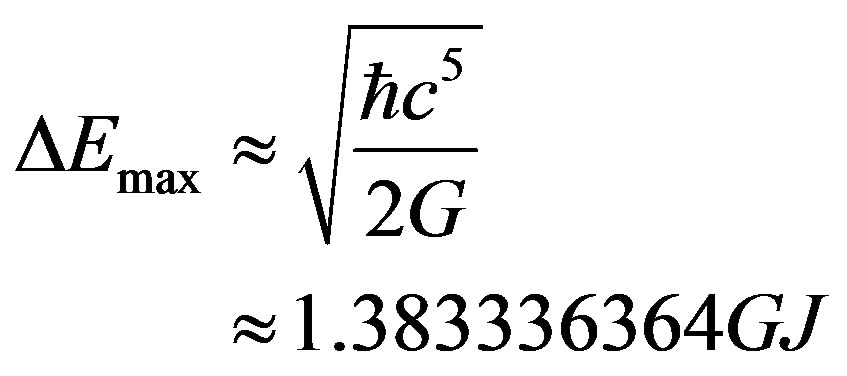(17)

is the highest energy state of a space-time harmonic oscillator.

The radius of this unit volume is

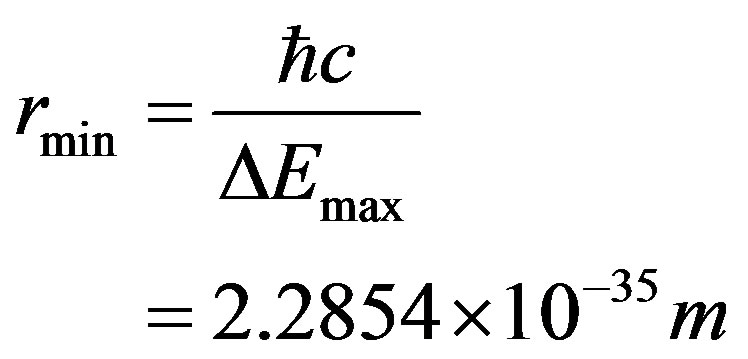(18)

The time interval associated with this volume element is

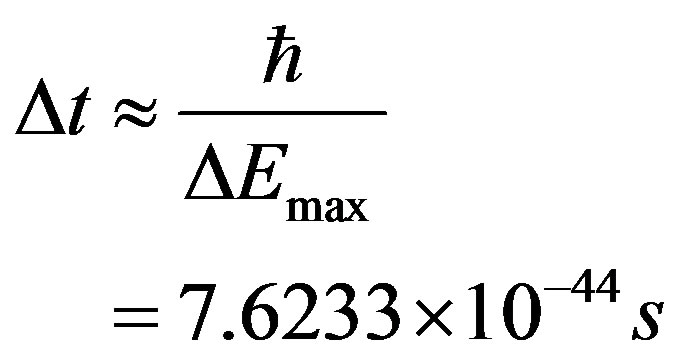(19)

The mass associated with this volume element

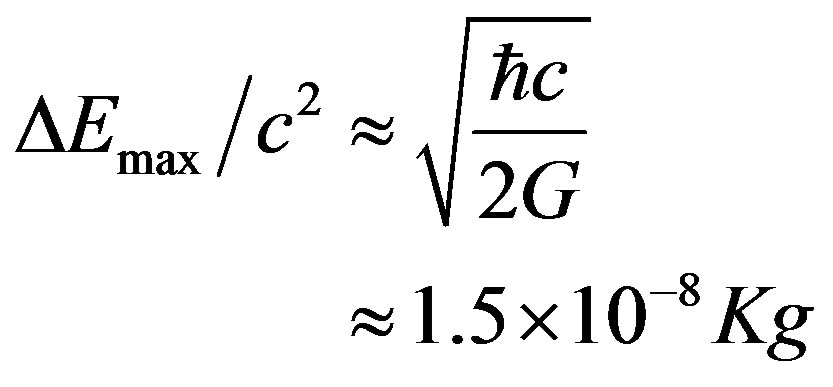(20)

These are Planck units multiplied or divided by.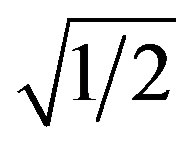

We now seek to find the energy of the lowest energy graviton. To this end we consider the natural four wave vector.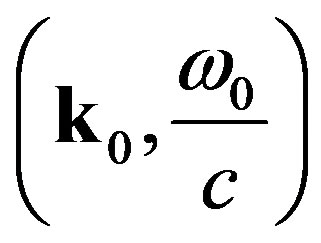

The wavelength of the fundamental harmonic is equal to twice the radius of the Hubble sphere and therefore implying that the natural wave number of the space time harmonic oscillator is

(21)

where r_HS is the radius of the Hubble sphere.

Here we see that is the natural frequency of the harmonic oscillator which is equal to Hubble’s constant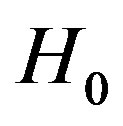. Thus the highest energy state or Planck state is

(22)

The above expression enables one to find N, the number of space-time energy states to be

(23)

Each separated by an energy gap

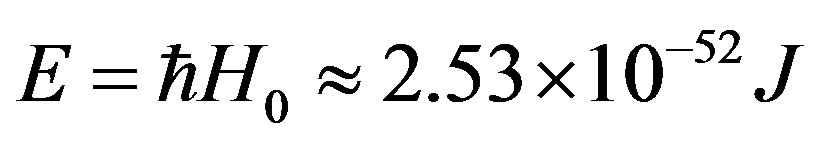(24)

2.3. Graviton Absorption and Emission by the Space-Time Lattice

From A. Friedmann’s Equation [16]

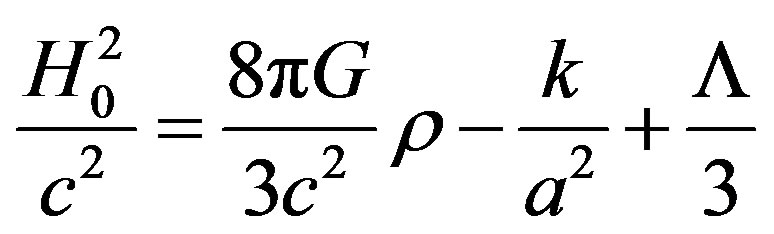(25)

We infer that for a flat Minkowskian space-time devoid of matter (ρ = 0 and k = 0) the cosmological constant is

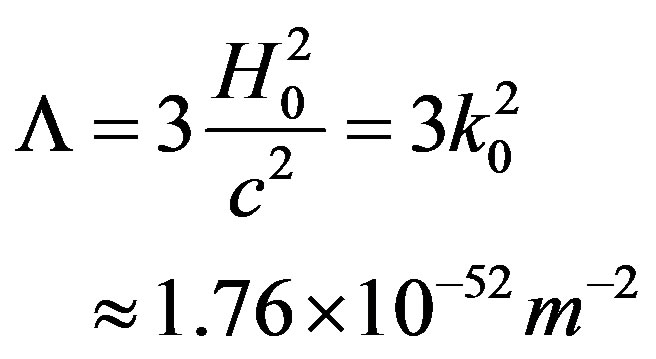(26)

This is approximately the same as the measured value of the cosmological constant [17,18].

Einstein’s field Equations which include the cosmological constant can now be seen as describing the absorption or emission of a graviton by the four vector elements of space-time depending on the sign in front of the cosmological constant which results in a new lattice quantum state

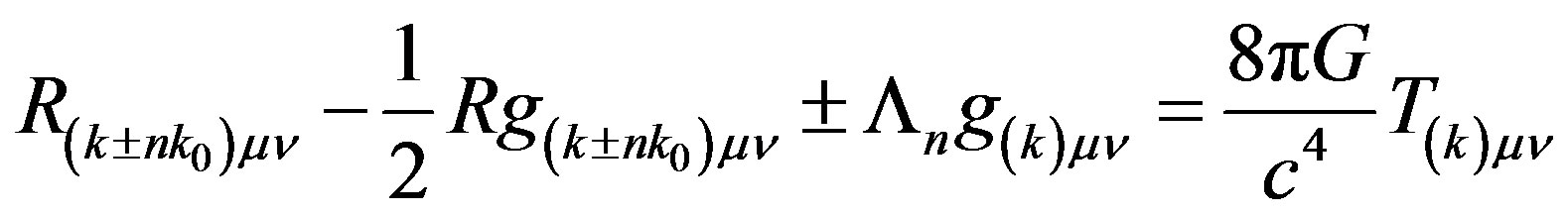
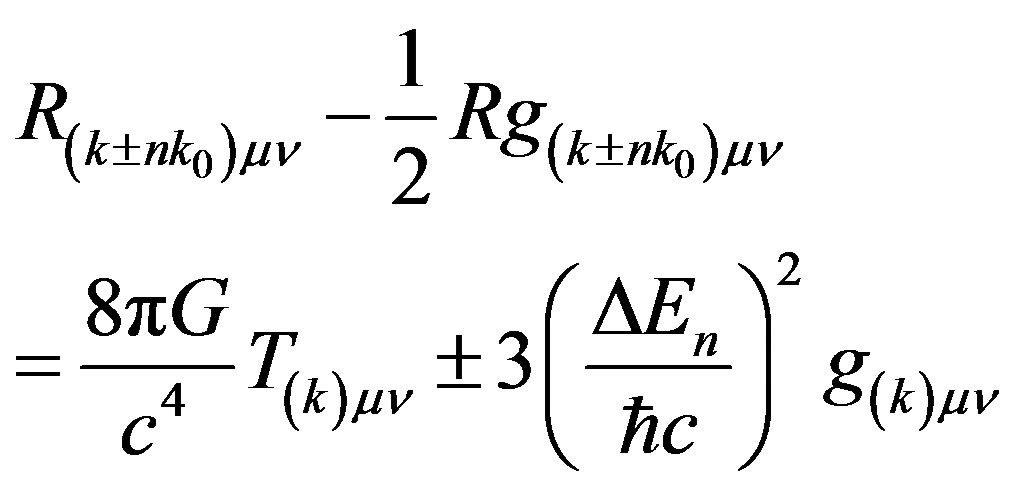(27)

where the graviton energy is

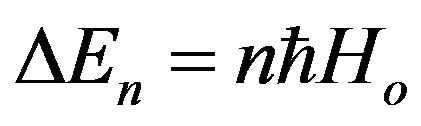(28)

Equation (27) is the nexus between the concepts of Quantum Theory and General Relativity.

The measured value (26) implies n = 1 and that every four vector element of space-time is emitting the lowest energy graviton (24), and transiting into an energy state lowered in energy by the loss of the graviton (24). The loss of the quantum expands the unit cell. That is, when the four momentum of the primitive cell is lowered, the Heisenberg uncertainty relations show that the size of the primitive cell is dilated. From the point of view of General Relativity, the loss of the graviton uncurves the four vector element or expands it.

This decay process is natural as the space-time lattice constantly seeks to assume a state of least potential energy. Also, these transitions are quantized time evolution processes. Without them, the arrow of time vanishes and events remain static.

The absorption of a graviton has the opposite effect. Absorption can be considered as a multiple site occupation by gravitons hence increasing the stress momentum tensor of the primitive cell. A particle of matter can be considered as associated with a graviton or elementary excitation of space-time, of four wave vector equal to the Compton four wave vector of the particle via the Uncertainty Principle. The particle’s graviton energy can also be expressed in the form (28) and is the gravitational energy of the particle. This is the weak equivalence principle (WEP) [19] in the sense that the energy of the particle is equal to its gravitational energy.

The absorption and emission of a rank 2 tensor field by space-time has also been explored by authors such as G. Liu [20] and in String Theory [21].

2.4. Dark Matter as a Consequence of Bose-Einstein Statistics

We consider the space-time crystal lattice in a particular eigen state E_n as a set of identical harmonic oscillators or gravitons in thermal equilibrium. Being spin 2 bosons, the ratio of the number of gravitons in their (n + 1)th quantum state of excitation to the number in the nth quantum state is

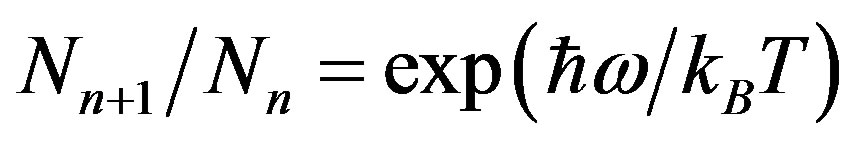(29)

where k_B is the Boltzmann constant and T the thermodynamic temperature of the space-time lattice. Thus the fraction of the total number of gravitons in the nth quantum state is

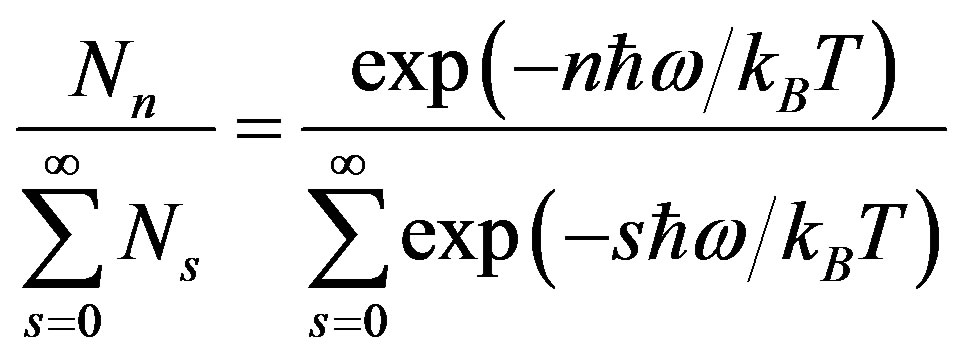(30)

We see that the average excitation quantum number of a graviton is

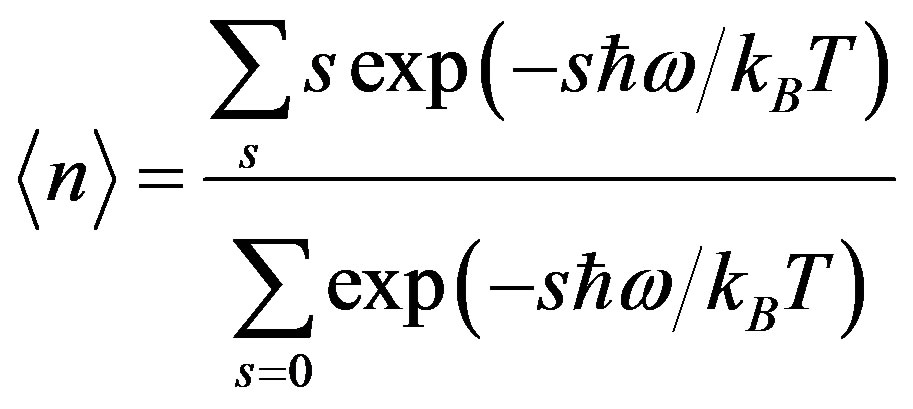(31)

On completing the summation we may rewrite equation (31) as the Planck distribution

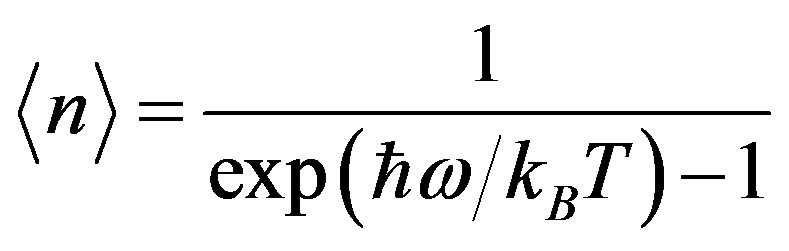(32)

The graviton thermal energy for the system is then

(33)

We observe that from a statistical point of view, the lattice cells have broken down from a state of equilibrium to a state in which some have gained extra energy quanta or gravitons from others in accordance to the Planck distribution function. Thus a lattice cell in the nth quantum state characterized by a four wave vector k = nk₀, can be considered as a ground state graviton that has been promoted to the nth quantum state. We apply equation (27) to this process to obtain:

(34)

where  is the stress momentum tensor for a lattice cell in the ground state. Here we see a lattice cell that has changed its radius of curvature from the radius of the Hubble sphere, r_HS, to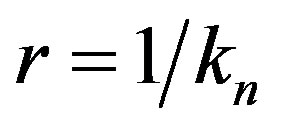. We therefore have in the lattice, regions in which cells are more energetic and highly curved while others are in lower energy states and relatively more expanded. Starting from the assumption that the energy density within each cell in nth quantum state is uniformly distributed we thus have uniform spacetime curvature (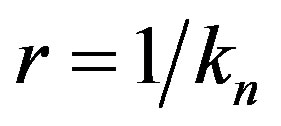) within each cell. This will result in a constant rotational velocity within it and the velocity can be calculated using Hubble’s Law.

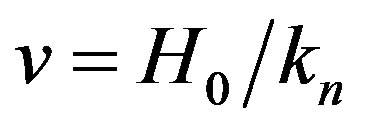(35)

Hubble’s Law itself is a consequence of the emission of a graviton of least energy (24) by higher energy gravitons E_n which constitute the elements of the spacetime lattice. Thus by the law of conservation of momentum the recoil speed v in each cardinal direction of the more energetic gravitons (graviton expansion rate) can be calculated from

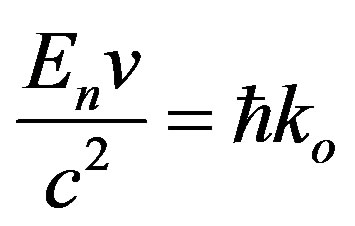
or

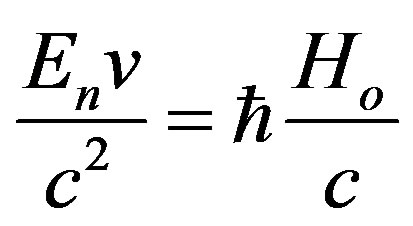(36)

The left side can be expressed as

or

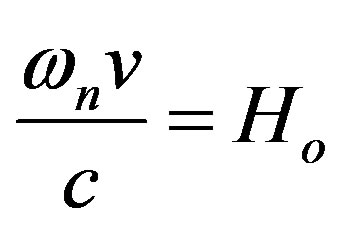(37)

Which reduces to

or

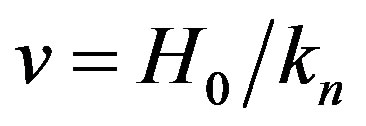(38)

Thus we predict that a test particle inside a lattice cell of radius 0.1 Mlyrs will experience a rotational speed of approximately

(39)

Whereas a test particle inside a lattice cell of radius 10 Mlyrs will experience a rotational speed of 220km/s. These large lattice cells can overlap resulting in cluster of dark matter cells having a dense oval core in the region of overlap. Dark Matter should therefore exhibit the following properties:

• Because Dark Matter is a graviton in the nth quantum state, it curves space-time uniformly and manifest constant rotational velocity within the graviton. Matter found within or passing through the graviton/lattice cell will thus experience an additional uniform rotational velocity.

• Since gravitons are waves they pass through each other and interact through superposition, and so will dark matter.

• The effects of dark matter are appreciable at very large scales because of the small value of the Hubble constant.

Hence the curvature of space-time around galaxies is due to baryonic matter and dark matter which can be expressed from Equation (27) as

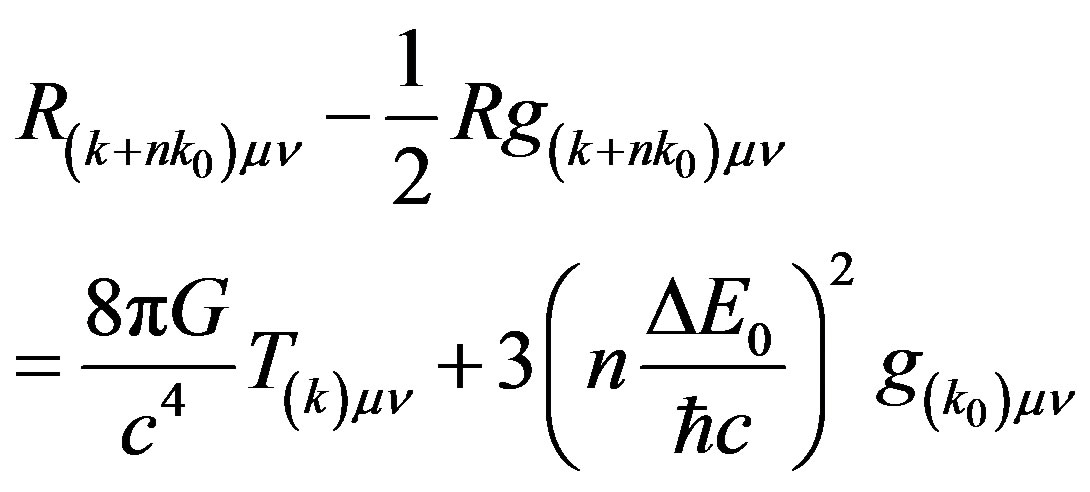(40)

where 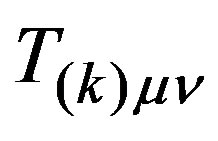 is the stress momentum tensor due to baryonic matter and the last term expresses the dark matter contribution. If we include dark energy contribution to the curvature, Equation (40) becomes

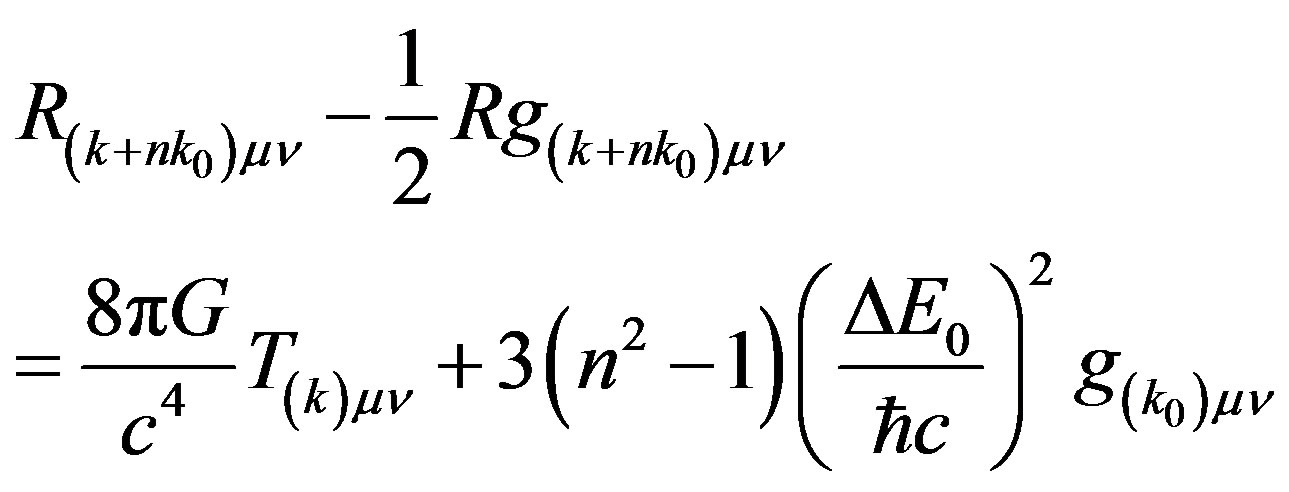
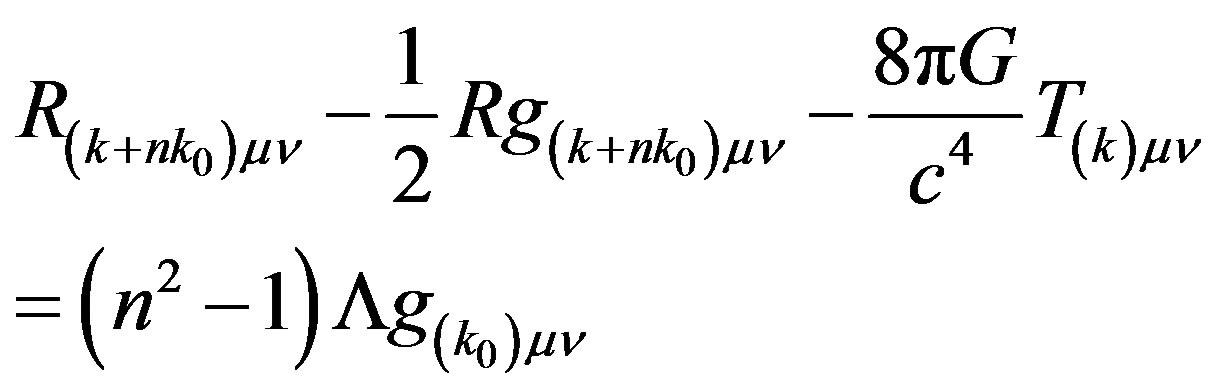(41)

We immediately notice that when n = 10⁶⁰ at the Planck energy state, the dark energy term Λ is 10¹²⁰ times smaller than the dark matter term. An observer within a lattice cell in the n-th quantum state can choose to ignore the background curvature by allotting a value of 0 or −1 to n in Equation (41) which then reduces to Einstein’s field Equations with or without the cosmological constant respectively.

Here we have a model of Dark Matter modeled entirely from the graviton concept and unrelated to the Scalar Field Dark Matter Bose Einstein Condensate (SFDM/BEC) [22-24] models. The beauty of the current model compared to others is found in its simplicity in the sense that it shows Dark Matter as a different manifestation of the same underlying graviton field. This highlights the interconnectedness of the Dark Matter phenomenon with the other fundamental phenomena in the universe. More importantly, DM in this model is seen to induce a constant rotational velocity and not gravity.

The thermal analogy also implies that graviton transfer through the crystal lattice is a random process. The graviton flux does not proceed directly in a straight path, but diffuses through the lattice, suffering frequent collisions with it. If we use the same method applied by Debye [25] to describe the thermal conductivity of dielectric solids we obtain the following expression for graviton thermal conductivity K

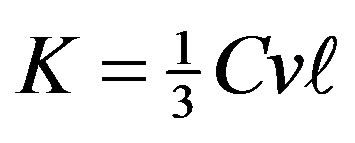(42)

where C is the heat capacity of the gravitons v the graviton velocity and the mean free path. The net graviton energy flux is therefore

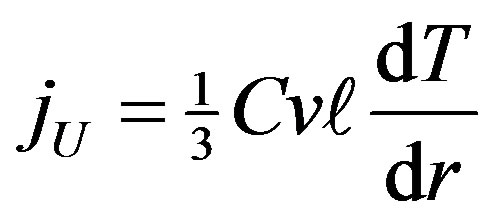(43)

The mean free path depends on the spacing between lattice sites which for a given space-time eigen state is its elementary wave length (). This implies that high energy graviton diffusion is slower than low energy graviton diffusion. This may explain the apparent difficulty in detecting gravity waves of sufficiently high enough energies to be detected. These gravity waves will consist of slowly diffusing gravitons. Travelling at small drift velocities over large distances means that gravity wave information takes a long time to reach us compared to luminal information.

Here we see a thermodynamic aspect of gravity. The deep connection of gravity and thermodynamics has also emerged in theoretical works by S. Hawkings, Berkenstein, T. Jacobson and E. P. Verlinde [26-28].

3. Graviton Transmutations

The graviton is a composite particle made from a combination of the components of the four vector element making up a quantum of space-time. The spin symmetry of the graviton can breakdown giving rise to other bosons. For the graviton, the spin states are

The available combinations which result in spin 1 bosons are

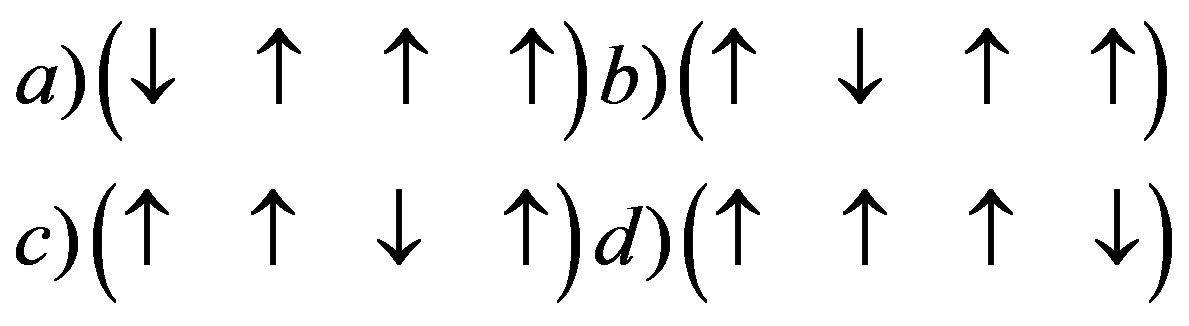
The problem is to identify which one of these bosons is a gluon, W, Z, or a photon.

And for spin 0 bosons

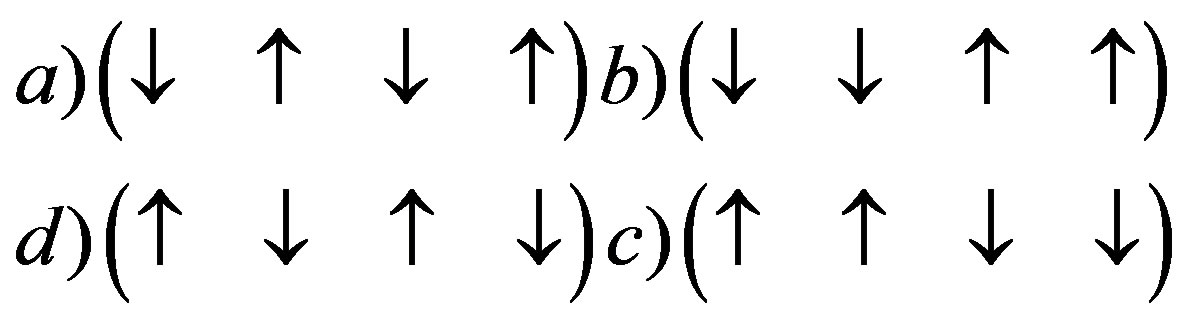
These could be either four Higgs Bosons or the Higgs boson and three yet to be detected scalar fields. Gravity therefore, is the primordial Unified Field! At Planck energies the graviton may resonate in all the nine states.

The entropy inside a Black Hole may increase if the spin symmetry of its constituent gravitons/unit cells breaks down giving rise to other vector or scalar bosons.

4. Summary

In this paper, the author has put forward a hypothesis that endeavors to harmonize two of the most fundamental ideas of the observable physical universe using the concept of gravitons which are space-time quanta. The very fabric of space-time is seen as consisting of a superposetion of vibrating spin 2 elements of the world line called gravitons. These gravitons together with the quantum vacuum form a crystal lattice that can assume different eigen states. The stress momentum tensor of each graviton generates constant curvature. A particle of matter is associated with a graviton of frequency and wavelength equal to the particle’s Compton four-wave vector. The particle’s graviton is then absorbed by the space-time lattice, distorting it in the process and generating more curvature. The paper also highlights the following:

• The transportation of gravitons through the spacetime lattice is analogous to the flow of phonons in a conductor. High energy gravitons have a low rate of diffusion than low energy gravitons.

• Dark matter is seen as a space-time lattice cell in the nth quantum state whose spatial dimensions can be large or small depending on the energy of the cell. The constant curvature of the cell induces a uniform rotational velocity.

• Dark energy is due to the emission of low energy gravitons by the space-time lattice.

• Gravitational free fall is manifested when there is transition from a lower to a higher quantum state of spacetime.

• The graviton is a spin 2 composite boson which can transmute into spin 1 and 0 bosons by changing the spin states of its constituent fermions.

The findings from this paper may provide other avenues of detecting dark matter that exploit its property of inducing constant rotational motion. Remarkably, we do not encounter any energy divergences in this paper both ultraviolet and infrared.

5. Acknowledgements

I would like to thank the anonymous peers who reviewed this paper for their constructive critique and funding from the Department of Research Science and Technology of the Ministry of Infrastructure Science and Technology (Botswana).

REFERENCES