International Journal of Astronomy and Astrophysics
Vol.3 No.2A(2013), Article ID:33314,5 pages DOI:10.4236/ijaa.2013.32A005
Confrontation between Quantized Periods of Some Extra-Solar Planetary Systems and Observations
1Department of Astronomy, National Research Institute of Astronomy and Geophysics, Cairo, Egypt
2Center of Theoretical Physics (CTP), British University in Egypt (BUE), Cairo, Egypt
3Egyptian Relativity Group, Cairo, Egypt
Email: fadymorcos@hotmail.com
Copyright © 2013 A. B. Morcos. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 23, 2013; revised March 25, 2013; accepted April 2, 2013
Keywords: Quantization; Periods; Extra-Planetary; Extra-Solar Planet
ABSTRACT
A simple formula, using the quantum numbers of solar system planets and some quantized extra-solar planets, to estimate the periods, is done. The quantum numbers, calculated by other authors, have been used to find the orbital periods of solar system planets and some extra-solar planets. Observed periods have been used to compare them with the estimated periods from the given formula. It is found that the given relation is applicable perfectly for the solar system planets. Some extra-solar planets, of stars having approximately the same mass as the sun, are chosen to apply the same relation. The differences between the observed and calculated periods for the extra-solar systems have been calculated and tabulated. It is found that the percentage errors between the predicted values and the corresponding observed values for extra-planetary systems are controlled by the star’s mass and its quantum number. The percentage error decreases by increasing the quantum number, for quantum numbers over 4. When the quantum number is less than or equal 4, it is found that the percentage error decreases by decreasing the quantum number.
1. Introduction
The main idea of quantization starts by the discovery of the electron spin. Millikan and Einstein show that in the photoelectric effect, light is absorbed in quanta, each carrying energy 4πsv. Planck said that oscillators do not emit light continuously but in quanta with energies as given by Einstein equation. Also he mentioned that light quantum sometimes behaves as waves and other times as a corpuscle, De Broglie recognized that the nature seems to have a symmetries performance and since the light behaves in dualistic manner, then particles should also behave at time by the same way. Particle waves should also exist with wavelength equal to 4π× (the ratio between the spin of the particle to its momentum). Heisenberg showed that the simultaneous observation of conjugate quantities always involves an error equal to 2 S of electron.
Schrӧdinger solved this problem by setting a partial differential equation which leads for negative energies to discrete eigenvalues, that is by substitution in the Hamiltonian with a new variable S = K lnψ where K = 2 Se. Reference [1] suggested a formula to compute the quantum number of the solar system planets. He concluded that the results obtained by the given formula for the quantum number are completely random. Nottale in a series of papers started at 1993, in the frame work of the theory of Scale-Relativity, quantized the period of solar system planets and semi-major axes of extra solar planet. Reference [2] put a formula for the effective quantum number n. References [3,4] suggested that the periodic motion of celestial bodies can be described by tuned action discretization for periodic motions on the atomic scale, in order to take into account the gravitational field instead of the electrostatic one to calculate a few mechanical quantities related to the periodic motions of celestial objects. In the following section, we are going to give brief notes about these different methods of quantization of orbits of celestial objects. In Section 3 a new formula for quantized periods is given and used to calculate the periods of solar system planets and some of extra-solar planets. The differences between observed and calculated periods are represented in Table 1 for planets of solar system and in Table 2 for extra-solar planets under consideration. In Section 4 concluding remarks are given.
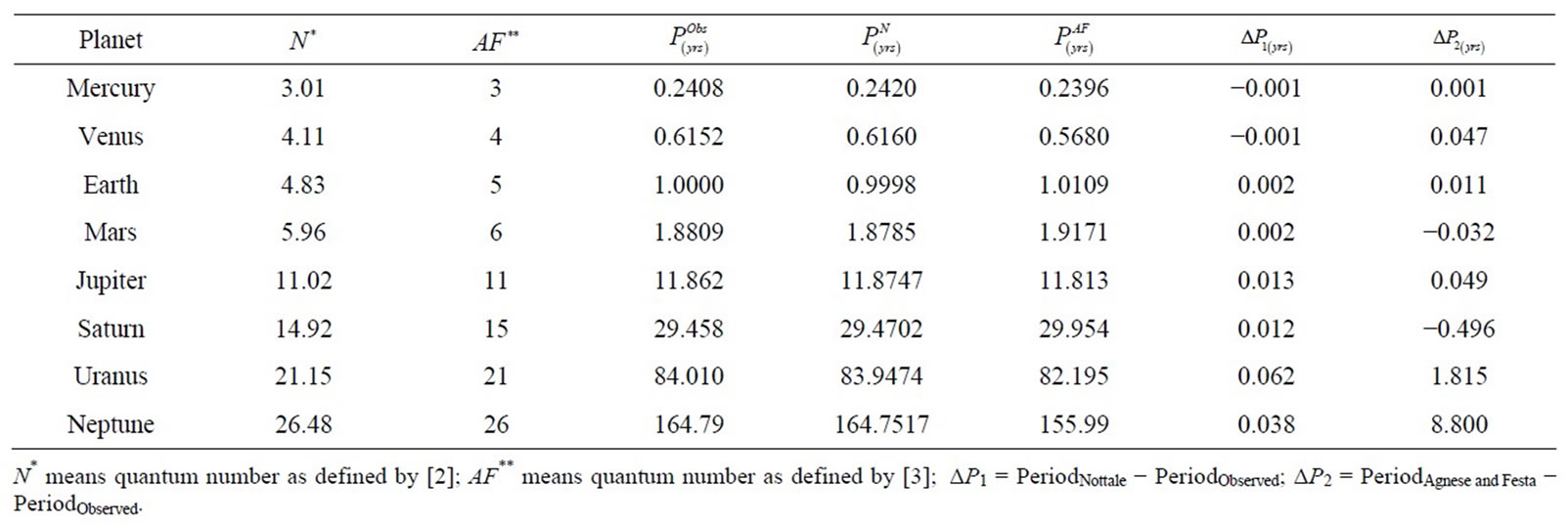
Table 1. Comparison between calculated periods and observed periods of solar planetary system.

Table 2. Comparison Between calculated periods and observed periods of solar planetary system.
2. Quantization of Macro Bodies
Many authors made many trials to quantize macro-bodies. Reference [1] put the first idea for quantization of planets of solar system by new concept of understanding of Schrӧdinger equation. He put a formula for finding the quantization number of solar system. References [2,5-7], in the framework of scale-relativity theory, tried to quantize the orbital periods of solar system planets and extra solar planet orbital semi-major axes. Reference [3,4] defined new structure constant in the framework of old quantum mechanics αg to discretize solar and 5 of extra solar planets. In what follows a short note about each of these methods will be given.
2.1. Baranothy Quantization
Reference [1] put a general form for constant K in Schrodinger equation as
 (1)
(1)
where k is a small positive integer or zero and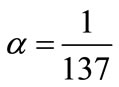 .
.
He put the following relation to find the quantum number of planets of the solar system planets as
 (2)
(2)
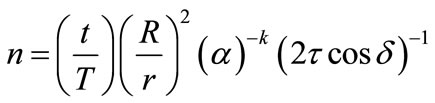 (3)
(3)
where r and t are radius and period of rotation of the planet. T and R are the orbital period and distance from Sun. 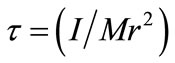 is the moment of inertia factor and
is the moment of inertia factor and 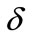 the inclination of the equator to the orbital plane.
the inclination of the equator to the orbital plane.
2.2. Nottale Quantization
Nottale in a series of papers started at 1993, in the frame work of the theory of Scale-Relativity, quantized the period of solar system planets and semi-major axes of extra-solarplanet. References [2,6] derived simple formulae to the motion of the solar planets. They found some relations between quantum numbers and speed quantization rule using a new gravitational constant. They calculated the quantum numbers of some extra-solar systems. Reference [2] put a simple formula for the effective quantum number n as
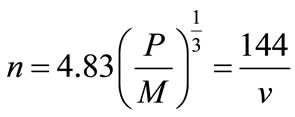 (4)
(4)
where M is the parent star mass in unit of solar mass and its uncertainty, the orbital period P in years, and a is the semi-major axis and  the average velocity in km/s.
the average velocity in km/s.
2.3. Agnese and Festa Quantization
Reference [3] suggested that the periodic motion of celestial bodies can be described by tuned action discretization. They expressed Planck’s constant as
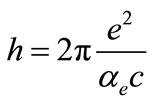 (5)
(5)
where 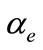 is the fine structure constant and
is the fine structure constant and 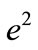 is the product of proton charge times electron charge in H atom.
is the product of proton charge times electron charge in H atom.
They put some formulae to the motion of the solar planets, these relations are
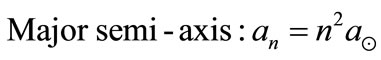 (6)
(6)
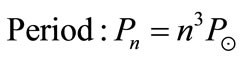 (7)
(7)
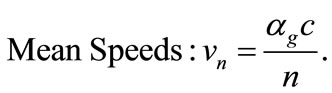 (8)
(8)
Where 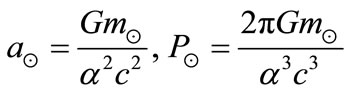 and
and 
Also they defined the Boher radius for each planet as
 (9)
(9)
where 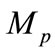 is the planet’s mass and
is the planet’s mass and  is the mass of the sun.
is the mass of the sun.
3. New Quantized Period Formula and Results
It is clear from [2] that there is a clear relation between the quantum number and both of mass and period of the star, of the system. If we write Equation (4) in the following form
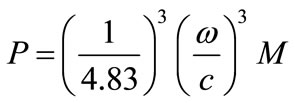 (10)
(10)
By using Equation (7) and keeping in mind that
 , we have
, we have

Since 3 preceding  in the previous equation, is the quantum number of Mercury, then it can be generalized to be (n), and this equation takes the form
in the previous equation, is the quantum number of Mercury, then it can be generalized to be (n), and this equation takes the form
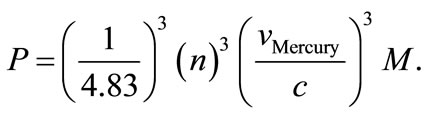 (11)
(11)
From Equations (11) and (7), considering that the mass of the star is taken in terms sun’s mass, we can write
 (12)
(12)
By using, as it is given by [3], we conclude that
 is equal approximately to one. Now Equation
is equal approximately to one. Now Equation
(11) can be written in the simple form as:
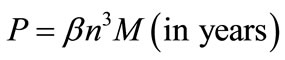 (13)
(13)
where M is the mass of the system star in terms of sun’s mass, n is the quantum number and  is a coupling constant and equal to
is a coupling constant and equal to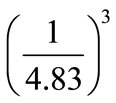 . The value of the coupling constant
. The value of the coupling constant 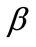 is equal approximately
is equal approximately .
.
The simple form (13) can be used to calculate the orbital period of solar system or extra-solar planets. In what follows we are going to apply this relation on solar System and some extra-solar planets of some star of approximately have the same solar mass. The quantum numbers for the solar system planets, obtained by [2,3]will be used in the Equation (13) to calculate the periods of these planets. The obtained periods, compared with the observed values and tabulated in Table 1.
It is clear from Table 1,that the estimated values for periods of solar system planets from relation (13), which depends on the quantum numbers, have a reasonable values with respect to the observed values.
From Table 1, the periods obtained from Nottale’s quantum numbers are too near to the observed period, than Agnese & Festa quantum values.
The main problem in Nottale’s values is that these quantum numbers are not whole numbers. One can says in general that the maximum difference between using Agnese & Festa quantum numbers in the relation (13) and the observed periods is not more than error 5%. It is noticed also that the values of error increase by increasing the quantum number.
In what follows we are going to use the relation (13) to find the periods of some extra-solar planets. These planets are chosen such that their stars are of the same sun’s mass or too near to it. A comparison between the estimated and observed values will be given in Table 2. The percentage errors in each period to the observed one are given to clarify the trend of this error.
It is noticed from Table 2 that, for short intervals periods, of few days, the difference between calculated and observed periods is in the range of 0.8 day to 1.3 day. Also when the quantum number becomes 6 or 7 this difference becomes less and the estimated value becomes more reasonable values. It is noticed also that the percentage errors in periods decreases increasing the star’s mass for the systems having the same quantum number. It is worth f mentioning that this trend will be reversed for quantum numbers greater than 5. As it is mentioned before, the error in periods of the solar system planets increases by increasing the quantum number. A different behavior appears, whenever the percentage error increases by increasing the quantum number till the quantum number becomes 4. For quantum numbers more than or equal 5, the percentage error deceases by increasing the quantum number until it reaches to the minimum value 6% for quantum number 7 and star’s mass 0.98 solar mass.
4. Concluding Remarks
The idea of quantization of macro-bodies in particularly in solar system planets was established by [1]. He obtained quantum numbers for solar systems, but he noticed that the quantum numbers for solar system planets running randomly. References [2-7] represent trials to establish a set of relations to quantize the periods, orbital velocities and radii of solar system planets. It is noticed from their calculations that the quantum numbers obtained for solar system planets are not running in a systematic way and start from quantum number 3 and move successively to 6 for inner planets, whenever for exterior planets it starts from 11 for Jupiter and move randomly to be 26 for Neptune. This may lead to one of the following events:
1) There are some minor or unseen bodies occupy the missed quantum numbers.
Or 2) There is another technique which may lead to successive quantum numbers.
The quantization numbers mentioned by [2,3], have been used in the relation (13), to find the periods of the solar system planets. The obtained values are tabulated in Table 1. In the same table a comparison between the obtained values and the corresponding observed results is done. The difference between observed and calculated values obtained by using Nottale quantum numbers and Agnese & Festa quantum numbers, respectively are given in the seventh and eighth columns of Table 1. The differences between observed and calculated periods when [2] quantum numbers are used, are less than that obtained by using [3] quantum numbers. But we prefer that of Agnese and Festa because it is more reasonable to consider the quantum numbers to be whole numbers not fractional. In general the differences between the observed and calculated values from Equation (13) are in the acceptable range. The quantum numbers given by [3], for some extra solar planets, have been used in the relation (13), to calculate the periods of some of these extra-solar planets. We choose the extra-planetary systems of Stars equal to the sun in mass from 0.70 to 1.3. The obtained results for periods are tabulated in Table 2. The percentage errors with respect to the observed values are listed in the last column of Table 2. It is noticed from Table 2 that, the percentage errors are related to star’s mass and the quantum number of the planet. When the quantum number of the extra-solar planet becomes 6 or 7, the percentage error becomes less and the estimated value for the period from the Equation (13), becomes more reasonable value when the star’s mass becomes too near to the solar mass. The percentage error for the extra-solar planets of quantum numbers less than or equal 5, increases by decreasing the star’s mass and for smaller quantum numbers than five the error decreases by increasing star’s mass. This may through a light on the value chosen for the parameter β and its relation with mass. It is expected that the value of this parameter will change due to the mass of the star of the extra-solar planets. In a future work the Equation (13), will be adapted, to be suitable to calculate the periods of extra-planetary systems of different stars masses.
5. Acknowledgements
The author would like to thank SOC of MG12, Cospar 38 and Cospar 39, for giving him the chance to present orally, some parts of this work.
REFERENCES
- J. M. Barnothy, “The Stability of the Solar Systemand of Small Stellar Systems,” Proceedings of the IAU Symposium 62, Warsaw, 5-8 September 1973, pp. 23-31.
- L. Nottale, “Scale-Relativity and Quantization of Exoplanet Orbital Semi-Major Axes,” Astronomy & Astrophysics, Vol. 361, 2000, pp. 379-387.
- A. G. Agnese and R. Festa, “Discretization on the Cosmic Scale Inspirred from the Old Quantum Mechanics,” 1998. http://arxiv.org/abs/astro-ph/9807186
- A. G. Agnese and R. Festa, “Discretizing ups-Andromedae Planetary System,” 1999. http://arxiv.org/abs/astro-ph/9910534
- L. Nottale, “Fractal Space-Time and Microphysics, Towards a Theory of Scale Relativity,” World Scientific, London, 1994.
- L. Nottale, “Scale-Relativity and Quantization of ExtraSolar Planetary Systems,” Astronomy & Astrophysics, Vol. 315, 1996, pp. L9-L12
- L. Nottale, G. Schumacher and J. Gay, “Scale-Relativity and Quantization of the Solar Systems,” Astronomy & Astrophysics letters, Vol. 322, 1997, pp. 1018-1025.

