International Journal of Astronomy and Astrophysics
Vol. 2 No. 2 (2012) , Article ID: 19744 , 4 pages DOI:10.4236/ijaa.2012.22013
Fundamental Way of Charge Formation and Relation between Gravitational Field and Electromagnetic Field
1Singhania University, Rajasthan, India
2Department of Electronics, Vidyasagar University, Paschim Midnapur, India
Email: *mukuldas.100@gmail.com
Received December 28, 2011; revised February 27, 2012; accepted March 8, 2012
Keywords: Superimposed Spins; Complex Momentum
ABSTRACT
A complex motion and complex momentum due to relativistic phenomenon has been deduced in this paper. This procedure leads to explain the generation of a field which is the result of energy momentum complexity (tensor). In this work, a form of complex momentum of photon has been derived. This momentum reveals the construction of electromagnetic field. These procedures have been applied to explain the electromagnetic field of fundamental charged particle and leads to the assumption of fundamental charge. In this works trial would be made to derive a relation between gravitational field and electromagnetic field.
1. Introduction
In the theory of relativity, mass velocity relation gives a large quantity of kinetic energy attributed to the particle of rigid configuration [1]. Again this expression (concept) would be same for a spinning particle of rigid configuration as in [2]. A particle can possess two or more superimposed motions to the view of an observer. In [3] Chandrau Iyer and G. M. Probhu describe a constructive method for the composition of two planar boosts with velocities 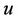 and
and 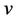 resulting in a velocity
resulting in a velocity . Composition of three linear velocities
. Composition of three linear velocities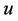 ,
, 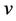 and
and 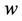 in different directions resulting in a single velocity has been developed in [4]. This leads to the assumption that a body can possess three simultaneous superimposed rotational or spin motions. In this paper, first, trials would be made to derive the energy momentum characteristic of a particle having two superimposed motions. An electromagnetic mass was possible due to Einstein [5]. Einstein strongly believed that field is the form of energy momentum tensor. A charged particle contains electromagnetic field. Again, photons contain electromagnetic field and also electric charge as in [6,7]. In this paper trial would be made to find out the complex characteristic of photon and following this consideration trial would be made to find out the source of fundamental charge of an elementary particle. Gravity is the four dimensional interaction. It is the space-time curvature, basically stress energy tensor. The principles of General Relativity imply that gravity and electrodynamics affect each other. According to Einstein all forces of nature are rooted in gravity. He dreamed of unification in between gravity and electrodynamics in much the same way as electricity and magnetism had been combined by Maxwell and Lorenz. But his unified field theory was not particularly successful. Following the general relativistic approach unified field theory has been developed. In [8] it is said that change of both electric and gravitational field results in the creation of a magnetic field in the region of space time which has a dual electro-gravitational nature. Change in magnetic field results in the creation of both electric and gravitational field. Rotating gravitational masses generate magnetic field B and which generates electric field E and gravitational field G. In this work trial would be made to derive the unification of gravity and electrodynamics following the combination of electricity and magnetism.
in different directions resulting in a single velocity has been developed in [4]. This leads to the assumption that a body can possess three simultaneous superimposed rotational or spin motions. In this paper, first, trials would be made to derive the energy momentum characteristic of a particle having two superimposed motions. An electromagnetic mass was possible due to Einstein [5]. Einstein strongly believed that field is the form of energy momentum tensor. A charged particle contains electromagnetic field. Again, photons contain electromagnetic field and also electric charge as in [6,7]. In this paper trial would be made to find out the complex characteristic of photon and following this consideration trial would be made to find out the source of fundamental charge of an elementary particle. Gravity is the four dimensional interaction. It is the space-time curvature, basically stress energy tensor. The principles of General Relativity imply that gravity and electrodynamics affect each other. According to Einstein all forces of nature are rooted in gravity. He dreamed of unification in between gravity and electrodynamics in much the same way as electricity and magnetism had been combined by Maxwell and Lorenz. But his unified field theory was not particularly successful. Following the general relativistic approach unified field theory has been developed. In [8] it is said that change of both electric and gravitational field results in the creation of a magnetic field in the region of space time which has a dual electro-gravitational nature. Change in magnetic field results in the creation of both electric and gravitational field. Rotating gravitational masses generate magnetic field B and which generates electric field E and gravitational field G. In this work trial would be made to derive the unification of gravity and electrodynamics following the combination of electricity and magnetism.
2. Complex Momentum of a Particle
For composition of three velocities 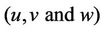 we may visualize six inertial frames as discussed in [4] where, co-ordinate of an event from frame S to frame S5 would be
we may visualize six inertial frames as discussed in [4] where, co-ordinate of an event from frame S to frame S5 would be
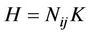 (1)
(1)
Inverse of this operation would be
 (2)
(2)
Considering four inertial frames  where, velocity
where, velocity 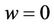 and angle
and angle 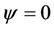 in [4] then matrix
in [4] then matrix 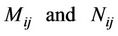 respectively turn out as
respectively turn out as
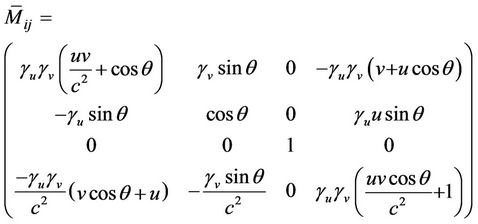 (3)
(3)
 (4)
(4)
Above conditions imply that Frames 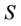 and
and  have both their co-ordinate axes aligned and
have both their co-ordinate axes aligned and  is moving at a velocity
is moving at a velocity  along
along 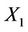 axis as observed by
axis as observed by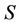 . The inertial frame
. The inertial frame 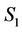 has another co-ordinate reference frame
has another co-ordinate reference frame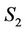 , where
, where 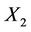 axis of
axis of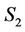 , is rotated by an angle
, is rotated by an angle 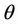 counter clockwise with respect to
counter clockwise with respect to 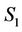 on
on 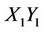 plane. Frames
plane. Frames 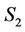 and
and 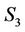 have both their co-ordinate axes aligned and
have both their co-ordinate axes aligned and 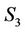 is moving at a velocity
is moving at a velocity 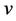 along
along 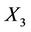 axis as observed by
axis as observed by 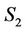 [3]. Then magnitude of resultant velocity of an event of
[3]. Then magnitude of resultant velocity of an event of 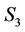 as observed by
as observed by 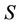 would be
would be
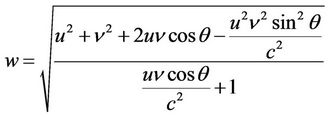 (5)
(5)
In (5) it is clear that 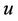 and
and 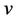 are two linear velocities in different directions and rotational angle between
are two linear velocities in different directions and rotational angle between 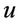 and
and  is
is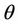 . From these implications we get Case-1: When
. From these implications we get Case-1: When 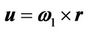 and
and 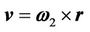 as in [4] then it may be called rotation-rotation interaction (i.e. R-R interaction) where, respectively
as in [4] then it may be called rotation-rotation interaction (i.e. R-R interaction) where, respectively  and
and 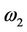 are angular velocities of
are angular velocities of 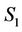 and
and 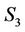 about
about  and
and 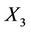 axes. It is also pointed out that origin of frames are same with respect to
axes. It is also pointed out that origin of frames are same with respect to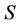 . If the particle is imagined at the origin of frame
. If the particle is imagined at the origin of frame  then it possesses two superimposed spins i.e. spin-spin interaction (S-S interaction) which is homogeneous with R-R interaction.
then it possesses two superimposed spins i.e. spin-spin interaction (S-S interaction) which is homogeneous with R-R interaction.
Case-2: When 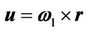 but
but 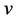 is linear then it may be called rotation-linear (i.e. R-L) interaction and that will be S-L interaction if the particle is present at the origin of
is linear then it may be called rotation-linear (i.e. R-L) interaction and that will be S-L interaction if the particle is present at the origin of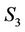 .
.
Case-3: When 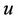 and
and 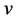 both are linear motions then it is called L-L interaction.
both are linear motions then it is called L-L interaction.
![]()
![]() Following [9] this may be written as
Following [9] this may be written as
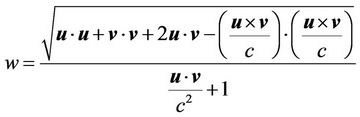 (6)
(6)
So
 (7)
(7)
where,  also,
also, 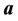 and
and  are normal to each other.
are normal to each other.
 represents velocity along space coordinate and
represents velocity along space coordinate and
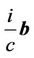 represents velocity along time coordinate. So,
represents velocity along time coordinate. So, 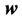
in (7) is a four velocity and from it we get a four velocity matrix 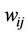 where,
where,
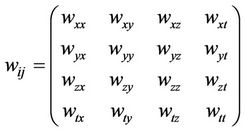 (7a)
(7a)
Hence to an observer in 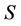 resultant velocity
resultant velocity 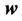 in (7) is of complex nature. And the relativistic mass of the particle
in (7) is of complex nature. And the relativistic mass of the particle
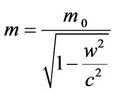 (8)
(8)
and relativistic Lagrangian would be
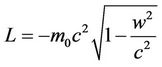 (9)
(9)
which leads to the form of relativistic momentum
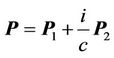 (10)
(10)
where, 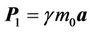 ,
,  and
and 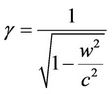
when θ = 90˚, then we get from (7)
 (11)
(11)
where, 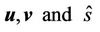 are mutually normal to each other which leads to the form of momentum
are mutually normal to each other which leads to the form of momentum
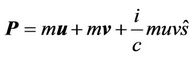 (12)
(12)
where, 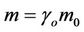 and
and
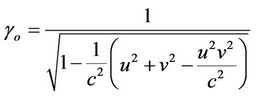
It is seen that Equations (10) and (12) represents a complex momentum of the particle. For a relativistic particle taking 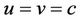 we get from (11)
we get from (11)
 (13)
(13)
For R-R interaction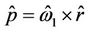 ,
, 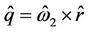 and
and  .
.
For R-L interaction  and
and  (i.e. direction of linear velocity of
(i.e. direction of linear velocity of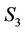 )
)
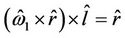
So, following (12) momentum would be
 (14)
(14)
It is understood that due to every relativistic motion kinetic energy respective virtual mass 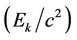 is attributed to the particle and due to every relativistic spin it rotates about the axis with relativistic velocity approaching that of light [2]. So S-S interaction or S-L interaction or L-L interaction of the particle implies that
is attributed to the particle and due to every relativistic spin it rotates about the axis with relativistic velocity approaching that of light [2]. So S-S interaction or S-L interaction or L-L interaction of the particle implies that 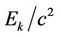 performing two superimposed motions with velocity as in (13) reveals one kind of stress energy tensor (i.e. one kind of field). Following Equation (14) we get momentum-density
performing two superimposed motions with velocity as in (13) reveals one kind of stress energy tensor (i.e. one kind of field). Following Equation (14) we get momentum-density
 (15)
(15)
So, we can write a function of field 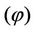 as below
as below
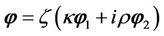 (16)
(16)
where, 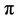 is canonically conjugate to
is canonically conjugate to 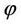
here, 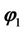 and
and 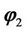 are real fields,
are real fields,  and
and 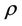 are constants.
are constants.
3. Complex Momentum and Field of Photon
Light is electromagnetic wave. It carries electric and magnetic fields which is proved by Faraday effect and Kerr effects. But photon is a particle whose kinetic energy is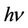 , having mass
, having mass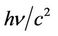 . Photon has spin motion about an axis and it may be considered as a small mass
. Photon has spin motion about an axis and it may be considered as a small mass  concentrated in a ring of radius
concentrated in a ring of radius 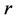 and rotates at velocity of light
and rotates at velocity of light 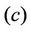 and it also has linear motion with velocity
and it also has linear motion with velocity 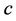 along the axis of rotation [10, 11]. It is one kind of S-L interaction which is homogeneous with R-L interaction. So resultant velocity would be as in (13) which gives the complex momentum of photon as shown below
along the axis of rotation [10, 11]. It is one kind of S-L interaction which is homogeneous with R-L interaction. So resultant velocity would be as in (13) which gives the complex momentum of photon as shown below
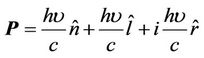 (17)
(17)
This leads to the electromagnetic wave function as specified in [12,13] respectively
 (18)
(18)
 (19)
(19)
where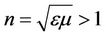 , Now we can write
, Now we can write 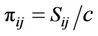 and
and
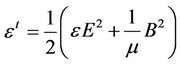 where,
where, 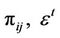 and
and 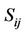 are respectively the momentum density energy density and poynting vector of electromagnetic field of photon, So we can write stress energy tensor of this field as
are respectively the momentum density energy density and poynting vector of electromagnetic field of photon, So we can write stress energy tensor of this field as
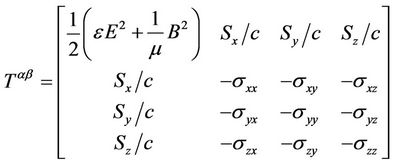 (20)
(20)
where 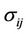 is the Maxwell stress tensor [14]. Since
is the Maxwell stress tensor [14]. Since 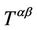 is the basis of electromagnetic field so,
is the basis of electromagnetic field so, 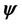 in (18) would be four dimensional wave function as
in (18) would be four dimensional wave function as
 (21)
(21)
Again from [6,7,15] a concept is that photon charge is possible with both types, positive and negative, and also upper limit of photon charge is 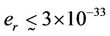 of elementary charge. It is also possible that photon has two types of spins (i.e. clockwise or anti-clockwise). Since directions of field depend on the direction of momentum so, nature of charges (i.e. positive or negative) would be determined by the type of spins. It is understood that
of elementary charge. It is also possible that photon has two types of spins (i.e. clockwise or anti-clockwise). Since directions of field depend on the direction of momentum so, nature of charges (i.e. positive or negative) would be determined by the type of spins. It is understood that 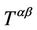 reveals the field. Photon carries electric and magnetic fields which are functions of energy
reveals the field. Photon carries electric and magnetic fields which are functions of energy 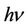 (or virtual mass
(or virtual mass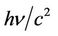 ) and momentum as given in Equation (17). From the concept of photon we can write energy-momentum tensor due to S-L interaction of a particle which appears as an electromagnetic field. From this we can assume that tensor due to S-S interaction of the particle generates electromagnetic field and the particle would be a rest charged element to the view of an observer in S. So a particle of rigid configuration may be charged having electromagnetic field if it possesses S-S or S-L interaction with corresponding relativistic speed. It is to be pointed out that electron, proton carry electric charge as well as electromagnetic field with its rigid configuration. Hence we can write,
) and momentum as given in Equation (17). From the concept of photon we can write energy-momentum tensor due to S-L interaction of a particle which appears as an electromagnetic field. From this we can assume that tensor due to S-S interaction of the particle generates electromagnetic field and the particle would be a rest charged element to the view of an observer in S. So a particle of rigid configuration may be charged having electromagnetic field if it possesses S-S or S-L interaction with corresponding relativistic speed. It is to be pointed out that electron, proton carry electric charge as well as electromagnetic field with its rigid configuration. Hence we can write, 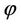 in (16) is an electromagnetic field function and to make a rest charged particle S-S interaction of it is required.
in (16) is an electromagnetic field function and to make a rest charged particle S-S interaction of it is required.
4. Field Transformation
Let gravitational field function in the frame 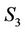 in Section 2 be
in Section 2 be  and which would be
and which would be 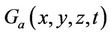 as observed by
as observed by 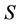
where 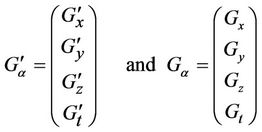
Then using (3) and (4) we get the relation between 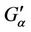 and
and 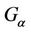 as
as
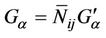 (22)
(22)
Inverse of this operation is given as
 (23)
(23)
It is understood that a particle of rigid configuration may be charged having S-S or S-L interaction with relativistic speed as in [2,10]. So we can write 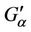 performing two superimposed motions (which is associated with
performing two superimposed motions (which is associated with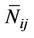 ) generates electromagnetic field function
) generates electromagnetic field function 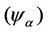 which would be homogeneous with
which would be homogeneous with 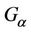 in (22). So we can consider a relation
in (22). So we can consider a relation
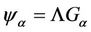 (24)
(24)
This leads to the form
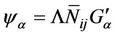 (25)
(25)
Similarly, using four velocity matrix as in (7A) we can consider the above relation as
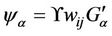 (26)
(26)
where  and
and 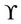 are two constants which depend on the medium.
are two constants which depend on the medium.
5. Conclusion
A particle can possess two simultaneous superimposed spins (i.e. S-S interaction). To get an electromagnetic field, energy-momentum tensor due to complex motion as well as complex momentum of a relativistic particle as in (7) and (10) are required. But to make an elementary rest charged particle, to the view of an observer, S-S interaction of it is required. In such manners a particle of rigid configuration having gravitational field generates electromagnetic field. Equation (26) reveals the relations between electromagnetic field and gravitational field.
6. Acknowledgements
Author thanks the authorities of Satmile High School, Satmile-721452, W. B., India for their continuous encouragements.
REFERENCES
- R. Resnick, “Introduction to Special Relativity,” Wiley India Pvt. Ltd., New Delhi, 2009.
- M. C. Das and R. Misra, “Relativistic Spin of an Arbitrary Body,” Advance Studies in Theoretical Physics, Vol. 6, No. 3, 2012, pp. 135-138.
- C. Iyer and G. M. Prabhu, “Composition of Two Lorenz Boosts through Spatial and Space-Time Rotations,” Journal of Physical and Natural Sciences, Vol. 1, No. 2, 2007.
- M. C. Das and R. Misra, “Three Lorentz Transformations Considering Two Rotations,” Advance Studies in Theoretical Physics, Vol. 6, No. 3, 2012, pp. 139-145.
- A. Einstein, S. Preuss and A. Wiss, “The Principal of Relativity,” Dover, 1952, pp. 190-198.
- V. V. Kobychev and S. B. Porov, “Constraints on the Photon Charge from Observations of Extragalactic Sources,” Astronomy Letters, Vol. 31, No. 3, 2005, pp. 147-151. doi:10.1134/1.1883345
- C. Sivaram, “Constraints on the Photon Mass and Charge and Test of Equivalence Principle from GRB 990123,” Bulletin of the Astronomical Society of India, Vol. 27, No. 4, 1999, pp. 627-630.
- V. Y. Kosyev, “Electromagnetic Gravitational Interaction,” Conference “Time Machine”, Moscow, 12 April 2003.
- C. I. Mocanu, “Is Thomas Rotation a Paradox,” Apeiron, Vol. 16, 1993.
- Y. Rocard, “Thermodynamique,” Masson & Cie, Paris, 1957, p. 250.
- C. V. Raman and S. Bhagavantam, “Experimental Proof of the Spin of the Photon,” Indian Journal of Physics, Vol. 6, 1931, pp. 353-366.
- I. I. Popescu, P. Sterian and M. Dobre, “The Photon Wave Function and the Fresnel Formulas,” Romanian Reports in Physics, Vol. 62, No. 2, 2010, pp. 360-368.
- R. E. Nistor, “Quantum Aspects of Photon Propagation in Transparent Infinite Homogeneous Media,” Romanian Reports in Physics, Vol. 60, No. 3, 2008, pp. 471-491.
- J. B. Hartle, “Gravity: An Introduction to Einstein’s General Relativity,”3rd Edition, 2009, p. 512.
- L. B. Okun, “On the Charge of the Photon,” 2005. http://arXiv:hep-ph/0505250v1
NOTES
*Corresponding author.

