International Journal of Astronomy and Astrophysics
Vol.1 No.3(2011), Article ID:7366,9 pages DOI:10.4236/ijaa.2011.13020
Effect of Altitude, Right Ascension of Ascending Node and Inclination on Lifetime of Circular Lunar Orbits
1Applied Mathematics Division, Vikram Sarabhai Space Centre, Thiruvananthapuram, India
2Present Address: Department of Aerospace Engineering, School of Mechanical Sciences, Karunya University, Coimbatore, India
E-mail: *sddgupta@gmail.com, ramkrishansharma@gmail.com
Received June 23, 2011; revised July 25, 2011; accepted August 8, 2011
Keywords: Lifetime of Lunar Orbits, Transition Altitude, Right Ascension of Ascending Node, Polar Orbits, Long-Periodic Effects of Earth’s Gravity
Abstract
The lifetime of a lunar satellite orbit is constrained by the non-spherical nature of the Moon’s gravity field. The orbital lifetime of lunar orbits depends significantly on the initial conditions of the orbit. Right ascension of ascending node (Ω) is one of the important orbital parameter affecting the orbital lifetime. In the present work we have analyzed the effect of Ω on the variation of lifetime with altitude for circular lunar orbits. It is found that at a particular initial altitude, a small increase in the altitude results in substantial increase in the orbital lifetime due to effect of the long periodic terms of Earth’s gravity on eccentricity and this transition altitude is different for different Ω. Further, it is observed that the variation of transition altitude with Ω follows a definite, but different trend for orbits with different inclinations. The transition altitude for polar orbits is found to be higher without the effect of Sun and Earth gravity. Variation of transition altitude with orbital inclination is also analyzed. Lifetimes of high altitude circular lunar orbits are analyzed and it is observed that at high altitudes lifetime decreases with altitude.
1. Introduction
It is well known that the orbit of a lunar satellite and consequently its orbital lifetime is mainly influenced by the gravitational field of Moon, Earth and Sun [1-6]. The primary perturbation on a low-altitude (100 km or 300 km) lunar parking orbit is mainly due to Moon’s nonspherical gravity field which also has mascons. An unstable satellite orbit around moon will have more fuel requirements for orbit maintenance without which it will crash into moon’s surface. Hence lunar orbits need to be designed in such a way that they not only meet ideal observation conditions but also have less fuel requirements for orbit maintenance. In this regard it is crucial to understand the factors affecting the stability and lifetime of lunar orbits. Various studies have been carried out to analyze the behavior of low lunar orbits which minimizes the mission cost by providing efficient mapping orbits [3-6]. Tzirti Tsiganis, Varvoglis [7] and Melo, Winter, Neto [8] employed periodic orbit approach to find stable orbits around Moon.
The orbital lifetime depends on the initial orbital parameters of the satellite. Some of the important contributions on the study of dependence of lunar orbital lifetime on initial orbital parameters are by Mayer, Buglia and Desai [9], Ramanan and Adimurthy [10], Wang and Lin [11] and Zeile et al. [12].
In their study [9], Mayer, Buglia and Desai analyzed the dependence of lifetime on initial inclination and argument of perigee and its sensitivity to lunar gravity harmonics. Ramanan and Adimurthy [10] analyzed the effect on initial inclination on lifetime of 100 km circular orbit. They also analyzed the influence of the higher order harmonics of the lunar gravity field. Wang and Lin [11] carried out a detailed theoretical analysis on the orbital lifetime and orbital inclination of a low moonorbiting satellite. They also validated their results numerically. Zeile et al. [12] investigated the effect of initial inclination, right ascension of ascending node and argument of perigee on the orbital lifetime along with the ground coverage analysis.
In this paper we study the effect of altitude, right ascension of ascending node and inclination on lifetime of circular lunar orbits. Detailed simulations are carried out to analyze the effect of altitude on lifetime. It is found that at a particular orbital altitude the lifetime increases substantially. This is due to the effect of long periodic terms of Earth’s gravity (zonal and tesseral harmonics) on the eccentricity of the lunar satellite orbits. Effect of inclination and right ascension of ascending node on the lifetime variation due to altitude is also studied. Further the effect of the Sun and the Earth gravity on the orbital lifetime of circular polar orbits of Moon is analyzed.
2. Propagation Model Description and Model Validation
2.1. Propagation Model Description
The analysis is carried out with the lunar orbit propagation software “lprop” available in public domain (http://www.cdeagle.com). The propagator takes orbital parameters in the lunar mean equator and IAU node of J2000 as initial conditions. The initial orbit epoch can be given in Barycentric Dynamical Time (TDB) and Coordinated Universal Time (UTC). It can take different lunar gravity models with variable degree and order terms. Effect of Sun and Earth point mass gravity is also available in the orbit propagator and is optional. The propagation duration is given in days. The output of the software is a file which gives the state vectors and orbital elements in the specified time interval up to 16 decimal places of accuracy.
2.2. Model Validation
We have validated the software with the published results as well as with STK, which is widely used commercial software developed by the AGI Corporation.
a) Validation with STK
Table 1 gives the lifetime of a circular polar orbit with 100 km altitude calculated using lprop and STK for various initial orbit epochs using LP150Q lunar gravity model. The estimated lifetimes with ‘lprop’ show a close match with that calculated from STK. The maximum percentage error in the lifetimes calculated from “lprop”

Table 1. Comparison of lifetime of circular polar orbit with different initial orbit epoch.
is 0.11% as compared with the lifetimes obtained from STK.
b) Validation with the results in [10]
Lifetime of 100 km circular polar orbit is assessed for various orbital inclinations using LP100J and LP150Q lunar gravity model and is plotted in Figure 1. The figure shows a close resemblance with the result given in [10].
c) Validation with the results in [13]
The lifetime computed using different gravity terms of LP165P gravity model and without considering gravity due to Sun and Earth point mass gravity, is provided in Table 2. The results are compared with those given in [13]. The maximum percentage error is only 1.35%. Figure 2 shows the difference in lifetime computed using Sun and Earth gravity and without considering it for a 100 km circular polar orbit using LP165P (50 × 50) model. The result is comparable with the result given in [13].
3. Orbital Lifetime
3.1. Analysis on Orbital Lifetime
For the simulations presented here, the LP150Q gravita-

Figure 1. Effect of inclnation on orbital life time.
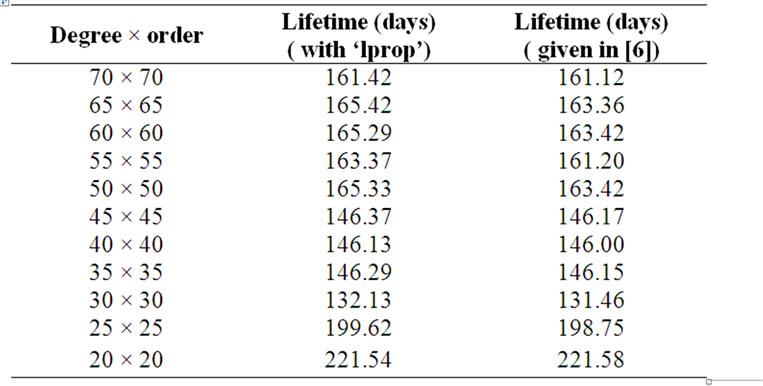
Table 2. The effect of different harmonics of lunar gravity on the life time of the 100 km circular lunar orbit.

Figure 2. Effects of Earth and Sun gravity on the circular lunar polar orbit.
tional model with degree and order 50 is used. The lunar gravity field, LP150Q, is a 150th spherical harmonic degree and order model. This gravity field was developed using the available data from past US missions to Moon including the Lunar Orbiter missions, the Apollo 15 and Apollo 16 sub-satellites, Clementine, and the Lunar Prospector Doppler and range data [14].
In the present study, the radius of moon is taken to be 1738 km. The values of 
 and
and  (gravitational constants of Moon, Earth and Sun, respectively) used in the simulations are 4902.800076 km3/s2, 398,600.436233 km3/s2 and 132,712,440,040.944 km3/s2, respectively. For every simulation, the orbit is propagated taking January 1, 2010 (TDB) as initial epoch. Lifetime is calculated as the time from the initial epoch to the time at which the periapsis altitude becomes zero.
(gravitational constants of Moon, Earth and Sun, respectively) used in the simulations are 4902.800076 km3/s2, 398,600.436233 km3/s2 and 132,712,440,040.944 km3/s2, respectively. For every simulation, the orbit is propagated taking January 1, 2010 (TDB) as initial epoch. Lifetime is calculated as the time from the initial epoch to the time at which the periapsis altitude becomes zero.
3.2. Lifetime of Low Altitude Lunar Orbits
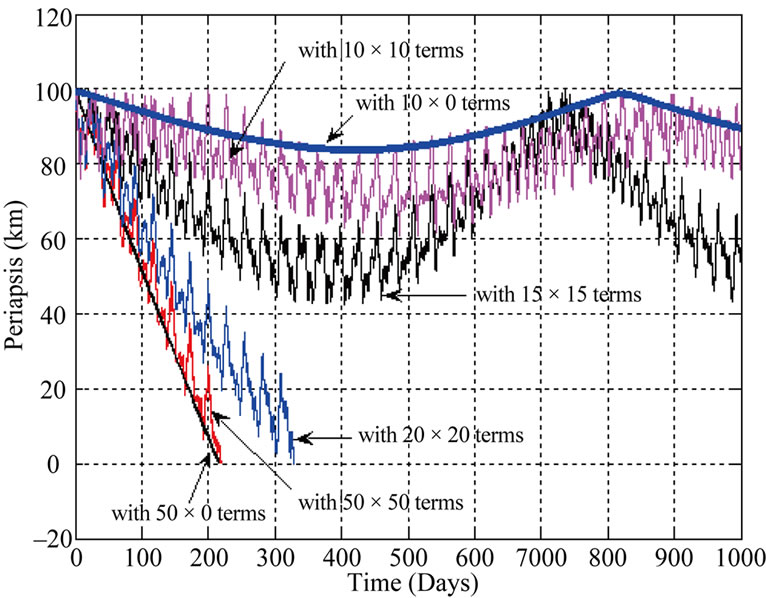
The estimation of lifetime of a lunar orbit strongly depends on the lunar gravity model and the number of the gravity terms. Figure 3(a) shows the variation in periapsis of a 100 km circular polar lunar orbit using 10 × 0, 10 × 10, 15 × 15, 20 × 20, 50 × 0 and 50 × 50 terms of the lunar gravity model LP150Q. Vast difference is seen in lifetime estimated by (10 × 10) and (50 × 50) terms. Assessment from Figure 3(b) shows that the lifetime estimated using 50 × 50 and 60 × 60 terms are comparable.
A comparison of lifetime estimated with 5 lunar gravity models (LP75G, LP100K, LP100J, LP165P, and LP150Q) using 50 × 50 gravity terms for a circular polar lunar orbit of 125 km altitude is shown in Figure 4. It can be observed that the lifetime calculated with the models LP75G and LP100 K is around 384 days while that computed with the models LP100J, LP165P and LP150Q is 411 days.
 (a)
(a) (b)
(b)
Figure 3. (a). Variation of periapsis of a 100 km circular polar lunar orbit using different gravity terms of lp150q; (b). Variation of periapsis of a 100 km circular polar lunar orbit using 50 × 50 and 60 × 60 terms.
Table 4 shows the comparison of lifetime of lunar orbits estimated with 50 × 50 gravity terms and with 50 zonal harmonics terms of LP150Q model without including Sun and Earth point mass gravity effect. It can be observed that the orbital lifetime predicted using only zonal harmonics gives higher values as compared to the orbital lifetime computed with 50 zonal and 50 tesseral terms in most of the cases. This indicates the significance of tesseral harmonics terms in lunar gravity model for assessing the orbital lifetimes of lunar satellites.
It is noticed that for a fixed value of Ω, the lifetime increases significantly after a particular altitude. This is essentially due to the gradual reduction of the effect of the long periodic terms of Moon’s gravity on eccentricity of the orbit. It is depicted from Figures 5(a) and 5(b)

Figure 4. Variation of periapsis for last 31 days of a 125 km circular orbit using different lunar gravity model.
 (a)
(a)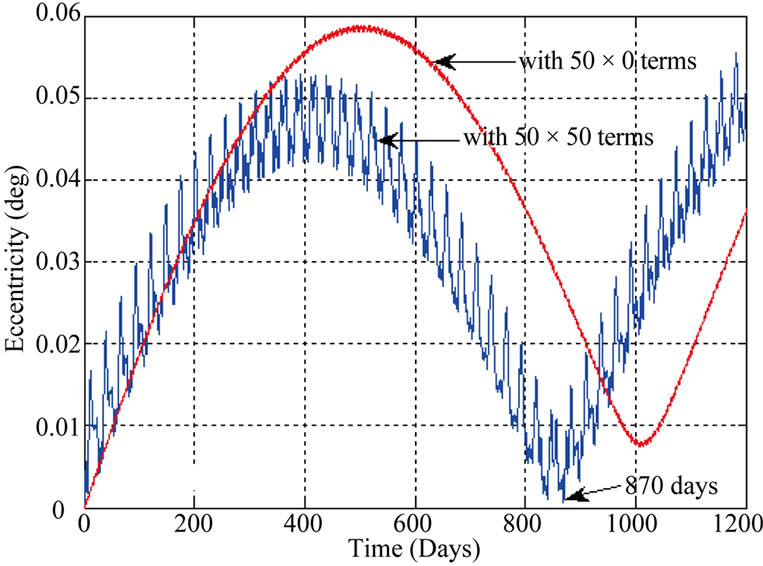 (b)
(b)
Figure 5. (a) Evolution of eccentricity of a 138 km circular polar orbit (Ω = 25˚); (b) Evolution of eccentricity of a 99 km circular polar orbit (Ω = 125˚).
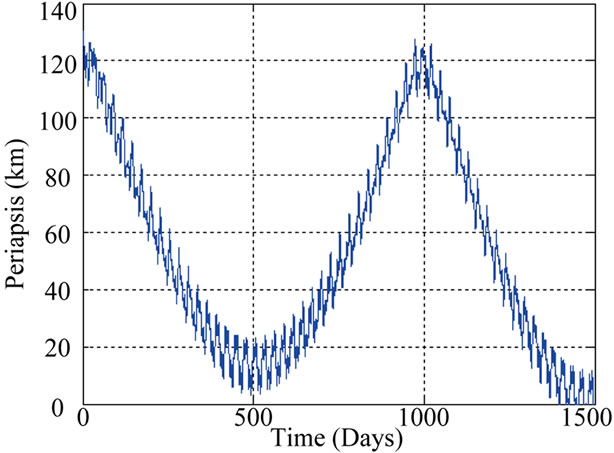
where the period of the long periodic term on eccentricity for two orbits with initial altitude 138 km (Ω = 25˚) and 99 km (Ω = 125˚) are 920 days and 870 days, respectively. It may be noted that the long periodic terms due to 50 × 50 Moon’s gravity have different period of long periodic terms on eccentricity than the 50 × 0 Moon’s gravity which may be seen in Figures 5(a) and 5(b). Initially the periapsis starts decreasing and if it does not reaches to zero altitude, it again starts increasing. Then it has to take at least one cycle to reach to zero altitude resulting in higher orbital lifetime. As observed in Figure 6, for the case where Ω = 60˚ and the initial altitude of 130.25 km, the periapsis becomes zero after 414 days. In Figure 7, for initial altitude of 130.50 km, it is observed that the periapsis first starts decreasing and has periapsis altitude slightly greater than zero and then again starts increasing. Thus, it leads to a higher orbital lifetime.

Figure 6. Periapsis variation of a circular polar orbit with initial altitude 130.25 km and Ω = 60˚.
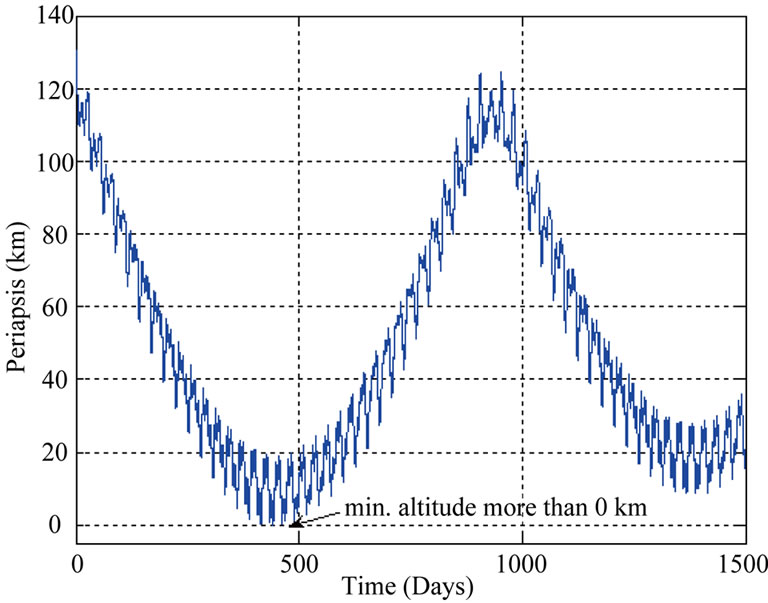
Figure 7. Periapsis variation of a circular polar orbit with initial altitude 130.50 km and Ω = 60˚.
Depending on the initial altitude, the altitude of the orbit can be zero in the first cycle itself, if not, the periapsis increases due to long periodic terms and comes down in next cycle and can become zero. Hence for a particular initial altitude, periapsis can vanish in its first cycle while for a little higher altitude it lifts and lifetime can be much higher. We define the transition altitude as the altitude for which the orbital lifetime increases substantially (at least one cycle more) with a very small increase (of the order of 0.1 to 0.2 m) in the altitude. Figure 8 shows the variation of transition altitude with Ω for circular polar orbit. The transition altitude is different for different values of Ω and follows a definite trend. The plot also shows the difference in transition altitude when Sun and Earth gravity are ignored. It is observed from Figure 8 that for circular polar orbits the transition altitude computed without considering Sun and Earth gravity is more than that computed using Sun and Earth gravity effect. It is essentially due to the effect of the long periodic terms of Earth’s gravity on the eccentricity of the lunar satellite orbit.
On considering Sun and Earth gravity effects for circular polar orbits, the transition altitude decreases from 138 km (Ω = 30˚) to 99 km (Ω = 120˚) and again in-
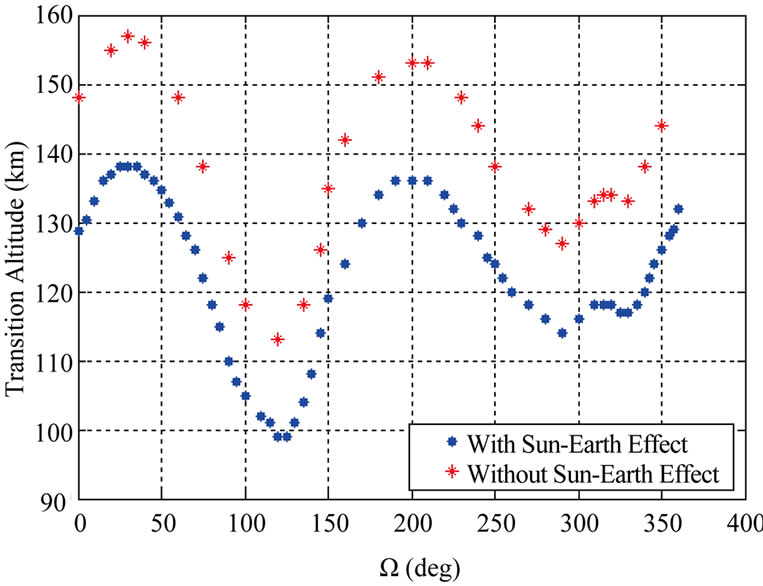
Figure 8. Variation of transition altitude with Ω for circular polar orbit.
creases to 136 km (Ω = 210˚) and then decreases to 114 km (Ω = 290˚). It can be seen that for circular polar lunar orbit, for a given Ω, the lifetime will be of the order of 300 days to 400 days for the altitudes below this curve, while for the altitudes above this curve lifetime will be of the order of 3 years or more. As a particular case, Figure 9 shows the variation of orbital lifetime with altitude for a circular polar orbit with Ω = 0˚. Table 3 gives the lifetime of circular polar orbit at transition altitudes.
Figure 10 shows the periapsis variation for an orbit with an initial altitude of 140 km for 10,000 days. From this figure, it can be inferred that if the long periodic terms due to Moon’s gravity on eccentricity are not able to bring down the periapsis to zero then the lifetime will be very long.
Figures 11, 12 and 13 show the variation in transition altitude for circular orbits with initial orbital inclination 10˚, 50˚ and 70˚ and the transition altitude varies from 138 km to 182 km, 40 km to 156 km, and 33 km to 270 km, respectively. It may be noted that different trends in transition altitudes are seen for different inclinations with variation of Ω from 0 to 360 degrees. The effect of altitude on lifetime of circular lunar orbit of different incli
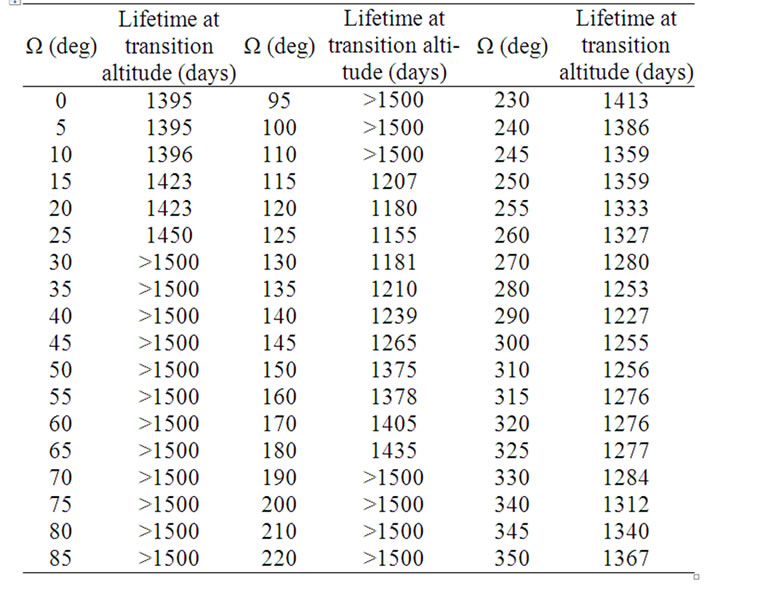
Table 3. Lifetime of circular polar orbits at transition altitudes.
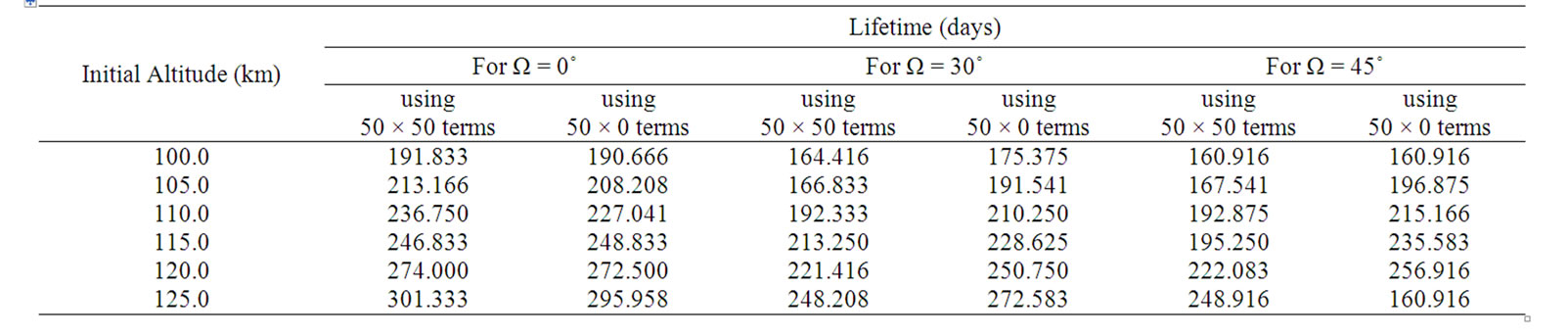
Table 4. Comparison of lifetime of lunar polar orbit estimated using 50 × 50 and 50 × 0 lunar force model.
nation is also analyzed for Ω = 0˚. Figure 14 shows the variation of transition altitude with orbital inclination. For all the results presented here for circular orbits, the argument of periapsis and the true anomaly are taken as zero for the initial conditions. Ω is varied from 0˚ to 360˚ in the intervals of 1˚ to 10˚ depending upon the trend in variation. For each value of Ω, the lifetime is calculated for different altitudes ranging from 30 to 500 km.
Figures 15(a) to 15(f) show the variation in orbital parameters of a 130 km altitude circular polar orbit. As seen from Figure 15(d) Variation of nearly 2 degrees in inclination is noticed.
3.3. Lifetime of High Altitude Lunar Orbits
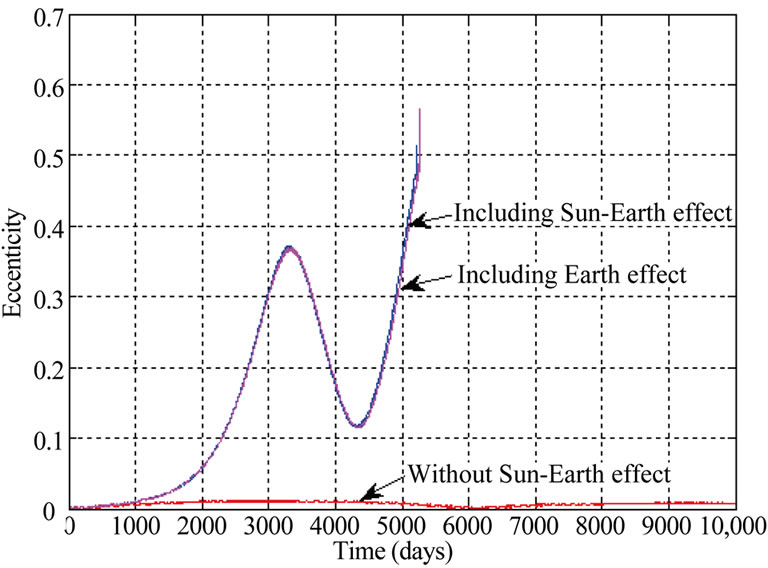
Apart from the gravity field of Moon, lifetime of high altitude lunar orbit is mostly influenced by gravitational field of Earth. At higher altitudes, the perturbations due to Earth’s gravity have significant effect on the lifetime of lunar orbits. The variation of periapsis of 1200 km circular orbit (inclination = 55˚) without considering Earth and Sun gravity, considering the Earth’s gravity alone and considering both Sun and Earth gravity is given in Figure 16(a). Figure 16(b) gives the variation in eccentricity of the orbit. It can be seen that gravity effect of Sun causes very less variation on the periapsis variation and hence on the orbital lifetime. The perigee variation shows a very high lifetime if the gravity effect of Sun and Earth are not considered. Hence for the lifetime estimation of lunar orbits, the gravity effect of Earth is essential.
Figures 17(a), 17(b), 17(c) and 17(d) give the variation in lifetime with altitude for circular orbits with inclinations of 60˚, 65˚, 63.4˚ and 90˚. For an orbit with

Figure 9. Variation of orbital lifetime with altitude for Ω = 0˚.

Figure 10. Periapsis variation of a 140 km altitude circular orbit during 10,000 days.

Figure 11. Variation of transition altitude with Ω (inclination = 10˚).
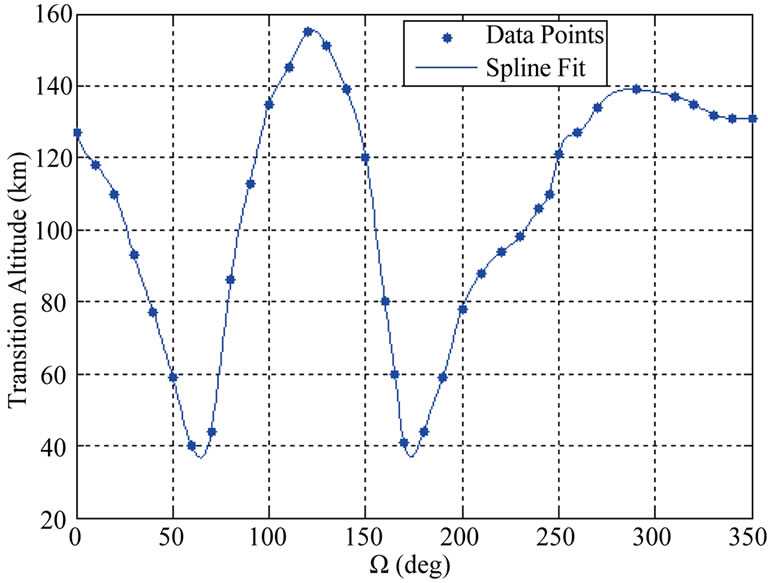
Figure 12. Variation of transition altitude with Ω (inclination = 50˚).

Figure 13. Variation of transition altitude with Ω (inclination = 70˚).
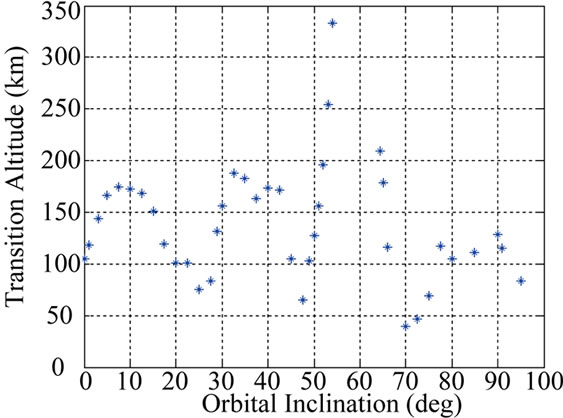
Figure 14. Variation of transition altitude with orbital inclination.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)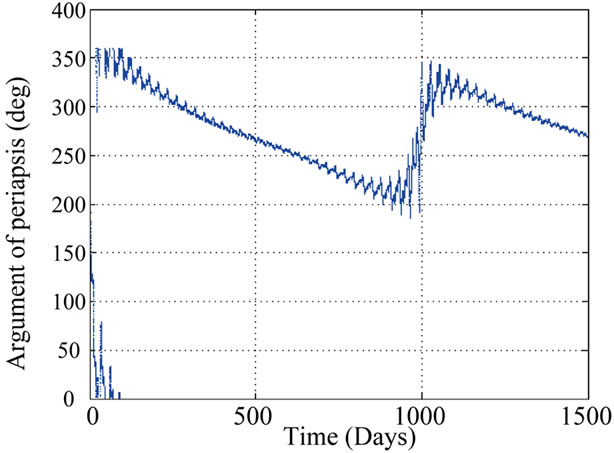 (e)
(e) (f)
(f)
Figure 15. Variation in Orbital Parameter of a 130 km initial altitude polar orbit (Initial Ω = 0˚). (a) Periapsis variation; (b). Apoapsis variation; (c). Variation in eccentricity; (d). Variation in inclination; (e). Variation in argument of periapsis; (f). Variation in Ω.
 (a)
(a)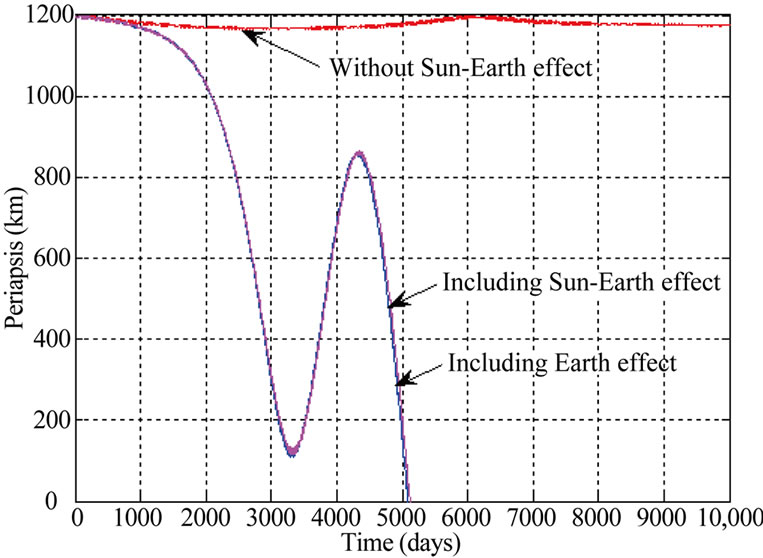 (b)
(b)
Figure 16. (a). Variation of periapsis of 1200 km circular orbit (i = 55˚); (b). Variation of eccentricity of 1200 km circular orbit (i = 55˚).
 (a)
(a)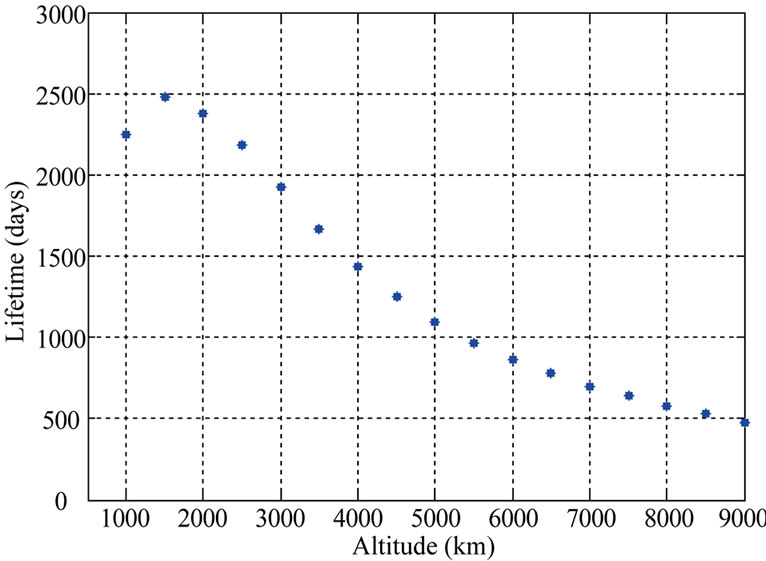 (b)
(b)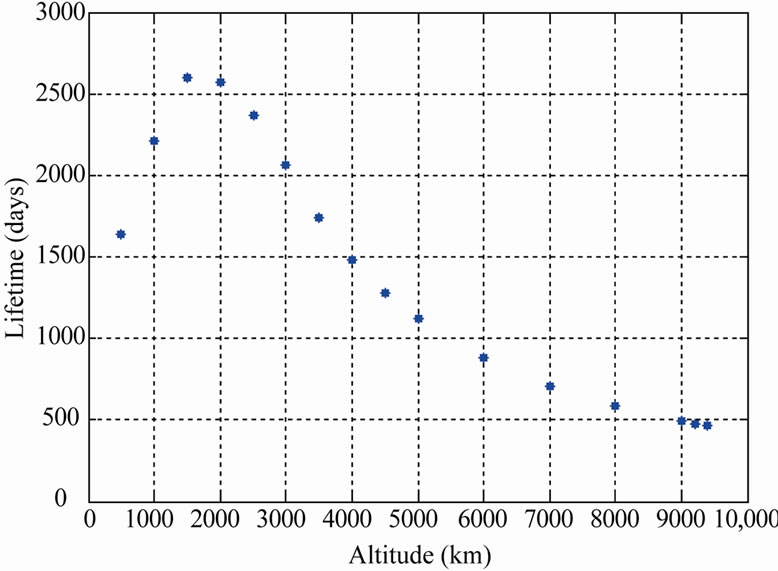 (c)
(c)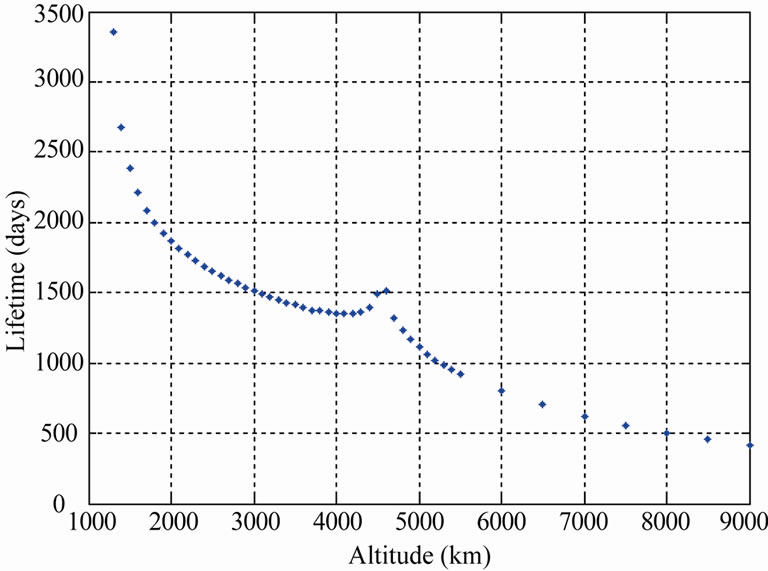 (d)
(d)
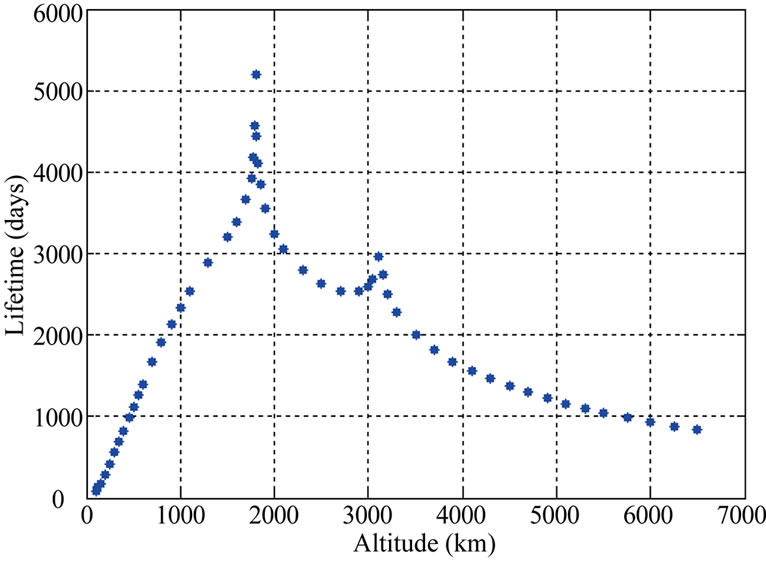
Figure 17. (a). Variation of lifetime with altitude for circular orbit (i = 60˚); (b). Variation of lifetime with altitude for circular orbit (i = 65˚); (c). Variation of lifetime with altitude for circular orbit (i = 63.4˚); (d). Variation of lifetime with altitude for circular orbit (i = 90˚).
inclination 60˚, the altitude is varied from 100 km to 6500 km (cf. Figure 17(a)). The lifetime first increases from 83 days (for 100 km orbit) and becomes maximum (5197 days) at an altitude of 1800 km and then it starts decreasing. At an altitude of 6500 km, the lifetime becomes 845 days. In Figure 17(b), altitude is varied from 1000 km to 9000 km. The lifetime first increases and it is maximum at 1500 km altitude and then starts decreasing. Same trend in lifetime variation can be observed in Figure 17(c). For circular polar orbit the altitude is varied from 1200 km to 9000 km. The variation of lifetime with altitude for circular polar orbit is shown in Figure 17(d).
Lifetime of high altitude circular lunar orbits decreases with altitude. This is due to the increase of Earth’s gravitational effect on long periodic terms in eccentricity i.e. the eccentricity starts increasing resulting in the decrease of perigee altitude to zero.
4. Conclusions
The effect of right ascension of ascending node (Ω) on the variation of lifetime with altitude is assessed. It is found that for a given Ω, the lifetime increases with altitude and at a particular altitude defined as transition altitude lifetime increases substantially due to the effect of long periodic terms of Earth’s gravity (zonal and tesseral harmonics) on eccentricity of the orbit. Earth’s gravity dominates over the Moon’s gravity with respect to the long periodic effect on eccentricity of the orbit. The transition altitude varies from 138 km to 182 km, 40 km to 156 km, 33 km to 270 km and 99 km to 138 km for orbits with inclination of 10˚, 50˚, 70˚ and 90˚, respectively. There is significant effect of Earth gravity on transition altitudes while the effect of Sun’s gravity is very marginal. Variation of transition altitude with orbital inclination is also analyzed. Lifetime of high altitude circular lunar orbits is analyzed and it is observed that at high altitudes lifetime decreases with altitude.
5. References
[1] P. M. Muller and W. L Sjogren, “Mascons: Lunar Mass Concentrations,” Science, Vol. 161, No. 3482, 1968, pp. 680-684.
[2] A. Konopliv, S. W. Asmar, E. Carranza, W. L. Sjogren and D. N. Yuan, “Recent Gravity Models As a Result of the Lunar Prospector Mission,” Icarus, Vol. 150, No. 1, 2001, pp. 1-18.
[3] A. Abad, A. Elipe and E. Tresaco, “Analytical Model to Find Frozen Orbits for a Lunar Orbiter,” Journal of Guidance, Control, and Dynamics, Vol. 32, No. 3, 2009, pp. 888-898. doi:10.2514/1.38350
[4] D. Folta and D. Quinn, “Lunar Frozen Orbits,” AIAA 2006-6749, AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, 21-24 August, 2006.
[5] S. Y. Park and J. L. Junkins, “Orbital Mission Analysis for a Lunar Mapping Satellite,” Journal of the Astronautical Sciences, Vol. 43, No. 2, 1995, pp. 207-217.
[6] R. P. Russell and M. Lara, “Long-Life Lunar Repeat Ground Track Orbits,” Journal of Guidance, Control, and Dynamics, Vol. 30, No. 4, 2007, pp. 982-993. doi:10.2514/1.27104
[7] S. Tzirti, K. Tsiganis and H. Varvoglis, “Effect of 3rd -Degree Gravity Harmonics and Earth Perturbations on Lunar Artificial Satellite Orbits,” Celestial Mechanics and Dynamical Astronomy, Vol. 108, No. 4, 2010, pp. 389-404. doi:10.1007/s10569-010-9313-3
[8] C. F. de Melo, O. C. Winter and E. Vieira Neto, “Numerical Study of Low-Cost Alternative Orbits around the Moon,” Advances in Space Research, Vol. 36, No. 3, 2005, pp. 552-560. doi:10.1016/j.asr.2005.07.052
[9] K. W. Meyer, J. J. Buglia and P. N. Desai, “Lifetimes of Lunar Satellite Orbits,” NASA Technical Paper 3394, March 1994.
[10] R. V. Ramanan and V. Adimurthy, “An Analysis of near Circular Lunar Mapping Orbits,” Journal of Earth System Science, Vol. 114, No. 6, 2005, pp. 619-626. doi:10.1007/BF02715946
[11] H.-H. Wang and L. Lin, “A Study on the Relationship between the Orbital Lifetime and Inclination of Low Lunar Satellites,” Chinese Journal of Astronomy and Astrophysics, Vol. 5, No. 6, 2005, pp. 665-670. doi:10.1088/1009-9271/5/6/012
[12] O. Zeile, M. Lachenmann, E. Baumstark, A. Mohr, D. Bock, R. Laufer, N. Sneeuw and H.-P. R¨oser, “Analyses of Orbital Lifetime and Observation Conditions of Small Lunar Satellites,” Acta Astronautica, Vol. 66, No. 3-4, 2010, pp. 516-527. doi:10.1016/j.actaastro.2009.07.008
[13] Y.-J. Song, S.-Y. Park, H.-D. Kim and E.-S. Sim, “Development of Precise Lunar Orbit Propagator and Lunar Polar Orbiter’s Lifetime Analysis,” Journal of Astronomy and Space Sciences, Vol. 27, No. 2, 2010, pp. 97-106.
[14] R. B. Roncoli, “Lunar Constants and Models Document, [JPL D-32296],” Jet Propulsion Laboratory, Pasadena, 2005.

