International Journal of Astronomy and Astrophysics
Vol.1 No.2(2011), Article ID:5671,10 pages DOI:10.4236/ijaa.2011.12008
Comprehensive Research on the Origin of the Solar System Structure by Quantum-Like Model
College of Physics and Electronics, Shandong Normal University, Jinan, China
E-mail: nqx2000cn@yahoo.com
Kuiper Belt, Asteroid Belt
Received April 10, 2011; revised May 17, 2011; accepted May 27, 2011
Keywords: Schrödinger Equation, Planetary Distances and Masses, Satellites Distribution, Rings Structure,
Abstract
A quantum-like model of gravitational system is introduced to explore the formation of the solar system structure. In this model, the chaos behavior of a large number of original nebular particles in a gravitational field can be described in terms of the wave function satisfying formal Schrödinger equation, in which the Planck constant 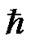 is replaced by a constant
is replaced by a constant 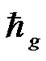 on cosmic scale. Numerical calculation shows that the radial distribution density of the particles has the character of wave curves with decreasing amplitudes and elongating wavelengths. By means of this model, many questions of the solar system, such as the planetary distance, mass, energy, angular momentum, the distribution of satellites, the structure of the planetary rings, and the asteroid belt and the Kuiper belt etc., can be explained in reason. In addition, the abnormal rotations of Venus and Mercury can be naturally explained by means of the quantum-like model.
on cosmic scale. Numerical calculation shows that the radial distribution density of the particles has the character of wave curves with decreasing amplitudes and elongating wavelengths. By means of this model, many questions of the solar system, such as the planetary distance, mass, energy, angular momentum, the distribution of satellites, the structure of the planetary rings, and the asteroid belt and the Kuiper belt etc., can be explained in reason. In addition, the abnormal rotations of Venus and Mercury can be naturally explained by means of the quantum-like model.
1. Introduction
There are many quantization phenomena on cosmic scale in the solar system, such as the planetary distance, orbital energy and angular momentum, the distribution of regular satellites of giant planets, planetary ring system, and so on. Among these phenomena, the planetary distance law, called Titius-Bode law [1], is the most famous one. Although this law has been studied for over two hundred years, its physical explanation remains open so far. Titius-Bode law is generally denoted as
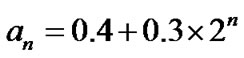 , (1)
, (1)
where 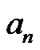 is the planetary orbital semi-major axis in astronomical units (AU),
is the planetary orbital semi-major axis in astronomical units (AU), 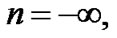 0, 1, 2, 4, 5 for the Mercury, Venus, Earth, Mars, Jupiter and Saturn. But Neptune and Pluto are not consistent with the law. Titius-Bode law means the planetary distance into a quantization series. The series are later also denoted by formulas [2-11]
0, 1, 2, 4, 5 for the Mercury, Venus, Earth, Mars, Jupiter and Saturn. But Neptune and Pluto are not consistent with the law. Titius-Bode law means the planetary distance into a quantization series. The series are later also denoted by formulas [2-11]
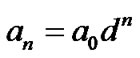 or
or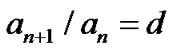 , (2)
, (2)
where 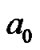 and d are constants and are given different values in different articles in order to fit in with the observations. Although the two formulas are still imprecise, the quantization series of the planetary orbits is more obvious. So some hypotheses on quantum theory of gravitational field have been continually raised [11-21]. The common view of these hypotheses is that the quantum mechanics theory can be applied not only to the microscopic field, but also possibly to the gravitational field in the cosmic scale, with the large scale Planck constants. Among these researchers, some used the analogy between the planetary orbits and Bohr-Sommerfeld quantization orbits, while others applied the Schrödinger equation or Schrödingerlike equation to planetary system. Despite some exciting results, the phenomena are far from being completely explained due to the complexity of the formation and evolution of the solar system. In addition, some other phenomena, such as the planetary mass, energy, angular momentum, and the structure of rings, are rarely studied yet, and to explain them requires a uniform theory.
and d are constants and are given different values in different articles in order to fit in with the observations. Although the two formulas are still imprecise, the quantization series of the planetary orbits is more obvious. So some hypotheses on quantum theory of gravitational field have been continually raised [11-21]. The common view of these hypotheses is that the quantum mechanics theory can be applied not only to the microscopic field, but also possibly to the gravitational field in the cosmic scale, with the large scale Planck constants. Among these researchers, some used the analogy between the planetary orbits and Bohr-Sommerfeld quantization orbits, while others applied the Schrödinger equation or Schrödingerlike equation to planetary system. Despite some exciting results, the phenomena are far from being completely explained due to the complexity of the formation and evolution of the solar system. In addition, some other phenomena, such as the planetary mass, energy, angular momentum, and the structure of rings, are rarely studied yet, and to explain them requires a uniform theory.
The fact that Titius-Bode law can be denoted by several different formulas with imprecision means that there is no real law in planetary distance, and this so-called “law” is obscure. In fact, the formation of the planetary distance is complex, which depends on the initial distribution of the solar nebula and the gravitational interaction between the planets. It should be an obvious fact that unlike the particles in nebula gas, the planets are too large to be dominated by quantum law.
By means of the Schrödinger-like equation of microscopic particles in the gravitational field, Nie et al. have made preliminary interpretations on the planetary distance [17], the population of Kuiper belt objects [22], and the unusual rotation of Venus and Mercury [23]. This paper attempts to systematically illustrate the origin of the solar system structure including planetary distance and mass, distribution of regular satellites, the asteroid belt and Kuiper belt, the structure of rings and so on.
2. A Quantum Clue on the Solar System
The similarities between quantum mechanics and stochastic motion of particles have been noticed in some early papers. Comisar (1965) has introduced a Brownian motion model to explain the behavior of electron described in quantum mechanics [24]. Nelson (1966) has given a derivation of the Schrödinger equation for an electron motion from the theory of Brownian motion [25]. Following Nelson, Nottale et al. (1997) have applied a Schrödinger-like equation to planets in the solar system [21].
The quantization character of planetary orbits has been expressed in teams of Bohr orbit 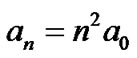 by some researchers (e.g., Yang [19], Agnese & Festa [20]), where
by some researchers (e.g., Yang [19], Agnese & Festa [20]), where  is the “Bohr radius” of planetary system with different values in various literatures, and n is the principal quantum number. The difficulty in applying Bohr orbit is that the values of n must be discrete integer in order to fit the planets and satellites.
is the “Bohr radius” of planetary system with different values in various literatures, and n is the principal quantum number. The difficulty in applying Bohr orbit is that the values of n must be discrete integer in order to fit the planets and satellites.
If we divide the planets into two groups, the first group including the Mercury, Venus, Earth, Mars and asteroid belt, the second group including the Jupiter, Saturn, Uranus, Neptune and Kuiper belt, the different characteristics in two groups of planets can be shown, and planetary distances, energies and angular momentums carried by unit mass can approximately form two same successive sequences with the continuous integer . It is important that the ratio of the mean “Bohr radius” of two groups of planetary orbits is approximately 16, i.e.
. It is important that the ratio of the mean “Bohr radius” of two groups of planetary orbits is approximately 16, i.e.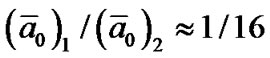 . Comparing the format between gravitational force and Coulomb force,
. Comparing the format between gravitational force and Coulomb force,
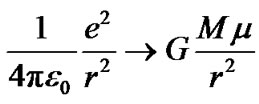 , (3)
, (3)
using the analogy ,
, 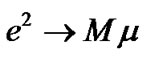 and
and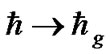 , the following relation between Coulomb field in a hydrogen atom and gravitational field in the solar system can be obtained:
, the following relation between Coulomb field in a hydrogen atom and gravitational field in the solar system can be obtained:
 , (4)
, (4)
where 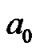 is the Bohr radius, M the mass of the Sun, and
is the Bohr radius, M the mass of the Sun, and 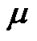 the mass of the particle. From Equation (4), it can be supposed that the formation of the proto-planets in two groups are related to the particles with different masses
the mass of the particle. From Equation (4), it can be supposed that the formation of the proto-planets in two groups are related to the particles with different masses  and
and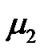 , and
, and . This ratio happens to be the mass ratio of H atom and He atom, which are the most abundant elements in the universe.
. This ratio happens to be the mass ratio of H atom and He atom, which are the most abundant elements in the universe.
Equation (4) seems to remind us of Bohr-Sommerfeld theory, which is an old quantum theory. But our numerical simulation, in which 28000 test particles in Keplerian motion are distributed on the 28 different Sommerfeld’s elliptical orbits, shows that the radial distribution of the particles are irrelevant to the distances of planets. The model of old quantum theory is not reliable. As the progress from the old quantum theory to the new theory, the application of Schrödinger equation in gravitational field should be naturally thought of.
The quantum-like model in this paper is different from the others. The basic assumption is that the chaos behavior of a large number of micro-particles around a gravitational center can be described in terms of the wave function satisfying formal Schrödinger equation, in which a constant  on cosmic scale replaces the Planck constant
on cosmic scale replaces the Planck constant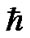 . Applying the model to solar system, we can reasonably explain many phenomena on the solar system.
. Applying the model to solar system, we can reasonably explain many phenomena on the solar system.
3. Schrödinger Equation in GravitationalField
According to the modern hypothesis of the origin of the solar system, the solar system forms from a rotary gas nebula. This paper attempts to explore the slow shrinking phase of the nebula, which can be regarded as stable in a long time. The object studied here is the large number of micro-particles around the Sun. The motion tracks of the particles are chaotic due to the superposition of Brownian motion with Kepler motion. The Kepler orbit is only the probability orbit of the large number of particles. This behavior of the gas particles is very similar to the electrons’. Therefore, we attempt to borrow a time-independent Schrödinger equation in gravitational field to describe the motion of nebular gas particles. The equation can be written as
 , (5)
, (5)
where E and V are the total energy and potential energy of a particle respectively,  is the mass of the particle, and
is the mass of the particle, and 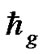 a constant on cosmic scale with the same meaning to the Planck constant. The density of the nebular gas is
a constant on cosmic scale with the same meaning to the Planck constant. The density of the nebular gas is .
.
The potential energy of the particle in gravitational field is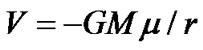 , where r is the distance of the particle from the gravitational center. From quantum theory, on condition of
, where r is the distance of the particle from the gravitational center. From quantum theory, on condition of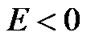 , the normalized radial function of Equation (5) in spherical coordinate is
, the normalized radial function of Equation (5) in spherical coordinate is
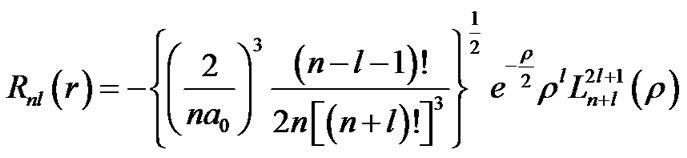 ,
,
 ,
,  , (6)
, (6)
where 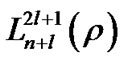 is an associated Laguerre polynomial,
is an associated Laguerre polynomial,
 .
.
The allowed values of quantum numbers are 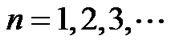 and
and . The “Bohr radius”
. The “Bohr radius”  is consistent with Equation (4). According to the shape and the initial revolving angular momentum of observed proto-planetary nebula disks, most of the nebular particles should be in states of the azimuthal quantum number ml = l, in which the particles revolve in the same direction around the equatorial plane of the system. The numerical simulation shows that all particles in these states form a gas disk similar to the observed nebular disk.
is consistent with Equation (4). According to the shape and the initial revolving angular momentum of observed proto-planetary nebula disks, most of the nebular particles should be in states of the azimuthal quantum number ml = l, in which the particles revolve in the same direction around the equatorial plane of the system. The numerical simulation shows that all particles in these states form a gas disk similar to the observed nebular disk.
The key question is what particles have affected the formation of planets. Though the old quantum model is rough, it still indicates some valuable information: the formation of the distances of inner and outer proto-planets might be the result of the different distribution of hydrogen and helium particles. It is known that the mass of the proto-solar nebula is mostly made of hydrogen (71%) and helium (27%) gases, with tiny traces of other chemical elements and tiny dust particles. Therefore, hydrogen and helium, the most abundant gas particles, will be given the special attention.
Based on the Boltzmann equiprobability principle, we can assume that the particles distribute in each of the states described by above quantum number with equal probability. Since radial probability density of particles is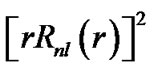 , which can affect planetary distances, if the number of particles in every state is N, the radial mass density of some kind of particle with the mass
, which can affect planetary distances, if the number of particles in every state is N, the radial mass density of some kind of particle with the mass 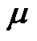 in all these states can be written as
in all these states can be written as
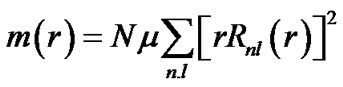 . (7)
. (7)
Analytical expression of m(r) is very complicated, so the numerical calculating is adopted. It can provide a clear nature of the radial mass density. In calculation, the unit of distance is 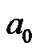 of hydrogen atom, and N is an appropriate constant due to the unimportance of its absolute magnitude. Though n may be all integers, numerical experiments show that when
of hydrogen atom, and N is an appropriate constant due to the unimportance of its absolute magnitude. Though n may be all integers, numerical experiments show that when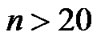 , the increase of n has almost no influence on the characteristic of m(r) curve used in this paper. Here the maximum of n is set at >30 for accuracy. The numerical experiments also show that only when l is all the allowed values, the regular fluctuation of the m(r) curve can appear. In this case, the spatial periods of the fluctuation correspond to the spacing of planets or satellites of the solar system.
, the increase of n has almost no influence on the characteristic of m(r) curve used in this paper. Here the maximum of n is set at >30 for accuracy. The numerical experiments also show that only when l is all the allowed values, the regular fluctuation of the m(r) curve can appear. In this case, the spatial periods of the fluctuation correspond to the spacing of planets or satellites of the solar system.
4. Planetary Distances
4.1. Correspondences between Planetary Distances and 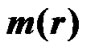
This model is first applied to the planets of the solar system. Based on the phenomena and analysis in the above sections, H, H2 and He, the most abundant particles in nebular disk, are chosen as the investigated objects. The plots of m(r) are shown in Figure 1, where the 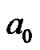 of the H atom is set as 1 AU, and the ratios of the m(r) values for the three curves have no real significance. The curves in Figure 1 have the following properties: 1) The wave amplitudes of m(r) values is decreasing but wavelengths increasing with the distance r. 2) The wave cycles of H curve from the first to the sixth correspond to the terrestrial planets, Jupiter, Saturn, Uranus, and Kuiper belt, respectively. 3) Six cycles of the He curve are included within the first cycle of the H curve, and the wave cycles of He curve from the second to the fifth respectively correspond to the Mercury, Venus, Earth and Mars, while the mean distance of asteroids belt is just at the sixth He wave crest but H wave trough.
of the H atom is set as 1 AU, and the ratios of the m(r) values for the three curves have no real significance. The curves in Figure 1 have the following properties: 1) The wave amplitudes of m(r) values is decreasing but wavelengths increasing with the distance r. 2) The wave cycles of H curve from the first to the sixth correspond to the terrestrial planets, Jupiter, Saturn, Uranus, and Kuiper belt, respectively. 3) Six cycles of the He curve are included within the first cycle of the H curve, and the wave cycles of He curve from the second to the fifth respectively correspond to the Mercury, Venus, Earth and Mars, while the mean distance of asteroids belt is just at the sixth He wave crest but H wave trough.
There is no good correspondence between the wave cycles of the H2 curve and the planets, so we will not pay any more attention to it in the following discussions. But it should be noticed that the wave crests of H curve from the first to the fifth overlap with H2 cure crests, and these are the places that large planets exist. There is no large planet in the overlapping position of the sixth crest of H curve and the trough of the H2 curve, Kuiper belt exist right there.
It is noticeable that the positions of planets are not exactly consistent with the wave crests of the m(r) curves of H or He, especially in terrestrial planets. These deviations are actually reasonable, which will be further specially explained.
4.2. Significance of the Correspondences
The above correspondences and deviation can be easily understood once the model is accepted. The fluctuation of mass density of nebula is an important initial condition for the proto-planet formation. Numerical integration reveals that there are gravitational potential wells at the wave crests of the m(r) curve. This means that the formation of proto-planets is the easiest at these radial density peaks. In the terrestrial region, the oscillation of radial density of helium particles is comparatively obvious, i.e., the action of the potential wells of helium is stronger than that of other kinds of particles. Therefore, the particles can be aggregated more easily in these regions to form the proto-planets. This is just the reason why the terrestrial planets correspond to the m(r) waves of He. But the influence of the hydrogen particles is also important on the formation of the terrestrial planets, because the largest gravity potential well caused by the first peak of the H curve lies in the middle of the terrestrial region, and it might cause the planetesimals or embryo in the region to move towards it during their growth. This can explain why the terrestrial planets all deviate from the He curve peaks, where planets should lie on, towards the first peak of the H curve. In the giant planet region, the oscillation amplitude of the He curve becomes much smaller, and the potential wells correspond to wave crests of the H curve act as the local gravity center. Therefore there exists a good correspondence between the giant planets and the m(r) peak of H.
From modern hypothesis on planetary formation [26,27], giant planets are formed because of the gravitational instability of gas in the accretion disk around young star, and terrestrial planets are formed by continuous collision and accumulation of larger planetesimals and planetary embryos. If it is true, the gravitational instability could be caused by the gravitational potential wells in the gas disk, and larger planetesimals and planetary embryos should be firstly formed nearby the potential wells. Actually, the quantum-like model can give the planetary formation mechanism a convincing support. From Figure 1, it can be seen that there are higher frequency and greater intensity radial density wave of heavier elements in terrestrial region in comparison with giant planets region. Accordingly, it can be speculated that: 1) Formation of planetesimals is easier, and the number is larger in terrestrial region than in outer solar system. So the collision probability of planetesimals is larger, and the planetary embryos form easily and grow quickly at the wave crests of He. 2) In giant planets region, for the lack of heavier particles and the weakness of the fluctuation of their density, the formation of planetesimals is more difficult. But because of the strong fluctuations of the radial density of hydrogen gas, the proto-planets are most possibly formed because of gravitational instability of the gas.
4.3. Signification of the Deviation
The deviation of the planetary positions will be discussed here. The locations of curve crests are about , 4.4
, 4.4 10.3
10.3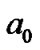 , 18.6
, 18.6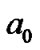 , 29.5
, 29.5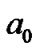 , 42.9
, 42.9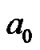 , etc, where
, etc, where 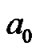 is equal to 1 AU for H, and about 1/16 AU for He. Figure 1 (b) displays the obvious deviation of the position of each terrestrial planet from the corresponding wave crest of He curve towards the first crest of H curve. It is worth noticing that the planetary deviation degree is roughly related to the slope of the H curve at the planetary corresponding position, and larger deviation corresponds to larger slope in either side of the crest of H. For example, the deviation of the Mercury is larger than that of the Venus in inner side of the H wave crest, while the deviation of the Mars is larger than that of the Earth in outer side. Since the sixth crest of the He curve is near the minimum point of H curve, where the slope is the smallest, the deviation of the asteroids from the He crest is also the smallest. If the matter distribution of the proto-solar system is surely similar to that in Figure 1, these deviations are reasonable. As explained above, the formation of the terrestrial planetary positions depends not only on the distribution of helium, but also on that of hydrogen. If an embryo formed at the wave crest of He, it should shift from the crest towards the location with larger density of hydrogen in later accretion process. Besides, other mechanisms, such as their mutual gravitation, can also cause them to congregate. So we can speculate that if there is no strong tidal force from the Sun and Jupiter, a giant planet might be formed. Since the distribution of He atoms and other heavier particles lean to the interior of nebula disk, the position of this aborted giant planet should lie at the first crest of the H curve but deviate a little towards the Sun, i.e., its distance from the Sun should be less than 1 AU. Such giant planets are possible in extrasolar systems.
is equal to 1 AU for H, and about 1/16 AU for He. Figure 1 (b) displays the obvious deviation of the position of each terrestrial planet from the corresponding wave crest of He curve towards the first crest of H curve. It is worth noticing that the planetary deviation degree is roughly related to the slope of the H curve at the planetary corresponding position, and larger deviation corresponds to larger slope in either side of the crest of H. For example, the deviation of the Mercury is larger than that of the Venus in inner side of the H wave crest, while the deviation of the Mars is larger than that of the Earth in outer side. Since the sixth crest of the He curve is near the minimum point of H curve, where the slope is the smallest, the deviation of the asteroids from the He crest is also the smallest. If the matter distribution of the proto-solar system is surely similar to that in Figure 1, these deviations are reasonable. As explained above, the formation of the terrestrial planetary positions depends not only on the distribution of helium, but also on that of hydrogen. If an embryo formed at the wave crest of He, it should shift from the crest towards the location with larger density of hydrogen in later accretion process. Besides, other mechanisms, such as their mutual gravitation, can also cause them to congregate. So we can speculate that if there is no strong tidal force from the Sun and Jupiter, a giant planet might be formed. Since the distribution of He atoms and other heavier particles lean to the interior of nebula disk, the position of this aborted giant planet should lie at the first crest of the H curve but deviate a little towards the Sun, i.e., its distance from the Sun should be less than 1 AU. Such giant planets are possible in extrasolar systems.
The deviation of the Jupiter and Saturn shown in Figure 1(a) can be explained by resonance mechanism. The resonance can cause changes of some planetary positions in later evolvement [28]. Among all giant planets, since Jupiter and Saturn both have the largest mass and the shortest distance between them, their strong mutual attraction can easily draw themselves close to each other. It is known that the mean-motion resonance of 5:2 exists in the Jupiter-Saturn system. If the mass ratio of the Jupiter to Saturn remains a constant in evolvement, and the initial distances were 4.4 AU for the Jupiter and 10.3 AU for the Saturn, the ratio of the initial angular momentum of the Jupiter-Saturn system to modern that, 10.2/10.7, can be obtained. Obviously, the ratio approximately obeys the conservation law of angular momentum. The increase of 5% of modern angular momentum may be explained by the action of the solar wind or the other mechanism.
5. Planetary Masses
Another interesting phenomenon in Figure 1 is the correspondence order between the mass of a planet and the value of m(r) curve of H. This relationship is clearly shown in Figure 2, where the height of vertical bar represents the mass of the planet. Apparently, except the Neptune, two corresponding relations appear in two sets of planets respectively. This correlation can be understood easily because hydrogen is the most abundant component of the solar system, and the final mass of planet should mainly depend on the radial density and the total mass of hydrogen in the region of planet formed. The larger radial density can cause the proto-planet to form earlier and grow more quickly, and so become a larger mass planet. The mass of the Neptune is slightly larger than Uranus, which is an intelligible exception. The Neptune is the outermost giant planet, and its region of provisioning material can be extended outwards into the Kuiper belt, so its mass can become larger.
6. Asteroid Belt and Kuiper Belt
An interesting coincidence between the asteroid belt and Kuiper belt can be seen from Figure 1. Asteroid belt and Kuiper belt respectively correspond to the sixth wave cycle of the He curve and the H curve, and the asteroid belt lies at the overlapping region of the crest of He with the trough of the H curve, while the Kuiper belt lies at the overlapping region of the crest of H with the trough of the H2 curve. This means that the material density in the two regions is too few to the formation of the planets. This might be one of the reasons why there are no large planets in these positions.
In Figure 1(b), the distance between the two troughs of the sixth wave of He curve is 2.2-3.1 AU. It is close to the width of about 2.1-3.3 AU of the asteroid belt shown in Figure 3, which is prepared on 2011 March 20 by IAU Minor Planet Center (MPC) [29].
The position of the sixth crest of the He curve is 2.7 AU, which is just the radial geometrical center of the asteroid belt.
Similarly, from Figure 1(a), the distance between the two troughs of the sixth wave of the H curve is 36-50 AU, which is consistent with the current observed range of Transneptunian Objects (TNOs), also called Kuiper belt objects (KBOs). Figure 4 is the statistics for population of 1163 TNOs promulgated by MPC in 2011 March [29]. Their orbital semi-major axis distribute between 35 - 50 AU, which is called the main Kuiper belt [30]. This population pattern has not changed since 2002 [22], although the number of observed objects has increased twice. In addition, we do not worry about the effect of Centanurs and SKBOs (scattered Kuiper belt objects), whose number is smaller, and the most of them distribute inside the Neptune orbit and outside 50AU respectively. They have properties different from the TNOs, and their population is not innate. So they are not considered here.
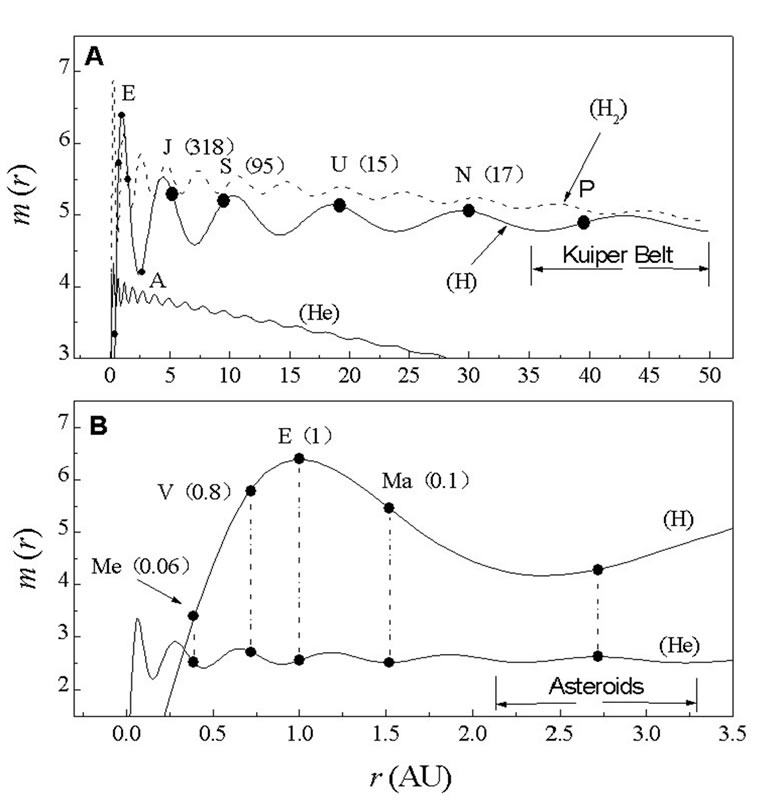
Figure 1. The m(r) curves of particles and planetary distances. The solid lines are m(r) curves of H and He particles, the dashed is one of H2, the filled circles represent the planetary positions, and the numbers in brackets are planetary masses.

Figure 2. Relation between the planetary mass and the radial density of H.
For the origin of the Kuiper belt, a representative viewpoint suggests that the Kuiper belt itself is a remnant of the solar nebula [30]. The quantum-like model supports this view. The major part of the KBOs possibly retains the characteristics of the radial distribution of the primeval material, and a fraction of them were turned into the 3:2 resonance region of Neptune or were scattered into the other space. There is an absence of objects between the resonance belt of 3:2 and 43 AU. The major part of these absent objects might have been removed. This characteristic of distribution of KBOs shown in Figure 4 cannot be completely illustrated by the mechanism of the Neptune resonance [31], unless the distribution of the initial material is the same as the m(r) curve shown in Figure 1.
Zuo et al. have simulated the evolution of the Kuiper belt by the time regression method, and have obtained the expected results that before 4.5 × 108 yrs the distribution pattern of the KBOs is almost same as theory using m(r) curve [32]. We can predict that despite the increasing of number of objects, the center of the Kuiper Belt should remain at about 43 AU, which is the wave crest of the m(r) curve.
Since Pluto is only the largest object lying in 3:2 resonance in the Kuiper belt, and have lost its large planetary status, no attention will be paid to it in this paper.

Figure 3. Distribution of the minor planets.
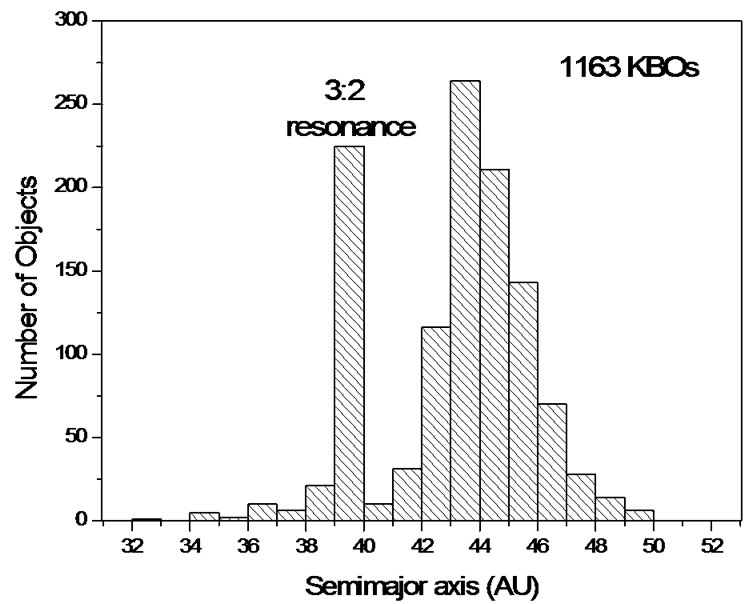
Figure 4. Distribution of KBOs.
7. Satellites and Ring System
The model can also be applied to explain the regular satellites and ring system of planets. Numerical fitting shows that if the “Bohr radius” of H particle in planetary gravitational field is  for Jupiter,
for Jupiter, 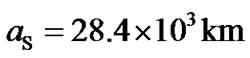 for Saturn, and
for Saturn, and  for Uranus, many corresponding relations in Figure 5 can be discovered.
for Uranus, many corresponding relations in Figure 5 can be discovered.
Figure 5(a) shows the relation between the regular satellites of Jupiter and the distribution of the materials in the model. The positions of the four Galilean satellites correspond to the four wave crests of H2 curve respectively, and the three larger satellites, Io, Ganymede, and Callisto, just locate at the superposition region of the wave crests of H and H2 curves. The Europa with smaller mass is at the crest of H2 curve but at the trough of H curve. Besides, most of the inner small moons of Jupiter also lie near crests of H2 curve. This means that the role of the hydrogen molecules in the formation of satellites might be more important than that of hydrogen atoms. The Jupiter has a ring system including a halo (89.4 - 123.0 × 103 km), the main (123.0 - 128.9 × 103 km) and a gossamer ring(128.9 - 242.0 × 103 km) [33]. The brighter halo and the main ring just occupy one wave of He curve, and the end of the gossamer ring is at the overlapping region of two trough of H and He waves.
The chief graph in Figure 5(b) mainly illustrates the relation between the distribution of H atoms and positions of six large satellites of Saturn. Two largest satellites, Titan and Rhea, accurately lay at the wave crests of H curve. The distribution of the other four smaller satellites, Mimas, Enceladus, Tethys, and Dione is very similar to that of the terrestrial planets. The inset graph shows clearly that the four satellites respectively correspond to the four wave cycles of He curve and are included in a wave cycle of H curve, and Enceladus, Tethys, and Dione all slide down the corresponding wave crests of He curve and are close to the crests of H curve except Mimas being at the trough of H curve.
It is impressive that the distribution of rings and the most of the moonlets of Saturn also accord with the fluctuation of He curve. The D ring (66.9 × 103 - 74.7 × 103 km) and C ring (74.7 × 103 - 92.0 × 103 km) occupy one wave cycle of He curve, B ring (92.0 × 103 - 117.5 × 103 km) just takes up the next one, the narrow F ring (140 × 103 km) and nearby five moonlets are at the He wave crest following B ring, while the French division (90 × 103- 92 × 103 km) and Cassini division (118 × 103 - 122 × 103 km) are exactly in the two troughs of wave corresponding B ring respectively. Another coincidence is that if E ring is really defined observationally to lie in the region about 3.3 - 6.5 Saturn radii [34], which is 60 × 103 km, it will be surprising again that E ring takes up a complete wave cycle of H curve, from about 200 × 103 km to 390 × 103 km.
Figure 5(c) displays that six larger satellites of Uranus correspond to the wave crests of H curve well, and the ring of Uranus is just at a wave crest.
From the above analysis we believe that the formation of the three planet systems is related to the distribution of initial hydrogen. The molecule composition of hydrogen around the Jupiter is more than that of the Saturn and Uranus due to larger gas density caused by large mass of the Jupiter, so the correspondences of them with H2 or H curve are reasonable. In addition, there is an absent object in every curve in Figure 5, while the masses of satellites near these spaces are all the largest, such as Ganymede of Jupiter, Titan of Saturn, and Titania of Uranus. It can be assumed that the materials here have been captured by these largest satellites for other mechanism.
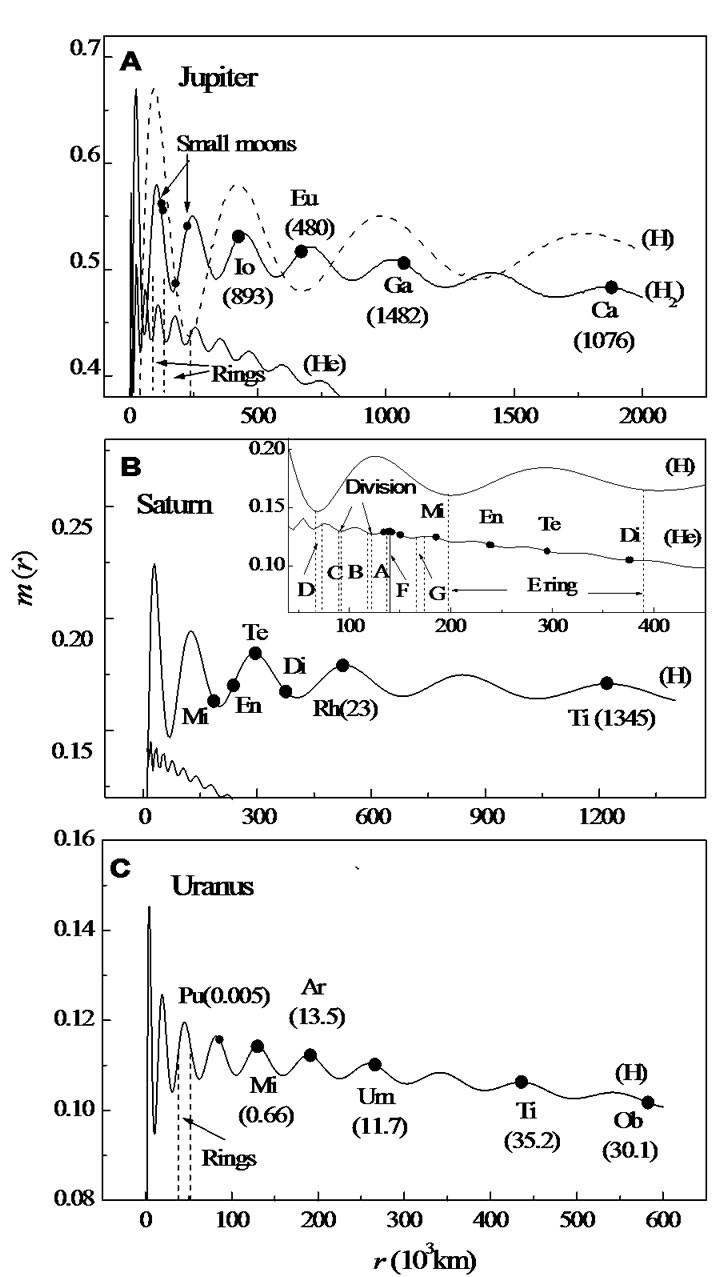
Figure 5. The correspondence of m(r) curves with the satellites and rings of planets. Here, every satellite is marked with the first two letters of its name. The dashed vertical lines give the locations of the rings. The numbers in the brackets are the mass of the satellites (in unit 1020 kg).
8. Energy and Angular Momentum of thePlanetary Region
Whether the original nebular radial density really follows m(r) curves, there are further evidence according to the comparison of the energy and angular momentum in planets districts. Considering interaction between planets during their formation and growth, the system is divided into four regions as given in Table 1, which adopts Dai method [35]. The inner boundary of the terrestrial region is the trough of the helium m(r) curve. Based on quantum mechanics, the energy of a particle with mass  in n state is
in n state is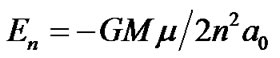 . From Equation (7), the radial number density of a certain particle is
. From Equation (7), the radial number density of a certain particle is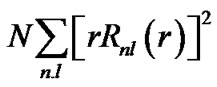 . The total energy of particles in a thin spherical shell with thickness dr is
. The total energy of particles in a thin spherical shell with thickness dr is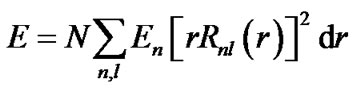 . If there are two kinds of particles, H and He atoms, the energy density in each of the regions can be expressed as
. If there are two kinds of particles, H and He atoms, the energy density in each of the regions can be expressed as , where
, where  and
and 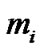 are the total energy and the total mass of a certain kind of particles respectively, and they can be written as
are the total energy and the total mass of a certain kind of particles respectively, and they can be written as
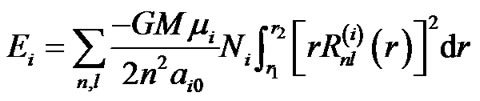 , (8)
, (8)
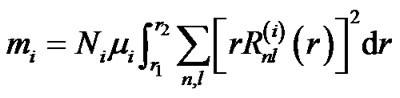 , (9)
, (9)
where 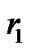 and
and  are the inner and the outer radii of the region respectively, and
are the inner and the outer radii of the region respectively, and 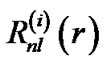 represents the radial wave function of a certain kind of particles. Based on the above two equations, the energy carried by the unit mass of the nebula (called energy density) in each of the four regions can be calculated by letting the ratio of the total mass
represents the radial wave function of a certain kind of particles. Based on the above two equations, the energy carried by the unit mass of the nebula (called energy density) in each of the four regions can be calculated by letting the ratio of the total mass 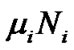 of H and He in the solar system be 71: 27, and the unknown
of H and He in the solar system be 71: 27, and the unknown 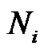 can be eliminated. The calculated values of
can be eliminated. The calculated values of 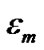 in unit (
in unit ( ) are given in Table 1, where
) are given in Table 1, where 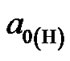 is “Bohr radius” of H particle. The actual energy of planets can be calculated by
is “Bohr radius” of H particle. The actual energy of planets can be calculated by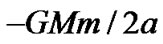 , where m and a are planetary mass and semi-major axis respectively. The energy density
, where m and a are planetary mass and semi-major axis respectively. The energy density  of every planetary district is also given in Table 1 for comparison. It is clear that the data of the model and the observation fit well.
of every planetary district is also given in Table 1 for comparison. It is clear that the data of the model and the observation fit well.
The similar method is used to calculate the angular momentum of the unit mass nebula (called angular mo

Table 1. The comparison of the angular momentum and energy.
mentum density). z axis component of the angular momentum of a particle in l states is written as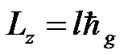 . In each region, the total angular momentum of a certain kind of particles can be written as
. In each region, the total angular momentum of a certain kind of particles can be written as
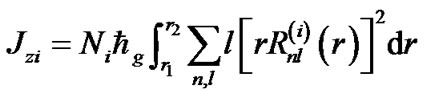 . (10)
. (10)
The angular momentum density in each region is calculated by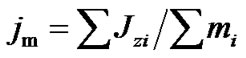 . Since
. Since 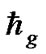 is unknown, we take the value of the Uranus region as unit. The approximate equation calculating of the angular momentum of the planet is
is unknown, we take the value of the Uranus region as unit. The approximate equation calculating of the angular momentum of the planet is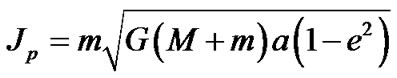 , where e is the orbital eccentricity. The angular momentum density of a planet is
, where e is the orbital eccentricity. The angular momentum density of a planet is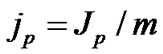 , the unit is that of the Uranus. The calculated values of nebular and the actual values of the planets in each region are listed in Table 1. It is also seen that the model is consistent with observation, except the terrestrial region.
, the unit is that of the Uranus. The calculated values of nebular and the actual values of the planets in each region are listed in Table 1. It is also seen that the model is consistent with observation, except the terrestrial region.
In conclusion, Table 1 shows a strong consistency between the theory and the observation in three giant planets regions, but the deviations in the terrestrial region are larger, especially for the angular momentum. Actually, this is reasonable as a result when most of the original gas materials have escaped from the terrestrial region. There are two reasons for the increase in the angular momentum of the unit mass of planets: 1) planets had captured particles with large angular momentum, 2) planets formation region had lost the materials with smaller angular momentum. In the terrestrial region,the maximum amount of the primordial materials is H particles which are in 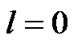 state with zero angular momentum, and the next is smaller ratio of helium and other heavier particles being in any possible l state with larger angular momentum. During the earlier period of the Sun formation, the solar wind is very weak, so that H particles with zero angular momentum can be easily captured by the Sun. In the later stage, the strong solar wind takes away the most of H particles again and left some angular momentum in the collision with planets materials. Both the mechanisms can all make terrestrial region lose a lot of mass carrying small amount of angular momentum. Even the angular momentum taken away by solar wind might be smaller than what is brought in. As a result, the angular momentum of the unit mass of planets in the terrestrial region is increased. We can make a simple estimation. Let the original total mass of terrestrial region be m, the lost mass with zero angular momentum be
state with zero angular momentum, and the next is smaller ratio of helium and other heavier particles being in any possible l state with larger angular momentum. During the earlier period of the Sun formation, the solar wind is very weak, so that H particles with zero angular momentum can be easily captured by the Sun. In the later stage, the strong solar wind takes away the most of H particles again and left some angular momentum in the collision with planets materials. Both the mechanisms can all make terrestrial region lose a lot of mass carrying small amount of angular momentum. Even the angular momentum taken away by solar wind might be smaller than what is brought in. As a result, the angular momentum of the unit mass of planets in the terrestrial region is increased. We can make a simple estimation. Let the original total mass of terrestrial region be m, the lost mass with zero angular momentum be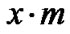 , and
, and  is planetary mass. Since the ratio of original 0.074 and modern 0.214 (see Table 1), the total original angular momentum is
is planetary mass. Since the ratio of original 0.074 and modern 0.214 (see Table 1), the total original angular momentum is 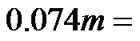
 . The ratio of lost mass can be obtained as
. The ratio of lost mass can be obtained as 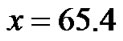 %, which is reasonable. In addition, since the energy of the particle is proportional to the mass, the energy will naturally decreases with the decrease of the mass, and the ratio of energy and mass will be a constant approximately. So there is only small deviation of energy of the unit mass in the terrestrial region.
%, which is reasonable. In addition, since the energy of the particle is proportional to the mass, the energy will naturally decreases with the decrease of the mass, and the ratio of energy and mass will be a constant approximately. So there is only small deviation of energy of the unit mass in the terrestrial region.
In this section, the planetary rotation has not been mentioned because the rotation energy and angular momentum are much smaller than the orbital ones.
9. Conclusions and Discussion
To conclude, in the study of the basic problems of the solar system origin, the quantum-like model described in this paper would be more efficient than others. Many correspondences mentioned above are neither far-fetched and obscure, nor haphazard coincidence. It is possible that an unknown truth will be revealed. Above research can inspire us to make the following hypotheses:
1) The chaos behavior of nebular particles in gravitational field can be described by the wave function satisfying the Schrödinger equation when we replace the 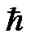 with
with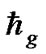 .
.
2) The distribution of H and He particles might play the important roles in formation of the planets. Waves of radial density of H atoms formed a series of largest rings, and the terrestrial planets, Jupiter, Saturn, Uranus, Neptune, as well as the Kuiper belt formed in these rings respectively. The rings of He atoms are thinner than those of H. The first H ring covers four He rings, where the original terrestrial planets formed respectively, but due to the influence of H ring, they have shifted toward the center of H ring.
3) The distribution of heavier elements is closer to the Sun than hydrogen and helium. The rings made from heavier particles are thinner and denser than those of He. A ring of He contains tens or hundreds of thin rings made of heavier particles, and the thin ring contains the thinner rings, which like the form of the observed rings of Saturn. With the decrease of the distance from the Sun, rings become denser and thinner gradually. They might be important for the formation of planetesimals. Due to more heavy elements and planetesimals in the terrestrial region than other regions, the formation of terrestrial planets is easier. As to the giant planets region, as the lack of heavy elements and planetesimals, the formation of proto-planets can only depend on the gravitational instability of gas.
4) The formation of the proto-planet was earlier on the higher crest of the matter radial density wave. In the giant planet region, the order of planetary formation is Jupiter, Saturn, Uranus and Neptune. Since Jupiter forms early and grows quickly, it can capture a large amount of materials of the terrestrial region and Saturn, then becomes into the largest planet. Though Neptune formed later, because a large amount of materials in the widest region outside its exterior boundary can contribute to it, the mass of Neptune is still larger than Uranus. Due to strong solar wind and the strong tidal forces from the Sun and Jupiter, the terrestrial region cannot form a giant planet.
5) The formation mechanism of satellites differs from that of planets. The regular satellites might form in a circumplanetary accretion disk produced by a slow inflow of gas and solids during the end of the planet formation [36]. The gas should form an envelope, in which the gas matter distribution is the same as shown in Figure 5. When the planetesimals in exterior space fall into the envelope, they should be likely to stay nearby the radial density crest of gas by the stickiness of gas, and finally form satellites. In this way, the mass of outer satellites is naturally greater than inner ones.
6) Due to the special position in H wave, the rotation speeds of Mercury and Venus gradually slow down by asymmetric viscous resistance. The resistance is so effective that the rotation direction of Venus is reversed. The results have already published [23], we did not discussed in this paper.
This paper shows a perfect structure of the solar system, which can be divided into two symmetrical quantum groups: 1) the Jupiter, Saturn, Uranus, Neptune and the Kuiper belt; 2) the Mercury, Venus, Earth, Mars and the asteroid belt. Their quantum orders are all described as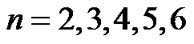 , and the width of the planetary districts of the giant planets group is 16 times that of the terrestrial group. This ratio is that of the atom mass square of helium and hydrogen, which are the main particles in primitive nebula of the solar system. According to these facts, it can be predicted that the structure of the solar system has been basically fixed, and it is impossible to find any major planets inside the orbit of Mercury and outside the Kuiper belt, but the minor planets or dwarf planets similar to Pluto may be found inside or outside the Kuiper belt.
, and the width of the planetary districts of the giant planets group is 16 times that of the terrestrial group. This ratio is that of the atom mass square of helium and hydrogen, which are the main particles in primitive nebula of the solar system. According to these facts, it can be predicted that the structure of the solar system has been basically fixed, and it is impossible to find any major planets inside the orbit of Mercury and outside the Kuiper belt, but the minor planets or dwarf planets similar to Pluto may be found inside or outside the Kuiper belt.
In addition, this paper provides an initial distribution state of the solar nebula, using the initial conditions, the formation of planets and satellites can be simulated, although the workload is quite large.
10. Acknowledgements
The author would like to thank Prof. Chuanfu Cheng, Prof. Qingtian Meng for their help in English writing of this paper, and would also thank the reviewers whose comments have caused great improvement of this paper. The author is grateful to David Jewitt for the data from his Internet Station. At last, the author would express her thanks to The SAO/NASA Astrophysics Data System for the consulting on references.
11. References
[1] M. M. Nieto, “Conclusions about the Titius Bode Law of Planetary Distances,” Astronomy and Astrophysics, Vol. 8, 1970, pp. 105-111.
[2] L. Basano and D. W. Hughes, “A Modified Titius-Bode Law for Planetary Orbits,” Nuovo Cimento C, Vol. 2C, No. 5, 1979, pp. 505-510. doi:10.1007/BF02557750
[3] E. Badolati, “A Supposed New Law for Planetary Distances,” Moon and the Planets, Vol. 26, May 1982, pp. 339-341. doi:10.1007/BF00928016
[4] V. Pletser, “Exponential Distance Laws for Satellite Systems,” Earth, Moon, and Planets, Vol. 36, 1986, pp. 193- 210. doi:10.1007/BF00055159
[5] R. Neuhaeuser and J. V. Feitzinger, “A Generalized Distance Formula for Planetary and Satellite Systems,” Astronomy and Astrophysics, Vol. 170, No. 1, 1986, pp. 174-178.
[6] P. Lynch, “On the Significance of the Titius-Bode Law for the Distribution of the Planets,” Monthly Notice of the Royal Astronomical Society, Vol. 341, No. 4, 2003, pp. 1174-1178. doi:10.1046/j.1365-8711.2003.06492.x
[7] L. Neslušan, “The Significance of the Titius-Bode Law and the Peculiar Location of the Earth’s Orbit,” Monthly Notice of the Royal Astronomical Society, Vol. 351, No. 1, 2004, pp. 133-136.
[8] G. Gladyshev, “The Physicochemical Mechanisms of the Formation of Planetary Systems,” Moon and the Planets, Vol. 18, April 1978, pp. 217-222. doi:10.1007/BF00896744
[9] J. J. Rawal, “Contraction of the Solar Nebula,” Earth, Moon, and Planets, Vol. 31, October 1984, pp. 175-182. doi:10.1007/BF00055528
[10] X. Q. Li, Q. B. Li and H. Zhang, “Self-similar Collapse in Nebular Disk and the Titius-Bode Law,” Astronomy and Astrophysics, Vol. 304, 1995, pp. 617-621.
[11] F. Graner and B. Dubrulle, “Titius-Bode Laws in the Solar System 1: Scale Invariance Explains Everything,” Astronomy and Astrophysics, Vol. 282, No. 1, 1994, pp. 262-268.
[12] R. Louise, “A Postulate Leading to the Titius-Bode Law,” Moon and the Planets, Vol. 26, February 1982, pp. 93-96. doi:10.1007/BF00941371
[13] R. Wayte, “Quantisation in Stable Gravitational Systems,” Moon and the Planets, Vol. 26, February 1982, pp. 11-32. doi:10.1007/BF00941366
[14] R. Louise, “The Titius-Bode Law and the Wave Formalism,” Moon and the Planets, Vol. 26, June 1982, pp. 389- 398. doi:10.1007/BF00941641
[15] R. Louise, “Quantum Formalism in Gravitation Quantitative Application to the Titius-Bode Law,” Moon and the Planets, Vol. 27, August 1982, pp. 59-63. doi:10.1007/BF00941557
[16] Daniel and M. Greenberger, Quantization in the Large,” Foundations of Physics, Vol. 13, No. 9, 1983, pp. 903- 951.
[17] Q. X. Nie, “Simulated Quantum Theory for Seeking the Mystery of Regularity of Planetary Distances,” Acta Astronomica Sinica, Vol. 34, No. 3, 1993, pp. 333-340.
[18] K. U. Lu, “Mathematical Investigation of Bode’s Law and Quantilization of Gravity,” Astrophysics and Space Science, Vol. 225, No. 2, 1995, pp. 227-235. doi:10.1007/BF00613237
[19] B. E. Yang, “Introduction to Quantum Theory on Planets and Satellites (in Chinese),” Dalian University of Technology Press, Dalian, 1996, pp. 27-32.
[20] A. G. Agnese and R. Festa, “Clues to Discretization on the Cosmic Scale,” Physics Letters A, Vol. 227, No. 3-4, 1997, pp. 165-171. doi:10.1016/S0375-9601(97)00007-8
[21] L. Nottale, G. Schumacher and J. Gay, “Scale Relativity and Quantization of the Solar System,” Astronomy and Astrophysics, Vol. 322, 1997, pp. 1018-1025.
[22] Q. X. Nie, “The Characteristics of Orbital Distribution of Kuiper Belt Objects,” Chinese Astronomy and Astrophysics, Vol. 27, No. 1, 2003, pp. 94-98.
[23] Q. X. Nie, Cuan Li and F.-S. Liu, “Effect of Interplanetary Matter on the Spin Evolutions of Venus and Mercury,” International Journal of Astronomy and Astrophysics, Vol. 1, No. 1, 2011, pp. 1-5. doi:10.4236/ijaa.2011.11001
[24] G. G. Comisar, “Brownian-Motion Model of Nonrelativistic Quantum Mechanics,” Physical Review, Vol. 138, No. 5B, 1965, pp. 1332-1337. doi:10.1103/PhysRev.138.B1332
[25] E. Nelson, “Derivation of the Schrödinger Equation from Newtonian Mechanics,” Physical Review, Vol. 150, No. 4, 1966, pp. 1079-1085. doi:10.1103/PhysRev.150.1079
[26] A. P. Boss, “Astrometric Signatures of Giant-planet Formation,” Nature, Vol. 393, No. 6681, 1998, pp. 141-143. doi:10.1038/30177
[27] A. P. Boss, “Rapid Formation of Outer Giant Planets by Disk Instability,” The Astrophysical Journal, Vol. 599, No. 1, 2003, pp. 577-581. doi:10.1086/379163
[28] N. Murray and M. Holman, “The Origin of Chaos in the Outer Solar System,” Science, Vol. 283, No. 5409, 1999, pp. 1877.doi:10.1126/science.283.5409.1877
[29] D. Jewitt, “Kuiper Belt,” 2011. http://www2.ess.ucla. edu/~jewitt/kb.html
[30] J. X. Luu and D. C. Jewitt, “Kuiper Belt Objects: Relics from the Accretion Disk of the Sun,” The Annual Review of Astronomy and Astrophysics, Vol. 40, 2002, pp. 63- 101. doi:10.1146/annurev.astro.40.060401.093818
[31] R. Malhotra, “The Origin of Pluto’s Orbit: Implications for the Solar System beyond Neptune,” Astronomical Journal, Vol. 110, 1995, pp. 420-429. doi:10.1086/117532
[32] Q. L. Zuo, Qing-xiang Nie, et al., “Simulations for Original Distribution of KBOs,” Acta Astronomica Sinica., Vol. 49, No. 4, 2008, pp. 413-418
[33] C. D. Murray and S. F. Dermott “Solar System Dynamics,” Cambridge University Press, Cambridge, 1999, pp. 532-533.
[34] J. A. van Allen, et al., “Saturn’s Magnetosphere, Rings, and Inner Satellites,” Science, Vol. 207, January 25 1980, pp. 415-421. doi:10.1126/science.207.4429.415
[35] W. S. Dai, “An Interpretation of the Titius-Bode Law,” Acta Astronomica Sinica, Vol. 16, No. 2, 1975, pp. 123- 130.
[36] R. M. Canup and W. R. Ward, “Formation of the Galilean Satellites: Conditions of Accretion,” The Astronomical Journal, Vol. 124, No. 6, 2002, pp. 3404-3423. doi:10.1086/344684

