World Journal of Nano Science and Engineering
Vol.05 No.03(2015), Article ID:59915,10 pages
10.4236/wjnse.2015.53012
Angular Dependence of the Second Harmonic Generation Induced by Femtosecond Laser Irradiation in Silica-Based Glasses: Variation with Writing Speed and Pulse Energy
Jing Cao, Bertrand Poumellec, François Brisset, Anne-Laure Helbert, Matthieu Lancry
Institut de Chimie Moléculaire et des Matériaux d’Orsay (ICMMO), CNRS-Université Paris Sud, Université Paris Saclay, Bât.420, Campus Orsay, 91405 Orsay, France
Email: bertrand.poumellec@u-psud.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 July 2015; accepted 22 September 2015; published 25 September 2015
ABSTRACT
To control second harmonic generation (SHG) in silica-based glasses is crucial for fabricating photonic devices, such as frequency doubling waveguides. Here, we investigated SHG of laser induced nonlinear optical crystals in silica-based glasses, according to writing speed and pulse energy. We observed two regions with different probing laser polarization angular dependence: a) a well-defined cosine-like curve with period of 180˚ at low pulse energy (0.8 µJ) whatever the writing speed or at high pulse energy (1.4 µJ) with high writing speed (25 µm/s). This is accounted for by a well-defined texture for the nano crystals with their polar axis oriented perpendicular to the writing laser polarization; and b) a double cosine-like curve revealing a second texture of the crystals at high pulse energy (1.4 µJ) with low writing speed (5 µm/s) and with the polar axis oriented closer parallel to the writing laser polarization. Therefore, a SHG dependence on probing laser polarization angle may show high contrast by a correct choice of the writing speed and pulse energy. These results pave the way for elaboration of nonlinear optical devices.
Keywords:
Nonlinear Optical Crystal, Glass Ceramics, Direct Writing, Ultrafast Processes, Waveguide

1. Introduction
Second harmonic generation (SHG) is a nonlinear optical effect, in which the frequency of incident light is doubled [1] [2] . Generally, SHG requires medium without inversion symmetry. In that case, breaking the centre symmetry of glass is necessary for obtaining SHG based devices. Modification of glasses by precipitation of second order nonlinear optical materials is an effective way to reach this goal [3] - [5] . On the other hand, excellent improved mechanical, optical properties can be obtained by combining glasses and crystals [6] . Recently, this field has received more and more attention because of the excellent optical properties and potential applications such as optical memory [7] and second harmonic generation waveguides [8] - [10] . To master the orientation of nonlinear optical crystal is an important topic for obtaining highly efficient optical devices [11] .
Thus far, various methods have been employed to obtain highly oriented nonlinear optical crystal [12] . Heat treatment is a traditional technique; however, the spatially precipitation of oriented crystal is limited and the process is time consuming [13] . Appling electric field, the spatial crystal orientation can be improved but it commonly needs complicated facilities and electric energy [14] . Compared with the above two methods, femtosecond laser induced crystallization in glasses is a promising tool in achieving nonlinear optical crystal orientation with three-dimensional, sub-micrometre spatial resolution [9] . Because of the nonlinear nature of light- matter interaction, pulse energy of femtosecond laser could be deposited in transparent materials [15] . At certain high repetition rate (e.g. >200 kHz), thermal accumulation effect occurs and the space-time profile can be controlled [16] [17] . In addition, it is a simple and flexible process just by adjusting the parameters of femtosecond laser [9] .
Recently, the orientation of nonlinear optical crystal has been controlled by adjusting the laser parameters such as writing direction [18] , pulse energy [9] . However, thus far, there is no systematic investigation of the relationship between SHG and laser parameters such as pulse energy, writing speed and writing orientation [19] , in particular, how to get well contrasted angular dependence of SHG with probing polarization.
Here, we investigated thus the SHG in femtosecond laser induced LiNbO3-like crystal in Li2O-Nb2O5-SiO2 system. It is a commonly used nonlinear optical crystal system due to the advantageous properties such as a wide range of chemical composition for glass formation, optically transparent and easy precipitation of crystals [20] .
2. Experimental Section
2.1. Femtosecond Laser-Induced Crystallization
A silica-based glass with composition of 32.5Li2O-27.5Nb2O5-40SiO2 (mol%) was prepared by the classical melt quenching technique. Details of the sample preparation were described elsewhere [21] . A Yb-doped fiber amplifier femtosecond laser (1030 nm, 300 fs, 250 kHz repetition rate, Satsuma, Amplitude Systèmes Ltd.) was focused 300 mm (in air) below the surface of glass using an objective (numerical aperture, NA = 0.6). Samples were mounted on a computer controlled three-dimensional stage and mechanically moved during laser fabrication process to obtain crystal lines.
2.2. Writing Configuration Definition
As a matter of fact, in previous experiments [19] , the angle between writing direction and writing laser polarization direction was found insufficient to differentiate experiments made with the same angle between laser polarization direction and writing direction but with different writing direction e.g. vertical or horizontal. We detected also an asymmetrical effect when we change the sense of writing [21] . Therefore, in this paper, we refer the vector orientations to a laboratory reference described in Figure 1(a), independently. In details, the geometry of the problem is denoted in terms of a set of Cartesian coordinate system along the laser propagating direction. The reference of writing configuration is based on the beam specifies at Cartesian coordinate system at the origin (in black). X0 and Y0 axes are defined as the horizontal and vertical directions, respectively; right (up) side of beam is donated as positive and left (down) as negative. +Z0 is the laser propagation direction. It changed to Cartesian coordinate system (in green) when arrived at the sample (because of the odd number of mirrors on the optical table, the sample coordinate system changed from right-handed one to left-handed one). We investigated various configurations considering different combinations of writing and laser polarization directions. Here, we take as example for the direction of writing +45˚ and +225˚ in reference to +X (in X, Y plane) with the

Figure 1. Schematic of experimental set up. (a) Femtosecond laser writing system, the reference of writing configuration is based on the beam specifies at Cartesian coordinate system at the origin (in black), and changed to Cartesian coordinate system when arrived at the sample (in green). N.B.: because of the odd number of mirrors on the optical table, the sample coordinate system changes from right-handed one to left-handed one; (b) Second harmonic generation measurement setup. It was measured in X, Y plane. All angles in this paper are referred to +X direction (in X, Y plane).
polarization direction parallel to Y. Femtosecond laser irradiation of the glass induced crystallization under specific conditions (repetition rate and pulse energy large enough) [9] . It is worth to note that the irradiated volume is smaller than the crystallized one. The threshold of crystallization for our glass is found at pulse energy of 0.4 μJ. Crystal seeds were produced by irradiating the sample without moving during 80 s before continuous irradiation in X, Y plane. The writing speed was varied from 1 to 25 μm/s.
2.3. Electron Backscatter Diffraction Measurement and Texture Analysis
Before to make further investigations, we observed the samples optically through a microscope with natural and polarized light and found strong index change and birefringence.
Samples were cut along the direction perpendicular to writing directions, polished and analyzed using a field-emission gun scanning electron microscope (FEG-SEM ZEISS SUPRA 55 VP) without HF etching.
Electron backscatter diffraction (EBSD) [22] , is a useful tool to determine the amount of crystallized matter, the size of the crystal, their spatial distribution and their orientation if any. The first step of the measurement is the recording of the Kikuchi lines [23] . This means that the matter is crystallized at the point of electron illumination. Then, by entering space group of the expected phase, here R3c and the crystal parameters for LiNbO3 [24] , we can get the indexation of the Kikuchi lines using Orientation Imaging Microscopy (OIM™) software. This software yields several facilities for texture analysis.
The first step is to examine the Orientation Distribution Function (ODF, the angular density of crystals among the Euler space) for determining if a texture exists. Then, we can plot the Inverse Pole Figure (IPF) for displaying the preferred orientations in choosing a sample direction suitable to show the detected texture.
2.4. Second Harmonic Generation Measurement
Polarized second harmonic generation (SHG) measurement was performed in transmission mode. As illustrated Figure 1(b), the fundamental beam from a Yb-doped fiber amplifier femtosecond laser system (1030 nm, 300 fs, 100 kHz repetition rate, Satsuma, Amplitude Systèmes Ltd.) was used as laser source. The polarization direction of the fundamental beam was varied by rotating a half-wave plate to obtain polarization dependent SHG signal. Sample was mounted on a stage which could be adjusted to let laser propagate perpendicular to sample X, Y plane. After passing a low-pass filter (used to block the fundamental beam), the intensity of SHG was detected by a photomultiplier. Data were recorded 5 times and we took the average value. Then intensity of data for each irradiated line was normalized at the largest value as 1. The error bars represent the standard error of mean. As a matter of fact, the absolute intensity cannot be compared because of different scattering from place to place. It is also worth to note that in a disordered material, we could expect a centre-symmetric material and from that the SHG is forbidden. This is obviously experimentally not the case and it is always the case in ceramics (a mixing between glass and nanocrystals). The explanation has been given by several authors and in particularly, Brevet et al. [25] have reported that the emission from a nanocrystal looses its phase relation with the other nanocrystals due to multiple scattering. Therefore, we can collect the sum of the intensity coming from each nanocrystal whatever their orientation.
3. Experimental Results
3.1. Second Harmonic Generation Properties of Irradiated Lines
For investigating the SHG properties, we recorded the SHG intensity according to two determinant laser parameters: writing speed and pulse energy.
3.1.1. Pulse Energy Effect
At low pulse energy (0.8 μJ, red curve in Figure 2), we obtain a well defined cosine-like curve with period of 180˚. The minimum SHG intensity is obtained at an angle close to writing laser polarization direction (90˚). When we increased the pulse energy to 1.4 μJ (green curve in Figure 2), the cosine-like curve is modified, a second maximum occurs at the place of the minimum on the simple cosine-like curve. This phenomenon becomes obvious at 1.8 μJ (blue curve in Figure 2). This observation is in agreement with a previous report [9] .
3.1.2. Writing Speed Effect
For investigating the dependence of SHG with the writing speed, we fixed the pulse energy at 0.8 μJ and changed the writing speed. We obtained well defined cosine-like curves whatever the writing speed in Figure 3(a). It is worth noting that, with the increase of writing speed, the minimum value of SHG shifts from 102˚ to 91˚, which is closer to the writing polarization angle (90˚). However, for high pulse energy (1.4 μJ), the result is quite different from the previous ones. With the decrease of the writing speed from 25 to 1 μm/s, the SHG curve changed from simple cosine-like curve (blue curve in Figure 3(b)) to the modified ones (green and red curves in Figure 3(b)).
Figure 2. Normalized second harmonic generation intensity of irradiated lines as function of probing laser polarization in the X, Y plane. The variable parameter is the pulse energy. Other parameters: writing speed 5 µm/s, writing direction is along 45˚ direction, laser polarization is parallel to Y.

Figure 3. Normalized second harmonic generation intensity of irradiated lines as function of probing laser polarization angle. The variable parameter is the writing speed at pulse energy of 0.8 µJ for (a) and 1.4 µJ for (b). Other parameter: writing direction is along 45˚ direction, laser polarization is parallel to Y.
3.1.3. Writing Orientation Effect
Orientation here means the movement along a given direction. As a matter of fact, there are two orientations for a given direction. According to a previous report, the orientation of writing is peculiar for ultra-brief laser-matter interaction [26] . The glass is centre-symmetric, considering that the laser beam is XY-symmetric and the experimental geometry is also XY-symmetric; there should be no difference between the orientation of writing i.e. between forward direction (here 45˚) and backward direction (here 225˚). However, experimentally, it is not the case. In both cases, there are two textures: one with polar axis of nanocystals (<0001>) perpendicular to the writing laser polarization, X direction and one with the polar axis close to Y direction. However, the ratio between the two components and the angular position of the maxima seems slightly different. This is particularly clear in Figure 4(a) when writing speed is at 1 μm/s and pulse energy is 1.4 μJ. This is an Asymmetric Orientational Writing (AOW). With the increase of writing speed from 1 μm/s to 25 μm/s, the curves are cosine-like ones and the AOW effect is reduced (Figure 4(b)). It is worth noting that it is the first time that an AOW effect is clearly demonstrated in SHG and related to photo precipitation of crystals in a silica-based glass.
3.2. Modification of Glasses
In order to find an explanation of the above angular dependence, we have investigated the modification of glasses after irradiation. Samples were cut along the direction perpendicular to writing direction. The morphology of the cross section has been analyzed by scanning electron microscopy (SEM, Figure 5). At low pulse energy (0.8 μJ), a ginseng like shape laser track with a width of 1.4 μm of and length of 30 μm is obtained (Figure 5(a)). From the Figure 5(b), a magnification of the previous figure, a rough structure with ribbon-like shape is obtained. With the increase of the pulse energy (1.4 μJ), the width of the laser trace increased to about 4 μm, another part appearing in white in Figure 5(c) is obtained around a rough structure.
The ODF showed that a preferential orientation has been developed. The Inverse Pole Figure (IPF, Figure 5(d) and Figure 5(e)) is used to display the crystal direction along the writing laser polarization direction. In the color coding, basic red is used for polar axis of the crystal (<0001> axis), green and blue for 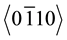 and
and 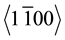 axes, respectively. The inter media orientations are colored by an RGB mixture of the primary components.
axes, respectively. The inter media orientations are colored by an RGB mixture of the primary components.
The first remark we can make from IPF is that at low pulse energy (0.8 μJ, Figure 5(d)), nano-sized crystals have been produced. We observed that the picture is completely green and blue, indicating that  and
and 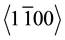 axes are parallel to the writing laser polarization direction so that the polar axis (i.e. <0001> axis) is perpendicular to the writing laser polarization direction. With the increase of pulse energy (1.4 μJ), sub-micro sized crystals are obtained, with nano-crystals in the core of laser track or in the tail; micro-sized crystals in the head part, especially outside of the core (Figure 5(e)). It should be noted that with the increase of pulse energy, the color of IPF changes from completely green to various colors, indicating that other orientations are appearing.
axes are parallel to the writing laser polarization direction so that the polar axis (i.e. <0001> axis) is perpendicular to the writing laser polarization direction. With the increase of pulse energy (1.4 μJ), sub-micro sized crystals are obtained, with nano-crystals in the core of laser track or in the tail; micro-sized crystals in the head part, especially outside of the core (Figure 5(e)). It should be noted that with the increase of pulse energy, the color of IPF changes from completely green to various colors, indicating that other orientations are appearing.

Figure 4. Normalized second harmonic generation intensity of irradiated lines as function of probing laser polarization angle. The writing orientation is the variable parameter for two writing speeds: (a) 1 µm/s and (b) 25 µm/s. Other parameters: pulse energy 1.4 µJ, laser polarization is parallel to Y.
Figure 5. Structure of the laser trace by scanning electron microscopy, the section is achieved perpendicularly to the writing direction. (a) The secondary electron image for 0.8 µJ; (b) The magnification of the part framed in red in (a). (c) A similar part of the laser trace but for 1.4 µJ; (d) The corresponding Inverse Pole Figures coding crystal direction along the writing laser polarization direction for 0.8 µJ; (e) Similar information for 1.4 µJ. N.B.: the color in IPF maps (inset at the right bottom) is based on R3c space group. All scale bars are 1 µm. Other parameters: writing speed 5 µm/s, writing direction along 45˚ and laser polarization direction parallel to Y.
Based on the above analysis, we can defined three regions of the laser traces exhibiting different morpholo- gies: region 1: in Figure 5(b) with nano-sized or sub-micro sized crystals or the core of the Figure 5(c); region 2: the white part at the border of the laser trace, with micro-sized crystals (Figure 5(c)); region 3: for high pulse energy, the tail of the laser trace with nano-sized crystals (Figure 5(e)). Clearly, the texture is stronger at low pulse energy, with the acuity of the 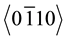 axis direction reinforced along Y.
axis direction reinforced along Y.
4. Discussion
4.1. Sum up of SHG Dependence
A quantity, named anisotropy magnitude, deduced from the angular dependence of the SHG in Figure 2 to Figure 3 and defined as 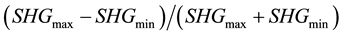 has been used to characterize the angular contrast. It is plotted in Figure 6. At the fix writing speed (5 µm/s), the anisotropy magnitude decreases with the increase of pulse energy (green line in Figure 6). At high speed (25 μm/s), the anisotropy magnitude is not dependent on pulse energy (blue line in Figure 6), whereas it is absolutely not the case when the writing speed is decreased, especially at high pulse energy (red line in Figure 6).
has been used to characterize the angular contrast. It is plotted in Figure 6. At the fix writing speed (5 µm/s), the anisotropy magnitude decreases with the increase of pulse energy (green line in Figure 6). At high speed (25 μm/s), the anisotropy magnitude is not dependent on pulse energy (blue line in Figure 6), whereas it is absolutely not the case when the writing speed is decreased, especially at high pulse energy (red line in Figure 6).
4.2. Modeling/Interpretation
We have analysed the shape of the curves in Figure 2 on the basis of SHG angular response of the single crystal. We used a programme previously used for poling for computing the coefficients in the following expression for simulating the angular dependence of SHG intensity with the probe polarization. It deduced from the theory with the second order nonlinear tensor for the symmetry R3c attached to LiNbO3 crystal, the largest SHG coefficient (d33 = 34.4 pm/V) is supplied in the <0001> crystal direction, i.e. along the polar axis. The other ones are d31 = 5.95 pm/V and d22 = 3.07 pm/V [27] , 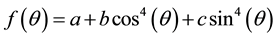 with a = 0.010, b = 0.033, c = −8.4 ´ 10−3. Note that this function is maximum for q = 0˚. From this, we built another expression that may be accounted for by two populations: one randomly oriented and one textured i.e.
with a = 0.010, b = 0.033, c = −8.4 ´ 10−3. Note that this function is maximum for q = 0˚. From this, we built another expression that may be accounted for by two populations: one randomly oriented and one textured i.e.
 where q1 is an angle shift from +X direction; a and b the weight of
where q1 is an angle shift from +X direction; a and b the weight of
the two populations. We obtained a fit with a = 0.013, b = 3.2 and q1 = 3.4˚. Result shown in Figure 7(a) for pulse energy of 0.8 μJ seems to indicate a large proportion of crystal with the polar axis oriented in the X direction versus non randomly oriented nanocrystals.
The same procedure has been applied to pulse energy of 1.8 μJ considering two oriented distributions. In this case, we adjusted the expression with three populations: one randomly oriented and two textured. . We obtained a reasonable fit with a = 0.0, b = 3.9, g = 2.0, q2 = 1.1˚ and q3 = 94˚. The result is shown in Figure 7(b) with one distribution with the polar axis oriented along X (at the level of 66%) and another with the polar axis oriented closely to Y (a few degrees away actually, at the level of 34%).
. We obtained a reasonable fit with a = 0.0, b = 3.9, g = 2.0, q2 = 1.1˚ and q3 = 94˚. The result is shown in Figure 7(b) with one distribution with the polar axis oriented along X (at the level of 66%) and another with the polar axis oriented closely to Y (a few degrees away actually, at the level of 34%).
Because EBSD is the tool for pointing out texture, we intend to get similar information with this method.
A texture has actually been detected and is shown in Figure 8 using pole figures. At low pulse energy (Figure 8(a)), we can see that the polar axis of the crystal (<0001>), is distributed perpendicular to the laser polarization direction (Y) like a fiber texture. The SHG intensity is mainly defined by the angle between the probe laser polarization direction and the polar axis. The width of this function at half maximum is just deduced from the equation 
Figure 6. Anisotropy magnitude of irradiated lines computed from Figure 2 to Figure 3. Here anisotropy magnitude is defined by the following ratio:

Figure 7. Experimental data and computered data of 0.8 µJ for (a) and 1.8 µJ for (b). Writing speed 5 µm/s, writing direction is along 45˚ direction, polarization is parallel to Y direction.
Figure 8. 0001 pole figure of texture calculated from electron backscatter diffraction (EBSD)-scans i.e. the polar axis from EBSD scans. At pulse energy of 0.8 µJ for (a) and 1.4 µJ for (b) and 1.8 µJ for (c), writing speed 5 µm/s, writing direction is along 45˚ direction, polarization is parallel to Y direction. The milky disks at the centre of the pole figures indicate the part of the distribution that should not be taken into account for SHG interpretation with probe polarization in X, Y plane (see text).
The same procedure, applied to the curves in Figure 2 green and blue curves (1.4 and 1.8 μJ), shows two textures: one with the polar axis perpendicular to Y like for low energy and another one at another angle from +X: 112˚ for 1.4 μJ or 140˚ for 1.8 μJ. This is not exactly consistent with the fit we have obtained in angular curve fitting but we have also to note that it is not exactly the same interaction volume considered in SHG analysis (X, Y plane) and cross section analysis (135, Z plane). In the case of SHG, the measurement is performed through the sample whereas for EBSD it is performed at the surface.
From the discussion in the section above, we see that the femtosecond laser induced crystallization leads to crystals not randomly oriented but with one or two textures. This means that some forces are active for orienting the crystals during their formation. The simple preferential orientation is such that the polar axis is perpendicular to the writing laser polarization direction. We have observed this texture in many cases with several orientations of the writing or laser polarization direction providing that the pulse energy is low enough [9] . The first kind of forces that can lead to an orientation is the thermal force due to large thermal gradient experienced in such focused irradiation. However, this can be ignored at once since in that case, there would be no effect of the laser polarization. If we observe such an effect, this is because the light is acting. The simplest idea is a torque exerted on a dipole of the nanocrystal during the nucleation. Assuming that the nuclei have already the structure of the final crystals, we can notice that LiNbO3 may have a spontaneous dipole (because it is ferroelectric), it has also an induced dipole, like any crystal, but with a anisotropic susceptibility in such a way that the dipole is not always parallel to the applied electric field


with 

relative permittivity 


matrix.
This torque aligns the dipole 









The existence of a second texture in the SHG angular response is more difficult to explain. There are two possibilities: this last is not at the same location in the laser track than the previous one and at that place the predominant electromagnetic force is of different origin (non-linear), or the force is of different nature and this last is predominant (e.g. thermal but this one is not dependent of the laser polarization). This discussion may become speculative but in previous papers we have proposed a theoretical approach for trying to understand this effect, it arises from the peculiarity of the femtosecond laser interaction with dielectrics [29] .
Briefly, the laser light is absorbed through multiphoton ionization or tunnelling ionization producing a quasi-free electron plasma in the conduction band. Then, the formed plasma may be further heated by the rest of the laser pulse through free carrier one or several-photon absorption and/or grows through avalanche ionization. In a previous publication [19] , for explaining the existence of the appearance of asymmetric effect in writing with the femtosecond laser like it is also described in Section 3.1.3 here, we have assumed that a ponderomotive force (the force created by the light on the electrons) increases the plasma density on a side of the beam and then that the trapping afterwards “records” the subsequent space charge in the materials, producing a DC field and a stress field that can act between the pulses (memory effect).
In such a way, a second torque is appearing based on the spontaneous dipole of the nanocrystal that may have a direction parallel to the polar axis. The direction of the polar axis is thus driven by the direction of the induced DC electric field that is discussed elsewhere [19] . It depends on the orientation of the pulse front tilt (PFT), of the writing laser polarization direction and of the direction of writing. The PFT has been measured here rotated by 142˚ around the Z axis from X (PFT azimuth) and tilted by 67˚ from the Z axis (PFT colatitude). The angle between the writing laser polarization and PFT makes 55.6˚. This means from the theory developed in [19] that the polarization can play a role. On the other hand, it is also noticed in this paper, that the stress field modify the kinetics and the stress field is dependent of the orientation of writing. We can also remark that the angles between the direction of writing and the PFT one are 83.6˚ (for 45˚ writing direction) and 96.4˚ (for 225˚ writing direction). Finally, the combination of a stress field differently oriented compared to the PFT vector may lead to a variation of the crystallization, here detected on the intensity of the second texture (the one aligned with the laser polarization).
5. Conclusion
In summary, we have demonstrated that second harmonic generation (SHG) can be obtained from a glass by femtosecond laser irradiation. This is a flexible method for controlling SHG three-dimension in silica matrix. By adjusting the pulse energy and writing speed, angular dependence of SHG with the probe laser polarization can be obtained with a high contrast. In our experiment conditions: a) a well-defined cosine-like curve with period of 180˚ could be obtained at low pulse energy or high pulse energy with high writing speed; b) a double cosine- like curve revealing a second texture of the crystals at high pulse energy (1.4 µJ) with low writing speed (5 µm/s) and with the polar axis oriented closer parallel to the writing laser polarization. An asymmetric orientational writing was observed, especially at high pulse energy with low writing speed so when the second texture was active. A discussion has been presented, including the mechanism for tentatively explain the above observations. The main force would be the effect of the electromagnetic polarization of the writing laser on the anisotropic induced dipole. We believe that this investigation contributes to a better understanding of the mechanism of the SHG orientations and contributes to revealing the technology potential in fabricating three-dimensional nonlinear optical devices.
Acknowledgements
The authors thank Prof. T. Baudin, Dr. D. Solas and K. Verstraete in Université Paris-Sud for useful discussions. The work has been done in the frame of FLAG (Femtosecond Laser Application in Glasses) consortium project with the support of Agence Nationale pour la Recherche (ANR-09-BLAN-0172-01). The authors extend thanks to China Scholarship Council and Université Paris-Sud.
Cite this paper
JingCao,BertrandPoumellec,FrançoisBrisset,Anne-LaureHelbert,MatthieuLancry, (2015) Angular Dependence of the Second Harmonic Generation Induced by Femtosecond Laser Irradiation in Silica-Based Glasses: Variation with Writing Speed and Pulse Energy. World Journal of Nano Science and Engineering,05,96-106. doi: 10.4236/wjnse.2015.53012
References
- 1. Franken, P.A., Hill, A.E., Peters, C.W. and Weinreich, G. (1961) Generation of Optical Harmonics. Physical Review Letters, 7, 118-119.
http://dx.doi.org/10.1103/PhysRevLett.7.118 - 2. Bloembergen, N. and Pershan, P.S. (1962) Light Waves at the Boundary of Nonlinear Media. Physical Review, 128, 606-622.
http://dx.doi.org/10.1103/PhysRev.128.606 - 3. Vigouroux, H., Fargin, E., Fargues, A., Garrec, B.L., Dussauze, M., Rodriguez, V., Adamietz, F., Mountrichas, G., Kamitsos, E., Lotarev, S. and Sigaev, V. (2011) Crystallization and Second Harmonic Generation of Lithium Niobium Silicate Glass Ceramics. Journal of the American Ceramic Society, 94, 2080-2086.
http://dx.doi.org/10.1111/j.1551-2916.2011.04416.x - 4. He, X., Poumellec, B., Liu, Q., Brisset, F. and Lancry, M. (2014) One-Step Photoinscription of Asymmetrically Oriented Fresnoite-Type Crystals in Glass by Ultrafast Laser. Optics Letters, 39, 5423-5426.
http://dx.doi.org/10.1364/OL.39.005423 - 5. Du, X., Zhang, H., Zhou, S., Zhang, F., Dong, G. and Qiu, J. (2015) Femtosecond Laser Induced Space-Selective Precipitation of a Deep-Ultraviolet Nonlinear BaAlBO3F2 Crystal in Glass. Journal of Non-Crystalline Solids, 420, 17-20.
http://dx.doi.org/10.1016/j.jnoncrysol.2014.12.023 - 6. Qiu, J., Miura, K. and Hirao, K. (2008) Femtosecond Laser-Induced Microfeatures in Glasses and Their Applications. Journal of Non-Crystalline Solids, 354, 1100-1111.
http://dx.doi.org/10.1016/j.jnoncrysol.2007.02.092 - 7. Dai, Y., Zhu, B., Qiu, J., Ma, H., Lu, B. and Yu, B. (2007) Space-Selective Precipitation of Functional Crystals in Glass by Using a High Repetition Rate Femtosecond Laser. Chemical Physics Letters, 443, 253-257.
http://dx.doi.org/10.1016/j.cplett.2007.06.076 - 8. Komatsu, T., Koshiba, K. and Honma, T. (2011) Preferential Growth Orientation of Laser-Patterned LiNbO3 Crystals in Lithium Niobium Silicate Glass. Journal of Solid State Chemistry, 184, 411-418.
http://dx.doi.org/10.1016/j.jssc.2010.12.016 - 9. He, X., Fan, C., Poumellec, B., Liu, Q., Zeng, H., Brisset, F., Chen, G., Zhao, X. and Lancry, M. (2014) Size-Controlled Oriented Crystallization in SiO2-Based Glasses by Femtosecond Laser Irradiation. Journal of the Optical Society of America B—Optical Physics, 31, 376-381.
http://dx.doi.org/10.1364/JOSAB.31.000376 - 10. Stone, A., Jain, H., Dierolf, V., Sakakura, M., Shimotsuma, Y., Miura, K., Hirao, K., Lapointe, J. and Kashyap, R. (2015) Direct Laser-Writing of Ferroelectric Single-Crystal Waveguide Architectures in Glass for 3D Integrated Optics. Scientific Reports, 5, 10391.
http://dx.doi.org/10.1038/srep10391 - 11. Komatsu, T., Ihara, R., Honma, T., Benino, Y., Sato, R., Kim, H.G. and Fujiwara, T. (2007) Patterning of Non-Linear Optical Crystals in Glass by Laser-Induced Crystallization. Journal of the American Ceramic Society, 90, 699-705.
http://dx.doi.org/10.1111/j.1551-2916.2006.01441.x - 12. Zeng, H., Poumellec, B., Fan, C., Chen, G., Erraji-Chahid, A., et al. (2012) Preparation of Glass-Ceramics with Oriented Nonlinear Crystals: A Review. Nova Science Publishers, New York, 89-134.
- 13. Ochi, Y., Meguro, T. and Kakegawa, K. (2006) Orientated Crystallization of Fresnoite Glass-Ceramics by Using a Thermal Gradient. Journal of the European Ceramic Society, 26, 627-630.
http://dx.doi.org/10.1016/j.jeurceramsoc.2005.07.044 - 14. Gerth, K., Rüssel, C., Keding, R., Schleevoigt, P. and Dunken, H. (1999) Oriented Crystallisation of Lithium Niobate Containing Glass Ceramic in an Electric Field and Determination of the Crystallographic Orientation by Infrared Spectroscopy. Physics and Chemistry of Glasses, 40, 135-139.
- 15. Stuart, B., Feit, M., Herman, S., Rubenchik, A., Shore, B. and Perry, M. (1996) Nanosecond-to-Femtosecond Laser-Induced Breakdown in Dielectrics. Physical Review B, 53, 1749-1761.
http://dx.doi.org/10.1103/PhysRevB.53.1749 - 16. Eaton, S., Zhang, H., Herman, P., Yoshino, F., Shah, L., Bovatsek, J. and Arai, A. (2005) Heat Accumulation Effects in Femtosecond Laser-Written Waveguides with Variable Repetition Rate. Optics Express, 13, 4708-4716.
http://dx.doi.org/10.1364/OPEX.13.004708 - 17. Gattass, R., Cerami, L. and Mazur, E. (2006) Micromachining of Bulk Glass with Bursts of Femtosecond Laser Pulses at Variable Repetition Rates. Optics Express, 14, 5279-5284.
http://dx.doi.org/10.1364/OE.14.005279 - 18. Stone, A., Sakakura, M., Shimotsuma, Y., Stone, G., Gupta, P., Miura, K., Hirao, K., Dierolf, V. and Jain, H. (2009) Directionally Controlled 3D Ferroelectric Single Crystal Growth in LaBGeO5 Glass by Femtosecond Laser Irradiation. Optics Express, 17, 23284-23289.
http://dx.doi.org/10.1364/OE.17.023284 - 19. Poumellec, B., Lancry, M., Desmarchelier, R., Hervé, E., Brisset, F. and Poulin, J.C. (2013) Asymmetric Orientational Writing in Glass with Femtosecond Laser Irradiation. Optical Materials Express, 3, 1586-1599.
http://dx.doi.org/10.1364/OME.3.001586 - 20. Todorovi&cacute, M. and Radonji&cacute, L. (1997) Lithium-Niobate Ferroelectric Material Obtained by Glass Crystallization. Ceramics International, 23, 55-60.
http://dx.doi.org/10.1016/0272-8842(95)00140-9 - 21. Fan, C. (2011) Directional Writing Dependence of Birefringence in Multicomponent Silica-Based Glasses with Ultrashort Laser Irradiation. Journal of Laser Micro/Nanoengineering, 6, 158-163.
- 22. Dingley, D.J. and Randle, V. (1992) Microtexture Determination by Electron Back-Scatter Diffraction. Journal of Materials Science, 27, 4545-4566.
http://dx.doi.org/10.1364/OL.37.002955 - 23. Fan, C., Poumellec, B., Lancry, M., He, X., Zeng, H., Erraji-Chahid, A., Liu, Q. and Chen, G. (2012) Three-Dimensional Photoprecipitation of Oriented LiNbO3-Like Crystals in Silica-Based Glass with Femtosecond Laser Irradiation. Optics Letters, 37, 2955-2957.
http://dx.doi.org/10.1364/OL.37.002955 - 24. Weis, R.S. and Gaylord, T.K. (1985) Lithium Niobate: Summary of Physical Properties and Crystal Structure. Applied Physics A, 37, 191-203.
http://dx.doi.org/10.1007/BF00614817 - 25. Butet, J., Russier-Antoine, I., Jonin, C., Lascoux, N., Benichou, E. and Brevet, P.-F. (2013) Effect of the Dielectric Core and Embedding Medium on the Second Harmonic Generation from Plasmonic Nanoshells: Tunability and Sensing. The Journal of Physical Chemistry C, 117, 1172-1177.
http://dx.doi.org/10.1021/jp310169u - 26. Yang, W., Kazansky, P.G. and Svirko, Y.P. (2008) Non-Reciprocal Ultrafast Laser Writing. Nature Photonics, 2, 99-104.
http://dx.doi.org/10.1038/nphoton.2007.276 - 27. Träger, F. (2007) Springer Handbook of Lasers and Optics. Springer, New York.
http://dx.doi.org/10.1007/978-0-387-30420-5 - 28. Zelmon, D.E., Small, D.L. and Jundt, D. (1997) Infrared Corrected Sellmeier Coefficients for Congruently Grown Lithium Niobate and 5 mol.% Magnesium Oxide—Doped Lithium Niobate. Journal of the Optical Society of America B, 14, 3319-3322.
http://dx.doi.org/10.1364/JOSAB.14.003319 - 29. Mao, S.S., Quéré, F., Guizard, S., Mao, X., Russo, R.E., Petite, G. and Martin, P. (2004) Dynamics of Femtosecond Laser Interactions with Dielectrics. Applied Physics A, 79, 1695-1709.
http://dx.doi.org/10.1007/s00339-004-2684-0








