Received 21 April 2014; revised 5 May 2014; accepted 12 May 2014

ABSTRACT

In this paper, molecular dynamics (MD) simulations of nano-sized wiredrawing are performed. The wiredrawing is a traditional plastic working method, but there has not been any insight to develop it in a nano-sized scale. Therefore, to materialize the concept of the nano-sized wiredrawing, a numerical modelling is pursued at first in this paper, and the interatomic potential, a crystalline orientation, the drawing condition realized by a die geometry are thoroughly investigated. In particular, to reduce the friction between a wire and a die, a simple friction model for the MD analysis is newly proposed, where the interatomic interaction is adequately modified by a single factor ω. Then, the fruitful results are obtained by using ω = 0.1. We checked the availability of such nano-sized MD simulation by constructing a two-dimensional wiredrawing model, at first. The analysis of atomic stress during drawing is also assessed. It is useful to use invariant of the atomic stress tensor, such as hydrostatic stress (average stress, σ_m) or von Mises equivalent stress (σ_eq). The former is related to the phase transformation from the body-centered-cubic (bcc) structure to the face-centered-cubic (fcc) one, which is found in the present MD simulation. It is observed that an initial α-iron crystal with bcc structure changes partially into the fcc phase. It is recognized that the phase transformation is caused by the positive hydrostatic stress values, which is occurring especially inside the die region. We observed that a lot of dislocation core structures occur in wiredrawing process and their existence and evolution are well related to the equivalent stress values.

Keywords:

Molecular Dynamics, Iron and Steel, Wiredrawing, Plastic Working, Nanotechnology, Materials Processing, Crystalline Structure

1. Introduction

There are many plastic working processes that are important for industry. Above all, drawing (wiredrawing) process is extensively used to fabricate axisymmetric metallic bars and wires into a prescribed diameter. It is interesting that the wiredrawing is basically using only a die. So far, for example, drawn wires made up of iron and steel have been applied to many industrial products, such as tire codes, piano (music) wire, and suspension wire of huge bridge. Today, materials are trending toward very narrow and small size. For the purpose of utilizing wire structures in the field of MEMS (Micro Electro Mechanical System) or small-sized electronic/computer devices, the dimension of wire material should be as small as possible. From now on, a diameter required in such purpose will become less than one micrometer, i.e. less than several hundreds of nano-meters. Certainly, there is another cutting-edge method to synthesize very tiny wire using nano-structured template [1] . But, it has to be based on chemical reaction process and spontaneous crystal growth technique, so it is not so easy to control the fabricating process. Therefore, as an effective method for the production of very narrow and small wires, the traditional plastic working technique using the die may be applied, by downsizing the wiredrawing process into a nano-meter scale. Indeed, it is, of course, just an idea with possibility now, but in near future it will be categorized as a prospective extension of the traditional wiredrawing method. So far, the smallest steel wire made by commercial drawing has just reached to several micrometers in diameter. Accordingly, “nanoscale wiredrawing” is one of prospective technologies. However, now, we do not have any evidence for feasibility of nano-meter wire drawing technique. For this reason, we need first to study the possibility of this new technique, and we should predict the material behaviors by numerical simulation.

In this study, the molecular dynamics (MD) method, which is one of theoretical and computational techniques for materials modelling and simulation, is applied to the nano-sized wiredrawing process. In numerical modelling, except for MD method, usually, finite element (FE) analysis, which is definitely based on some mathematical elastic-plastic continuum theory, has been widely applied to investigate the wiredrawing process. In recent years, since information about the crystalline change of metallic materials during wiredrawing is very crucial, the FE analysis including crystal plasticity theory (CPFE) [2] [3] is well being applied to the study. Though the FE analysis can produce many practical results, its material model must be constructed in mathematical fashion and the interaction between the die and the wire is still inevitably ambiguous. Namely, microscopic physics of a wire material is not sufficiently modeled by the conventional FE or even precise CPFE framework. The conventional FE is also unsuitable to analyze the texture and defects which are being nucleated and developing in the wire. To the contrary, the MD method is capable of modelling a wire material from atomic-scale physics and so the method has an advantage in predicting microscopic phenomena. It is well known that there are some drawbacks of MD, however. At the present, the largest three-dimensional computational size of atomic system treatable in the MD method is just limited to the range around several hundreds nano-meters. However, as stated above, there is a trend to make smaller metallic wire and this fact requires us to simulate the phenomena from the atomic scale to obtain a clear insight about wiredrawing. For those reasons, the present authors suppose that it is very worthwhile using the MD method to analyze the wiredrawing process.

So far, plasticity or plastic working process has been investigated by the MD method as follows. As for analyses of plastic working application, for example, the rolling [4] and the cutting [5] of metallic materials have been studied. As for unknown phenomena concerning plasticity, to name a few, dynamic recrystallization in Cu-Al system [6] , pencil glide dislocation motion in bcc (body-centered cubic) crystal [7] , and martensitic phase transformation of alloy [8] , have been studied. Unfortunately yet, there has not been any MD study concerning wiredrawing. In the wiredrawing process, the force and the contact conditions subjected to the wires are tremendously strong. Therefore, the wiredrawing is one of strong plastic working techniques, where the material is subjected to very strong multi-axial stress and strain. A similar viewpoint can be found in the MD analysis concerning severe plastic deformation (SPD) processes [9] , many of which have been experimentally invented as novel plastic processing method. Also, the nano-sized imprint (nano-imprint) technique of copper has been attempted in the MD simulation [10] , while the material implemented there is generally a soft polymer or a resin. Once again, to our knowledge, there has not yet been any MD study of nano-sized wiredrawing.

In this study, iron and steel wires are focused on, for they are extensively used with the wiredrawing in industry. In iron and steel, an impurity addition such as carbon, etc., is usually carried out. Consequently, both strength and ductility are enhanced at the same time, thanks to an eutectic phase called a pearlite phase. The pearlite phase is composed of ferrite (α-Fe) and cementite (Fe₃C) crystal as sub-structures inside. In the present MD simulation, however, some drastic simplification in the computational model is inevitable, especially for the modelling of interatomic potential function. So, at this point, it is reasonable to use a single crystal model comprising just the ferrite crystal and then a reliable potential function just between iron atoms will be successfully adopted.

In this study, an atomic-scale wiredrawing model is constructed for the MD simulation. The new knowledge of atomic mechanism in the wiredrawing which is presented in this study is useful for the future micro-scale or nano-scale wiredrawing process. Ideally, the wiredrawing includes an axisymmetric condition and so a full three-dimensional model would be optimum. But, for the simplification of the MD model, a two-dimensional drawing model using periodic boundary condition is adequate now and here. The realistic crystal rotation and the motion of lattice defects will be precisely captured by upcoming study of a full three-dimensional model [11] .

As one of topics in our study of MD modelling, a friction model is proposed and is evaluated. As frequently observed in MD analyses, a friction force between nano-sized solids becomes tremendously large, because of larger relative contacting area between surfaces. In our model, the interatomic potential between the die and the wire atoms is modified to conduct the drawing smoothly with a moderate lubricating condition. Since the present friction model requires somewhat parametric study, the first evaluation is provided here.

Understanding the stress or strain distribution inside a drawn wire, including the residual stress distribution, is important in discussing the result of wiredrawing process. In the history of studies of the wiredrawing [12] -[16] , hydrostatic and (von Mises) equivalent stress components are key factors which should be focused on. This paper shows that the atomic motion and behavior of lattice defects are closely related to their stress distribution. We also affirm the result of crystalline phase transition between bcc and fcc (face-centered cubic) in microscopic scale. This behavior has not yet observed experimentally in the drawing of steel wires. The present study shows that the mechanism of phase transition is also closely related to the stress distribution inside the wire.

2. Theory and Methods

2.1. Molecular Dynamics

Molecular dynamics (MD) is a microscopic numerical simulation technique, where the time evolution of atomic or molecular system is obtained. The interatomic interaction between atoms or molecules is prescribed. The equations of motions are numerically integrated, with a certain time increment (usually in the order of femto- second), to update positions and velocities of individual atoms. Using the atomic trajectories in the system, the development of crystal structure and material phase is captured. Accordingly, dynamics of phase transition can be simulated directly, and transport coefficients such as diffusion constant can be estimated effectively.

The equations of motion are given by Equation (1),

(1)

where m_i , r_i , F_i , and t are atomic mass, position, interatomic force, and time, respectively. The MD simulation is sometimes called a deterministic method, which is different from any stochastic method such as Monte Carlo method. The interatomic force is straightforwardly determined as the derivative of the potential energy of the total system E_tot. Though the MD method provides a high-resolution view of the material, the calculated size is only limited to very tiny portion of the material. In addition, the interatomic potential function is just an approximation of real material system. However, those drawbacks are being somewhat resolved by introducing ab- initio (first principle) method involving quantum mechanical formulation and also by utilizing a parallel algorithm to enable very larger-scale computations.

2.2. Interatomic Potential Function of Iron and Steel

The crystal structure of iron is bcc in the standard temperature and pressure, while it changes to fcc in high temperature or stress application. Accordingly, most of potential functions are formulated in the bcc structure. The potential function of the embedded atom method (EAM) is adopted in the present study. The EAM can reproduce the many-body effect around a metallic atom. We use the Finnis-Sinclair type potential (FS potential) [17] , which has been extensively used in other MD studies, because of its high accuracy in system energy and atomic behavior of iron system. In the FS potential formulation, the total energy of the system is given by,

(2)

where E_m means the many-body term, ρ_i is an electron density made up of interactions from surrounding atoms, and F(ρ) means a functional of the electron density. The second term E_p is a summation of usual pairwise interactions f(r).

2.3. The Concept of Nano-Scale MD Wiredrawing Model

Generally speaking, the wiredrawing is one of traditional plastic working processes, in which bar or rod is forced to go through the die, and is eventually given a narrower diameter (i.e. it is shrunk in diameter and is stretched in the longitudinal direction). Consequently, the wire material is given higher strength and ductility as well as a fine surface finish. The purpose of the present study is to build a nano-meter-sized simulation model for the wiredrawing process. The idea that a hollow die is used in the wiredrawing is straightforwardly adopted. Therefore, whether it will be actually better choice or not is, in fact, left to the future experimental study.

2.4. Nano-Scale MD Wiredrawing Model

It is true that a three-dimensional model is more precise for the wiredrawing as shown in Figure 1(b) which is being used in another study [11] [18] . But, in three-dimension, understanding the behavior of crystal transition and defects is quite complicated yet. Therefore, in the present study, an approximated two-dimensional model of the wiredrawing, as shown in Figure 1(a), is constructed and is applied to the MD simulation. The MD calculation is carried out in three-dimensional space, but the periodic boundary condition is imposed on in one direction

(in this case, y direction) which is perpendicular to the drawing direction (in this case, z direction). This model seems like the rolling process, but, since the deformation in periodic direction (y direction) is constrained, the stress state tends to be tri-axial similar to the wiredrawing.

The die semi-angle is 5.0 degrees and the length of the die slope is 5.0 nm, which are fixed through the present study. In fact, the die semi-angle in between 5 and 7 degrees is proved to be optimum in axisymmetric drawing by analytic consideration of theoretical plasticity. As recognized well, the choice of crystalline orientation relative to the drawing direction affects the mechanical property of the drawn wire. Therefore, [100] [111] orientations are compared here. All the calculation conditions are summarized in Table 1.

2.5. Construction of Friction Model

The plastic working technique usually copes with the problem of the friction between the die and the wire material [19] . Since the relative contact area is larger in nano-sized scale, the effect of friction becomes larger. It is supposed that the future nanotechnology should overcome the friction problem as a primal subject. The developing study of nano-imprint technique is one of the challenges [10] .

In this study, it is proposed that the friction is reduced by modifying the potential function between the die and the wire atoms as shown in Figure 2. The interatomic interaction is somewhat needed to make the friction,

but it is reduced not to adhere each other. The general formulation is shown as follows. For example for pairwise potentials, the cohesive energy (interatomic binding energy) is determined by the intensity of the potential function itself. Therefore, the potential function is reduced by an arbitrary factor ω, which is less than unity (ω < 1). At this point, the factor ω is completely ad-hoc parameter and it should be fitted by ab-initio calculation or experimental result in the future. So far, we have evaluated the adequate value of ω in our MD simulation. As an consequence, it is found that ω should be less than 0.1, and then it shows good results for most of wiredrawing conditions.

Generally, the original potential function V(r) is modified by Equation 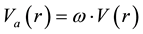(3).

(3)

The many-body potential is composed of the many-body term and the pairwise term, as shown in Equation (2). Interatomic bonding is largely contributed by the many-body term and it is usually a monotonically increasing function of the electron density ρ(r). Thus, for the FS potential in this study, ρ(r) is directly multiplied by the factor ω introduced above. The expression of the FS potential including the friction condition is given by Equation (4) together with Equation (2),

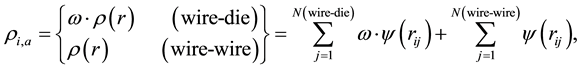(4)

where ψ(r) is a pairwise function for the electron density. The ω < 0.1 is found to show a relevant friction in the many-body case as well.

2.6. Analyzing Method of the MD Output

CNA Method: In order to detect a crystal type and its orientation, the common neighbor analysis (CNA) can be used effectively [20] [21] . By using the CNA, one can identify each atom as fcc, bcc or the other crystalline structures. Besides, by the CNA, we can determines atoms near a lattice defect such as dislocation, grain boundary or surface.

Atomic Stress: It is possible to calculate the atomic stress tensor (atomic stress) in MD calculation. The atomic stress tensor is derived along with the continuum concept of stress tensor. When an individual atomic volume is assumed, then strain energy stored inside the volume is evaluated from interatomic potential. The energy is mathematically differentiated by the strain tensor which assumes homogeneous deformation and is expressed by the distance between pair of atoms. This means that atomic stress corresponds to increase of the elastic strain energy per unit volume. Thus, the general formulation of atomic stress of atom i is defined by Equation 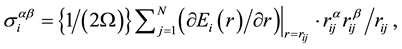(5).

(5)

where 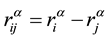is the difference of position vectors between i and j atoms, r_ij is their distance. E_i(r) is an effective energy contribution from i atom. Ω is the atomic volume for the reference structure. Generally speaking, the summation of many-body energy is unable to be divided into the energy of each atoms. However, for FS potential, we can do it only in considering an effective potential,

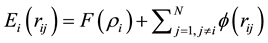(6)

In finite temperature, atomic stress inevitably contains large fluctuation due to the small number of atoms. So, it needs to be averaged in volume or in time interval to give continuous distribution. The averaged stresses are displayed without the atomic subscript i, like σ^αβ, and we use these values throughout this paper and call them only “stress”.

Once the components of the stress with regard to a set of coordinate axes (x, y, z) are obtained, effective stress invariants are calculated from them. They are, for instance, hydrostatic stress (mean stress) σ_m and von Mises equivalent stress σ_eq. σ_m is also the first invariant of stress tensor, defined by,

(7)

where p means hydrostatic pressure. The σ_m represents a tri-axial condition of the stress and it is related to the volume change. For example in the wiredrawing process, with increase of the σ_m in positive regime (i.e. tensile stress, σ_m > 0), an internal fracture (also called central burst or “cuppy” failure in the actual process) tends to take place. On the other hand, the σ_eq is related to the second invariant of stress. It combines the deviatric stress components and is defined by,

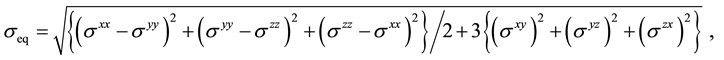(8)

Physically, the σ_eq value reflects a nucleation event of dislocation and its motion in a crystal. In the atomic system in MD simulation, the σ_eq, which is evaluated locally in an atomic system, exhibits the intensity of driving force for the nucleation or the mobility of dislocations.

3. Results and Discussion

3.1. Effect of the Factor ω on the Friction Behavior

Wiredrawing simulations are performed with the variety of friction factors, ω = 1.0, 0.1, 0.01 and 0.001, and the dependency on friction factor ω is investigated. The maximum stress value for components σ^zz, σ_m, and σ_eq, which are averaged over all atoms in the wire, are shown in Figure 3(a). Moreover, Figure 3(b) shows the time-averaged stress components. It is clear that the larger ω is, the larger the stresses are. It means that resistance of the wire material during the drawing process, is totally raised by larger ω near unity. The resistance is possibly caused by the friction at the wire surface between the die and the wire atoms as well as the plastic deformation occurring inside the wire. If we assume that the resistance due to plasticity provides a constant resistance, the friction at the wire surface is responsible for the change in the total resistance in the drawing process. Besides, the results for ω = 0.01 and ω = 0.001 are not so different and their difference in stresses is almost zero. Thus, we can apply the friction model with the factor ω = 0.001 in all the MD simulations presented here.

3.2. Stress Distribution and Its Change in Wiredrawing Process

3.2.1. Drawing Stress

Figure 4 shows the value of σ^zz which is the normal stress component in the direction of wiredrawing (i.e. σ^zz is a drawing stress) and σ^xx which is in the perpendicular direction and not in the direction of periodicity of the model. After a start-up period when the length 1.5 nm of the wire has been drawn, the stress component σ^xx tends to be negative (compressive) and then becomes stationary. On the other hand, the drawing stress, σ^zz, tends to be positive (tensile) and becomes stationary. The value of σ^zz reaches 6.0 GPa at maximum, the magnitude of

which is about twice the maximum value of the magnitude of σ^xx. As for comparison among crystalline orientations, the wiredrawing in [100] direction shows the largest stress values among three. If we assume the same effect of the friction at the surface, this fact means that the crystal arranged in [100] orientation shows the largest resistance to the plastic deformation among three orientations.

3.2.2. Hydrostatic Stress

In order to comprehend characteristics of the stress state in the wire, it is highly reasonable to look into both hydrostatic stress, σ_m, and equivalent stress, σ_eq. The normal stress components, σ^xx, σ^yy or σ^zz may be either tensile or compressive, but an averaged tri-axial stress state, i.e. σ_m tends to be in tension or in compression. The hydrostatic stress, σ_m, corresponds only to an elastic deformation, whereas equivalent stress, σ_eq, is derived from the deviatric stress tensors which are a residue of stress tensor in excluding isotropic contribution. Accordingly, the atomistic value of σ_eq shows a measure of the plastic working which those atoms have been experienced during the wiredrawing.

Time transition of σ_m and σ_eq during drawing is visualized in Figure 5. It is understood that σ_m is always positive (tensile stress). However, when the drawing speed is slower (condition (B)), the magnitude of σ_m is converging into zero. This means that, in the case with a higher drawing speed (such as v = 50 m/s, Figure 5(a)), the deformation velocity in plasticity is defeated by the traveling speed of the wire. As a result, the plastic deformation has not fully been carried out even after the wire comes out of the die region. To the contrary, in a slower drawing case, there is a plenty of time for the atoms to undertake a plastic deformation, including a nucleation of lattice defect such as dislocation. The whole crystalline structure is relaxed and the hydrostatic stress σ_m drops soon after that, in this case. As shown in Figure 5(b), the plastic deformation can proceed, not increasing the stress σ_eq and keeping the magnitude of σ_m at a low level.

Figure 6 shows the stress distribution when it is viewed in the cross-section of the wire (projected onto xz plane). This is the case of wiredrawing with [100]-orientation and v = 50 m/s. Those pictures are arranged as follows: (A) normal stress in drawing direction σ^zz, (B) hydrostatic (mean) stress σ_m, and (C) equivalent stress σ_eq, from the top to the bottom. Also, the pictures at 40, 80 and 120 ps are arranged from the left to the right.

The drawing stress σ^zz possesses a positive value after passing through the die region, whereas the trailing part shows a negative value (compressive). These plus and minus in the stress value seems balanced in the total region of the wire. The mean stress σ_m shows a larger value, especially near the exit of the die region, and it is decreasing with increase of the distance from the exit of the die. Besides, a v-shaped region of the compressive stress exists at the entrance of the die region. Since the wire is always compressed by the inclined surface of the die, it is reasonable that the atoms in the wire have always compressive stress.

Equivalent stress σ_eq shows a large value at the center of the die region. The stress value of the wire is increasing with increase of the distance from the exit of the die. It seems natural that the σ_eq is large around the region in which the wire material is experiencing a plastic deformation. As an example, an isolated dislocation structure is observed at the lower part in the cross-sectional picture which is taken outside the die region, as

shown in the figure at 120 ps. Discussion concerning the structure and the dynamics of dislocations will be shown in the subsequent section in relation to the CNA analysis.

3.3. Results of Crystal Change by Common Neighbor Analysis (CNA)

Figure 7 shows the distribution and its transition of the crystalline state which is analyzed by common neighbor analysis (CNA) during wiredrawing. It is found that, when the drawing velocity is high, there occurs a phase transformation from bcc into fcc in some part of the wire. This fact will be discussed in more detail later in this paper. For a slow drawing velocity, this type of phase transition certainly takes place, but the amount of it is much smaller compared with the fast drawing. Anyway, for both velocities, however, the transformed fcc phase does not stay alive so long time. Most of the transformed fcc phase disappears and changes back into a bcc phase spontaneously. This return event of the crystalline phase is observed, after the transformed fcc region of the wire just exits from the die region. It is guessed that the driving force needed to the phase transformation is no longer applied outside the die region.

Figure 8 shows the time transition of the ratio of fcc atoms to the whole wire atoms. As can be seen in the figures, the phase transformation takes place instantly after the drawing starts. There is a tendency that a higher drawing velocity promotes more atoms which are relating to the phase transformation.

Figure 9 shows a selected region of the atomic configurations including a dislocation core, which are analyzed by the CNA method. The arbitrarily selected time is 120 ps after the wiredrawing started.

This case is for the drawing of [100]-orientation. The series of pictures in Figure 9 are displayed to compare

between the atomic configuration, CNA analysis, the distribution of hydrostatic stress, and the distribution of equivalent stress, respectively. It is understood, from the atomic arrangement and the stress distribution, that this dislocation contains edge and screw components at the same time. The magnitude of the stress value is especially larger in the dislocation core. The dislocation is moving from upper-right to lower-left in angle of 45 degrees with regard to the horizontal axis in these pictures. By viewing pictures of the CNA analysis, it is confirmed that this dislocation is an isolated one, and it is atomistically composed of both less-coordinated and excessive-coordinated atoms which are located above and beneath the slip plane, respectively.

The hydrostatic stress of the atoms located above and beneath the slip plane have the opposite sign each other. The equivalent stress exhibits a large value widely around the dislocation core. The surface of the wire is seen at the bottom of these figures. When the dislocation reaches at the surface, the lattice imperfection due to the dislocation structure resolves naturally into a perfect crystal, where the wire surface is contacting strongly to the die surface. These MD results of the wiredrawing show that the events concerning generation, movement and annihilation of dislocation are all performed in the nano-sized scale and in a very short time.

Figure 10 shows stress components (hydrostatic stress σ_m, equivalent stress σ_eq and drawing stress σ^zz), all of which are averaged over atoms in each CNA categories. In the condition shown here (the [100]-oriented drawing and the drawing velocity of v = 50 m/s), it is observed that the phase transition into the fcc crystal occurs on a large area in this cross-section. All the stress values indicated in Figure 10 are averaged and normalized by the total average. At that moment, the ratio of categories is as follows: bcc = 85%, fcc = 3%, hcp (hexagonal close- packed) = 0%, surface (less coordinated) = 12%, and grain boundaries and defects (excessively coordinated) ≤ 1%. The fcc phase occupies relatively a large volume, but the fcc atoms there do not transform into a hcp phase (the hcp phase means regional stacking fault of the fcc crystal) at all. The hydrostatic stress is generally larger in the fcc-transformed region. The equivalent stress is also generally larger in the disordered (defected) region, such as the phase boundary around the fcc-transformed region, dislocation, or grain boundary.

From these facts, it is concluded that the hydrostatic stress component is responsible for the bcc → fcc phase transition. It can be said that the iron atomic system in our MD model undergoes a process of the severe plastic deformation (SPD). It also understood that such a strong plasticity condition can be realized by a nano-sized wiredrawing condition.

4. Conclusions

In order to assess the possibility of nano-sized wiredrawing, molecular dynamics (MD) modelling of α-iron is carried out. In the modelling, potential function, crystalline orientation and geometry of die etc. have to be considered so as to succeed in wiredrawing. In particular, introduction of friction model is inevitable. In this paper, to simplify the material behavior, the two-dimensional MD models with three different crystalline orientations are compared. Following results are obtained.

1) The interatomic function which is modified by the factor ω works well for reducing the friction between wire and die. The variety of ω values is compared. It is resulted that the smaller ω is, the smaller the resistance in drawing is obtained.

2) The invariant of atomic stress tensor is useful to recognize the status of atoms in the wire. Both hydrostatic stress σ_m and von Mises equivalent stress σ_eq are evaluated.

3) Phase transformation into fcc crystal occurs in wiredrawing of α-iron. It is caused by large hydrostatic stress σ_m in tensile regime (plus sign). The fcc phase is generally short-lived and is maintained only inside die region.

4) Dislocation structures are observed in wiredrawing. Atomistic equivalent stress clearly exhibits the core structure of a dislocation. A set of dislocation behaviors including nucleation, movement and annihilation at the wire surface completes in very small period.

Acknowledgements

This study is partly supported by the “Strategic Project to Support the Formation of Research Bases at Private Universities: Matching Fund Subsidy from MEXT (Ministry of Education, Culture, Sports, Science and Technology) (2012-2014)”. The authors also acknowledge Nippon Steel & Sumitomo Metal Co. Ltd. and Kurimoto Ltd. for financial support.

References

NOTES

^*Corresponding author.