Advances in Chemical Engineering and Science
Vol.07 No.03(2017), Article ID:77773,21 pages
10.4236/aces.2017.73023
Solvent Extraction of Citric Acid with Different Organic Phases
Estêvão Magno Rodrigues Araújo, Fabrício Eduardo Bortot Coelho, Julio Cézar Balarini, Tânia Lúcia Santos Miranda, Adriane Salum*
Chemical Engineering Department, Federal University of Minas Gerais (UFMG), Belo Horizonte, Brazil

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 26, 2017; Accepted: July 17, 2017; Published: July 20, 2017
ABSTRACT
The present work aimed at the study of citric acid solvent extraction in order to establish the composition of the organic phase and to obtain thermodynamic and kinetic data for the chosen system. Discontinuous extraction experiments in a single stage were performed from a synthetic solution of citric acid, with the typical concentration (10% w/v) observed in industrial fermented musts. Exploratory experiments were carried out using different organic phases in order to select the most suitable solvent phase to further continuous extraction tests in a mechanically agitated column. The selected organic phase composition was: Alamine® 336, Exxal™ 13 tridecyl alcohol, and the aliphatic diluent EscaidTM 110. Next, the effects of the contact time and of the concentrations of extractant and modifier on the citric acid extraction were studied. Among the investigated conditions, the best one was 10 minutes of contact time, 30% w/v of Alamine® 336, and 10% w/v of Exxal™ 13 tridecyl alcohol. For this condition, the equilibrium isotherm (28˚C ± 2˚C) was determined, and the equilibrium constant was calculated (36.8 (mol∙L−1)−1.5). It was considered that trioctylamine and citric acid complexation reaction occurs mainly with non-dissociated citric acid form, because the aqueous feed solutions’ pH is lower than the citric acid pKa1. It was found that 1.5 molecules of the extractant, on average, are required to react with one citric acid molecule, which can indicate that reactions with different extractant/citric acid ratios occur simultaneously. Next, the rate constants for the direct and inverse reactions, 2.10 (mol∙L−1)−1.5∙s−1 and 5.69 × 10−2 s−1, respectively, were calculated. Coefficients of determination (R2) values higher than 0.93 were found in these calculations, suggesting that the results obtained using a computer modeling would be very close to those results obtained experimentally. Therefore, the present work provides data required to future modelling, design, and simulation of citric acid solvent extraction processes.
Keywords:
Citric Acid, Solvent Extraction, Alamine 336, TOA, Equilibrium Isotherm

1. Introduction
Citric acid (2-hydroxypropane-1,2,3-tricarboxylic acid) is a tricarboxylic acid, naturally presents in several fruits, vegetables, and in the milk. Commercially, citric acid is usually found as a white crystalline solid and it has several industrial applications. This acid is widely used in food and pharmaceutical industries because of its various functions, as acidulant, food preservative, chelating agent, carbonic gas fixer, humectant, emollient, and others.
The ionization of one or more of the three carboxylic groups (-COOH) presenting in citric acid produces the citrate ions, which are good buffer agents in acid solutions. Citrate salts with metals can also chelate metallic ions. This property allows the use of citrates as water softeners and food preservatives. For instance, calcium citrate is an important food additive [1] .
Industrially, citric acid is produced mainly through the fermentation of sucrose, which is done by the fungi of Aspergillus genus, especially the Aspergillus niger one. After fermentation, the produced acid needs to be recovered. In the conventional processes, citric acid is recovered by its precipitation with calcium hydroxide. Then, the citric acid is regenerated by adding sulfuric acid to the precipitated calcium citrate. In the final step, the acid is crystalized and dried. The main problem, associated with this process, is the requirement of resins to purify liquid phases and the huge amount of calcium sulfate generated [2] . Thus, alternative processes for citric acid recovery and purification from fermented musts have been developed. In recent studies, involving the purification of citric acid, it is worth mentioning the use of a bipolar membrane electrodialysis [3] [4] and reactive extraction using a tertiary amine and supercritical carbon dioxide [5] .
In the solvent extraction, one of these alternative processes, the feed phase (fermented must) is contacted with an organic phase (solvent). These phases are mutually immiscible and the citric acid is selectively extracted from the feed to the organic phase. This process can be applied when the fermented musts contain a low amount of impurities, since the solvent may extract compounds rather than the citric acid. For instance, oxalic acid can be formed under an uncontrolled fermentation process, and this acid may be co-extracted by the solvent. In addition, the presence of solids can hamper the extraction. Hence, the fermentation and the must filtration should be properly done prior to the citric acid removal by solvent extraction.
The main advantage of the solvent extraction process is to eliminate the use of calcium hydroxide and sulfuric acid in the precipitation process. It also eliminates the generation of the byproduct calcium sulfate [6] . Although solvent extraction has been industrially applied to citric acid extraction, the access to actual process designs and operational parameters is quite restricted. According to Pazouki & Panda [7] , among several patents concerning this subject, only those in which tertiary amines are used as extractant and the stripping is made with hot water have feasible conditions to industrial application. The reason is that the citric acid extraction with tertiary amines is exothermic. Thus the extraction is favored at low temperatures [8] . Konzen [9] obtained good results for the citric acid extraction using a solvent composed by AlamineÒ 336, the poliamine Infineum 9268 (surfactant) and Exxsol™ D240/280, by liquid surfactant membranes technique, in a mechanically agitated column.
Processes that uses trioctylamine (TOA), a tertiary amine, as an extractant, require the use of a diluent with a high affinity with the amine-citric acid complex (generally polar organic solvents), or using a diluent with a modifier to avoid the formation of a third phase. Other authors have studied citric acid extraction with trioctylamine associated with chloroform [10] [11] [12] , MIBK (methyl isobutyl ketone) [10] [11] [13] and alcohols [14] [15] . Moreover, vegetable oils, such as rice, soy, sunflower, and sesame oils, have been tested as diluents [16] .
Few authors have discussed the citric acid extraction mechanism and there is no consensus among them. Malmary et al. [14] proposed that the formation of the complexes between the citric acid and the tertiary amine (triisooctylamine) occurs with the non-ionized acid form (amine acting as a solvation extractant). Bauer et al. [2] believe that the complexation reaction occurs with the citrate ions and trialkylamine in MIBK by an ionic association mechanism. Bízek et al. [17] , in their work with trialkylamine in MIBK, observed that both of the previously cited cases could occur simultaneously. Va?ura & Kuča [18] have found the presence of 2/1, 3/2, and 6/5 citric acid/amine complexes, in which the amine (trilaurylamine in toluene) acted as a solvation extractant. According to Bízek et al. [17] , the complexation of citric acid with trialkylamine can occur from both non-ionized and ionized citric acid forms.
In this context, the present work studied the solvent extraction of citric acid. The feed phase used was a synthetic solution of 100 g∙L−1 (10% w/v) of citric acid, in order to simulate a typical acid concentration found in industrial fermented musts. Concerning the past studies presented [8] [9] [11] [17] [19] and the reagents availability, it was studied the extraction with Alamine® 336, a trioctyl/decyl amine, mainly composed by the tertiary amine trioctylamine. The use of different diluents and modifiers was evaluated. EscaidTM 110, Exxsol™ D240/280, TBP (tributyl phosphate), chloroform, different alcohols (pentanol, decanol, dodecanol, tridecanol and mixtures of pentanol/dodecanol in several ratios) were investigated. TBP was tested, because it is already applied in the industrial purification of food grade phosphoric acid [20] [21] . TBP was also used for citric acid extraction by Thakre et al. [19] . The use of alcohols is common due to their amphiphilic characteristics: their polar part interacts with the polar portion of the complex and the non-polar part interacts with the diluent, favoring the solvation of the complex in the organic phase. Such reagents are effective to increase the solubility of amine complexes in aliphatic solvents [22] [23] .
Therefore, exploratory bench scale tests were made with Alamine® 336 with different diluents and modifiers. Then, after selecting the solvent components (AlamineÒ 336, Exxal™ 13 tridecyl alcohol, and EscaidTM 110), it was investigated the adequate concentrations of each component for further continuous extractions tests in a mechanically stirred column.
2. Materials and Methods
The reagents, used as supplied by the manufacturers, were: anhydrous citric acid (>99.5% purity―Vetec); Alamine® 336, extractant (>95% tertiary amine― BASF); EscaidTM 110, diluent (ExxonMobil), Exxsol™ D240/280 (ExxonMobil), TBP (tributilfosfato), chloroform, pentanol, decanol, dodecanol and tridecanol―Exxal™ 13 tridecyl alcohol (ExxonMobil).
For the organic phase preparation, Alamine® 336, modifier and diluent were weighted separately in order to obtain the desired concentration for each test and then mixed. The aqueous (feed) phase, prepared just before the beginning of each experiment, was composed by a citric acid solution 10% w/v (100 g∙L−1), whose pH value was around 1.5. This concentration was chosen, because the filtered fermented must has acid concentrations between 8 and 15% w/v, and pH values around 1.6 and 2.6 [24] [25] [26] . The mass of both phases were measured for the further mass balance calculations.
The batch solvent extraction experiments were performed in a single stage, using volumetric aqueous/organic phase ratio (A/O) of 1/1. Then, 40 mL of the aqueous phase was put in a beaker and the stirring system was turned on. The organic phase (40 mL) was slowly added during 10 seconds, when the contact time started to be measured. After a determined period of contact, stirring was turned off and the mixture was transferred to a separation funnel to allow aqueous phase decantation. Then, the phases were separated; each phase was weighted and stored for further determination of citric acid concentration.
The citric acid concentration was determined by complexometric titration with copper ions, using murexide as indicator [9] .
Initially, only the citric acid concentration of the aqueous phase was measured after the tests, since the analytical method is simple and the concentration of acid in the organic phase easily obtained, by a mass balance. However, in some experiments the concentration of citric acid was determined for both aqueous and organic phases by the same method. Then, the citric acid concentrations obtained for the organic phase were compared to the results obtained from the mass balance.
2.1. Definition of the Organic Phase Components
2.1.1. Experiments with Alamine® 336―Exxsol™ D240/280―TBP
Initially, exploratory experiments with the diluent Exxsol™ D240/280, without modifier, were done to evaluate the formation or not of a third phase, and, then, the need of adding a modifier to the solvent phase. The tests were carried out at 25˚C ± 2˚C, under a stirring speed of 500 rpm, for 15 min. The concentrations of the extractant, Alamine® 336, investigated were 10%, 20%, 30%, 40% and 50% w/v. Next, tests with Alamine® 336 (20% and 30% w/v) with TBP (10% and 20% w/v) in Exxsol™ D240/280 were done. Experiments with Alamine® 336 (10%, 20%, 30%, 40%, and 50% w/v) and TBP without Exxsol™ D240/280 were also carried out.
2.1.2. Experiments with Alamine® 336―Exxsol™ D240/280―Chloroform
Experiments with Alamine® 336 (20% and 30% w/v) with chloroform (10% and 20% w/v) in Exxsol™ D240/280 were done. For the chloroform, it was also studied the citric acid extraction without Exxsol™ D240/280, using extractant concentrations of 10%, 20%, 30%, 40% and 50% w/v. In addition, the extraction times of 2, 5, 7, 10, 15, and 20 min were studied for the Alamine® 336 concentration of 30% w/v.
2.1.3. Experiments with Alamine® 336―Escaid™ 110―Alcohols
Initially, tests with the diluent Escaid™ 110 without modifier were done for the extractant Alamine® 336 levels of 10%, 20%, 30%, 40% and 50% w/v. Then, for an Alamine® 336 concentration of 30% w/v, it was evaluated the addition of 10% w/v of mixtures of pentanol/dodecanol (molar ratios of 1/0, 5/1, 2/1, 1/1, 1/2, 1/4, and 0/1) at different temperatures (23˚C, 40˚C and 60˚C ± 2˚C).
Considering the obtained results, two other modifiers where studied for comparison purposes. Decanol, with a chain length between pentanol and dodecanol, was tested. Exxal™ 13 tridecyl alcohol, with a chain slightly longer than that of dodecanol, was also tested. In these experiments, the alcohol concentration was 10% w/v and the temperature was 30˚C.
2.2. Definition of the Organic Phase Components Proportion
Experiments with Alamine® 336―Escaid™ 110―Exxal™ 13 Tridecyl Alcohol
In the next part of the work, the components of the solvent phase were chosen, considering the obtained results and the feasibility of using this solvent phase in continuous test on a mechanically agitated column. Thus, experiments were performed to determine the best composition for the solvent phase composed of Alamine® 336 and Exxal™ 13 tridecyl alcohol in Escaid™ 110. The investigated parameters in these extraction experiments and their respective levels are presented in Table 1.
After establishing the best operational conditions among the investigated ones, the equilibrium isotherm was determined. Therefore, a series of experiments were done, by using the following volumetric phase ratios between aqueous and organic phases (A/O): 10/1, 5/1, 2/1, 1/1, 1/2 and 1/5.
2.3. Response Variables
The citric acid extraction percentage, used as response variable in the present work, refers to the amount of citric acid extracted from the aqueous phase (feed), as shown in Equation (1).
Table 1. Investigated and fixed parameters and their respective levels.
 (1)
(1)
In this equation, wA is the total aqueous phase mass; CA is the concentration of citric acid in % w/w; and the superscripts 0 and t refer to the initial condition and to the condition after the test, respectively.
3. Results and Discussion
3.1. Exploratory Experiments
3.1.1. Extraction Using Alamine® 336 and Exxsol™ D240/280
When amines are used as extractant, the complexes formed between citric acid and amines tend to form third phase. These complexes have a high polarity compared to diluents predominantly aliphatic, as commonly used in the organic phase (Exxsol™ D240/280, Escaid™ 110, and others). This fact makes the solubility of these complexes in the solvent more difficult [22] . On the other hand, the complex formed, due to its hydrocarbon chains, has a large non-polar portion, which means that it is also not soluble in the aqueous phase. Thus, in order to avoid the formation of a third phase in the experiment, it is necessary to use a modifier. A better solvation of the complex in the organic phase favors the extraction of the solute.
As in all tests there was the formation of a third phase, the extraction percentages of citric acid were not measured.
3.1.2. Extraction Using Alamine® 336 and TBP in Exxsol™ D240/280
In all experiments performed with TBP (10 or 20% mv) and Alamine® 336 (20% or 30% m/v), it was observed the third phase formation. Thus, it was decided to evaluate the action of TBP in the absence of ExxsolTM D240/280.
3.1.3. Extraction Using Alamine® 336 in TBP
The results for the extraction tests with Alamine® 336 in TBP are shown in Figure 1. From this figure, it can be noticed that the citric acid extraction increased
Figure 1. Citric acid extraction for different concentrations of Alamine® 336 in TBP. (Room temperature = 25˚C ± 2˚C, stirring speed = 500 rpm, contact time = 15 min, A/O = 1/1).
up to 98% by increasing the extractant concentration until 30% w/v. For higher concentrations, the extraction remained practically constant. However, in all tested conditions, after phase separation, the aqueous and organic phases presented a turbid aspect, even after the centrifugation of the phases.
In the test without Alamine® 336, i.e. only TBP, a citric acid extraction of 47% was obtained but, again, a stable turbidity in the organic phase was observed, which implies in a very difficult phase separation. In view of the foregoing, the use of TBP was considered unsuitable for the present work.
Thakre et al. [19] carried out experiments using the same concentration of citric acid (0.5 mol∙kg−1, that is equivalent to10% w/v), but using 30% TBP in different diluents. For each of the diluents used, different extraction percentages were obtained: 5%, 10%, and 14% for benzene, decanol, and n-butyl acetate, respectively.
3.1.4. Extraction Using Alamine® 336 and Chloroform in Exxsol™ D240/280
In the tests with Alamine® 336 and chloroform in Exxsol™ D240/280, again, a stable turbidity in the organic phase was observed. Therefore, the use of this organic phase composition was also discarded.
3.1.5. Extraction Using Alamine® 336 and Chloroform
The citric acid extraction results obtained only with Alamine® 336 and chloroform are shown in Figure 2. It can be seen that the extraction increases by increasing the extractant concentration. The highest extractions (99%) were obtained for extractant concentrations of 40% and 50% w/v, but the phase separation was easier and faster for concentrations of Alamine® 336 between 0% and 30% w/v. For these lower concentrations, the organic phases did not present turbidity and no centrifugation of the phases was required. The same was not observed at concentrations of 40% and 50% w/v, for which the organic phases
Figure 2. Citric acid extraction for different concentrations of Alamine® 336 in chloroform. (Room temperature = 25˚C ± 2˚C, stirring speed = 500 rpm, contact time = 15 min, A/O = 1/1).
viscosity and turbidity were higher and the phases had to be centrifuged. It should be noted that, since chloroform has a higher density than water (1.49 g∙cm−3), the organic phase, after decantation, is the lower phase, unlike that observed for TBP.
In the test performed in the absence of Alamine 336 (0% extractant), the extraction of citric acid with chloroform was 4.7%, and neither third phase formation nor a turbid organic phase was verified.
The extractant concentration of 30% w/v was considered the best among the studied levels, considering the extraction obtained (87%), the ease of phase separation and the absence of turbidity in the organic phase. With this Alamine® 336 concentration, experiments with different contact time were carried out. From the results (Figure 3), it can be noticed that an extraction of 89% was obtained after 2 minutes; after 5 minutes, the extraction reached 95%. Despite the good results obtained with chloroform, other organic phase compositions were investigated due to the toxicity of this reagent.
Procházka et al. [10] obtained a citric acid extraction of 95% for a solvent composed by 36.5% w/v of a trialkylamine (a Russian commercial product) in chloroform. In the present work, for such condition, the extraction would be approximately 95% (Figure 2).
3.1.6. Extraction Using Alamine® 336 in Escaid™ 110
In all the extraction experiments with this system (Alamine® 336 in Escaid™ 110), it was observed the formation of a third phase, which did not allow the evaluation of citric acid extraction.
3.1.7. Extraction Using Alamine® 336 with Pentanol, Dodecanol, and Mixture of Them in Escaid™ 110
The results of the tests with these modifiers, at several temperatures, are shown
Figure 3. Citric acid extraction with Alamine® 336 (30% w/v) in chloroform for different contact times. (Room temperature = 25˚C ± 2˚C, stirring speed = 500 rpm, contact time = 15 min, A/O = 1/1).
Figure 4. Evaluation of adding of modifier(s) (10% w/v) to an organic phase composed of 30% w/v of Alamine® 336 in EscaidTM110 (Contact time = 10 min, stirring speed = 500 rpm, A/O = 1/1).
in Figure 4. From this figure, it can be seen that, for a same temperature, no significant effect on citric acid extraction due to the variation of pentanol/dodecanol molar ratio. It can, also, be observed that, for each specific temperature, slightly higher extractions were obtained when using pure pentanol as a modifier, compared to pure dodecanol.
Concerning the effect of temperature, extraction percentages between 85% and 88%, at 23˚C ± 2˚C, 78% and 82%, at 40˚C ± 2˚C, 71% and 74%, at 60˚C ± 2˚C, were obtained. Therefore, higher temperatures lead to lower citric acid extractions. Bízek et al. [8] verified that the complexation reaction between citric acid with trialkylamine, in n-heptane, using 1-octanol as modifier, is exothermic. In view of the foregoing, the subsequent experiments were performed at room temperature.
It is important to notice that, in all tests, the loaded organic phase was initially turbid, due to the presence of aqueous phase droplets, but this turbidity disappeared with time. The higher the temperature, the faster the turbidity of the organic phase disappeared. But, at 60˚C, the organic phase became yellowish. Additionally, the organic phases obtained when using pure pentanol or pure dodecanol were the most turbid, while, when using pentanol/dodecanol ratios closer to equimolarity, the organic phases were clearer. In addition, organic phases with more dodecanol were less turbid than those phases with more pentanol.
The Winsor Solvation theory [22] provides a good explanation for these findings. According to this theory, the solubilization efficiency of an specific component added to a system, in the present case, the alcohol as a modifier, is a function of a parameter known as affinity ratio (R), defined by Equation (2), where Aco is the affinity of this additive to the non-polar phase and, Acw its affinity to the polar phase.
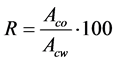 (2)
(2)
According to Shimidt [22] , the maximum increase in the solubilization promoted by each mol of the added component is obtained when R is equal to one, i.e., the additive has the same affinity for both polar and non-polar phases. Then, if the two liquids, the polar and the nonpolar, are immiscible and a third component, with a value of R greater than one, is added, this component will mainly pass into the non-polar phase, and the main effect will be the solubilization of the polar substance in the non-polar phase.
Appling this theory to the studied system, reported in this paper, the polar phase would be the complex between Alamine® 336 and citric acid; the non-polar phase would be Escaid™ 110, an aliphatic diluent; and the third component would be a long chain alcohol acting as a modifier. If the R value of this alcohol were greater than one, adding this alcohol would promote the solubilization of the complex in the diluent. On the contrary, if R were lower than one, the addition would result on the solubilization of the diluent in the polar phase. When R < 1 or R > 1, the amount of alcohol required for the solubilization is higher than the amount necessary when R = 1.
The effect of solubilization promoted by alcohols can be explained in terms of the interactions alcohol-complex and alcohol-diluent. The interaction between an alcohol and a low polar solvent, such as saturated hydrocarbons, involving only van der Waals forces, is much weaker than the interaction of the alcohol with the complex formed in the system, studied in the present work. Thus, the R values for the system in question are probably lower than one. This means that, in such cases, it is better to use alcohols with higher values of R in order to increase the solubilizing effect, i.e., to use alcohols with a longer aliphatic chain. Another important factor that affects the value of R is the steric hindrance of the groups that constitute the complex formed, which would increase the value of R (lower Acw).
In addition, as reported in the literature [22] , on a study of a system constituted by water and a non-polar solvent, it was observed that, using a mixture of two additives, one with R < 1 and other with R > 1, the resulting solubilization was much more effective than that using each additive individually, at the same concentration. A significant increase in solubilization is achieved when these additives are added in a proportion such that R is equal to one. This could explain the lower turbidity for the equimolar mixture pentanol/dodecanol.
3.1.8. Extraction using Alamine® 336 and an Alcohol (Pentanol, Decanol, Dodecanol, Tridecanol) in Escaid™ 110
In order to make a comparison with the previous results, experiments were performed using decanol, an alcohol with an intermediate chain between pentanol and dodecanol, and using tridecanol, added as the commercial reactant Exxal™ 13 tridecyl alcohol (ExxonMobil). The effect in citric acid extraction, by using different alcohols (10% w/v) with 30% w/v (37.5% w/w) of Alamine® 336 in Escaid™ 110, is shown in Figure 5. The citric acid concentration was measured in both extract (loaded organic phase) and raffinate (depleted aqueous phase) in order to verify the efficacy of the analytical method for the organic phase.
From this Figure, it can be seen that the applied analytical method was adequate to determine citric acid concentration also in the organic phase, since the extraction percentages calculated with the extract concentrations were practically the same of those obtained using only the raffinate concentrations and the mass balance.
Concerning the alcohols, the extraction percentages are practically the same
Figure 5. Citric acid extraction using 10% w/v of different alcohols as modifiers, with 30% w/v of Alamine® 336 in Escaid™ 110. (Room temperature = 30˚C ± 2 ˚C, stirring speed = 400 rpm, contact time = 10 min, A/O = 1/1).
for tridecanol, dodecanol and decanol (81%, 82%, and 83%, respectively), being slightly higher for pentanol (86%). The alcohols concentration of 10% m/v are equivalent to 1.14, 0.64, 0.54 and 0.51 mol∙L−1 for pentanol, decanol, dodecanol and tridecanol, respectively. As the number of moles of pentanol is much higher than the others, since it has the lower molar mass, it is difficult to compare these results.
With respect to the turbidity of the organic phases, as it was expected, considering the Winsor theory, decanol resulted in the less turbid one, probably because the R value was closer to one. The most turbid organic phase was the one obtained when using pentanol. Moreover, as expected, tridecanol resulted in an organic phase slightly more turbid than that obtained when dodecanol was used.
However, in all tests the turbidity dissipated with time, indicating that a longer decantation time was needed. In none of the experiments, a third phase formation was observed. It is worth to notice that the high stirring speed used (400 rpm) may also have been responsible for the turbidity of the organic phase and for the higher difficulty in phase separating.
Poposka et al. [27] studied the citric acid extraction from a solution containing 10% w/v of this acid. These authors used the extractant TOA (~43% w/w) in a mixture of isodecanol (~26% w/w) and a paraffinic diluent (~31% w/w). At such conditions, the obtained raffinate presented an acid concentration of 2.3% w/v, which corresponds to an extraction of, approximately, 77%, considering the phases’ volumes constant.
3.2. Studies with the Organic Phase Composed by Alamine® 336 and Exxal™ 13 Tridecyl Alcohol in Escaid™ 110
Considering the preliminary results, as reported in section 3.1, the organic phase components were defined and it turned out to be Alamine® 336 as the extractant, Exxal™ 13 tridecyl alcohol as the modifier and Escaid™ 110 as the diluent.
3.2.1. Definition of the Modifier Concentration
Figure 6 shows the results of the extraction experiments, for different tridecanol (Exxal™ 13 tridecyl alcohol) concentrations, using Alamine® 336 (30% w/v). In this Figure, it is observed a small increase in citric acid extraction with the increase of tridecanol concentration. Increasing this modifier concentration from 2% to 20% w/v has increased the extraction from 79% to 87%, respectively. The concentration of 2% w/v led to the formation of a third phase in the system, and the concentration of 8% w/v, considering its visual aspect, seemed to be the limiting minimum concentration, below which a third phase formation occurs. By varying the tridecanol concentration from 10% w/v to 20% w/v, the extraction increased from 82% to 87%, an increase that, in our understanding, is too small considering the cost of this reagent. Therefore, the concentration of 10% w/v was the one chosen to be used in further experiments.
3.2.2. Definition of the Extractant Concentration
Once defined the modifier concentration the next step was to investigate the in-
Figure 6. Citric acid extraction for different tridecanol concentrations. (Alamine® 336 concentration = 30 % w/v, A/O ratio = 1/1, room temperature = 28˚C ± 2˚C, stirring velocity = 400 rpm, and contact time = 10 min).
Figure 7. Citric acid extraction for different extractant concentrations. (Tridecanol concentration = 10% w/v, A/O ratio = 1/1, temperature = 28˚C ± 2˚C, stirring velocity = 400 rpm, and contact time = 10 min).
fluence of the extractant Alamine® 336 in the citric acid extraction process. The results obtained for the different extractant concentrations tested (Table 1) are presented in Figure 7. It can be noticed that the extraction percentage was extensively affected by the concentration of Alamine® 336. Without this extractant in the organic phase only 0.9% of citric acid was extracted, while in the highest concentration studied (50% w/v) the acid extraction was up to 95%. However, the organic phase viscosities for the two highest extractant concentrations tested were quite high. This fact would hinder the organic phase pumping in an industrial process. Thus, the Alamine® 336 concentration of 30% w/v was chosen for the forthcoming experiments. Using this concentration level, in a single stage, an extraction of 82% was obtained.
Experiments with different contact times were done using the organic phase composition defined in the previous tests (modifier concentration of 10% w/v and extractant concentration of 30% w/v). The results are shown in Figure 8. From this figure, it can be seen, that the extraction is quite fast. The equilibrium was reached after 5 minutes. Therefore, 10 minutes was used as the contact time of the phases in the experiments for the determination of the equilibrium isotherm.
3.2.3. Equilibrium Isotherm
The equilibrium isotherm for citric acid (Figure 9) was determined by varying the volumetric ratio between aqueous and organic phase (A/O). The following operations conditions were used: tridecanol concentration of 10% w/v; Alamine® 336 concentration of 30% w/v; room temperature (29˚C ± 2˚C); stirring speed of 400 rpm; contact time of 10 min; and A/O ratios of 10/1, 5/1, 2/1, 1/1, 1/2 and 1/5.
As previously mentioned, the reaction between a tertiary amine and the citric acid can occur with both non-dissociated (Equation (3)) and non dissociated (Equation (4)) forms of citric acid [17] .
 (3)
(3)
 (4)
(4)
In these equations, the subscripts aq and org refer to the aqueous and to the organic phases, respectively; R3N is a tertiary amine; n is the number of amine
Figure 8. Citric acid extraction for different contact times. (Tridecanol concentration = 10% w/v, Alamine® 336 concentration = 30% w/v. A/O ratio = 1/1, room temperature = 28˚C ± 2˚C, stirring velocity = 400 rpm, contact time = 10 min).
Figure 9. Equilibrium isotherm obtained by varying the volumetric ratio between phases (A/O). (Tridecanol concentration = 10% w/v, Alamine® 336 concentration = 30% w/v, room temperature = 29˚C ± 2˚C, stirring velocity = 400 rpm, contact time = 10 min).
molecules that reacts with one citric acid molecule and, also, the number of hydrogen ions lost by the citric acid.
However, once the aqueous phase (feed) pH value was 1.5, below citric acid pKa1 of 3.13, practically all the acid should be in its non-dissociated form. Thus, the complexation reaction is taken as occurring mainly with the non-dissociated form, as represented in Equation (5), where trialkylamine (R3N) of Equation (3) is replaced by TOA (trioctylamine), the main component of Alamine® 336.
 (5)
(5)
The equilibrium constant for this extraction reaction is given by Equation (6), where the concentrations are in moles per liter. It was considered that the activities of the species in equilibrium are equal to their concentrations. In this equation, the ratio between the equilibrium concentrations of citric acid in the organic and in the aqueous phase ([(TOAH)n∙H3−nCit]org/[H3Cit]aq) can be substituted by the distribution coefficient (m), as shown in Equation (7). Then, after mathematical treatment, the logarithm of the distribution coefficient (log m) can be expressed as a function of the logarithm of the free extractant concentration (log[TOA]org), as represented in Equation (8).
 (6)
(6)
 (7)
(7)
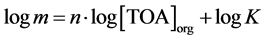 (8)
(8)
The number of amine extractant molecules that complexes with each citric
Figure 10. Logarithm of the distribution coefficient m as a function of the logarithm of the free extractant concentration (Room temperature = 29˚C ± 2˚C).
acid molecule, n, is unknown. However, it can be obtained by making a linear regression to a plot of Equation (8), the slope of the adjusted line being equal to n and the intercept being equal to log K. This plot is shown in Figure 10. The concentrations are in mol∙L−1 and it was considered that the only active component of Alamine® 336 is the trioctylamine (TOA).
From Figure 10, n is equal to 1.5 and K is equal to 36.8 (mol∙L−1)−1.5, at 29˚C ± 2˚C. This value of n implies that it is necessary, in average, 1.5 molecules of TOA to complex with each molecule of citric acid. According to Equation (5), the complexes formation occurs with an integer number (n = 1, 2, …) of extractant molecules. Thus, it can be said that reactions with different n vales are occurring simultaneously.
Using the obtained values for K and n, the equilibrium curve for the system was calculated (Figure 11). It was also calculated, according to Equation (9), the coefficient of determination (R2), which is an indication of the adequacy of the model [28] .

In Equation (9), SQE and SQT are the error sum of squares and the total sum of squares, respectively; n is the number of experimental points; 

From Figure 11, it can be seen that the calculated and the experimental curves are very close. A R2 value of 0.93 was obtained, which indicates that the model for the chosen extraction reaction (Equation (5)), with the obtained values for n and K is able to explain 93% of the results. For the isotherm curve ends, the
Figure 11. Experimental and calculated equilibrium isotherm.
higher deviations observed were probably due to experimental errors. Particularly, in regions of low concentrations, the curve presents a higher slope, and small variations on the acid concentration determination in the raffinate can cause large displacements in the equilibrium point. In the highly concentrated region, there is a greater loading of the organic phase, which probably could be better described by other model (other n and K values).
3.2.4. Kinetic Parameters Estimation
Considering the direct and inverse reactions, described by Equation (5), as elementary, the reaction rate can be written as:

In Equation (10), the index i refers to the aqueous or to the organic phase, Vi is the volume of the phase i, and 
tric acid moles with time in phase i, k1 and k−1 are the rate constants of the direct and of the inverse reactions, respectively, the equilibrium constant being K = k1/k−1. Equation (11) is obtained considering that the phase volumes are constant.

From the mass balance, it can be shown that the number of moles of citric acid that leaves the aqueous phase is equal to the number of moles of this acid that goes to the organic phase:

The integration of Equation (10), knowing k1 and k−1 values, results in citric acid concentration profiles with time.

Equation (13) can be solved numerically by finite difference method. Although the values of the rate constants (k1 and k−1) are initially unknown, citric acid concentrations at different times are available from experimental data. Therefore, an initial value for k1 was defined, k−1 = k1/K and the concentration profiles were calculated using the initial conditions (t = 0). The quadratic errors between these calculated profiles and the experimental ones were calculated before the equilibrium (t = 1, 3, and 5 min). In an iterative procedure, new values of k1 were calculated in order to minimize the sum of the quadratic errors. The values of k1 and k−1 obtained were 2.10 (mol∙L−1)−1.5∙s−1 and 5.69 × 10−2 s−1, respectively. In Figure 12, the calculated concentrations profiles (dashed line) and the experimental data (points) are represented.
Using Equation (9), in which the values for 

It was obtained a value of k1 much higher than k−1, as expected considering the equilibrium constant value found, K = 36.8 (mol∙L−1)−1.5. This indicates that a high extraction is achieved, i.e., the concentration of citric acid is higher in the extract than in the raffinate. In addition, with a value of k1 ? k−1, the reaction can be considered irreversible, at the beginning, when the concentration profile is practically linear.
Figure 12. Calculated (dashed lines) and experimental (points) concentration profiles, and concentration of free extractant (TOA) along time.
Bízek et al. [8] stated that citric acid extraction is exothermic, and it is possible to strip the citric acid from the loaded organic phase (extract) by simply raising the temperature. Therefore, the speed of the inverse reaction (stripping) is much more favored, with temperature increase, than the direct reaction (extraction). This indicates that the activation energy of the inverse reaction is higher, and it is more sensible to a temperature rise.
In the calculation of the equilibrium constant (K), of the extractant stoichiometric coefficient (n), of the citric concentrations in the raffinate and in the extract and of the free extractant concentration, values of the determination coefficients (R2) equal or superior than 0.93 were found. This can be taken as an evidence that the results obtained through computer modeling and the experimental ones would be very close.
4. Conclusions
Citric acid solvent extraction using commercial extractant AlamineÒ 336 was investigated. Tests with this extractant diluted in TBP led to organic phases with high turbidity, which is not reduced by phase centrifugation. The use of chloroform as diluent promotes a high extraction, but its use is not recommended because of its toxicity. In the experiments with aliphatic diluents, Exxsol™ D240/280 and Escaid™ 110, it was required to add a modifier. No significant citric acid variation was observed among the tested alcohol modifiers, pentanol, decanol, dodecanol, and tridecanol in Escaid™ 110.
After selecting the organic phase components (Alamine® 336, Exxal™ 13 tridecyl alcohol and Escaid™ 110), the effects of varying the contact time, and the modifier and extractant concentrations were evaluated. Using the selected conditions (10 minutes, 10% w/v of modifier, and 30% w/v of extractant, room temperature (29˚C ± 2˚C), the equilibrium isotherm was determined. It was considered that TOA and citric acid complexation reaction occurs mainly with the non-dissociated citric acid form, because of the initial pH of citric acid solution (pH < pKa1). It was found that, on average, 1.5 molecules of TOA were required to react with each acid molecule. This indicates that reactions with different extractant/citric acid ratios occur simultaneously. The equilibrium constant obtained was K = 36.8 (mol∙L−1)−1.5. The rate constant for the direct reaction, k1 = 2.10 (mol∙L−1)−1.5∙s−1 was much higher than that for the inverse reaction, k−1 = 5.69 × 10−2 s−1.
In the calculation of the equilibrium constant (K), of the extractant stoichiometric coefficient (n), of the citric acid concentrations in the raffinate and in the extract and of the free extractant concentration, values of the determination coefficients (R2) equal or superior than 0.93 were found, representing an evidence that the results obtained through computer modeling would be very close to those results obtained experimentally. Therefore, the present work provides data required for modelling, design, and simulation of citric acid extraction processes.
Acknowledgements
The authors would like to acknowledge CAPES, CNPq, FAPEMIG and PRPq for the financial support.
Cite this paper
Araújo, E.M.R., Coelho, F.E.B., Balarini, J.C., Miranda, T.L.S. and Salum, A. (2017) Solvent Extraction of Citric Acid with Different Organic Phases. Advances in Chemical Engineering and Science, 7, 304-324. https://doi.org/10.4236/aces.2017.73023
References
- 1. Fani, M. (2011) ácido Cítrico ou Citrato de Hidrogênio. In: Fani, M., Ed., Aditivos e Ingredientes, Editora Insumos, São Paulo, 30-35.
http://aditivosingredientes.com.br/upload_arquivos/201604/2016040746833001460591974.pdf - 2. Bauer, U., Marr, R., Rückl, W. and Siebenhofer, M. (1989) Reactive Extraction of Citric Acid from an Aqueous Fermentation Broth. Berichte der Bunsengesellschaft für Physikalische Chemie, 93, 980-984.
https://doi.org/10.1002/bbpc.19890930911 - 3. Sun, X., Lu, H. and Wang, J. (2017) Recovery of Citric Acid from Fermented Liquid by Bipolar Membrane Electrodialysis. Journal of Cleaner Production, 143, 250-256.
https://doi.org/10.1016/j.jclepro.2016.12.118 - 4. Luo, H., Cheng, X., Liu, G., Zhou, Y., Lu, Y., Zhang, R., Li, X. and Teng, W. (2017) Citric Acid Production Using a Biological Electrodialysis with Bipolar Membrane. Journal of Membrane Science, 523, 122-128.
https://doi.org/10.1016/j.memsci.2016.09.063 - 5. Djas, M. and Henczka, M. (2016) Reactive Extraction of Citric Acid Using Supercritical Carbon Dioxide. The Journal of Supercritical Fluids, 117, 59-63.
https://doi.org/10.1016/j.supflu.2016.05.005 - 6. Yokoya, F. (1992) Fermentaçoes Industriais 1. Fundação Tropical de Pesquisas e Tecnologia André Tosello Press, Campinas.
- 7. Pazouki, M. and Panda, T. (1998) Recovery of Citric Acid—A Review. Bioprocess Engineering, 19, 435-439.
https://doi.org/10.1007/PL00009029 - 8. Bizek, V., Horácek, J., Rericha, R. and Kousova, M. (1992) Amine Extraction of Hydroxycarboxylic Acids. 1. Extraction of Citric Acid with 1-Octanol/n-Heptane Solutions of Trialkylamine. Industrial & Engineering Chemistry Research, 31, 1554-1562.
https://doi.org/10.1021/ie00006a019 - 9. Konzen, C. (2013) Projeto e Montagem de uma Unidade Piloto para Operação de um Sistema de Membranas Líquidas Surfatantes Utilizando-Se uma Coluna Mecanicamente Agitada. Ph.D. Thesis, Federal University of Minas Gerais, Belo Horizonte.
- 10. Procházka, J., Heyberger, A. and Volaufová, E. (1997) Amine Extraction of Hydroxycarboxylic Acids. 3. Effect of Modifiers on Citric Acid Extraction. Industrial & Engineering Chemistry Research, 36, 2799-2807.
https://doi.org/10.1021/ie9607107 - 11. Maurer, G. (2006) Modeling the Liquid-Liquid Equilibrium for the Recovery of Carboxylic Acids from Aqueous Solutions. Fluid Phase Equilibria, 241, 86-95.
https://doi.org/10.1016/j.fluid.2005.11.005 - 12. Kirsch, T. and Maurer, G. (1998) Distribution of Binary Mixtures of Citric, Acetic and Oxalic Acid between Water and Organic Solutions of Tri-N-Octylamine. Part III. Organic Solvent Chloroform. Fluid Phase Equilibria, 146, 297-313.
https://doi.org/10.1016/S0378-3812(98)00209-X - 13. Nikhade, B.P., Moulijn, J.A. and Pangarkar, V.G. (2004) Extraction of Citric Acid from Aqueous Solutions with Alamine 336: Equilibrium and Kinetics. Journal of Chemical Technology & Biotechnology, 79, 1155-1161.
https://doi.org/10.1002/jctb.1109 - 14. Malmary, G., Albet, J., Putranto, A.M.H. and Molinier, J. (2001) Recovery of Carboxylic Acids from Aqueous Solutions by Liquid-Liquid Extraction with a Triisooctylamine Diluent System. Brazilian Journal of Chemical Engineering, 18, 441-447.
https://doi.org/10.1590/S0104-66322001000400008 - 15. Bressler, E. and Braun, S. (1999) Separation Mechanisms of Citric and Itaconic Acids by Water-Immiscible Amines. Journal of Chemical Technology and Biotechnology, 74, 891-896.
https://doi.org/10.1002/(SICI)1097-4660(199909)74:9<891::AID-JCTB113>3.0.CO;2-E - 16. Keshav, A., Norge, P. and Wasewar, K.L. (2012) Reactive Extraction of Citric Acid Using Tri-N-Octylamine in Nontoxic Natural Diluents: Part 1—Equilibrium Studies from Aqueous Solutions. Applied Biochemistry and Biotechnology, 167, 197-213.
https://doi.org/10.1007/s12010-012-9682-z - 17. Bízek, V., Horácek, J., Kousová, M., Heyberger, A. and Procházka, J. (1992) Mathematical Model of Extraction of Citric Acid with Amine. Chemical Engineering Science, 47, 1433-1440.
https://doi.org/10.1016/0009-2509(92)80288-N - 18. Vaňura, P. and Kuca, L. (1976) Extraction of Citric Acid by the Toluene Solutions of Trilaurylamine. Collection of Czechoslovak Chemical Communications, 41, 2857-2877.
https://doi.org/10.1135/cccc19762857 - 19. Thakre, N., Prajapati, A.K., Mahapatra, S.P., Kumar, A., Khapre, A. and Pal, D. (2016) Modeling and Optimization of Reactive Extraction of Citric Acid. Journal of Chemical Engineering, 61, 2614-2623.
https://doi.org/10.1021/acs.jced.6b00274 - 20. Jin, Y., Zou, D., Wu, S., Cao, Y. and Li, J. (2015) Extraction Kinetics of Phosphoric Acid from the Phosphoric Acid-Calcium Chloride Solution by Tri-N-Butyl Phosphate. Industrial & Engineering Chemistry Research, 54, 108-116.
https://doi.org/10.1021/ie503273j - 21. Shlewit, H. and Alibrahim, M. (2008) Counter Current Extraction of Phosphoric Acid: Food Grade Acid Production. Periodica Polytechnica Chemical Engineering, 52, 7-9.
https://doi.org/10.3311/pp.ch.2008-1.02 - 22. Schimidt, V.S. (1971) Amine Extraction. John Wiley & Sons Incorporated, New York.
- 23. Canari, R. and Eyal, A. (2004) Temperature Effect on the Extraction of Carboxylic Acids by Amine-Based Extractants. Industrial & Engineering Chemistry Research, 43, 7608-7617.
https://doi.org/10.1021/ie034127j - 24. Lima, U.A., Aquarone, E. and Borzani, W. (1975) Biotecnologia Tecnologia das Fermentaçoes. Edgard Blücher, São Paulo.
- 25. Rohr, M., Kubicek, C.P. and Kominek, J. (1983) Citric Acid. In: Reed, G., Ed., Biotecnology, Wenheim, New York, 440-442.
- 26. Garibay, M.G., Ramirez, R.Q. and Canales, A.L.M. (1993) Biotecnología Alimentaria. Editorial Limusa, Mexico, 562-564.
- 27. Poposka, F.A., Nikolovski, K. and Tomovska, R. (1998) Kinetics, Mechanism and Mathematical Modelling of Extraction of Citric Acid with Isodecanol/N-Paraffins Solutions of Trioctylamin. Chemical Engineering Science, 53, 3227-3237.
https://doi.org/10.1016/S0009-2509(98)00125-0 - 28. Montgomery, D.C. and Runger, G.C. (2010) Applied Statistics and Probability for Engineers. John Wiley & Sons, New York.














