Advances in Chemical Engineering and Science
Vol.4 No.2(2014), Article ID:44758,6 pages DOI:10.4236/aces.2014.42017
Calculating Efficiency of Separation of Aerosol Particles from Gases in Packed Apparatuses
Anatoly G. Laptev1,2, Marat M. Basharov1, Timur M. Farakhov1,2, Albert R. Iskhakov1
1Department of Technology of Water and Fuel, Kazan State Power Engineering University, Kazan, Russia
2Engineering-Promotional Center “Inzhekhim”, Kazan, Russia
Email: info@ingehim.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 23 January 2014; revised 23 February 2014; accepted 1 March 2014
ABSTRACT
A mathematical model for the process of removal of aerosols from gases in channels filled with packing is considered. Equations for transport of aerosol particles and results of their numerical solution are given. Influence of operating conditions and of design characteristics of the packed apparatus on gas purification efficiency is analyzed.
Keywords:Gas Purification, Aerosols, Packing, Mathematical Model, Numerical Solution, Turbulent Migration

1. Introduction
Gaseous environments are often used in chemical and petrochemical industries and power engineering. As a rule, the gaseous environments are of a non-uniform composition and are contaminated by disperse phase admixtures causing problems through exerting negative influence on efficiency of technological processes and the process equipment operation; therefore, they must be removed from gases.
Disperse phase separation efficiency can be determined through using the value of disperse phase content in the gas before the point of entrance into the gas purification apparatus and the value after the point of exit from the apparatus via the following expression:
 , (1)
, (1)
where C is the particle concentration (kg/m3); Q is the gas flow rate (m3/s); subscripts i and f refer to the initial and final values, respectively.
One usually adopts for apparatuses the equality Qi = Qf.
As is known, particle deposition in apparatuses can be due to several mechanisms such as gravitational, inertial, turbulent, centrifugal and other mechanisms. Most industrial apparatuses operate through utilizing several of these mechanisms by combining them together. Hence, disperse phase separation efficiency is dependent of many different parameters.
In case of several mechanisms acting simultaneously or in case of purification of gases being carried out in series in back-to-back apparatuses (zones), the overall efficiency is calculated through using the additivity rule in the following manner:
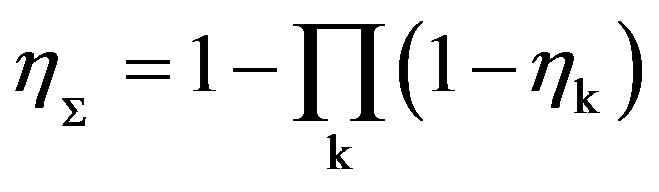 , (2)
, (2)
where ηk is the separation mechanism due to the kth mechanism in the kth apparatus (zone).
In the present, work we use the approach of F. P. Zaostrovsky and K. N. Shabalin developed within the years 1951-1953 and improved further by E. P. Mednikov and other authors [1] -[3] for the case when aerosol deposition was considered as a sub-set of the diffusion process and the equations from the mass transfer theory and the turbulent migration theory were used for determining the aerosol deposition.
2. Equations Governing Aerosol Transport
Packed gas separators are used for removal of liquid aerosols from gases in cases when there is no solid phase present in the gas. Below is given a mathematical model for the process of removal of liquid aerosol particles from the gas in the apparatus (channel) free from packing and in the apparatus filled with fine random packing.
For evaluating separation efficiency of the packed layer, we will use the equation for convective mass transfer of particles.
Assume that a gas under turbulent conditions containing a finely dispersed phase of concentration Ci is fed to the inlet of the packed layer. As the gas flows, the dispersed phase migrates toward the walls of the packing elements by means of various mechanisms.
The following assumptions are adopted for the mathematical model [1] :
· The wall material of the packing elements is well wetted by the deposited liquid phase.
· The particle diameter dp is small compared to the scale L of pulsation vortices carrying the particles: dp = L.
· The particle polydispersity is accounted for by considering particles by fractions.
· At C < 0.2 kg/m3, the particles do not collide and do not coalesce with each other.
Then, a three-dimensional equation governing steady-state transport of aerosol particles in the gas takes the form
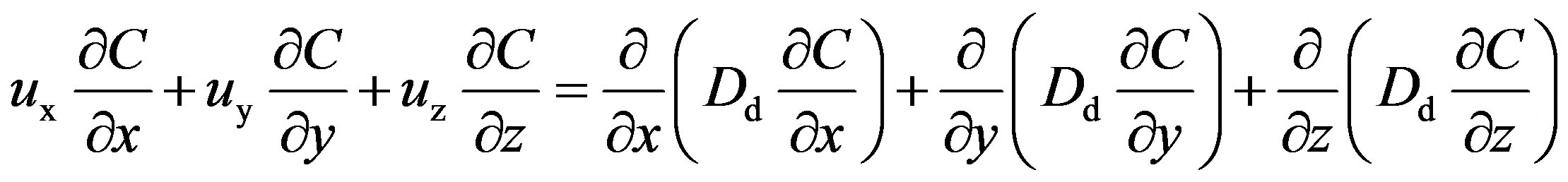 , (3)
, (3)
where x, y, z are spatial coordinates (m); Dd is the turbulent diffusion coefficient for particles (m2/s).
The Brownian diffusion is neglected here, since it plays only a very small role in turbulent flows.
For solving Equation (3), a 3-D velocity field (ux, uy, uz) and a spatial distribution of the coefficient of turbulent transfer of particles Dd(x, y, z) are required. Then, Equation (1) can be solved using the preset concentrations at the boundaries to obtain a spatial distribution of particles along the coordinate axes 0x, 0y, and 0z. As it was noted in [1] , it is not easy to set values of aerosol concentrations at the walls of packing elements due to some uncertainties. Besides, it must be kept in mind that packing elements are distributed randomly within the gas separator volume. Therefore, below we will use an approach to the simulation that considers transfer of the dispersed phase mass toward the wall (or toward the phase interface) as a volumetric source of mass in the particle transport equation.
The source of mass is presented in the general form as follows
 , (4)
, (4)
where M is particle flux (kg/s); F is area of contact of gas with the walls of the channel filled with packing (m2); V is working volume of the contact unit (m3); j is the average value of specific particle flux toward the wall at the wall surface (kg/(m2s)).
In the theory of gas treatment, the specific flux of the dispersed phase mass can be written in the form of an analog of the mass transfer equation as follows: j = utC∞, where C∞ is the particle concentration in the flow core taken as cross sectional area-average particle concentration (kg/m3); ut is the turbulent migration velocity (m/s).
The so-called turbulent particle deposition velocity, ut, characterizes the intensity of particle deposition from the turbulent flow onto the walls, i.e. it represents the quantity of particles (weight or number) being deposited from the stream containing aerosols onto the walls of area 1 m2 per 1 s divided by a unit particle concentration [1] .
With the assumptions made, Equation (3) for a cylindrical channel filled with packing takes the form:
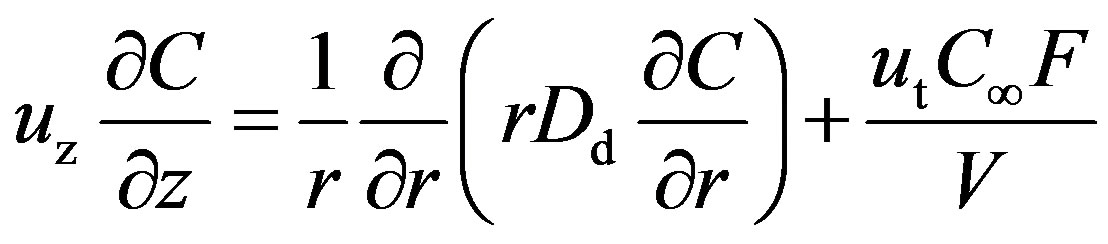 , (5)
, (5)
where r is radial distance from the channel’s axis (m); z is vertical coordinate (in the direction of the gas flow) (m).
3. Turbulent Particle Deposition Velocity
A number of empirical and semi-empirical dependencies can be used for calculation of reduced rate of particle deposition ut+=ut/u* which is related to particle relaxation time
 , (6)
, (6)
where dp is particle diameter (m); ρp is density of particle material (kg/m3); νg is kinematic viscosity of the gas (m2/s); μg is dynamic viscosity of the gas (Pa·s); ρg is density of the gas (kg/m3).
Dimensionless relaxation time is defined as:
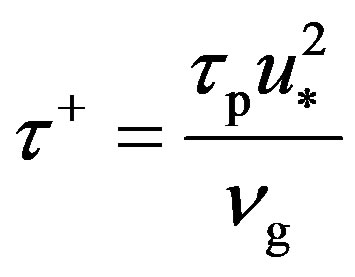 , (7)
, (7)
where 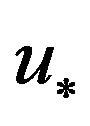 is friction velocity on the wall (m/s).
is friction velocity on the wall (m/s).
Generalized expression for ut takes the form [1] :
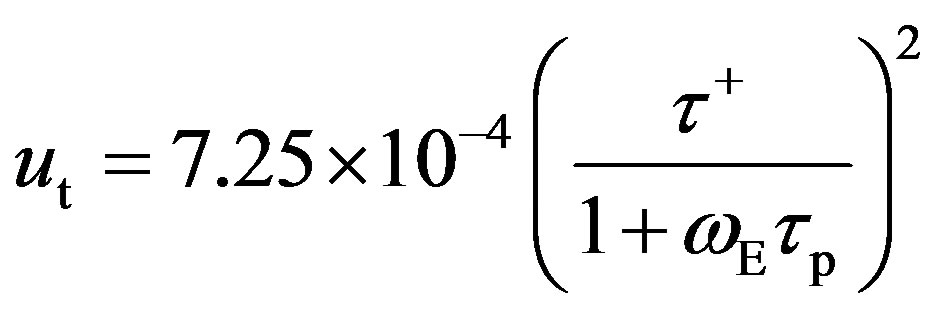 , (8)
, (8)
where ωE = u*/(0.1R) is angular velocity of energy-intensive pulsations (1/s); R is the channel radius (m).
From Equations (7) and (8) it follows that separation rate ut depends to a large extent on friction velocity u* or wall shear stress τw (u* = (τw/ρg)0.5).
The average value of friction velocity on the surfaces of random packing elements can be determined through using the average energy dissipation rate expressed through pressure drop.
Numerous calculations of u* carried out for packed separators agree with accuracy ±18% with the expression [3] :
 , (9)
, (9)
where the average energy dissipation rate is determined through the pressure drop as follows:
 , (10)
, (10)
where Vfree is free volume of the packed layer (m3); S is cross-sectional area of the packed layer (apparatus) (m2); l is length (height) of the packed layer (m); εfree is specific free volume of the packing, where uave is average velocity of gas flow in the packing (m/s); uave = wg/εfree; wg is gas flow velocity in the channel free from packing (m/s).
4. Turbulent Diffusion Coefficient for Particles
Turbulent diffusion coefficient for particles can be determined using the following expression [1] :
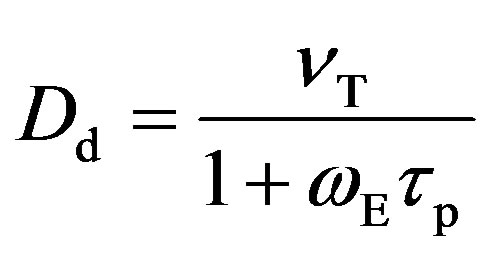 , (11)
, (11)
where νT is the turbulent viscosity coefficient in a single-phase flow (m2/s);
For a channel free from packing, the average value of νT at y > δ can be calculated using the Karman–Prandtl model:
 , (12)
, (12)
where χ = 0.4 is a turbulence constant; δ is the average thickness of the near-wall layer (m).
Turbulent viscosity coefficient in the packed layer is determined using the following semi-empirical expression [4] :
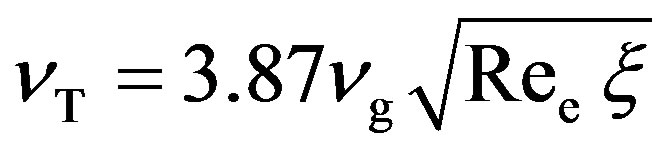 , (13)
, (13)
where Ree is the Reynolds number defined as Ree = uavede/νg; is the hydraulic resistance coefficient for the packing [3] .
5. Numerical Results
Results of the numerical solution of Equation (5) by the finite-difference method are shown below.
Figure 1 presents concentration profiles along the channel length l for a hollow tube and for a tube filled with steel Raschig rings. The gas-liquid mixture is air containing water droplets. Initial data are following: d = 0.017 m; Ci = 5 wt%; uave = 30 m/s; dp = 9 μm. Apparently, a tube filed with packing ensures better purification efficiency compared to a hollow tube.
Figure 2 shows change in separation efficiency η with the channel length l for different Reynolds numbers. In the calculations, a tube filled with random packing was assumed. The contact devices are the Raschig rings. The gas-liquid mixture is air containing water droplets. Initial data are following: d = 0.017 m; Ci = 5 wt%; dp = 9 μm. It can be seen that the smaller the channel length is, the greater the Reynolds number must be for high purification efficiency. Conversely, as the channel length increases, the Reynolds number can be reduced without loss in separation efficiency.
Figure 3 shows change in separation efficiency η with the Reynolds number for different channel lengths l. The tubes are assumed to be filled with steel Raschig rings. The gas-liquid mixture is air containing water droplets. Initial data are following: d = 0.017 m; Ci = 5 wt%; dp = 9 μm.
It can be seen from the figure that the increase in the channel length and the Reynolds number leads to an increase in separation efficiency.
Figure 4 shows change in separation efficiency η with the Reynolds number for particles of different sizes.

Figure 1. Concentration profiles for a tube filled with Raschig rings and a hollow tube: 1—Tube filled with packing; 2—Hollow tube.

Figure 2. Change in separation efficiency with the channel length for different Reynolds numbers.
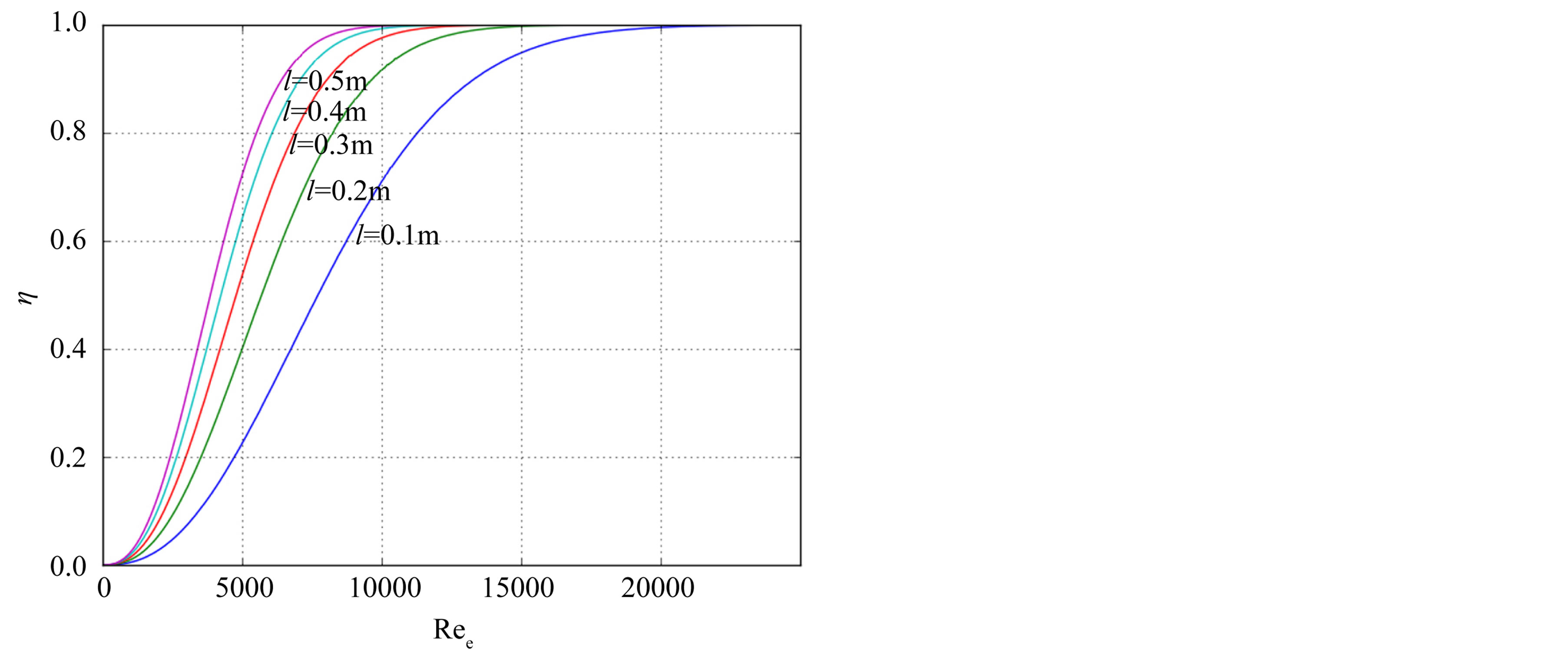
Figure 3. Change in separation efficiency with the Reynolds number for different channel lengths.

Figure 4. Change in separation efficiency with the Reynolds number for particles of different sizes.
The tubes are assumed to be filled with steel Raschig rings. The gas-liquid mixture is air containing water droplets. Initial data are following: d = 0.017 m; Ci = 5 wt%; l = 0.2 m.
Apparently, the increase in the particle size and the Reynolds number leads to an increase in separation efficiency.
If the Peclet number Pee = uavel/Dmix > 10, the model of ideal displacement in the channel can be used, where Dmix is mixing coefficient (m2/s).
The mixing coefficient can be calculated using the following empirical expression [4] .
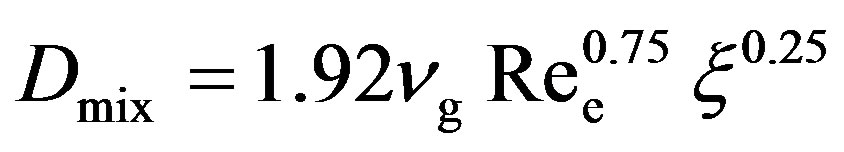 . (14)
. (14)
As is known, for Pee > 10, solution to Equation (5) takes the form
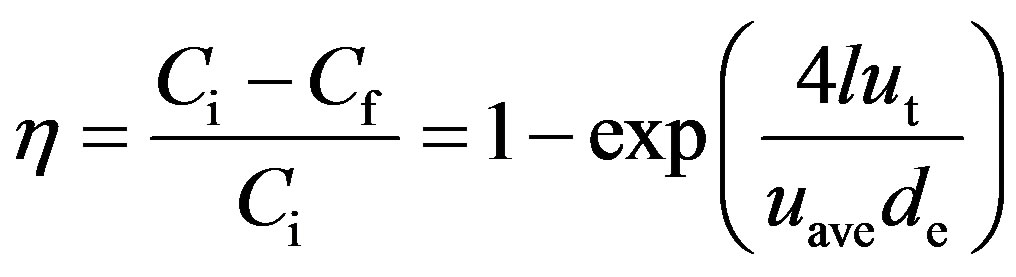 . (15)
. (15)
Calculations carried out with the use of the above expression agree satisfactorily with experimental data [1] -[6] .
6. Conclusion
The considered approach to determination of particle concentration profiles in contact devices and to calculation of separation efficiency which is based on the turbulent migration theory allows carrying out calculations with the use of hydraulic resistance of the apparatus. The obtained equations can be used for calculating industrial gas separators present at petrochemical and gas producing enterprises.
References
- Mednikov, E.P. (1980) Turbulent Transport and Deposition of Aerosols. Nauka, Moscow.
- Sugak, E.V., Voinov, N.A. and Nikolaev, N.A. (2010) Cleaning of Off-Gases in Apparatuses with Intense Hydrodynamic Regimes. ZAO Novoe Znanie Press, Kazan.
- Laptev, A.G. and Farakhov, M.I. (2006) Separation of Heterogeneous Mixtures in Packed Apparatuses. Kazan State Power Engineering University Press, Kazan.
- Laptev, A.G., Farakhov, T.M. and Dudarovskaya, O.G. (2013) Models of Turbulent Viscosity and Mixing in Channels and Packed Flow-Through Mixers. Russian Journal of Applied Chemistry, 86, 1046-1055. http://dx.doi.org/10.1134/S1070427213070173
- Laptev, A.G. and Basharov, M.M. (2013) Efficiency of Aerosol Deposition in Gas Separators of Various Designs. Russian Journal of Applied Chemistry, 86, 1190-1196. http://dx.doi.org/10.1134/S1070427213080077
- Laptev, A.G. and Basharov, M.M. (2013) Determination of Efficiency of Removal of Disperse Phase from Gases by Vortical Elements. Izvestiya VUZov Khimiya i Khimicheskaya Tekhnologiya, 56, 101-104.

