Journal of Signal and Information Processing
Vol.07 No.01(2016), Article ID:63872,5 pages
10.4236/jsip.2016.71005
A New Scheme to Construct Orthogonal Channel Matrix for MIMO STBC by Givens Rotation
Huanming Zhang, Kaiyi Xian, Lijun Feng, Chaokang Hu
Electronics and Information Engineering Institute, Foshan University, Foshan, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 July 2015; accepted 23 February 2016; published 26 February 2016
ABSTRACT
This paper proposes a scheme to construct orthogonal channel matrix for full rate quasi-ortho- gonal STBC based on givens rotation with lower bit error rate. The transmission diversity method rotates every single information symbol. The scheme can suppress channel noise and eliminate the interference term well. Simulation results show that the method can improve performance better than conventional algorithm without increasing decoding complexity.
Keywords:
QO-STBC, MIMO, Givens Rotation

1. Introduction
Because of its efficient maximum likelihood decoding, MIMO (Multiple-Input Multiple-Output) system has been received the significant amount of attention. In 1998, Alamouti proposed orthogonal STBC applied on two transmitting antennae firstly which is usually regarded as the OSTBC with full diversity and full transmission rate and has been used in mobile communication system [1] . More antennas can get more diversity gain. But it has been proved that full diversity and full rate complex design exists only for two transmit antennas. Due to this drawback, various linear quasi-orthogonal STBCs have been proposed to achieve a full rate (R = 1) for more than 2 transmit antennas at the expense of loosing the diversity gain and increasing the decoding complexity.
2. Background
For O-STBC with N transmitting antennas, coding matrix S has following equation:
 (1)
(1)
where SH is conjugate transpose of S, 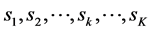 are transmitting symbols,
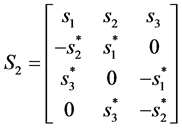
are transmitting symbols,  is identity matrix with order N. And up to now, (2), (3) and (4) are orthogonal STBC be found with rate 1, 3/4, 3/4 respectively, as following Equations (2)-(4) [2] :
is identity matrix with order N. And up to now, (2), (3) and (4) are orthogonal STBC be found with rate 1, 3/4, 3/4 respectively, as following Equations (2)-(4) [2] :
 (2)
(2)
 (3)
(3)
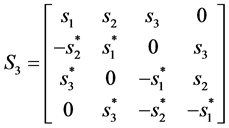 (4)
(4)
And for QO-STBC, proposed by Jafarkhani [3] , has following signal matrix:
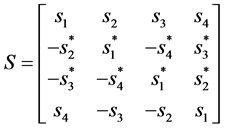 (5)
(5)
S is an orthogonal matrix, it has the following feature:
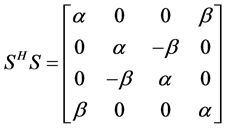 (6)
(6)
where,  represents channel gain for the four transmit antennas, and
represents channel gain for the four transmit antennas, and  represents interference terms from neighboring signals.
represents interference terms from neighboring signals.
 (7)
(7)
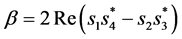 (8)
(8)
So S is a quasi-orthogonal matrix. And it is well known that the presence of the channel dependent interference can cause the performance degradation in contrast to the optimal orthogonal design.
3. Constructing Orthogonal Channel Matrix by Givens Rotation
For a MIMO system, the received signal r is expressed as:
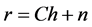 (9)
(9)
where C represents signal matrix and n is noise, the equivalent equation 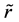 of r is given by
of r is given by
 (10)
(10)
When C is chose suitably [4] , H can satisfy the following format:



Considering a flat fading channel over four time slots with 4 transmit antennas and 1 receive antenna, the channel gain is denoted by

The symbol matrix 


So, although the new coding matrix 




The encoding matrix after rotation is described as:

Especially, when 

If we define D as the estimating error, 

Here, 


rank matrix. So S gets coding gain.
4. Simulation Results and Performance Analysis
In this section, we make simulation for ABBA scheme, Jafarkhani scheme [8] and the new code by Figure 1 as following.
Figure 2 shows the BER performance of the three schemes. It can be seen that the new scheme has better performance.
5. Conclusion
Maximum transmit rate and diversity gain can be improved by givens rotation to non-orthogonal channel correlation of STBC. And also linear decoding complexity can be decreased at receive terminal. Transposition of
Figure 1. Simulation block diagram of QO-STBC.
Figure 2. BER versus SNR of three QO-STBC schemes.
channel matrix and Givens rotation are applied to eliminate part of interference terms and achieve a triangular matrix.
Cite this paper
HuanmingZhang,KaiyiXian,LijunFeng,ChaokangHu, (2016) A New Scheme to Construct Orthogonal Channel Matrix for MIMO STBC by Givens Rotation. Journal of Signal and Information Processing,07,34-38. doi: 10.4236/jsip.2016.71005
References
- 1. Alamouti, S.M. (1998) A Simple Transmitter Diversity Scheme for Wireless Communications. IEEE Journal on Selected Areas in Communications, 16, 1451-1458.
http://dx.doi.org/10.1109/49.730453 - 2. Xu, C.L., Gong, Y. and Letaief, K.B. (2004) High-Rate Complex Orthogonal Space-Time Block Codes for High Number of Transmit Antennas. 2004 IEEE International Conference on Communications, 2, 823-826.
- 3. Jafarkhani, H. (2001) A Quasi-Orthogonal Space-Time Block Code. IEEE Transactions on Communications, 49, 1-4.
http://dx.doi.org/10.1109/26.898239 - 4. Park, U., Lim, K. and Li, J. (2008) A Novel QO-STBC Scheme with Linear Decoding for Three and Four Transmit Antennas. IEEE Communications Letters, 12, 868-870.
http://dx.doi.org/10.1109/LCOMM.2008.081323 - 5. Jia, M.-R. and Xiao, L.-P. (2010) Improved QO-STBC for Three and Four Transmit Antennas. The Journal of China Universities of Posts and Telecommunications, 17, 42-46.
- 6. Wang, L., Zhu, S.-H. and Wang, J. (2005) An Orthogonal Space-Time Block Coded on Matrix Rotation. Journal of Electronics & Information Technology, 27, 397-401.
- 7. Teng, Z.-J., Zhang, W. and Wang, N. (2012) An Improved Space-Time Block Coded Based on Matrix Rotation. Journal of Northeast Dianli University, 32, 8-13.
- 8. Tarokh, V., Jafarkhani, H. and Calderbank, A.R. (1999) Space Time Block Coding for Wireless Communications: Perfromance Results. IEEE Transactions on Information Theory, 45, 1456-1467.
http://dx.doi.org/10.1109/18.771146



