Journal of Signal and Information Processing
Vol. 4 No. 1 (2013) , Article ID: 28284 , 9 pages DOI:10.4236/jsip.2013.41005
Accurate Tools for Analyzing the Behavior of Impulse Noise Reduction Filters in Color Images
![]()

Dipartimento di Ingegneria e Architettura, University of Trieste, Trieste, Italy.
Email: rusfab@univ.trieste.it
Received October 1st, 2012; revised November 1st, 2012; accepted November 23rd, 2012
Keywords: Color Image Denoising; Image Analysis; Vector Filters; Impulse Noise
ABSTRACT
Effective cancellation of noise and preservation of color/structural information are features of paramount importance for any filter devoted to impulse noise removal in color images. In this paper novel full-reference tools for analyzing the behavior of this family of filters are presented. The proposed approach is based on the classification of color errors into two main classes that separately take into account the inaccuracy in removing noise pulses and the filtering distortion. The distortion errors are then classified into two subclasses for a deeper analysis of the filtering behavior. Computer simulations show that the proposed method gives more accurate results than using other measures of filtering performance in the literature. Furthermore, the method can easily yield the spatial location of the different filtering features in the image.
1. Introduction
Impulse noise filtering in color images is a very dynamic branch of digital image processing [1-3]. Indeed, many different approaches have been proposed in the literature in order to reach better and better results in terms of cancellation of noise and preservation of edge and color information. The accurate measurement of these key features is thus of paramount importance to analyze the behavior of any new filter and to assess its performance with respect to the available ones. The commonly used approach to performance analysis of color filters resorts to visual inspection and objective measurements based on the computation of pixelwise differences between the original and the processed image. In this respect, the ability to cancel noise pulses is very often estimated by evaluating the mean squared error (MSE) or the peak signal-to-noise ratio (PSNR), whereas the ability to preserve edges is taken into account by computing the mean absolute error (MAE). All the aforementioned measures are typically evaluated in the RGB color space, that is the most popular color coordinate system for image storing, display and processing [1]. Since the RGB space is not adequate for describing the human perception of colors, the perceptual closeness of the filtered picture to the uncorrupted original image is generally considered by computing the normalized color difference (NCD) in the perceptually uniform CIE Luv (or CIE Lab) color spaces [1-3]. As an example, the family of weighted vector directional filters was studied and optimized by minimizing MAE, MSE and NCD to achieve the best balance between noise attenuation and preservation of the color/ structural information [4]. The same set of objective measures was adopted to numerically evaluate the performance of the sigma vector median filter [5]. A collection of four criteria including the MSE, the normalized mean square error (NMSE), the PSNR and the NCD was considered to validate weighted median filters for multichannel signals [6]. The results of many computer simulations were presented to assess the performance of the fuzzy two-step filter in [7]. Here, the PSNR was adopted as a measure of objective dissimilarity between a filtered image and the original one. The performance of the fuzzy filtering method [8] was deeply investigated in terms of PSNR and NCD for different parameter settings and different densities of impulse noise. An effective switching median filtering scheme was developed for grayscale pictures and extended to color images [9]. The performance of the method was quantified by the PSNR (for monochrome images) and by color difference measurements in the CIE Lab color space. The accuracy of the noise detection algorithm was also investigated by computing the number of false positives and false negatives. Similar approaches were adopted to validate the directional weighted median filter [10] and the robust neurofuzzy network [11]. MAE, PSNR, and NCD evaluations were provided to measure the performance of the denoising filters presented in [12,13]. Even most recent filters in the literature have been evaluated by resorting to the aforementioned measures (or combinations of them) [14-16]. The major drawback of such evaluation methods, however, is the fact that they have limited accuracy in estimating the different filtering features. As already observed for grayscale images [17,18], MSE and MAE cannot yield accurate measures of noise cancellation and detail preservation, because they cannot totally separate these effects. Although the MSE is more sensitive to residual noise than the MAE, it takes into account the amount of distortion produced by a filter too. The MAE is more sensitive to distortion than the MSE, however it depends upon the remaining noise too. The NCD focuses on the human perception of colors, so it computes all the filtering errors in perceptually uniform color spaces without distinguishing error components due to structural distortion and those that are caused by insufficient (or excessive) removal of noise. Other metrics that aim at mimicking the human perception yield a subjecttive evaluation of image quality in the form of a single score, so, again, they cannot distinguish between detail preservation and noise cancellation given by a filter. Furthermore, most of them deal with grayscale images only [19]. Measures such as the vector root mean squared error (VRMSE) have been just developed to yield a separate evaluation of the aforementioned error components. However, they operate in the RGB [20] and YUV [21] non-uniform color spaces and compute the noise cancellation and the detail preservation in the luminance component of the image only.
In this paper new tools for performance evaluation of impulse noise removal filters for color images are presented. The approach is based on the classification of color errors into different components that separately consider the inaccuracy in cancelling noise pulses and the distortion affecting originally noise-free pixels. Unlike our previous techniques, the proposed method operates in the CIE Luv color space. Furthermore, it performs a novel classification of filtered pixels for a deeper analysis of the filtering distortion. The rest of this paper is organized as follows. Section 2 focuses on the limitations of current approaches, Section 3 describes the proposed method, Section 4 discusses the results of many computer simulations and, finally, Section 5 reports the conclusions.
2. Limitations of Current Approaches
As mentioned above, MSE and MAE cannot yield very accurate measurements of the noise cancellation and detail preservation given by a filter. As an example, Figure 1 shows portions of two processed images with different properties in terms of noise cancellation and detail preservation but having the same MSE and the same MAE with respect to the original picture. To obtain this result, we considered a 512 × 512 version of the 24-bit color image “Parrots” and two filters with different window sizes, such as the 5-point and the 5 × 5 vector median filters [1]. We generated the noisy input picture as follows. We considered versions of the “Parrots” image corrupted by different densities of noisy pixels, i.e. pixels where each channel component is incremented (or decremented) by a fixed value. We searched for the noise density p and the noise amplitude d such that these medians yield filtered images with the same RMSE and the same MAE. A satisfactory result was obtained by choosing p = 39% and d = 37. Clearly, the 5 × 5 operator (Figure 1(b)) is more effective than the 5-point filter (Figure 1(a)) in removing noise at the price of a worse detail blur, but these very different features are not apparent from RMSE and MAE measurements that yield RMSE = 8.8 and MAE = 3.6 for both filtered images.
A similar situation occurs when scalar indexes that follow human perception are adopted for this specific purpose. As aforementioned, few metrics of this kind have been developed to address color images. Just as an example, let us briefly consider the application of the color quality index CQI [22]. Portions of filtered images having the same score (CQI = 0.7661) are depicted in Figures 2(a) (5-point vector median) and (b) (5 × 5 vector median). It is apparent that different mixtures of residual noise and detail blur can produce the same loss of perceived image quality and thus lead to the same score.
3. The Proposed Tools
Formally, let 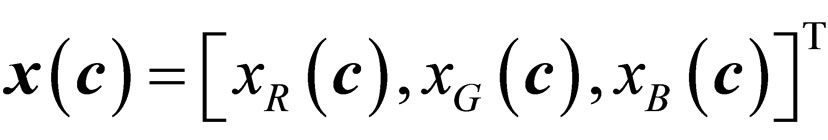 be the vector (in the RGB color space) representing the pixel at spatial position
be the vector (in the RGB color space) representing the pixel at spatial position  in the noisy image. Let
in the noisy image. Let  be the corresponding pixel in the filtered picture and
be the corresponding pixel in the filtered picture and 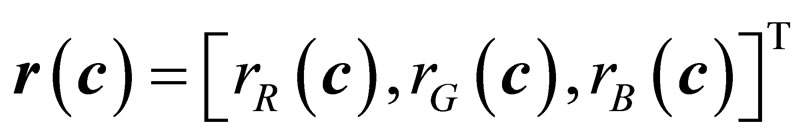 be the RGB pixel at spa-
be the RGB pixel at spa-
 (a) (b)
(a) (b)
Figure 1. Portions of filtered images showing very different combinations of noise cancellation and detail-preservation but having the same MSE and the same MAE with respect to the original picture.
 (a) (b)
(a) (b)
Figure 2. Portions of filtered images showing different combinations of noise cancellation and detail-preservation but having the same value of CQI with respect to the original picture.
tial position c in the original noise-free image. Thus, let us define two subsets of pixel coordinates A and B, as follows:
 (1)
(1)
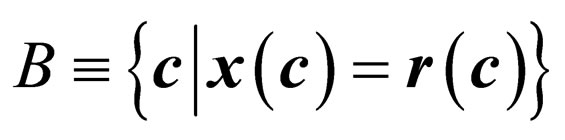 (2)
(2)
It can be easily seen that the subset A includes the spatial positions of noise pulses (i.e. the locations of pixels that changed values for effect of the noise), whereas B yields the set of coordinates of uncorrupted pixels possibly affected by distortion caused by the filtering. Now, let  and
and 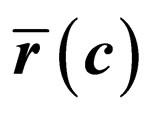 respectively represent the filtered and the original noise-free pixel in the Luv color space [1]:
respectively represent the filtered and the original noise-free pixel in the Luv color space [1]:
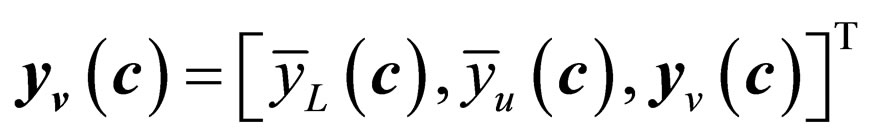 (3)
(3)
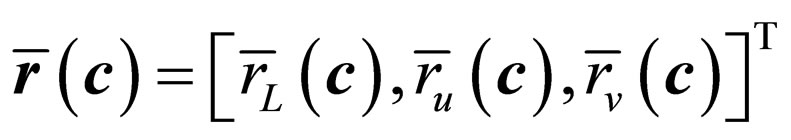 (4)
(4)
Thus, we shall define two new full-reference metrics, called unfiltered color noise (UCN) and total color distortion (TCD), as follows:
 (5)
(5)
 (6)
(6)
where 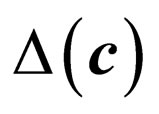 is the color difference (or error) evaluated in the Luv perceptually uniform color space:
is the color difference (or error) evaluated in the Luv perceptually uniform color space:
 (7)
(7)
Since the UCN evaluates the errors in restoring pixels corrupted by noise pulses, it measures the noise cancellation ability of the filter. On the contrary, the TCD computes the errors that affect the originally uncorrupted pixels, so it measures the data preservation capability of the filter.
A deeper analysis can be performed if more data are available, such as the picture that is produced when the original noise-free image is filtered adopting the same parameter settings. Let  briefly denote the pixel at spatial position
briefly denote the pixel at spatial position 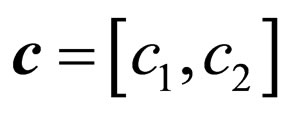 in this filtered picture. Now, let us consider the pixel subset B1 where the distortion does not depend upon the noise (basic distortion):
in this filtered picture. Now, let us consider the pixel subset B1 where the distortion does not depend upon the noise (basic distortion):
 (8)
(8)
Conversely, let B2 denote the pixel subset where the distortion is influenced by the presence of noise pulses (additional distortion).
 (9)
(9)
As shown in the next section, a useful index for further characterizing the filtering behavior is the additional to total distortion ratio (ATDR), that is defined as follows:
 (10)
(10)
4. Results and Discussion
In order to assess the performance of the proposed tools, we performed many computer simulations based on pictures of the well-known Kodak test set [23]. Four images from this set are considered in the following experiments. They are shown in Figure 3. All of these pictures are 24-bit color images whose size is 512-by-512 pixels.
4.1. Color Preservation Tests
In this first experiment (color preservation test) we focused on the sensitivity of TCD and MAE to this kind of filtering distortion. We considered the images corrupted by different amounts of impulse noise and we exploited the different behavior of the 5 × 5 scalar (SMF) and vector (VMF) median filters. It is known that the application of scalar filters on each channel separately can destroy the correlation between the color components of natural images thus producing color artifacts in the filtered data. For this reason, a more appropriate approach is vector filtering that treats color pictures as vector fields [1,2]. The corresponding TCD and MAE values are listed in Tables 1-4. The color artifacts given by the SMF are typically large, those yielded by the VMF are signifi-
 (a) (b)
(a) (b) (c) (d)
(c) (d)
Figure 3. Test images used in the experiments: (a) Parrots; (b) Girl; (c) Houses; (d) Lighthouse.
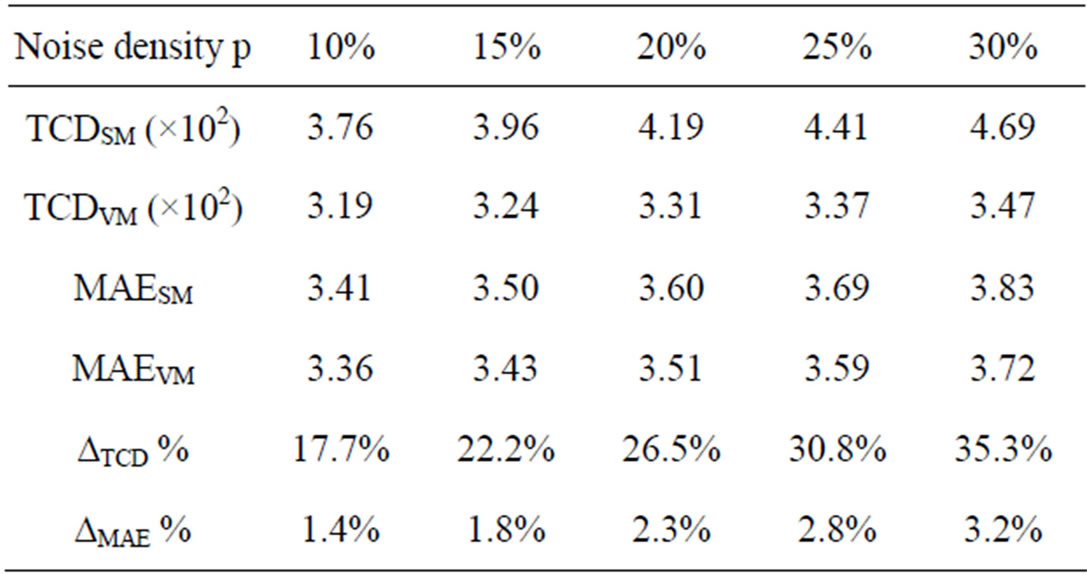
Table 1. TCD and MAE sensitivities to color artifacts given by 5 × 5 SMF and VMF filters (“Parrots” corrupted by impulse noise with d = 100 and noise density p ranging from 10% to 30%).

Table 2. TCD and MAE sensitivities to color artifacts given by 5 × 5 SMF and VMF filters (“Girl” corrupted by impulse noise with d = 100 and noise density p ranging from 10% to 30%).

Table 3. TCD and MAE sensitivities to color artifacts given by 5 × 5 SMF and VMF filters (“Houses” corrupted by impulse noise with d = 100 and noise density p ranging from 10% to 30%).
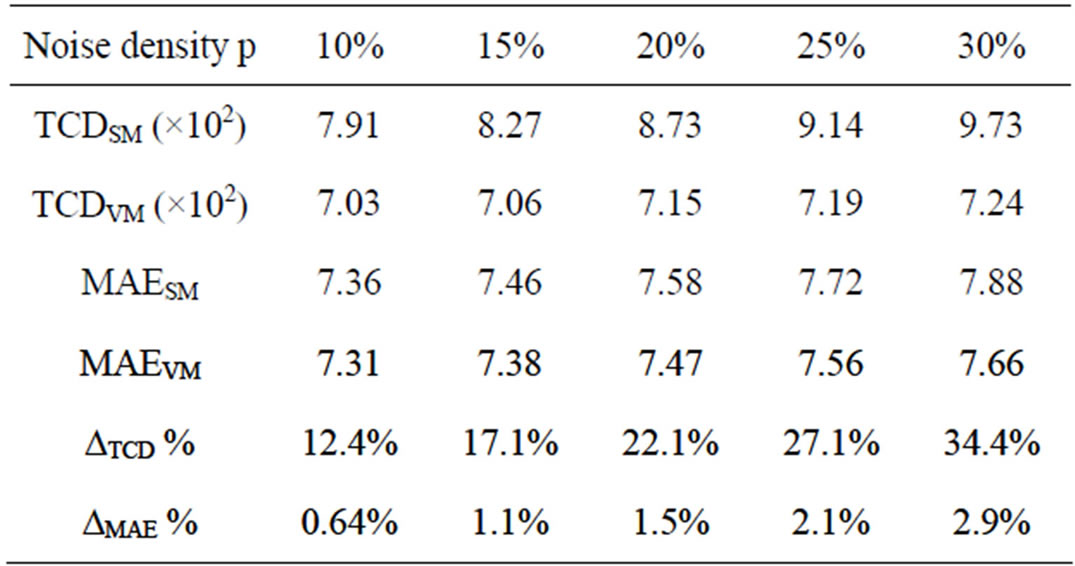
Table 4. TCD and MAE sensitivities to color artifacts given by 5 × 5 SMF and VMF filters (“Lighthouse” corrupted by impulse noise with d = 100 and noise density p ranging from 10% to 30%).
cantly smaller (almost negligible), whereas both filters produce similar distortion in terms of detail blur. Thus, a simple way to estimate the sensitivity of a given measure G to this kind of distortion is to evaluate the (relative) difference , where GSM and GVM address scalar and vector median filtering, respectively.
, where GSM and GVM address scalar and vector median filtering, respectively.
It can be seen that, in all the tests, the proposed TCD largely outperforms the MAE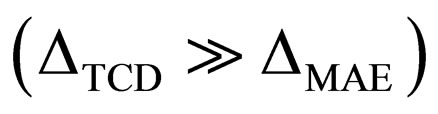 . A sample of the processed data is reported in Figure 4 for visual inspection. These data include a portion of the original noise-free image “Girl”, (Figure 4(a)), the corresponding data corrupted by impulse noise with density 30% (Figure 4(b)), the result given by SMF filter (Figure 4(c)) and the result yielded by the VMF operator (Figure 4(d)). Many color artifacts are apparent in Figure 4(c), whereas they are negligible in Figure 4(d). The same amount of detail blur is perceivable in both images.
. A sample of the processed data is reported in Figure 4 for visual inspection. These data include a portion of the original noise-free image “Girl”, (Figure 4(a)), the corresponding data corrupted by impulse noise with density 30% (Figure 4(b)), the result given by SMF filter (Figure 4(c)) and the result yielded by the VMF operator (Figure 4(d)). Many color artifacts are apparent in Figure 4(c), whereas they are negligible in Figure 4(d). The same amount of detail blur is perceivable in both images.
4.2. Detail Preservation Tests
In the second group of experiments (detail preservation tests) we compared the abilities of TCD and MAE to measure the detail preservation. We considered vector filtering in order not to be deceived by color artifacts. We chose the sigma vector median filter (SVMF) [5] because
 (a) (b)
(a) (b)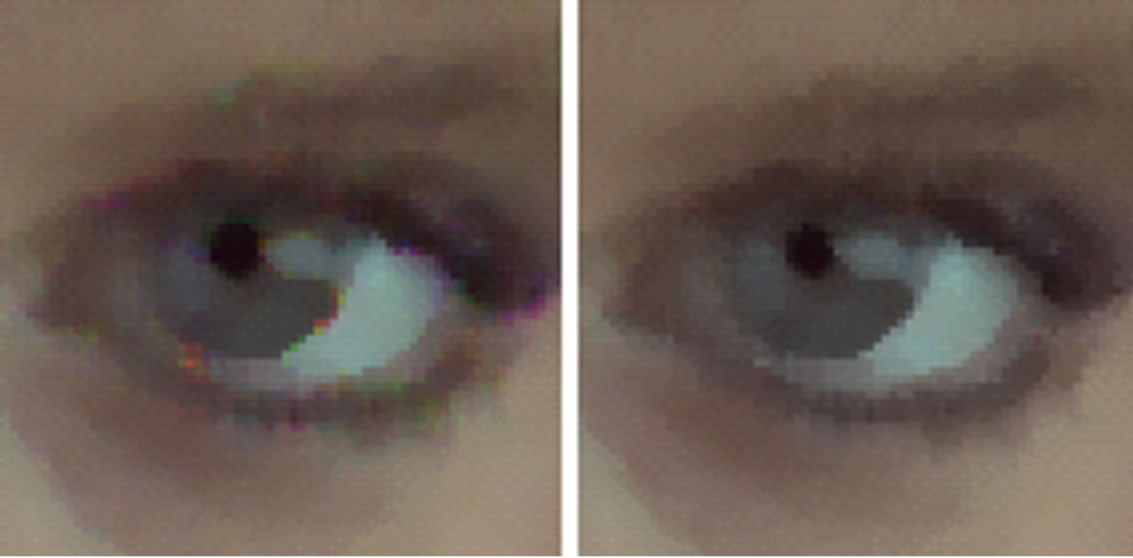 (c) (d)
(c) (d)
Figure 4. (a) Detail from the Girl image; (b) Noisy data; (c) Result of scalar filtering; (d) Result of vector filtering.
this is a powerful technique that preserves the details for large values of the tuning parameter λ. On the contrary, the SVMF yields a growing smoothing action as λ decreases. TCD and MAE evaluations are reported in Tables 5-8.
As a first example, let us focus on the data in Table 5. These data are graphically depicted in Figures 5 and 6. It can be observed that the TCD correctly characterizes the mentioned filtering behavior, whereas the MAE does not. Indeed, the maximum TCD is obtained for λ = 1 (minimum detail preservation) and the TCD decreases for larger values of λ, as it should be (Figure 5). Conversely, very similar values of MAE are achieved for λ = 1 and λ = 10 (Figure 5). The reason for this erroneous behavior can be easily understood if we decompose the MAE into the subsets of pixel coordinates A and B. The wrong MAE component (subset A) is sensitive to the unfiltered noise, and it becomes very annoying as λ increases (Figure 6). Similar results are shown in Tables 6-8 for different test images and different amounts of impulse noise.
A sample of the processed data is reported in Figure 7 for visual inspection (enlarged detail of the “Houses” picture). Strong smoothing (causing detail blur) is obtained by choosing λ = 1 (Figure 7(c)), whereas weak smoothing (preserving details and noise as well) is achieved by λ = 10 (Figure 7(d)).
4.3. Noise Cancellation Tests
In the third group of experiments (noise cancellation tests) we compared the abilities of UCN and MSE to measure the noise removal. We corrupted the test images by superimposing different amounts of impulse noise and we considered the results yielded by the 5 × 5 SVMF.
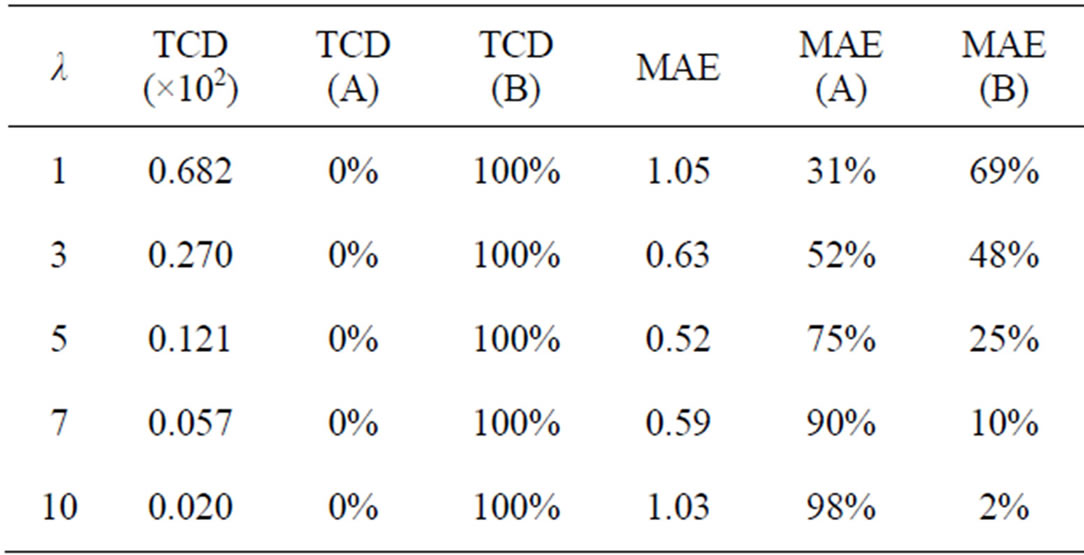
Table 5. TCD vs. MAE in measuring the detail preservation given by the 3 × 3 SVMF filter (“Parrots” corrupted by impulse noise with d = 200 and p = 10%).
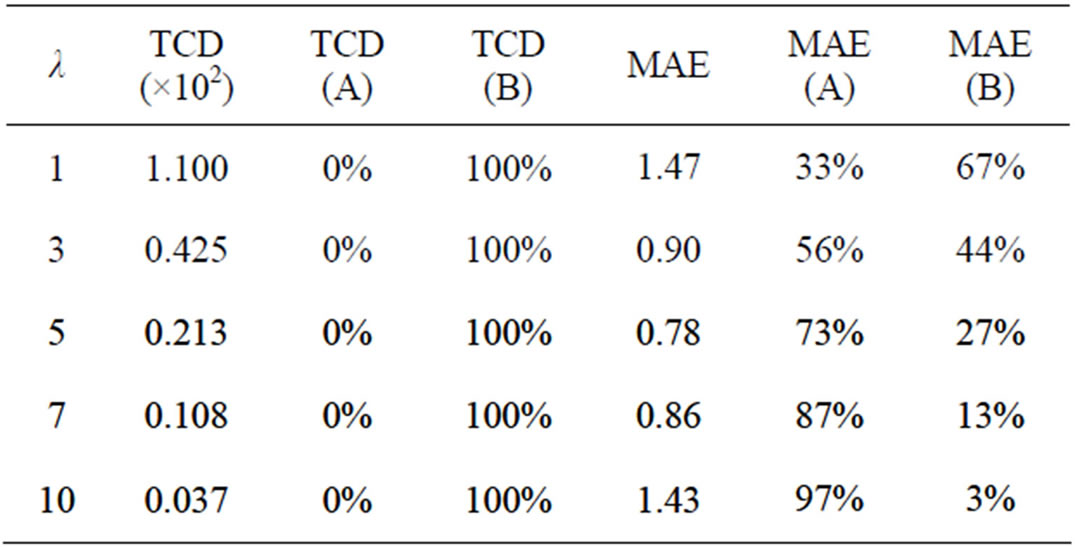
Table 6. TCD vs. MAE in measuring the detail preservation given by the 3 × 3 SVMF filter (“Girl” corrupted by impulse noise with d = 150 and p = 12%).
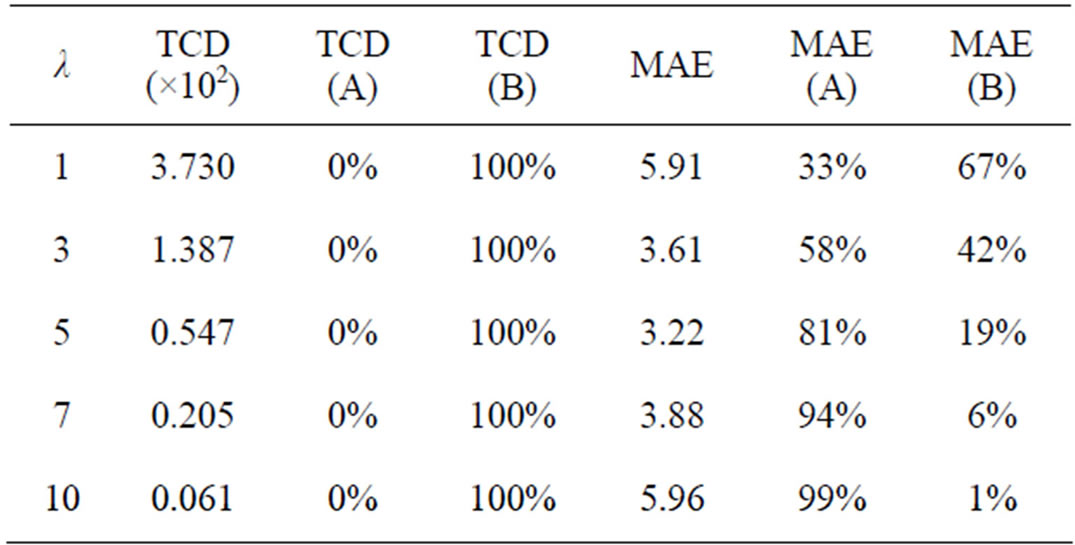
Table 7. TCD vs. MAE in measuring the detail preservation given by the 3 × 3 SVMF filter (“Houses” corrupted by impulse noise with d = 150 and p = 16%).
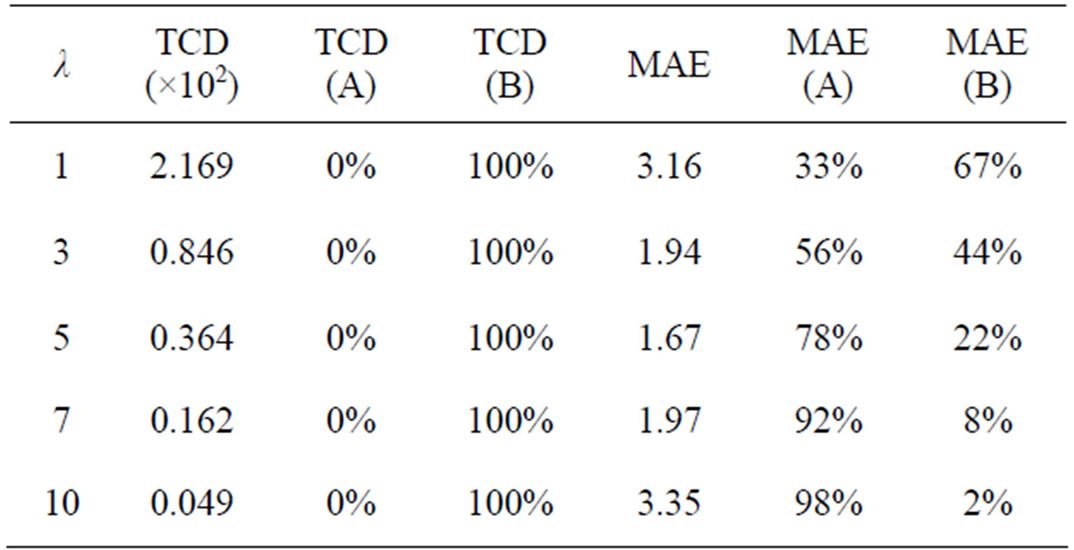
Table 8. TCD vs. MAE in measuring the detail preservation given by the 3 × 3 SVMF filter (“Lighthouse” corrupted by impulse noise with d = 150 and p = 15%).
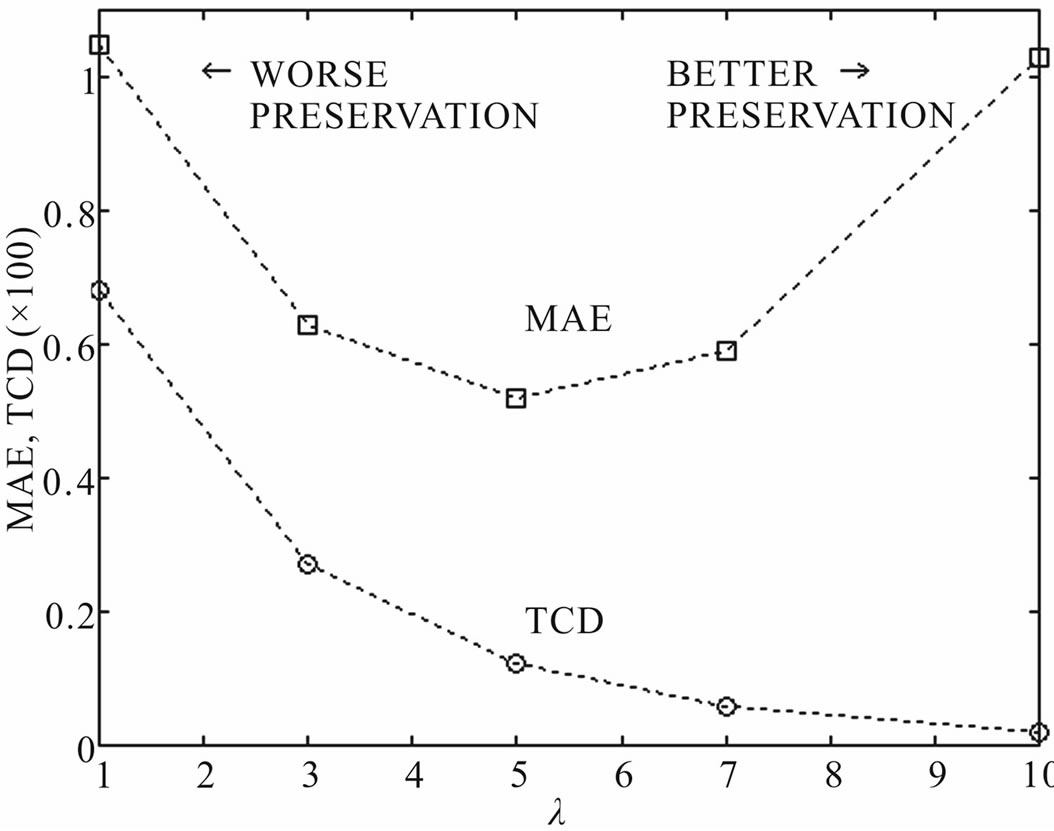
Figure 5. TCD vs. MAE in measuring the detail preservation given by the 3 × 3 SVMF filter.

Figure 6. Right and wrong MAE components (3 × 3 SVMF filter).
 (a) (b)
(a) (b) (c) (d)
(c) (d)
Figure 7. (a) Detail from the “Houses” image; (b) Noisy data; (c) Filtered with λ = 1 (TCD = 3.730 × 10−2, MAE = 5.91); (d) Filtered with λ = 10 (TCD = 0.061 × 10−2, MAE = 5.96).
The corresponding UCN and MSE evaluations are listed in Tables 9-12. It can be seen that the UCN correctly characterizes the aforementioned filtering behavior, whereas the MSE cannot.
As an example, let us focus on the data reported in Table 9. These data are graphically depicted in Figures 8 and 9. The minimum UCN is obtained for λ = 2 (maximum noise cancellation) and it increases for larger values of λ, as it should be. On the contrary, very similar values of MSE are achieved for λ = 2 and λ = 18. The wrong MSE component (subset B) is sensitive to detail blur, and it makes the result even more erroneous as λ decreases. Similar results are listed in Tables 10-12. A sample of

Table 9. UCN vs. MSE in measuring the noise cancellation given by the 5 × 5 SVMF filter (“Parrots” corrupted by impulse noise with d = 200 and p = 25%).
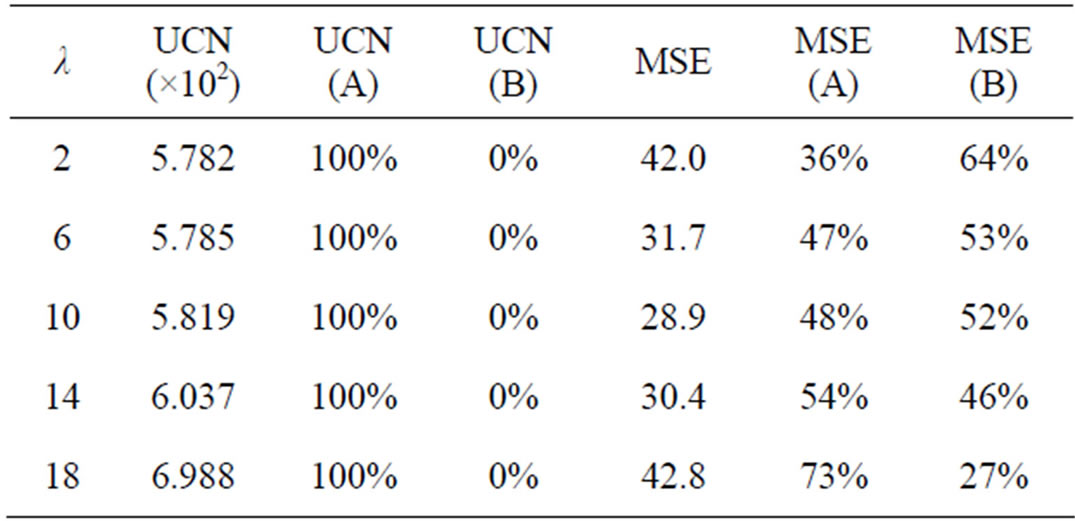
Table 10. UCN vs. MSE in measuring the noise cancellation given by the 5 × 5 SVMF filter (“Girl” corrupted by impulse noise with d = 200 and p = 25%).

Table 11. UCN vs. MSE in measuring the noise cancellation given by the 5 × 5 SVMF filter (“Houses” corrupted by impulse noise with d = 250 and p = 25%).
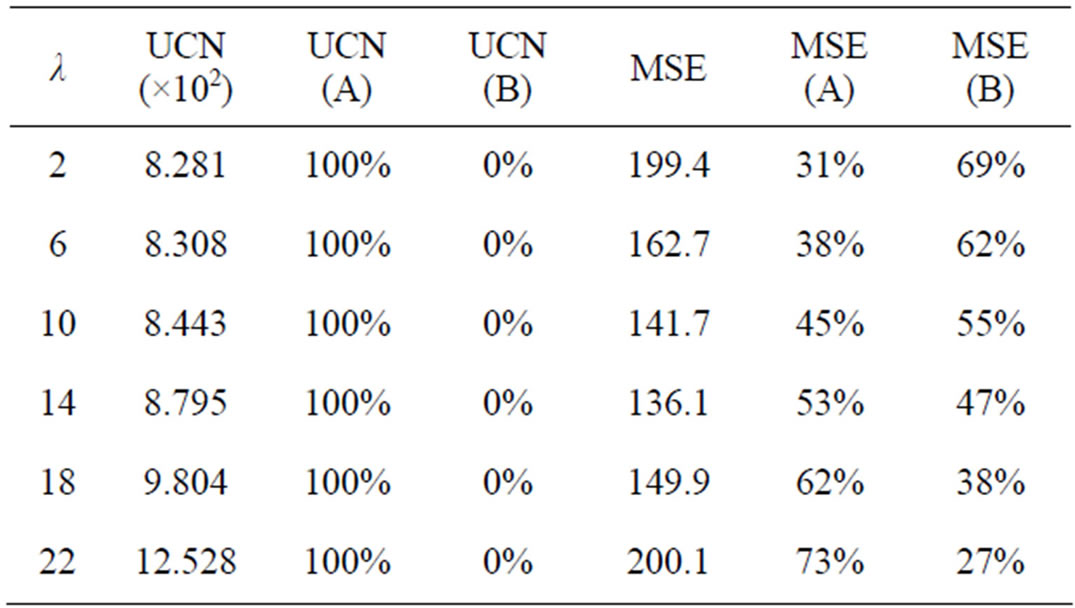
Table 12. UCN vs. MSE in measuring the noise cancellation given by the 5 × 5 SVMF filter (“Lighthouse” corrupted by impulse noise with d = 250 and p = 25%).

Figure 8. UCN vs. RMSE in measuring the noise cancellation given by the 5 × 5 SVMF filter.
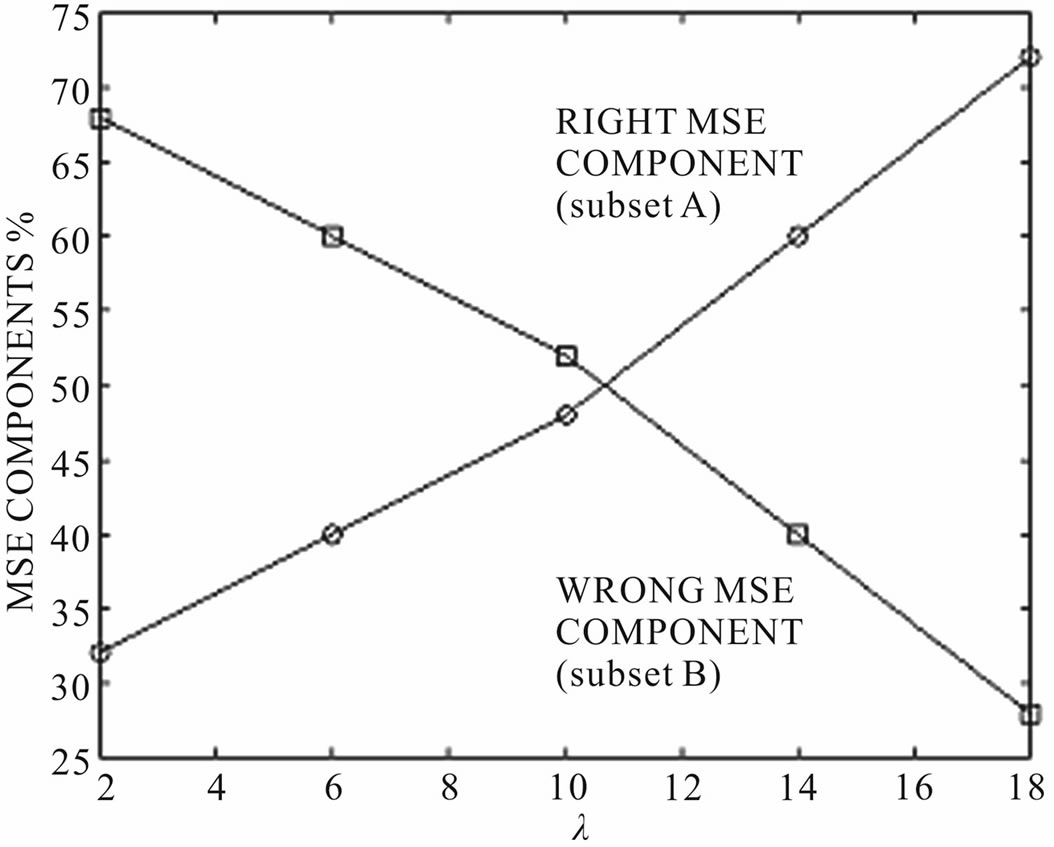
Figure 9. Right and wrong MSE components (5 × 5 SVMF filter).
the processed data is reported in Figure 10 for visual inspection (enlarged detail of the “Lighthouse” picture). The proposed UCN clearly distinguishes where the noise cancellation is better (Figure 10(c), λ = 2) and where it is worse (Figure 10(d), λ = 22), whereas the MSE cannot (MSE  200 for both, see Table 12).
200 for both, see Table 12).
4.4. ATDR Evaluation and Error Maps
Finally, let us show how the novel pixel classification can improve our analysis of scalar and vector approaches, which is a key issue in color filtering. A list of ATDR evaluations is reported in Table 13. Larger values characterize the scalar medians with respect to the vector operators. It can be seen that the sensitivity of the ATDR to the filtering behavior is significantly higher than in any previous method (see Table 1).
The different behavior becomes even more apparent if we provide a graphical representation of the errors 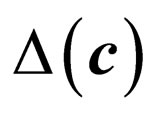 in the three subsets of pixel coordinates A, B1 and B2. As an example, let us consider the “Parrots” image corrupted by impulse noise with p = 10% and d = 100 (Figure 11(a)). The result given by the 5 × 5 SMF is shown in Figure 11(b). As expected, some color distortion is perceivable in the filtered picture. The better result given by the 5 × 5 VMF is depicted in Figure 11(c). Error maps showing where the filters give inaccuracy in removing
in the three subsets of pixel coordinates A, B1 and B2. As an example, let us consider the “Parrots” image corrupted by impulse noise with p = 10% and d = 100 (Figure 11(a)). The result given by the 5 × 5 SMF is shown in Figure 11(b). As expected, some color distortion is perceivable in the filtered picture. The better result given by the 5 × 5 VMF is depicted in Figure 11(c). Error maps showing where the filters give inaccuracy in removing
 (a) (b)
(a) (b) (c) (d)
(c) (d)
Figure 10. (a) detail from the “Lighthouse” image; (b) Noisy data; (c) Filtered with λ = 2 (UCN = 8.281 × 10−2, MSE = 199.4); (d) Filtered with λ = 22 (UCN = 12.528 × 10−2, MSE = 200.1).
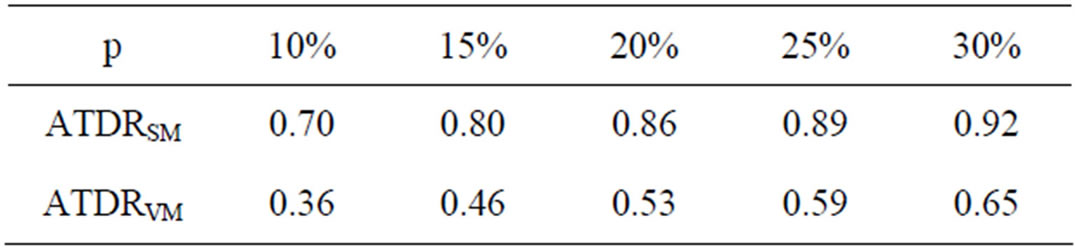
Table 13. ATDR values given by 5 × 5 SMF and VMF filters (“Parrots” corrupted by impulse noise with d = 100 and p ranging from 10% to 30%).
 (a)(b)(c)(d)(e)
(a)(b)(c)(d)(e) (f)(g)(h)(i)(j)
(f)(g)(h)(i)(j) (k)(l)(m)(n)(o)
(k)(l)(m)(n)(o)
Figure 11. Noisy input image, result yielded by the 5 × 5 scalar median filter (SMF), result yielded by the 5 × 5 vector median filter (VMF) and corresponding error maps evaluated in the CIE Luv space for different densities of impulse noise: p = 10% (a)-(e), p = 1% (f)-(j), p = 50% (k)-(o).
noise (green), basic distortion (blue) and additional distortion (red) are reported in Figures 11(d) (SMF) and (e) (VMF).
This effect also occurs for lower and higher densities of noise pulses. Figures 11(f)-(j) address the case p = 1%, where the basic distortion is the main effect, as denoted by the large number of blue pixels. On the contrary, Figures 11(k)-(o) consider the case p = 50%, where the errors in noise removal increase, especially for the SMF (green pixels).
A deeper analysis of the proposed method is a subject of present investigation. It suffices here to observe that the effectiveness in measuring color artifacts just resides in the adoption of a perceptually uniform color space, such as the CIE Luv color system. On the other hand, vector filtering can satisfactorily preserve the correlation between the color components of a natural image, whereas scalar filtering cannot. The results in Figure 11 are in good agreement with these theoretical considerations.
Finally, we can observe that, in all the experiments, we adopted a two-parameter model of noise where density and amplitude of noise pulses can be chosen to highlight the different behavior of classical and new metrics. The most apparent failure of a given quality index likely occurs when it yields the same value for different combinations of noise cancellation and image preservation. For this reason, we searched for this kind of result in many of the reported experiments, by appropriately choosing the mentioned noise parameters. Clearly, different amounts of noise could also be used to highlight the limitations of MAE and MSE. Their decomposition into the subsets of pixel coordinates A and B offers a simple and effective way to measure their erroneous behavior in any case.
5. Conclusions
Validation of impulse noise removal filters for color images requires full-reference metrics able to yield separate evaluations of noise cancellation and image preservation. In this respect, the contribution of this paper is twofold:
• to clearly show (and measure) the inaccuracies and limitations of classical metrics;
• to present a simple and new approach based on pixel classification.
Computer simulations have shown that the proposed approach, although simple, offers the following advantages:
1) only two measures (TCD and UCN) suffice; 2) TCD and UCN are much more accurate than the mentioned classical metrics; 3) furthermore, the proposed method can offer a deeper analysis of the filtering distortion (ATDR), at the price of one more processed image. 4) finally, the approach can easily provide a comprehensive error map (filter’s signature) showing the spatial location of different kinds of filtering errors, whereas classical metrics cannot.
REFERENCES
- K. N. Plataniotis and A. N. Venetsanopoulos, “Color Image Processing and Application,” Springer Verlag, New York, 2000.
- R. Lukac, B. Smolka, K. Martin, K. N. Plataniotis and A. N. Venetsanopoulos, “Vector Filtering for Color Imaging, ” IEEE Signal Processing Magazine, Vol. 22, No. 1, 2005, pp. 74-86. doi:10.1109/MSP.2005.1407717
- R. Lukac and K. N. Plataniotis, “A Taxonomy of Color Image Filtering and Enhancement Solutions,” In: P. W. Hawkes, Ed., Advances in Image and Electron Physics, Vol. 140, Elsevier, New York, 2006, pp. 187-264.
- R. Lukac, B. Smolka, K. N. Plataniotis and A. N. Venetsanopoulos, “Selection Weighted Vector Directional Filters,” Computer Vision and Image Understanding, Vol. 94, No. 1-3, 2004, pp. 140-167. doi:10.1016/j.cviu.2003.10.013
- R. Lukac, B. Smolka, K. N. Plataniotis and A. N. Venetsanopoulos, “Vector Sigma Filters for Noise Detection and Removal in Color Images,” Journal of Visual Communication and Image Representation, Vol. 17, No. 1, 2006, pp. 1-26. doi:10.1016/j.jvcir.2005.08.007
- Y. Li, G. R. Arce and J. Bacca, “Weighted Median Filters for Multichannel Signals,” IEEE Transactions on Signal Processing, Vol. 54, No. 11, 2006, pp. 4271-4281. doi:10.1109/TSP.2006.881208
- S. Schulte, V. De Witte, M. Nachtegael, D. Van der Weken and E. E. Kerre, “Fuzzy Two-Step Filter for Impulse Noise Reduction from Color Images,” IEEE Transactions on Image Processing, Vol. 15, No. 11, 2006, pp. 3568-3579.
- S. Schulte, S. Morillas, V. Gregori and E. E. Kerre, “A New Fuzzy Color Correlated Impulse Noise Reduction Method,” IEEE Transactions on Image Processing, Vol. 16, No. 10, 2007, pp. 2565-2575. doi:10.1109/TIP.2007.904960
- P.-E. Ng and K.-K. Ma, “A Switching Median Filter with Boundary Discriminative Noise Detection for Extremely Corrupted Images,” IEEE Transactions on Image Processing, Vol. 15, No. 6, 2006, pp. 1506-1516. doi:10.1109/TIP.2005.871129
- Y. Q. Dong and S. F. Xu, “A New Directional Weighted Median Filter for Removal of Random-Valued Impulse Noise,” IEEE Signal Processing Letters, Vol. 14, No. 3, 2007, pp. 193-196. doi:10.1109/LSP.2006.884014
- Y. Y. Li, F.-L. Chung and S. T. Wang, “A Robust Neurofuzzy Network Approach to Impulse Noise Filtering for Color Images,” Applied Soft Computing, Vol. 8, No. 2, 2008, pp. 872-884.
- Z. Y. Xu, H. R. Wu, B. Qiu and X. H. Yu, “Geometric Features-Based Filtering for Suppression of Impulse Noise in Color Images,” IEEE Transactions on Image Processing, Vol. 18, No. 8, 2009, pp. 1742-1759. doi:10.1109/TIP.2009.2022207
- S. Morillas, V. Gregori and A. Hervás, “Fuzzy Peer Groups for Reducing Mixed Gaussian-Impulse Noise From Color Images,” IEEE Transactions on Image Processing, Vol. 18, No. 7, 2009, pp. 1452-1466. doi:10.1109/TIP.2009.2019305
- T. Melange, M. Nachtegael and E. E. Kerre, “Fuzzy Random Impulse Noise Removal from Color Image Sequences,” IEEE Transactions on Image Processing, Vol. 20, No. 4, 2011, pp. 959-970. doi:10.1109/TIP.2010.2077305
- S. Esakkirajan, T. Veerakumar, A. N. Subramanyam and C. H. PremChand, “Removal of High Density Salt and Pepper Noise through Modified Decision Based Unsymmetric Trimmed Median Filter,” IEEE Signal Processing Letters, Vol. 18, No. 5, 2011, pp. 287-290. doi:10.1109/LSP.2011.2122333
- M. E. Yuksel and A. Basturk, “Application of Type-2 Fuzzy Logic Filtering to Reduce Noise in Color Images,” IEEE Computational Intelligence Magazine, Vol. 7, No. 3, 2012, pp. 25-35. doi:10.1109/MCI.2012.2200624
- F. Russo, “New Method for Performance Evaluation of Grayscale Image Denoising Filters,” IEEE Signal Processing Letters, Vol. 17, No. 5, 2010, pp. 417-420. doi:10.1109/LSP.2010.2042516
- F. Russo, “Design of Fuzzy Relation-Based Image Sharpeners,” In: A. Ruano and A. R. Várkonyi-Kóczy, Eds., New Advances in Intelligent Signal Processing, Springer-Verlag, Berlin, 2011, pp. 115-131. doi:10.1007/978-3-642-11739-8_6
- N. Ponomarenko, F. Battisti, K. Egiazarian, J. Astola and V. Lukin, “Metrics Performance Comparison for Color Image Database,” 4th International Workshop on Video Processing and Quality Metrics for Consumer Electronics, Scottsdale, 14-16 January 2009.
- F. Russo, A. De Angelis and P. Carbone, “A Vector Approach to Quality Assessment of Color Images,” IEEE Instrumentation and Measurement Technology Conference Proceedings, Victoria, 12-15 May 2008, pp. 814- 818.
- A. De Angelis, A. Moschitta, F. Russo and P. Carbone, “A Vector Approach for Image Quality Assessment and Some Metrological Considerations,” IEEE Transactions on Instrumentation and Measurement, Vol. 58, No. 1, 2009, pp. 14-25. doi:10.1109/TIM.2008.2004982
- A. Medda and V. DeBrunner, “Color Image Quality Index Based on the UIQI,” 2006 IEEE Southwest Symposium on Image Analysis and Interpretation, Denver, 26-28 March 2006, pp. 213-217. doi:10.1109/SSIAI.2006.1633753
- R. Franzen, “Kodak Lossless True Color Image Suite.” http://r0k.us/graphics/kodak/

