Journal of Signal and Information Processing
Vol.3 No.4(2012), Article ID:24962,4 pages DOI:10.4236/jsip.2012.34059
PAPR Distribution Analysis at the Output of Nonlinear PAPR Reducers
![]()
1AFRIQIS Technology, Lannion, France; 2SUPELEC/IETR, Campus de Rennes, Cesson-Sévigné, France.
Email: gueldesi@yahoo.fr, jacques.palicot@supelec.fr
Received July 23rd, 2012; revised August 27th, 2012; accepted September 6th, 2012
Keywords: Orthogonal Frequency Division Multiplexing (OFDM); Peak-To-Average Power Ratio (PAPR); Distribution; Nonlinear PAPR Reducers
ABSTRACT
Nonlinear PAPR reducers, such as clipping and companding techniques, are some simple methods used to reduce the Peak-to-Average Power Ratio (PAPR). In this paper, assuming that the baseband OFDM signal is characterized as a band-limited complex Gaussian process, we investigate the PAPR distribution of an OFDM signal when it is passed through a nonlinear PAPR reducer. The obtained PAPR distribution depends on the nonlinear function which characterizes the PAPR reducer. Later in this paper, we apply the obtained PAPR distribution in the clipping case. The comparisons made between the proposed distribution and that obtained thanks to computer simulations show good agreement.
1. Introduction
Orthogonal Frequency Division Multiplexing (OFDM) is an attractive modulation technique for the next generation of high bit rate wireless transmission due to its high robustness to multipath fading and its great simplification of channel equalization [1]. However, one of the main problems of the OFDM modulation technique is the large peak-to-average power ratio (PAPR) of the transmitting signals. This high PAPR causes in-band and out-band interferences when the OFDM signals are passed through a high power amplifier (HPA) which does not have enough linear range. Several PAPR reduction techniques have been proposed [2] to reduce the PAPR of OFDM signals. To well understand this PAPR problem and to predict possible gain thanks to reduction techniques, many papers were interested in the PAPR distribution analysis. The pionneer work was the work of R. van Nee and A. de Wild in [3]. But this expression was obtained at the Nyquist frequency and therefore did not represent a realistic value of the continuous signal PAPR distribution. Then, using a probabilistic approach, Ochiai et Imai proposed a more realistic expression in [4]. Later, Zhou et Caffery in [5] proposed an upper bound of the Complementary Cumulative Distribution Function (CCDF) of the PAPR. Louet and Hussain in [6] proposed a new expression for continuous baseband OFDM signals. This latter expression was very close to the continuous signal PAPR simulation.
But, only few papers are dealing with PAPR distribution analysis at the output of PAPR reducers. Some researchers proposed a PAPR distribution analysis when there is unequal power allocation between carriers [7]. In [8], YOO et al. studied the PAPR distribution at the ouput of probabilistic PAPR reducer. In this paper we are interrested in the PAPR distribution analysis at the output of PAPR reducers. We will, first of all, focus on the class of PAPR reduction techniques known as nonlinear PAPR reducers, i.e. the schemes for PAPR reduction that use spectrum distortion or spectral regrowth. This class of nonlinear PAPR reducers includes mainly clipping techniques [9] and companding techniques [10]. We derive a general expression of the CCDF at the ouput of non-linear reducers. Then, we apply this expression to the Soft Envelop Clipping (SEC) reducer.
The remainder of this paper is organized as follows: Section 2 briefly introduces nonlinear PAPR reducers. In Section 3, the PAPR distribution is analyzed through its Complementary Cumulative Distribution Function (CCDF). Then in Section 4 results of previous analysis is applied to Soft Enveloppe Clipping reducer. In this section, we provided some results which show good agreement between simulation and theoretical expressions. Finally in Section 5, a conclusion is drawn.
2. Characterization of Nonlinear PAPR Reducers
Let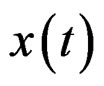 , be the baseband equivalent time-domain OFDM signal.
, be the baseband equivalent time-domain OFDM signal. 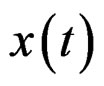 can be written as
can be written as
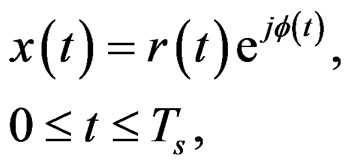 (1)
(1)
where 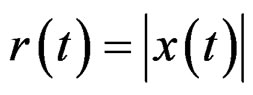 is the OFDM magnitude,
is the OFDM magnitude, 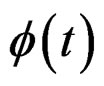 is the OFDM phase and
is the OFDM phase and 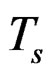 is the OFDM symbol period.
is the OFDM symbol period.
The PAPR of  may be defined as
may be defined as
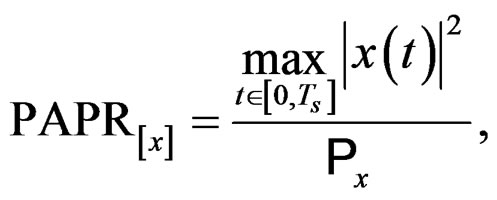 (2)
(2)
where 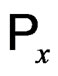 is the signal
is the signal 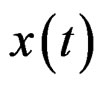 average power.
average power.
In nonlinear PAPR reducers (clipping, companding techniques), the data signal PAPR is reduced by a nonlinear function as shown in Figure 1.
Now, let us suppose 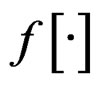 the nonlinear function that characterizes the nonlinear PAPR reducer shown in Figure 1, the PAPR reduced signal
the nonlinear function that characterizes the nonlinear PAPR reducer shown in Figure 1, the PAPR reduced signal 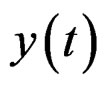 at the output of PAPR reduction scheme is expressed as
at the output of PAPR reduction scheme is expressed as
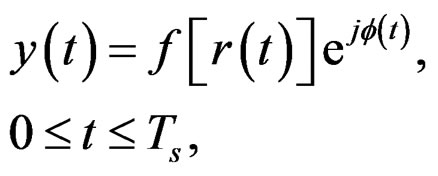 (3)
(3)
where 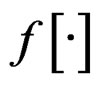 is nonlinear positive function also called function for PAPR reduction.
is nonlinear positive function also called function for PAPR reduction.
3. PAPR Distribution Analysis
In the literature, it is customary to use the Complementary Cumulative Distribution Function (CCDF) of the PAPR as a performance criterion. Let us consider 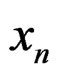 and
and 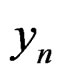 the discrete-time signals at the Nyquist rate of the OFDM signal
the discrete-time signals at the Nyquist rate of the OFDM signal 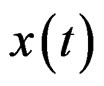 and its PAPR reduced version
and its PAPR reduced version 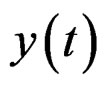 respectively. For a large number of subcarriers, the OFDM envelope converges to a Rayleigh envelope distribution. Therefore, the probability density function (PDF)
respectively. For a large number of subcarriers, the OFDM envelope converges to a Rayleigh envelope distribution. Therefore, the probability density function (PDF)  of the OFDM envelope can be expressed as
of the OFDM envelope can be expressed as
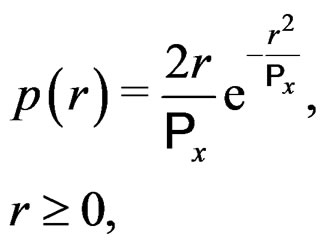 (4)
(4)
where  is the mean power OFDM signal.
is the mean power OFDM signal.
Using (4), it was shown in [4] that, the OFDM PAPR CCDF could be approximated by the following expression:
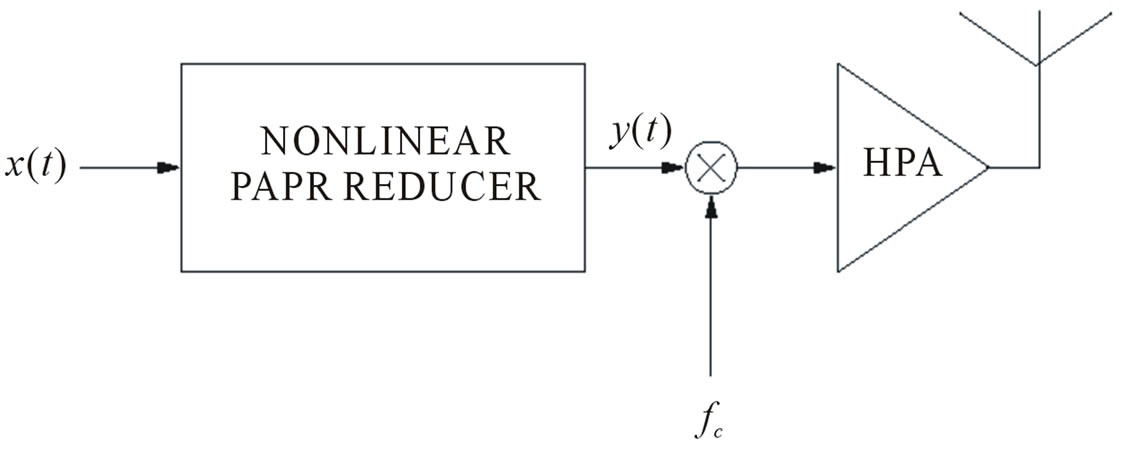
Figure 1. Nonlinear PAPR reducer scheme.
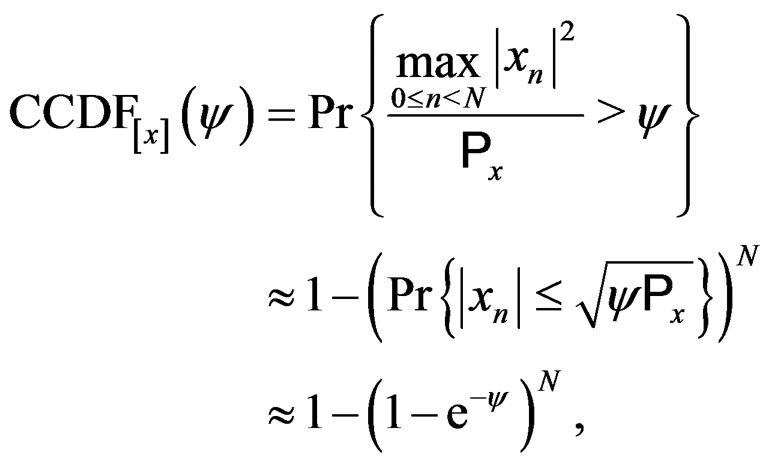 (5)
(5)
where, 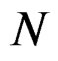 is the number of samples per OFDM symbol period. This PAPR CCDF expression has been proved for the first time by R. van Nee and A. de Wild in [3].
is the number of samples per OFDM symbol period. This PAPR CCDF expression has been proved for the first time by R. van Nee and A. de Wild in [3].
In the same way as (5), we show that the PAPR distribution of the ouput signal  could be approximated by Equation (6):
could be approximated by Equation (6):
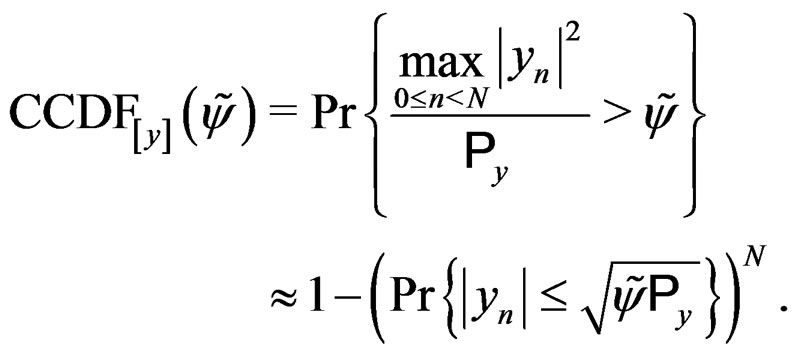 (6)
(6)
Using (2), it can be shown that, 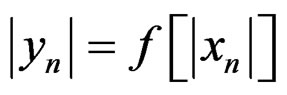 and Equation (6) becomes
and Equation (6) becomes
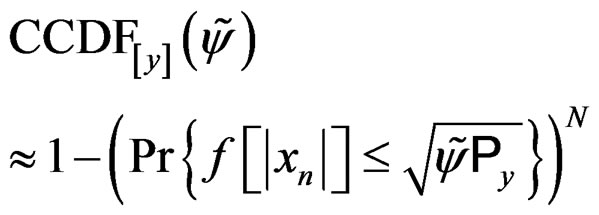 (7)
(7)
Equation (7) shows that, the expression of 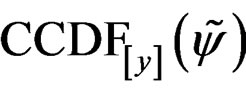 depends on the function
depends on the function  for PAPR reduction. In the following section of this paper, an exact expression of
for PAPR reduction. In the following section of this paper, an exact expression of 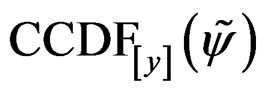 is given in the soft envelop clipping’s case [9].
is given in the soft envelop clipping’s case [9].
4. PAPR Distribution in the Soft Envelope Clipping Technique’s Case
In this section, in order to illustrate the theoretical results obtained for nonlinear PAPR reducers, we consider one nonlinear PAPR reducer which is commonly studied in the literature: The Soft Envelop Clipping (SEC) [9].
The nonlinear function 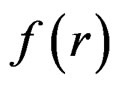 of SEC is expressed as
of SEC is expressed as
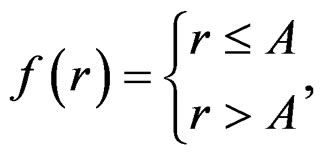 (8)
(8)
where 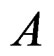 is the magnitude threshold and commonly known as clipping threshold.
is the magnitude threshold and commonly known as clipping threshold.
It is shown in [11] that the PDF 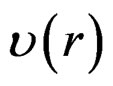 of the clipped signal envelope can be written as
of the clipped signal envelope can be written as
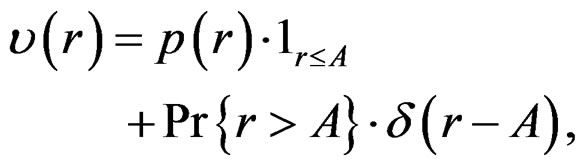 (9)
(9)
where  is the Dirac impulse. From (9), we show that,
is the Dirac impulse. From (9), we show that,
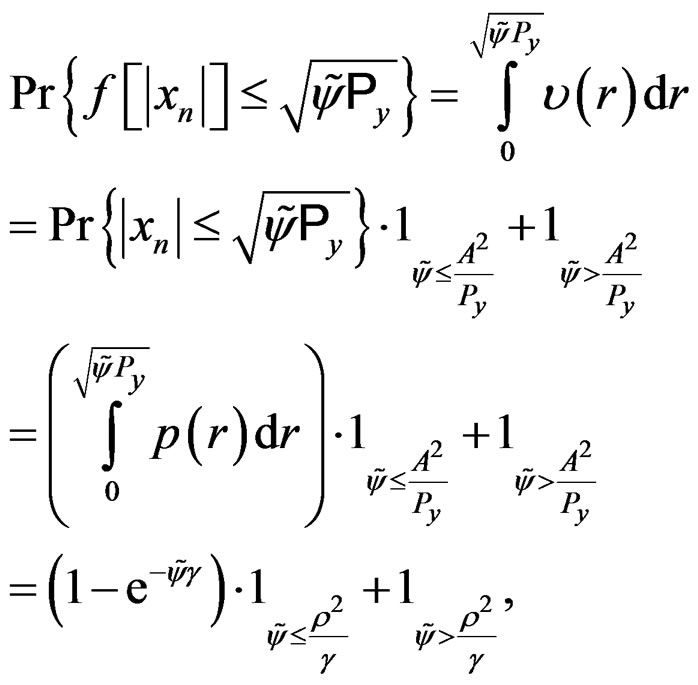 (10)
(10)
where 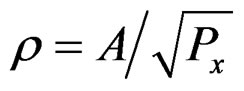 is the clipping ratio (CR) and
is the clipping ratio (CR) and 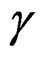 is the output-to-input average power ratio defined as
is the output-to-input average power ratio defined as
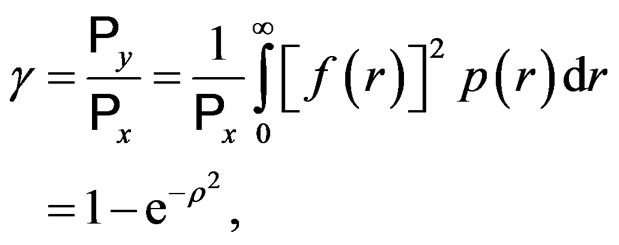 (11)
(11)
where 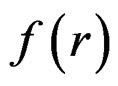 is the function for PAPR reduction defined in (8) and
is the function for PAPR reduction defined in (8) and 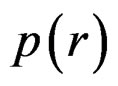 is the PDF of the OFDM signal expressed in (4).
is the PDF of the OFDM signal expressed in (4).
Substituting (10) into (7), we show that, the expression of 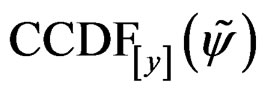 for SEC is expressed as
for SEC is expressed as
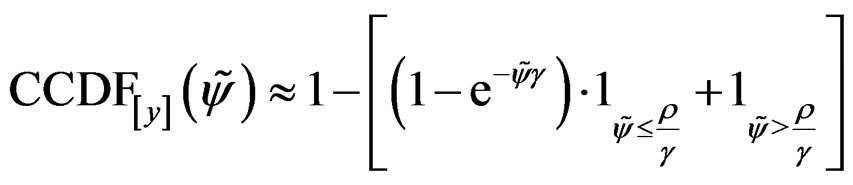 (12)
(12)
when 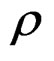 becomes great and tends to infinity, then
becomes great and tends to infinity, then 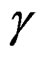 tends to
tends to  and expression 12 is equal to classical expression 5 of the CCDF at the input of the clipping.
and expression 12 is equal to classical expression 5 of the CCDF at the input of the clipping.
Figure 2 compares the theoretical CCDF of the signal’s PAPR at the output of the PAPR reduction scheme expressed by (7), and this for simulation results obtained with three different values of . The OFDM signal comprises
. The OFDM signal comprises 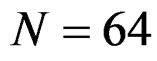 subcarriers and is simulated with an oversampling factor of
subcarriers and is simulated with an oversampling factor of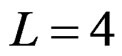 . It should be noted that, the theoretical
. It should be noted that, the theoretical 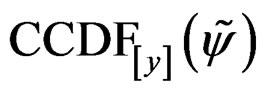 shows good agreement with the simulation results. Nevertheless, where
shows good agreement with the simulation results. Nevertheless, where 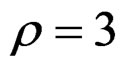 dB and 5 dB, the theoretical
dB and 5 dB, the theoretical 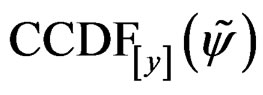 is less accurate with the simulation results where
is less accurate with the simulation results where 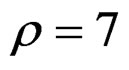 dB. The reason for this is that, for low values of
dB. The reason for this is that, for low values of , the theoretical
, the theoretical  tends to be a Dirac and becomes very sensitive to approximation errors.
tends to be a Dirac and becomes very sensitive to approximation errors.
5. Conclusions
In this paper, assuming that the baseband OFDM signal is characterized as a band-limited complex Gaussian process, we have investigated the PAPR distribution of an OFDM signal at the output of a nonlinear PAPR reducer. The obtained PAPR distribution has been applied in the clipping case, which is a well-known example of nonlinear PAPR reducer used for OFDM PAPR reduction.
The comparisons made between the proposed PAPR

Figure 2. Comparison of the proposed distributions for the PAPR related to the clipping technique (12) with simulation results for ρ = 3 dB, 5 dB and 7 dB.
distribution at the output of clipping and with that obtained thanks to computer simulations show good agreement.
REFERENCES
- A. R. S. Bahai and B. R. Saltzberg, “Multi-Carrier Digital Communications: Theory and Applications of OFDM,” Kluwer Academic/Plenum Publishers, New York, 1999.
- Y. Louet and J. Palicot, “A Classification of Methods for Efficient Power Amplification of Signals,” Annals of Telecom, Vol. 63, No. 7-8, 2008, pp. 351-368.
- R. J. Van Nee and A. De Wild, “Reducing Peak-To-Average Power Ratio of OFDM,” Proceedings of IEEE VTC 96, Atlanta, 1996, pp. 2072-2076.
- H. Ochiai and H. Imai, “On the Distribution of the PeakTo-Average Power Ratio in OFDM Signals,” IEEE Transactions on Communications, Vol. 49, No. 2, 2001, pp. 282- 289. doi:10.1109/26.905885
- X. Zhou and J. J. Caffery, “A New Distribution Bound and Reduction Scheme for OFDM PAPR,” Proceedings of 5th International Symposium on Wireless Personal Multimedia Communications, Vol. 1, 2002, pp. 158-162. doi:10.1109/WPMC.2002.1088152
- Y. Louet and S. Hussain, “Peak-To-Mean Envelope Power Ratio Statistical Analysis of Continuous OFDM Signal,” Proceedings of IEEE Vehicular Technology Conference VTC Spring 2008, 11-14 May 2008, pp. 1681- 1685. doi:10.1109/VETECS.2008.387
- T. Jiang, D. M. Qu and P. Gao, “Distribution of Peak-ToAverage Power Ratio and Its Applications in OFDM Systems with Unequal Power Allocation,” IEEE WICON, Singapore, 2010. doi:10.4108/ICST.WICON2010.8618
- H. Yoo, F. Guilloud and R. Pyndiah, “Amplitude PDF Analysis of OFDM Signal Using Probabilistic PAPR Reduction Method,” EURASIP Journal on Wireless Communications and Networking, Vol. 2011, 2011, Article ID: 983915. doi:10.1155/2011/983915
- X. Li and L. J. Cimini Jr., “Effects of Clipping and Filtering on the Performance of OFDM,” IEEE on Communications Letters, Vol. 2, No. 5, 1998, pp. 131-133. doi:10.1109/4234.673657
- X. Wang, T. Tjhung and C. S. Ng, “Reduction of Peak to Average Power Ratio of OFDM System Using a Companding Technique,” IEEE Transactions on Broadcasting, Vol. 45, No. 3, 1999, pp. 303-307.
- P. Banelli, G. Leus and G. B. Giannakis, “Bayesian Estimation of Clipped Gaussian Processes with Applicaiton to OFDM,” Proceedings of the European Signal Processing Conference (EUSIPCO), Toulouse, 3-6 September 2002, pp. 181-184.

