Open Journal of Modelling and Simulation
Vol.04 No.02(2016), Article ID:65850,9 pages
10.4236/ojmsi.2016.42006
The Optimal Investment Strategy Based on the DEA Model
Yulei Zhang, Shuai Zhang, Xinxin Zhang, Zhenping Li*
School of information, Beijing Wuzi University, Beijing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 March 2016; accepted 23 April 2016; published 26 April 2016
ABSTRACT
The Goodgrant Foundation is a charitable organization that wants to improve education performance of undergraduates attending colleges and universities in the US. So the foundation plans to contribute a total of US 50 million for a suitable team of schools per year under the condition of avoiding repeated other large grant organizations’ investment. The DEA (Data Estimate Analysis) model is developed to determine an optimal investment strategy for the Goodgrant Foundation. In this paper, two questions were solved: how to choose a suitable team of schools and how to allocate the investment. Before the establishment of the model, the EXCEL software is used to preprocess data. Then the DEA model which includes two models in the paper is developed. For the first question, the CCR model is established to rank schools which used efficiency from DEAP 2.1. For the second question, the resource allocation model is established to allocate investment amount by weights of allocation from MATLAB software. Accordingly, the optimal investment strategy is received for the Goodgrant Foundation. Through the analysis above, 23 from 293 schools are selected to invest. Then the schools are ranked and the investment of US 50 million for 23 schools is allocated.
Keywords:
The DEA Model, Optimal Investment Strategy, DEAP 2.1 Software

1. Introduction
In the ever-changing today’s society, talent has increasingly become the key topic. As the cradle of talent training, colleges and universities also attract people’s focus of attention. Colleges and universities shoulder the responsibilities for conveying fresh blood for society and making basic research. The development of colleges is closely related to the development of country. So many charitable organizations dedicate to donations to improve educational performance.
Zhang and Guo [1] proposed a new model to measure the relative efficiency of the assessed DMU (Decision Making Unit) through analyzing its disadvantages based on DEA model and compare the DMUs’ efficiency rates and give their order. Li and Zuo [2] established the optimal investment bilevel programming models of prior development colleges as well as that of indiscriminate investment in all colleges and given the optimal investment scheme of both upper and lower level. Cai [3] introduced the higher education evaluation model of investment benefit based on DEA, collected a university’s data according to the time series and conducted empirical research investment benefit from 2001 to 2009. Ma [4] analyzed Inner Mongolian University’s scientific and technological input-output efficiency quantitatively applying generalized data envelopment analysis method. Gan [5] built input-output index of the Graduate School, screened index based on the factor analysis and DEA methods to analysis panel data. Juan [6] proposed a series of DEA models to accommodate settings where non- homogenous sub-units operate in parallel network structures with intermediate measures or links. Chang [7] developed a new type of DEA model referred to as intertemporal DEA model that can be used to fully measure a firm’s efficiency by explicitly considering its key inputs and outputs involving the past-present-future time span. Fuentes [8] analyzed the productivity growth of the SUMA tax offices located in Spain evolved between 2004 and 2006 by using Malmquist Index based on Data Envelopment Analysis (DEA) models. Merkert [9] applied two-stage Data Envelopment Analysis (DEA) models to estimate a single efficiency measure that combines the potentially conflicting indicators of perceived service quality and profitable for the airport context. Li [10] re- estimate the TFEE (Total-Factor Energy Efficiency) using an improved DEA model, which combines the super- efficiency and sequential DEA models to avoid “discriminating power problem” and “technical regress”, and then used it to calculated the TEI (target for energy intensity). Adel [11] proposed an alternative DEA model for centrally imposed resource or output reduction across the references set and determined the amount of input and output reduction needed for each DMU to increase the efficiency score of all the DMUs.
The Goodgrant Foundation is a charitable organization that wants to improve educational performance of undergraduates attending colleges and universities in the US. So the Foundation plans to contribute 50 million money for a suitable team of schools per year under the condition of avoiding repeated other large grant organizations’ investment.
To do this, two questions are solved for the Goodgrant Foundation: how to choose a suitable team of schools and how to allocate the investment. In order to solve the two questions, the DEA model is established to determine an optimal investment strategy, including the selection of schools and determination of investment amount. In this process, DEAP software and MATLAB software are used to solve the questions we face.
2. The DEA Model
2.1. Assumptions
Before solving the questions above, some assumptions are made as follows:
1) Since the period of education investment return is long, only one cycle is considered.
2) Assume that the paper does not consider the school’s ownership such as Public, Private nonprofit and Private for-profit is not considered.
3) Assume that the wages of students after graduation directly reflected in the return on investment.
4) Assume that the school’s all indicators are static.
2.2. The Essential Definitions
Let us consider a set of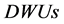 ,
, 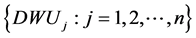 , where
, where 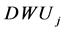 consumes multiple positive inputs
consumes multiple positive inputs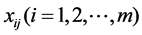 to produce multiple positive outputs
to produce multiple positive outputs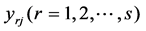 . Suppose that inputs and outputs for
. Suppose that inputs and outputs for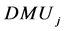 are denoted by
are denoted by 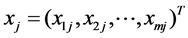 and
and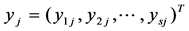 , and
, and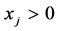 ,
, 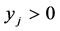 for
for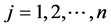 .
. 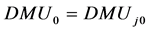 is the evaluated unit, whose input vector and output vector are respectively recorded as
is the evaluated unit, whose input vector and output vector are respectively recorded as 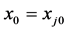 and
and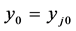 . Let
. Let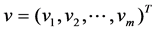 , where
, where 




2.3. The CCR Model
DEA (Data Environment Analysis) [12] is a nonparametric technique for measuring the relative efficiencies of a set of decision-making units (
DEA has become increasingly popular for efficiency analysis in practical viewpoint of management, economics, especially the education. So it is meaningful and necessary to apply DEA model in this question.
There exist various DEA models with different economic meanings. The CCR model is chosen in this paper, CCR model which measures the efficiency is the first model of DEA displayed as follows.

where

Due to the fractional programming model, the model is reformed into a linear programming model to solve as follows.

where

The fractional programming and linear programming are equivalent [13] .
The dual problem of Equation (3) is as follows.

Both Equation (3) and Equation (5) have the optimal solution, and the optimal value 
If the optimal solutions are
1) If the optimal value of Equation (5) is 


2) If the optimal value of Equation (5) is

3) If the optimal value of Equation (5) is


2.4. The Resource Allocation Model
According to the CCR model, an equivalent change is made on the first equation of the model [14] .

For the

where k represents the kth DMU, 

3. DEA Model to the Goodgrant’s Investment Strategy
3.1. Data Preprocessing
Because the formats of the data are various and missing values are different, the data should be preprocessed to avoid inaccuracy and instability caused by redundant data in the data mining. Firstly, the irrelevant or redundant data are deleted to make dimensionality reduced. For example, the name of schools are omitted, the schools’ official website and other characters data are not considered. Secondly, the reasonable data are used to deal with missing values. For example, the plural are used to fill the scalar data such as the index “LACALE “in the data and the mean value of no missing values is used to fill the numerical data.
To be clear, the EXCEL software is used to manipulate the data by the approaches we discussed above. Finally, some appropriate inputs and outputs are chosen. Through the data preprocessing and simple analysis, eight key factors are chosen: 6 inputs and 2 outputs. The DMUs are denoted as schools. After the data preprocessing, the number of schools decreased from 293 to 23. The inputs and outputs considered are as Table 1.
3.2. Establishment of the CCR Model and Resource Allocation Model
The CCR model is as follows:

The allocation model is as follows:


According to our analysis, the variables in the model are
3.3. Solving the Case
1) School ranking. The software DEAP 2.1 is used to implement CCR case of DEA. Owing to the data, the efficiency scores are got according to the DEA model. Then the schools are ranked according to the efficiency scores. So the schools are sorted by “crste” in the below chart. The degression of scale benefits show investment will not increase efficiency. So schools that are in the condition of scale benefit degression are deleted. Finally, the schools based on the overall efficiency are re-ranked. And the results are listed as Table 2.
2) Allocation of investment. Firstly, 

3.4. Results
After a series of analysis, the optimal investment strategy is obtained. The efficiency of schools is measured with the DEA model, and the efficiency scores are used to rank schools. Then, the investment amount is allocated based on the rank and weights of allocation solved by DEA model. So the Goodgrant Foundation can make optimal strategy for future educational investment.
4. Sensitivity Analysis
If the efficiency remains unchanged, but the inputs increase (


Table 1. Inputs and outputs.
Table 2. The efficiency and rank.
Notes: crste is the Overall efficiency; vrste is the True technical efficiency; scale is the Scale efficiency; rts is the Scale Report, irs is increase, - is constant; drs is decrease.
Table 3. The school investment table.

Then we can select 
5. Conclusions
To deal with the investment strategy problem for the Goodgrant Foundation, the DEA model is used to determine an optimal investment strategy in this paper. And two questions are solved about how to choose a suitable team of schools and how to allocate the investment. The CCR model is used to rank schools which use efficiency from DEAP 2.1 in order to solve the first question. Then, the resource allocation model is established to allocate investment. Finally, the optimal investment strategy is obtained for Goodgrant Foundation.
But in the analysis process, data processing may have tolerance, because the initial data have so many indexes and we have obtained part of indexes of every school. Because only the representative indexes are considered in this paper, some important indexes might be ignored; so some errors might appear in the result of data process- ing. And in model assumptions, the results will have a certain impact without considering some variables such as investment cycle. In the future, these factors in the improved model are investigated.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (71540028, F012408), and Major Research Project of Beijing Wuzi University. Beijing Key Laboratory (NO: BZ0211), Beijing Intelligent Logistics System Collaborative Innovation Center.
Cite this paper
Yulei Zhang,Shuai Zhang,Xinxin Zhang,Zhenping Li, (2016) The Optimal Investment Strategy Based on the DEA Model. Open Journal of Modelling and Simulation,04,46-54. doi: 10.4236/ojmsi.2016.42006
References
- 1. Zhang, J. and Guo, Y. (2004) A Comprehensive DEA Model Based on Advantages and Disadvantages Analysis. Journal of Southwest China Normal University (Natural Science Edition), 29, 358-360.
- 2. Li, X. and Zuo, L. (2004) High Education Optimal Investment Bilevel Programming Models on Strategy of Prior Development. Journal of Shandong University, 39, 35-46. (In Chinese)
- 3. Cai, X. (2011) Evaluation of an Investment Benefit of Higher Education Based on DEA Model. Academic Dissertation, Harbin Engineering University. (In Chinese)
- 4. Ma, Z. (2014) Analysis on Scientific and Technological Input-Output Efficiency of Inner Mongolian University Based on DEA Model. Academic Dissertation, Mongolian University, 93, 11-34. (In Chinese)
- 5. Gan, C. (2014) Study of Input-Output Efficiency Evaluation of Universities—As an Example to Graduate Universities. Academic Dissertation, Southwest Jiaotong University. (In Chinese)
- 6. Du, J. (2015) DEA for Non-Homogenous Parallel Networks. Omega, 56, 122-132. http://dx.doi.org/10.1016/j.omega.2014.10.001
- 7. Chang, T. (2015) Past-Present-Future Intertemporal DEA Models. Journal of the Operational Research Society, 66, 16-32. http://dx.doi.org/10.1057/jors.2013.139
- 8. Fuentes, R. (2015) Smoothed Bootstrap Malmquist Index Based on DEA Model to Compute Productivity of Tax Offices. Expert Systems with Applications, 42, 2442-2450. http://dx.doi.org/10.1016/j.eswa.2014.11.002
- 9. Merkert, R. and Assaf, A. (2015) Using DEA Models to Jointly Estimate Service Quality Perception and Profitability- Evidence from International Airports. Transportation Research Part A, 75, 42-50. http://dx.doi.org/10.1016/j.tra.2015.03.008
- 10. Li, K. and Lin, B. (2015) The Improvement Gap in Energy Intensity: Analysis of China’s Thirty Provincial Regions Using the Improvement DEA Model. Energy, 84, 589-599. http://dx.doi.org/10.1016/j.energy.2015.03.021
- 11. Adel, H. (2015) A Common-Weights DEA Model for Centralized Resource Reduction and Target Setting. Computer & Industrial Engineering, 79, 195-203. http://dx.doi.org/10.1016/j.cie.2014.10.024
- 12. Ghobadi, S. and Jahangiri, S. (2015) Inverse DEA: Review, Extension and Application. International Journal of Information Technology & Decision Making, 14, 805-824. http://dx.doi.org/10.1142/S0219622014500370
- 13. Wei, Q., Zhang, J. and Zhang, X. (2000) An Inverse DEA Model for Inputs/Outputs Estimate. European Journal of Operational Research, 121, 151-163. http://dx.doi.org/10.1016/S0377-2217(99)00007-7
- 14. Li, L. (2013) Study on DEA and Inverse DEA Model and Algorithm. http://www.doc88.com/p-9933788337530.html
Appendix
MATLAB Program
clear;
formatshortg
X = load('c:\x.txt');
Y = load('c:\y.txt');
n = size(X',1); m = size(X,1); s = size(Y,1);
A = [-X' Y'];
b = zeros (n, 1);
LB = zeros(m + s, 1); UB = [];
for i = 1:n;
f = [zeros (1, m) -Y(:,i)'];
Aeq = [X(:,i)' zeros(1,s)]; beq = 1;
w(:,i) = LINPROG(f, A, b, Aeq, beq, LB, UB);
E(i, i) = Y(:,i)'*w(m + 1:m + s,i);
end
Omega = w(1:m,:)
mu = w(m + 1:m + s,:)
NOTES
*Corresponding author.



