Received 7 May 2015; accepted 29 June 2015; published 2 July 2015

ABSTRACT

We consider a SIR epidemic model with saturated incidence rate and treatment. We show that if the basic reproduction number, R₀ is less than unity and the disease free equilibrium is locally asymptotically stable. Moreover, we show that if R₀ > 1, the endemic equilibrium is locally asymptotically stable. In the end, we give some numerical results to compare our model with existing model and to show the effect of the treatment term on the model.

Keywords:

SIR Epidemic Model, Basic Reproduction Number, Local Stability, Treatment, Saturated Incidence Rate

1. Introduction

While mathematical modeling of infectious diseases could be traced back to 1760 when Bernoulli used mathematical models for small pox [1] , the research in infectious diseases, using deterministic mathematical models actually began in 20^th century.

Bilinear and standard incidence rates have been frequently used in classical epidemic models [2] . Several different incidence rates have been proposed by researchers. After a study of the cholera epidemic spread in Bari in 1973, Capasso and Serio [3] introduced a saturated incidence rate g(I)S into epidemic models. Ruan and Wang

[4] studied an epidemic model with specific nonlinear incidence rate of the form where l and h were

positive constants and obtained lots of interesting dynamical behaviour of the model such as a limit cycle, two limit cycles and homoclimic loop etc. In 2000, van den Driessche and Watmough [5] studied an SIS epidemic

model with the incidence rate of the form 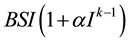where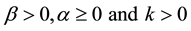. Xiao and Ruan [6] considered a special nonlinear incident rate of the form 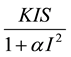where g(I) is non-monotone.

Jasmine and Amirtharaj [7] on account of the effect of limited treatment resources on the control of epidemic disease incorporated a modified SIR epidemic model with generalized incidence rate. They discussed the stability analysis of the disease-free equilibrium and endemic equilibrium with a nonlinear incidence rate. Chauhan et al. [8] discussed the stability analysis pf SIR epidemic model with and without vaccination. They discussed the local and global stability of the model through the basis reproduction number

In a recent paper, Kaddar [9] considered a delayed SIR epidemic model with a saturated incidence rate of the form 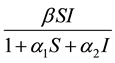and Pathak et al. [10] also considered the transmission rate 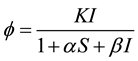which dis-

played a saturation effect accounting for the fact that the number of contacts in individual reaches some maximal value done to spatial or social distribution of the population.

In this paper, we extend the work of Pathak et al., by considering a transmission rate where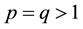. We also look at the effect of the transmission rate on the SIR epidemic model and we include the treatment term 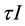where.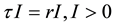

2. The Basic Mathematical Model

We modify the model of Pathak et al., by extending the transmission rate to nonlinear orders and also include the treatment term.

Pathak et al. Model

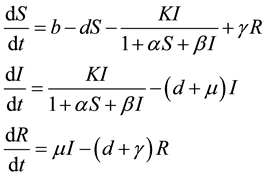(1)

Modified Model

The modified model is as follows:

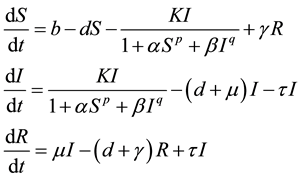(2)

where the transmission rate 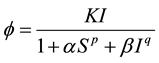and.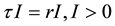

where 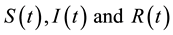represent the number of susceptible, infective and recovered individuals at time t, respectively, b is the recruitment rate of the population, d is the natural death rate of the population, k is the proportionality constant, 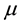is the natural recovery rate of the infective individuals, is the rate at which recovered individuals lose immunity and return to the susceptible class, are the parameters which measure the effects of sociological, psychological or other mechanisms and p and q are positive constants which are greater than unity.

3. Steady State and Local Stability of the Critical Points

In this section, we discuss the local stability of the disease-free equilibrium and endemic equilibrium of system (2).

The system (2) has a disease free of. Further, system (2) admits a unique endemic equilibrium

Proposition 1: If R₀ < 1, then the disease free equilibrium E₀ is locally asymptotically stable.

Proof:

(3)

Obviously, (3) has three roots,.

Let

Hence, if R₀ < 1, then the disease free equilibrium point E₀ is locally asymptotically stable.

Proposition 2: as for

Proof:

i.e.

Hence, , as

4. Stability Analysis of the Endemic Equilibrium

Let the endemic equilibrium where each component corresponds an earlier value.

Let

Then,

Then

where

by solving, the characteristic equation is

where

A straight forward calculation yields Then, it follows from Routh-Hurwitz criteria that all characteristics roots have negative real parts. Thus, the endemic equilibrium is locally asymptotically stable.

5. Numerical Simulations

To see the dynamical behavior of system (2), we solve the system by Runge-Kutta Felhberg 45(RKF 45) method using the parameters;, , , q = 2, b = 3.1, d = 2.29, k = 9, and with different values for the treatment term

a) In Figure 1, r = 0.1.

b) In Figure 2, r = 0.4.

c) In Figure 3, r = 0.7.

6. Conclusion

In this paper, we have carried out the stability of the equilibrium states using some of the tested parameters from literature reviewed in this paper. The simulation is carried out using numerical software called “maple”. The effect of the treatment term in the model has been investigated and it shows that treatment has a positive effect on the endemic nature of the disease. The more the treatment is applied, the faster the disease fades out.

References

NOTES

^*Corresponding author.