International Journal of Geosciences
Vol.07 No.07(2016), Article ID:68607,13 pages
10.4236/ijg.2016.77068
Occam Inversion of Transient Electromagnetic Data in a Layered Medium with Azimuthal Anisotropy
Wangwang Wang1, Changhong Lin1, Handong Tan1, Honglei Liu2
1School of Geophysics and Information Technology, China University of Geosciences, Beijing, China
2SINOPEC Petroleum Exploration and Production Research Institute, Beijing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 June 2016; accepted 16 July 2016; published 19 July 2016
ABSTRACT
In recent years, the anisotropic study has become a hot topic in the field of electromagnetics. Currently, inversion technologies of transient electromagnetic sounding data are mainly based on the case of an isotropic medium. However, the actual underground electrical structure tends to be complicated and anisotropic. It is often found that the isotropic inversion technologies do not lead to good results for field transient electromagnetic sounding data. We have developed an algorithm for calculating the transient electromagnetic response in a layered medium with azimuthal anisotropy. An occam inversion algorithm has also been implemented to invert the transient electromagnetic data induced by a grounded horizontal electric dipole in a layered medium with azimuthal anisotropy. Synthetic examples demonstrate the stability and validity of the inversion algorithm. Experimental results show different data for inverting have great influence on the inversion results.
Keywords:
Azimuthal Anisotropy, Layered Medium, Occam Inversion, Horizontalelectric Dipole, Transient Electromagnetic Data

1. Introduction
Electrical anisotropy in the Earth has recently gained attention as a significant linking factor between electrical models and underlying structural and tectonic patterns. This factor has motivated more and more studies into the anisotropic electrical structures. For the direct current resistivity method, Herwanger and Pain (2004) proposed the anisotropic resistivity tomography inversion technique [1] . Zhou and Greenhalgh (2009) used a new Gaussian quadrature grids scheme to achieve the two and a half dimensional (2.5D)/three dimensional (3D) resistivity- modelling in anisotropic media [2] . Later, a rapid finite element resistivity modelling algorithm for 3D arbitrary anisotropic structures was presented [3] . More recently, Wang et al. (2013) developed a 3D direct current ani- sotropic resistivity modelling method using a finite-element method [4] .
Compared with the direct current method, the anisotropy in the magnetotelluric method has been more widely researched. Abramovici and Shoham (1977) considered the generalized matrix inversion to invert the one dimensional (1D) anisotropic magnetotelluric data [5] . Osella and Martinelli (1993) have introduced a modified Rayleigh modelling technique to calculate the magnetotelluric response in two dimensional (2D) anisotropic structures [6] . Later, a finite-difference solution was presented to calculate the magnetotelluric response of 2D anisotropic media [7] . Li (2002) developed a finite-element algorithm to model the magnetotelluric field in 2D anisotropic conductivity structures [8] . Four years later, a magnetotelluric inversion technique for anisotropic conductivities in layered media also was implemented [9] . Recently, Qin and Yang (2012) studied a 1D anisotropic magnetotelluric inversion method to invert the whole tensor impedance data [10] . More recently, an artificial neural networks method was applied to magnetotelluric inversion for azimuthally anisotropic medium [11] . Huo et al. (2015) have analysed the example of magnetotelluric modeling for 2D anisotropic conductivity structure with topography [12] .
In the controlled-source electromagnetic method, Li and Pedersen (1991 and 1992) computed electromagnetic fields induced by grounded electric diploes in a half-space or layered medium with azimuthal anisotropy [13] [14] . The inversion of controlled-source tensor magnetotelluric data in a layered earth with azimuthal anisotropy has also been presented [15] . One year later, Yin and Maurer (2001) calculated the electromagnetic induction in a layered earth with arbitrary anisotropy [16] . Li and Dai (2011) proposed a finite element technology to model the marine controlled-source electromagnetic responses in 2D dipping anisotropic conductivity structures [17] . An adaptive finite element method for modelling the marine controlled-source electromagnetic fields in 2D general anisotropic medium has also been implemented [18] . Recently, Cai and Xiong (2014) have presented a linear edge-based finite element method for numerical modeling of 3D controlled-source electromagnetic data in an anisotropic conductive medium [19] . More recently, a 3D marine controlled-source electromagnetic method for arbitrarily anisotropic media has been presented [20] .
After a period of rapid development, the transient electromagnetic method, with its high detection and resolution, has become a widely used exploration method. However, most of the current data processing is based on the isotropic technique. Compared with the isotropic investigation of the transient electromagnetic method, the investigation of anisotropy is less robust. Yu and Evans (1997) presented an algorithm to calculate the transient electromagnetic responses generated by an electric dipole source over a triaxially anisotropic seafloor [21] . Collins and Everett (2006) detected the near-surface horizontal anisotropy in a weathered metamorphic schist using transient electromagnetic induction [22] . Dennis and Cull (2012) used the transient electromagnetic method to survey the near-surface electrical anisotropy characters [23] .
Occam inversion method is a widely used method for electromagnetic inversion [24] . The advantage of the occam inversion is the data fitting can achieve a prescribed tolerance, meanwhile, the model of inversion is smooth enough. Based on the occam inversion method, we have developed a transient electromagnetic inversion algorithm in a layered medium with azimuthal anisotropy. The outline of the paper is as follows. First, we describe the forward problem in 1D azimuthal anisotropic conductivity structures. Next, we validate the accuracy and validity of the transient electromagnetic modelling code. We then introduce the verification of the inversion program. Finally, different inversion results from inverting different synthetic data will be analyzed.
2. Forward Method Theory
2.1. Forward Theory
Consideran M-layer model with azimuthal anisotropy. The model is shown in Figure 1. An x-directed horizon- tal electric dipole source is located at the origin of the coordinate system. The electric conductivity tensor of the mth layer can be defined as:
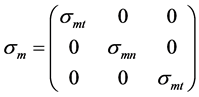 (1)
(1)
Figure 1. The m-layer azimuthal anisotropic model.
where σmt is the x-directed conductivity in the mth layer. σmn is the y-directed conductivity in the mth layer. Both the x-directed conductivity and z-directed conductivity are consistent in the azimuthal anisotropic medium. hm is the thickness of the mth layer. The base is a half-space. A useful parameter is the anisotropy coefficient: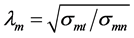 .
.
To obtain the transient electromagnetic responses at the surface, we need to know the electromagnetic field in the frequency domain. Assuming a time variation e−iωt, the governing equations in the quasi-stationary approximation can be written as:
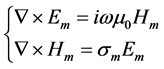 (2)
(2)
where σm is the electric conductivity tensor, ω is the angular frequency, μ0 is the magnetic permeability of free space. Introducing a vector potential A and a scalar potential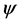 . There is relation in the mth layer as follows:
. There is relation in the mth layer as follows:
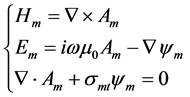 (3)
(3)
The differential equations for vector potential components can be shown as:
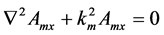 (4)
(4)
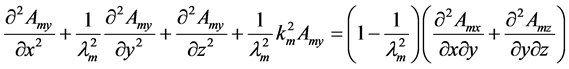 (5)
(5)
 (6)
(6)
where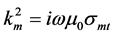 ; and Amx, Amy and Amz represent the components of the three directions, respectively.
; and Amx, Amy and Amz represent the components of the three directions, respectively.
According to the continuity of the tangential electric and magnetic fields, the boundary conditions for vector potential components in the wavenumber domain satisfy:
 (7)
(7)
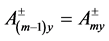 (8)
(8)
 (9)
(9)
 (10)
(10)
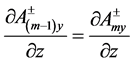 (11)
(11)

Then, after substantial derivations, the ground electric and magnetic response in the wavenumber domain can be expressed as follows:





where “+” and “−” refer to downward and upward traveling waves, respectively. The above detailed derivation is based on previous work by Li and Pedersen (1992).
Using a 2D Fourier transform, the components of the responses can be transformed from the wave number domain to the space domain.
Then, with the help of the inverse Fourier transform, we determine the transient electromagnetic responses in a layered medium with azimuthal anisotropy. Using the x-directed horizontal electric field as an example, we introduce the derivation process of the transient electromagnetic response. The derivation of the other responses follows the same process.
As we know, the following relationship exists between the response of frequency domain and the transient electromagnetic response

Basing on the Euler’s formula, Equation (18) will become the follows:

where ω is the angular frequency and t is the time point. Considering the general form, the x-directed horizontal electric field can be divided into two parts for calculation:

Using the digital filter algorithm of the sine and cosine transform [25] , we can continue doing the derivation. For the Hankel transform formula

With the digital filtering algorithm, the expression can be transformed into

where Jv is v order of the first kind Bessel function. Δ is defined as the sampling interval, and 
According to the relationship between the Bessel function and the trigonometric function:

Expression (20) can be written as


According the digital filtering algorithm, expression (24) and expression (25) can transform into the following formulae:


where




sine and cosine filter coefficient, respectively. Based on the above derivation, we can obtain the transient electromagnetic horizontal x-directed electric field. The derivation process for other responses is similar.
2.2. Validation of the Forward Code
It is important to demonstrate that the results of a numerical method are reliable. In order to demonstrate the accuracy of the forward code. We designed a two-layer model that the conductivity of the first layer is 0.01 s/m and the conductivity of the second layer is 0.05 s/m. The thicknesses were identified as 100 m and half-spaces. The observation point was placed at (500, 500) m.
We calculate the numerical results and the corresponding analytic results [26] , respectively. Using ex, hy, and hz as examples, we took 101 time sampling points at equal logarithm intervals. The comparison result of the numerical solution and the analytic solution is shown in Figure 2, the range of data fitting error is less than 2.23%, and it is considered to be an acceptable degree.
The forward verification results indicate that the forward program is accurate to an acceptable degree.
3. Inversion Method Theory
3.1. The Objective Function
Using the occam inversion method, we have presented the transient electromagnetic inversion algorithm in a layered medium with azimuthal anisotropy. The core though of the occam inversion is to fit the data to a prescribed tolerance, mean while, the model of inversion should be smooth as possible. The objective function of 1D azimuthal anisotropy inversion of transient electromagnetic measurement is defined as:

where 
vative with respect to depth, μ is Lagrange multiplier, d is a vector for the observed transient electromagnetic response, F(m) is the forward operator to calculate the response, and W is the diagonal matrix which represents the data weights assigned according to the standard deviation of the data noise. 

Figure 2. Forwarding modeling results from the numerical and analytic results.
3.2. The Calculation of the Sensitivity Matrix
The series expansion of the transient electromagnetic forward response F(m) can be expressed as follows:

where ε is a vector whose magnitude is



3.3. The Inversion Process
The general process for the occam inversion of the transient electromagnetic method in a layered medium with azimuthal anisotropy can be described as follows:
(1) The electromagnetic responses are calculated using a forward modeling code for a given initial model
(2) Calculate the data misfit, the sensitivity matrix and the roughness for the given current model.
(3) Compare the data misfit of the current model with desired data misfit
(4) Take the objective function’s gradient into zero to update the model and use a 1D line search way to choose the appropriate μ to minimize the data misfit. The value of μ is between 1 and 105.
(5) Compare the data misfit of the new model with the data misfit of the previous model. If the data misfit does not decrease, save the previous model, decrease the step length by half and update the sensitivity matrix, return to step (4) to update the model, then continue at the beginning of step (5). If the data misfit of the new model is smaller than the data misfit of the previous model, consider whether the data misfit achieves the expected value or not. If yes, compare the roughness of the current model with the roughness of the previous model. When the roughness decreases, choose the model with maximum μ, save it, and exit the program. Otherwise decrease the step length by half and update the sensitivity matrix, and return to step (4) to update the model. If the data misfit does not achieve the expectation, choose and save the model with minimum X2 and return to step (4) to execute the program.
4. Inversion Examples with Synthetic Data
In order to obtain synthetic transient electromagnetic data, we design some 1D azimuthal anisotropic synthetic geologic models to test. The x-directed horizontal electric dipole sources were located at the coordinate origin, and the corresponding responses were calculated by using the above-mentioned forward modeling program. One percent of Gaussian random noise was added to the data. For the anisotropy inversion of synthetic data, we chose a twenty-layer isotropic model where the conductivity is 0.01 s/m and the thickness is 25 m for every layer as the initial model.
4.1. Model 1
Our first test employs a simple two-layer model. The parameters of the model are given in Table 1. To prove the azimuthal anisotropy inversion algorithm is more reliable than the isotropic inversion algorithm in inverting the data with anisotropic medium, synthetic data (ex, ey, hx, hy) were used in the isotropic inversion algorithm and the azimuthal anisotropic inversion algorithm, respectively. The observation point was placed at (500, 500) m.
The comparison between the isotropic inversion and azimuthal anisotropy inversion results is shown in Figure 3. The resistivity inversion results and the anisotropy coefficient from the azimuthal anisotropy inversion algorithm are very close to the theoretical model. However, the inversion results from the isotropic inversion algorithm are not satisfied. The data root mean squared (RMS) misfit changed from an initial value of 67.47 to a final one of 0.94 for the azimuthal anisotropy inversion algorithm. However, the data RMS misfit changed from an initial value of 67.47 to a final one of 27.69 for the isotropic inversion algorithm.
Figure 3. The comparison between the isotropic inversion and azimuthal anisotropy inversion results. The previous plot is the comparison of resistivity results, and the latter plot is the comparison of the anisotropy coefficient results.
Table 1. Parameters of model 1.
The test result proves that the proposed azimuthal anisotropy inversion algorithm is reliable and the isotropic inversion algorithm cannot deal with an azimuthal anisotropic medium well.
4.2. Model 2
To demonstrate the azimuthal anisotropy inversion algorithm can also be used in the inversion of isotropic medium, the next experiment used a two-layer isotropic model. The parameters of the model are given in Table 2. Synthetic data (ex, ey, hx, hy) were used in the azimuthal anisotropic inversion algorithm. The observation point was placed at (500, 500) m.
The inversion result from the azimuthal anisotropy inversion algorithm is shown in Figure 4. Clearly, the resistivity inversion result is very close to the theoretical model. Meanwhile, the anisotropy coefficient is close to one, which means that there is no anisotropic property. The data RMSm is fit changed from an initial value of 60.35 to a final one of 3.29. The data fitting result is shown in Figure 5.
The test proves that the proposed azimuthal anisotropy inversion algorithm can also invert synthetic data generated from isotropic media well.
4.3. Model 3
In order to verify the azimuthal anisotropy inversion algorithm is applicable to different receiving points, we design a three-layer anisotropic model. The parameters of the model are given in Table 3. The Model 3’s observation points are placed at (500, 500) m and (1500, 1500) m, respectively.
The different inversion results for different receiver points are shown in Figure 6. Obviously, the inversion parameter result is very close to the theoretical model for different receiver points. The RMS misfit for observation point (500, 500) m changed from an initial value of 163.83 to a final one of 0.91. Meanwhile, the RMS misfit for observation point (1500, 1500) m changed from an initial 145.01 to a final 0.99.
The test illustrates that the proposed azimuthal anisotropy inversion algorithm can achieve satisfactory results for different observation points.
5. Experimental Results and Discussions
When we use different constraining data in the inversion program, we get different inversion results. To compare
Figure 4. The inversion result of the azimuthal anisotropy algorithm for the isotropic layered medium. The previous plot is the resistivity inversion result, and the latter plot is the inversion result of the anisotropy coefficient.


Figure 5. Data fitting results from the synthetic data and the inversion data: (a) x-directed horizontal electric field data fitting result; (b) y-directed horizontal electric field data fitting result; (c) x-directed horizontal magnetic field data fitting result; (d) y-directed horizontal magnetic field data fitting result.
Table 2. Parameters of model 2.
Table 3. Parameters of model 3.
the inversion results with different synthetic data, the transient electromagnetic azimuthal anisotropy inversion algorithm were carried out in the following eight scenarios: 1) inverting only ex; 2) inverting only ey; 3) inverting only hx; 4) inverting only hy; 5) inverting only hz; 6) inverting two elements, ex and hy; 7) inverting four elements, ex, ey, hx, and hy; 8) inverting five elements, ex, ey, hx, hy, and hz.
We designed a two-layer model with the observation point placed at (500, 500) m and a three-layer model with the observation point placed at (1500, 1500) m. The parameters of the two models are given in Table 4 and Table 5, respectively.
We compared the different inversion results for the different synthetic data for the two-layer model (shown in Figure 7). The following conclusions can be drawn:
a) When only inverting the horizontal electric field which is parallel to the source, we can get better inversion results than inverting any of the other single response.
b) When the more synthetic data are used in the inversion, the better inversion results we can achieve.
The comparison of different inversion results from different synthetic data for the three-layer model are shown in Figure 8. According to the experimental results, we can get the same conclusions as the former two- layer model test.
6. Conclusions
We have developed an algorithm for calculating the transient electromagnetic response in a layered medium with azimuthal anisotropy. The validation results of the forward code have demonstrated its validity.
Figure 6. The comparison of the anisotropic inversion result for different observation points. The previous plot is the resistivity inversion results, and the latter plot is the inversion results for the anisotropy coefficient.
Figure 7. The comparison of different inversion results from the different synthetic data at the observation point (500, 500) m. The previous plot is the inversion result comparison of resistivity, and the latter plot is the inversion result comparison of the anisotropy coefficient.
Figure 8. The comparison of different inversion results from the different synthetic data for the observation point (1500, 1500) m. The previous plot is the inversion result comparison of resistivity, and the latter plot is the inversion result comparison of the anisotropy coefficient.
Table 4. Parameters of the two-layer model.
Table 5. Parameters of the three-layer model.
Based on the occam inversion,we have presented a1D azimuthal anisotropic inversion algorithm for inverting transient electromagnetic data. Inversion examples for the synthetic data show the stability and validity of the inversion algorithm.
On the other hand, we have found different data for inverting have great influence on the inversion results by the experiment. The comparison of different inversion results show that inverting horizontal electric field which is parallel to the source can get a better inversion result than inverting any other single response. With the increase of the synthetic data, the inversion result will be closer to the target geology.
Considering the above research, we suggest that the field transient electromagnetic sounding data collect horizontal electric field data which is parallel to the source. If allowed, we should collect the field transient elec- tromagnetic sounding data with multi-components.
Acknowledgements
This study was jointly supported by the National Natural Science Foundation of China (Nos. 41004028, 41374078), the Special Fund for Basic Scientific Research of Central Colleges, Beijing Higher Education Young Elite Teacher Project and Program of Geological Survey (Nos. 12120113100800).
Cite this paper
Wangwang Wang,Changhong Lin,Handong Tan,Honglei Liu, (2016) Occam Inversion of Transient Electromagnetic Data in a Layered Medium with Azimuthal Anisotropy. International Journal of Geosciences,07,915-927. doi: 10.4236/ijg.2016.77068
References
- 1. Herwanger, J.V., Pain, C.C. and Binley, A. (2004) Anisotropic Resistivity Tomography. Geophysical Journal International, 158, 409-425.
http://dx.doi.org/10.1111/j.1365-246X.2004.02314.x - 2. Zhou, B., Greenhalgh, M. and Greenhalgh, S.A. (2009) 2.5-D/3-D Resistivity Modelling in Anisotropic Media Using Gaussian Quadrature Grids. Geophysical Journal International, 176, 63-80.
http://dx.doi.org/10.1111/j.1365-246X.2008.03950.x - 3. Wang, W. and Wu, X.P. (2010) Rapid Finite Element Resistivity Forward Modeling for 3D Arloitrary Anisotropic Structures. Progress in Geophysiscs, 25, 1365-1371.
- 4. Wang, W., Wu, X.P. and Spitzer, K. (2013) Three-Dimensional DC Anisotropic Resistivity Modelling Using Finite Elements on Unstructured Grids. Geophysical Journal International, 193, 734-746.
http://dx.doi.org/10.1093/gji/ggs124 - 5. Abramovici, F. and Shoham, Y. (1977) Inversion of Anisotropic Magnetotelluric Data. Geophysical Journal of the Royal Astronomical Society, 50, 55-74.
http://dx.doi.org/10.1111/j.1365-246X.1977.tb01324.x - 6. Osella, A.M. and Martinelli, P. (1993) Magnetotelluric Response of Anisotropic 2D Structures. Geophysical Journal International, 115, 819-828.
http://dx.doi.org/10.1111/j.1365-246X.1993.tb01494.x - 7. Pek, J. and Verner, T. (1997) Finite-Difference Modelling of Magnetotelluric Fields in Two-Dimensional Anisotropic Media. Geophysical Journal International, 128, 505-521. http://dx.doi.org/10.1111/j.1365-246X.1997.tb05314.x
- 8. Li, Y.G. (2002) A Finite-Element Algorithm for Electromagnetic Induction in Two-Dimensional Anisotropic Conductivity Structures. Geophysical Journal International, 148, 389-401.
http://dx.doi.org/10.1046/j.1365-246x.2002.01570.x - 9. Pek, J. and. Santos, F.A.M. (2006) Magnetotelluric Inversion for Anisotropic Conductivities in Layered Media. Physics of the Earth and Planetary Interior, 158, 139-158.
http://dx.doi.org/10.1016/j.pepi.2006.03.023 - 10. Qin, L.J., Yang, C.F. and Sun, C.C. (2012) A Magnetotelluric Inversion Method of the Whole Tensor Impedance Response to One-Dimensional Anisotropic Structure. Chinese Journal of Geophysics, 55, 693-701. (In Chinese)
- 11. Montahaei, M. and Oskooi, B. (2014) Magnetotelluric Inversion for Azimuthally Anisotropic Resistivities Employing Artificial Neural Networks. Acta Geophysica, 62, 12-43.
http://dx.doi.org/10.2478/s11600-013-0164-7 - 12. Huo, G.P., Hu, X.Y. and Huang, Y.F. (2015) MT Modeling for Two-Dimensional Anisotropic Conductivity Structure with Topography and Examples of Comparative Analyses. Chinese Journal of Geophysics, 58, 4696-4708. (In Chinese)
- 13. Li, X.B. and Pedersen, L.B. (1991) The Electromagnetic Response of an Azimuthally Anisotropic Half-Space. Geophysics, 56, 1462-1473.
http://dx.doi.org/10.1190/1.1443166 - 14. Li, X.B. and Pedersen, L.B. (1992) Controlled-Source Tensor Magnetotelluric Responses of a Layered Earth with Azimuthal Anisotropy. Geophysical Journal International, 111, 91-103.
http://dx.doi.org/10.1111/j.1365-246x.1992.tb00557.x - 15. Li, X.B., Oskooi, B. and Pedersen, L.B. (2000) Inversion of Controlled-Source Tensor Magnetotelluric Data for a Layered Earth with Azimuthal Anisotropy. Geophysics, 65, 452-464.
http://dx.doi.org/10.1190/1.1444739 - 16. Yin, C. and Maurer, H.M. (2001) Electromagnetic Induction in a Layered Earth with Arbitrary Anisotropy. Geophysics, 66, 1405-1416.
http://dx.doi.org/10.1190/1.1487086 - 17. Li, Y.G. and Dai, S.K. (2011) Finite Element Modelling of Marine Controlled-Source Electromagnetic Responses in Two-Dimensional Dipping Anisotropic Conductivity Structures. Geophysical Journal International, 185, 622-636.
http://dx.doi.org/10.1111/j.1365-246X.2011.04974.x - 18. Li, Y.G., Luo, M. and Pei, J.X. (2013) Adaptive Finite Element Modeling of Marine Controlled-Source Electromagnetic Fields in Two-Dimensional General Anisotropic Media. Journal of Ocean University of China, 12, 1-5.
http://dx.doi.org/10.1007/s11802-013-2110-3 - 19. Cai, H.Z., Xiong, B. and Han, M. (2014) 3D Controlled-Source Electromagnetic Modeling in Anisotropic Medium Using Edge-Based Finite Element Method. Computers & Geosciences, 73, 164-176.
http://dx.doi.org/10.1016/j.cageo.2014.09.008 - 20. Yin, C.C., Ben, F. and Liu, Y.H. (2014) MSCEM 3D Modeling for Arbitrarily Anisotropic Media. Chinese Journal of Geophysics, 57, 4110-4112. (In Chinese)
- 21. Yu, L., Evans, R.L. and Edwards, R.N. (1997) Transient Electromagnetic Responses in Seafloor with Triaxial Anisotropy. Geophysical Journal International, 129, 292-304.
http://dx.doi.org/10.1111/j.1365-246X.1997.tb01582.x - 22. Collins, J.L., Everett, M.E. and Johnson, B. (2006) Detection of Near-Surface Horizontal Anisotropy in a Weathered Metamorphic Schist at Llano Uplift (Texas) by Transient Electromagnetic Induction. Physics of the Earth and Planetary Interiors, 158, 159-173.
http://dx.doi.org/10.1016/j.pepi.2006.05.008 - 23. Dennis, Z.R. and Cull, J.P. (2012) Transient Electromagnetic Surveys for the Measurement of Near-Surface Electrical Anisotropy. Journal of Applied Geophysics, 76, 64-73.
http://dx.doi.org/10.1016/j.jappgeo.2011.10.014 - 24. Steven, C.C., Robert, L.P. and Catherine, G.C. (1987) Occam’s Inversion: A Practical Algorithm for Generating Smooth Models from Electromagnetic Sounding Data. Geophysics, 52, 289-300.
http://dx.doi.org/10.1190/1.1442303 - 25. Wang, H.J. (2004) Digital Filter Algorithm of the Sine and Cosine Transform. Chinese Journal of Engineering Geophysics, 1, 329-335.
- 26. Gong, Q., Hu, X.Y. and Meng, Y.L. (2008) Linear Dimension forward Solution of CSAMT by Hankel Transformation Method. Coal Geology & Exploration, 36, 71-73.










