International Journal of Geosciences
Vol.4 No.10A(2013), Article ID:41565,13 pages DOI:10.4236/ijg.2013.410A005
New Computerized Method for the Geochemical Classification of Precambrian Carbonate Rocks: Case of a Set of African Cap Carbonates
1Aix-Marseille Université, CNRS, IRD, CEREGE UM 34, Aix en Provence, France
2Université d’Avignon et des pays du Vaucluse, INRA, EMMAH, UMR 1114, LHA, Avignon, France
3Département de Géologie, Faculté des Sciences et Techniques, Université Marien Ngouabi de Brazzaville, Brazzaville, République du Congo
4Département de Géologie, Université des Sciences et Techniques de Masuku, Franceville, Gabon
Email: *miche@cerege.fr
Copyright © 2013 Hélène Miche et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Hélène Miche et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received September 20, 2013; revised October 23, 2013; accepted November 21, 2013
Keywords: Carbonate Rock; Cap Carbonate; Ternary Diagram; Software; Calcite; Dolomite
ABSTRACT
Post-sedimentary transformations have masked or completely obliterated the structures and textures of Precambrian carbonate rocks. Therefore, methods of classification of the carbonate rocks founded on the observation of primary structures or textural characteristics are ill-adapted. Consequently, only certain geochemical classification methods allow us to distinguish the various rock-types in the case of Neoproterozoic carbonates. After presenting the most suitable geochemical classifications, we propose a new classification into 14 groups based on a regular ternary diagram with computerized data input. For each sample of carbonate rock, analysis of calcium and magnesium contents allows us to calculate the input data for our diagram i.e. the percentages of Calcite, Dolomite and Insoluble Residue. To automate the application of this diagram, input parameters are created in a descriptive file “Roches.ternaires.txt” using an option called “Ternaires” in the “Diagrammes” software developed by Roland Simler. Thirty cap carbonates of Africa are used to validate this new method.
1. Concerning the Classification of Precambrian Carbonate Rocks
Among the rocks of sedimentary origin, carbonate rocks represent a very important and varied group that typically has a mineralogical composition primarily made up of carbonates. Indeed, the two main components of carbonate rocks are calcite (CaCO3) and dolomite
[CaMg(CO3)2], which are also the most widespread carbonate minerals. Based solely on the variation of the relative proportions of these two carbonate minerals and the insoluble residue [assumed to be made up of chert], it is possible to define more than fifteen carbonate rock types (Figure 1(b)). In such a series of rocks, the two most important end-members are represented by limestone and dolomite, which are themselves made up of at least 90% calcite or dolomite, respectively. It is easy to recognize a limestone by its reaction producing effervescence in contact with cold 10% HCl, whereas dolomite only reacts with hot HCl at this dilution. On the other hand, it is practically impossible to identify the intermediate types of carbonate rock without using generally complex criteria of classification.
The most currently-used classifications of the carbonate rocks are generally based on their textural or petrographic characteristics, which are closely dependent on the origin of the primary sediments, their depositional environment, and partly on their diagenetic evolution [1- 5].
Thus, the definition of numerous carbonate rock-types (such as mudstone, wackestone, packstone, grainstoneboudstone, cemenstone…) depends on the nature of the grains or the allochem constituents (peloids, ooids, bioclasts, extraclasts and intraclasts), the relative abundance of the matrix coating certain visible grains, the primary texture of the sediments or the biogenic constructions forming certain carbonate rocks, or even the diagenetic transformations leading to the lithification of materials or primary sediments. In practice, these textural or petrographic classifications can only be applied to Phanerozoic carbonate rocks where primary structures are still recognizable. In the case of very ancient carbonate rocks, post-sedimentary transformations (such as induration, compaction, cementation, recrystallization, dissolution, epigenisation, metasomatism, etc.) are very pervasive and have already masked or obliterated most of the sedimentary structures. This applies to most Precambrian carbonate rocks (>540 Ma), particularly the Neoproterozoic cap carbonates making up the reference series studied here (Table 1). Only geochemical classifications allow us to identify the various types represented by such ancient carbonate rocks.
Geochemical classifications based on the Ca and Mg ratios [6,7] of the carbonate rocks could not be applied to our reference samples. Indeed, such an approach does not take into account the uncarbonated portion and depends on limits that are partially determined by the origin of the rocks. For example, Ca/Mg < 3.5 would imply a chemical precipitation of calcite or almost complete dolomitezation, whereas Ca/Mg > 105 would indicate either a chemical precipitation of calcite or dedolomitisation.
On the other hand, the geochemical classifications most commonly used for such ancient carbonate rocks are based on the weight percentages of carbonate minerals in these rocks and on the relative abundance of calcite and dolomite [8-10] in the total carbonate fraction (i.e. sum of these two carbonate minerals). These weight percentages and relative abundances of carbonate minerals are obtained by recalculation of the Ca and Mg contents determined in the laboratory, by chemical analysis of each sample of the carbonate rocks concerned. Such an approach allows a relatively precise characterization of the various types of carbonate rocks (Figure 1).
This same geochemical approach led [11] to propose a precise graphic classification of about fifteen carbonate rock-types intermediate between limestone and dolomite, these latter representing the end-member facies of carbonate rock series. More precisely, the proposed diagram makes it possible to specify, for a given sample of carbonate rock of known Ca and Mg contents, the percentage of dolomite in the total carbonate fraction, the percentage of dolomite in the sample considered and the percentage of insoluble residue (quartz, feldspar, clays...).
Given that MgCO3 accounts for only 2% to 3% of the solid solution in the calcite of Paleozoic carbonate rocks, whereas it makes up nearly 15% in more recent rocks [9, 12], [11] propose that MgCO3 is only found as dolomite in Precambrian carbonate rocks. This amounts to assuming that the geochemical classification of [11] integrates all the processes of transformation related to the lithification of primary carbonate sediments and materials, and can be regarded as a very interesting approach to be developed.
After presenting the geochemical classification of Precambrian carbonate rocks proposed by [11] in Section 2, we develop the construction of our classification in Section 3. For this, we detail the data-processing parameters of the created software option and calculations to obtain the input data of our new representation. Then, in the same section, we validate the application of our ternary diagram. Finally, in Section 4, we compare the petrographic classifications and the two geochemical approaches. Then, we present the advantages of our automatic geochemical classification of the carbonate rocks.
2. Development of Martinet and Sougy’s Classification
The geochemical classification scheme of [11] is based on the contents of CaO and MgO in the whole rock, expressed as the weight percentage compositions of calcium and magnesium (i.e. Ca (wt%) and Mg (wt%)). In the present study, the chemical method of determination initially suggested by [13] is modified according to our new approach, which is described below.
2.1. Determination of Ca (wt%) and Mg (wt%)
All of the carbonate rocks sampled in the field undergo a preparatory treatment including several stages before being submitted to geochemical analysis. Indeed, each sample of carbonate rock is cleaned and cut up into several small pieces with a saw. These pieces of solid rock are dried and crushed in a jaw crusher before being ground to approximately 50 μm in a jar mill with stainless steel balls.
To determine the Ca (%) and Mg (%) contents of each powdered carbonate rock, the samples are digested in ultrapure nitric acid (SCP-Science), using bi-distilled water to make up aliquots for analysis, and two certified standard materials (Calcite n 701-1 and Dolomite n 702-1 from IRSID-France) are used to check the accuracy of the analytical results.
In practice, a homogeneous subsample of the powdered carbonate rock is ground manually in an agate mortar to obtain a very fine powder (<20 µm).
A 200 mg portion of this powder is weighed in a porcelain crucible, which is then placed in a drying oven and kept at 110˚C for 30 minutes [14]. After drying, the
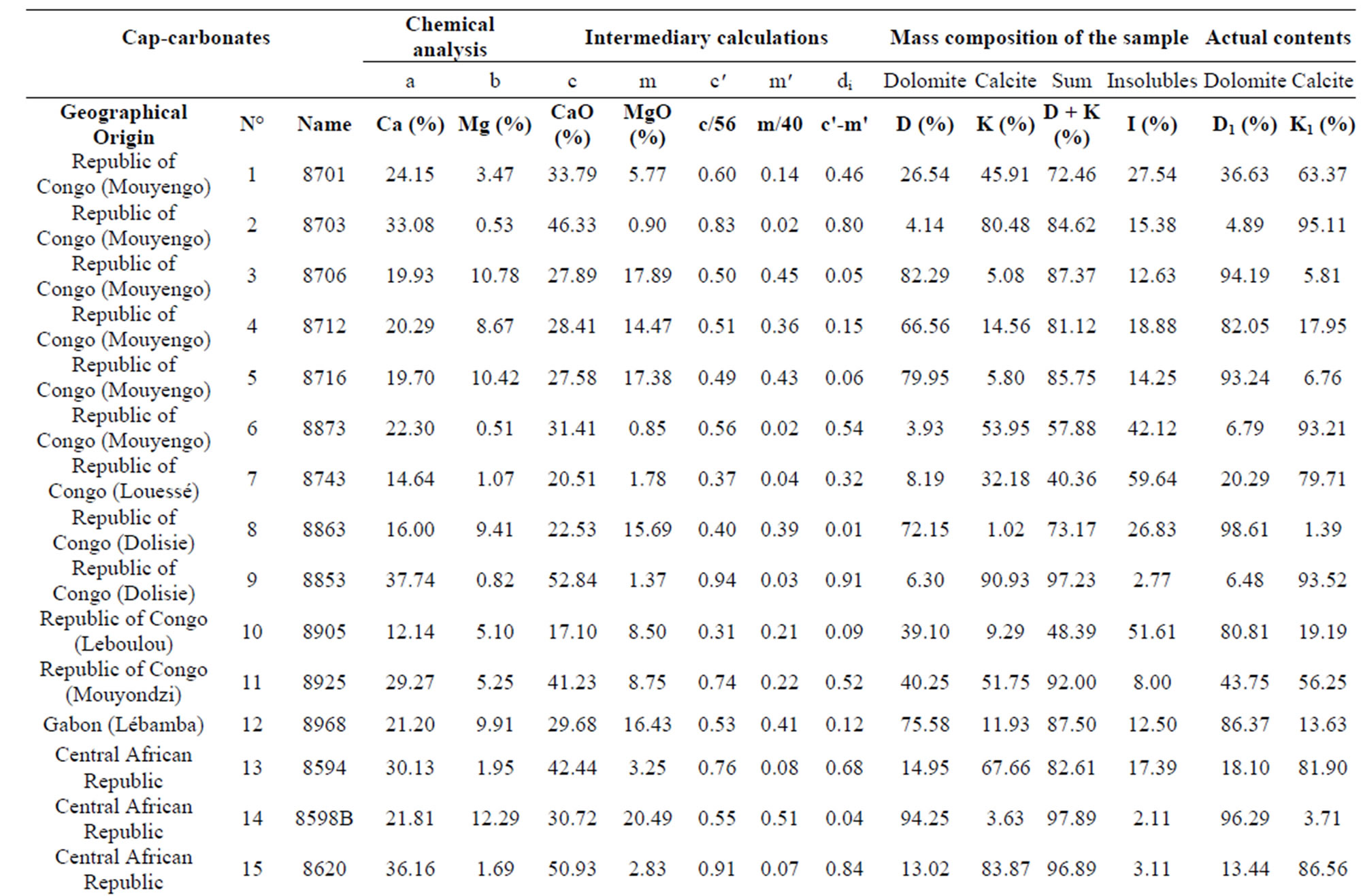

Table 1. Calculation method of Martinet and Sougy applied to 30 reference samples of cap carbonates.
.
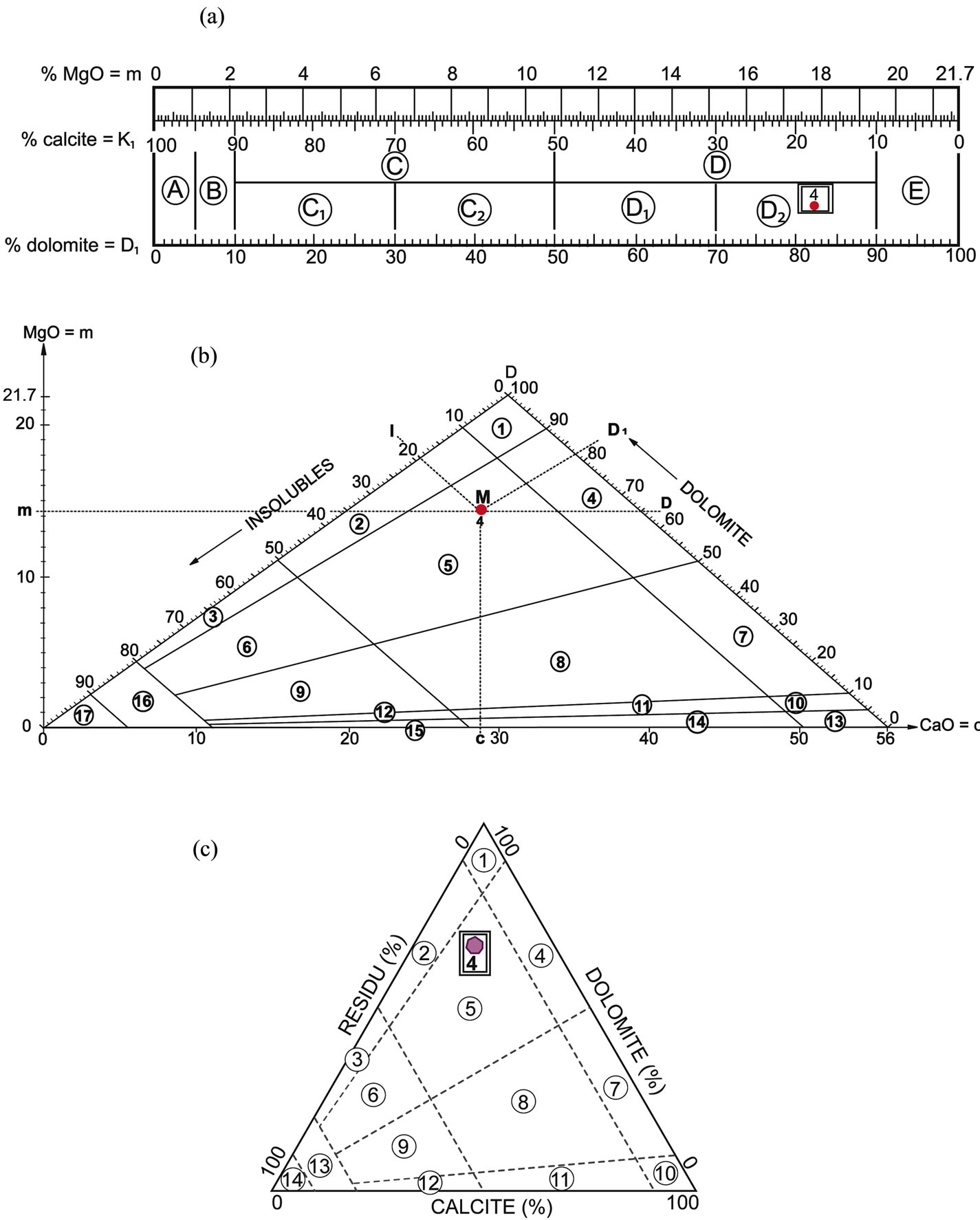
Figure 1. (a) Rapid method for classifying carbonate rocks from their chemical analysis. A: dolomitic limestones; B: magnesian limestones; C: limestones sensu lato; C1: slightly dolomitic limestones; C2: dolomitic limestones sensu stricto; D: calcareous dolomites sensu lato; D1: calcareous dolomites sensu stricto, D2: slightly calcareous dolomites; E: dolomites; (b) Diagram of Martinet and Sougy [11] for classifying carbonate rocks from their chemical analysis. 1: dolomites; 2: siliceous dolomites; 3: dolomitic cherts; 4: calcareous dolomites; 5: calcareous-siliceous dolomites; 6: dolomitic-calcareous cherts; 7: dolomitic limestones; 8: dolomitic-siliceous limestones; 9: calcareous-dolomitic cherts; 10: magnesian limestones; 11: siliceous magnesian limestones; 12: calcareous-magnesian cherts; 13: limestones; 14: siliceous limestones; 15: calcareous cherts; 16: impure cherts; 17: cherts. (c) Proposed regular ternary diagram for classifying carbonate rocks from their weight percentage contents of calcite (%), dolomite (%) and residue (%). 1: dolomites; 2: siliceous dolomites; 3: dolomitic cherts; 4: calcareous dolomites; 5: calcareous-siliceous dolomites; 6: dolomitic-calcareous cherts; 7: dolomitic limestones; 8: dolomitic-siliceous limestones; 9: calcareous-dolomitic cherts; 10: more or less magnesian limestones; 11: more or less magnesian siliceous limestones; 12: more or less magnesian calcareous cherts; 13: impure cherts; 14: cherts.
powder is weighed again, and the mass of dry sample is taken into account in later calculations.
The dried powder sample is introduced into in a 30 ml Teflon vessel and left to react with 10 ml of 2 M nitric acid for 2 hours at 120˚C, in a closed reactor. After cooling, the sample is filtered on a Büchner funnel, using an acetate filter with a mesh of 0.45 mm. The filtrate is diluted with bi-distilled water up to approximately 30 ml in a polyethylene container. The mass dilution factor f1 is determined by differential weighing of the container. Before the analysis, the filtrate (already diluted with water) is rediluted in 5% nitric acid to obtain a mass dilution factor f2 of approximately 50 (i.e. 0.6 ml of 5% nitric acid in 30 ml of diluted filtrate). In this way, we determine the final mass dilution factor F (i.e. F = f1 × f2), which is approximately 7500. The concentrations of Ca and Mg in solution are determined by ICP-AES (Horiba Jobin-Yvon Ultima C), using wavelengths of 317.933 nm and 279.553 nm [15], respectively, after calibration against standard solutions in 5% HNO3 containing between 0 and 80 mg/kg Ca and between 0 and 40 mg/kg Mg. From this, we can determine the weight percentages of Ca and Mg in the sample of analyzed carbonate rock, as follows:
a = % Ca and b = % Mg The values of a and b so obtained allow us to determine the weight percentages c and m of the oxides CaO and MgO, by using rounded molar masses (MCa = 40 g; MMg = 24 g and MO =16 g), which gives:
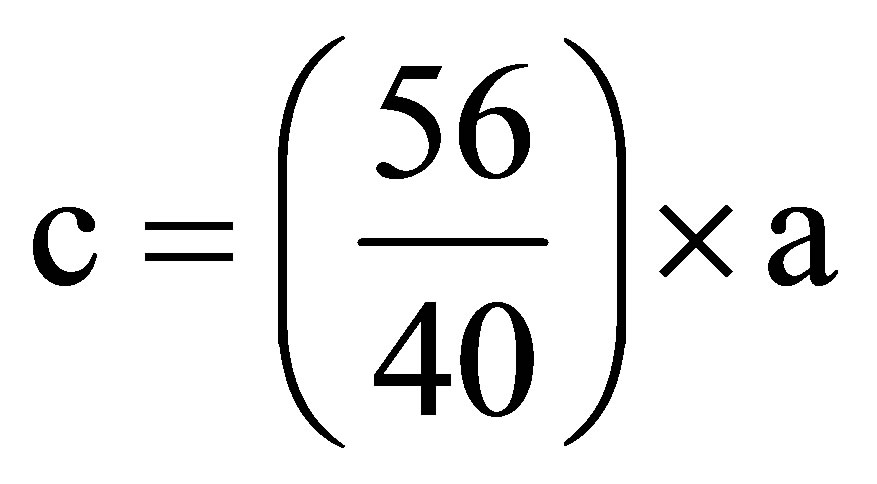 and
and , (1)
, (1)
with c = % CaO and m = % MgO (2)
2.2. Construction of Martinet and Sougy’s Diagram
Assuming that the chemical formulae of calcite and dolomite are CaCO3 and CaMg(CO3)2, respectively, [11] and [16] propose using the virtual contents D of dolomite and K of calcite in the analyzed sample of carbonate rock to derive a parameter I, which is considered as the percentage of insoluble residue representing the total content of other components not analyzed in the sample (in particular, silica and silicate minerals). With M(dolomite) = 184 g and M(calcite) = 100 g, they deduce:
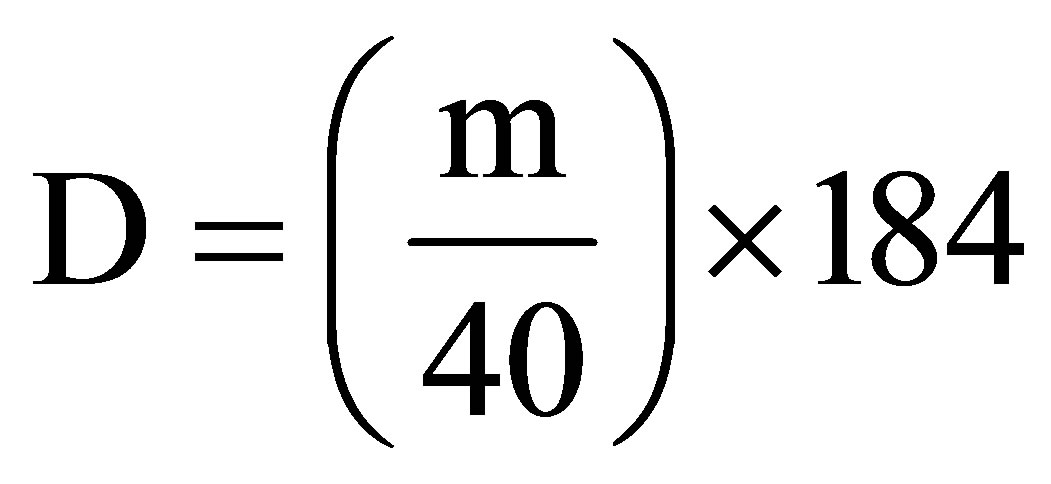 (3)
(3)
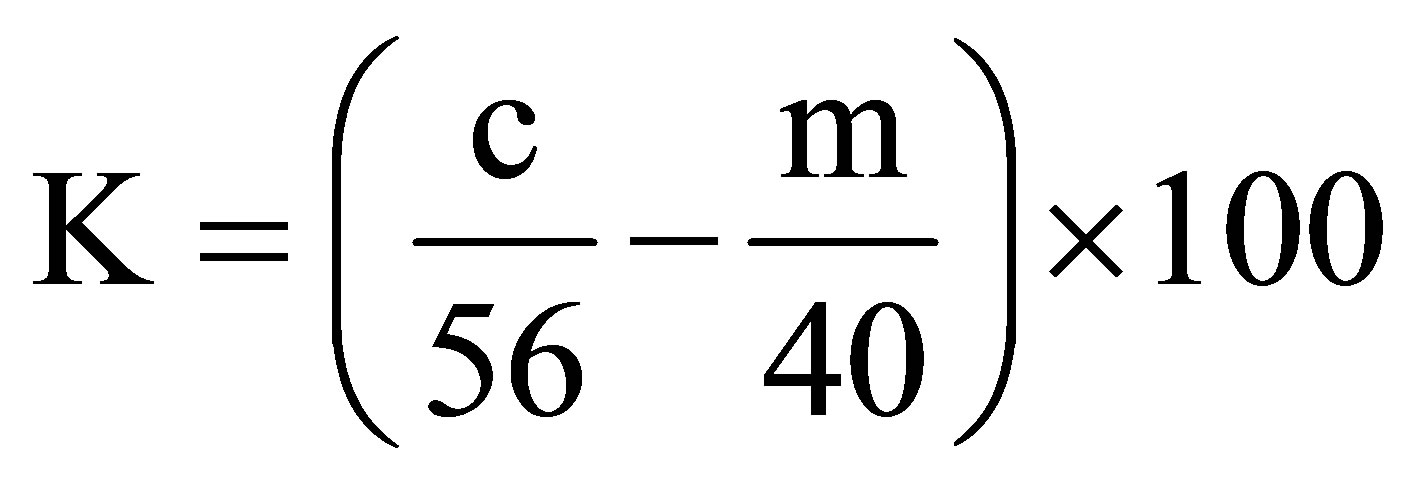 (4)
(4)
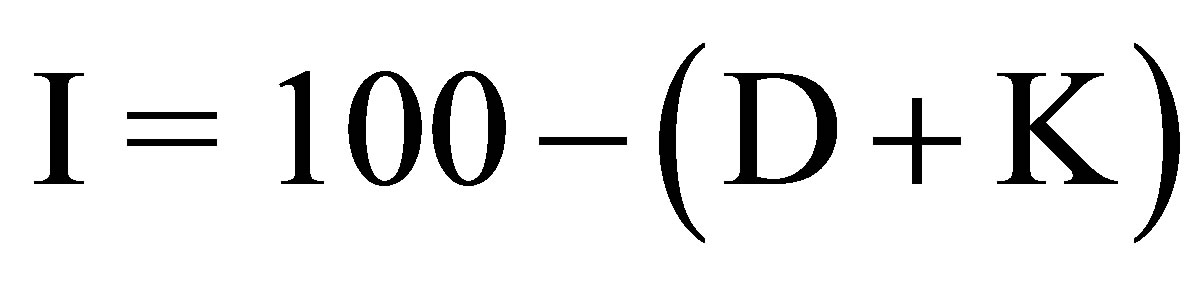 (5)
(5)
As a concrete example, let us consider the case of sample 8712 (corresponding to sample 4 of our reference series; Table 1) from a cap-carbonate section (at Mouyengo) in the Republic of Congo. By applying the techniques of sample preparation and analysis described above, we obtain:
a = 20.29 (% Ca) and b = 8.67 (% Mg)
for sample 8712, from which we can calculate:
c = 28.41 (% CaO) and m = 14.47 (% MgO).
These CaO and MgO contents are projected directly at point M (Figure 1(b)), using a binary system in the irregular triangular diagram of [11] and [16]. From this, we can conclude that sample 8712 corresponds to a siliceous calcareous dolomite, composed of 16% calcite (=K), 65% dolomite (=D) and 19% of insoluble residue (=I). In the rectangular diagram, this sample 8712 is defined, with less precision, as simply a calcareous dolomite.
Using Equations (3) and (4), we can estimate the virtual contents of calcite and dolomite, K1 and D1, that is to say:
 (6)
(6)
 (7)
(7)
From Equations (3) to (7), we can calculate D = 66.56%, K = 14.56% and I = 18.88% for sample 8712 and determine its calcite and dolomite contents, K1 (=17.95%) and D1 (=82.05%).
Projected in the classical rectangular diagram (Figure 1(a)), the results of these calculations indicate that sample 8712 is a calcareous dolomite.
On the whole, using solely the contents of CaO and MgO, or the K1 contents of calcite and D1 of dolomite, we arrive at practically the same classification for sample 8712.
Within the framework of this study, we carried out systematic calculations based on the Ca and Mg contents of about thirty samples of Neoproterozoic cap carbonates coming from sites geographically remote from each other and forming our reference series (Table 1). By using only the CaO and MgO contents of this series of samples (Figure 2), it is possible to distinguish six calcareoussiliceous dolomites (samples 4, 12, 18, 21, 22 and 25), three dolomitic-siliceous limestones (samples 1, 13 and 29), three dolomites (samples 14, 19 and 27), three calcareous dolomites (samples 17, 26 and 28), three siliceous dolomites (samples 3, 5, and 8), two limestones (samples 16 and 30), two dolomitic limestones (samples 11 and 15), two magnesian limestones (samples 20 and 9), one siliceous magnesian limestone (sample 6), one siliceous limestone (sample 2), one calcareous-dolomitic chert (sample 7), one dolomitic-calcareous chert (sample 10), one dolomitic chert (sample 23) and one impure chert (sample 24).
The recalculated dolomite and calcite contents (D1 and K1) of these same samples yield less detailed results (see Figure 3). Indeed, this diagram results in discriminating only seven main compositional facies (limestones, magnesian limestones, slightly dolomitic limestones, dolomitic limestones, calcareous dolomites, slightly calcareous dolomites and dolomites). From this, we may conclude that the rectangular diagram of Figure 1(a) leads to a less precise geochemical classification than the diagram (Figure 1(b)) [11,16].
To a first approximation, use of Martinet and Sougy’s diagram appears to yield some very interesting results. In

Figure 2. Diagram of martinet and Sougy [11] applied to 30 reference samples analysed in this study.

Figure 3. Rapid graphical representation applied to 30 reference samples analysed in this study.
particular, this diagram allows us to determine the virtual contents of calcite, dolomite and insoluble residue in each sample of carbonate rock analyzed for its Ca and Mg contents. Unfortunately, this irregular triangular diagram is only of relatively limited use since it depends on manual plotting of the data. Consequently, it cannot be applied to the rapid treatment of a large number of analyzed samples of carbonate rocks, or the computerized processing of geochemical data. For these reasons, we propose a regular ternary diagram that can be easily computerized and capable of ensuring the rapid treatment of very large amounts of geochemical data.
3. Development of the Regular Ternary Diagram
To validate our approach, it is firstly necessary to develop the construction of the regular ternary diagram, followed by its application to sample 8712 and the reference series of cap carbonates (Table 1).
3.1. Construction of the Regular Ternary Diagram
3.1.1. New Representation
To represent a large number of samples of carbonate rocks, in a fast and easy way, and automatically determine their classification, we need to transform irregular triangular diagram [11] (Figure 1(b)) into a regular ternary diagram (Figure 1(c)).
This transformation involves using an equilateral triangle where the input data for each sample of carbonate rock are represented by the percentages of calcite, dolomite and insoluble residue. This last component corresponds to the percentage fraction that remains unaffected by the chemical preparation, i.e. the percentage of insoluble residue as defined above.
Based on the weight percentages of Ca and Mg in a sample of carbonate rock (analyzed according to the techniques and procedures presented above), the real contents of calcite, dolomite and residue are calculated with Excel software, and then plotted in the new ternary diagram. For reasons of simplification compared to the initial diagram with 17 fields, our new diagram has only 14 fields (Figure 1(c)). This allows a better consistency compared with the results of laboratory analyses. Indeed, to estimate the percentages of calcite and dolomite in a given sample of carbonate rock, we analyze the weight percentage compositions of Ca and Mg, which amounts to determining the contents of Ca (%) and Mg (%) after dissolution of a fraction of the carbonate rock. The relative analytical error on Ca or Mg is generally lower than or equal to 5%. Consequently, the relative analytical error on the calcite and dolomite contents is lower than or equal to 10%. Thus, from an analytical point of view, there is little point in establishing a classification of the carbonate rocks that has a precision higher than 5%. This explains why the fields “12 and 15”, “11 and 14” and 10 and 13” as defined on the irregular triangular diagram (Figure 1(b)) are reduced to fields 12, 11 and 10, respectively, in the regular ternary diagram (Figure 1(c)). These latter fields represent more or less magnesian limestones, more or less siliceous magnesian limestones and more or less dolomitic calcareous cherts.
To facilitate the computer display of our regular ternary diagram, a new option was created in the “Diagrammes” software (hydrochemistry application developed and named by Roland Simler) which can be used under Windows. After publication of this article, this option called “Ternaires” [20] on the home page of the software and the descriptive file “Roches.ternaires.txt” will be made accessible on line by the following link:
http://www.lha.univ-avignon.fr/
3.1.2. Data-Processing Parameters Settings for the Development of the Regular Ternary Diagram
The diagram is subdivided into 20 elementary areas grouped into 14 fields. This subdivision is carried out using 7 lines defined by pairs of points in the reference square, whose origin O is located at top left (0,0), with 1000 units on each side. The slope and the ordinate at the origin are calculated for each pair of points (Table 2). The equilateral triangle of this diagram is thus defined by the three following points: S (50,900), T (500,120) and U (950,900).
In this diagram, each group corresponds to a specific field and is defined by its own data-processing conditions, based on a reference mark pointing downwards and the following conventions: a point A is denoted “–A” when it is located above the line and “+A” when it is below. For example, Group 1: s: = “−A − B − C − D − E − F − G” indicates that the point is above all of the seven lines; on the other hand, Group 2: s: = “−A − B − C + D − E − F − G” corresponds to the same type of configuration except that the point is below the line D.
The groups 1 to 14 were made up in this manner, with:

Table 2. Co-ordinates of the points used to generate the 7 straight lines dividing up the ternary diagram into 20 elementary areas and 14 zones corresponding to the various types of rocks.
Group 1: s: = “−A − B − C − D − E − F − G”;
Group 2: s: = “−A − B − C + D − E − F − G”;
Group 3: s: = “−A − B + C + D − E − F − G”;
Group 4: s: = “−A − B − C − D + E − F − G”;
Group 5: s: = “−A − B − C + D + E − F − G”;
Group 6: s: = “−A − B + C + D + E − F − G”;
Group 7: s: = “−A − B − C − D + E + F − G”;
Group 8: s: = “−A − B − C + D + E + F − G”;
Group 9: s: = “−A − B + C + D + E + F − G”;
Group 10: s: = “−A − B − C − D + E + F + G”;
Group 11: s: = “−A − B − C + D + E + F + G”;
Group 12: s: = “−A − B + C + D + E + F + G”;
Group 13: s: = “+A − B + C + D − E − F − G”;
Group 13: s: = “+A − B + C + D + E − F − G”;
Group 13: s: = “+A − B + C + D + E + F − G”;
Group 13: s: = “+A − B + C + D + E + F + G”;
Group 14: s: = “+A + B + C + D − E − F − G”;
Group 14 s: = “+A + B + C + D + E − F − G”;
Group 14: s: = “+A + B + C + D + E + F − G”;
Group 14 s: = “+A + B + C + D + E + F + G”
The separation of the fields by linear equations is used here to represent the various different carbonate rocktypes (“Diagrammes” software, “Ternaires” option on the home page with the descriptive file “Roches.ternaires. txt”). This representation is easily transposable to another family of rocks, by simply changing the pairs of points (defining up to ten lines) as well as the conditions of inclusion, using the relative position of the points compared to each line. This parameter-adaptive option will be developed later on.
3.2. Application of Our Method
The calculation of the input parameters for a sample of carbonate rock involves the transformation of the results (a and b obtained by geochemical analysis) into total weight percentage compositions of X and Y of the carbonates CaCO3 and MgCO3, and the determination of the percentage R of insoluble residue. Since (MC = 12.011 g; MCa = 40.08 g; MMg = 24.305 g and MO = 15.9994 g) and the chemical analysis yields the percentages of Ca and Mg (a and b) in a given sample, we can estimate X, Y and R as follow:
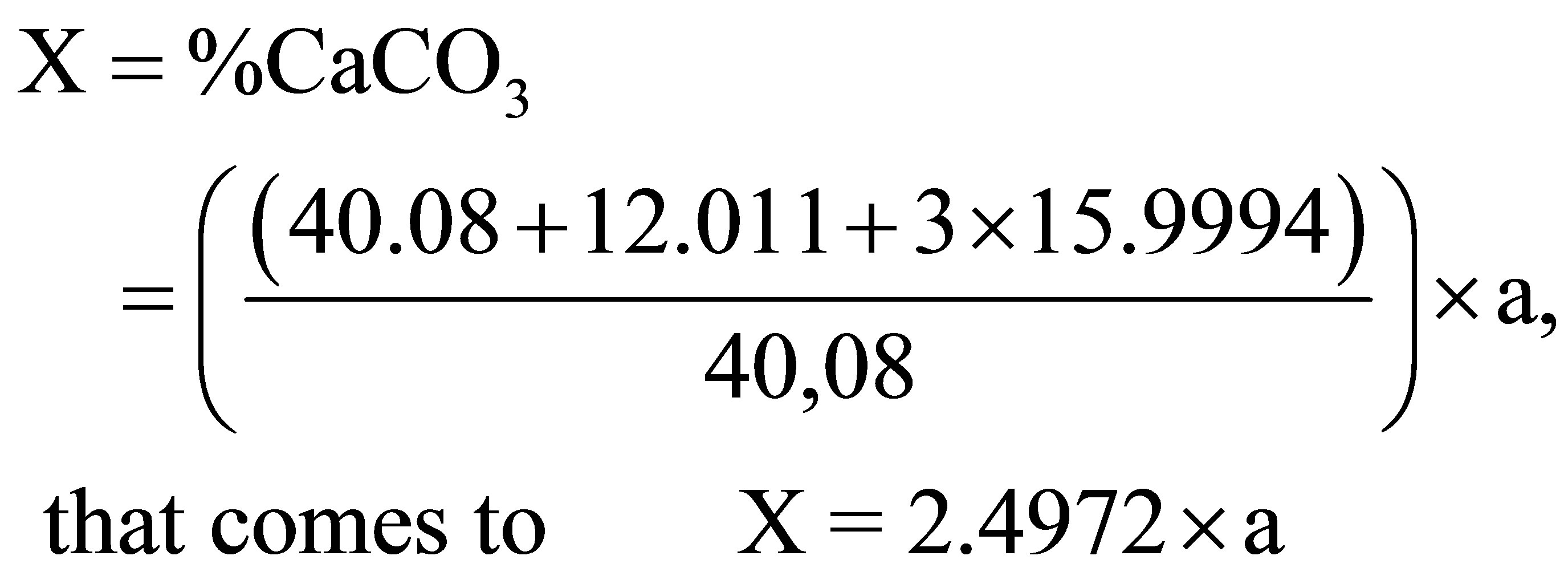 (8)
(8)
 (9)
(9)
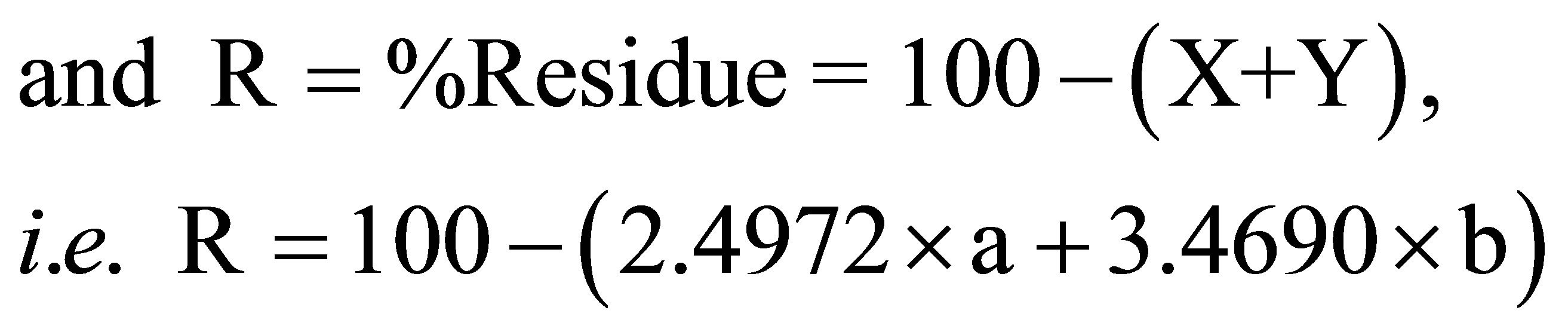 (10)
(10)
The second stage is the transformation into weight percentage compositions, i.e. D for dolomite (CaMg(CO3)2) and K for calcite (CaCO3). It is generally accepted that Paleozoic carbonate rocks contain a maximum of 2% to 3% of solid solution “MgCO3” in calcite [9]. The examination of all our samples of our carbonate rocks by X-ray diffraction indicates the absence of MgCO3 in solid solution, but the presence of calcite, dolomite and silicates. Assuming, like [11], that the carbonate fraction of Neoproterozoic samples of cap carbonates are made up solely of calcite and dolomite, we can write:
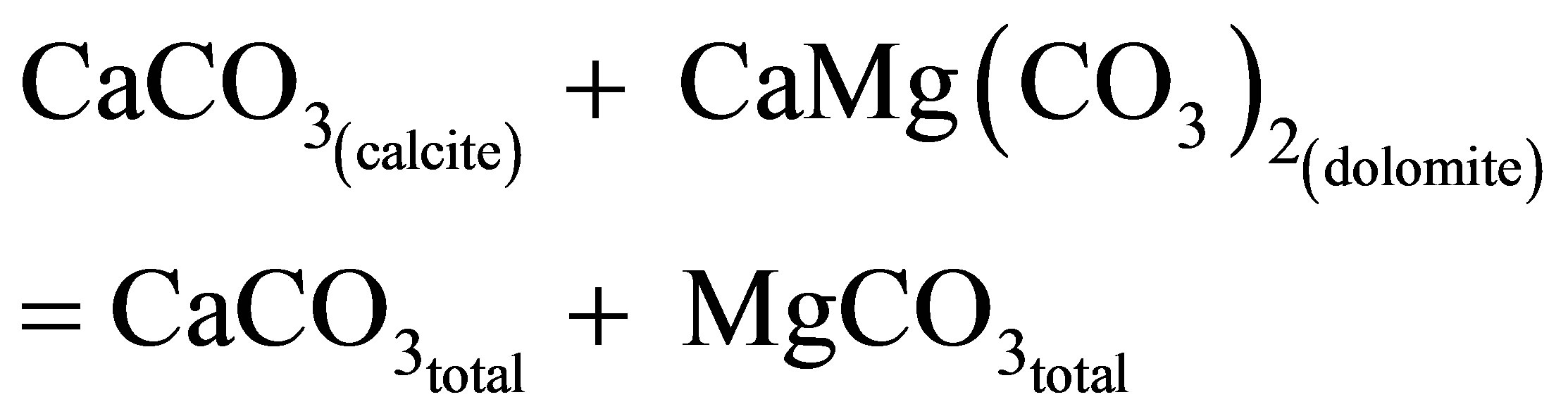
which corresponds to:
K + D = X + Y (11)where K is the percentage of calcite, D the percentage of dolomite and X and Y are the total percentages of magnesium and calcium carbonate components.
By using the ratio of the molar masses, we obtain the percentage of dolomite D as follows:
 (12)
(12)
Then, we can express the percentage of dolomite as a function of b, i.e. the percentage of magnesium determined by chemical analysis of a given sample of carbonate (from the Equations (9) and (12)):
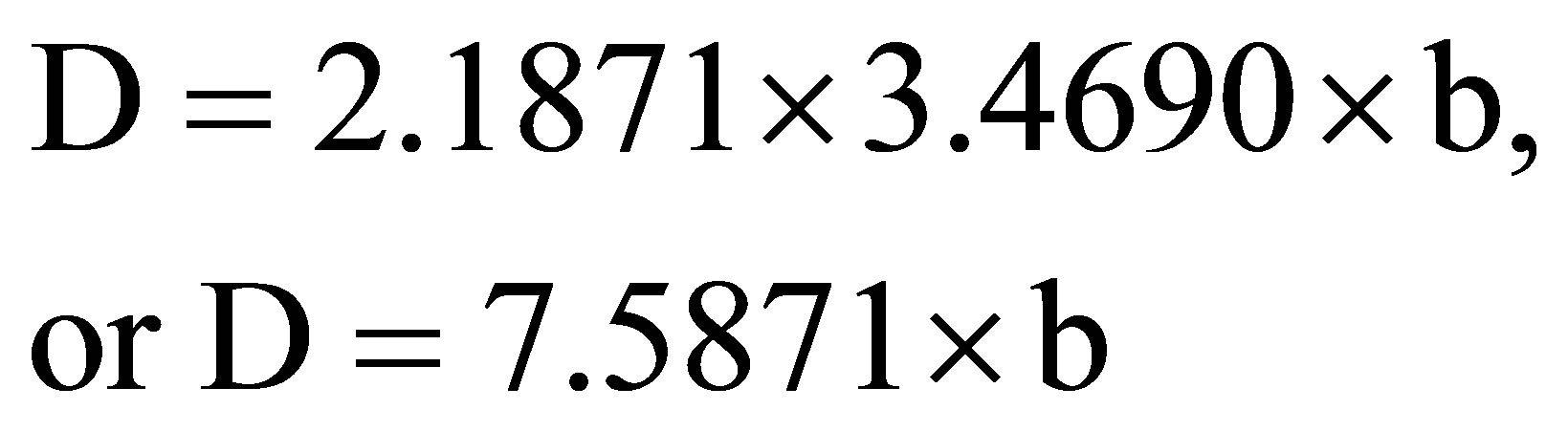 (13)
(13)
Similarly, the percentage K of calcite can be expressed as a function of X and Y, and then of a and b, which are the percentages of calcium and magnesium in the carbonate rock (from the Equations (8), (9) and (11)):
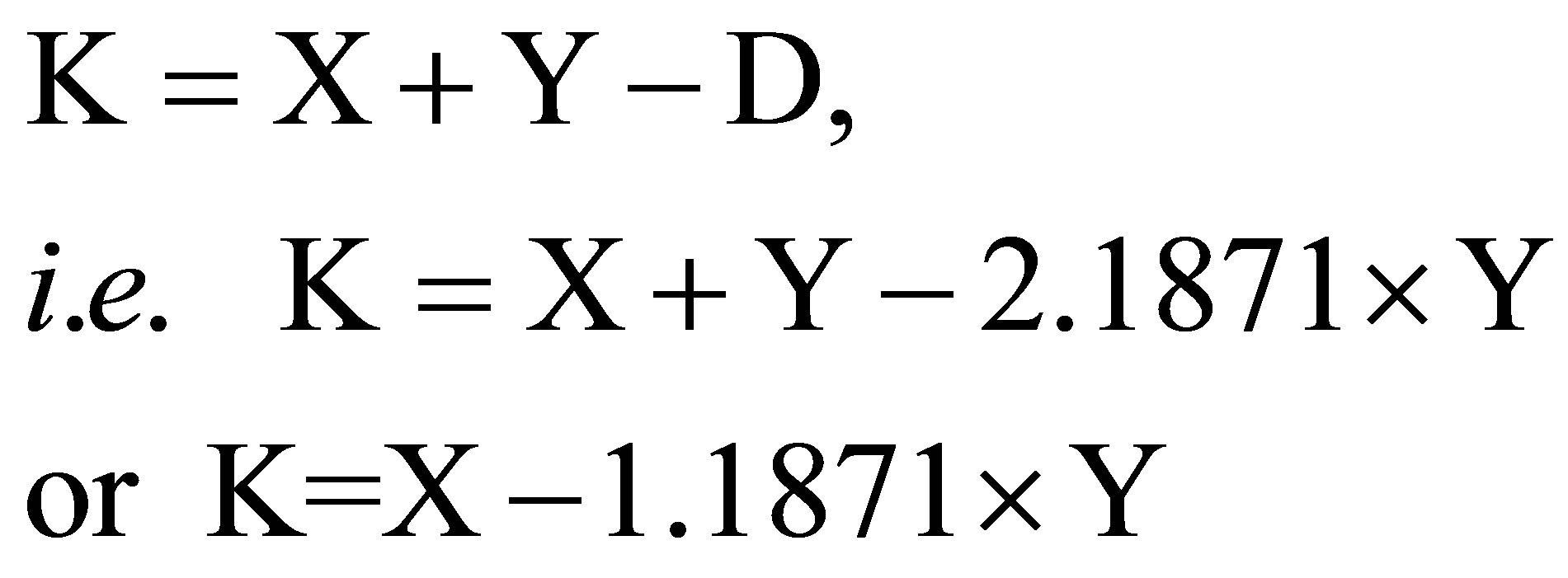 (14)
(14)
and
 (15)
(15)
To summarize, knowing only the weight percentage compositions of calcium (a) and magnesium (b) in a sample of analyzed carbonate rock, we can directly obtain the weight percentages of calcite K and dolomite D, as well as residue R, using the equations resumed below:
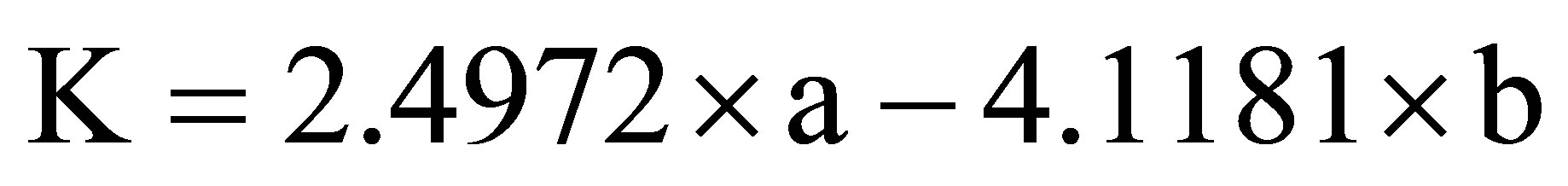 (15)
(15)
 (13)
(13)
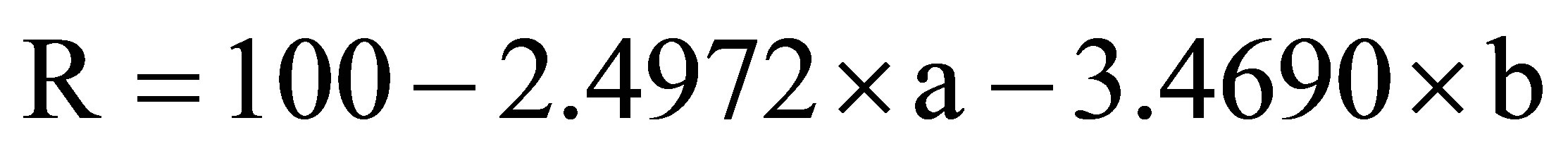 (10)
(10)
At this stage, it should be noted that:
i) for K ≥ 0, we need to apply 4.1181 × b ≤ 2.4972 × a, i.e. b ≤ (2.4972/4.1181) × a, which leads to b ≤ 0.6064 a;
ii) for 100 % calcite, we need to apply a = (100/2,4972) = 40.04 and b = 0;
iii) for 100% dolomite, b = (100/7.5871) = 13,18 and a = (4.1181/2.4972) × (100/7.5871) = 21.74;
iv) For our calculation method, we therefore select the following values: a ≤ 40.04 and b ≤ 13.18, with a = Ca(%) and b = Mg(%), i.e. X £ 2.4972 × 40.04, which leads to X £ 99.88, and Y £ 3.4690 × 13.18, which leads to Y £ 45.72.
By applying our calculation method to the data (a and b) for sample 8712 from the Mouyengo cap-carbonate section (in the Congo), we obtain results, which within the rounding errors of the calculations are comparable with those derived from the method of [11] (Table 1). The columns of results (Table 3) indicate the percentages of components in the samples [with D (%), K (%) and R (%)], which are plotted as data points on the ternary diagram. Thus, sample 8712 is still defined as a calcareous-siliceous dolomite (Figure 1(b)).
For the systematic processing of a set of data, we use the same types of calculations as for sample 8712. In this way, we obtain Tables 3 and 4, where the columns [D (%), K (%) and R (%)] correspond to the input data to the software application.
Once again, we note that the results obtained for the percentages of calcite, dolomite and insoluble residue are closely comparable, to within the rounding errors, with the values acquired by the method of [11] for the same series of samples. This fully validates our method of calculation.
Table 4 summarizes the data entered into the new option of the “Diagrammes” software, which is used to plot the results on a regular ternary diagram.
Using the data given in Table 4 [columns “Sequence N”, “CALCITE (%)”, “RESIDUE (%)” and “DOLOMITE (%)”], our samples can be plotted on Figure 4 using the “Diagrammes” software, the “Ternaires” option and the descriptive file “Roches.ternaires.txt” parameterized according to Section 3.1.2. [20].
The groups to which the samples are attributed [i.e. their rock-type names], which are derived from this equilateral ternary diagram, are reported in the column “Diagram results” of Table 4. From this, we are able to compare the results obtained using our method (see Figure 4) with the attribution of the same samples according to [11] (Figure 3).
In the ternary diagram presented here (Figures 1(c) and 4), our reference samples (Table 4) are projected
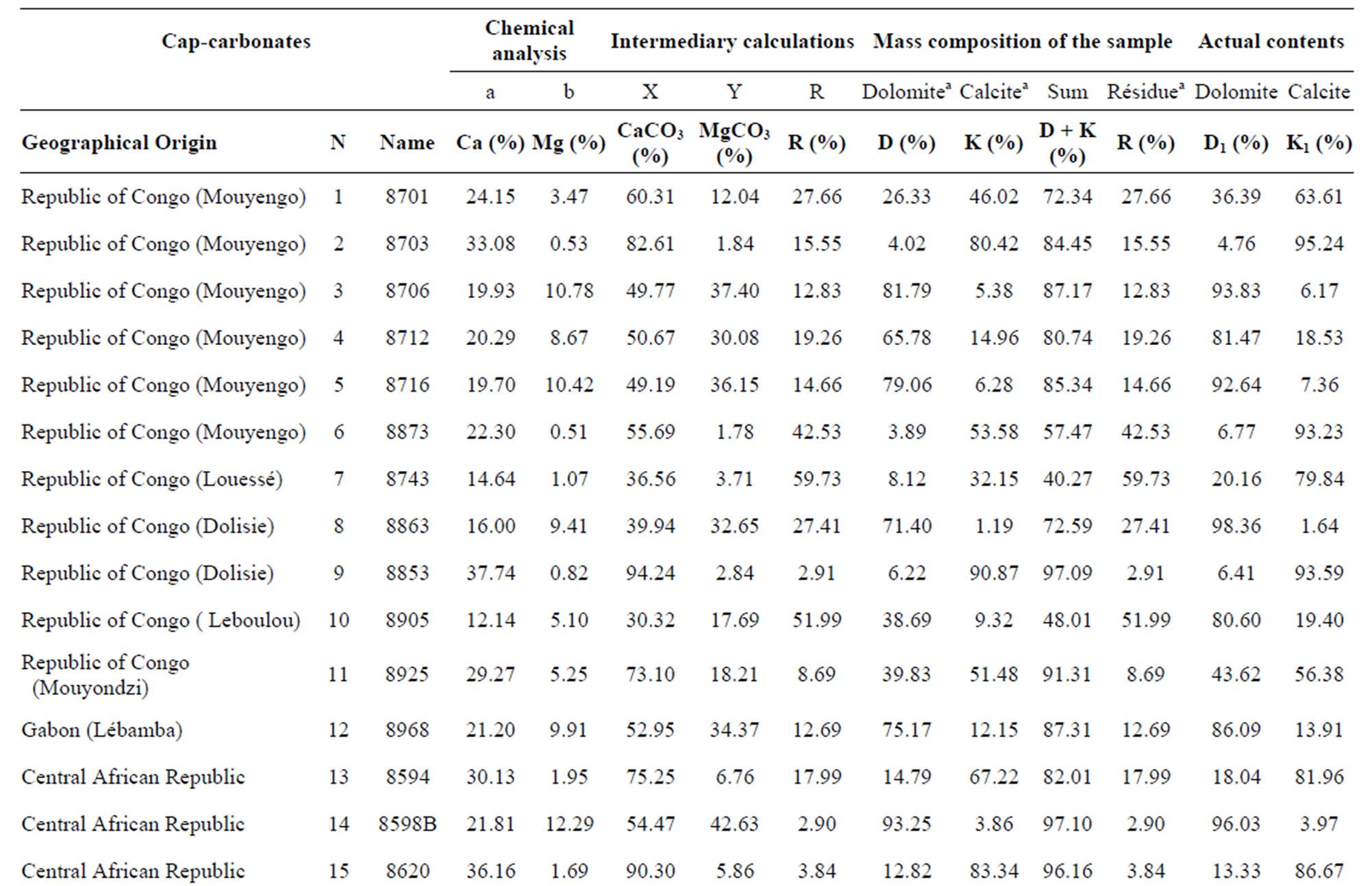
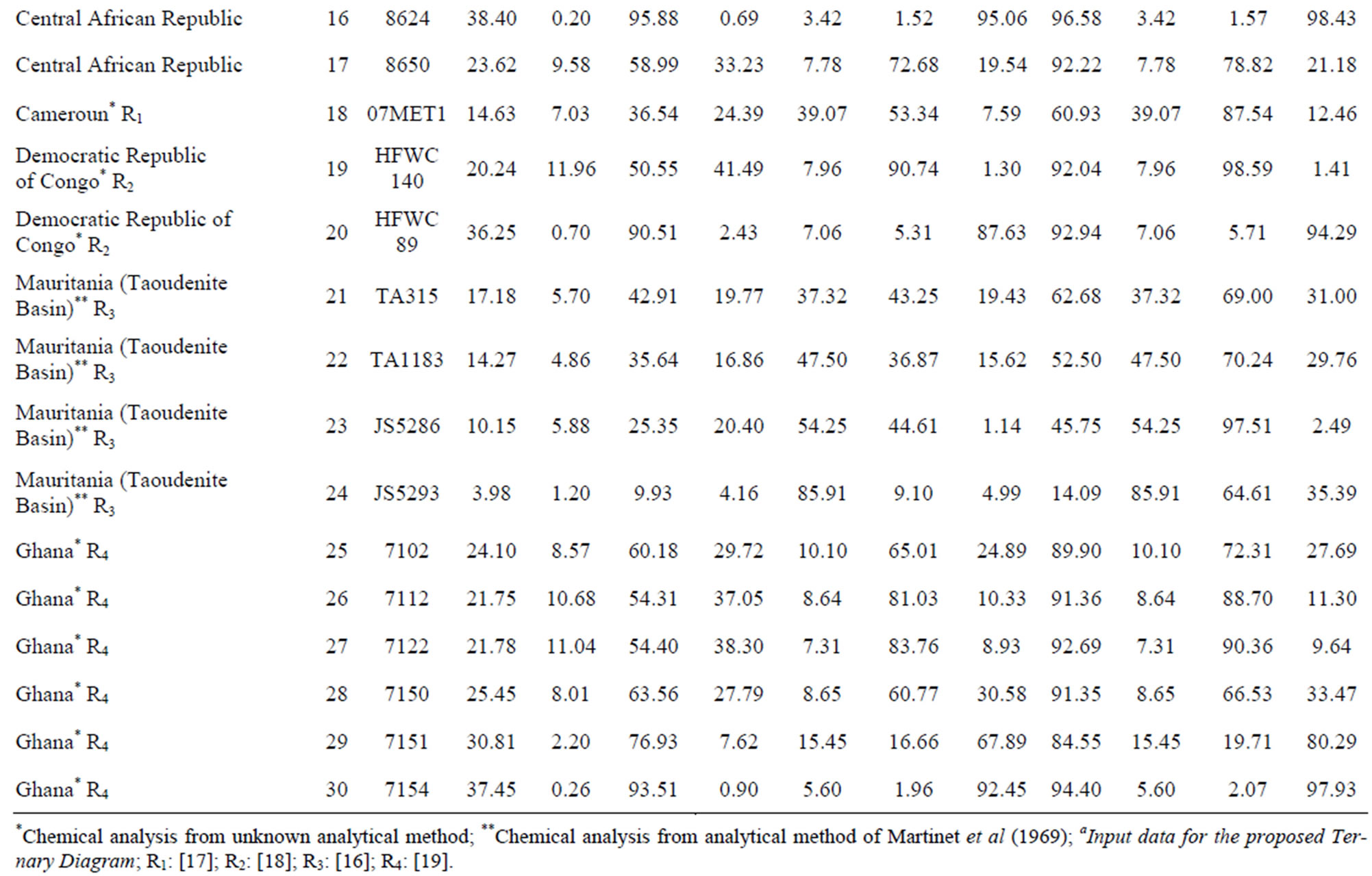
Table 3. Application of our proposed calculation method to the 30 reference samples of cap carbonates.
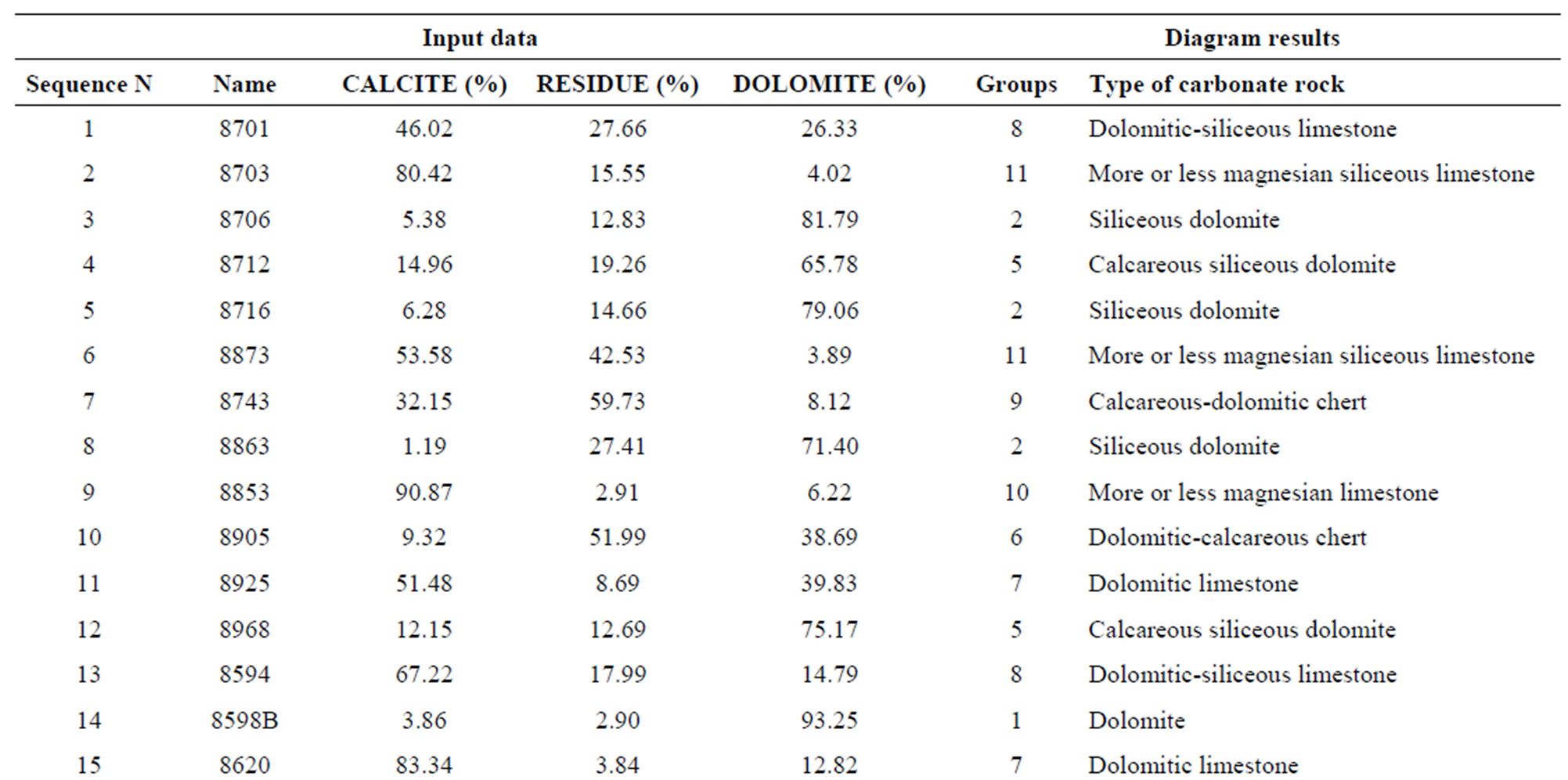

Table 4. Excel table of weight percent contents of components in the 30 reference samples (CALCITE (%), RESIDUE (%) and DOLOMITE (%)) used as input data to the “Diagrammes” software with the option “Ternaires” and the descriptive file “Roches.ternaires.txt”. Attribution of the various groups or types of rocks after plotting on the regular ternary diagram.
into fields defined by the input data (the percentages of calcite, dolomite and residue).
According to this diagram, samples 1, 13 and 29 of the series are defined as siliceous dolomitic limestones; 2 and 6 are more or less magnesian siliceous limestones; 3, 5 and 8 are siliceous dolomites; 4, 12, 18, 21, 22 and 25 are calcareous-siliceous dolomites; 7 is a calcareousdolomitic chert 9; 16, 20 and 30 are more or less magnesian limestones; 10 is a dolomitic-calcareous chert; 11 and 15 are dolomitic limestones; 14, 19 and 27 are dolomites; 17, 26 and 28 are dolomites limestones; 23 is a dolomitic chert and 24 is an impure chert.
On our diagram (Figure 4) which has 14 fields compared with the 17 fields of Martinet and Sougy [11], the only differences in classification concerns samples 6, 9 and 20. These three samples belong to groups that are simplified in our classification. Sample 6, which was defined as a siliceous magnesian limestone, now corresponds to a more or less magnesian siliceous limestone. And the samples 9 and 20, which were regarded as magnesian limestones, now plot in the group of more or less magnesian limestones.
All of the other carbonate rock samples are distributed in the same groups as given on the diagram of [11]. Such
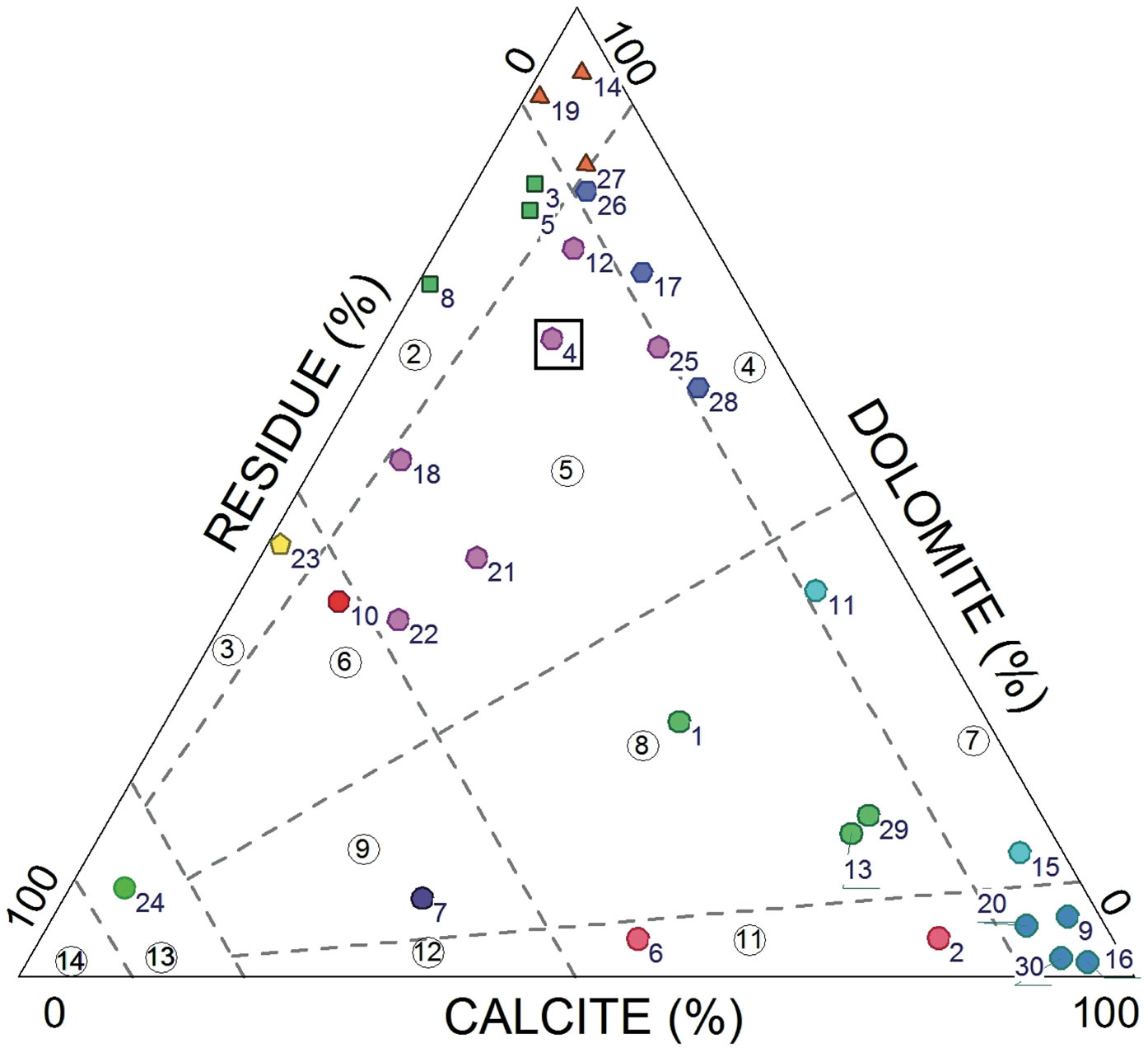
Figure 4. Diagram showing 30 reference samples of carbonate rocks plotted on regular ternary diagram proposes in this study.
results are indeed comparable with those obtained from plotting the same data on the irregular triangular diagram (Figure 3).
These results represent a good validation for the application of our ternary diagram.
4. Discussion and Conclusion
4.1. Concerning Structural, Textural and Petrographic Classifications
The methods of classification based on structural/textural characteristics [1-5] or mineralogical determinations under the optical microscope are inappropriate for the naming of very ancient carbonate rocks, in particular those dating from the Precambrian.
Indeed, subsequent to their deposition, carbonate rocks undergo transformation related to diagenetic processes (such as compaction, cementing, recrystallization, “feeding”, pressure solution, etc.), and very-low-grade metamorphism, as well as due to burial and sometimes hydrothermalism. In addition, classical methods of classification do not allow an estimate of the percentages of calcite and dolomite, which would facilitate the precise naming of rock-types.
4.2. Comparison of the Geochemical Result Approaches
The former method of geochemical classification, based on a rectangular diagram, does not require complex calculations and appears very easy to use. However, we consider that it is not very effective for determining a detailed classification of Precambrian carbonate rocks. Indeed, it can only distinguish seven different types of such rocks. This is why we pay particular attention to the two geochemical approaches, which are studied in detail here, to provide a classification of Precambrian carbonate rocks into 14 or 17 different groups (Figures 1(b) and 1(c)).
These two main methods of geochemical classification, presented in Sections 2 and 3 above, are based on chemical analysis of the calcium and magnesium contents (a and b) of each sample of carbonate rock. Due to the conversion of these simple chemical parameters (a and b) into percentages of CaO and MgO, the diagram of [11] (method presented in section II) allow us to finely classify ancient carbonate rocks, in particular according to groups defined by the contents of calcite, dolomite and insoluble residue. For this purpose, [11] propose the use of an irregular triangular diagram that is not easily computerized (Figures 1(b) and 3). In spite of its high degree of accuracy, resulting in distinguishing 17 different types of carbonate rock, this manual classification cannot be applied for the easy and rapid determination of a large number of samples.
The regular ternary diagram presented in Section 3. (Figures 1(c) and 4) makes direct use of the three input parameters [K = calcite (%), D = dolomite (%) and R = residue (%)], which define 14 groups discriminating the different types of Precambrian carbonate rocks. This diagram is only applicable if the total magnesium content analyzed in the sample is less than or equal to 13.2%, assuming Mg is present only in the form of dolomite. The regular ternary diagram depends on precise geochemical calculations and can be computerized owing to the new option in version 5.9 of the “Diagrammes” software written by Roland Simler. Using this new ternary diagram, it is possible to classify Precambrian carbonate rocks into 14 different groups or types. It also allows a rapid comparison between many carbonate rocks sampled from both far and near. It can also be applied in a systematic way to a given geological section to allow the determination of the various lithostratigraphic facies of a series.
Our method could be generalized to more recent carbonate rocks without Mg(CO3) in their composition.
Moreover, our automated chemical classification may have some industrial interest to evaluate the durability of building stones for example. Our chemical classification is well correlated with the geotechnical classification [21] based on porosity and swelling strain of the rocks.
4.3. Automatic Geochemical Classification of the Carbonate Rocks
Within the framework of this study, we propose a new diagram for the classification of Precambrian carbonate rocks. This approach uses a regular ternary diagram, and can be easily applied and computerized for a large number of samples.
This new geochemical classification only requires the parameters a and b, which correspond to the mass percentages of Ca and Mg determined in the analyzed carbonate rock. By calculation (Equations (15), (13), and (10)), we obtain the virtual percentages of calcite K, dolomite D and residue R making up the sample of carbonate rock in question:

These percentages of calcite, dolomite and residue represent the input data to our computerized diagram, based on the “Ternaires” option and based on the file “Roches. ternaires.txt” of the “Diagrammes” software developed by Roland Simler [20]. This option will be available after publication of the present article (with the link):
http://www.lha.univ-avignon.fr
Setup_Diagrammes Version 5.9 or more). In summary, the ternary diagram proposed here will enable a rapid and easy classification of many different Precambrian carbonate rocks of varied geographical origins. It will also facilitate the detailed characterization of a geological section, by determining the various lithostratigraphic facies present.
5. Acknowledgements
We thank Mr. Maurille Ouamba, Dean of the Faculty of Sciences in Marien Ngouabi University (BrazzavilleCongo), and the Scholarships National Agency of Gabon. This work is supported by the authorities of INSU/CNRS (GLANEC Projects 1 and 2). We thank Ms Laurence Vidal, Mr Didier Vandamme and the other members of the GLANEC Project. Our study has benefited from scientific and technical support from CEREGE in the Pytheas Institute. We also thank Mr. Bruno Tourlière for his pre-review and Mr. Michael Carpenter for his translation.
REFERENCES
- R. J. Dunham, “Classification of Carbonate Rocks According to Their Depositional Texture,” In: W. E. Ham, Ed., Classification of Carbonate Rocks: Tulsa, OK, American Association of Petroleum Geologist Memoirs, 1962, pp. 108-121.
- A. F. Embry and J. E. Klovan, “A Late Devonian reef tract on northeastern Banks Island,” Bulletin of Canadian Petroleum Geology, Vol. 19, No. 4, 1971, pp. 730-781.
- R. L. Folk, “Practical Petrographic Classification of Limestones,” American Association of Petroleum Geologist Bulletin, Vol. 43, No. 1, 1959, pp. 1-38.
- R. L. Folk, “Spectral Subdivision of Limestones Types,” In: W. E. Ham, Ed., Classification of Carbonates Rocks. A Symposium, Tulsa, OK, American Association of Petroleum Geologist Memoirs, 1962, pp. 62-84.
- V. P. Wright, “A Revised Classification of Limestones,” Sedimentary Geology, Vol. 76, No. 3-4, 1992, pp. 177- 185. http://dx.doi.org/10.1016/0037-0738(92)90082-3
- G. V. Chilingar, “Use of Ca/Mg ratio of Limestones and Dolomites as a Geological Tool,” Ph.D. Dissertation, Univ. Southern California, 1956.
- G. V. Chilingar, “Classification of Limestones and Dolomites on Basis of Ca/Mg Ratio,” Journal of Sedimentary Petrology, Vol. 27, No. 2, 1957, pp. 187-189.
- A. Carrozi, “Petrographie des Roches Sédimentaires,” F. Rouge et cie, Lausanne, 1953, 250 p.
- R. W. Fairbridge, “The Dolomite Question,” In: R. J. Le Blanc and J. G. Breeding, Eds., Regional Aspects of Carbonate Deposition, Tulsa Society of Economic Paleontologists and Mineralogists, Special Publications, 1957, p. 128. http://dx.doi.org/10.2110/pec.57.01.0125
- J. Rodgers, “Terminology of Limestone and Related Rocks: An Interim Report,” Journal of Sedimentary Petrology, Vol. 24, No. 4, 1954, pp. 225-234.
- B. Martinet and J. Sougy, “Utilisation Pratique des Classifications Chimiques des Roches Carbonatées,” C. R. Somm. Soc. Géol. Fr., 1957, p 367 (résumé), Annales de la Faculté des Sciences de Dakar, 1957[1961], pp. 81-92.
- K. E. Chave, “Aspects of the Biochemistry of Magnesium,” Journal of Geology, Vol. 62, 1954, pp. 266-283.
- B. Martinet, M. Deynoux and R. Trompette, “Méthode de Dosage de CaO et MgO dans les Roches Carbonatées,” Travaux des Laboratoires des Sciences de la Terre, Série B, No. 2, St Jérôme, Marseille, 1969.
- W. E. Dean, “Determination of Carbonate and Organic Matter in Calcareous Sediments and Sedimentary Rocks by Loss on Ignition: Comparison with Other Methods,” Journal of Sedimentary Petrology, Vol. 44, No. 1, 1974, pp. 242-248.
- R. W. Murray, D. J. Miller and K. A. Kryc, “Analysis of Major and Trace Elements in Rocks, Sediments, and Interstitial Waters by Inductively Coupled Plasma-Atomic Emission Spectrometry (ICP-AES),” ODP Technical Note, Vol. 29, 2000. http://dx.doi.org/10.2973/odp.tn.29.2000
- J. Sougy, “Les Formations Paléozoïques du Zemmour noir (Mauritanie septentrionale): Etude Stratigraphique, Pétrographique et Paléontologique,” Thèse d’Etat, Université de Nancy, 1964, 695 p.
- V. Caron, E. Ekomane, G. Mahieux, P. Moussango and E. Ndjeng, “The Mintom Formation (New): Sedimentology and Geochemistry of a Neoproterozoic, Paralic Succession in South-East Cameroon,” Journal of African Earth Sciences, Vol. 57, No. 4, 2010, pp. 367-385. http://dx.doi.org/10.1016/j.jafrearsci.2009.11.006
- H. E. Frimmel, L. Tack, M. S. Basei, A. P. Nutman and A. Boven, “Provenance and Chemostratigraphy of the Neoproterozoic West Congolian Group in the Democratic Republic of Congo,” Journal of African Earth Sciences, Vol. 46, No. 3, 2006, pp. 221-239. http://dx.doi.org/10.1016/j.jafrearsci.2006.04.010
- A. Nédélec, P. Affaton, C. France-Lanord, A. Charrière and J. Alvaro, “Sedimentology and Chemostratigraphy of the Bwipe Neoproterozoic cap Dolostones (Ghana, Volta Basin): A Record of Microbial Activity in a Peritidal Environment,” Comptes Rendus Geoscience, Vol. 339, No. 3-4, 2007, pp. 223-239. http://dx.doi.org/10.1016/j.crte.2005.06.002
- R. Simler, Software “Diagrammes,” Laboratoire d’Hydrologie d’Avignon, Université d’Avignon et pays du Vaucluse, France. http://www.lha.univ-avignon.fr
- J. Delgado Rodrigues, “Proposed Geotechnical Classification of Carbonate Rocks Based on Portuguese and Algerian Examples,” Engineering Geology, Vol. 25, No. 1, 1988, pp. 33-43. http://dx.doi.org/10.1016/0013-7952(88)90017-8
NOTES
*Corresponding author.

