Journal of Flow Control, Measurement & Visualization
Vol.07 No.01(2019), Article ID:90108,12 pages
10.4236/jfcmv.2019.71005
Active Stall Control System on NACA0012 by Using Synthetic Jet Actuator
Hiroaki Hasegawa1*, Shigeru Obayashi2
1Department of Mechanical & Intelligent Engineering, Utsunomiya University, Utsunomiya, Japan
2Institute of Fluid Science, Tohoku University, Sendai, Japan
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC 4.0).
http://creativecommons.org/licenses/by-nc/4.0/



Received: August 29, 2018; Accepted: December 8, 2018; Published: January 23, 2019
ABSTRACT
Flow separation is typically an undesirable phenomenon, and boundary layer control is an important technique for the separation problems on airfoils. The synthetic jet actuator is considered as a promising candidate for flow control applications because of its compact nature and ability to generate momentum without the need for fluidic plumbing. In the present study, an active separation control system using synthetic jets is proposed and practically applied to the stall control of the NACA0012 airfoil in a wind tunnel test. In our proposed system, the flow conditions (stalled or unstalled) can be judged by calculating from two static pressure holes on the airfoil upper surface alone. The experimental results indicate that the maximum lift coefficient increases by 11% and the stall angle rises by 4˚ in contrast to the case under no control. It is confirmed that our proposed system can suppress the stall on the NACA0012 airfoil and that the aerodynamic performance of the airfoil can be enhanced. The proposed system can also be operated prior to the onset of stall. Therefore, separation control is always attained with no stall for all flow fields produced by changing the angle of attack that were examined.
Keywords:
Active Control, Airfoil, Lift, Separation, Stall, Synthetic Jet

1. Introduction (Heading 1)
Currently, development of the economy and human life in developed nations depends on fossil fuels, and the exhaustion of this limited resource has become a serious social issue. Furthermore, global warming is accelerated by the massive consumption of fossil fuels, and there are concerns with regard to a rise in sea level, abnormal weather, floods, and food shortages, all of which may progress rapidly. In our social environment, improving the efficiency of fluid machinery in order to use energy effectively is a critical theme. The losses caused by fluid are largely related to the flow separation phenomenon owing to the development of the boundary layer. Flow separation is a mostly undesirable phenomenon, and boundary layer control is an important technique when dealing with separation problems on airfoils. Methods have been devised to prevent this separation, and boundary layer control has been widely used in aerodynamic applications to inhibit flow separation [1] [2] [3] [4] .
The synthetic jet is a method of boundary layer control to suppress flow separation [5] , and synthetic jet actuators have been shown to be a useful tool for flow control in applications such as mixing enhancement, separation control, and thrust vectoring [6] . A typical synthetic jet actuator consists of a small cavity with an oscillating diaphragm on its bottom and an orifice plate on the opposite side. As a result of alternating suction and blowing produced by a diaphragm movement, a succession of vortex rings is produced and propagates away from the orifice. A synthetic jet is created from the ambient fluid by impressing an oscillating pressure gradient across an orifice. The jet is synthesized by a two-phase cycle composed of suction and ejection.
During the suction phase, the diaphragm moves away from the orifice, thus increasing the cavity volume, and fluid is subsequently drawn into the cavity from the surroundings. During the ejection phase, the diaphragm moves toward the orifice, resulting in fluid expulsion through the orifice, while doing so separates from the edges. If the jet is sufficiently strong, the resulting free shear layer then rolls up to form a vortex ring at the exit of the orifice. Consequently, net momentum is transferred to the surrounding fluid even though the net mass flux is zero because of the self-induced velocity of the vortex ring, and synthetic jets can be effective for enhanced mixing.
The control system of synthetic jets can be constructed using small-scale equipment because jets can be generated without external devices such as compressors and complex piping, in contrast to the control system of vortex generator jets that can adaptively suppress the flow separation for a time-varying flow. The strength of a synthetic jet can be varied by changing the voltage and excitation frequency of an actuator. Therefore, synthetic jets in a crossflow adaptively create effective stall control of the airfoil in a time-varying flow field. In the present study, an active separation control system using synthetic jets to attain the airfoil stall suppression is developed. The active separation control system is practically applied to the stall control of the NACA0012 airfoil in a wind tunnel test.
2. Experimental Apparatus and Methods
2.1. Experimental Apparatus
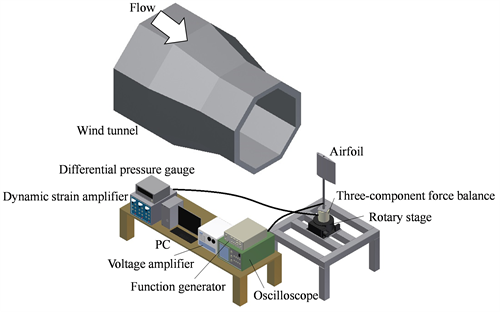
The experiments were carried out in a low-turbulence wind tunnel at the Institute of Fluid Science, Tohoku University, Japan, the freestream turbulence intensity was less than 0.05% within the operating range. A schematic diagram of the experimental apparatus is shown in Figure 1. The test section is octagonal, 0.81 m wide by 0.81 m high. Aerodynamic forces acting on the airfoil were measured by using a three-component force balance (LMC-3501-100N, NISSHO-ELECTRIC-WORKS) with a rotary stage, and the surface pressure was measured using a differential pressure gauge (PDV-25GA, KYOWA). The force measurements were sampled by an AD converter at 10 kHz and the error in the measurements was less than 0.1%.
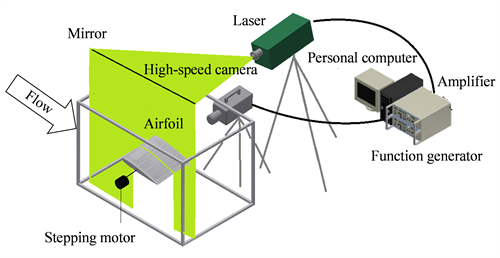
Figure 2 shows a schematic diagram of the flow visualization experiments. A high-speed camera (FASTCAM-SA3; Photron Ltd.) and Nd-YAG laser (G8000; Katoukouken Co.) were used to capture the smoke pattern around the airfoil in this experiment. The smoke pattern was made visible with a smoke-seeding freestream by using a smoke generator (PORTA SMOKE PS-2002, DAINICHI). The test model of the airfoil is shown in Figure 3. The NACA0012 airfoil had a chord C of 200 mm and a span S of 200 mm. There were eight jet orifices on the suction surface, and the jet array was placed at 40 mm from the leading edge (20% of the chord). The jet array position is determined by checking the detachment position on the airfoil’s upper surface in a stall state using the oil-flow visualization. The maximum thickness of the NACA0012 airfoil was at 30% of the chord. Then, the synthetic jet actuators were installed near the location of the maximum thickness of the airfoil.
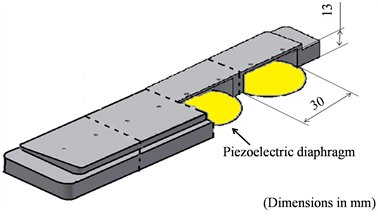
The jet was issued normal to the airfoil surface. Each jet orifice diameter D0 was 2 mm (D0 = 2 mm). Figure 4 shows an enlarged view of the cavities. Four cavities were provided in the synthetic jet actuators. The height of each cavity was 13 mm. Each cavity had a piezoelectric diaphragm with a diameter of 30 mm and two orifices. The jets were ejected by changing of cavity volume that occurs during the vibration of the piezoelectric diaphragm.
The freestream velocity U0 was varied from 5 to 30 m/s corresponding to the Reynolds number Re based on the chord length C of 0.75 × 105 - 4.5 × 105. The strength of the synthetic jet was determined by the jet-to-freestream velocity ratio VR (= Vj/U0), where Vj is the jet mean velocity. Vj was measured by an I-type hot-wire probe that was placed at the center of the orifice, and the height from the orifice of y = 2 mm. The strength of the synthetic jet was varied by changing the voltage and the excitation frequency of the actuator. The length of the fluid column that was blown from an orifice can be determined by the dimensionless stroke length L0 (= Vj/fD0), where f is the excitation frequency. The excitation frequency of the actuator was 500 Hz.
2.2. Experimental Method
Our proposed system operates by detecting the precursor of a stall in order to prevent a control delay owing to the response characteristics of the measurement system. A flowchart of this system is shown in Figure 5. This system initially samples a differential pressure to judge the flow situation. If a flow separation from the airfoil’s upper surfaceis detected, the system operates automatically to suppress the flow separation. The system uses feedback and determines whether the control target is attained. When the system determines that stall control has been attained, the system maintains the synthetic jet operation (the present speed of the synthetic jets).
Figure 1. Schematic diagram of experimental apparatus and force measurement system, lance measurement system.
Figure 2. Schematic diagram of flow visualization experiments.
Figure 3. NACA0012 airfoil model with synthetic jets.
Figure 4. Enlarged view of synthetic jet cavity.
Figure 5. Flowchart of active stall control system.
The system senses the unstalled flow field and cuts off the synthetic jets completely when no stall occurs. This system can determine the flow condition by using only the output signal of differential pressure dp between the two static pressure holes alone. In other words, information concerning the freestreamvelocity and the angle of attack of the airfoil is not needed for stall control in our proposed system. In the present study, two static pressure holes on the airfoil’s upper surface are used to determine the flow situation (stalled or unstalled).
In our proposed system, the control function is determined from dp, and attainment of the control target is judged by this control function. dp increases as the angle of attack increases. Therefore, the system can judge whether the angle of attack increases or decreases. In addition, if a separation occurs at the upper surface of the airfoil, dp decreases. When the control system detects a sudden decrement in the pressure difference, the synthetic jet device operates automatically to suppress the flow separation. Then, the system uses feedback and determines whether the control target is attained. When the system achieves sufficient pressure recovery and determines that the control target has been attained, the system continues to maintain control. The system senses the unstalled flow field and cuts off the jets completely when no flow separation occurs. Eventually, the synthetic jet actuator is operated by an on/off function, and the jet velocity is not adjusted during operation of the system in the present study.
3. Results and Discussion
3.1. Aerodynamic Characteristics
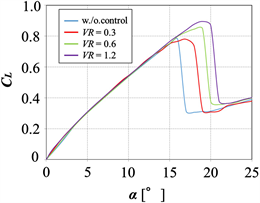
Figure 6 shows the life coefficient CL, the drag coefficient CD, and the polar curve. The solid and dotted lines indicate the cases with and without control, respectively. In the case with control, the synthetic jet actuator is initially operated (from α = 0 deg). CL increases as the angle of attack increases, and CL decreases at α = 16˚ for the case without control. The stall angle was 16˚ at Re = 1.5 × 105. CL increases until the angle of attack reaches 20˚ under control. The maximum lift coefficient CLmax increases 11% in contrast to the case without control. On the other hand, CD variations indicate almost the same tendency for cases with and without control, and the increment of drag does not occur for the synthetic jet issuing at the upper surface of the airfoil. The CL/CD ratio around a stall angle of attack increases under control and can be improved by operating the control system using the synthetic jets. The effect of VR on the maximum lift coefficient and the stall angle of attack in this experiment is shown in Figure 7. The stall characteristics are effectively improved for VR = 1.2, and the jet speed condition used in our proposed system mentioned later is set at VR = 1.2.
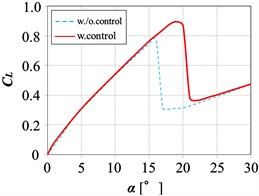

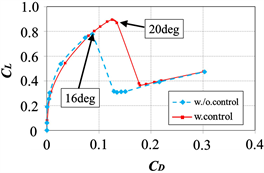
Figure 6. Aerodynamic characteristics curve. Solid and dotted lines denote with and without control (VR = 1.2, Re = 1.5 × 105). (a) lift curve; (b) drag curve; (c) polar curve.
Figure 7. Lift coefficients (Re = 1.5 × 105).
In order to investigate the effect of operating timing in the control system on the aerodynamic performance of the airfoil, the synthetic jets are operated by using several operation timings. Figure 8 shows the CL curves when the angle of attack of the airfoil changes from 0˚ to 25˚ at a constant angular velocity of 3.3˚/s, and the system is performed by using open loop control. The solid and dotted lines indicate the cases with and without control, respectively. Figure 8(a)-(c) shows the aerodynamic performance of the airfoil under different operation timings of the stall control system. When the system operates after the stall occurs (Figure 8(a)), the lift force recovers at the instant of starting operation. However, the value of the lift force after the operation is smaller than that of the maximum lift force before the stall.
When the system starts just after a stall occurs (Figure 8(b)), the lift force increases and the maximum lift coefficient becomes almost the same as the maximum value under no control without a stall. However, the decrement of the lift force cannot be avoided because the stall occurs for a short time. By contrast, when the system starts just before the onset of a stall, the lift force increases slightly over the stall angle without the occurrence of a decrement of lift (Figure 8(c)). Superior stall control can be achieved by operating the system to detect the onset of a stall.
3.2. Flow Visualization around the Airfoil under Control
Figure 9 shows a schematic of the input signal and position of each phase. In our proposed system, the input waveform of the synthetic jet actuator uses a rectangular wave. Figure 10 shows the instantaneous images visualized by smoke-seeding the freestream for each phase. In order to make the flow pattern visible at the leading edge, flow visualization was performed using a smoke method mentioned earlier and a schematic view of flow visualization set-up is given in Figure 2. A high-speed camera was used to capture the vortex behavior in the separated shear layer at the leadingedge of the airfoil. Phases ② and ④ correspond to the blowing and suction situations, respectively. Phases ① and ③ indicate the situations just after blowing and suction, respectively. Figure 10(a) clearly shows that the flow in the absence of jets separates at the leading edge. The flow separates upper the surface at α = 16˚, and the airfoil indicates a stall state under no control.
It is seen from Figure 10(a) that the leading edge vortices are not attached to the upper surface of the airfoil. A periodic excitation produced by the synthetic jets occurs in the separated shear layer under control (Figure 10(b)), and vortex growth occurs in the separated shear layer from the leading edge under control during the blowing phase. In Figure 10(b), with synthetic jets acting for control, the flow has less of tendency to separate, and Figure 10(b) shows a reduction in the tendency toward stall when compared with the no control case. The instability in the separated shear layer is promoted, and a large-scale vortex attaches to the airfoil surface (Figure 10(c) and Figure 10(d)). After that time, the attached vortex is elongated toward the orifice during the suction phase, and the attaching region expands (Figure 10(e)). These results suggest that vortex formation and evolution is responsible for enhanced boundary layer mixing of the airfoil upper surface.
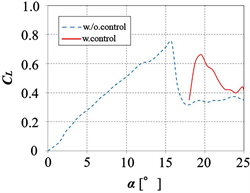
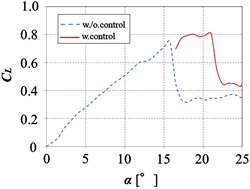
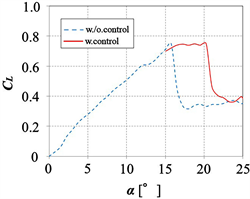
Figure 8. Lift curves in cases of different timing of jet operation (Re = 1.5 × 105, VR = 1.2, L0 = 12). (a) system operates after stall; (b) system operates just after stall; (c) system operates just before stall.
Figure 9. Schematic diagram of input signal.




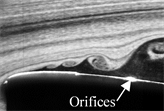
Figure 10. Schematic behavior of leading edge vortex at Re = 5.0 × 105, L0 = 12, AOA = 16˚. (a) under no control, (b) phase ①, (c) phase ②, (d) phase ③, (e) phase ④.
3.3. Applications to Time-Varying Flow with Changes in Angle of Attack
In order to adaptively suppress a stall, the proposed system was applied to time-varying flowfields caused by changes in the angle of attack of the airfoil. Figure 11 shows a time history of the differential pressure and lift coefficient when the angle of attack changes. Blue and red lines indicate the cases without and with control, respectively. In this example, the angle of attack is varied by α = 0˚ → 19˚ → 10˚ → 19˚ → 0˚ with a rate of change in the angle of attack of ω = 3.3˚/s, and the variation of the angle of attack is depicted by a green line. In these figures, the yellow circle and blue triangle symbols indicate the points of the angle of attack variations at which the jet starts (jet on) and stops (jet off) under the control system operation, respectively.
The synthetic jet is not issued when the system starts because a stall does not occur initially. Then, as the angle of attack increases, the system operates and starts the synthetic jets when in the middle of increasing the angle of attack for the case with control. The system senses a precursor of stall at this point because the tendency of differential pressure variation switches from increment to decrement. The yellow circle symbol indicates that the system senses the precursor of a stall owing to the differential pressure variation just before the whole separation occurs on the upper surface of the airfoil and starts the operation. In our proposed system, information about the angle of attack and the freestream velocity is not used to operate the system.


Figure 11. Time history of differential pressure and lift coefficient when our active stall control system operates to the time-varying flow fields. (a) differential pressure; (b) lift coefficient.
The flow conditions are judged only from the control variable corresponding to the differential pressure dp between two static pressure holes alone. If flow separation from the airfoil surface is detected and dp starts to decrease, the flow control starts to operate and the differential pressure can always be recovered. As shown in Figure 11(b), CL decreases when the angle of attack exceeds 16˚ ((α = 16˚) for the case without control, and does not decrease after issuing the synthetic jets for the case with control despite the increase in the angle of attack. After that, when the angle of attack is decreasing from 19˚ to 10˚ (0˚), the system stops operating the synthetic jets (indicated by the blue triangle symbols) owing to the unstalled flow field. The system detects the avoidance of a stall state at this angle of attack. Thus, the results of these tests confirm that our proposed system can sense the precursor of a stall and can completely attain the flow field with no stall under various changes in the angle of attack of the airfoil tasted in this experiment.
4. Conclusions
In the present study, an active separation control system using synthetic jets to attain airfoil stall suppression was developed and was practically applied to the stall control of the NACA0012 airfoil in a wind tunnel test. The main conclusions of this study are summarized as follows:
1) The maximum lift coefficient can be increased and a stall delay occurs by using the synthetic jets for freestream conditions examined in the present study.
2) The instability in the separated shear layer is promoted, and a large-scale vortex is observed by the periodic excitation of the synthetic jets. Furthermore, during the suction phase, the attached vortices are elongated along the upper surface of the airfoil, and the attaching region expands.
3) The active stall control system using synthetic jets successfully attains airfoil stall suppression, and can adaptively achieve the suppression of an airfoil stall for a time-varying flow field by changing the angle of attack.
4) Our proposed stall control system can be operated prior to the onset of a stall by sensing the precursor of a separation of the upper surface of the airfoil. Therefore, a flow condition with no separation on the upper surface can always be attained for time-varying separated flow fields.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Hasegawa, H. and Obayashi, S. (2019) Active Stall Control System on NACA0012 by Using Synthetic Jet Actuator. Journal of Flow Control, Measurement & Visualization, 7, 61-72. https://doi.org/10.4236/jfcmv.2019.71005
References
- 1. Johnston, J.P. (1999) Pitched and Skewed Vortex Generator Jets for Control of Turbulent Boundary Layer Separation: A Review. Proceedings of the 3rd ASME/JSME Joint Fluids Engineering Conference, San Francisco, CA, 18-23 July 1999, 1-10.
- 2. Zaman, K.B.M.Q. (1992) Effect of Acoustic Excitation on Stalled Flows over an Airfoil. AIAA Journal, 6, 1492-1499.
- 3. Hasegawa, H. and Kumagai, S. (2010) Active Boundary Layer Control System Using Vortex Generating Jets and Operating by the Detection of Precursor of Flow Separation. International Journal of Flow Control, 2, 155-167. https://doi.org/10.1260/1756-8250.2.3.155
- 4. Zhao, G.Q., Zhao, Q.J., Gu, Y.S. and Chen, X. (2016) Experimental Investigations for Parametric Effects of Dual Synthetic Jets on Delaying Stall of a Thick Airfoil. Chinese Journal of Aeronautics, 29, 246-357. https://doi.org/10.1016/j.cja.2016.02.010
- 5. Glezer, A. and Amitay, M. (2002) Synthetic Jets. Annual Review of Fluid Mechanics, 34, 503-529. https://doi.org/10.1146/annurev.fluid.34.090501.094913
- 6. Nicholas, W.R., Matthew J.B. and Michael A. (2014) Performance Enhancement of a Vertical Tail Using Synthetic Jet Actuators. AIAA Journal, 52, 810-820.
Nomenclature
A projected area of airfoil, m2
C cord length, m
CD drag coefficient (=L/(0.5ρ A))
CL lift coefficient (=D/(0.5ρ A))
D0 diameter of orifice, m
D drag, N
dP differential pressure, Pa
f diaphragm oscillation frequency, Hz
L0 dimensionless stroke length (=Vj/(fD0))
L lift, N
Re Reynolds number (=U0C/ν)
S span length, m
t time, s
T time period of a diaphragm oscillation cycle, s
U0 freestream velocity, m/s
VR jet-to-freestream velocity ratio (=Vj/U0)
Vj jet mean velocity, m/s
α angle of attack, deg
ν kinematic viscosity, m2/s
ρ density, kg/m3
ω rate of change in the angle of attack, deg/s