Journal of Flow Control, Measurement & Visualization
Vol.2 No.3(2014), Article ID:48099,5 pages
DOI:10.4236/jfcmv.2014.23014
Numerical Study on Nonlinear Sound Propagation for Parametric Array*
Kei Fujisawa
Department of Ocean Technology, Policy, and Environment, University of Tokyo, Tokyo, Japan
Email: fujisawa_ocean_eng@yahoo.co.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 April 2014; revised 26 April 2014; accepted 30 April 2014
ABSTRACT
This paper presents the numerical study on the nonlinear sound propagation for the parametric array using the compressible form of Navier-Stokes equations combined with the mass and energy conservation equations and the state equation. These governing equations are solved by finite difference time domain (FDTD) based method. The numerical result is shown for the parametric sound propagation in the near field of the sound source in cylindrical coordinate. The result indicates the generation of low-frequency unsteady beat by the interaction of two frequency sound waves in the near field, which grows to a difference frequency sound in the far field.
Keywords: Numerical Simulation, Nonlinear Sound Propagation, Parametric Array, FDTD

1. Introduction
The parametric array is a nonlinear transduction mechanism, which generates difference frequency sound of low frequency through the interaction of high-frequency sound waves of fundamental frequencies. The low-frequency sound generated from the parametric array is nearly side-lobe free and propagates for a long distance, while the emitted higher-frequency sound and the higher harmonics of nonlinear sound are attenuated during the propagation process due to the nonlinear effect of the fluid properties. Such parametric array has been applied to the highly directional loudspeaker, parametric sonar and so on.
The theory of nonlinear sound propagation of parametric array is first studied by Westervelt [1] , who derives the equations of low-frequency sound under the approximation of the nonlinear terms in the full second order wave equation. Later, Khokhlov-Zaboloskya-Kuznetsov (KZK) equation is derived from the Wetervelt equation under the assumption of parabolic approximation [2] . The KZK equation is solved numerically by Aanonsen et al. [3] and Kamakura et al. [4] for the study of parametric array, and the usefulness of this equation is experimentally confirmed by Garrett et al. [5] . It should be mentioned that the application of the KZK equation is limited to the far-field acoustics due to the parabolic nature of the KZK equations. In order to solve this problem, a few attempts have been carried out using the numerical technique for solving the full governing equations of nonlinear sound propagation for parametric array [6] [7] , while the mechanism of sound propagation in the near field has not been studied in detail. Such direct approach to the nonlinear sound propagation is important and should be further studied.
The purpose of this paper is to study the nonlinear sound propagation of parametric array based on the compressible form of Navier-Stokes equations combined with the mass and energy conservation equations and the state equation without the use of parabolic approximation. A few computational results are shown to visualize the interaction of sound waves in the near field of parametric array.
2. Numerical Methods
The nonlinear sound propagation is described by the compressible form of Navier-Stokes equations, the mass and energy conservation equations and the state equation, which can be written in the following form in cylindrical coordinate system under the axisymmetric assumption [7] :
 (1)
(1)
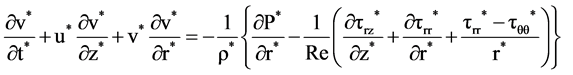 (2)
(2)
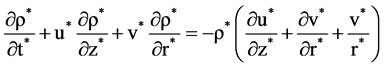 (3)
(3)
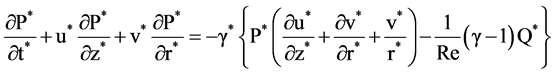 (4)
(4)
 (5)
(5)
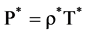 (6)
(6)
where the physical quantities with * are non-dimensional variables, such
as r* = k0r,
 ,
,
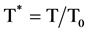 ,
,
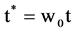 ,
,
 ,
,
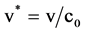 ,
,
 ,
,
 ,
,
 , where subscript 0 denotes the reference quantities.
r and z are radial and axial coordinates, respectively, u and v are velocity components
in axial and radial directions, respectively, P is the pressure, T is the temperature,
ρ is the density and τ is the stress tensor.
, where subscript 0 denotes the reference quantities.
r and z are radial and axial coordinates, respectively, u and v are velocity components
in axial and radial directions, respectively, P is the pressure, T is the temperature,
ρ is the density and τ is the stress tensor.
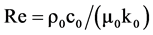 is the Reynolds number and
is the Reynolds number and
 is the Prandtl number, where Cp: specific heat at constant pressure,
c0: sound velocity, k0: wave number and μ0: viscosity.
Then, the governing equations are summarized in the following compact form using
the operator splitting method [7]
.
is the Prandtl number, where Cp: specific heat at constant pressure,
c0: sound velocity, k0: wave number and μ0: viscosity.
Then, the governing equations are summarized in the following compact form using
the operator splitting method [7]
.
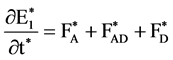 (7)
(7)
where
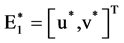 (8)
(8)
 (9)
(9)
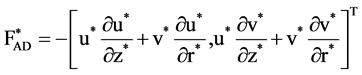 (10)
(10)
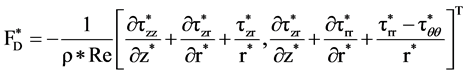 (11)
(11)
 (12)
(12)
where
 (13)
(13)
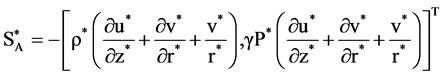 (14)
(14)
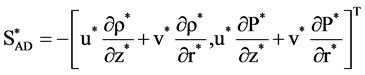 (15)
(15)
 (16)
(16)
The subscripts A, AD and D denote the acoustic term, advection term and dissipative term, respectively. These equations are discretized using FDTD based method and the velocities u, v, density ρ, pressure P are solved by numerical computation. It should be mentioned that the 2nd order difference scheme is applied to the acoustic terms in space and time, the 1st order upwind difference scheme is used for the advection terms and the 2nd order central difference scheme is used for the dissipative terms. In the numerical simulation, the staggered grid system is used. The computational domain in cylindrical coordinate is illustrated in Figure 1. The boundary condition for sound pressure at the inlet is prescribed by the two sinusoidal frequencies f1 and f2 with an amplitude Pm, which is written by the following equation.
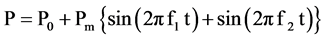 (17)
(17)
The surrounding boundary condition for sound pressure is given by the Mur 1st absorbing condition to minimize the reflection of sound at the boundary [8] .
3. Results and Discussions
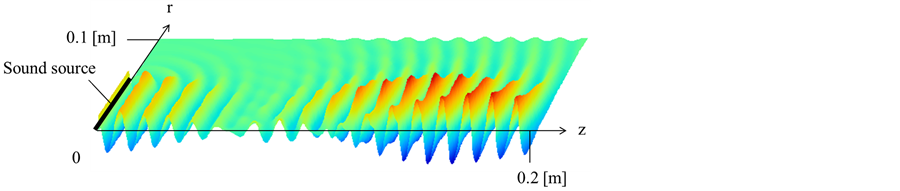
The numerical simulation is carried out for the parametric sound propagation from a circular disk sound source in a fluid of air at temperature 293 K, as shown in Figure 1. The sound source is set to z = 0 m and the height is 0.05 m with a uniform sound intensity. The characteristic properties of the air used in the present computation is as follows: the sound speed c0 = 3.468 × 102 m/s, the density ρ0 = 1.184 kg/m3, the pressure P0 = 1.013 × 105 Pa, the viscosity μ0 = 1.802 × 10−5 Pas, the thermal conductivity κ0 = 2.600 × 10−2 W/(m·K), the specific heat at constant pressure Cp = 1.006 × 103 J/(kg·K) and the specific heat ratio γ = 1.403. The two frequencies of parametric sound is set to f1 = 30 kHz and f2 = 32 kHz with the same amplitude Pm = 500 Pa, while the comparative study is carried out for the single frequency sound at f1 = 30 kHz. In the numerical simulation, the cell size is set to Δz = Δr = λ/40 (λ: wavelength of sound), which corresponds to the number of grids 692 × 692 in the present computational domain of interest 0.2 m × 0.2 m. The increment of time step (=0.235 μs) is determined to satisfy Courant-Friedrichs-Lewy (CFL) condition [9] . It should be mentioned that the validation of the present simulation code is confirmed in comparison with the reported result in literature [7] .
Figure 2 shows the numerical results of sound wave propagation in the near field, which compares the sound propagation of the parametric sound with frequencies f1 = 30 kHz and f2 = 32 kHz (a) and that of the single frequency f1 = 30 kHz (b). Both results are compared at the same computational time of 4000 steps, which corresponds to the time t = 0.94 ms after the sound emission. The observation of the sound propagation for parametric sound indicates that the low amplitude of sound pressure is found around x = 0.08 m and the high amplitude is detected around x = 0.16 m along the axis of sound propagation. These are due to the result of

Figure 1. Computational domain for parametric array.
 (a)
(a)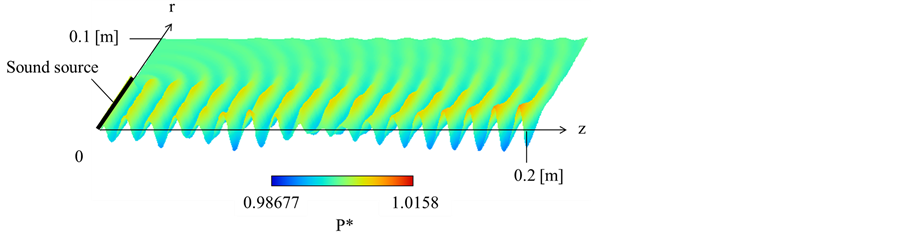 (b)
(b)
Figure 2. Visualization of sound wave propagation. (a) Parametric array; (b) Single frequency sound.
sound interference of two fundamental sound frequencies which is known as beat, and is perceived by the periodic variations in pressure wave whose rate is the difference of the two frequencies. The highest peak of the pressure wave does not necessary locate in the centerline of the sound, which shows the interference of the sound wave emitted from various radial positions of the sound source. The sound wave in the outer part of the sound source indicates the circular development of the sound wave from the edge of the sound source. On the other hand, the sound propagation of the single frequency (b) indicates almost uniform sound wave propagation in axial direction and the magnitude of the sound wave is smaller than the parametric case.
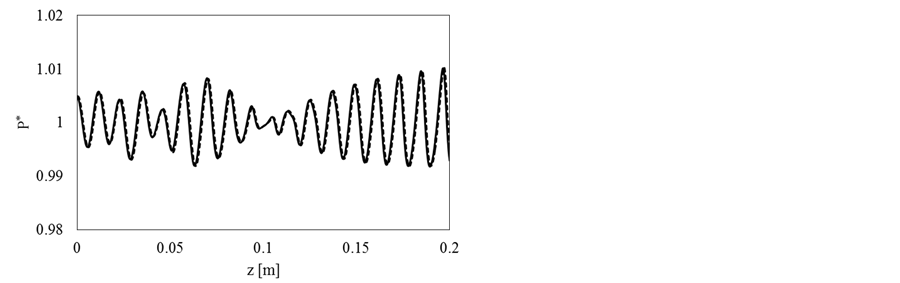
Figure 3 shows the comparison of the pressure waves at two different time steps for the parametric array (a) and for the single frequency sound (b). Although the pressure wave for the single frequency does not change with the time steps, the pressure wave of the parametric sound varies with the time steps and the result indicates the generation of unsteady low frequency beat in the near field. Note that the modulation of the pressure wave for the single frequency case is also due to the non-linear effect of sound propagation. This result suggests that the difference frequency sound is generated in the near field due to the interference of two fundamental frequencies of emitted sound from the parametric array. This result may not be obtained from the computation under the assumption of parabolic approximation in literature.
4. Conclusion
The propagation of sound emitted from the parametric array is numerically studied by solving compressible
 (a)
(a) (b)
(b)
Figure 3. Sound pressure distribution along sound axis (-4000 step, t = 0.94 ms; - - - 5000 step, t = 1.18 ms). (a) Parametric array; (b) Single frequency sound.
form of Navier-Stokes equations combined with the mass and energy conservation equations and the state equation without assuming parabolic approximation. The numerical result shows the generation of low-frequency unsteady beat due to the interference of two fundamental frequency sounds in the near field, which grows to a difference frequency sound in the far field.
Acknowledgements
The authors would like to thank to Prof. H. Nomura and Prof. T. Kamakura from the University of ElectroCommunications and Prof. Y. Kawaguchi and Prof. A. Asada from the University of Tokyo for their helpful advices during the course of this study.
References
- Westervelt, P.J. (1963) Parametric Acoustic Array. Journal of Acoustical Society of America, 35, 535-537. http://dx.doi.org/10.1121/1.1918525
- Kuznetsov, V.P. (1975) Equations of Nonlinear Acoustics. Soviet Physics Acoustics, 16, 467-470.
- Aanonsen, S.I., Tjotta, J.N. and Tjotta, S. (1984) Distortion and Harmonic Generation in the Nearfield of a Finite Amplitude Sound Beam. Journal of Acoustical Society of America, 75, 749-768. http://dx.doi.org/10.1121/1.390585
- Kamakura, T., Hamada, N., Aoki, K. and Kumamoto, Y. (1989) Nonlinearly Generated Spectral Components in the Nearfield of a Directive Sound Source. Journal of Acoustical Society of America, 85, 2331-2337. http://dx.doi.org/10.1121/1.397778
- Gaete-Garreton, G.S. and Gallego-Juarez, J.A. (1983) Propagation of Finite-Amplitude Ultrasonic Waves in Air: Part 2 Plane Waves in Air. Journal of Acoustical Society of America, 74, 1013-1020.
- Huijssen, J., Bousakaz, A., Verweij, M.D. and De Jong, N. (2003) Simulation of the Nonlinear Acoustic Pressure Field without Using the Parabolic Approximation. IEEE Ultrasonic Symposium, No. 1854.
- Nomura, H., Hedberg, C.M. and Kamakura, T. (2012) Numerical Simulation of Parametric Sound Generation and Its Application to Length-limited Sound Beam. Applied Acoustics, 73, 1231-1238. http://dx.doi.org/10.1016/j.apacoust.2012.02.016
- Mur, G. (1981) Absorbing Boundary Condition for the Finite-Difference Approximation of the Time-Domain Electromagnetic-Field Equation. IEEE Transaction on Electromagnetic Compatibility, EMC-23, 377-382. http://dx.doi.org/10.1109/TEMC.1981.303970
- Lax, P.D. and Wendroff, B. (1964) Difference Schemes for Hyperbolic Equations with High Order of Accuracy. Communications on Pure and Applied Mathematics, 17, 381-398. http://dx.doi.org/10.1002/cpa.3160170311
NOTES

*Short paper.

