ABSTRACT

In this paper, a variable metric algorithm is proposed with Broyden rank one modifications for the equality constrained optimization. This method is viewed expansion in constrained optimization as the quasi-Newton method to unconstrained optimization. The theoretical analysis shows that local convergence can be induced under some suitable conditions. In the end, it is established an equivalent condition of superlinear convergence.

1. Introduction & Algorithm

This In this paper, it is proposed to consider the following nonlinear mathematical programming problem:

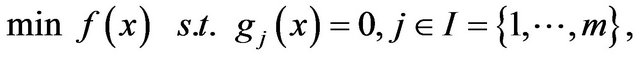(1)

where are continuously differentiable functions. Denote the feasible set as follows:

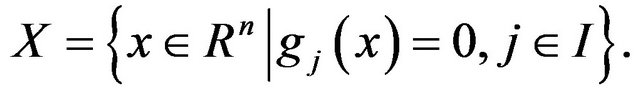
Let 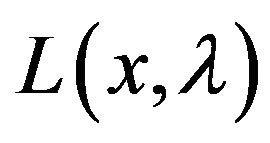be Lagrangian function of (1), and

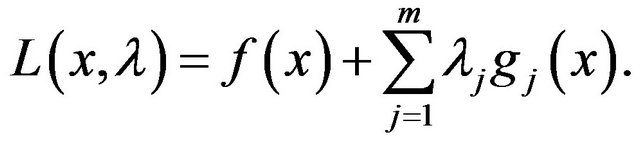
If is a KKT point pair of Equation (1), then

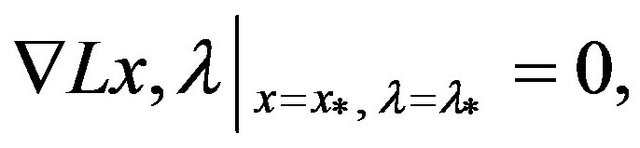i.e.,

(2)

where

At the point pair, the Newton’s iteration of (2) is defined as follows:

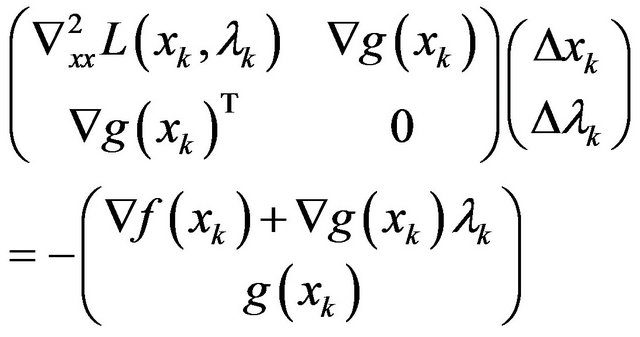(3)

Later, a positive definite matrix 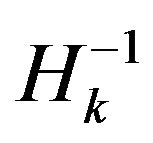is replaced for

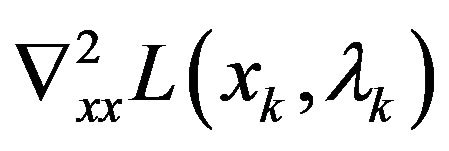by a lot of authors to develop some kinds of variable metric methods, such as sequential quadratic programming (SQP) methods [1-5], sequential systems of linear equations (SSLE) algorithms [6-8]. In general, the computational cost of those methods is large.

In this paper, a new variable metric method is presented, in which the following fact is based on: a positive definite matrixis replaced for the matrix

.

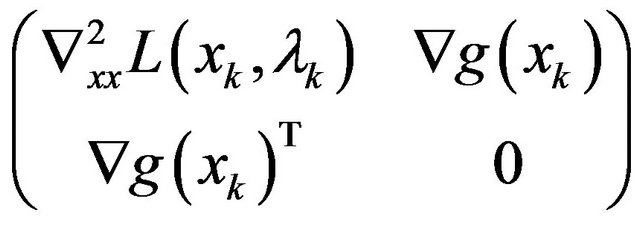In the sequel, we describe the algorithm for the solution of (1). Denote

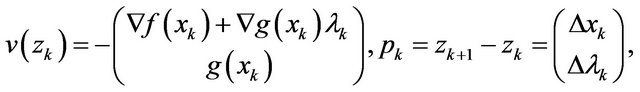
It is obvious that and from Equation (3), we have

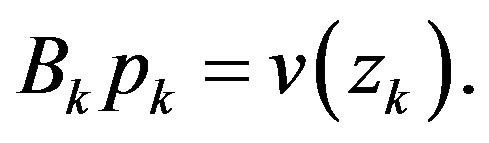(4)

To the system of linear Equations (4), like unconstrained optimization, 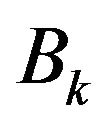is dealt with using Broyden rank one modifications as follows:

(5)

Now, the algorithm for the solution of Equation (1) can be stated as follows:

Algorithm A:

Step 1: Initialization: Given a starting point (i.e.,), and a initial positive definite matrix.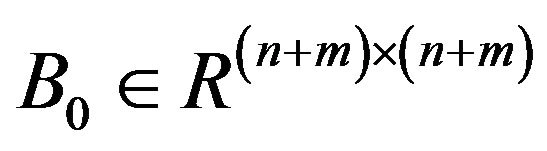

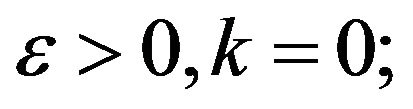
Step 2: Compute. If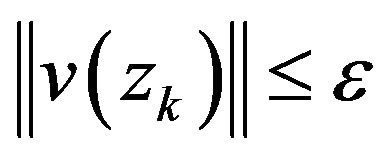, stop;

Step 3: Compute;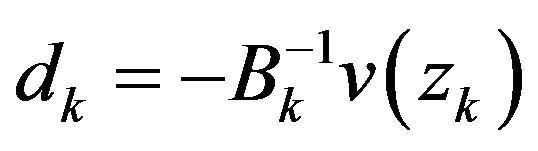

Step 4: Let, and obtain according to (5). Set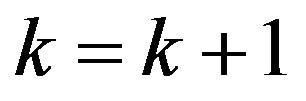. Go back to step 2.

2. Convergence of Algorithm

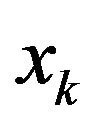If the algorithm stops at, then is a KKT point of (1). In the sequel, we suppose that algorithm generates an infinite sequence.

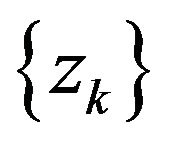Four basic assumptions are given as follows:

A1 The feasible set 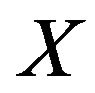is nonempty; The functions

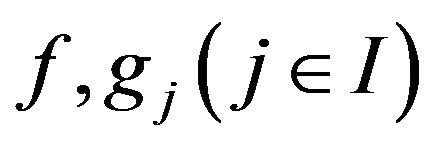are two-times continuously differentiable;

A2 For all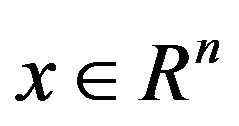, the vectors are linearly independent;

A3 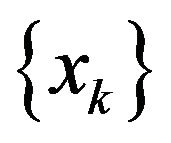and 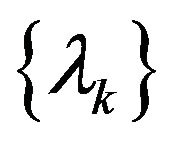are bounded. There exists a KKT point pair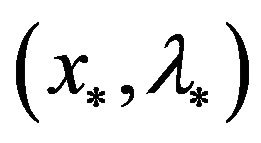, such that is positive definite;

A4 There exists a ball 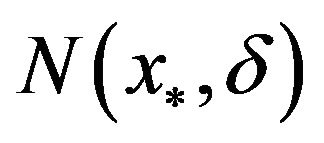of radius 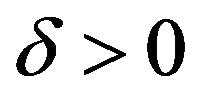about, where 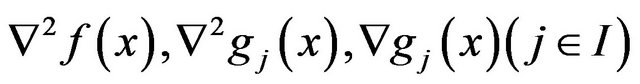satisfy the Lipschitz condition on.

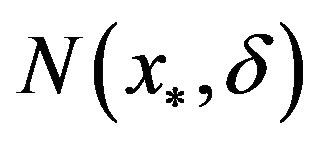Lemma 1 [9] Let 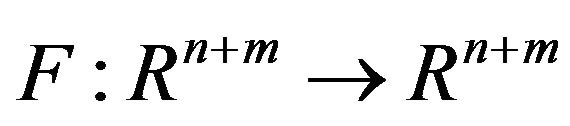be continuously differentiable in some open and convex set, and 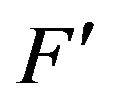is Lipschitz continuous in, then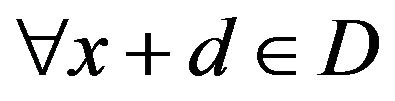, it holds that

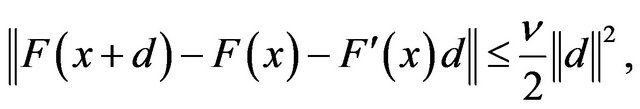
where 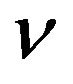is the Lipschitz constant. Moreover,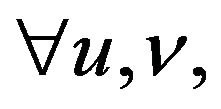

, it follows that

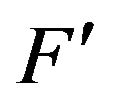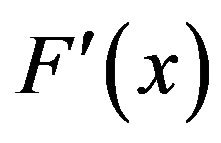Lemma 2 [9] Let be continuously differentiable in some open and convex set, and is Lipschitz continuous in. Moreover, assume is invertible for some, then there exist some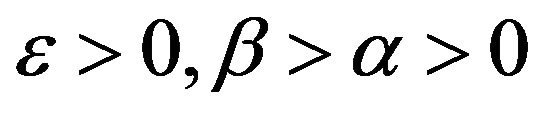, such that for all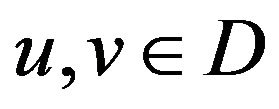, the fact

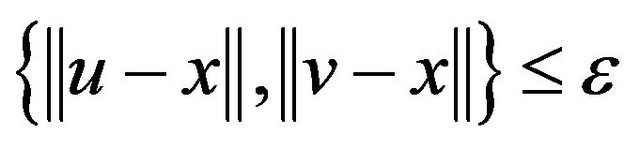implies that

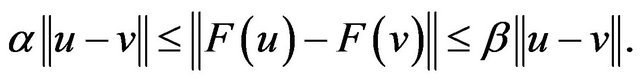
Lemma 3 [9] For operator, which satisfies:

R1 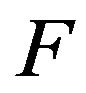is continuously differentiable on;

R2 There exists a point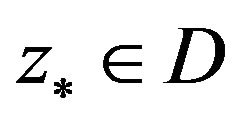, such that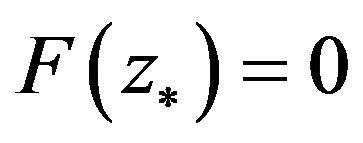, and is reversible;

R3 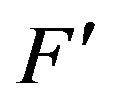is Lipschitz continuous at, i.e., there exists a constant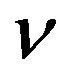, such that

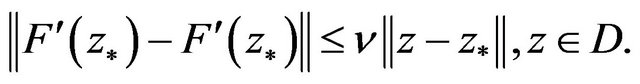
Let, where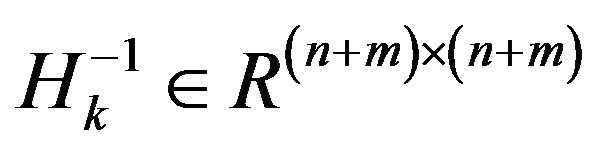, and it holds that

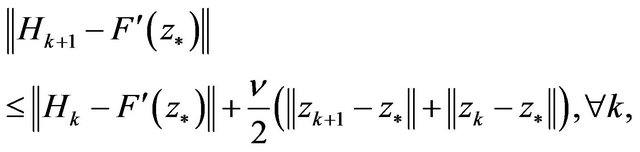(6)

then there exist 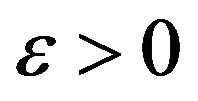and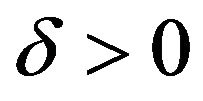, when

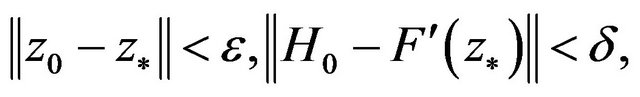
it is true that is meaning, and is linearly convergent to. Thereby, we can conclude that is superlinearly convergent to, if and only if

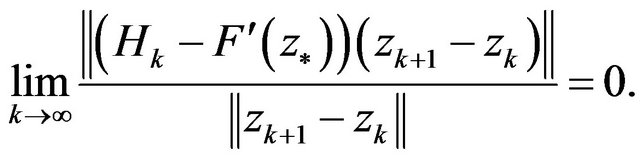(7)

In the sequel, we prove the convergence Theorem as follows:

Theorem 1 If there exist constants and such that

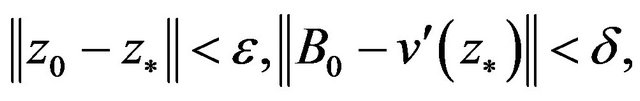
then 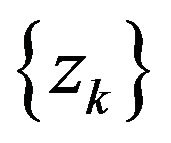is meaning, and 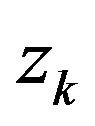is linearly convergent to

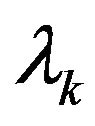, thereby and are linearly convergent to and respectively.

Proof: From Lemma 3, we only prove that 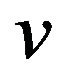and 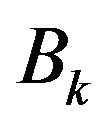satisfy conditions R1, R2, R3 and the inequality (6). From assumption A1, it is obvious that is continuously differentiable. From A3, it holds that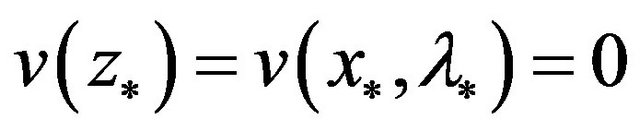, and

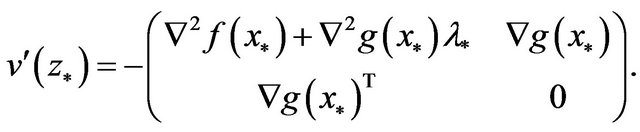
While is positive definite, and 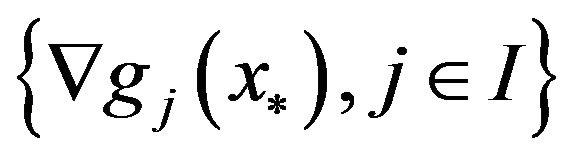are linearly independent. So, it is easy to see that 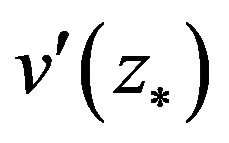is reversible. In addition,

From assumption A4, it holds that 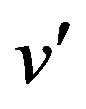is Lipschitz continuous at. In a word, 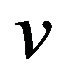satisfies the conditions R1, R2, R3.

Now, we prove that, for and generated according to (5), (6) is satisfied.

In fact, from (5), we have

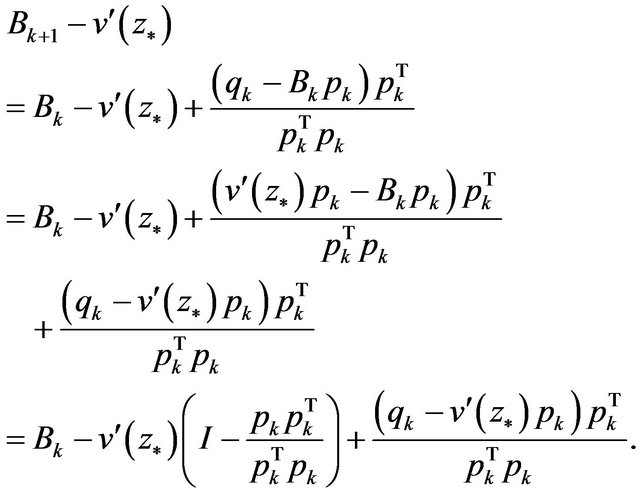(8)

So,

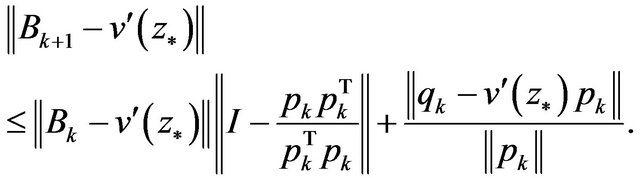
While

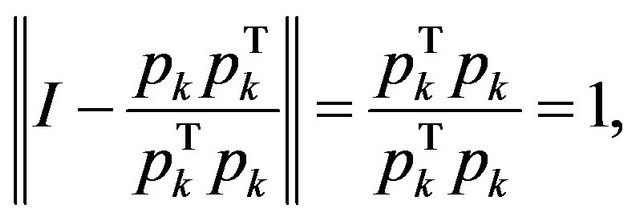
and from Lemma 1, we have

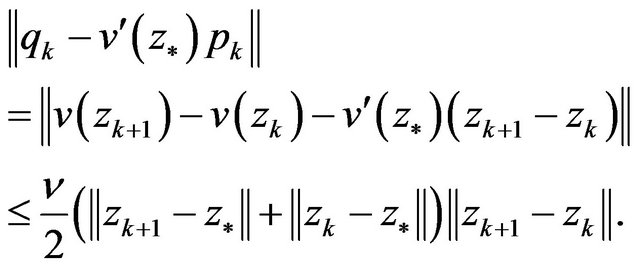(9)

So,

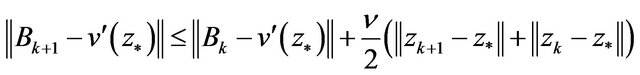i.e., (6) is true, thereby, from Lemma 3, we get

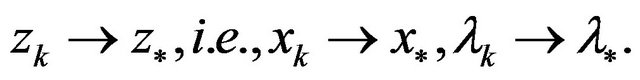
The claim holds.

Theorem 2 Under above-mentioned assumptions, if, in Theorem 1 satisfy that

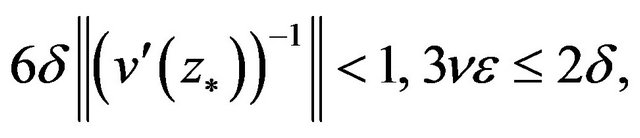(10)

then is superlinearly convergent to, i.e.,

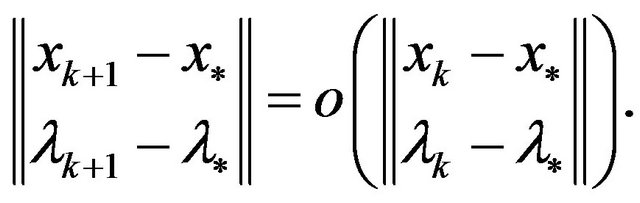
Proof. From Lemma 3, we only prove that 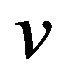and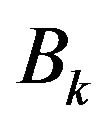

satisfy (7). Denote, 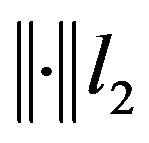norm, 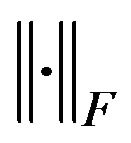Frobenius norm. From (8),

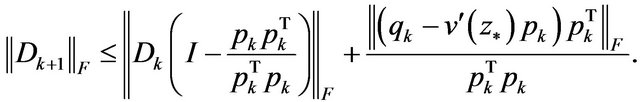(11)

Since

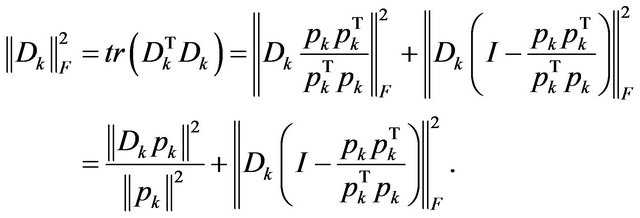
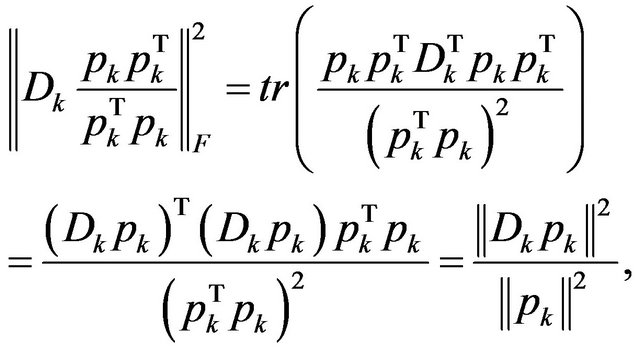
So,

(12)

In addition, from (6), (10), using the method of mathematical induction, it is not difficult to prove that

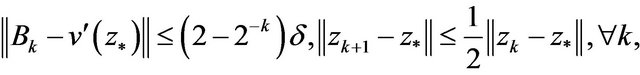(13)

thereby,

(14)

Thus, from (9), (12), (13), we have

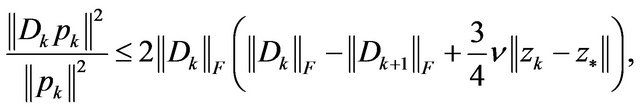
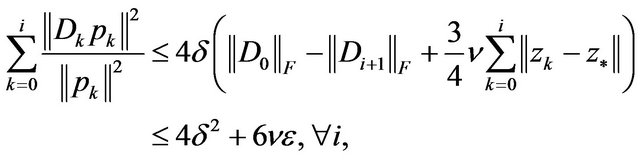
i.e. 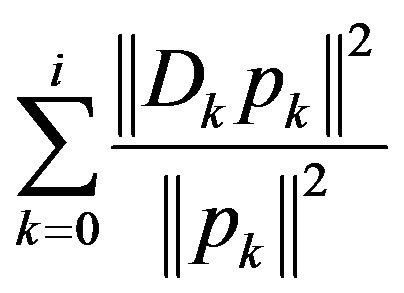is convergent, thereby,

From Theorem 2, we don’t conclude that 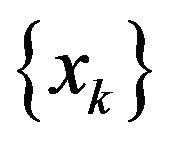is superlinearly convergent to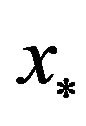, i.e.,

In the sequel, we discuss one condition which assures that 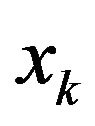is superlinearly convergent to.

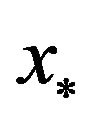Lemma 4 Let be a function defined by

where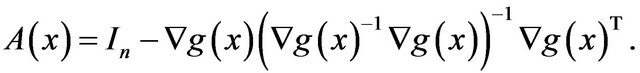

Then, 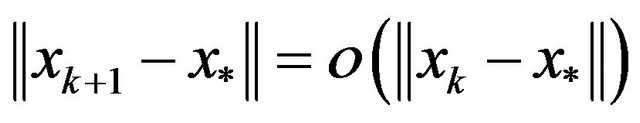, if and only if

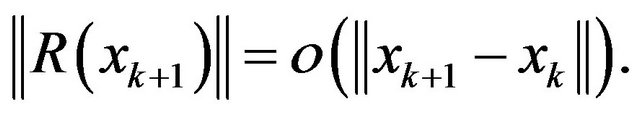
Proof. Obviously, using the triangle inequality, it holds that

In addition, from A1, we know that 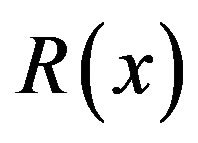is continuously differentiable, and

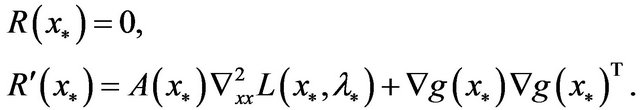(15)

It holds that is nonsingular. In fact, let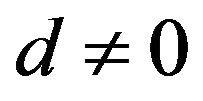, and

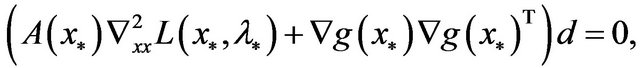
the facts that 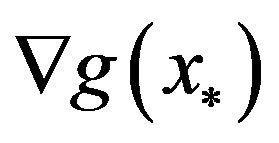has full rank, 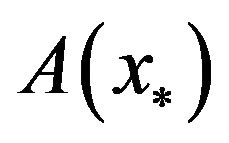is semi-positive definite and 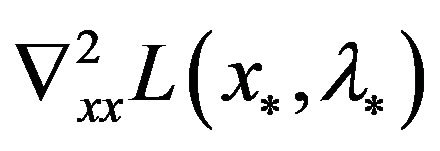is positive definite imply that

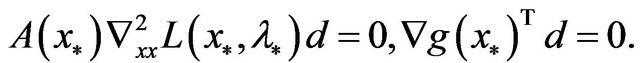
So,

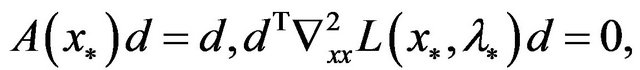
which is a contradiction.

Thereby, from A4 and Lemma 2, there exist , such that

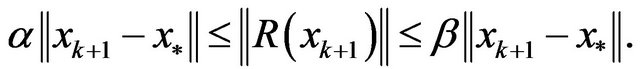
So,

.

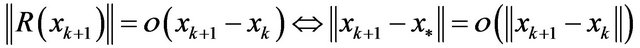The claim holds.

Theorem 3 Under above-mentioned conditions,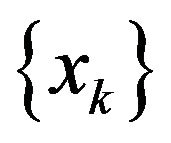

is superlinearly convergent to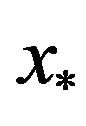if and only if

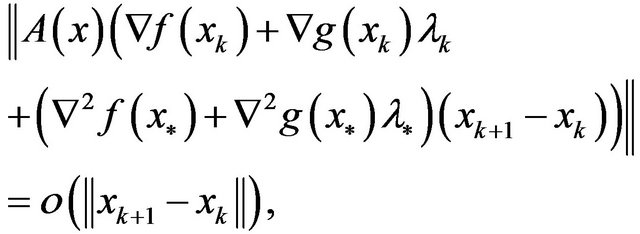
and 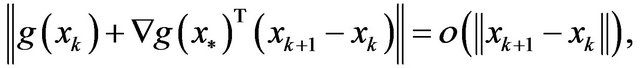i.e.,

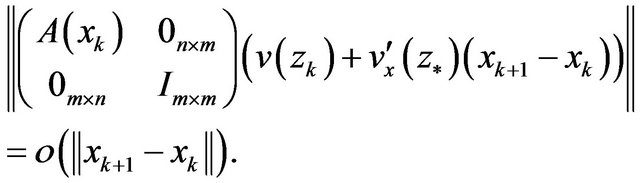(16)

Proof. The sufficiency: Suppose that (16) holds. We only prove that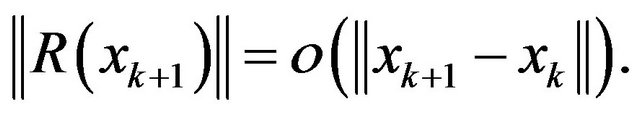

From (4), we have

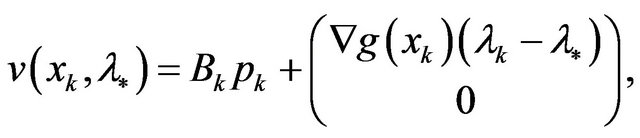
So, the fact 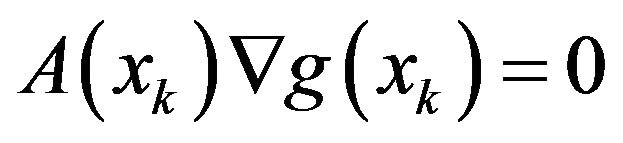implies that

thereby,

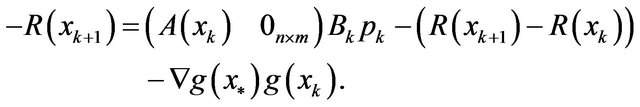
From (15), we have

So,

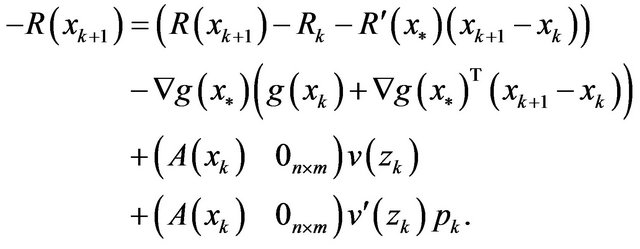
While

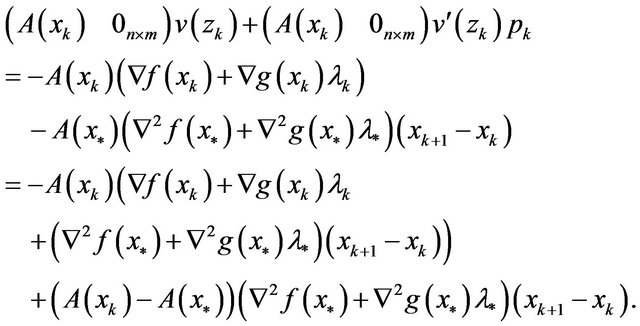
In addition, according to Lemma 1, we have

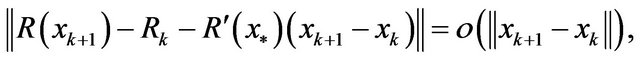
so, from (16), it holds that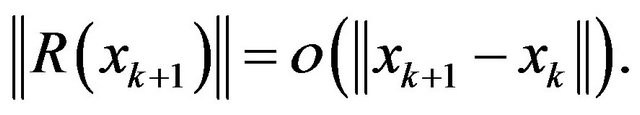

The necessity: Suppose that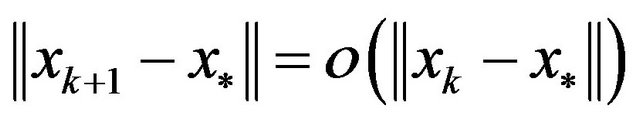

i.e.,

On one hand,

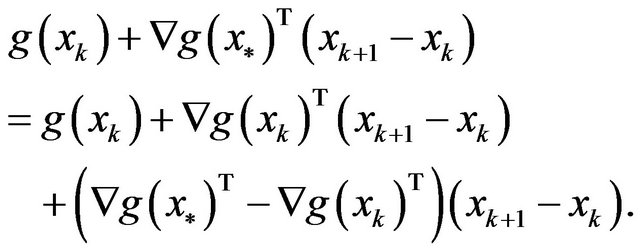
So, in order to prove that

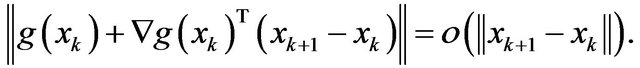
While

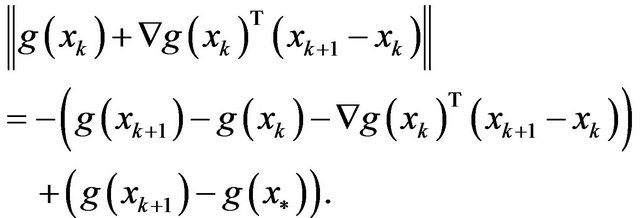
According to Lemma 1, we have

and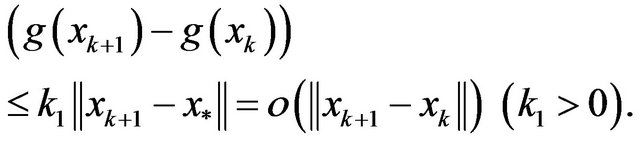

So,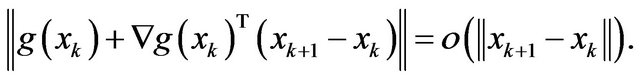

On the other hand, the fact 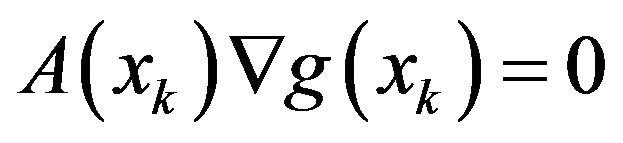implies that

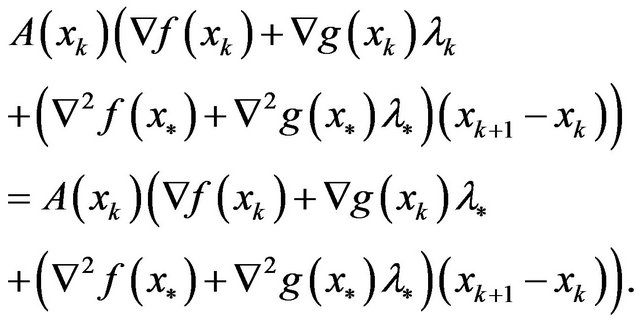
Let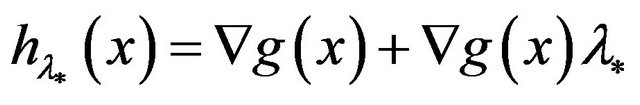, then

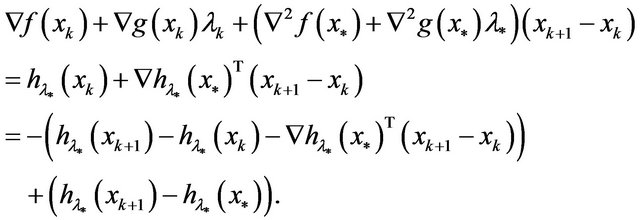It is easy to see that

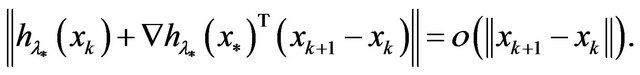
Thereby,

The claim holds.

3. Acknowledgements

This work was supported in part by NNSF (No. 11061 011) of China and Guangxi Fund for Distinguished Young Scholars (2012GXSFFA060003).

REFERENCES