Journal of Minerals and Materials Characterization and Engineering
Vol.02 No.06(2014), Article ID:51283,12 pages
10.4236/jmmce.2014.26058
Optimization of Carburized UNS G10170 Steel Process Parameters Using Taguchi Approach and Response Surface Model (RSM)
Olawale Samuel Fatoba1*, Olaitan Lukman Akanji1, Abiodun Samson Aasa2
1Department of Chemical, Metallurgical and Materials Engineering, Tshwane University of Technology, Pretoria, South Africa
2Department of Mechanical Engineering, University of Pretoria, Pretoria, South Africa
Email: *fatobaolawale@yahoo.com, *FatobaOS@tut.ac.za
Academic Editor: Jiann-Yang (Jim) Hwang, Michigan Technological University, USA
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 July 2014; revised 9 October 2014; accepted 30 October 2014
ABSTRACT
The utilization of carburizing materials in surface engineering has undergone many tremendous changes. Effective quality control is possible through carburizing the steel components under optimal conditions. In this research work, process parameters like furnace temperature, soaking time and particle size of energizer were taken for optimization of carburized UNS-G10170 steel to yield maximum hardness using Taguchi’s design of experiment concepts and Response Surface Model. Nine experimental runs based on Taguchi’s L9 orthogonal array were performed; signal to noise (S/N) ratios, analysis of variance (ANOVA) and regression analysis were used with hardness as response variable. From the optimization and experimental analyses conducted, it was observed that furnace temperature, soaking time and particle size had significant influence in obtaining a better surface integrity. The optimal values obtained during the study optimization by Taguchi approach and Response Surface Model (RSM) were validated by confirmation experiments.
Keywords:
ANOVA, S/N Ratios, Taguchi Method, Hardness, RSM, Optimization

1. Introduction
Steels are alloys of iron and carbon containing up to 1.5% of carbon. There are many forms of steel each of which is designed to serve a particular application in the field of engineering. An active research area is the surface engineering of components to improve the life and performance of parts used in automobiles and aerospace [1] .
Mild steel, by reasons of its dominance and workability among the classes of steel [2] , has found a broad relevance in the production of engineering components like cams, gears, shafts, pinions, keys, hand tools, agricultural equipment, etc. These components require the mechanical properties of impact strength, hardness and tensile strength for their safe and durable purposes.
The addition of carbon to the surface of low-carbon steels at temperatures within the austenitic region of the steel concern is called carburizing, which usually is between 850˚C and 950˚C for mild steels. Within this austenite temperature range, there is high solubility for carbon which is the stable crystal structure. When the subsequent high-carbon surface layer is quenched to form martensite hardening is accomplished, so that a high-carbon martensitic case with good fatigue and wear resistance is superimposed on a tough, low carbon steel core [3] -[5] .
The inward diffusion of carbon takes place at a rate which depends on the chemical composition of the steel, the carburizing temperature and the chemical composition of the carburizing mixture [6] [8] [10] [12] . For a successful carburization, a control of all these parameters; the carburizing temperature, carburizing time, and chemical composition of the carburizing compound must be achieved [7] [9] [11] . The study of process parameters in metals during heat treatment has been of considerable interest for some years [7] -[9] [13] ; but there has been relatively little work on optimization of process variables during the surface hardening process [14] since controlling parameters in carburization is a complex problem. Thus, the optimization of particle sizes, volume fractions of energizer, carburizing temperature and soaking time becomes imperative.
Response Surface Model (RSM) is a statistical tool and powerful mathematical method with a collection of statistical techniques by which interaction between multiple process variables can be identified with fewer experimental trials. It is widely used to examine and optimize the operational variables for experimental design, model development, test variables and condition optimization. While two major tools used in Taguchi method are the orthogonal array (OA) and the signal to noise ratio (SNR or S/N ratio). OA is a matrix of numbers arranged in rows and columns. Taguchi’s methods in general provide a significant reduction in the size of experiments, thereby speeding up the experimental process [15] . Efficiency of this method depends on the selection of suitable orthogonal array. The S/N ratio is expressed in decibels (dB). Theoretically, the S/N ratio is the ratio of signal to noise in terms of power.
Noorul and Jeyapaul [16] adopted orthogonal array, Grey relational analysis in the ANOVA using Taguchi method to find suitable level of indentified parameters, and significant association of parameters in order to increase response efficiency of the parameters. [15] -[19] proposed the efficient use of Taguchi’s parameter design to obtain optimum condition because it leads to minimum number of experimental and lower cost. Palanikumar et al. [20] adopted Response Surface Methodology in analyzing the variance for verification model in order to increase efficiency of cutting parameters for surface roughness. Statistical methodologies give rapid and reliable short-listing of process conditions, understanding interaction among them, and a tremendous reduction in total number of experiments, resulting in saving time, materials, chemicals and manpower. In spite of various advantages, statistical designs have been applied only to limited number of manufacturing processes.
This research work mainly focuses on the carburizing process parameters optimization of Graphite/Seashell media using UNS-G10170 steel specimen by Taguchi’s L9 orthogonal array concept and Response Surface Model (RSM), and thereby determining the optimum values which will maximize the hardness value.
2. Experimental Procedure
2.1. Materials and Preparation
A flat bar of mild steel obtained was analyzed and its nominal chemical composition is given in Table 1.
Table 1. Chemical composition of UNS-G10170 steel.
The prepared UNS-G10170 steel samples were embedded in the carburizing box, which was first filled with the carburizing agent (Graphite) with appropriate energizer (Graphite/Sea shell) of particles 45 µm, 60 µm and 90 µm with volume fraction of 90/10%, 80/20% and 70/30% which was then tightly sealed with clay cover to prevent unwanted furnace gas from entering the carburizing box during heating. The furnace temperatures were adjusted to the required temperature (870˚C, 910˚C & 940˚C), and the loaded steel carburizing box was charged into the furnace. When each of the furnace temperature reaches the required carburizing temperature, it was then soaked at the temperature for the required time (3, 6 and 9 hours). The material was held at the specified time, the steel carburizing box was removed from the furnace and the material was quenched in oil. The typical characteristic of the quenching oil is shown in Table 2. The carburizing process was carried out in various batches in accordance with volume fraction set.
Table 2. Typical characteristics of the quenching oil (As specified by the producer. Petro-Canada).
The carburized test samples were tempered at a temperature of 200˚C held for an hour and then quenched in oil. Hardness of the carburized UNS-G10170 steel was determined using a Rockwell micro-hardness tester. The same trial was repeated three times to reduce experimental errors, and the average value was quoted as the final hardness.
2.2. Design of Experiment (Taguchi’s Technique)
Taguchi method based design of experiments has been used to study the effects of three process parameters i.e. temperature, soaking time and particle size on hardness output parameter. Taguchi approach provides a new experimental strategy in which a modified and standardized form of design of experiment (DOE). This technique helps to study effect of many factors (variables) on desired quality characteristic most economically. By studying the effect of individual factors on the results, the best factor combination can be determined [21] . Experiments were conducted based on the Taguchi’s method at three levels, each level with three factors. The values taken by a factor are termed to be levels. The factors to be studied and their levels chosen are detailed in Table 3.
Table 3. Carburization parameters and their levels.
2.2.1. Signal-to-Noise Ratio (S/N Ratio)
Taguchi recommends the use of the S/N ratio to measure the quality characteristic deviating from the desired values. The method of modelling the S/N ratio depends on whether the quality characteristic is smaller-the-better, larger-the-better, or nominal-the-best [22] -[25] . The S/N ratio for micro-hardness is calculated using the higher- the-better criterion as depicted in Equation (1).
2.2.2. Higher-the-Better
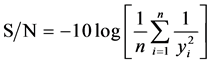 (1)
(1)
where 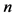 is the number of experiments in the orthogonal array and
is the number of experiments in the orthogonal array and 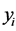 the
the 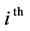 value measured. From the orthogonal array used, it is possible to get the effects of each factor at different levels. For instance, the average S/N ratio for factor A at levels 1, 2, and 3 can be obtained by calculating the mean of S/N ratios for trials 1 - 3, 4 - 6, and 7 - 9 respectively. The mean S/N ratio for each level of all other factors is computed in similar fashion. Here, the L9 orthogonal array is used for experimental investigations. The L9 experimental micro-hardness results are tabulated, and the corresponding mean S/N ratio results are calculated by using Equation (1). Table 4 shows the input into the Design Expert 6.0.6 and Minitab 16 software to design the experiment. The software generated the designed experiment as presented in Table 4. Regardless of the category of the performance characteristics, the larger algebraic value of S/N ratio corresponds to the better performance characteristic, and hence the optimal level of the parameter is the level with the highest S/N. In Taguchi method, optimal parameters are usually determined using the analysis of means [ANOM] as shown in Table 5. ANOM is a statistical
value measured. From the orthogonal array used, it is possible to get the effects of each factor at different levels. For instance, the average S/N ratio for factor A at levels 1, 2, and 3 can be obtained by calculating the mean of S/N ratios for trials 1 - 3, 4 - 6, and 7 - 9 respectively. The mean S/N ratio for each level of all other factors is computed in similar fashion. Here, the L9 orthogonal array is used for experimental investigations. The L9 experimental micro-hardness results are tabulated, and the corresponding mean S/N ratio results are calculated by using Equation (1). Table 4 shows the input into the Design Expert 6.0.6 and Minitab 16 software to design the experiment. The software generated the designed experiment as presented in Table 4. Regardless of the category of the performance characteristics, the larger algebraic value of S/N ratio corresponds to the better performance characteristic, and hence the optimal level of the parameter is the level with the highest S/N. In Taguchi method, optimal parameters are usually determined using the analysis of means [ANOM] as shown in Table 5. ANOM is a statistical
Table 4. Orthogonal Experimental results for micro-hardness and S/N ratio.
Table 5. Response table for signal to noise ratios.
approach of estimating the mean S/N ratios for each parameter and each of its levels. However, when there are significant interactions between factors, the optimal parameter levels are more accurately determined using the analysis of variance [ANOVA] and by considering the interaction plots. Analysis of variance (ANOVA) is performed to see which process parameters are statistically significant. With the S/N and ANOVA analyses, the optimal combination of the process parameters can be predicted. Finally, a confirmation experiment is conducted to verify the optimal process parameters obtained from the parameter designed [26] .
3. Results and Discussion
The Taguchi optimization method consists of the following steps: Each S/N ratio can be obtained from observations according to the formula of higher the better. For each significant factor, the level corresponding to the highest S/N ratio is chosen as its optimum level. A search for the factors that have a significant effect on the S/N ration is then performed through analysis of variance (ANOVA) of the S/N ratios [22] [23] .
Table 4 shows the average value of the hardness for each experimental point, as well as S/N ratios calculated by Equation (1). Average effect of each factor on the multiple quality characteristic at different levels was calculated. This is equal to the sum of all S/N ratios corresponding to a factor at a particular level divided by the number of repetitions of the factor level [23] . For example, the average S/N ratio of factor C at level 3 is calculated as being
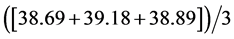
Response graphs shown in Figures 1(a)-(e) are drawn using the values in Table 5 through Design Expert 6.0.6 statistical software (α = 0.05) and Minitab 16 statistical software. The factor levels corresponding to the maximum average effect are selected as the optimum level. The average factor effect is shown in Table 5, and the main effect plotted for SNR is shown in Figure 1(a). The delta values from Table 5 were calculated by subtracting the largest value from the lowest among the values in each column. Optimum condition for surface hardness is found by adopting the higher the S/N ratio is better as strategy. The largest S/N ratio for each factor would be preferred. Hence, the optimum (Maximum Hardness) setting of the parameters is A2B3C1. Corresponding parameter values are listed in Table 6.
Table 6. Optimum parameters.
Main effects plots of factors can be used to depict a prelude conclusion about effects of processing parameters. These plots are shown in Figures 1(a)-(e). The furnace temperature peaked at 910˚C at soaking time of 9 hrs with energizer (seashell) particle size of 45 micron at hardness and S/N ratio values of 92 HRB and 39.28 dB for both plots in Figure 1(a) & Figure 1(b).
Figures 1(c)-(e) showed the interactions between processing parameters. Out of the three furnace temperatures (870˚C, 910˚C, 940˚C), 910˚C performed better at different particle sizes and gave increased hardness values at increasing soaking time as shown in Figure 1(c). Temperature 910˚C increased with an increased soaking





Figure 1. (a) Main effects plot for S/N ratio; (b) Main effects plot for Means; (c) Interaction plot for S/N ratio (Temperature and Particle Size); (d) Interaction plot for S/N ratios (Temperature and Soaking Time); (e) Interaction plot for S/N ratios (Soaking Time and Particle Size).
time while other temperatures (870˚C, 940˚C) showed increase and decrease as the soaking time increases. This is indicated in Figure 1(d).
Soaking time of 9 hrs and particle size of 45 micron interaction gave highest hardness value as shown in Figure 1(e). Particle size of 60 micron gave reasonable hardness value at soaking time of 3 hrs but later dropped with particle size of 90 micron showing good sign of hardness value. Particle size of 90 micron gave an increased hardness value with increasing soaking time but later decreased after soaking time of 6 hrs. The response graphs (Figures 1(a)-(e)) show the change in the hardness values when a given factor goes from lower level to higher level. The slope of the line determines the power of the control factors (temperature, soaking time and particle size) influence on surface hardness. Figure 1(a) clearly suggests a dominant influence, in a quantitative sense, of furnace temperature on the surface hardness.
The effect of furnace temperature can be explained by the fact that as the temperature increases the interaction between particle size and hardness value decreases i.e. decrease in particle size increases the hardness values. From Figures 1(a)-(e), it can be observed that the optimal combination of carburizing process parameters is A2B3C1. In other words, using furnace temperature of 910˚C at soaking time of 9 hrs with energizer particle size of 45 micron is beneficial for surface hardness maximization. However, to find the relative contribution of each process parameters on the surface hardness and confirm initial assumption of the optimal condition, the statistical analysis through ANOVA was performed. The ANOVA results of S/N ratios are shown in Table 7. Figures 2-4 represent surface plots of hardness against process parameters.
3.1. ANOVA Analysis
Statistical methods are powerful tools for extracting useful information contained in data and ANOVA is one of the most frequently used tools [27] . ANOVA is the quantitative measure of the influence of individual factors/ parameters. It is important for determining the relative importance of the various factors/parameters [28] . ANOVA analysis is carried out to determine the influence of main variables on surface hardness and case depth, and also to determine the percentage contributions of each variable. The results of the S/N analysis were used for realization of ANOVA, allowing defining which factor and level influences the final results of experiments [29] . ANOVA was performed for the S/N ratios using Design Expert 6.0.6 statistical software (α = 0.05) and Minitab 16 statistical software. ANOVA table for the S/N ratios is given in Table 7.
Table 7. Analysis of variance (ANOVA) table for the S/N ratio of Hardness.
The model F-value of 20.43 implies the model is significant. There is only a 2.31% chance that a “Model F-Value” this large could occur due to noise. Values of “Prob > F” less than 0.0500 indicate model terms are significant. In this case A and C are significant model terms. Values greater than 0.1000 indicate the model terms are not significant. Table 6 shows the standard deviation, R-squared (R2), Adj R-squared. etc, which are important for further analysis of the model. “R-Squared” of 0.9839 is in reasonable agreement with the “Adj R-Squared” of 0.9358. “Adj Precision” measures the signal to noise ratio. A ratio greater than 4 is desirable. In this case, the Adeq Precision ratio is 14.143 which indicate an adequate signal/noise ratio. It may therefore be concluded that this model is adequate, and could be used to navigate the design space. The sum of squares, the mean square, the F value as well as the residual and percentage contribution of each factor are shown in the ANOVA tables.
According to Table 7, the value of R2 is 98.4%. The expressiveness of this model is high. Furnace Temperature (A) and particle size (C) are found to be significant and contributed more for the average hardness at 95 percent confidence levels according to the ANOVA Table 7. The contribution of different factors in a decreasing order of S/N ratio for hardness in Table 7 is as follows: furnace temperature (62.16%), soaking time (0.23%), particle size of energizer (36.01%), and residual error are (1.61%). This shows that furnace temperature is having a significant effect on obtainable surface hardness. The present study shows that higher furnace temperature (910˚C), soaking time of 9hrs and particle size of 45micron gives high surface hardness.
3.2. Confirmation Experiment
A verification experiment is the final step of the design of an experiment. Its purpose is to verify that the optimum conditions suggested by the matrix experiment do indeed give the improvement projected. The verification experiment is performed by conducting a test with optimal settings of the factors and levels previously evaluated. The predicted value of the multiple S/N ratio at the optimum level 

where 


From Taguchis’ methodology, Equation (2) can be used to predict the surface hardness obtainable. The S/N ratio calculated for the optimum level is as follows:

where 




If the S/N ratio is known and we want to learn about the expected result that will make the S/N, the procedure is to back-transform S/N to find the performance value expected which is equivalent to 89.85 HRB.
3.3. Numerical Analysis for the Response Surface Model
A quadratic regression model was developed for surface hardness based on experimental results using MINITAB software of version 16.0 and Design Expert Software of version 6.0.6. The model helped to predict the response as a function of independent variables and their interactions. The effects of furnace temperature, soaking time and particle size on surface hardness are shown graphically in Figures 2-4 by constructing the response surface diagrams.
A second-order response surface model equation is as follows [30] .

where 










Figure 2. Surface plot of hardness versus temperature, soaking time.
Figure 3. Surface plot of hardness versus temperature, particle size.
Figure 4. Surface plot of hardness versus soaking time, particle size.
Figure 5. Response optimization plot for carburizing process parameters.
where, A is Furnace temperature (˚C), B is Soaking time (hrs) and C is the Particle size (micron). Therefore, mathematic model suitable for predicting UNS-G10170 steel hardness is quadratic model (Linear and Square) as shown in Equation (5), with the full regression ANOVA table for hardness shown in Table 8.
Figure 5 shows the response optimization plot for carburizing process parameters using Response Optimizer function of Minitab Software 16. Desirability function was selected to find suitable value of the factors. It is observed from this figure that the objective optimization of the response (hardness) was achieved at furnace temperature of 910.30˚C, soaking time of 9 hrs and particle size of energizer at 45 micron. Therefore, it can be deduced that proposed empirical models [Taguchi and RSM] can successfully predict the hardness value during carburizing process as shown in Table 9.
Table 8. ANOVA regression analysis.
Table 9. The comparison of hardness values predicted by Taguchi model and RSM.
4. Conclusions
This paper presents the Taguchi approach and Response Surface Model for optimization of hardness in carburized UNS-G10170 steel. The influence of carburizing parameters on hardness has been investigated. Taguchi technique, Response Surface Model and ANOVA were used for the numerical modeling and analysis. From the experimental results and derived models, the following conclusions can be drawn:
v It was observed that the furnace temperature should be kept at 910˚C, soaking time at 9 hrs, while energizer particle size of 45micron should be used in order to obtain optimal hardness value.
v The correlation between process parameters and hardness was derived using a regression analysis and an optimum parameter combination (A2B3C1) for the maximum hardness was obtained by using the analysis of S/N ratios.
v The developed mathematical models through Taguchi approach and Response Surface Model correlate with experimental results of hardness which proved that the mathematical models derived are effective.
References
- Oyetunji, A. and Adeosun, O.S. (2012) Effects of Carburizing Process Variables on Mechanical and Chemical Properties of Carburized Mild Steel. Journal of Basic and Applied Science, 8, 319-324.
- Kanisawa, H.O. and Koyasou, Y.K. (1995) Development of High Strength Carburized Steels for Automobile Gears. Nippon Steel Technical Report, 65, 234-237.
- Gupta, R.C. and Kumar, M.O. (1995) Abrasive Wears Characteristics of Carbon and Low Alloy Steels for Better Performance of Farm Implements. Journal of Material Science and Technology, 11, 91-96.
- Tucas, J.O. (2010) Tribology of 316L Austenitic Stainless Steel Carburized at Low Temperature. M.Sc. Thesis, Case Western Reserve University, Cleveland.
- Osma, A.U. (2009) Effect of High Temperature Gas Carburizing on Fatigue Bending Strength of SAE 8620 Steel. Materials and Design, 30, 1792-1797.
- Wang, S.W., Lin, Y.C. and Chen, T.M. (2002) A Study on the Behavior of Hardened Medium Carbon Steel. Journal of Materials Processing Technology, 120, 126-132. http://dx.doi.org/10.1016/S0924-0136(01)01195-5
- Aramide, F.O., Ibitoye, S.A. and Oladele, I.O. (2009) Effects of Carburizing Time and Temperature on the Mechanical Properties of Carburized Mild Steel, Using Activated Charcoal as Carburizer. Material Research, 12, 483-487. http://dx.doi.org/10.1590/S1516-14392009000400018
- Gupta, R.C. (2009) Effect of Carburizing Temperatures on the Mechanical and Wear Behavior of Mild Steels. M.Sc. Thesis, National Institute of Technology Rourkela, India.
- Atanda, P.O., Umoru, L.E. and Adeyeye, A.D. (2009) Effects of Carburizing Variables on the Case Properties of C2R Steel. Journal of Minerals and Materials Characterization and Engineering, 8, 79-92.
- Muhammad, H.J. (2000) Effect of Various Heat Treatments on Microstructure and Mechanical Properties of Low Carbon Steel. ISIJ International, 34, 34-38.
- Sarkar, S. (2008) Two Dimensional Mathematical Modeling in Cylindrical Coordinate for Simulating the Pack Carburization Process. ASM International, 39A, 46-48.
- Kumar, M.O. (1994) Studies on the Abrasive Wear of Carburized Mild Steels. Transactions of the Indian Institute of Metals, 47, 417-420.
- Ohize, E.J. (2009) Effects of Local Carbonaceous Materials on the Mechanical Properties of Mild Steel. AU Journal of Technology, 13, 107-113.
- Preciado, M.J., Bravo, P.M. and Alegre, J.M. (2006) Effect of Low Temperature Tempering Prior Cryogenic Treat- ment on Carburized Steels. Journal of Materials Processing Technology, 176, 41-44. http://dx.doi.org/10.1016/j.jmatprotec.2006.01.011
- Thamizhmanil, S., Saparudin, S. and Hasan, S. (2007) Analyses of Surface Roughness by Turning Process Using Taguchi Method. Journal of Achievements in Materials and Manufacturing Engineering, 20, 503-505.
- Noorul, H.A., Marimuthu, P. and Jeyapaul, R. (2008) Multi-Response Optimization of Machining Parameters of Drilling Al/SiC Metal Matrix Composite Using Grey Relational Analysis in the Taguchi Method. International Journal of Advanced Manufacturing Technology, 37, 250-255.
- Surace, R., De Filippis, L.A.C., Ludovico, A.D. and Boghetich, G. (2010) Application of Taguchi Method for the Multi-Objective Optimization of Aluminium Foam Manufacturing Parameters. International Journal of Material Forming, 3, 1-5.
- Tosun, N. and Ozler, L. (2004) Optimization for Hot Turning Operations with Multiple Performance Characteristics. International Journal of Advanced Manufacturing Technology, 23, 777-782.
- Lin, T.R. (2002) Experimental Design and Performance Analysis of TiN-Coated Carbide Tool in Face Milling Stainless Steel. Journal of Materials Processing Technology, 127, 1-7. http://dx.doi.org/10.1016/S0924-0136(02)00026-2
- Palanikumar, K., Shanmugam, K. and Paulo, D.J. (2010) Analysis and Optimization of Cutting Parameters for Surface Roughness in Machining Al/SiC Particulate Composites by PCD Tool. International Journal of Materials and Product Technology, 37, 117-128. http://dx.doi.org/10.1504/IJMPT.2010.029463
- Kaladhar, M., Subbaiah, K.V., Rao, C.S. and Rao, K.N. (2011) Application of Taguchi Approach and Utility Concept in Solving the Multi-Objective Problem When Turning AISI 202 Austenitic Stainless Steel. Journal of Engineering Science and Technology, 4, 55-61.
- Park, C.K. and Ha, J.Y. (2005) A Process for Optimizing Sewing Conditions to Minimize Seam Pucker Using the Taguchi Method. Textile Research Journal, 75, 245-252. http://dx.doi.org/10.1177/004051750507500310
- Taguchi, G., Chowdhury, S. and Wu, Y. (2005) Taguchi’s Quality Engineering Handbook. John Wiley & Sons, Inc., Hoboken, 1662.
- Roy, R.K. (2001) Design of Experiment Using Taguchi Approach. Wiley-Interscience Publication, Hoboken, 538.
- Ross, P.J. (1996) Taguchi Techniques for Quality Engineering. Mcgraw-Hill International Editions, New York, 329.
- Kamaruddin, S., Khan, Z.A. and Foog, S.H. (2010) Application of Taguchi Method in the Optimization of Injection Moulding Parameters for Manufacturing Products from Plastic Blend. International Journal of Engineering and Technology, 2, 574-580. http://dx.doi.org/10.7763/IJET.2010.V2.184
- Khosla, A., Kumar, S. and Aggarwal, K.K. (2006) Identification of Strategy Parameters for Particle Swarm Optimizer through Taguchi Method. Journal of Zhejiang University Science A, 7, 1989-1994. http://dx.doi.org/10.1631/jzus.2006.A1989
- Mel, M., Karim, M.I.A., Jamal, P., Salleh, M.R.M. and Zakaria, R.A. (2006) The Influence of Process Parameters on Lactic Acid Fermentation in Laboratory Scale Fermenter. Journal of Applied Sciences, 6, 2287-2291. http://dx.doi.org/10.3923/jas.2006.2287.2291
- Chen, Q.H., Au, K.F., Yuen, C.W.M. and Yeung, K.W. (2003) Effects of Yarn and Knitting Parameters on the Spirality of Plain Knitted Wood Fabrics. Textile Research Journal, 73, 421-426. http://dx.doi.org/10.1177/004051750307300508
- Subrata, M., Asish, B. and Pradip, K. (2011) Ni-Cr-Mo Cladding on Mild Steel Surface Using CO2 Laser and Process Modeling with Response Surface Methodology. International Journal of Engineering Science and Technology, 3, 6805-6816.
- Montgomery, D.C. (2001) Design and Analysis of Experiments. 5th Edition, John Wiley & Sons Ltd., New York.
- Wang, J.P., Chen, Y.Z., Ge, X.W. and Yu, H.Q. (2007) Optimization of Coagulation-Flocculation Process for a Paper- Recycling Wastewater Treatment Using Response Surface Methodology. Colloids and Surfaces A, 302, 204-210. http://dx.doi.org/10.1016/j.colsurfa.2007.02.023
NOTES
*Corresponding author.








