Graphene
Vol.2 No.2(2013), Article ID:30886,8 pages DOI:10.4236/graphene.2013.22013
Lifshitz Transition Including Many-Body Effects in Bi-Layer Graphene and Change in Stacking Order
Physics Department, D.B. College, University of Delhi, New Delhi, India
Email: physicsgoswami@gmail.com
Copyright © 2013 Partha Goswami. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 27, 2013; revised March 28, 2013; accepted April 20, 2013
Keywords: AB-(Bernal) Stacking; Trigonal Warping; Lifshitz Transition; Logarithmic Renormalizations; Inverted Sombrero
ABSTRACT
We consider the AB-(Bernal) stacking for the bi-layer graphene (BLG) system and assume that a perpendicular electric field is created by the external gates deposited on the BLG surface. In the basis (A1, B2, A2, B1) for the valley K and the basis (B2, A1, B1, A2) for the valley K′, we show the occurrence of trigonal warping [1], that is, splitting of the energy bands or the density of states on the kx-ky plane into four pockets comprising of the central part and three legs due to a (skew) interlayer hopping between A1 and B2. The hopping between A1 - B2 leads to a concurrent velocity v3 in addition to the Fermi velocity vF. Our noteworthy outcome is that the above-mentioned topological change, referred to as the Lifshitz transition [2,3], is entirely bias-tunable. Furthermore, the many-body effects, which is known to yield logarithmic renormalizations [4] in the band dispersions of monolayer graphene, is found to have significant effect on the biastunability of this transition. We also consider a variant of the system where the A atoms of the two layers are over each other and the B atoms of the layers are displaced with respect to each other. The Fermi energy density of states for zero bias corresponds to the inverted sombrero-like structure. The structure is found to get deformed due to the increase in the bias.
1. Introduction
In two very exhaustive review articles Castro Neto et al. [5,6] have discussed many peculiar properties of graphene. These peculiarities have greatly intrigued physicists in recent years. In the monolayer graphene (MLG), the charge carriers are mass-less Dirac particles of chiral nature near neutrality points. The spin-degenerate bilayer grapheme (BLG) presents an entirely different landscape where the two layers are coupled by weak van der Waals forces. The carriers, for example, in the Bernal AB-stacked BLG are neither Dirac nor Schrodinger fermions. Unlike MLG, an energy gap can be opened in BLG in a controlled manner by applying an external electrical field [7,8]. In the Bernal stacking, the two layers in the bi-layer graphene consisting of two coupled honeycomb lattices with basis atoms (A1, B1) and (A2, B2) in the bottom and the top layers, respectively, are arranged in (A2, B1) fashion. That is, the A-carbon of the upper sheet lies on top of the B-carbon of the lower one. The intra-layer coupling between A1 and B1 and A2 and B2 is . The strongest interlayer coupling is between A2 and B1 with coupling constant
. The strongest interlayer coupling is between A2 and B1 with coupling constant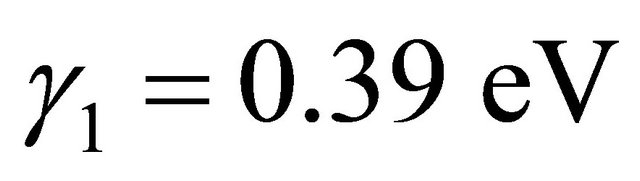 . We consider a (skew) interlayer hopping between A1 and B2 with strength
. We consider a (skew) interlayer hopping between A1 and B2 with strength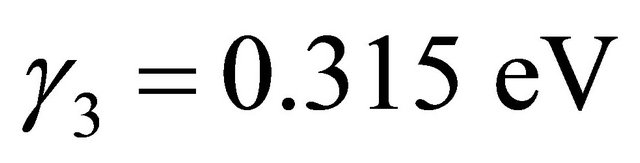 . This introduces an additional velocity
. This introduces an additional velocity 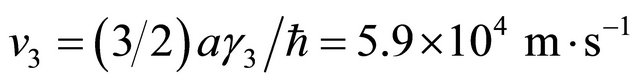 and causes a significant trigonal warping [1,9] of the energy dispersion, that is, splitting of the energy bands or the density of states on the kx-ky plane into four pockets comprising of the central part and three legs due to the skew interlayer hopping. Another important fact is that in undoped BLG, there are two pairs of energy bands as in Figure 1—a low-energy pair and a high-energy pair. When a band gap is induced by a transverse electric field, the low-energy bands develop a Mexican-hat-like dispersion at conduction and valence band edges near the band gap [10]. This rather flat dispersion leads to two distinct van Hove singularities in the density of states [11,12] (see also Figure 2). We shall, however, not look in to this aspect here apart from a sketchy allusion towards the end. The values of the hopping integrals will be taken to be same as in ref. [13] in our calculation below. Our significant outcome is that the above-mentioned topological
and causes a significant trigonal warping [1,9] of the energy dispersion, that is, splitting of the energy bands or the density of states on the kx-ky plane into four pockets comprising of the central part and three legs due to the skew interlayer hopping. Another important fact is that in undoped BLG, there are two pairs of energy bands as in Figure 1—a low-energy pair and a high-energy pair. When a band gap is induced by a transverse electric field, the low-energy bands develop a Mexican-hat-like dispersion at conduction and valence band edges near the band gap [10]. This rather flat dispersion leads to two distinct van Hove singularities in the density of states [11,12] (see also Figure 2). We shall, however, not look in to this aspect here apart from a sketchy allusion towards the end. The values of the hopping integrals will be taken to be same as in ref. [13] in our calculation below. Our significant outcome is that the above-mentioned topological
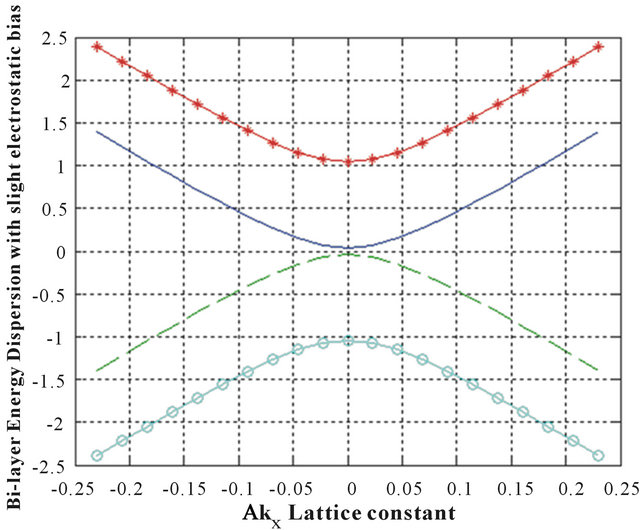
Figure 1. A plot of the bi-layer energy dispersion around Dirac point K for aδky = 0, with vanishing electrostatic bias and no trigonal warping, as a function of momentum (aδkx).
change in the single-particle excitation spectrum and the density of states, referred to as the Lifshitz transition [2, 3], is entirely bias-tunable. Furthermore, the many-body effects, engineered or otherwise, is known to yield logarithmic renormalizations [4] in the band dispersions of monolayer graphene, is found to have significant effect on the bias-tunability of this transition as shown in this paper. Our key motivation for the present study of the honeycomb bi-layer is the fact that, despite the promise afforded by bi-layer graphene as building blocks for electronic devices and circuitry, the actual development till date is limited. It is being hoped that the alluded tunability and the many-body effect driven band dispersion reconstruction (together with many exotic possibilities, such as the potential for excitonic condensation [14], an unexpected negative differential resistance at the Dirac energy as revealed by tunneling spectroscopy [15], the “spontaneous symmetry breaking” (see Section 4) when the concentration of electrons on the BLG sheet is close to zero, etc.) may hold some clues for the actual realization of the status of BLG as a suitable candidate for graphene-based nanoelectronic/optoelectronic applications.
The paper is organized as follows: In Section 2, starting with a lattice model in real space for the spin-degenerate BLG system, we present the integration of a selfenergy term involving logarithmic correction due to electron-electron interaction in the model Hamiltonian in the momentum space δkx - δky where δk refers to deviation from momentum corresponding to Dirac neutrality point. In Section 3 we discuss the issue of the biastunability of the Lifshitz transition. The paper ends in Section 4 with the brief discussion on sombrero-like structure of electron spectrum and concluding remarks.
2. Electron-Electron Interaction Related Self-Energy
The lattice model in real space for the spin-degenerate BLG system, assuming one free 2pz electron provided by each carbon atom, can be written in the tight-binding form with an electrostatic bias V as
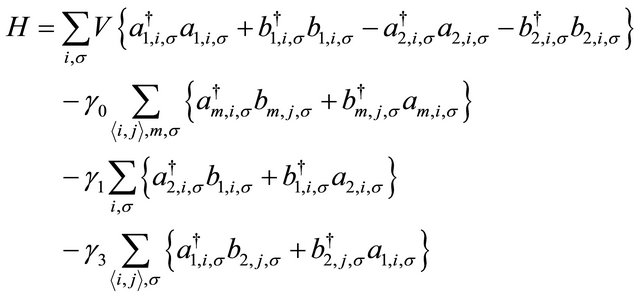 (1)
(1)
where the NN hopping integral corresponds to the index  in the second term in (1). The operators
in the second term in (1). The operators  and
and 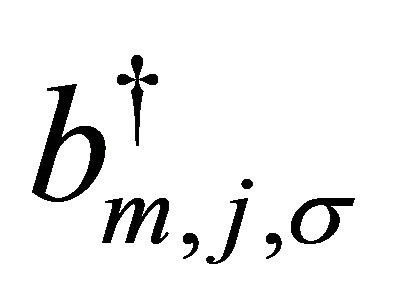 with spin σ, respectively, correspond to the fermion creation operators for A and B sub-lattices in the m = 1,2 layer. Close to the Dirac point in the Brillouin zone, upon expanding the momentum, the low-energy, spin-degenerate Hamiltonian for the Bernal AB-stacked BLG could be written in a compact form
with spin σ, respectively, correspond to the fermion creation operators for A and B sub-lattices in the m = 1,2 layer. Close to the Dirac point in the Brillouin zone, upon expanding the momentum, the low-energy, spin-degenerate Hamiltonian for the Bernal AB-stacked BLG could be written in a compact form 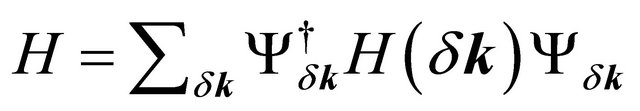 in the basis (A1,B2,A2,B1) in the valley K. The row vector
in the basis (A1,B2,A2,B1) in the valley K. The row vector

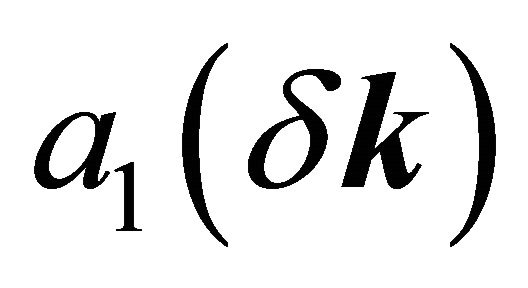 ,
, 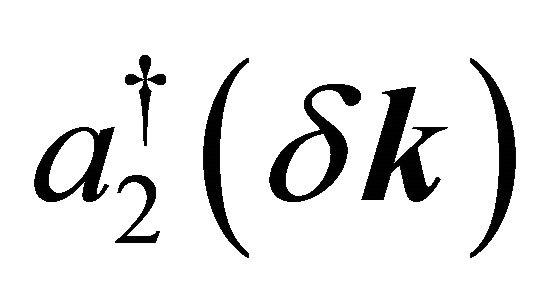 ,
, 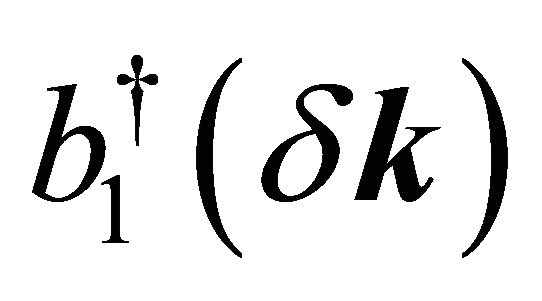 , etc. stand for the low-energy fermion annihilation/creation operators in the momentum space. For the valley K′, the appropriate basis is (B2,A1,B1,A2). We assume that a perpendicular electric field is (electrostatic bias V) created by the external gates deposited on the BLG surface. This induces a gap in the energy spectrum through a charge imbalance between the two graphene layers. The Hamiltonian matrix
, etc. stand for the low-energy fermion annihilation/creation operators in the momentum space. For the valley K′, the appropriate basis is (B2,A1,B1,A2). We assume that a perpendicular electric field is (electrostatic bias V) created by the external gates deposited on the BLG surface. This induces a gap in the energy spectrum through a charge imbalance between the two graphene layers. The Hamiltonian matrix 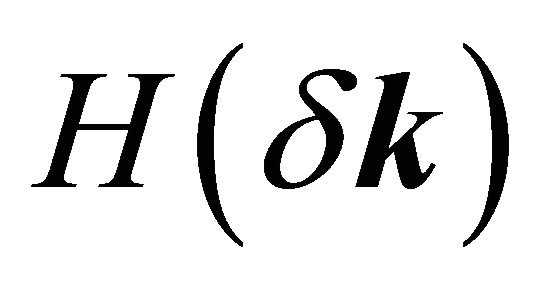 is given by
is given by
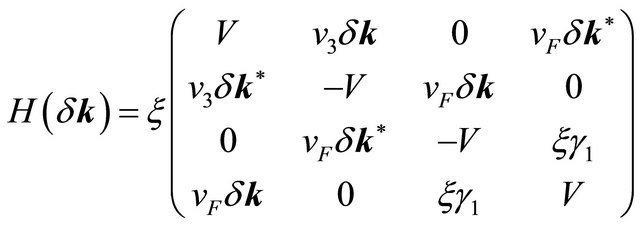 (2)
(2)
where  is Fermi velocity (the speed of electrons in the vicinity of a Dirac point in the absence of interlayer hopping and is equal to 8 × 105 m·s−1),
is Fermi velocity (the speed of electrons in the vicinity of a Dirac point in the absence of interlayer hopping and is equal to 8 × 105 m·s−1), 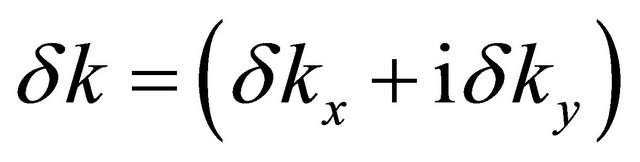 is a complex number and ξ = ±1; ξ = +1 corresponds to the valley K and ξ = −1 to the valley K′. We shall now consider the many-body effects only on the dominant terms
is a complex number and ξ = ±1; ξ = +1 corresponds to the valley K and ξ = −1 to the valley K′. We shall now consider the many-body effects only on the dominant terms  above. A similar exercise for all the terms has been carried out by C. T’oke and V. I. Fal’ko [16] in the Hartree-Fock approximation. We feel that a recently reported crucial many-body effect [4] in the band dispersions of monolayer graphene needs to be included in a description of the bi-layer system. In other
above. A similar exercise for all the terms has been carried out by C. T’oke and V. I. Fal’ko [16] in the Hartree-Fock approximation. We feel that a recently reported crucial many-body effect [4] in the band dispersions of monolayer graphene needs to be included in a description of the bi-layer system. In other
 (a)
(a) (b)
(b)
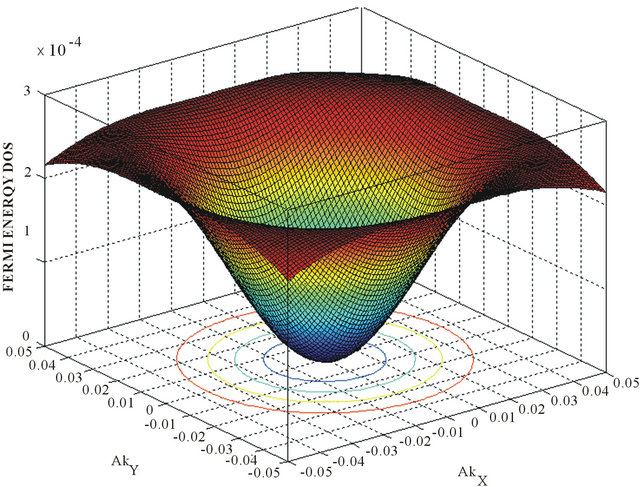
Figure 2. The 3D plots of the Fermi energy density of states corresponding to the AA-stacking, in the momentum space, for (V/γ1) = 0.0 (a), and (V/γ1) = 0.17 (b). The inverted sombrero-like structure in (a) gets deformed due to the increase in bias.
previous approaches [4,17] for BLG, all effects of Coulomb interactions are ignored except the Coulomb interaction for an electron and hole adjacent to each other but in opposite layers. It may be noted that the path integral approach requires no single-particle approximation and therefore many-body effects emerge naturally. Since we shall not adopt this rigorous formalism in the present paper, our approach is essentially a mean-field approximation requiring the introduction of the many-body effects by using the Dyson’s equation.
For the purpose stated above, one may write few unperturbed thermal averages determined by the Hamiltonian in (2), viz.

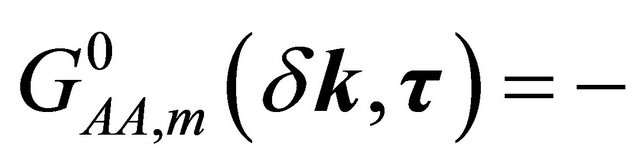
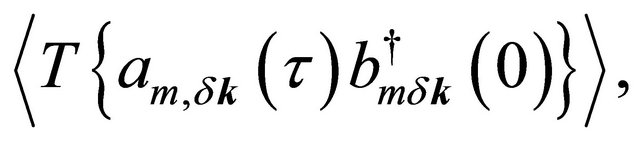
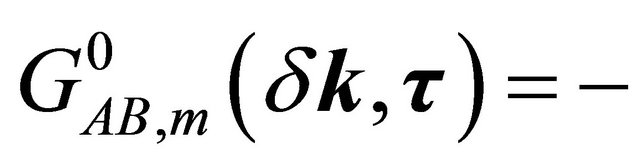
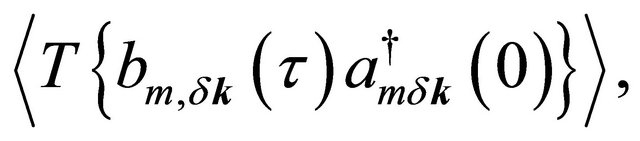
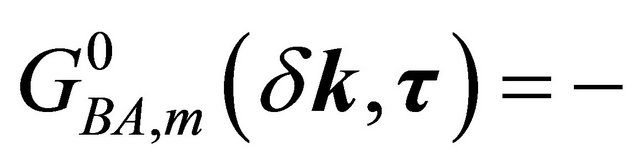

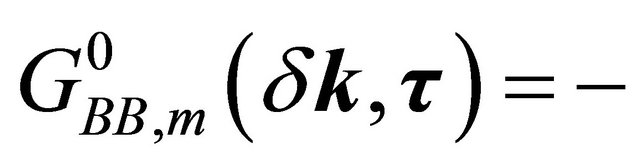
with m = 1,2. Here T is the time-ordering operator which arranges other operators from right to left in the ascending order of imaginary time τ. The Fourier coefficients of these temperature functions are
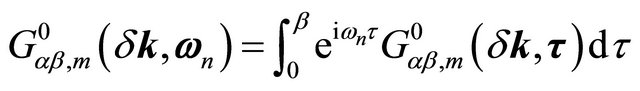
where the Matsubara frequencies are with
with 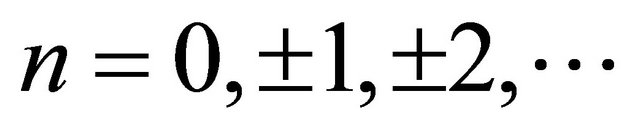 and
and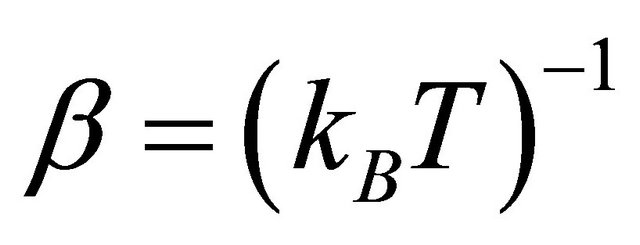 ). We obtain for the mth sheet
). We obtain for the mth sheet

and so on. In Equation (2), upon retaining only the terms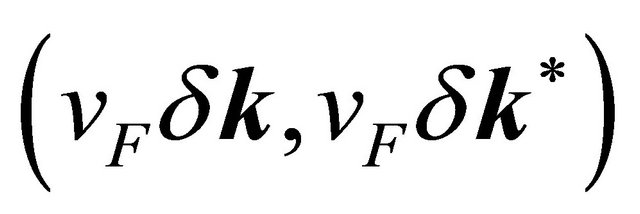 , we obtain
, we obtain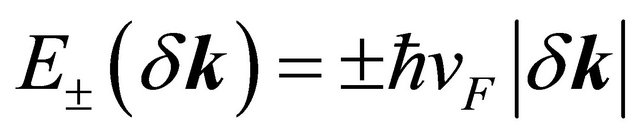 . It was proposed by Castro Neto et al. [5] that, unlike the linear real self-energy of a Fermi liquid, when monolayer graphene (MLG) is near the charge neutrality point the electron-electron interaction leads to a self-energy involving logarithmic term given by
. It was proposed by Castro Neto et al. [5] that, unlike the linear real self-energy of a Fermi liquid, when monolayer graphene (MLG) is near the charge neutrality point the electron-electron interaction leads to a self-energy involving logarithmic term given by
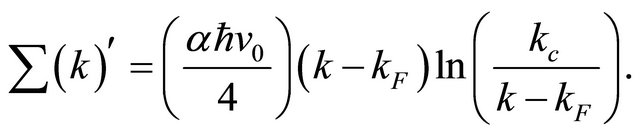
This is the “so called” marginal Fermi liquid self-energy function for MLG. Here kF = 1.703 Å −1 is the Fermi wave-number along the Г-K direction, 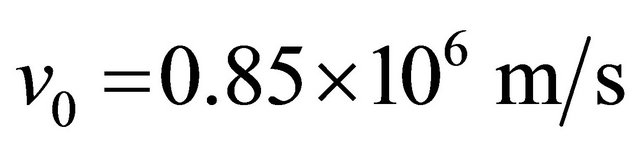 is the Fermi velocity for the dielectric constant ε = 6.4 ± 0.1,
is the Fermi velocity for the dielectric constant ε = 6.4 ± 0.1, 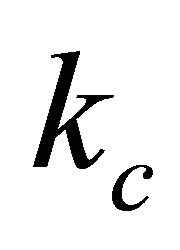 is the momentum cut-off
is the momentum cut-off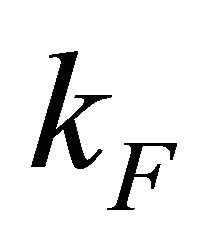 , and α= 0.40 ± 0.01 is a dimensionless fine-structure constant (or the strength of electron-electron interactions) defined as
, and α= 0.40 ± 0.01 is a dimensionless fine-structure constant (or the strength of electron-electron interactions) defined as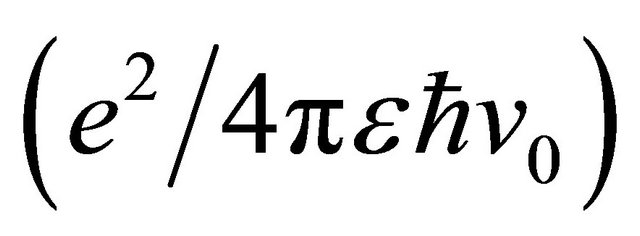 . In terms of the logarithmic self-energy, using the Dyson’s equation, a full propagator for the mth sheet
. In terms of the logarithmic self-energy, using the Dyson’s equation, a full propagator for the mth sheet 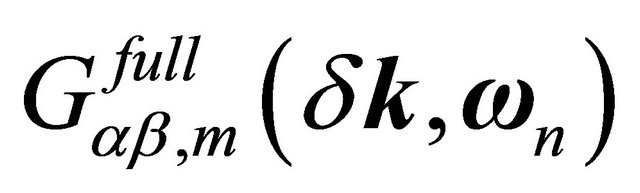 could be approximated as
could be approximated as
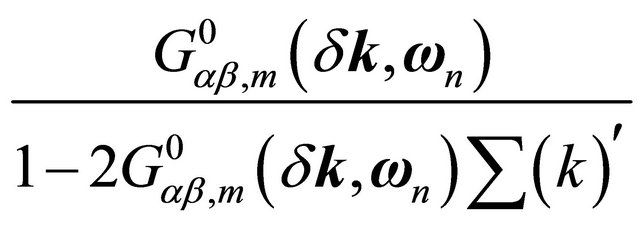
where the self energy contribution
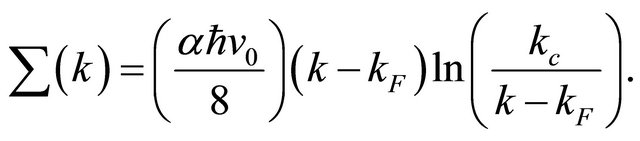
The approximate analytic form of the full propagator is
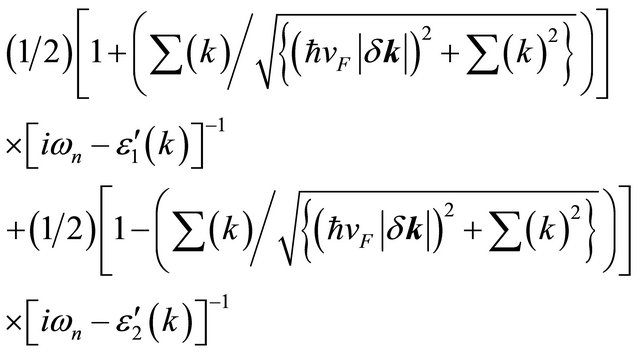
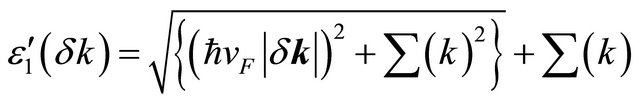 ,
,
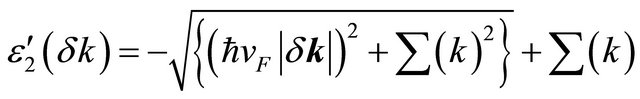 (3)
(3)
The poles  allow us to re-construct the intra-layer coupling between A1 and B1 and A2 and B2; the interlayer coupling between A2 and B1 (with coupling constant γ1) and the (skew) interlayer hopping between A1 and B2 (with strength γ3 ) remains unaffected by the reconstruction as stated above. Effectively, we have assumed here that the inter-layer separation is larger than the intra-layer nearest neighbor separation. An analysis of the ratio Re(∑′(k))/γ1 as a function of momentum, close to the Dirac points
allow us to re-construct the intra-layer coupling between A1 and B1 and A2 and B2; the interlayer coupling between A2 and B1 (with coupling constant γ1) and the (skew) interlayer hopping between A1 and B2 (with strength γ3 ) remains unaffected by the reconstruction as stated above. Effectively, we have assumed here that the inter-layer separation is larger than the intra-layer nearest neighbor separation. An analysis of the ratio Re(∑′(k))/γ1 as a function of momentum, close to the Dirac points 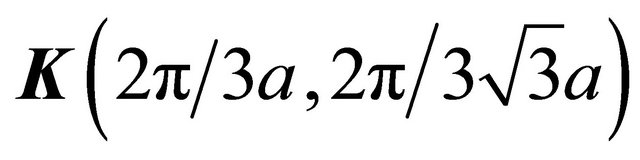 and
and 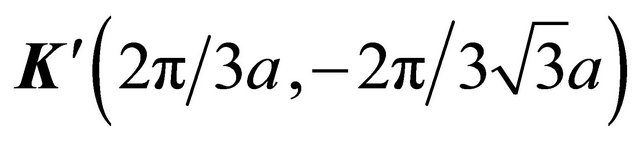 where
where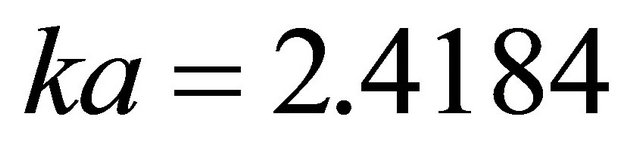 , shows that the self-energy corrections are very significant as these may be greater than the linear terms in momentum in
, shows that the self-energy corrections are very significant as these may be greater than the linear terms in momentum in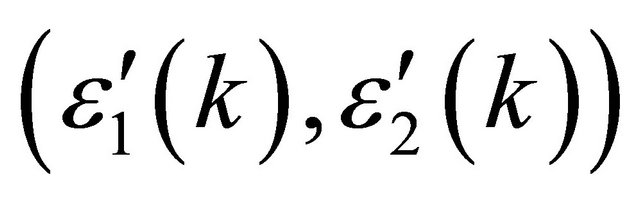 . It must be added here that in principle, bi-layer graphene could have arbitrarily large coupling at low carrier density where disorder effects are also important.
. It must be added here that in principle, bi-layer graphene could have arbitrarily large coupling at low carrier density where disorder effects are also important.
With the self-energy correction, the matrix in (2) may be re-written as
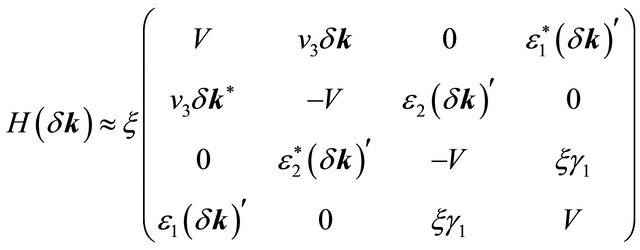 (4)
(4)
where

and
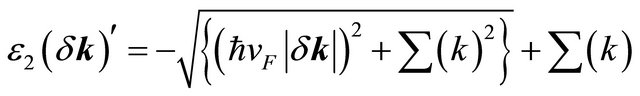
The eigenvalue (denoted by λ) equation of the matrix in (4) is a quartic:
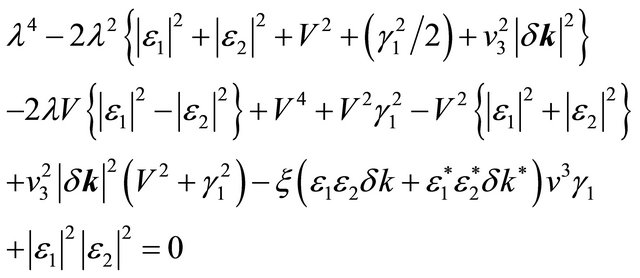 (5)
(5)
If one ignores the self-energy correction altogether, Equation (5) reduces to a bi-quadratic whose solutions are easy to obtain. We obtain four bands, 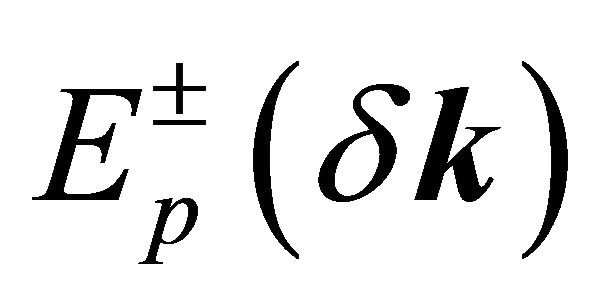 ,
,  1, 2, as reported by Fal’ko et al. [9,10] with
1, 2, as reported by Fal’ko et al. [9,10] with
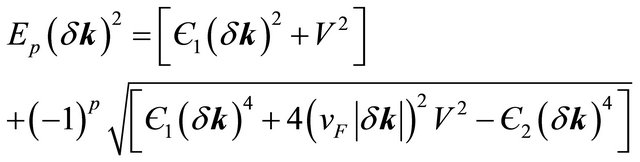 (6)
(6)
where E1 and E2, respectively, describes the lower and higher energy bands, and
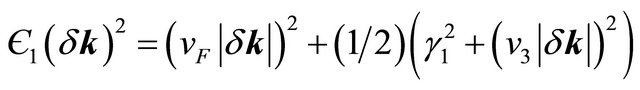
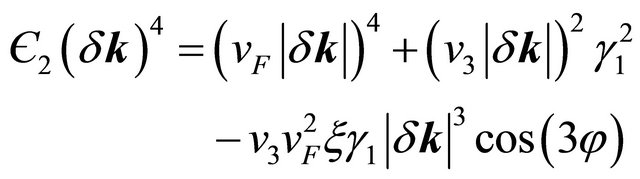 (7)
(7)
We have parameterized δk writing  and
and 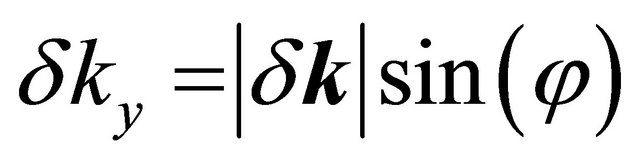 which gives
which gives . The effect of valley state plus the skew interlayer hopping between A1 - B2, given by the last term in Є2(δk)4, on the four bands are found to be extremely sensitive to the bias. The bands Ep (δk) splits into four pockets comprising of the central part and three legs [2] for φ = {0, 2π/3, 4π/3}, {π/3, π, 5π/3}. We note that such splitting is an indication of the Lifshitz transition [8]. In the next section this topological change will be displayed graphically.
. The effect of valley state plus the skew interlayer hopping between A1 - B2, given by the last term in Є2(δk)4, on the four bands are found to be extremely sensitive to the bias. The bands Ep (δk) splits into four pockets comprising of the central part and three legs [2] for φ = {0, 2π/3, 4π/3}, {π/3, π, 5π/3}. We note that such splitting is an indication of the Lifshitz transition [8]. In the next section this topological change will be displayed graphically.
3. Bias-Tunability of Lifshitz Transition
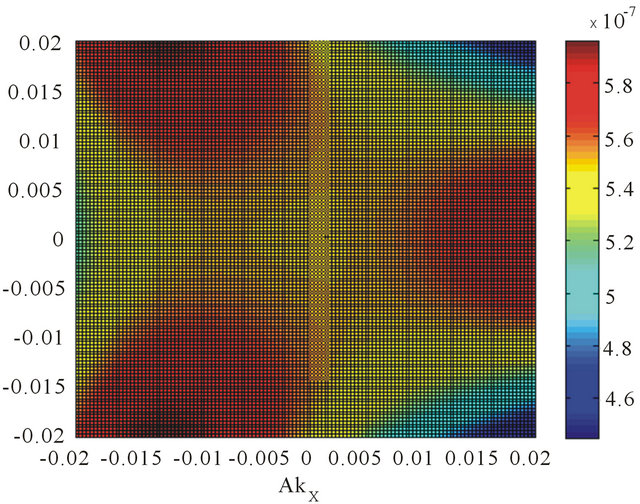
We have shown in Figure 3 the topological change in the Fermi surface density of states (DOS) obtainable from Equation (6) in the momentum space with an artificial level broadening (Ѓ/γ1) = 0.0001. We have started with the electrostatic bias (V/γ1) = 0.1 at which the change sets in. The plots in Figures 3(a) and 3(b) correspond to (V/γ1) = 0.107. A higher value of (V/γ1), as much as 0.17, almost obliterates the four-pocket feature from the DOS. Thus, the transition appears to be bias-tunable or concentration dependent.
We obtain the solutions of Equation (5) using the Ferrari’s method of solving a quartic. Given the general quartic , its solution could be found by means of the following algebra: We introduce
, its solution could be found by means of the following algebra: We introduce
 (a)
(a)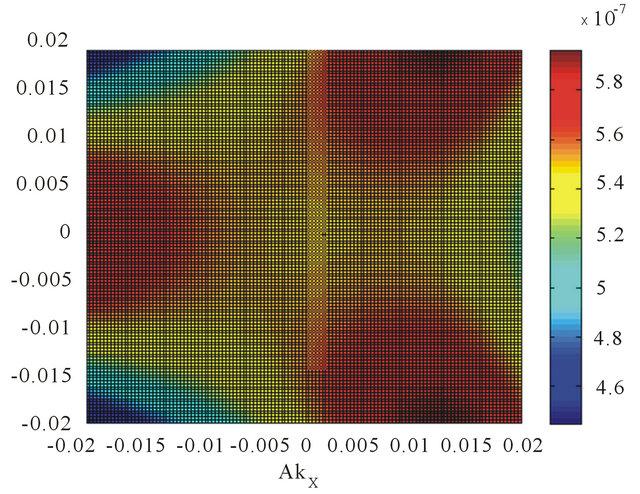 (b)
(b)
Figure 3. We have contour plotted the Fermi surface DOS obtainable from Equation (6) in the momentum space with an artificial level broadening (Ѓ/γ1) = 0.0001. We find that the DOS is given by a sum of four δ functions at the quasi-particle energies. We notice that the trigonal warping splits the surface into four pockets comprising of the central part and three legs both for the valley states ׀ (a) and ׀
(a) and ׀ (b). The splitting for ׀
(b). The splitting for ׀ and ׀
and ׀ are in the opposite sense. We have assumed (vF/aγ1) = 7.9. The remaining numerical values are (V/γ1) = 0.1 and (v3/aγ1) = 0. 7949.
are in the opposite sense. We have assumed (vF/aγ1) = 7.9. The remaining numerical values are (V/γ1) = 0.1 and (v3/aγ1) = 0. 7949.

and

In the present problem, A = 1, B = 0, so α = C, β = D, and γ = E. We further define
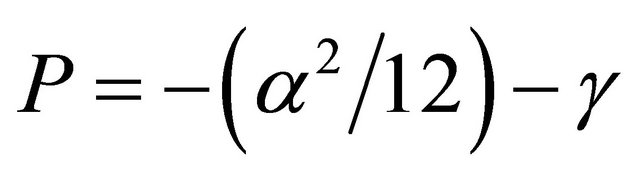
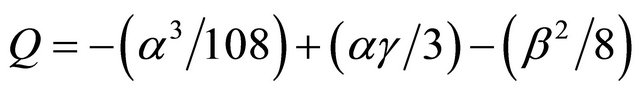
and
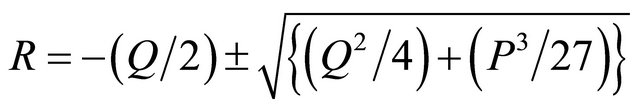
This ultimately yields the single-particle excitation spectra 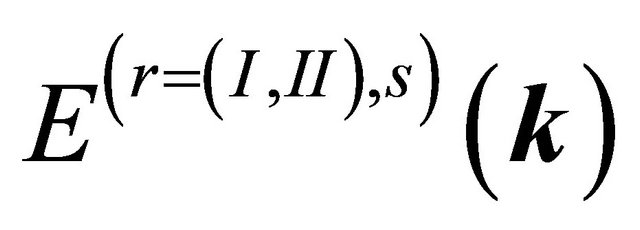 given by
given by
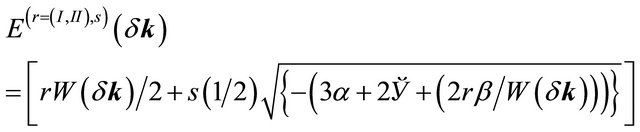
where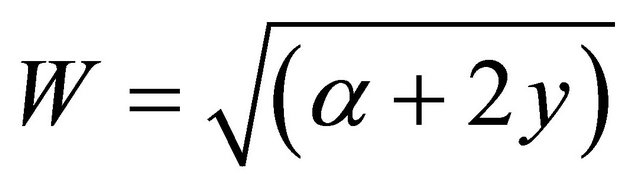 ,
, 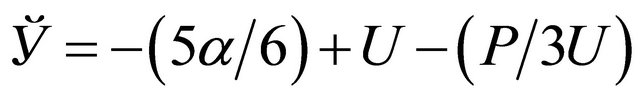 ,
, 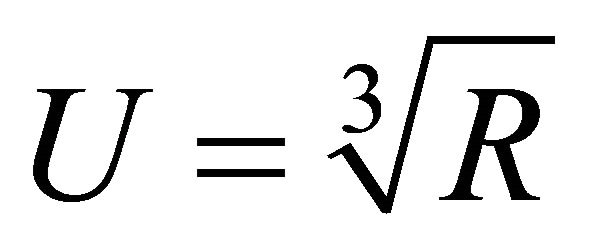 , r is equal to (±1) with r = +1 corresponding to the branch (I) and r = −1 to the branch (II) and for a given r we have
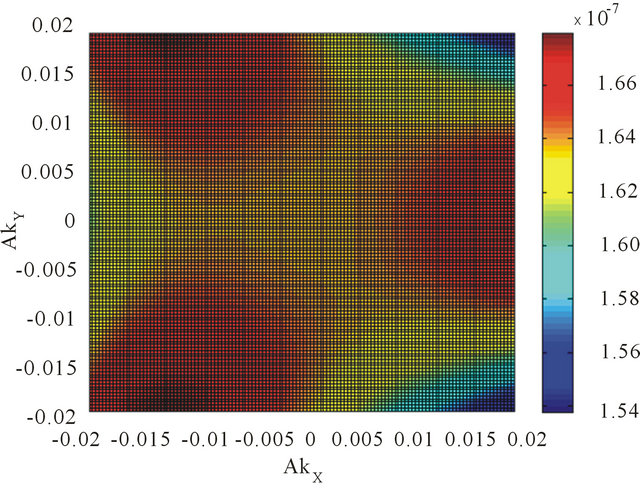
, r is equal to (±1) with r = +1 corresponding to the branch (I) and r = −1 to the branch (II) and for a given r we have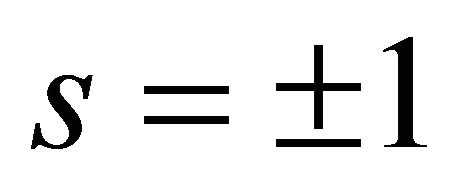 . The single-particle spectral function or density of states (DOS) is given by a retarded Green’s function. We find that the DOS is given by a sum of four δ functions at the quasi-particle energies. We have plotted in momentum space (see Figure 4) the Fermi surface DOS with these bands and an artificial level broadening (Ѓ/γ1) = 0.0001 once again. We have assumed
. The single-particle spectral function or density of states (DOS) is given by a retarded Green’s function. We find that the DOS is given by a sum of four δ functions at the quasi-particle energies. We have plotted in momentum space (see Figure 4) the Fermi surface DOS with these bands and an artificial level broadening (Ѓ/γ1) = 0.0001 once again. We have assumed  . The remaining numerical values are
. The remaining numerical values are 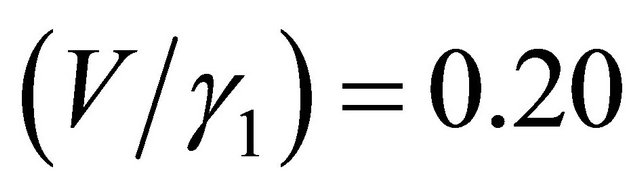 and
and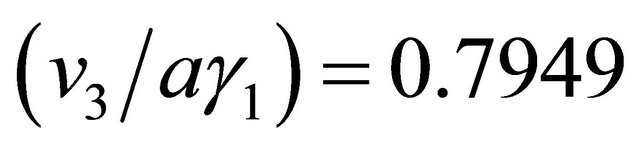 . We find that in this case the Lifshitz transition [2,3] sets in at (V/γ1) ~ 0.17 and a higher value of (V/γ1), as much as 0.22, almost obliterates the four-pocket feature from the DOS. We, thus, find that in the presence of many-body effects higher bias is required for the occurrence of the transition. It may be pointed out that the mean-field approach here has one major disadvantage. It does not take into account the logarithmic divergence in the similar manner as a renormalization group theory does, and therefore may not lead to results that are quantitatively correct.
. We find that in this case the Lifshitz transition [2,3] sets in at (V/γ1) ~ 0.17 and a higher value of (V/γ1), as much as 0.22, almost obliterates the four-pocket feature from the DOS. We, thus, find that in the presence of many-body effects higher bias is required for the occurrence of the transition. It may be pointed out that the mean-field approach here has one major disadvantage. It does not take into account the logarithmic divergence in the similar manner as a renormalization group theory does, and therefore may not lead to results that are quantitatively correct.
4. Sombrero-Like Structure and Concluding Remarks
We now work on the pending task, that is to have an indication of the Mexican-hat-like structure alluded to in Section 1. We find it convenient to consider a variant of the system above where the A atoms of the two layers are over each other and the B atoms of the layers are displaced with respect to each other. It must be made clear though that there is slight difference in environment in Bernal stacking as an A site has three in-plane nearest-neighbor B sites and one neighboring A site in the opposite layer at a distance c and a B site has only the three surrounding in-plane A sites as nearest neighbors. As before, the band structure of bi-layer graphene can be described within the tight-binding formalism. In this description [5], assuming one free 2pz electron provided by each carbon atom, the Hamiltonian with the electrostatic bias (V) is given by
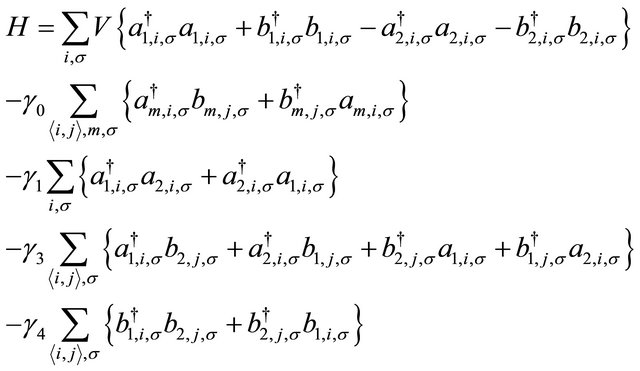 (8)
(8)
 (a)
(a)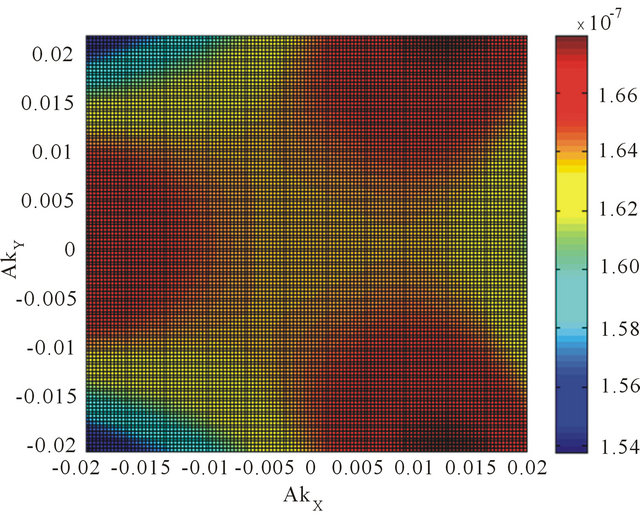 (b)
(b)
Figure 4. We have contour plotted the Fermi surface DOS obtainable from Equation (5) including the many-body effect in the momentum space with an artificial level broadening (Ѓ/γ1) = 0.0001. The trigonal warping splits the surface into four pockets comprising of the central part and three legs both for the valley states ׀ (a) and ׀
(a) and ׀ (b) as before. We have assumed (vF/aγ1) = 7.9. The remaining numerical values are (V/γ1) = 0.20 and (v3/aγ1) = 0. 7949.
(b) as before. We have assumed (vF/aγ1) = 7.9. The remaining numerical values are (V/γ1) = 0.20 and (v3/aγ1) = 0. 7949.
The intra-layer coupling between A1 and B1 and A2 and B2 is γ0 = 3.16 eV. The strongest direct interlayer coupling is between A1 and A2 with coupling constant γ1 = 0.39 The skew interlayer hopping between A1 and B2 (and between A2 and B1) with strength γ3 = 0.315 eV introduces an additional velocity 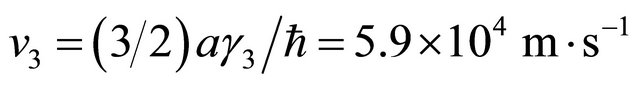 . These numerical values are almost the same as in ref. [13]. Close to the Dirac point K in the Brillouin zone, upon expanding the momentum, this Hamiltonian with the electrostatic bias could be written in the compact form
. These numerical values are almost the same as in ref. [13]. Close to the Dirac point K in the Brillouin zone, upon expanding the momentum, this Hamiltonian with the electrostatic bias could be written in the compact form  in the basis (A1,B1,A2,B2) in the valley K where the row vector
in the basis (A1,B1,A2,B2) in the valley K where the row vector
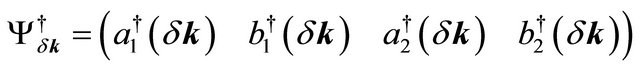 ,
,
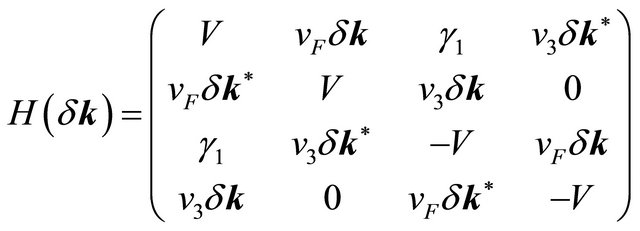 (9)
(9)
As before,  is a complex number. For thevalley
is a complex number. For thevalley , the basis would be (B1,A1,B2,A2). In writing Equation (9) we have ignored γ4 term as this term is smaller than the others. As before, the density of states (DOS) is given by a re traded green’s function. We find that the DOS is given by a sum of four δ functions at the quasi-particle energies. We have also contour plotted the DOS (Figure 2) with an artificial level broadening (Ѓ/γ1) = 0.0001. The Figures 2(a) and 2(b), respectively, correspond to the (V/γ1) = 0, and (V/γ1) = 0.17. We notice a Mexican-hat-like structure mentioned in Section 1 and a bias induced slight deformation in the topology of the Fermi surface DOS.
, the basis would be (B1,A1,B2,A2). In writing Equation (9) we have ignored γ4 term as this term is smaller than the others. As before, the density of states (DOS) is given by a re traded green’s function. We find that the DOS is given by a sum of four δ functions at the quasi-particle energies. We have also contour plotted the DOS (Figure 2) with an artificial level broadening (Ѓ/γ1) = 0.0001. The Figures 2(a) and 2(b), respectively, correspond to the (V/γ1) = 0, and (V/γ1) = 0.17. We notice a Mexican-hat-like structure mentioned in Section 1 and a bias induced slight deformation in the topology of the Fermi surface DOS.
The focal point of this paper though is the trigonal warping (which is important only at extremely low densities), we wish to mention an important, experimentally not yet established fact [19] that, at zero temperature and zero field, for the BLG system the leading instability corresponds to the quantum anomalous Hall (QAH) state. Since this issue will be a part of the future investigation, one may mention that the first step, to this end, is the calculation of Hall conductivity using a Kubo formula [20]. The formula requires the identification of velocity operators which, in turn, is easily possible if the BLG Hamiltonian is written in terms of 4 × 4 Dirac matrices (γµ) in the ordinary or Weyl representation [21]. The trigonal warping is masked by uncontrolled disorder. In the absence of warping, the single-particle Hamiltonian in units such that ħ = 1 may be written in a compact form in terms of 4 × 4 Dirac matrices (γµ), say, in the Weyl representation as 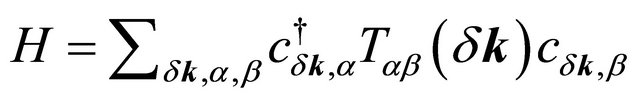 where the matrix
where the matrix
 ,
,
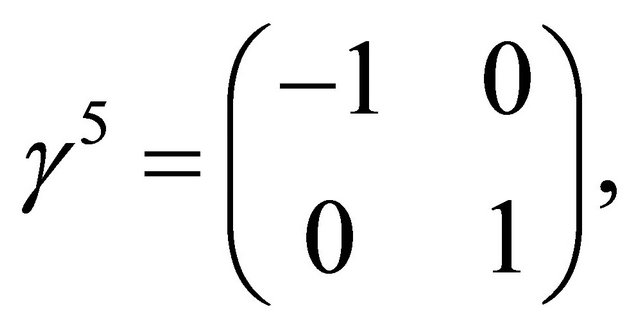
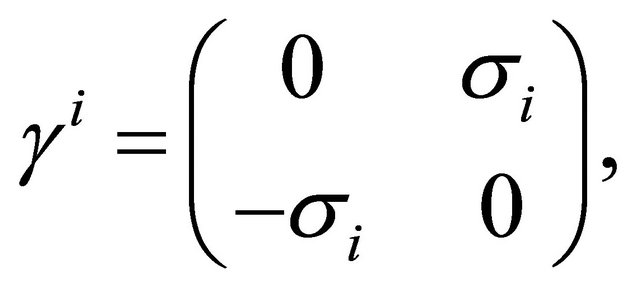
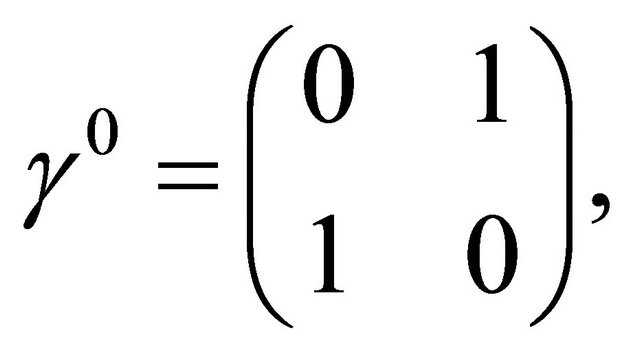
1 denotes the 2 × 2 identity matrix,  denote the Pauli matrices, and the Greek indices α and β account for the sub-lattice degrees of freedom in top and bottom layers. The required velocity operators correspond to the matrices
denote the Pauli matrices, and the Greek indices α and β account for the sub-lattice degrees of freedom in top and bottom layers. The required velocity operators correspond to the matrices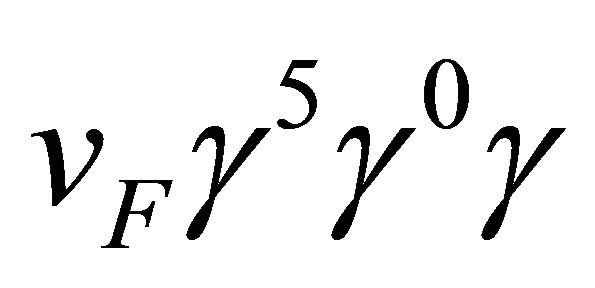 . It is evident from the form of
. It is evident from the form of 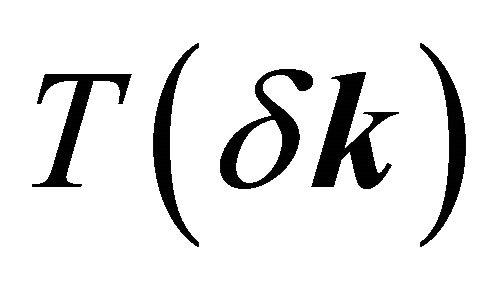 that the “spontaneous symmetry breaking” (it is the same principle that “endows” mass for particles in high energy physics) when the concentration of electrons on the BLG sheet is close to zero, as mentioned in Section 1, is initiated by the inter-layer hopping term
that the “spontaneous symmetry breaking” (it is the same principle that “endows” mass for particles in high energy physics) when the concentration of electrons on the BLG sheet is close to zero, as mentioned in Section 1, is initiated by the inter-layer hopping term  in
in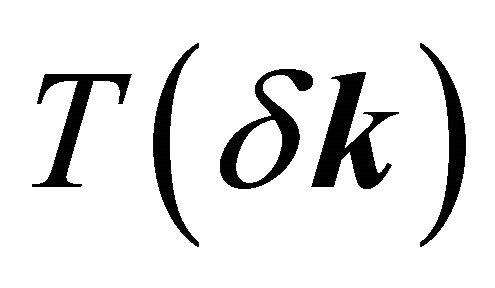 .
.
In conclusion, the striking reconstruction of the Fermi surface at low densities presented here leads to an enhancement in the conductivity for pristine BLG as well as under electron or hole doping. For example, neglecting trigonal warping, the minimal conductivity is predicted to be 8e2/(πh)—twice the value in monolayer grapheme [22,23]. Because of multiple Fermi surface pockets at low energy, in the presence of trigonal warping, it is larger and equal to 24e2/(πh) [24]. We have, however, only estimated the change in the electronic specific heat due to this bias-tunable transition. It is found to be close to 10%. Thus, the Lifshitz transition, in principle, is detectable also in the heat capacity measurements. It must be added that the experimental observation of the change is quite a difficult proposition, for the dominant phononic contribution is expected to over-shadow the anomaly in the measurements.
REFERENCES
- A. S. Nunez, E. Suarez Morell, and P. Vargas, “Trigonal Distortion of Topologically Confined Channels in Bilayer Grapheme,” Applied Physics Letters, Vol. 98, No. 26, 2011, Article ID: 262107. doi:10.1063/1.3605568
- A. A. Abrikosov, “Fundamentals of the Theory of Metals,” Elsevier, Amsterdam, 1988.
- Y. Lemonik, I. L. Aleiner and V. I. Fal’ko, “Competing Nematic, Antiferromagnetic, and Spin-Flux Orders in the Ground State of Bilayer Grapheme,” Physical Review B, Vol. 85, No. 24, 2012, Article ID: 245451. doi:10.1103/PhysRevB.85.245451
- C. Hwang, D. A. Siegel, S.-K. Mo, W. Regan, A. Ismach, Y. Zhang, A. Zettl and A. Lanzara, “Fermi Velocity Engineering in Graphene by Substrate Modification,” Scientific Reports, Vol. 2, 2012, p. 590.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, “The Electronic Properties of Grapheme,” Reviews of Modern Physics, Vol. 87, No. 1, 2009, pp. 109-162. doi:10.1103/RevModPhys.81.109
- V. N. Kotov, B. Uchoa, V. M. Pereira, F. Guinea, and A. H. Castro Neto, “Electron-Electron Interactions in Graphene: Current Status and Perspectives,” Reviews of Modern Physics, Vol. 84, No. 3, 2012, pp. 1067-1125. doi:10.1103/RevModPhys.84.1067
- J. B. Oostinga, H. B. Heersche, X. Liu, A. F. Morpurgo, L. M. K. Vandersypen, “Gate-Induced Insulating State in Bilayer Graphene Devices,” Nature Materials, Vol. 7, 2008, pp. 151-157. doi:10.1038/nmat2082
- Y. Zhang, T.-T. Tang, C. Girit, Z. Hao, M. C. Martin, A. Zettl, M. F. Crommie, Y. R. Shen, F. Wang, “Direct Observation of a Widely Tunable Bandgap in Bilayer Graphene,” Nature, Vol. 459, No. 7248, 2009, pp. 820-823. doi:10.1038/nature08105
- K. Kechedzhi, V. I. Fal’ko, E. McCann, and B. L, “Influence of Trigonal Warping on Interference Effects in Bilayer Graphene,” Physical Review Letters, Vol. 98, No. 7, 2007, Article ID: 176806. doi:10.1103/PhysRevLett.98.176806
- E. McCann and V. I. Fal’ko, “Landau-Level Degeneracy and Quantum Hall Effect in a Graphite Bilayer,” Physical Review B, Vol. 96, 2006, Article ID: 086805.
- F. Guinea, A. H. Castro Neto, and N. M. R, Peres, “Electronic States and Landau Levels in Graphene Stacks,” Physical Review B, Vol. 73, No. 24, 2006, Article ID: 245426. doi:10.1103/PhysRevB.73.245426
- A. Ramasubramaniam, D. Naveh, and E. Towe, “Tunable Band Gaps in Bilayer Graphene-BN Heterostructures,” Nano Letters, Vol. 11, No. 3, 2006, pp. 1070-1075. doi:10.1021/nl1039499
- M. S. Dresselhaus and G. Dresselhaus, “Intercalation Compounds of Graphite,” Advances in Physics, Vol. 51, No. 1, 2002, pp. 1-186. doi:10.1080/00018730110113644
- Y. Barlas, R. Côté, J. Lambert and A. H. MacDonald, “Anomalous Exciton Condensation in Graphene Bilayers,” Physical Review Letters, Vol. 104, No. 9, 2010, Article ID: 096802. doi:10.1103/PhysRevLett.104.096802
- K. S. Kim, T.-H. Kim, A. L. Walter, Th. Seyller, H. W. Yeom, E. Rotenberg and A. Bostwick, “Visualizing Atomic-Scale Negative Differential Resistance in Bilayer Graphene,” Physical Review Letters, Vol. 110, No. 3, 2013, Article ID: 036804.
- C. Toke and V. I. Fal’ko, “The Effect of the ElectronElectron Interaction on the Lifshitz Transition Density in Bilayer Graphene,” Unpublished.
- H. Min, R. Bistritzer, J. J. Su and A. H. MacDonald, “Room-Temperature Superfluidity in Graphene Bilayers,” Physical Review B, Vol. 78, No. 12, 2008, Article ID: 121401. doi:10.1103/PhysRevB.78.121401
- B. Seradjeh, J. E. Moore and M. Franz, “Exciton Condensation and Charge Fractionalization in a Topologic,” Physical Review Letters, Vol. 103, No. 6, 2009, Article ID: 06642.
- R. Nandkishore, and L. Levitov, “Quantum Anomalous Hall State in Bilayer Grapheme,” Physical Review B, Vol. 82, No. 11, 2010, Article ID: 115124.
- E. Akkermans and G. Montambaux, “Mesoscopic Physics of Electrons and Photons,” Cambridge University Press, New York, 2007.
- M. Maggiore, “A Modern Introduction to Quantum Field Theory,” Oxford University Press, Oxford, 2005.
- J. Cserti, “Minimal Longitudinal dc Conductivity of Perfect Bilayer Grapheme,” Physical Review B, Vol. 75, No. 3, 2007, Article ID: 033405.
- I. Snyman and C. W. J. Beenakker, “Ballistic Transmission through a Graphene Bilayer,” Physical Review B, Vol. 75, No. 4, 2007, Article ID: 045322.
- J. Cserti, A. Csordas and G. David, “Role of the Trigonal Warping on the Minimal Conductivity of Bilayer Graphene,” Physical Review Letters, Vol. 99, 2007, Article ID: 066802.

