Advances in Remote Sensing
Vol.05 No.02(2016), Article ID:67551,13 pages
10.4236/ars.2016.52010
Assessing Net Primary Production in Montane Wetlands from Proximal, Airborne, and Satellite Remote Sensing
Michael Maguigan1, John Rodgers2, Padmanava Dash2, Qingmin Meng2
1National Strategic Planning and Analysis Research Center, Mississippi State University, Starkville, MS, USA
2Department of Geosciences, Mississippi State University, Mississippi State, MS, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2016; accepted 18 June 2016; published 21 June 2016
ABSTRACT
In this study, several vegetation indices were examined in order to determine the most sensitive vegetation index for monitoring southern Appalachian wetlands. Three levels of platforms (in situ, airborne, and satellite) for sensors were also examined in conjunction with vegetation indices. Net primary production (NPP) data were gathered to use as a measure of wetland function. Along with the in situ radiometers, National Agricultural Imagery Program (NAIP) data and Landsat 8 Operational Land Imager (OLI) data were gathered in order to calculate vegetation indices at three platforms. At the in situ level, VARI700 was the most sensitive vegetation index in terms of NPP (r2 = 0.65, p < 0.05). At the airborne level, the NDVI was the most sensitive vegetation index to NPP (r2 = 0.35, p = 0.11). At the satellite level, the DVI appeared to have a positive relationship with NPP. For most indices there was a drop in the coefficient of determination with NPP when the platform altitude increased, with the exception of NDVI when increasing altitude from in situ to airborne. This study provides a novel methodology comparing reflectance and vegetation indices at three platform levels.
Keywords:
Net Primary Production, Montane Wetland, In Situ, Airborne, Satellite

1. Introduction
The use of remote sensing in vegetation-related studies is a rising trend as it allows for the estimation of vegetation characteristics (chlorophyll content and net primary production, NPP) over large areas [1] . Remote sensing is beneficial because of the low cost and short analysis time, both of which are advantageous for the monitoring of wetland health. Proximal sensing, the use of hand-held radiometers in the field, is becoming a larger part in the field of remote sensing than it has been previously [2] - [5] .
In all of the aforementioned in-situ remote sensing studies, two inter-calibrated hyperspectral radiometers were used. This methodology was employed because the use of two radiometers allows for one to capture incoming radiation while the other captures the ground reflectance simultaneously [3] [4] . This practice allows for smaller errors when estimating irradiance because irradiance is being captured while the upwelling radiance is also captured, resulting in more accurate reflectance values [3] [4] . Computing radiance is also possible during times of inconstant irradiance [4] , which might be a difficulty with remote sensing.
Remote sensing allows for the estimation of vegetation characteristics over large areas in a short amount of time, though error is introduced because of atmospheric interference (e.g. Rayleigh and Mie scattering). Differences in platform (airborne vs. satellite) might determine the amount of the aforementioned error due to the amount of atmosphere with which light must interact. Thus, using data from an airborne platform for comparison to proximally sensed data might serve as an intermediate step between comparing proximally sensed and satellite data.
The National Agricultural Imagery Program (NAIP) generates plane platform data that served the purpose of this comparison. NAIP was selected among the varieties of remotely sensed data for a few reasons. The spatial resolution of NAIP data is 1 m of ground distance with ground control points within 6 m [6] . High spatial resolution was a top priority for this study given the size of the wetlands in this study (average = 0.06 ha, n = 3) as well as the quadrats within the wetlands (0.09 m2) [5] . The other priority for remotely sensed data were the spectral resolution, specifically focusing on the need for green, red, and near infrared (NIR) bands. NAIP data records visible bands (red, green, and blue) for all states with some states having NIR data recorded as well. The NIR band is important for most, if not all, of the vegetation indices that have been generated [2] . However, NIR is not available for all states and NAIP has low temporal resolution relative to many satellite sensors, like Landsat 8 Operational Land Imager (OLI).
While Landsat 8 OLI has limitations associated with spatial resolution (30 m) for visible and NIR bands, imagery from Landsat 8 is available at 16 day intervals [7] . Landsat 8 OLI also offers 11 bands, including three bands covering the visible portion of the electromagnetic spectrum (band 2-blue, band 3-green, band 4-red) and NIR (band 5) [7] . With high temporal and spectral resolution, Landsat 8 OLI provides useful imagery for management of sensitive areas, such as southern Appalachian wetlands.
Attempts to estimate biomass from remotely sensed data have been numerous [8] . Over forty vegetation indices have been developed [9] but the primary vegetation index used in remote sensing is the normalized difference vegetation index (NDVI). Wetlands are not a typical environment for the use of vegetation indices to predict biomass or NPP, but [10] found that NDVI can be used but it can be modified to improve its prediction of biomass. This lack of biomass prediction accuracy is in part due to the saturation of NDVI and a traditional non- linear relationships with aboveground vegetation characteristics [10] - [14] , though it is still useful for measuring biomass and should be the starting point for any study trying to predict biomass from vegetation indices. For that reason, efforts have been made to improve NDVI and develop other vegetation indices [14] . However, the NDVI still serves as a point against which to measure any new vegetation index. The difference vegetation index (DVI) has shown the ability to explain a high amount of variance in biomass estimates (r2 = 0.8546) [8] [15] . The DVI is calculated as:
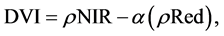 (1)
(1)
where ρNIR is the reflectance of NIR, ρRed is the red reflectance, and α = 0.96916 [16] [17] . The wide dynamic range vegetation index (WDRVI) was found to have the best correlation (r2 = 0.52) with biomass in the coastal marsh study conducted by [5] . According to [13] , the WDRVI is calculated as:
 (2)
(2)
where a serves as an estimation of the vegetation fraction (VF) and can range from 0.05 to 0.2. Other vegetation indices that have been found to have linear relationships with aboveground vegetation characteristics are the modified simple ratio (MSR) [14] [18] , calculated as:
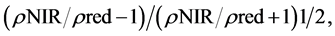 (3)
(3)
and the Renormalized Difference Vegetation Index (RDVI) [14] [19] , which is calculated as:
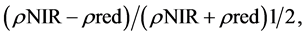 (4)
(4)
The Soil-Adjusted Vegetation Index (SAVI), which was developed by [20] , was created in an attempt to improve upon the NDVI through transformation that allowed for the physical effect of soil interference through reflectance to be eliminated. SAVI is useful for examining wetland vegetation, like reeds [21] , especially when vegetation cover is low and soil exposure is high [22] . SAVI is calculated as:
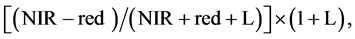 (5)
(5)
where L is a correction factor based on LAI [20] .
Two indices were developed by [23] based on the Atmospherically Resistant Vegetation Index (ARVI), called the Visible Atmospherically Resistant Index, using green reflectance in one calculation (VARIGreen) and red edge reflectance in the other (VARI700) [23] . They are calculated as:
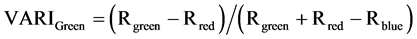 (6)
(6)
and
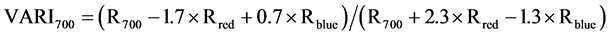 (7)
(7)
where Rgreen is green reflectance, Rred is red reflectance, Rblue is blue reflectance, and R700 is the reflectance at 700 nm (red edge).
All vegetation indices have benefits and drawbacks (Table 1). Methods for examining ecosystems, NPP in particular, have evolved and will continue to evolve as knowledge and technology expand.
NPP is an important indicator of ecosystem function. Gross primary productivity (GPP) is the amount of carbon (C) converted from inorganic forms in the atmosphere to part of the plant body through the process of photosynthesis. NPP is the GPP minus the amount of C lost to the environment through cellular respiration in the root system and herbivory. NPP is important because it serves as a marker of C storage as well as an indication of ecosystem function, where more productive systems will result in higher NPP values. Thus, NPP is important as a measure of both C sequestration and ecological function. The importance of this study is, in part, tied to the importance of NPP.
The significance of this research lies in the study of NPP in montane wetlands, an ecosystem that is little studied, as well as the methods used in this study. As already discussed, NPP is an important factor to study and the development of a model that can estimate NPP in southern Appalachian montane wetlands using vegetation indices would provide a useful tool in management of montane wetlands with less disturbance. In order to create this model, we employed a methodology using proximally sensed data to help improve the accuracy of remotely sensed data for the model. The model developed in this study could be employed in other settings to also improve management, while limiting disturbance.
Table 1. Summary of vegetation index needs.
The objective of this study was to create a model using vegetation indices generated from remotely sensed data in order to estimate NPP to best serve in the management of southern Appalachian wetlands. Among the myriad of vegetation indices in existence, NDVI, DVI, RDVI, WDRVI, SAVI, MSR, and VARI will be examined. The model is designed to inform wetland managers to which type of data acquired and used (platform, spatial resolution, spectral resolution, and temporal resolution) to the appropriate needs of and resources allocated to the wetland managers. Many vegetation indices were tested to provide the best estimate for NPP throughout southern Appalachian wetlands.
2. Materials and Methods
2.1. Study Area
Three wetland sites in the southern Appalachians, one in Alabama and two in Tennessee (Figure 1 and Figure 2) were selected from southern Appalachian wetlands based on the presence of emergent wetland vegetation and the lack of forest using the Wetlands Mapper website operated by the US Fish and Wildlife Service. Tennessee and Alabama sites provided a low amount of surrounding forest cover, which was desirable for the remote sensing portion of this research. Tree cover would limit the capture of images by creating shadows or by being captured within a pixel for Landsat 8 OLI.
2.2. Vegetation Sampling
Leaf area index (LAI) data were collected along with peak standing aboveground biomass, which was assumed to be NPP, for each quadrat [5] . Vegetation was sampled within a 0.09 m2 quadrat along 10-m transects for each wetland site [5] . The biomass collected from each quadrat was assumed to be NPP and NPP values were generated for each quadrat. Biomass samples were refrigerated until further analysis. For biomass sample analysis, samples
Figure 1. Site map for southern Appalachian wetlands in this study.
Figure 2. Landsat 8 OLI imagery for southern Appalachian wetlands in this study. Red dots mark the field sites.
were oven-dried for 12 hours at 50˚C [5] . Biomass samples were massed before and after drying. One above canopy and four below canopy LAI values were taken for each quadrat [5] . LAI served as an ancillary value for WDRVI as well as calculating the L value for SAVI.
2.3. Proximally Sensed Data Collection
Generating a spectral signature involved collecting top of canopy reflectance using OceanOptics JAZ hyperspectral radiometers (OceanOptic Inc., Dunedin, FL, USA) following [5] . Each of the radiometers was calibrated for white, using a Spectralon white reference board (ASD Inc., Boulder, CO), and dark by covering the end of the radiometer. Radiance and irradiance were collected from the two calibrated hyperspectral radiometers, which were operated at least 1 m above the canopy [3] [5] . One of the radiometers was pointed toward the sky in order to collect one sample of incoming irradiance [5] . The other radiometer was pointed toward the ground with 25˚ field of view (FOV) to collect one sample of upwelling radiance [5] . One signature was collected for each biomass sample by collecting one sample of irradiance and one sample of radiance from the vegetation.
After field collection of radiometer data, a reflectance value was generated for each proximally sensed data sample. Radiance and irradiance data were downloaded from the radiometers and a reflectance value was generated by dividing the radiance by the irradiance. The reflectance value generated was a measure of the percentage of irradiance that was radiated back by the vegetation (radiance) for each band, unless vegetation indices dictated otherwise (e.g. VARIGreen). Reflectance values generated from the radiometers were averaged over the bandwidths of NAIP radiometers. For example, the red band for NAIP captured by an ADS radiometer is 607 - 662 nm, thus the values for the reflectance of radiometers were averaged over the same range in order to generate a red reflectance for the radiometers for comparison to NAIP data.
2.4. Remotely Sensed Data Acquisition and Calibration
NAIP data were acquired by downloading data from the USDA Geospatial Data Gateway (http://datagateway.nrcs.usda.gov/). The year of the field work was used for the data collection. If the year of the field work was not available, the closest year was used. Local governments proximal to each site were contacted to inquire about data collected closer to field work dates. GPS coordinates were used to find the pixel associated with the NPP sample collection point and reflectance values for red, green, and NIR were recorded for vegetation index calculations.
NAIP imagery was calibrated using ERDAS Imagine (Hexagon Geospatial, Norcross, GA). NAIP images were calibrated using the empirical line calibration (ELC). Images were calibrated by band by using a spectral library (ASTER). Ground cover types were selected (e.g. grass, asphalt) that occurred near the site and five points were taken of each ground cover within the image. The spectral signatures for the ground points were run against the spectral library signatures for that band. A new image was generated from the ELC. Brightness values were taken from that image for vegetation indices.
Landsat 8 OLI images were downloaded from the USGS Earth Explorer website (http://earthexplorer.usgs.gov/). Imagery was downloaded for the date closest to the date of field work before field work was conducted. 20% cloud cover was the maximum cloud cover; if an image exceeded 20% cloud cover for the collection date, the image from the previous collection period was used. GPS coordinates were used to locate the pixel for each quadrat. Brightness values were recorded for blue, green, red, and NIR for each pixel in order to calculate vegetation indices.
2.5. Vegetation Indices
After reflectance values were generated from radiometer and brightness values were recorded from NAIP data, vegetation indices were calculated for all NPP sites using combinations of green, red, and NIR reflectance data, depending on the vegetation index equation. NDVI was employed because it is the most common vegetation index and generally accepted as the best vegetation index for estimating biomass. The MSR (Equation (3)), RDVI (Equation (4)), DVI (Equation (1)), and WDRVI (Equation (2)) were also used because success has been found in estimating biomass from these indices [5] [14] . LAI was used in order to estimate for VF to calculate WDRVI. LAI values were put into 15 categories to account for the 15 values (0.05 - 0.2) within the range of the VF value used by [14] with the lowest LAI category representing 0.05 and the highest LAI category representing 0.2.
2.6. Data Analysis
The objectives of this study were to determine which vegetation index best identifies variance in NPP and, thus, best informs wetland managers on wetland health. Linear regressions of the vegetation indices calculated for each sample point for in situ and NAIP data and compared to NPP will determine which of the vegetation indices was best able to explain variance in NPP. Because Landsat has coarser spatial resolution than in situ and NAIP imagery, NPP values that fell within one Landsat pixel were averaged [5] and the vegetation index for the pixel was compared to the average NPP value within the pixel via scatter plot.
3. Results
3.1. Abbreviations and Acronyms
There was a large amount of variability in NPP among sites in this chapter as well as a smaller amount of variability in NPP within each site (Figure 3). The range in NPP among all sites was 915 g/m2/yr, with an NPP maximum of 1101 g/m2/yr (sd = 470 g/m2/yr, n = 2) at TN-1 and an NPP minimum of 185 g/m2/yr (sd = 66 g/m2/yr, n = 9) at AL-1. TN-1 and AL-1 were also the sites in this study with the highest and lowest amount of intra-site variability, respectively.
Figure 3. Variability in NPP among sites. Error bars represent one standard deviation.
3.2. Vegetation Indices from in Situ Radiometer Data
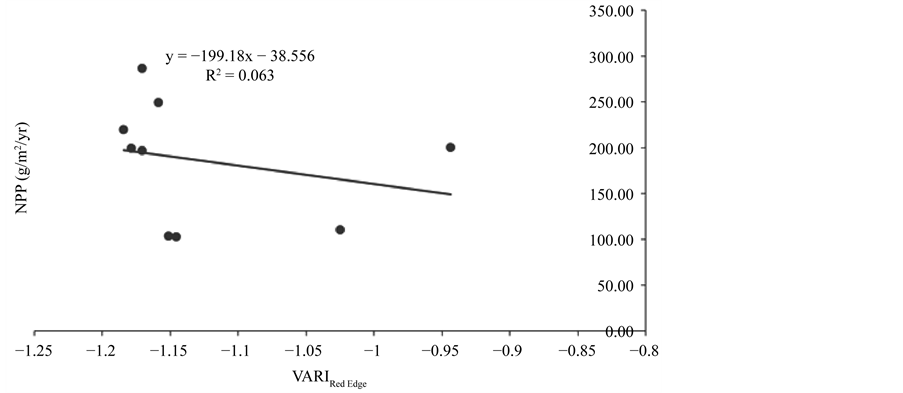
Vegetation indices calculated from in situ radiometer data were able to explain a moderate amount of variance in NPP in southern Appalachian wetlands (Figure 4). The VARI700 showed the most sensitivity to NPP and was
Figure 4. Linear regressions between NPP and the vegetation indices calculated from in situ radiometers.
able to explain the most amount of variance in NPP (r2 = 0.65, p < 0.05), though all of the index values were negative and there appeared to be an outlier. After removing the outlier, it appears as though VARI700 is not as sensitive to NPP (Figure 5). The SAVI was able to explain 39% of variance in NPP and the VARIGreen index was able to explain 32% of variance in NPP. Five of the eight vegetation indices used to estimate NPP were able to explain less than 30% of variance in NPP.
3.3. Vegetation Indices from NAIP Data
Most of the vegetation indices calculated from NAIP data were unable to explain more than 10% of variance in NPP in southern Appalachian wetlands (Figure 6). The NDVI was able to explain 35% of variance in NPP, ranking as the most sensitive vegetation index for NAIP. The WDRVI and MSR were able to explain 8% of variance in NPP and the SAVI was able to explain 6% of variance in NPP. The DVI and RDVI were the least sensitive vegetation indices and were able to explain the least amount of variance in NPP.
3.4. Vegetation Indices from Landsat 8 OLI Data
The amount of variance in NPP by vegetation indices from Landsat 8 OLI were the lowest among all vegetation indices tested in this study (Figure 7). The DVI was able to explain the most amount of variance in NPP (r2 = 0.37, p = 0.10) among vegetation indices calculated from Landsat 8 OLI. The MSR was able to explain 5% of variance in NPP. All other vegetation indices calculated from Landsat 8 OLI were not able to explain more than 2% of variance in NPP.keep using lower-cased.
3.5. Trends among Vegetation Indices by Platform Level
In examining NPP by vegetation indices at three platform levels, a trend was noted for most of the vegetation indices along a change in height of the platform (Figure 8). Generally the highest coefficients of determination between NPP and vegetation indices were noted for the in situ radiometer. As the platform level moves from the in situ radiometer to airborne (NAIP), there is a sharp decline in coefficients of determination for all vegetation indices except NDVI, which increased from 0.28 to 0.35. The coefficient of determination for NDVI dropped sharply when the platform increased in elevation from airborne to satellite. The coefficients of determination for all other vegetation indices, except for the DVI, decreased with an increase in elevation from airborne to satellite platforms.
4. Discussion
4.1. Performances of the Vegetation Indices
There was a disparity in the ability of vegetation indices to explain variance in NPP at all levels, though no ve-
Figure 5. Linear regression between NPP and VARI700 without the outlier.
Figure 6. Linear regressions between NPP and the vegetation indices calculated from NAIP.
getation index was best able to explain variance consistently at all levels. The difference in the ability of vegetation indices to explain variance in NPP is due in part to differences in the indices themselves, but also is related to the type of vegetation and ecosystems in which the indices were employed. No vegetation indices have been developed to specifically study montane wetland NPP. Another cause for the lack of a vegetation index that was able to explain NPP variance at all three levels is that the data is different for all three levels. At the in situ level, hyperspectral radiometers were employed and thousands of bands were used at a high spatial resolution. At the airborne level, NAIP data are limited in the context of spectral resolution, though spatial resolution is still high. At the satellite level, spatial resolution is low, though spectral resolution is higher than NAIP.
At the in situ level, the VARI700 was best able to explain variance in NPP and the SAVI was the second most sensitive vegetation index with respect to NPP. The VARI700 was only applicable to the in situ radiometers because the VARI700 requires hyperspectral data. The VARI700 is a useful vegetation index that was developed by [4] , which estimated canopy chlorophyll content well for maize (r2 = 0.93), however, VARI700 was not as strong at estimating NPP in this study (r2 = 0.65). Like the VARI700, the SAVI requires field work to establish an L value which is based on soil exposure. SAVI was sensitive to NPP variations when radiometers are used in the field but it is not as sensitive at remote or airborne platforms. While the SAVI, which was developed by [19] , is useful for
Figure 7. Linear regressions between NPP and the vegetation indices calculated from Landsat 8 OLI.
Figure 8. Ability of vegetation indices to explain NPP variance at in situ and airborne platform levels.
examining reeds [20] , especially when vegetation cover is low and soil exposure is high [21] , it was not as effective in estimating NPP in this study concerning emergent vegetation.
The NDVI, which is one of the main vegetation indices used for examining or monitoring vegetation, was the most sensitive vegetation index for NAIP data. While the NDVI may be criticized, it is still very useful in monitoring vegetation. The NDVI was one of the original vegetation indices developed by [23] and [24] and has since been modified to better estimate vegetation characteristics (e.g. WDRVI) [9] [14] . The NDVI serves well in any land management where vegetation biomass or LAI is low before the NDVI is saturated [2] . NDVI was able to explain a similar amount of variation in NPP (35%) as in [10] (39%) using imagery with high spatial resolution. Other than the problem of saturation, the NDVI would provide a useful tool for wetland management if NAIP data were used.
The DVI was the most sensitive vegetation index when using Landsat 8 OLI data. Similarly, [14] found a high amount of variance in wetland biomass (r2 = 0.85) was explained by the DVI calculated from Landsat 7 ETM+ [8] . The DVI would be useful for Landsat 8 OLI data, which is available at a high temporal resolution (16 days). For constant monitoring of montane wetland vegetation, the use of the DVI calculated from Landsat 8 OLI data would serve as the best tool.
4.2. Limitations
There were some limitations associated with this research. More specifically, there was a lack of sample size to examine the associations between field NPP estimates and the estimates gathered from vegetation indices. There were limitations associated with the congruence of dates between the field work and the collection of remotely sensed data. Also, there might be some differences in the season in which the biomass was collected and when the imagery was collected. For imagery with lower spatial resolution (i.e. Landsat 8 OLI), there may exist a difference in the NPP from field samples and the ecosystem NPP. There might also exists differences between scales concerning NPP and imagery.
5. Conclusions
This study provided valuable tools for wetland managers in the southern Appalachians and contributes to the scientific community with intellectual merit. By conducting an examination on vegetation indices and NPP, the people in charge of southern Appalachian wetlands can now make better informed decisions on how to monitor wetlands with remote sensing data. The results of this study also contribute to the scientific community by further testing vegetation indices in an environment where few, if any, similar studies have been conducted.
The choice in vegetation index depends on the platform that is being used to examine southern Appalachian wetlands. At the in situ level, the VARI700 (r2 = 0.65) was most sensitive to changes in NPP, with SAVI (r2 = 0.39) and VARIGreen (r2 = 0.33) also showing sensitivity toward NPP. At the airborne level, most vegetation indices saw a drop in coefficient of determination with NPP. The exception was the NDVI, which was more sensitive to NPP at the airborne level (r2 = 0.35) than the in situ level (r2 = 0.28). All other vegetation indices were insensitive to changes in NPP. At the satellite platform, the DVI (r2 = 0.37) was the most sensitive vegetation index.
Within the broader context of vegetation index usage across ecosystems and in different areas of the world, it would appear that a variety of indices should be tested and performance may depend on the platform level. For future studies concerning the use of vegetation indices, it is important to start with the NDVI as that is still the main index and was effective at the airborne level with high spatial resolution. It is also important to consider the ecosystem in which the study takes place. As few studies have been focused on remote sensing use in wetlands, it is important to expand efforts to study wetlands with remote sensing so as not to disturb these sensitive ecosystems, yet to understand them because of their sensitivity, especially as it relates to climate change.
Acknowledgements
First and foremost, we would like to thank Chanda Maguigan for all of her hard work in this study. We would like to thank the Department of Geosciences for partial funding through an assistantship and use of the department truck. We would also like to thank the permitting agencies including The Nature Conservancy of Shady Valley, TN and Lake Guntersville State Park. This material is based upon work supported by the National Science Foundation under Grant No. DGE-0947419 at Mississippi State University. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
Cite this paper
Michael Maguigan,John Rodgers,Padmanava Dash,Qingmin Meng, (2016) Assessing Net Primary Production in Montane Wetlands from Proximal, Airborne, and Satellite Remote Sensing. Advances in Remote Sensing,05,118-130. doi: 10.4236/ars.2016.52010
References
- 1. Cramer, W., Kicklighter, D., Bondeau, A., Moore, B., Churkina, G., Nemry, B., Ruimy, A. and Schloss, A., the Participants of the Potsdam NPP Model Intercomparison (1999) Comparing Global Models of Terrestrial Net Primary Productivity (NPP): Overview and Key Results. Global Change Biology, 5, 1-15.
http://dx.doi.org/10.1046/j.1365-2486.1999.00009.x - 2. Gitelson, A., Vina, A., Arkebauer, T., Rundquist, D., Keydan, G. and Leavitt, B. (2003) Remote Estimation of Leaf Area Index and Green Leaf Biomass in Maize Canopies. Geophysical Research Letters, 30, 1248.
http://dx.doi.org/10.1029/2002GL016450 - 3. Rundquist, D., Perk, R., Leavitt, B., Keydan, G. and Gitelson, A. (2004) Collecting Spectral Data over Cropland Vegetation Using Machine-Positioning versus Hand Positioning of the Sensor. Computers and Electronics in Agriculture, 43, 173-178.
http://dx.doi.org/10.1016/j.compag.2003.11.002 - 4. Gitelson, A., Vina, A., Verma, S., Rundquist, D., Arkebauer, T., Keydan, G., Leavitt, B., Ciganda, V., Burba, G. and Suyker, A. (2006) Relationship between Gross Primary Production and Chlorophyll Content in Crops: Implications for the Synoptic Monitoring of Vegetation Productivity. Journal of Geophysical Research: Atmospheres, 111, D08S11.
http://dx.doi.org/10.1029/2005JD006017 - 5. Mishra, D.R., Cho, H., Ghosh, S., Fox, A., Downs, C., Merani, P., Kirui, P., Jackson, N. and Mishra, S. (2012) Post-Spill State of the Marsh: Remote Estimation of the Ecological Impact of the Gulf of Mexico Oil Spill on Louisiana Salt Marshes. Remote Sensing of Environment, 118, 176-185.
http://dx.doi.org/10.1016/j.rse.2011.11.007 - 6. United States Department of Agriculture. NAIP Imagery. Last Modified August 26, 2013.
https://www.fsa.usda.gov/programs-and-services/aerial-photography/imagery-programs/naip-imagery/ - 7. United States Geological Survey. What Are the Band Designations for the Landsat Satellites? Last Modified June 19, 2014.
http://landsat.usgs.gov/band_designations_landsat_satellites.php - 8. Adam, E., Mutanga, O. and Rugege, D. (2010) Multispectral and Hyperspectral Remote Sensing for Identification and Mapping of Wetland Vegetation: A Review. Wetlands Ecology and Management, 18, 281-296.
http://dx.doi.org/10.1007/s11273-009-9169-z - 9. Bannari, A., Morin, D., Bonn, F. and Huete, A. (1995) A Review of Vegetation Indices. Remote Sensing Reviews, 13, 95-120.
http://dx.doi.org/10.1080/02757259509532298 - 10. Mutanga, O., Adam, E. and Cho, M. (2012) High Density Biomass Estimation for Wetland Vegetation Using World-View-2 Imagery and Random Forest Regression Algorithm. International Journal of Applied Earth Observation and Geoinformation, 18, 399-406.
http://dx.doi.org/10.1016/j.jag.2012.03.012 - 11. Myneni, R.B., Hall, F.G., Sellers, P.J. and Marshak, A.L. (1995) The Interpretation of Spectral Vegetation Indexes. IEEE Transactions on Geoscience and Remote Sensing, 33, 481-486.
http://dx.doi.org/10.1109/36.377948 - 12. Myneni, R.B., Hoffman, S., Knyazikhin, Y., Privette, J.L., Glassy, J., Tian, Y., Wang, Y., Song, X., Zhang, Y., Smith, G.R., Lotsch, A., Friedl, M., Morisette, J.T., Votava, P., Nemani, R.R. and Running, S.W. (2002) Global Products of Vegetation Leaf Area and Fraction Absorbed PAR from Year One of MODIS Data. Remote Sensing of Environment, 83, 214-231.
http://dx.doi.org/10.1016/S0034-4257(02)00074-3 - 13. Huete A.R., Didan, K., Miura, T., Rodriguez, E.P., Gao, X. and Ferreira, L.G. (2002) Overview of Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sensing of Environment, 83, 195-213.
http://dx.doi.org/10.1016/S0034-4257(02)00096-2 - 14. Gitelson, A. (2004) Wide Dynamic Range Vegetation Index for Remote Quantification of Crop Biophysical Characteristics. Journal of Plant Physiology, 161, 165-173.
http://dx.doi.org/10.1078/0176-1617-01176 - 15. Tan Q., Shao Y., Yang S. and Wei Q. (2003) Wetland Vegetation Biomass Estimation Using Landsat-7 ETM+ Data. IEEE Transactions on Geoscience and Remote Sensing, 3, 2629-2631.
- 16. Richardson, A. and Everitt, J. (1992) Using Spectral Vegetation Indices to Estimate Rangeland Productivity. Geocarto International, 1, 63-77.
http://dx.doi.org/10.1080/10106049209354353 - 17. Lyon, J., Ding Y., Lunetta, R. and Elvidge, C. (1998) A Change Detection Experiment Using Vegetation Indices. Photogrammetric Engineering and Remote Sensing, 64, 143-150.
- 18. Chen, J.M. and Cihlar, J. (1996) Retrieving Leaf Area Index of Boreal Conifer Forests Using Landsat TM Images. Remote Sensing of Environment, 55, 153-162.
http://dx.doi.org/10.1016/0034-4257(95)00195-6 - 19. Roujean J-L., Breon, F-M. (1995) Estimating PAR Absorbed by Vegetation from Bi-Directional Reflectance Measurements. Remote Sensing of Environment, 51, 375-384.
http://dx.doi.org/10.1016/0034-4257(94)00114-3 - 20. Huete, A.R. (1988) A Soil-Adjusted Vegetation Index (SAVI). Remote Ssensing of Environment, 25, 295-309.
http://dx.doi.org/10.1016/0034-4257(88)90106-X - 21. Poulin, B., Davranche, A. and Lefebvre, G. (2010) Ecological Assessment of Phragmitesaustralis Wetlands Using Multi-season SPOT-5 Scenes. Remote Sensing of Environment, 114, 1602-1609.
http://dx.doi.org/10.1016/j.rse.2010.02.014 - 22. Zhang, M., Ustin, S.L., Rejmankova, E. and Sanderson, E.W. (1997) Monitoring Pacific Coast Salt Marshes Using Remote Sensing. Ecological Applications, 7, 1039-1053.
http://dx.doi.org/10.1890/1051-0761(1997)007[1039:MPCSMU]2.0.CO;2 - 23. Gitelson, A.A., Kaufman, Y.J., Stark, R. and Rundquist, D. (2002) Novel Algorithms for Remote Estimation of Vegetation Fraction. Remote Sensing of Environment, 80, 76-87.
http://dx.doi.org/10.1016/S0034-4257(01)00289-9 - 24. Rouse, J.W. (1973) Monitoring the Vernal Advancement and Retrogradation of Natural Vegetation. NASA/GSFCT Type II Report, Greenbelt, MD.