Advances in Remote Sensing
Vol.04 No.03(2015), Article ID:59977,13 pages
10.4236/ars.2015.43019
Actual Evapotranspiration Estimation Using Remote Sensing: Comparison of SEBAL and SSEB Approaches
Bergson G. Bezerra1, Bernardo B. da Silva2, Carlos A. C. dos Santos3, José R. C. Bezerra4
1Program of Post-Graduate in Climatic Sciences, Federal University of Rio Grande do Norte (PPGCC/UFRN), Natal, Brazil
2Department of Geographical Sciences, Federal University of Pernambuco, Recife, Brazil
3Department of Atmospheric Science, Federal University of Campina Grande, Campina Grande, Brazil
4Brazilian Agricultural Research Company/National Centre of Cotton Research (EMBRAPA/Algodão), Campina Grande, Brazil
Email: bergson.bezerra@gmail.com, bbdasilva.ufpe@gmail.com, carlos@dca.ufcg.edu.br, carlostorm@gmail.com, renato.cortez-bezerra@embrapa.br
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 June 2015; accepted 25 September 2015; published 28 September 2015
ABSTRACT
The main objective of this paper was to evaluate the daily actual evapotranspiration (ET) accuracy obtained by remote sensing algorithms when compared with Bowen ratio measurements performed in the cotton fields. The experiment was conducted in a cotton experimental field of EMBRAPA located in Ceará State, Brazil. Seven TM Landsat-5 images acquired in 2005 and 2008 were used to perform SEBAL and SSEB algorithms. The comparison between the estimated values by remoting sensing algorithms and the measured values in situ showed an acceptable accuracy. Besides, SSEB algorithm showed to be an important tool for ET analysis in the semi-arid regions, due to the fact that it does not need the meteorological data to solve the energy balance, but only the average temperature of the “hot” and “cold” pixels. Additionally, SSEB presents simpler pro- cessing than SEBAL algorithm that needs to solve an iterative process to obtain the sensible heat flux values.
Keywords:
Energy Balance, Landsat, Evapotranspiration, Bowen Ratio, Semi-Arid

1. Introduction
Monitoring the spatial and temporal distribution of actual evapotranspiration (ET) is critically important for water management and crop water requirements, particularly in water-scarce regions [1] - [3] . Most studies have demonstrated that the temporal and spatial patterns of ET depend on a large variety of influencing factors, specifically vegetation and soil types, topography, the meteorological conditions, spatial and temporal variations of soil water content [1] [4] [5] . The primary methods used conventionally to measure ET are based on field scales (Bowen ratio, Eddy covariance method, soil water balance), but do not allow the estimation of fluxes when dealing with larger spatial scales because of the heterogeneity inherent in land surfaces and the dynamic nature of water vapor transport processes [6] . Thus, they are unable to provide estimates of spatially distributed ET.
According to [2] remote sensing by satellite has long been identified as a technology capable of monitoring ET spatially distributed. However [2] emphasizes that ET cannot be measured directly from satellites, but can be estimated based on surface radiation fields through semi-empirical remote sensing approaches such as SEBAL (Surface Energy Balance Algorithm for Land) [7] [8] and its variant METRIC (Mapping Evapotranspiration at High Resolution with Internalized Calibration) [9] [10] , and M-SEBAL (Modified Surface Energy Balance Algorithm for Land) [11] , beyond S-SEBI (Simplified Surface Energy Balance) [12] .
The SEBAL approach uses spectral radiance recorded by satellite sensors and meteorological data to solve the energy balance at the land surface. A relevant procedure of SEBAL algorithm is the methodology to compute daily ET from instantaneous latent heat flux (LE) (satellite overpass time). The original approach of SEBAL [8] [13] is based on the use of the evaporative fraction, Λ, which is defined as ratio between latent heat flux and available energy [12] , as temporal-integration quantity. This approach assumes two main hypotheses: 1) the amount to 24-h soil heat flux is negligible if compared to 24-h net radiation, and 2) the instantaneous value of evaporative fraction (Λ) can be assumed equal to the average daytime value. This hypothesis is based on some studies, i.e., [14] [15] which provided evidence of self-preservation (i.e., constancy) of Λ. Some modifications in the SEBAL algorithm have been proposed by [16] [17] that initially was called SEBALID (reference to Idaho state) and later METRIC [9] [10] , for the calculation of daily ET based on the reference evapotranspiration fraction (ETrF), that according to [16] is equal to crop coefficient discussed by FAO-56 [18] . The ET calculated based on ETrF offers larger reliability, because it is strongly linked with the reference evapotranspiration (ETr), recommended method by FAO-Penman-Monteith [18] for the alfalfa, which is based on several meteorological parameters, regard the eventual cloudiness presence. Thus, ETrF is calculated by the ratio between instantaneous ET and ETr and admitted as being constant during the daytime.
However, the core of the SEBAL algorithm is the approach for estimating the sensible heat flux (H), which is based in a complex procedure involving micrometeorological concepts for calculating parameters for atmospheric stability corrections, and aerodynamic resistance [2] [9] [13] [16] .
The SSEB (Simplified Surface Energy Balance) approach was proposed by [19] , that unlike SEBAL, the ET is calculated based on simpler methodology. The SSEB approach is based on assumption that the latent heat flux (actual ET) varies linearly with land surface temperature (LST) [19] -[21] . This method presupposes that LST is related to soil moisture and then to the atmospherics fluxes. This assumption was previously used in the construction of S-SEBI algorithm [12] . The ET is calculated from evapotranspiration fraction (ETf) which is calculated from average temperature of “hot” and “cold” pixels [19] . The hot pixel correspond to bare soil or sparse vegetation areas with lesser ET and cold pixels represent maximum ET throughout the study area and should be chosen in irrigated or dense vegetation areas [16] [19] . This method has been tested presenting strong correlations with the SEBAL and METRIC estimates [19] [21] .
The main goal of this study is evaluating the daily ET based on the energy balance obtained by SEBAL and SSEB algorithms. The estimates of these methods are compared with the ET obtained by Bowen Ratio Energy Balance (BREB) method on fields of cotton and castor bean, under full irrigation conditions. The studied areas in this research were located in a semi-arid region of Brazil. Therefore, the applications and accuracy analyses of different remote sensing algorithms to obtaining ET are necessary and important to identify the performance of the simple SSEB algorithm.
2. Data and Method
2.1. Study Area
This study was conducted in two sites of Brazilian Semi Arid region: experimental field of EMBRAPA―Brazilian Agricultural Research Company, located in Barbalha (07˚19'S, 39˚18'W, 415 m) in Ceará (CE) state and Experimental Station of EMPARN―Agricultural Research Company of Rio Grande do Norte State, located in Apodi-RN (05˚37'S, 37˚49'W 138 m) in Rio Grande do Norte (RN) state (Figure 1).
Although both the sites are located in Brazilian Semi-Arid region (Figure 1), Barbalha-CE and Apodi-RN has different climates. According to [22] the climate of Apodi-RN is semiarid while Barbalha-CE has dry sub humid climate. The average air temperature of Apodi-RN ranges from 23.5˚C (August) to 28.3˚C (December) while in Barbalha-CE this variation is from 23.8˚C (July) to 26.8˚C (November) (Figure 2). The average annual rainfall in Apodi-RN is 920 mm with average annual potential evapotranspiration equal to 1632 mm while in Barbalha-CE average annual rainfall is 1001 mm and average annual potential evapotranspiration is equal to 1392 mm. More details about study sites can be found in [5] [23] [24] .
In this study the ET was calculated from SEBAL and SSEB approaches using seven TM-Landsat 5 images whose details are shown in Table 1. The images were acquired from INPE―National Institute of Space Research of Brazil.
Figure 1. The region highlighted in Blue on the South America map is the Brazilian Semiarid, in which the location of the studied area in Barbalha-CE and Apodi-RN are shown on the right figure.
Figure 2. Monthly average of the rainfall and air temperature in Barbalha-CE and Apodi-RN.
Table 1. Details of the TM-Landsat 5 images used in this study.
2.2. SEBAL Approach Descriptions
The ET is calculated using SEBAL from resolution of energy balance equation. The first step is to obtain the net radiation (Rn) pixel by pixel using the following equation:
 (1)
(1)
where a is the albedo (dimensionless), 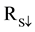 is the incoming solar radiation (W∙m−2),
is the incoming solar radiation (W∙m−2),  is the incoming longwave radiation (W∙m−2),
is the incoming longwave radiation (W∙m−2),  is the outgoing longwave radiation (W∙m−2), and ε0 is the surface thermal emissivity (dimensionless).
is the outgoing longwave radiation (W∙m−2), and ε0 is the surface thermal emissivity (dimensionless).
To obtain Rn (Equation (1)) it is necessary several computational steps such as the spectral radiance, reflectivity, albedo, emissivity, and land surface temperature. These computational steps are described in [16] and [25] .
The second step is computation of the soil heat flux (G), which is the rate of heat storage into the soil and vegetation due to conduction, which was computed using the following empirical equation proposed by [13] :
 (2)
(2)
where LST is the Land Surface Temperature obtained by the modified Planck equation based on thermal radiance of TM Landsat 5 and NDVI is the Normalized Difference Vegetation Index [26] .
Sensible heat flux (H) is the rate of heat loss to the air by convection and conduction, due to a temperature difference. It is computed using the following equation for heat transport [7] :
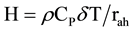 (3)
(3)
where ρ is the air density (kg∙m−3), cp is the air specific heat (1004 J∙kg−1∙K−1) at constant pressure, rah is the aerodynamic resistance to heat transport (s∙m−1) between two near surface heights, z1 and z2 (0.1 a 2 m, respectively), dT (K) represents the near surface temperature difference between the levels z1 and z2. According to [9] , dT is used in Equation (3) because of the difficulty in estimating LST accurately from satellite due to uncertainty in atmospheric attenuation or contamination and radiometric calibration of the sensor. Still according to [9] , dT is designed to “float” above the surface, beyond the height for sensible heat roughness (z0h) and zero plane displacement (d), and can be approximated as a relatively simple linear function of LST.
Equation (3) is difficult to solve because there are two unknowns, rah and dT. The calculations of rah, dT and H uses wind speed extrapolated from some blending height above the ground surface (in this study equal to 100 m) and an iterative stability correction scheme based on the Monin-Obhukov functions [9] . To facilitate this computation, we utilize the two “anchor” pixels (where reliable values for H can be predicted and a dT estimated). More details can be found in [16] and [25] .
Latent heat flux (LE) is the rate of latent heat loss from the surface due to evapotranspiration. It is computed as the residual of the energy balance for each pixel using the following equation:
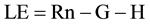 (4)
(4)
The daily ET was derived from evaporative fraction (Λ) which is calculated from instantaneous value of the LE pixel by pixel using the following equation:
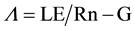 (5)
(5)
Considering that the instantaneous value of Λ is similar to its 24 h counterpart because the difference between the instantaneous Λ at the satellite overpass and the Λ derived from the 24-h integrated energy balance is marginal and may be neglected [14] [15] [27] , and G for daily period can be ignored and net available energy (Rn − G) reduces to Rn, ET was calculated from:
 (6)
(6)
The daily net radiation (Rn24) was estimated using 24-h integrated meteorological variables by the Equation of [28] :
 (7)
(7)
where the daily surface albedo (α0) is assumed to be similar to the surface albedo during the morning overpass [13] , 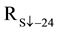 is the 24 h incoming solar radiation,
is the 24 h incoming solar radiation, 
 is the atmospheric transmittance,
is the atmospheric transmittance, 
The computational steps for calculating energy balance and instantaneous latent heat flux (for satellite overpass time) are shown in the Figure 3.
2.3. SSEB Approach Descriptions
According to [19] [20] [29] [30] the obtaining of daily ET using SSEB algorithm is based on the evapotranspiration fraction (ETf) which is calculated pixel by pixel using the Equation (8), whose computational steps are illustrated in the flow chart which is shown in Figure 4:

where LSTHP is the average temperature of the three hot pixels selected for a given scene, LST is the land surface temperature pixel-by-pixel in the composite scene, and LSTCP is the average of the three cold pixels selected for the scene.
The calculation of daily ET has been made using a similar methodology of the classic method of the crop coefficient (Kc) [18] . As presented previously, [19] affirm that the ETf is similar to Kc. Thus, ET was calculated using the following equation:

where ETr(d) is the daily reference evapotranspiration, whose calculation already mentioned.
2.4. Validation of SEBAL and SSEB Approaches
The data used to validate the approaches were collected in experimental campaigns accomplished on the cotton and castor bean crop fields in Barbalha-CE and cotton field in Apodi-RN, all under full irrigation conditions, using Bowen Ratio Energy Balance―BREB method. The characteristics of experimental fields in Barbalha-CE and Apodi-RN were shown in Table 2.
The daily ET was estimated, from the latent heat flux (LE) which was obtained from the following equation [24] [31] :

where Rn is the net radiation (W×m−2), G is the soil heat flux (W×m−2) and b is the Bowen ratio. According to the method proposed by [31] , for calculating the latent heat flux, for the period of the day with positive energy available (Rn − G > 0), b was calculated from the following equation:

where g is the psychometric constant (kPa∙˚C−1), dT and de above canopy vertical gradients of air temperature (˚C) and vapor pressure (kPa), respectively.
Rn measurements were obtained by a NR-LITE net radiometer (Kipp & Zonen, Delft, The Netherland) in
Figure 3. Flow chart of the computational steps of SEBAL algorithm.
Table 2. Characteristics of experimental field.
Figure 4. Flow chart of the computational steps of SSEB algorithm.
stalled at 2 m above canopy, while G was measured by two soil heat flux plates, model HFP01SC Self-Calibra- tion Soil Heat Flux Plate (Hukseflux Thermal Sensors, Delft, The Netherland), burried at 0.02 m depth. The gradients of the air temperature (˚C) and vapor pressure (kPa) were measured using psychrometers constructed with thermocouples type T (copper?constantan), installed at 0.5 and 2.0 m above canopy. More details about field experimental procedures can be found in [5] [23] [24] .
2.5. Error Analysis
To evaluate the level of difference between the observed ET data (BREB) and estimated values (SEBAL and SSEB), the Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE) and Root Mean Square Error (RMSE) were computed as given by [32] :



where ET(Mod)i and ET(Obs)i was the ET values estimated by SEBAL or SSEB approaches and observed on field by BREB, respectively.
3. Results and Discussion
Surface energy fluxes for satellite overpass time estimated by SEBAL approach and observed on field were shown in Table 3. Note that the greatest uncertainty associated to SEBAL was verified in the estimates of H (MAPE > 60%) and G (MAPE~40%). On the other hand the estimates of Rn and LE using SEBAL approach were the most accurate when compared to field observations, i.e., MAPE lower than 10% corroborating to [8] .
One of probable sources of uncertainties in the validation of SEBAL estimates can be associated to instantaneous energy balance closure (satellite overpass time). While the SEBAL approach forces the energy balance closure and calculates LE as a residual of the energy balance equation, the residue of the energy balance (i.e., LE = Rn − G − H) from field observation using BREB method, in turn, ranged from −22.8 W∙m−2 to 142 W∙m−2. This imbalance in instantaneous measurements of energy balance is common and is associated to different sensibili-
Table 3. Comparison of surface energy fluxes observed on field and estimated by SEBAL approach.
ties of the different sensors which compose the Bowen ratio system beyond to the different footprint of measures of Rn, G, H and LE [8] .
The high uncertainty associated to G is considered a minor problem by [8] , because microscale soil heat flux measurements are representative of a very small sphere of influence and therefore incompatible with the size of one Thematic Mapper pixel anyhow. Moreover, uncertainty decreases with increasing scale [8] [33] . According to [33] , the error (1-ha resolution) varies from 10% to 20%. For an area of 1000 ha, the error is reduced to 5% and for farmland regions of 1 million ha the error becomes negligibly small.
However it should be noted the good performance of SEBAL approach in estimating the LE or ET. The difference of 19.4 W∙m−2 in LE is equivalent to MAPE less than 5% and should be seen as encouraging. Errors of this magnitude against the limitations previously described are within the range of uncertainty of the field instruments [8] .
The validation of daily ET outputs of the SEBAL and SSEB approaches are shown in Table 4 and Table 5. It is found satisfactory performance of SEBAL approach (Table 4) since the MAE was less than 0.5 mm, RMSE equal to 0.40 mm and MAPE about 6%.
In different places around the world SEBAL and/or METRIC have been applied and their results have shown similar performances. In agreement with [34] the differences between SEBAL and observed measurements were less than 0.3 mm ∙day−1, while [35] found differences between the SEBAL estimates and soil water balance observations less than 1.0 mm∙day−1, and absolute error comparing the ET monthly estimates in sorghum in September, October and November, were 4%, 4% and 19%, respectively. Using METRIC [10] compared its estimates with lysimeter measurements of sugar beet crop, in four analyzed dates from April to September of 1989, and found differences less than 7%.
The validation of the SSEB approach is shown in Table 5. Note that SSEB performance was poorer than that of SEBAL since the MAE and RMSE were about 60% higher and MAPE about 10%. SSEB approach was previously validated on Texas High Plains by comparison with lysimeter data [36] . In this study was found RMSE equal to 1.2 mm and MBE (Mean Bias Error) of −0.6 mm∙day−1, while [37] validated by comparison with latent heat flux data from 60 FLUXNET eddy covariance sites for the years 2001 to 2007 and found RMSE ranging from 24 to 30 mm∙month−1.
Figure 5 shows the scatter plot between daily ET observed in field using BREB method and daily ET estimate by SEBAL (left) and SSEB (right). The daily ET outputs of both SEBAL and SSEB approaches were
Figure 5. Scatter plot of daily ET observed in field using Bowen ratio method and estimated by SEBAL (left) and SSEB (right).
Table 4. Comparison of surface energy fluxes observed on field and estimated by SSEB approach.
Table 5. Observed daily evapotranspiration in the cotton crop field using the Bowen ratio energy balance method (BREB) and the estimated value by SSEB algorithm using Landsat 5-TM images.
strongly correlated with field observations, i.e., R2 equal to 0.90 and 0.71, respectively. The R2 between SSEB approach and BREB method is within the range of R2 found by [21] (from 0.42 to 0.90) comparing SSEB estimate with eddy covariance data observed on diverse ecosystems including cropland, cropland/natural, forest, woody savanna, grassland, scrubland, and urban. On the other hand [36] compared ET provided by SSEB with ET observed from lysimeter on dryland and irrigated areas on Texas High Plains and found R2 of 0.84. However, in terms of magnitude, it is noted that both SEBAL and SSEB approaches underestimated the field observations because more points fall below the one-to-one lines.
The best performance of SEBAL approach is expected due to some details which involves the formulation of both SEBAL and SSEB approaches. SEBAL approach is based on concepts physically complex, such as laws of radiation [38] [39] procedures of atmospheric corrections beyond concepts and procedures of micrometeorology such as Monin-Obukhov Similarity theory, correction of atmospheric instability conditions, concept of constancy or self-preservation of the fluxes [2] [7] [9] [27] [40] , while SSEB algorithm is based on a simpler theory, considering only that surface temperature is related to soil moisture and then the atmospherics fluxes [12] [19] .
Nevertheless, a problem that should be emphasized in the validation of ET results obtained using satellite images is the “thermal contamination” [8] [10] [17] . The “thermal contamination” occurs because there are differences between spatial resolution of the visible and near infrared channels and thermal infrared channel. Thus, experimental areas with reduced size can be composed of pixel with radiometric information of adjacent area with different soil vegetation cover. According to [10] “thermal contamination” becomes more important when the size of the experimental area is compatible with the spatial resolution of the pixel in thermal channel. In this specific case of TM Landsat 5 is of 120 m corresponding to a scanned area of about 1.5 ha. In SEBAL and/or METRIC validations the “thermal contamination” has been a problem as shown in [10] [17] . The errors attribute to this contamination between METRIC estimations and lysimeter measurements ranged between 23% and 139% on four dates of study [10] .
In the validation of the SSEB approach the “thermal contamination” should be more impactful because ET is only based on data provided by the thermal channel. This can be seen in Figure 6 which shows the images of ET on December 19, 2008 provided by SEBAL (left) and SSEB (right). As can be seen in the areas highlighted in the two images, the ET estimated based on SEBAL offers more sensibility to coverage and land use. In other words, the SEBAL is able to provide values of ET in accordance with a range of soil coverage greater than that detected by the SSEB approach. This occurs because the SEBAL approach uses numerous input variables to calculate ET such as albedo and vegetation index which are calculated based on high resolution reflectance of channels 1, 2, 3, 4, 5 and 7 of TM-Landsat 5 (spatial resolution of 30 m), although the radiance of thermal channel is critical in determining the surface temperature and thus the sensible heat flux and ET. On the other hand, ET output of the SSEB approach is based only on low resolution reflectance of channel 7 (spatial resolution 120 m).
The effect of images resolution in the accuracy of ET was evaluated by [2] which compared evapotranspiration calculated from high resolution Landsat/ASTER images and low resolution MODIS images and concluded that the use of remote sensing ET algorithm developed at fine resolution (Landsat/ASTER) to coarse-
Figure 6. Daily ET maps of 2008 dec-19 provided by SEBAL (left) and SSEB (right).
resolution (MODIS) data will result in underestimating low ET rates (<1 mm/day) and overestimating high ET rates; the overestimation is within 20%.
Figure 7 shows the scatter plot of the dataset of daily ET provided by SEBAL approach correlated with correspondent data provided by SSEB approach for each scene and for each date of study. As can be seen on Figure 7 there is considerable scatter around the one-to-one line. However, there is a reasonable relationship with R2 ranging from 0.63 to 0.90 and slope ranging from 0.69 to 1.05 (Table 6). The RMSE, still according to Table 6, ranged from 0.37 to 1.2 mm. Analyzing the seven studied days together, R2 was of 0.70, RMSE of 0.60 mm and slope of 0.86.
The validation of the SSEB performance was undertaken using field crop data in the United States. Corn and soybean fields in two South Dakota counties, Brookings and Moody, were used to compare model results with the SEBAL and METRIC methods, as well as, Landsat thermal images to assess the SSEB performance were
Figure 7. Scatter plot of daily ET estimated by SEBAL and SSEB approach.
Table 6. Statistical analysis between daily ET provided by SEBAL and SSEB approach.
where N is the sample size.
used. The R2 of the relationship between SSEB and METRIC varied from 0.94 to 0.99 and with SEBAL between 0.55 and 0.79 [19] . On the other hand [20] compared SSEB with METRIC approach on south central Idaho and found R2 which ranged from 0.27, in more complex (mountain) areas with elevation greater than 2000 m, to 0.90 in less complex topography (elevation less than 2000 m).
The SSEB approach has evolved from a focus on large irrigation basins, which is uniform hydro climatic zones, to a continent scale with diverse ecosystems [21] . This study contribute to the algorithm validation which can improve the continental application that is an innovative parameterization using pre-defined hot and cold boundary conditions, which prompted the renaming of the model to indicate its potential use for routine operational applications [21] . This simplicity is particularly important for the Brazilian semi-arid region to quantify and map year to year variability in consumptive water use. This method application can produce ET maps at a large scale on a regular basis with minimal computational requirements; generate operational monthly and annual ET anomaly maps for drought monitoring purposes. Additionally, this method can easily be applied to the recently launched LDCM (Landsat Data Continuity Mission) satellite data with its improved TIRS bands.
4. Conclusions
In this paper, the methods developed by [7] [8] (SEBAL) and [19] (SSEB) for ET retrieval were applied. The SEBAL algorithm has been applied around the world presenting good results. However, the process to obtain the ET needs meteorological parameter information, and to obtain the sensible heat flux an iterative process following the Monin-Obukhov theory is applied. In SSEB algorithm, the ET estimation does not use the solution of the energy balance as the SEBAL algorithm, but uses the crop coefficient method proposed by FAO-56 [18] .
The SEBAL and SSEB algorithms have shown similar results. The comparison between the estimated values by remote sensing (SEBAL and SSEB) and the field measurements (BREB) showed that the methods presented acceptable accuracy. However, the best performance of the SEBAL algorithm was evident. In general, the SSEB performance has been similar to those presented by SEBAL. Errors showed by SSEB must be associated to the “thermal contamination” of the pixels chosen. The analysis of the correlation between both the algorithms presented good agreement.
These results evidenced that the SSEB algorithm was a promising tool to be applied in semi-arid regions of Brazil where few weather stations were in operation. Thus, the SEBAL and other remote sensing algorithms application in that region have been difficult.
Acknowledgements
The first author is grateful for the Ph.D. scholarship provided by National Council for Scientific and Technological Development (CNPq). The second and third authors are grateful for the productivity scholarship provided by CNPq, and the EMBRAPA (Brazilian Company of Agricultural Research) for providing the cotton field data.
Cite this paper
Bergson G.Bezerra,Bernardo B. daSilva,Carlos A. C. dosSantos,José R. C.Bezerra, (2015) Actual Evapotranspiration Estimation Using Remote Sensing: Comparison of SEBAL and SSEB Approaches. Advances in Remote Sensing,04,234-247. doi: 10.4236/ars.2015.43019
References
- 1. Bouwer, L.M., Biggs, T.W. and Aerts, C.J.H. (2008) Estimates of Spatial Variation in Evaporation Using Satellite-Derived Surface Temperature and a Water Balance Model. Hydrological Processes, 22, 670-682.
http://dx.doi.org/10.1002/hyp.6636 - 2. Gebremichael, M., Wang, J. and Sammis, T.W. (2010) Dependence of Remote Sensing Evapotranspiration Algorithm on Spatial Resolution. Atmospheric Research, 96, 489-495.
http://dx.doi.org/10.1016/j.atmosres.2009.12.003 - 3. Kamble, B., Irmak, A., Hubbarb, K. and Gowda, P. (2013) Irrigation Scheduling Using Remote Sensing Data Assimilation Approach. Advances in Remote Sensing, 2, 258-268.
http://dx.doi.org/10.4236/ars.2013.23028 - 4. Allen, R.G., Pereira, L.S., Howell, T.A. and Jensen, M.E. (2011) Evapotranspiration Information Reporting: I. Factors Governing Measurement Accuracy. Agricultural Water Management, 98, 899-920.
http://dx.doi.org/10.1016/j.agwat.2010.12.015 - 5. Bezerra, B.G., Santos, C.A.C., Silva, B.B., Perez-Marin, A.M., Bezerra, M.V.C., Bezerra, J.R.C. and Ramana Rao, T.V. (2013) Estimation of Soil Moisture in the Root-Zone from Remote Sensing Data. Revista Brasileira de Ciência do Solo, 37, 595-603.
http://dx.doi.org/10.1590/S0100-06832013000300005 - 6. Gao, Y., Long, D. and Li, Z. (2008) Estimation of Daily Evapotranspiration from Remotely Sensed Data under Complex Terrain over the Upper Chao River Basin in North China. International Journal of Remote Sensing, 29, 3295-3315.
http://dx.doi.org/10.1080/01431160701469073 - 7. Bastiaanssen, W.G.M., Menenti, M., Feddes, R.A. and Holtslag, A.A.M. (1998) A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL) 1. Formulation. Journal of Hydrology, 212-213, 198-212.
http://dx.doi.org/10.1016/S0022-1694(98)00253-4 - 8. Bastiaanssen, W.G.M., Pelgrum, H., Wang, J., Ma, Y., Moreno, J.F., Roenrink, G.J. and van der Wal, T. (1998) A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL) 2. Validation. Journal of Hydrology, 212-213, 213-229.
http://dx.doi.org/10.1016/S0022-1694(98)00254-6 - 9. Allen, R.G., Tasumi, M. and Trezza, R. (2007) Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Model. Journal of Irrigation and Drainage Engineering, 133, 380-394.
http://dx.doi.org/10.1061/(ASCE)0733-9437(2007)133:4(380) - 10. Allen, R.G., Tasumi, M., Morse, A., Trezza, R., Wright, J.L., Bastiaanssen, W., Kramber, W., Lorite, I. and Robinson, C.W. (2007) Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Applications. Journal of Irrigation and Drainage Engineering, 133, 395-406.
http://dx.doi.org/10.1061/(ASCE)0733-9437(2007)133:4(395) - 11. Long, D. and Singh, V.P. (2012) A Modified Surface Energy Balance Algorithm for Land (M-SEBAL) Based on a Trapezoidal Framework. Water Resources Research, 48, W02528.
http://dx.doi.org/10.1029/2011WR010607 - 12. Roerink, G.J., Su, Z. and Menenti, M. (2000) S-SEBI: A Simple Remote Sensing Algorithm to Estimate the Surface Energy Balance. Physics and Chemistry of the Earth—Part B: Hydrology, Oceans and Atmosphere, 25, 147-157.
http://dx.doi.org/10.1016/S1464-1909(99)00128-8 - 13. Bastiaanssen, W.G.M. (2000) SEBAL-Based Sensible and Latent Heat Fluxes in the Irrigated Gediz Basin, Turkey. Journal of Hydrology, 229, 87-100.
http://dx.doi.org/10.1016/S0022-1694(99)00202-4 - 14. Shuttleworth, W.J., Gurney, R.J., Hsu, A.Y. and Ormsby, J.P. (1989) FIFE: The Variation in Energy Partition at Surface Flux Sites. IAHS Publicationi, 186, 67-74.
- 15. Farah, H.O., Bastiaanssen, W.G.M. and Feddes, R.A. (2004) Evaluation of the Temporal Variability of the Evaporative Fraction in a Tropical Watershed. International Journal of Applied Earth Observation and Geoinformation, 5, 129-140.
http://dx.doi.org/10.1016/j.jag.2004.01.003 - 16. Allen, R., Tasumi, M. and Trezza, R. (2002) SEBAL (Surface Energy Balance Algorithms for Land)-Advanced Training and User’s Manual-Idaho Implementation, Version 1.0.
- 17. Tasumi, M., Trezza, M., Allen, R.G. and Wright, J.L. (2005) Operational Aspects of Satellite-Based Energy Balance Models for Irrigated Crops in the Semi-Arid U.S. Irrigation and Drainage Systems, 19, 355-376.
http://dx.doi.org/10.1007/s10795-005-8138-9 - 18. Allen, R.G., Pereira, L.S., Raes, D. and Smith, M. (1998) Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements. FAO Irrigation and Drainage Paper 56. Food and Agriculture Organization of the United Nations (FAO), Rome.
- 19. Senay, G.B., Budde, M., Verdin, J.P. and Melesse, A. (2007) A Coupled Remote Sensing and Simplified Surface Energy Balance Approach to Estimate Actual Evapotranspiration from Irrigated Fields. Sensors, 7, 979-1000.
http://dx.doi.org/10.3390/s7060979 - 20. Senay, G.B., Budde, M.E. and Verdin, J.P. (2011) Enhancing the Simplified Surface Energy Balance (SSEB) Approach for Estimating Landscape ET: Validation with the METRIC Model. Agricultural Water Management, 98, 606-618.
http://dx.doi.org/10.1016/j.agwat.2010.10.014 - 21. Senay, G.B., Bohms, S., Singh, R.K., Gowda, P.H., Velpuri, N.M., Alemu, H. and Verdin, J.P. (2013) Operational Evapotranspiration Mapping Using Remote Sensing and Weather Datasets: A New Parameterization for the SSEB Approach. Journal of the American Water Resources Association, 49, 577-591.
http://dx.doi.org/10.1111/jawr.12057 - 22. Thornthwaite, C.W. (1948) An Approach toward a Rational Classification of Climate. Geographical Review, 38, 55-94.
http://dx.doi.org/10.2307/210739 - 23. Bezerra, J.R.C., Azevedo, P.V., Silva, B.B. and Dias, J.M. (2010) Evapotranspiração e coeficiente de cultivo do algodoeiro BRS-200 Marrom, irrigado. Revista Brasileira de Engenharia Agrícola e Ambiental, 14, 625-632.
http://dx.doi.org/10.1590/S1415-43662010000600009 - 24. Bezerra, B.G., Silva, B.B., Bezerra, J.R.C., Sofiatti, V. and Santos, C.A.C. (2012) Evapotranspiration and Crop Coefficient for Sprinkler-Irrigated Cotton Crop in Apodi Plateau Semiarid Lands of Brazil. Agricultural Water Management, 107, 86-93.
http://dx.doi.org/10.1016/j.agwat.2012.01.013 - 25. Bezerra, B.G., Silva, B.B. and Ferreira, N.J. (2008) Assessment of Daily Actual Evapotranspiration Using TM— Landsat 5 Digital Images. Revista Brasileira de Meteorologia, 23, 305-317. (In Portuguese)
http://dx.doi.org/10.1590/S0102-77862008000300005 - 26. Julien, Y., Sobrino, J.A., Mattar, C., Ruescas, A.B., Jiménez-Muñoz, J.C., Sòria, G., Hidalgo, V., Atitar, M., Franch, B. and Cuenca, J. (2011) Temporal Analysis of Normalized Difference Vegetation Index (NDVI) and Land Surface Temperature (LST) Parameters to Detect Changes in the Iberian Land Cover between 1981 and 2001. International Journal of Remote Sensing, 32, 2057-2068.
http://dx.doi.org/10.1080/01431161003762363 - 27. Brutsaert, W. and Sugita, M. (1992) Application of Self-Preservation in the Diurnal Evolution of the Surface Energy Budget to Determine Daily Evaporation. Journal of Geophysical Research, 97, 377-382.
http://dx.doi.org/10.1029/92JD00255 - 28. De Bruin, H.A.R. (1987) From Penman to Makkink. In: Hooghart, J.C., Ed., Proceedings and Information: TNO Committee on Hydrological Research N°39. The Netherlands Organization for Applied Scientific Research TNO, Den Haag, 5-31.
- 29. Senay, G.B., Leake, S., Nagler, P.L., Artan, G., Dickinson, J., Cordova, J.T. and Glenn, E.P. (2011) Estimating Basin Scale Evapotranspiration (ET) by Water Balance and Remote Sensing Methods. Hydrological Processes, 25, 4037-4049.
http://dx.doi.org/10.1002/hyp.8379 - 30. Gowda, P.H., Chavez, J.L., Colaizzi, P.D., Evett, S.R., Howell, T.A. and Tolk, J.A. (2008) ET Mapping for Agricultural Water Management: Present Status and Challenges. Irrigation Science, 26, 223-237.
http://dx.doi.org/10.1007/s00271-007-0088-6 - 31. Perez, P.J., Castellvi, F., Ibañez, M. and Rosell, J.I. (1999) Assessment of Reliability of Bowen Ratio Method for Partitioning Fluxes. Agricultural and Forest Meteorology, 97, 141-150.
http://dx.doi.org/10.1016/S0168-1923(99)00080-5 - 32. Wilks, D.S. (2006) Statistical Methods in the Atmospheric Science. Academic Press, San Diego.
- 33. Bastiaanssen, W.G.M., Molden, D.J. and Makin, I.W. (2000) Remote Sensing for Irrigated Agriculture: Examples from Research and Possible Applications. Agricultural Water Management, 46, 137-155.
http://dx.doi.org/10.1016/S0378-3774(00)00080-9 - 34. Kimura, R., Bai, L., Fan, J. and Takayama, N. (2007) Evapotranspiration Estimation over the River Basin of the Loess Plateau of China Based on Remote Sensing. Journal of Arid Environments, 68, 53-65.
http://dx.doi.org/10.1016/j.jaridenv.2006.03.029 - 35. Bashir, M.A., Hata, T., Tanakamaru, H., Adelhadi, A.W. and Tada, A. (2008) Satellite-Based Energy Balance Model to Estimate Seasonal Evapotranspiration for Irrigated Sorghum: A Case Study from the Gezira Scheme, Sudan. Hydrology and Earth System Sciences, 12, 1129-1139.
http://dx.doi.org/10.5194/hess-12-1129-2008 - 36. Gowda, P.H., Senay, G.B., Howell, T.A. and Marek, T.H. (2009) Lysimetric Evaluation of Simplified Surface Energy Balance Approach in the Texas High Plains. Applied Engineering in Agriculture, 25, 665-669.
http://dx.doi.org/10.13031/2013.28855 - 37. Velpuri, N.M., Senay, G.B., Singh, R.K., Bohms, S. and Verdin, J.P. (2013) A Comprehensive Evaluation of Two MODIS Evapotranspiration Products over the Conterminous United States: Using Point and Gridded FLUXNET and Water Balance ET. Remote Sensing of Environment, 139, 35-49.
http://dx.doi.org/10.1016/j.rse.2013.07.013 - 38. Iqbal, M. (1983) An Introduction to Solar Radiation. Academic Press, Toronto.
- 39. Liou, K.N. (2002) An Introduction to Atmospheric Radiation. 2nd Edition, Academic Press, San Diego.
- 40. Stull, R.B. (1988) An Introduction to Boundary Layer Meteorology. Kluwer Academic Publishers, Boston.
http://dx.doi.org/10.1007/978-94-009-3027-8









